- Research Article
- Open access
- Published:
Distributed Antenna Channels with Regenerative Relaying: Relay Selection and Asymptotic Capacity
EURASIP Journal on Wireless Communications and Networking volume 2007, Article number: 021093 (2007)
Abstract
Multiple-input-multiple-output (MIMO) techniques have been widely proposed as a means to improve capacity and reliability of wireless channels, and have become the most promising technology for next generation networks. However, their practical deployment in current wireless devices is severely affected by antenna correlation, which reduces their impact on performance. One approach to solve this limitation is relaying diversity. In relay channels, a set of wireless nodes aids a source-destination communication by relaying the source data, thus creating a distributed antenna array with uncorrelated path gains. In this paper, we study this multiple relay channel (MRC) following a decode-and-forward (D&F) strategy (i.e., regenerative forwarding), and derive its achievable rate under AWGN. A half-duplex constraint on relays is assumed, as well as distributed channel knowledge at both transmitter and receiver sides of the communication. For this channel, we obtain the optimum relay selection algorithm and the optimum power allocation within the network so that the transmission rate is maximized. Likewise, we bound the ergodic performance of the achievable rate and derive its asymptotic behavior in the number of relays. Results show that the achievable rate of regenerative MRC grows as the logarithm of the Lambert W function of the total number of relays, that is,
wireless nodes aids a source-destination communication by relaying the source data, thus creating a distributed antenna array with uncorrelated path gains. In this paper, we study this multiple relay channel (MRC) following a decode-and-forward (D&F) strategy (i.e., regenerative forwarding), and derive its achievable rate under AWGN. A half-duplex constraint on relays is assumed, as well as distributed channel knowledge at both transmitter and receiver sides of the communication. For this channel, we obtain the optimum relay selection algorithm and the optimum power allocation within the network so that the transmission rate is maximized. Likewise, we bound the ergodic performance of the achievable rate and derive its asymptotic behavior in the number of relays. Results show that the achievable rate of regenerative MRC grows as the logarithm of the Lambert W function of the total number of relays, that is, . Therefore, D&F relaying, cannot achieve the capacity of actual MISO channels.
. Therefore, D&F relaying, cannot achieve the capacity of actual MISO channels.
References
Telatar I: Capacity of multi-antenna Gaussian channels. European Transactions on Telecommunications 1999,10(6):585-595. 10.1002/ett.4460100604
Alamouti SM: A simple transmit diversity technique for wireless communications. IEEE Journal on Selected Areas in Communications 1998,16(8):1451-1458. 10.1109/49.730453
Vishwanath S, Jindal N, Goldsmith A: Duality, achievable rates, and sum-rate capacity of Gaussian MIMO broadcast channels. IEEE Transactions on Information Theory 2003,49(10):2658-2668. 10.1109/TIT.2003.817421
Tse D, Viswanath P: Fundamentals of Wireless Communications. 1st edition. Cambridge University Press, Cambridge, UK; 2005.
Zimmermann E, Herhold P, Fettweis G: On the performance of cooperative relaying protocols in wireless networks. European Transactions on Telecommunications 2005,16(1):5-16. 10.1002/ett.1028
Kramer G, Gastpar M, Gupta P: Cooperative strategies and capacity theorems for relay networks. IEEE Transactions on Information Theory 2005,51(9):3037-3063. 10.1109/TIT.2005.853304
Chen D, Laneman JN: The diversity-multiplexing tradeoff for the multiaccess relay channel. Proceedings of the 40th Annual Conference on Information Sciences and Systems, March 2006, Princeton, NJ, USA 1324-1328.
Sendonaris A, Erkip E, Aazhang B: User cooperation diversity—part I: system description. IEEE Transactions on Communications 2003,51(11):1927-1938. 10.1109/TCOMM.2003.818096
Høst-Madsen A, Zhang J: Capacity bounds and power allocation for wireless relay channels. IEEE Transactions on Information Theory 2005,51(6):2020-2040. 10.1109/TIT.2005.847703
Cover T, El Gamal A: Capacity theorems for the relay channel. IEEE Transactions on Information Theory 1979,25(5):572-584. 10.1109/TIT.1979.1056084
Laneman JN: Cooperative diversity in wireless networks: algorithms and architectures, Ph.D. Dissertation. 2002.
Laneman JN, Tse D, Wornell GW: Cooperative diversity in wireless networks: efficient protocols and outage behavior. IEEE Transactions on Information Theory 2004,50(12):3062-3080. 10.1109/TIT.2004.838089
Dana AF, Sharif M, Gowaikar R, Hassibi B, Effros M: Is broadcast plus multiaccess optimal for Gaussian wireless networks? Proceedings of the 37th Asilomar Conference on Signals, Systems, and Computers, November 2003, Pacific Grove, Calif, USA 2: 1748-1752.
Nabar R, Bölcskei H, Kneubühler FW: Fading relay channels: performance limits and space-time signal design. IEEE Journal on Selected Areas in Communications 2004,22(6):1099-1109. 10.1109/JSAC.2004.830922
del Coso A, Ibars C: Achievable rate for Gaussian multiple relay channels with linear relaying functions. Proceedings of IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP '07), April 2007, Honolulu, Hawaii, USA 3: 505-508.
El Gamal A, Mohseni M, Zahedi S: Bounds on capacity and minimum energy-per-bit for AWGN relay channels. IEEE Transactions on Information Theory 2006,52(4):1545-1561.
del Coso A, Ibars C: Partial decoding for synchronous and asynchronous Gaussian multiple relay channels. Proceedings of the International Conference on Communications (ICC '07), June 2007, Glasgow, Scotland, UK 713-718.
Høst-Madsen A: On the capacity of wireless relaying. Proceedings of the 56th IEEE Vehicular Technology Conference (VTC '02), September 2002, Vancouver, BC, Canada 3: 1333-1337.
El Gamal A: Capacity theorems for relay channels. Proceedings of MSRI Workshop on Mathematics of Relaying and Cooperation in Communication Networks, April 2006, Berkeley, Calif, USA
Laneman JN, Wornell GW: Distributed space-time-coded protocols for exploiting cooperative diversity in wireless networks. IEEE Transactions on Information Theory 2003,49(10):2415-2425. 10.1109/TIT.2003.817829
Dohler M: Virtual antenna arrays, Ph.D. thesis. King's College London, London, UK; 2003.
Maric I, Yates R: Bandwidth and power allocation for cooperative strategies in Gaussian relay networks. Proceedings of the 38th Asilomar Conference on Signals, Systems and Computers, November 2004, Pacific Grove, Calif, USA 2: 1907-1911.
Corless RM, Gonnet GH, Hare DEG, Jeffrey DJ, Knuth DE:On the Lambert
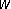 function. Advances in Computational Mathematics 1996,5(4):329-359.
function. Advances in Computational Mathematics 1996,5(4):329-359.Cover T, Thomas J: Elements of Information Theory, Wiley Series in Telecommunications. Wiley-Interscience, New York, NY, USA; 1991.
David H: Order Statistics. 2nd edition. John Wiley & Sons, New York, NY, USA; 1981.
Boyd S, Vandenberghe L: Convex Optimization. 1st edition. Cambridge University Press, Cambridge, UK; 2004.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
del Coso, A., Ibars, C. Distributed Antenna Channels with Regenerative Relaying: Relay Selection and Asymptotic Capacity. J Wireless Com Network 2007, 021093 (2007). https://doi.org/10.1155/2007/21093
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2007/21093
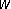 function. Advances in Computational Mathematics 1996,5(4):329-359.
function. Advances in Computational Mathematics 1996,5(4):329-359.