- Research Article
- Open access
- Published:
Performance Analysis of SSC Diversity Receivers over Correlated Ricean Fading Satellite Channels
EURASIP Journal on Wireless Communications and Networking volume 2007, Article number: 025361 (2007)
Abstract
This paper studies the performance of switch and stay combining (SSC) diversity receivers operating over correlated Ricean fading satellite channels. Using an infinite series representation for the bivariate Ricean probability density function (PDF), the PDF of the SSC output signal-to-noise ratio (SNR) is derived. Capitalizing on this PDF, analytical expressions for the corresponding cumulative distribution function (CDF), the moments of the output SNR, the moments generating function (MGF), and the average channel capacity (CC) are derived. Furthermore, by considering several families of modulated signals, analytical expressions for the average symbol error probability (ASEP) for the diversity receivers under consideration are obtained. The theoretical analysis is accompanied by representative performance evaluation results, including average output SNR (ASNR), amount of fading (AoF), outage probability , average bit error probability (ABEP), and average CC, which have been obtained by numerical techniques. The validity of some of these performance evaluation results has been verified by comparing them with previously known results obtained for uncorrelated Ricean fading channels.
, average bit error probability (ABEP), and average CC, which have been obtained by numerical techniques. The validity of some of these performance evaluation results has been verified by comparing them with previously known results obtained for uncorrelated Ricean fading channels.
References
Rappaport TS: Wireless Communications. Prentice-Hall PTR, Upper Saddle River, NJ, USA; 2002.
Simon MK, Alouini M-S: Digital Communication over Fading Channels. 2nd edition. John Wiley & Sons, New York, NY, USA; 2005.
Sagias NC, Karagiannidis GK: Gaussian class multivariate Weibull distributions: theory and applications in fading channels. IEEE Transactions on Information Theory 2005,51(10):3608-3619. 10.1109/TIT.2005.855598
Corazza GE, Vatalaro F: A statistical model for land mobile satellite channels and its application to nongeostationary orbit systems. IEEE Transactions on Vehicular Technology 1994,43(3, part 2):738-742. 10.1109/25.312773
Wakana H: A propagation model for land mobile satellite communications. Proceedings of IEEE Antennas and Propagation Society International Symposium, June 1991, London, Ont, Canada 3: 1526-1529.
Lutz E, Cygan D, Dippold M, Dolainsky F, Papke W: The land mobile satellite communication channel-recording, statistics, and channel model. IEEE Transactions on Vehicular Technology 1991,40(2):375-386. 10.1109/25.289418
Simon MK, Alouini M-S:A unified performance analysis of digital communication with dual selective combining diversity over correlated Rayleigh and Nakagami-
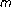 fading channels. IEEE Transactions on Communications 1999,47(1):33-43. 10.1109/26.747811
fading channels. IEEE Transactions on Communications 1999,47(1):33-43. 10.1109/26.747811Chen Y, Tellambura C:Distribution functions of selection combiner output in equally correlated Rayleigh, Rician, and Nakagami-
 fading channels. IEEE Transactions on Communications 2004,52(11):1948-1956. 10.1109/TCOMM.2004.836596
fading channels. IEEE Transactions on Communications 2004,52(11):1948-1956. 10.1109/TCOMM.2004.836596Karagiannidis GK, Zogas DA, Sagias NC, Kotsopoulos SA, Tombras GS: Equal-gain and maximal-ratio combining over nonidentical Weibull fading channels. IEEE Transactions on Wireless Communications 2005,4(3):841-846.
Ismail MH, Matalgah MM: Performance of dual maximal ratio combining diversity in nonidentical correlated Weibull fading channels using Padé approximation. IEEE Transactions on Communications 2006,54(3):397-402.
Sagias NC: Capacity of dual-branch selection diversity receivers in correlative Weibull fading. European Transactions on Telecommunications 2006,17(1):37-43. 10.1002/ett.1082
Khatalin S, Fonseka JP:Capacity of correlated Nakagami-
 fading channels with diversity combining techniques. IEEE Transactions on Vehicular Technology 2006,55(1):142-150. 10.1109/TVT.2005.861206
fading channels with diversity combining techniques. IEEE Transactions on Vehicular Technology 2006,55(1):142-150. 10.1109/TVT.2005.861206Iskander C-D, Mathiopoulos PT:Performance of dual-branch coherent equal-gain combining in correlated Nakagami-
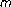 fading. Electronics Letters 2003,39(15):1152-1154. 10.1049/el:20030727
fading. Electronics Letters 2003,39(15):1152-1154. 10.1049/el:20030727Abu-Dayya AA, Beaulieu NC: Switched diversity on microcellular Ricean channels. IEEE Transactions on Vehicular Technology 1994,43(4):970-976. 10.1109/25.330159
Ko Y-C, Alouini M-S, Simon MK: Analysis and optimization of switched diversity systems. IEEE Transactions on Vehicular Technology 2000,49(5):1813-1831. 10.1109/25.892586
Tellambura C, Annamalai A, Bhargava VK: Unified analysis of switched diversity systems in independent and correlated fading channels. IEEE Transactions on Communications 2001,49(11):1955-1965. 10.1109/26.966072
Alouini M-S, Simon MK: Dual diversity over correlated log-normal fading channels. IEEE Transactions on Communications 2002,50(12):1946-1959. 10.1109/TCOMM.2002.806552
Zogas DA, Karagiannidis GK: Infinite-series representations associated with the bivariate Rician distribution and their applications. IEEE Transactions on Communications 2005,53(11):1790-1794. 10.1109/TCOMM.2005.858659
Simon MK: Probability Distributions Involving Gaussian Random Variables: A Handbook for Engineers and Scientists. Kluwer Academic Publishers, Norwell, Mass, USA; 2002.
Bithas PS, Sagias NC, Mathiopoulos PT: Dual diversity over correlated Ricean fading channels. Journal of Communications and Networks 2007,9(1):67-74.
Gradshteyn IS, Ryzhik IM: Table of Integrals, Series, and Products. 6th edition. Academic Press, New York, NY, USA; 2000.
Abramowitz M, Stegun IA: Handbook of Mathematical Functions with Formulas, Graphs and Mathematical Tables. 9th edition. Dover, New York, NY, USA; 1972.
Abu-Dayya AA, Beaulieu NC: Analysis of switched diversity systems on generalized-fading channels. IEEE Transactions on Communications 1994,42(11):2959-2966. 10.1109/26.328977
Papoulis A: Probability, Random Variables, and Stochastic Processes. 2nd edition. McGraw-Hill, New York, NY, USA; 1984.
Nuttal A: Some integrals involving the Q-function. In Tech. Rep. 4297. Naval Underwater Systems Center, New London, Conn, USA; 1972.
Lee WCY: Estimate of channel capacity in Rayleigh fading environment. IEEE Transactions on Vehicular Technology 1990,39(3):187-189. 10.1109/25.130999
The Wolfram functions site http://functions.wolfram.com/
Adamchik VS, Marichev OI: The algorithm for calculating integrals of hypergeometric type functions and its realization in REDUCE system. Proceedings of International Symposium on Symbolic and Algebraic Computation (ISSAC '90), August 1990, Tokyo, Japan 212-224.
Sagias NC, Zogas DA, Karagiannidis GK: Selection diversity receivers over nonidentical Weibull fading channels. IEEE Transactions on Vehicular Technology 2005,54(6):2146-2151. 10.1109/TVT.2005.853452
Bithas PS, Karagiannidis GK, Sagias NC, Mathiopoulos PT, Kotsopoulos SA, Corazza GE: Performance analysis of a class of GSC receivers over nonidentical Weibull fading channels. IEEE Transactions on Vehicular Technology 2005,54(6):1963-1970. 10.1109/TVT.2005.858194
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Bithas, P.S., Mathiopoulos, P.T. Performance Analysis of SSC Diversity Receivers over Correlated Ricean Fading Satellite Channels. J Wireless Com Network 2007, 025361 (2007). https://doi.org/10.1155/2007/25361
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2007/25361
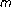 fading channels. IEEE Transactions on Communications 1999,47(1):33-43. 10.1109/26.747811
fading channels. IEEE Transactions on Communications 1999,47(1):33-43. 10.1109/26.747811 fading channels. IEEE Transactions on Communications 2004,52(11):1948-1956. 10.1109/TCOMM.2004.836596
fading channels. IEEE Transactions on Communications 2004,52(11):1948-1956. 10.1109/TCOMM.2004.836596 fading channels with diversity combining techniques. IEEE Transactions on Vehicular Technology 2006,55(1):142-150. 10.1109/TVT.2005.861206
fading channels with diversity combining techniques. IEEE Transactions on Vehicular Technology 2006,55(1):142-150. 10.1109/TVT.2005.861206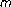 fading. Electronics Letters 2003,39(15):1152-1154. 10.1049/el:20030727
fading. Electronics Letters 2003,39(15):1152-1154. 10.1049/el:20030727