- Research Article
- Open access
- Published:
Error Probability of Binary and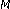 -ary Signals with Spatial Diversity in Nakagami-
-ary Signals with Spatial Diversity in Nakagami- (Hoyt) Fading Channels
(Hoyt) Fading Channels
EURASIP Journal on Wireless Communications and Networking volume 2007, Article number: 053742 (2007)
Abstract
We analyze the exact average symbol error probability (SEP) of binary and -ary signals with spatial diversity in Nakagami-
-ary signals with spatial diversity in Nakagami- (Hoyt) fading channels. The maximal-ratio combining and orthogonal space-time block coding are considered as diversity techniques for single-input multiple-output and multiple-input multiple-output systems, respectively. We obtain the average SEP in terms of the Lauricella multivariate hypergeometric function
(Hoyt) fading channels. The maximal-ratio combining and orthogonal space-time block coding are considered as diversity techniques for single-input multiple-output and multiple-input multiple-output systems, respectively. We obtain the average SEP in terms of the Lauricella multivariate hypergeometric function . The analysis is verified by comparing with Monte Carlo simulations and we further show that our general SEP expressions particularize to the previously known results for Rayleigh (
. The analysis is verified by comparing with Monte Carlo simulations and we further show that our general SEP expressions particularize to the previously known results for Rayleigh ( = 1) and single-input single-output (SISO) Nakagami-
= 1) and single-input single-output (SISO) Nakagami- cases.
cases.
References
Simon MK, Alouini M-S: A unified approach to the performance analysis of digital communication over generalized fading channels. Proceedings of the IEEE 1998,86(9):1860-1877. 10.1109/5.705532
Simon MK, Alouini M-S: Digital Communication over Fading Channels: A Unified Approach to Performance Analysis. Wiley-Interscience, New York, NY, USA; 2000.
Annamalai A, Tellambura C:Error rates for Nakagami-
 fading multichannel reception of binary and
fading multichannel reception of binary and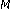 -ary signals. IEEE Transactions on Communications 2001,49(1):58-68. 10.1109/26.898251
-ary signals. IEEE Transactions on Communications 2001,49(1):58-68. 10.1109/26.898251Shin H, Lee JH:On the error probability of binary and
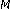 -ary signals in Nakagami-
-ary signals in Nakagami-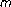 fading channels. IEEE Transactions on Communications 2004,52(4):536-539. 10.1109/TCOMM.2004.826373
fading channels. IEEE Transactions on Communications 2004,52(4):536-539. 10.1109/TCOMM.2004.826373Efthymogloua GP, Piboongungon T, Aalo VA:Error rates of
 -ary signals with multichannel reception in Nakagami-
-ary signals with multichannel reception in Nakagami-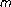 fading channels. IEEE Communications Letters 2006,10(2):100-102. 10.1109/LCOMM.2006.02022.
fading channels. IEEE Communications Letters 2006,10(2):100-102. 10.1109/LCOMM.2006.02022.Aalo VA, Piboongungon T, Efthymoglou GP:Another look at the performance of MRC schemes in Nakagami-
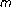 fading channels with arbitrary parameters. IEEE Transactions on Communications 2005,53(12):2002-2005. 10.1109/TCOMM.2005.860089
fading channels with arbitrary parameters. IEEE Transactions on Communications 2005,53(12):2002-2005. 10.1109/TCOMM.2005.860089Lu J, Tjhung TT, Chai CC:Error probability performance of
 -branch diversity reception of MQAM in Rayleigh fading. IEEE Transactions on Communications 1998,46(2):179-181. 10.1109/26.659476
-branch diversity reception of MQAM in Rayleigh fading. IEEE Transactions on Communications 1998,46(2):179-181. 10.1109/26.659476Tellambura C, Mueller AJ, Bhargava VK:Analysis of
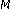 -ary phase-shift keying with diversity reception for land-mobile satellite channels. IEEE Transactions on Vehicular Technology 1997,46(4):910-922. 10.1109/25.653065
-ary phase-shift keying with diversity reception for land-mobile satellite channels. IEEE Transactions on Vehicular Technology 1997,46(4):910-922. 10.1109/25.653065Ekanayake N:Performance of
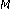 -ary PSK signals in slow Rayleigh fading channels. Electronics Letters 1990,26(10):618-619. 10.1049/el:19900405
-ary PSK signals in slow Rayleigh fading channels. Electronics Letters 1990,26(10):618-619. 10.1049/el:19900405Shin H, Lee JH:Performance analysis of space—time block codes over keyhole Nakagami-
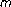 fading chanels. IEEE Transactions on Vehicular Technology 2004,53(2):351-362. 10.1109/TVT.2004.823540
fading chanels. IEEE Transactions on Vehicular Technology 2004,53(2):351-362. 10.1109/TVT.2004.823540Shin H, Lee JH: Effect of keyholes on the symbol error rate of space—time block codes. IEEE Communications Letters 2003,7(1):27-29. 10.1109/LCOMM.2002.807428
Shin H, Win MZ: MIMO diversity in the presence of double scattering. to appear in IEEE Transactions on Information Theory, http://arxiv.org/abs/cs.IT/0511028 to appear in IEEE Transactions on Information Theory,
Alamouti SM: A simple transmit diversity technique for wireless communications. IEEE Journal on Selected Areas in Communications 1998,16(8):1451-1458. 10.1109/49.730453
Tarokh V, Jafarkhani H, Calderbank AR: Space—time block codes from orthogonal designs. IEEE Transactions on Information Theory 1999,45(5):1456-1467. 10.1109/18.771146
Zogas DA, Karagiannidis GK, Kotsopoulos SA:Equal gain combining over Nakagami-
 (Rice) and Nakagami-
(Rice) and Nakagami- (Hoyt) generalzied fading channels. IEEE Transactions on Wireless Communications 2005,4(2):374-379.
(Hoyt) generalzied fading channels. IEEE Transactions on Wireless Communications 2005,4(2):374-379.Fraidenraich G, Filho JCSS, Yacoub MD: Second-order statistics of maximal-ratio and equal-gain combining in Hoyt fading. IEEE Communications Letters 2005,9(1):19-21.
Youssef N, Wang C-X, Pätzold M: A study on the second order statistics of Nakagami-Hoyt mobile fading channels. IEEE Transactions on Vehicular Technology 2005,54(4):1259-1265. 10.1109/TVT.2005.851353
Radaydeh RM:Average error performance of
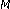 -ary modulation schemes in Nakagami-
-ary modulation schemes in Nakagami- (Hoyt) fading channels. IEEE Communications Letters 2007,11(3):255-257.
(Hoyt) fading channels. IEEE Communications Letters 2007,11(3):255-257.Exton H: Multiple Hypergeometric Functions and Applications. John Wiley & Sons, New York, NY, USA; 1976.
Erdelyi A: Higher Transcendental Functions. Volume 1. McGraw-Hill, New York, NY, USA; 1953.
Tirkkonen O, Hottinen A: Square-matrix embeddable space-time block codes for complex signal constellations. IEEE Transactions on Information Theory 2002,48(2):384-395. 10.1109/18.978740
Fraidenraich G, Yacoub MD:The
 -
- general fading distribution. Proceedings of the SBMO/IEEE MTT-S International Microwave and Optoelectronics Conference (IMOC '03), September 2003, Foz do Iguacu, Brazil 1: 49-54.
general fading distribution. Proceedings of the SBMO/IEEE MTT-S International Microwave and Optoelectronics Conference (IMOC '03), September 2003, Foz do Iguacu, Brazil 1: 49-54.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Duong, T.Q., Shin, H. & Hong, EK. Error Probability of Binary and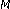 -ary Signals with Spatial Diversity in Nakagami-
-ary Signals with Spatial Diversity in Nakagami- (Hoyt) Fading Channels.
J Wireless Com Network 2007, 053742 (2007). https://doi.org/10.1155/2007/53742
(Hoyt) Fading Channels.
J Wireless Com Network 2007, 053742 (2007). https://doi.org/10.1155/2007/53742
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2007/53742
 fading multichannel reception of binary and
fading multichannel reception of binary and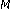 -ary signals. IEEE Transactions on Communications 2001,49(1):58-68. 10.1109/26.898251
-ary signals. IEEE Transactions on Communications 2001,49(1):58-68. 10.1109/26.898251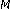 -ary signals in Nakagami-
-ary signals in Nakagami-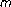 fading channels. IEEE Transactions on Communications 2004,52(4):536-539. 10.1109/TCOMM.2004.826373
fading channels. IEEE Transactions on Communications 2004,52(4):536-539. 10.1109/TCOMM.2004.826373 -ary signals with multichannel reception in Nakagami-
-ary signals with multichannel reception in Nakagami-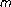 fading channels. IEEE Communications Letters 2006,10(2):100-102. 10.1109/LCOMM.2006.02022.
fading channels. IEEE Communications Letters 2006,10(2):100-102. 10.1109/LCOMM.2006.02022.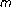 fading channels with arbitrary parameters. IEEE Transactions on Communications 2005,53(12):2002-2005. 10.1109/TCOMM.2005.860089
fading channels with arbitrary parameters. IEEE Transactions on Communications 2005,53(12):2002-2005. 10.1109/TCOMM.2005.860089 -branch diversity reception of MQAM in Rayleigh fading. IEEE Transactions on Communications 1998,46(2):179-181. 10.1109/26.659476
-branch diversity reception of MQAM in Rayleigh fading. IEEE Transactions on Communications 1998,46(2):179-181. 10.1109/26.659476 -ary phase-shift keying with diversity reception for land-mobile satellite channels. IEEE Transactions on Vehicular Technology 1997,46(4):910-922. 10.1109/25.653065
-ary phase-shift keying with diversity reception for land-mobile satellite channels. IEEE Transactions on Vehicular Technology 1997,46(4):910-922. 10.1109/25.653065 -ary PSK signals in slow Rayleigh fading channels. Electronics Letters 1990,26(10):618-619. 10.1049/el:19900405
-ary PSK signals in slow Rayleigh fading channels. Electronics Letters 1990,26(10):618-619. 10.1049/el:19900405 fading chanels. IEEE Transactions on Vehicular Technology 2004,53(2):351-362. 10.1109/TVT.2004.823540
fading chanels. IEEE Transactions on Vehicular Technology 2004,53(2):351-362. 10.1109/TVT.2004.823540 (Rice) and Nakagami-
(Rice) and Nakagami- (Hoyt) generalzied fading channels. IEEE Transactions on Wireless Communications 2005,4(2):374-379.
(Hoyt) generalzied fading channels. IEEE Transactions on Wireless Communications 2005,4(2):374-379. -ary modulation schemes in Nakagami-
-ary modulation schemes in Nakagami- (Hoyt) fading channels. IEEE Communications Letters 2007,11(3):255-257.
(Hoyt) fading channels. IEEE Communications Letters 2007,11(3):255-257. -
- general fading distribution. Proceedings of the SBMO/IEEE MTT-S International Microwave and Optoelectronics Conference (IMOC '03), September 2003, Foz do Iguacu, Brazil 1: 49-54.
general fading distribution. Proceedings of the SBMO/IEEE MTT-S International Microwave and Optoelectronics Conference (IMOC '03), September 2003, Foz do Iguacu, Brazil 1: 49-54.