- Research Article
- Open access
- Published:
Performance of Selection Combining Diversity in Weibull Fading with Cochannel Interference
EURASIP Journal on Wireless Communications and Networking volume 2007, Article number: 060408 (2007)
Abstract
We evaluate the performance of selection combining (SC) diversity in cellular systems where binary phase-shift keying (BPSK) is employed and the desired signal as well as the cochannel interferers (CCIs) is subject to Weibull fading. A characteristic function-(CF-) based approach is followed to evaluate the performance in terms of the outage probability. Two selection criteria are adopted at the diversity receiver: maximum desired signal power and maximum output signal-to-interference ratio (SIR). We study the effect of the fading parameters of the desired and interfering signals, the number of diversity branches, as well as the number of interferers on the performance. Numerical results are presented and the validity of our expressions is verified via Monte Carlo simulations.
References
Simon MK, Alouini MS: Digital Communication over Fading Channels. John Wiley & Sons, Hoboken, NJ, USA; 2005.
Abu-Dayya AA, Beaulieu NC: Diversity MPSK receivers in cochannel interference. IEEE Transactions on Vehicular Technology 1999,48(6):1959-1965. 10.1109/25.806789
Yang H, Alouini M-S: Outage probability of dual-branch diversity systems in presence of co-channel interference. IEEE Transactions on Wireless Communications 2003,2(2):310-319. 10.1109/TWC.2003.808972
Sivanesan K, Beaulieu NC: Precise outage analysis of selection diversity in bandlimited micro-cellular systems with cochannel interference. Proceedings of 62nd IEEE Vehicular Technology Conference (VTC '05), September 2005, Dallas, Tex, USA 1494-1498.
Shepherd NH: Radio wave loss deviation and shadow loss at 900 MHz. IEEE Transactions on Vehicular Technology 1977,26(4):309-313.
Hashemi H: Indoor radio propagation channel. Proceedings of the IEEE 1993,81(7):943-968. 10.1109/5.231342
Coverage prediction for mobile radio systems operating in the 800/900 MHz frequency range IEEE Transactions on Vehicular Technology 1988,37(1):3-72.
Tzeremes G, Christodoulou CG: Use of Weibull distribution for describing outdoor multipath fading. Proceedings of IEEE Antennas and Propagation Society International Symposium (APS '02), June 2002, San Antonio, Tex, USA 1: 232-235.
Siqueira GL, Vásquez EJA: Local and global signal variability statistics in a mobile urban environment. Wireless Personal Communications 2000,15(1):61-78. 10.1023/A:1008920617967
Sagias NC, Zogas DA, Karagiannidis GK, Tombras GS: Channel capacity and second-order statistics in Weibull fading. IEEE Communications Letters 2004,8(6):377-379. 10.1109/LCOMM.2004.831319
Alouini M-S, Simon MK: Performance of generalized selection combining over Weibull fading channels. Proceedings of 54th IEEE Vehicular Technology Conference (VTC '01), October 2001, Atlantic City, NJ, USA 3: 1735-1739.
Sagias NC, Zogas DA, Karagiannidis GK, Tombras GS: Performance analysis of switched diversity receivers in Weibull fading. Electronics Letters 2003,39(20):1472-1474. 10.1049/el:20030956
Sagias NC, Mathiopoulos PT, Tombras GS: Selection diversity receivers in Weibull fading: outage probability and average signal-to-noise ratio. Electronics Letters 2003,39(25):1859-1860. 10.1049/el:20031189
Sagias NC, Karagiannidis GK, Zogas DA, Mathiopoulos PT, Tombras GS: Performance analysis of dual selection diversity in correlated Weibull fading channels. IEEE Transactions on Communications 2004,52(7):1063-1067. 10.1109/TCOMM.2004.831362
Karagiannidis GK, Zogas DA, Sagias NC, Kotsopoulos SA, Tombras GS: Equal-gain and maximal-ratio combining over nonidentical Weibull fading channels. IEEE Transactions on Wireless Communications 2005,4(3):841-846.
Ismail MH, Matalgah MM: Performance of dual maximal ratio combining diversity in nonidentical correlated Weibull fading channels using Padé approximation. IEEE Transactions on Communications 2006,54(3):397-402.
Ismail MH, Matalgah MM: On the use of Padé approximation for performance evaluation of maximal ratio combining diversity over Weibull fading channels. EURASIP Journal on Wireless Communications and Networking 2006, 2006: 7 pages.
Ismail MH, Matalgah MM:BER analysis of diversity
 -PSK receivers over the Weibull fading channel with cochannel interference. Proceedings of IEEE International Conference on Communications (ICC '06), June 2006, Istanbul, Turkey 11: 5134-5139.
-PSK receivers over the Weibull fading channel with cochannel interference. Proceedings of IEEE International Conference on Communications (ICC '06), June 2006, Istanbul, Turkey 11: 5134-5139.Sagias NC, Zogas DA, Karagiannidis GK: Selection diversity receivers over nonidentical Weibull fading channels. IEEE Transactions on Vehicular Technology 2005,54(6):2146-2151. 10.1109/TVT.2005.853452
Ismail MH, Matalgah MM: Downlink outage probability analysis in cellular systems with Weibull faded lognormal-shadowed links. IEE Proceedings: Communications 2006,153(6):949-954. 10.1049/ip-com:20050641
Beaulieu NC, Cheng J: Precise error-rate analysis of bandwidth-efficient BPSK in Nakagami fading and cochannel interference. IEEE Transactions on Communications 2004,52(1):149-158. 10.1109/TCOMM.2003.822187
Gil-Pelaez J: Note on the inversion theorem. Biometrika 1951,38(3-4):481-482. 10.1093/biomet/38.3-4.481
Gradshteyn IS, Ryzhik IM: Table of Integrals, Series and Products. Academic Press, San Diego, Calif, USA; 2000.
Prudinikov AP, Brychkov YuA, Marichev OI: Integrals and Series, Volume 3: More Special Functions. Gordon and Breach Science, Amsterdam, The Netherlands; 1990.
Suetin SP: Padé approximants and efficient analytic continuation of a power series. Russian Mathematical Surveys 2002,57(1):43-141. 10.1070/RM2002v057n01ABEH000475
Amindavar H, Ritcey JA: Padé approximations of probability density functions. IEEE Transactions on Aerospace and Electronic Systems 1994,30(2):416-424. 10.1109/7.272264
Karagiannidis GK:Moments-based approach to the performance analysis of equal gain diversity in Nakagami-
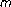 fading. IEEE Transactions on Communications 2004,52(5):685-690. 10.1109/TCOMM.2004.826255
fading. IEEE Transactions on Communications 2004,52(5):685-690. 10.1109/TCOMM.2004.826255
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Ismail, M.H., Matalgah, M.M. Performance of Selection Combining Diversity in Weibull Fading with Cochannel Interference. J Wireless Com Network 2007, 060408 (2007). https://doi.org/10.1155/2007/60408
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2007/60408
 -PSK receivers over the Weibull fading channel with cochannel interference. Proceedings of IEEE International Conference on Communications (ICC '06), June 2006, Istanbul, Turkey 11: 5134-5139.
-PSK receivers over the Weibull fading channel with cochannel interference. Proceedings of IEEE International Conference on Communications (ICC '06), June 2006, Istanbul, Turkey 11: 5134-5139.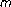 fading. IEEE Transactions on Communications 2004,52(5):685-690. 10.1109/TCOMM.2004.826255
fading. IEEE Transactions on Communications 2004,52(5):685-690. 10.1109/TCOMM.2004.826255