- Research Article
- Open access
- Published:
Handoff Triggering and Network Selection Algorithms for Load-Balancing Handoff in CDMA-WLAN Integrated Networks
EURASIP Journal on Wireless Communications and Networking volume 2008, Article number: 136939 (2008)
Abstract
This paper proposes a novel vertical handoff algorithm between WLAN and CDMA networks to enable the integration of these networks. The proposed vertical handoff algorithm assumes a handoff decision process (handoff triggering and network selection). The handoff trigger is decided based on the received signal strength (RSS). To reduce the likelihood of unnecessary false handoffs, the distance criterion is also considered. As a network selection mechanism, based on the wireless channel assignment algorithm, this paper proposes a context-based network selection algorithm and the corresponding communication algorithms between WLAN and CDMA networks. This paper focuses on a handoff triggering criterion which uses both the RSS and distance information, and a network selection method which uses context information such as the dropping probability, blocking probability, GoS (grade of service), and number of handoff attempts. As a decision making criterion, the velocity threshold is determined to optimize the system performance. The optimal velocity threshold is adjusted to assign the available channels to the mobile stations. The optimal velocity threshold is adjusted to assign the available channels to the mobile stations using four handoff strategies. The four handoff strategies are evaluated and compared with each other in terms of GOS. Finally, the proposed scheme is validated by computer simulations.
1. Introduction
There has been a huge development in wireless communication technologies: mobile and WLAN systems. Mobile technologies such as global system for mobile communications (GSM), general packet radio service (GPRS), universal mobile telecommunication system (UMTS), and CDMA (IS-95 A/B and CDMA2000) offer high mobility, long range always-connected access, but with high costs and low rates. In contrast, WLAN technologies offer higher rates and lower costs, but with low mobility and short-range coverage. Due to the complementary characteristics of mobile technologies and WLANs, the integration of mobile technologies and WLANs will help compensate for coverage, bandwidth, and mobility, and achieve the requirements imposed by the increased user demands. Therefore, the integration of such heterogeneous networks is expected to become a main focus in the development of the next generation of wireless networks. In order to provide a convenient access to both technologies in various environments, interworking and integration of the two types of networks are regarded as very important design objectives [1–6].
Recently, the 3rd-generation partnership project (3GPP), a standard body that developed and maintained GSM, GPRS, and UMTS, initiated the specification of interworking architecture for WLAN and 3GPP systems. In [7], six interworking scenarios have been identified under different supporting services and operational capabilities. The 3rd -generation partnership project 2 (3GPP2), such as IS-95, cdma2000, and 1xEV-DO [8], has been nation-widely deployed in Korea. As a result of the sequential and successful development of wireless networks, we address herein the integrated network between CDMA and WLAN. The combination of WLAN and CDMA technologies uses the best features of both systems. The key goal of this integration is to develop a heterogeneous mobile data network, capable of supporting ubiquitous data services with very high data rates in hotspots. The effort to develop such heterogeneous networks, especially seamless roaming, is linked with many technical challenges including seamless vertical handoff across WLAN and CDMA technologies, security, common authentication, unified accounting and billing, WLAN sharing, consistent QoS, service provisioning, and so forth [5].
For implementing the vertical handoff in heterogeneous wireless networks, the mobility management represents a main challenge. It relies on two main problems which are location management and handoff management [9, 10]. Location management tracks the mobile station (MS) for successful information delivery. For this purpose, Mobile IP (MIP), which enables seamless roaming, is the main engine for location management. Handoff management maintains the active connections for roaming mobile terminals as they change their point of attachment to the network. Handoff management is the main concern of this paper.
Handoff (or handover) is an event that takes place when an MS moves from one wireless cell to another. It can be classified into horizontal and vertical handoffs. A horizontal handoff is a handoff between base stations (BSs) that are using the same kind of wireless network interface, while a vertical handoff occurs between BSs that are using different wireless network interface. In WLANs, the BSs are called access points (APs). Several aspects can be considered in the handoff decision making to optimize the handoff performance (e.g., throughput and grade of service (GoS)). The decision about when and how this handoff is executed is assisted by the handoff policy. It can be classified into handoff triggering and network selection. First, the handoff trigger is the ability to decide when to perform the vertical handoff. Handoff trigger metrics are the qualities that are measured to indicate whether or not a handoff is needed. In traditional homogeneous networks, the physical layer parameters such as the received signal strength indication (RSSI) and signal to interference ratio (SIR) are regarded as classical handoff trigger metrics. However, these parameters are insufficient for the challenges raised by the next generation of heterogeneous wireless networks since there are many differences in the radio interface, cell coverage, traffic type, data rate, and so forth. Second, the network selection represents the ability to decide which system performs the network interface. In [11], a handoff decision is made based on the RSSI, available bandwidth, delay, user preference, and so forth. In order to quickly and accurately detect the signal decay, [11] proposed a signal decay detection approach referred to as the FFT-based decay detection. To decide the "best" network interface, a policy-based handoff scheme was proposed in [12], where a cost function is designed to decide the "best" network interface for various network conditions. In order to handle more sophisticated configurations, a smart decision model which employs the logarithmic function as the cost function, is proposed by [13], where cost function (network selection criteria) components such as like usage expanse, link capacity, and power consumption are considered. In [14], the vertical handoff is applicable to a wider set of context changes, including network QoS (e.g., bandwidth, loss rate, packet delay, and delay jitter), user device preferences, and so forth. In this case, a lot of criteria and objectives must be satisfied. To deal with these aims, the analytic hierarchy process (AHP) was exploited by [15]. In recent years, artificial intelligence-based decision algorithms have been proposed for adaptive decision. In order to take an intelligent and better decision as to which wireless network should be chosen, [16, 17] proposed a fuzzy logic scheme based on RSSI, service type, network conditions, system performance, mobile node capabilities, user preferences, and monetary cost.
In fast MSs, a handoff occurs frequently in WLANs due to their small coverage area. It implies that the frequency of handoffs will increase especially in WLANs, so a large number of handoff requests must be handled. Therefore, the handoff dropping probability is increasing, and the service quality (e.g., GoS) becomes worse. On the other hand, the CDMA system is large enough to accommodate fast MSs, and lower handoff request rates, thus resulting in lower burden and good service quality. It is safe to assume that either slow or stationary MSs transmit more data and that fast moving stations communicate at lower data rates. Therefore, according to the MS speed, the load balancing handoff between WLAN and CDMA results in good service quality and the avoidance of unnecessary handoffs. Our proposed methods adopt the mobility management concept through the MS speed cost function to minimize the GoS.
In this paper, we deal with a vertical handoff decision based on context information. In order to design new criteria with higher performance, we consider the RSSI, distance between BS and MS, MS speed, and grade of service related with the blocking probability with new traffic, dropping probability of the handoff traffic, and the number of handoff attempts per user. A good handoff algorithm is to be derived in order to satisfy the required objectives. Thus an appropriate handoff control is also an important issue in the system management for the sake of the benefits mentioned above in reference with overlay cell structures. We first propose in Section 2 a handoff triggering algorithm, a network selection method based on context information in Sections 2 and 3, and the corresponding communication mechanism from WLAN to the CDMA system, and vice versa, based on the wireless channel assignment in Section 3. Second, we present a handoff strategy for hierarchical overlay structured networks in Section 3. We consider also a handoff trigger based on the RSSI and distance between BS and MS. As a network selection criterion, the velocity threshold is determined to optimize the system performance (e.g., GoS and the number of handoffs per user). Combining WLAN and CDMA presents a unique dimensioning problem, in terms of determining the system performance given the number of radio channels, voice traffic, and data traffic (queuing delays). The proposed scheme is validated through analytical simulations and using a voice traffic model.
The rest of the paper is organized as follows. In Section 2, we describe the handoffs and the requirements of the handoff algorithms. In Section 3, the proposed vertical handoff decision making algorithms are presented, and several design problems are formulated including the core part of the algorithmic decision procedure for the optimal velocity threshold for the WLAN and CDMA selection schemes. Section 4 explains the architecture for the integrated networks, the mobility model, and the performance parameters (i.e., new call blocking probability and handoff call dropping probability, and grade of service (GoS)) for four handoff strategies. Simulations are performed in Section 5 to validate the proposed approach. Finally, a summary of the proposed results and future related research topics are presented in Section 6.
2. Wireless Overlays and Vertical Handoff
In this section, we describe the wireless overlay network and handoff concepts. WLANs are comprised of high-bandwidth wireless cells that cover a relatively small area, CDMA systems in the hierarchy provide a lower bandwidth per unit area connection over a larger geographic area. In our system, which consists of large CDMA cells and several small WLAN cells inside of them, vertical handoff may take place in two cases: handoff from CDMA to WLAN (downward vertical handoff) when the MS is in the coverage area of a CDMA cell and enters into the WLAN, handoff from WLAN to CDMA when the MS leaves the coverage area of a WLAN and enters that of a CDMA cell.
In general, even though the RSSI from CDMA is usually greater than that of WLAN, downward vertical handoff is done with high priority since connecting to WLAN is more desirable because it provides more bandwidth, is cost effective and power efficient, and reduces interference in the mobile network. However, in the case of fast MS, the frequency of handoffs will increase in WLAN. In order to overcome this problem, we propose a novel handoff algorithm in Sections 3 and 4. In contrast, we consider the upward vertical handoff.
The horizontal handoff is divided into two categories: handoff from CDMA to CDMA when the MS leaves the coverage area of a CDMA cell and enters other CDMA cell, handoff from WLAN to WLAN when the MS leaves the coverage area of a WLAN and enters other WLAN.
The requirements of the handoff algorithm in heterogeneous networks which should be considered in the design of the handoff algorithm are as follows [18]:
-
(i)
handoff should be done fast and its delay should be minimum;
-
(ii)
the number of handoffs should be minimal since excessive handoff results in signal quality degradation increased traffic dropping probability and additional loads on the network;
-
(iii)
the handoff procedure should be reliable and successful;
-
(iv)
when the traffic in the WLAN becomes too high and overflow occurs, the handoff to WLAN should be avoided;
-
(v)
fast MS should remain connected to CDMA and prevented from connecting to WLAN since the WLAN is designed for low-velocity MS and assumes a small coverage area (~100 m).
In order to satisfy the above requirements, we propose a handoff decision algorithm considering the MS speed, GoS, dropping probability, blocking probability, RSSI, and distance between BS (or AP) and MS.
3. A Vertical Handoff Decision and the Proposed Algorithm
A vertical handoff decision determines when to invoke a vertical handoff operation. The vertical handoff decision is rule based, and the rules decide whether the handoff is necessary and to which network to switch.
A vertical handoff in our system falls into two stages which are included during a vertical handoff decision: a handoff triggering and a network selection stage. In the handoff triggering stage, various parameters used for the handoff decision are continuously monitored by both networks (e.g., RSSI). In the network selection stage, the handoff target direction is chosen based on the predefined criterion (e.g., QoS and GoS).
3.1. Handoff Triggering
In this subsection, we discuss handoff triggering criteria for optimizing the GoS, low-latency handoff in MIPv4 and fast handoff in MIPv6.
3.1.1. Handoff Triggering with RSS
A vertical handoff decision process determines when to invoke a vertical handoff operation. The time for the handoff trigger is evaluated by the user location changes (as users may leave or enter into specific network coverage) and the network selection criterion is the context information (e.g., QoS, GoS, mobile speed, network preferences, etc.) of the current and alternative network(s). The evaluation of user location changes is carried out based on the RSS. Generally, a handoff trigger is decided by the RSS. This method is similar to movement detection in the MIP mobility management. This paper adopts a vertical handoff algorithm, where the criteria for handoff triggering and network selection are the RSS and mobile velocity for optimizing the GoS, respectively.
Our proposed vertical handoff algorithm between the WLAN and CDMA is shown in Figure 1. We assume the following variables to determine the vertical handoff:
-
(i)
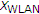 : predefined threshold value when the handoff is in WLAN;
: predefined threshold value when the handoff is in WLAN; -
(ii)
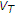 : velocity threshold whether a fast mobile station (MS) or a slow MS.
: velocity threshold whether a fast mobile station (MS) or a slow MS.
In the left-side operation of the vertical handoff procedure (upward vertical handoff), first, the RSS values are measured in sampling intervals and their average RSS is computed in the averaging window. If a neighbor WLAN does not exist, it prepares to handoff to CDMA. If a neighbor WLAN exists, it monitors the RSS of the neighbor WLANs. As the MS moves away from the coverage of the access point, the signal strength falls. The MS then scans the environment for other access points. If another access point is available, and the RSS of the neighbor WLAN is strong enough, then the network selection procedure prepares the information to which network to connect (either CDMA or WLAN). In the network selection stage, the velocity threshold ( ) is calculated while optimizing the GoS. When the MS speed is larger than the velocity threshold, it executes the handoff to CDMA. In this case, the MS is identified as a fast MS. Therefore, the requirements 2, 4, and 5 in Section 2 can be satisfied. The handoff algorithm uses this information (RSSI) along with other possible information (
) is calculated while optimizing the GoS. When the MS speed is larger than the velocity threshold, it executes the handoff to CDMA. In this case, the MS is identified as a fast MS. Therefore, the requirements 2, 4, and 5 in Section 2 can be satisfied. The handoff algorithm uses this information (RSSI) along with other possible information ( ) to make a decision on the handoff execution to the CDMA network. Notice also that the right-side operation of the vertical handoff procedure (downward vertical handoff) is similar with the upward vertical handoff except for the handoff direction.
) to make a decision on the handoff execution to the CDMA network. Notice also that the right-side operation of the vertical handoff procedure (downward vertical handoff) is similar with the upward vertical handoff except for the handoff direction.
3.1.2. Handoff Trigger with RSS and Distance
To reduce the likelihood of unnecessary handoffs, we consider a handoff triggering model based on the criteria of RSS and distance between BS (or AP) and MS.
Figure 2 illustrates the proposed vertical handoff procedure using the RSS and the distance between BS (or AP) and MS. We use the following variables to determine the vertical handoff:
-
(1)
 : predefined signal strength thresholds for the handoff in the CDMA network and WLAN, respectively;
: predefined signal strength thresholds for the handoff in the CDMA network and WLAN, respectively; -
(ii)
 : predefined distance thresholds for the CDMA network and WLAN, respectively;
: predefined distance thresholds for the CDMA network and WLAN, respectively; -
(iii)
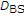 : current measured distance between BS and MS.
: current measured distance between BS and MS.
We notice that the measured criteria of signal level and distance for both RAN (radio access network) technologies cannot be directly compared since the monitored links come from different access networks, so different thresholds for the two access technologies are defined separately.
In the upward vertical handoff (the left-side of Figure 2), when the active MS is using the WLAN link, the handoff from WLAN to CDMA network will occur when the following condition is satisfied:

As the MS moves away from the coverage of the access point, the signal strength is falling down and the distance between BS and MS is decreasing.
On the other hand, the handoff from the CDMA network to WLAN will occur when the following condition is satisfied:

When the signal from the WLAN access point (AP) becomes strong and at the same time the distance between AP and MS is decreasing and MS speed is smaller than the velocity threshold (VT), the MS is connected to the WLAN. These two criteria (RSS and distance) reduce the unnecessary handoff probability and traffic-dropping probability [19]. Reference [19] mentioned that the probability of vertical handoff using both RSS and distance is smaller than that using only RSS. The handoff mechanism for this direction should consider the criteria of RSS and distance on the CDMA link, and the information brought by velocity. The latter is decided by the GoS-based network selection process, invoked when the GoS of an integrated network is below the perceived acceptance quality, or the GoS achieves a minimal value.
3.2. Network Selection Method
As network selection method, we propose a context-based network selection process between WLAN and the CDMA network, based on the wireless channel assignment information. We focus on the network selection method which uses the context information such as GoS and the number of handoff attempts. GoS is a function of the dropping and blocking probabilities. As a network selection parameter, the velocity threshold is determined to optimize the system performance. The optimal velocity threshold is adjusted to assign the available channels to the mobile stations.
3.2.1. Criteria Parameters: MS Speed and GoS
The proposed network selection algorithm between WLAN and CDMA cellular networks considers the velocity thresholds related to GoS performance and handoff rates as shown in Figures 1 and 2. In general, GoS is a measure of the probability that a percentage of the offered traffic will be blocked or delayed. As such, GoS is commonly expressed in terms of the fraction of calls failing to receive immediate service (blocked calls), or the fraction of calls forced to wait longer than a given time for service (delayed calls). In this paper, the call blocking and call dropping probabilities are used for GoS function because mobile users complain more about dropping calls due to handoff failures for voice call services.
In our proposed vertical handoff decision process, the estimation of the velocity threshold ( ) is carried out in the system shown in Figure 3. For the estimation of the mobile speed, global positioning system (GPS) or differential GPS can provide adequate location information. Using GPS and time-of-arrival (TOA) information from the user signal, we can estimate for user's velocity. We develop the handoff algorithm based on an optimal velocity threshold. The problem here is to find
) is carried out in the system shown in Figure 3. For the estimation of the mobile speed, global positioning system (GPS) or differential GPS can provide adequate location information. Using GPS and time-of-arrival (TOA) information from the user signal, we can estimate for user's velocity. We develop the handoff algorithm based on an optimal velocity threshold. The problem here is to find  that improves GoS and decreases the number of handoff attempts (
that improves GoS and decreases the number of handoff attempts ( ) with the given traffic parameters and MS mobility:
) with the given traffic parameters and MS mobility:  and
and  , which are the traffic load and velocity distribution of MS, respectively. We have to find the velocity threshold that satisfies the following optimality criterion:
, which are the traffic load and velocity distribution of MS, respectively. We have to find the velocity threshold that satisfies the following optimality criterion:

The procedure is now concerned with optimizing GoS in which the system-wide call blocking probability  and the handoff call dropping probability
and the handoff call dropping probability  are weighted and averaged as described later in (35). GoS can be written as a function of
are weighted and averaged as described later in (35). GoS can be written as a function of  , and hence finding the optimum value of
, and hence finding the optimum value of  minimizing the value of GoS and
minimizing the value of GoS and  is a typical minimization problem.
is a typical minimization problem.
3.2.2. Criteria Parameters: WLAN Throughput and Delay Jitter
The proposed network selection algorithm between WLAN and CDMA cellular networks considers the WLAN throughput and delay jitter related to the number of competing terminals as shown in Figure 4.
In the IEEE 802.11 medium access control (MAC) layer protocol, the basic access method is the distributed coordination function (DCF) which is based on the mechanism of carrier sense multiple access with collision avoidance (CSMA/CA). The performance strongly depends on the number of competing terminals. Therefore, if we know the number of competing terminals, then we can assess the current throughput in WLAN. As the number of competing terminals increases, the throughput is degraded. Therefore, when the WLAN networks present over maximum throughput and minimum delay jitter, we expect the handoff to WLAN be avoided and entrance into the CDMA cell be granted.
According to the network traffic class (e.g., conversational, streaming, interactive, or background class), the network selection algorithm exhibits different sensitivities to delays or delay jitters. In such scenarios, there is a tradeoff between the handoff delay and throughput during these handoff operations. Therefore, we propose a network selection algorithm by exploiting the information provided by both throughput and delay jitter.
In [20], the number of competing terminals is estimated using the extended Kalman filter approach. This approach shows both high accuracy as well as prompt reactivity to changes in the network occupancy status. Thus the estimated knowledge of traffic load and number of terminals sharing an 802.11 WLAN might effectively drive the load-balancing and handoff algorithms to achieve better network resource utilization. From these estimated values, we calculate the throughput and delay jitter. Provided that the throughput and delay jitter are satisfied based on a prespecified threshold value (e.g., maximum delay variation of 130 milliseconds), then the WLAN will be selected as the active network. Otherwise, the CDMA network is selected. As Figure 4 indicates, the proposed method allows the reservation of the CDMA resources, and therefore the channel capacity will increase. Generally, voice can tolerate a maximum delay variation of 130 milliseconds while preserving good real-time interactivity [21].
4. Performance Metrics and Analysis
In this section, we describe handoff strategies and metrics that we use to quantify the performance. We consider a large geographical area covered by contiguous WLANs. WLAN constitutes the lower layer of the two-layer hierarchy. All the WLANs are overlaid by a large CDMA system. The overlaying CDMA system forms the upper cell layer. Each CDMA system is allocated  traffic channels, and the number of channels allocated to the WLAN cell-
traffic channels, and the number of channels allocated to the WLAN cell- is
is  . In the case of speech calls, the number of WLAN channels is the maximum number of users who can communicate with the access point (AP) while satisfying both the QoS and delay jitter conditions at the same time. All channels are shared among new calls and handoff calls. In our system, mobile stations (MSs) are traversing randomly the coverage area of WLAN and CDMA systems. We distinguish two classes of MSs: fast and slow MSs, respectively. We further assume that an MS does not change its speed during a call.
. In the case of speech calls, the number of WLAN channels is the maximum number of users who can communicate with the access point (AP) while satisfying both the QoS and delay jitter conditions at the same time. All channels are shared among new calls and handoff calls. In our system, mobile stations (MSs) are traversing randomly the coverage area of WLAN and CDMA systems. We distinguish two classes of MSs: fast and slow MSs, respectively. We further assume that an MS does not change its speed during a call.
Figure 5 shows the traffic flows between different wireless networks with related parameters. In our system, we have classified them into four handoff strategies as follows:
-
(i)
strategy 1: no vertical handoff;
-
(ii)
strategy 2: only upward vertical handoff;
-
(iii)
strategy 3: upward and downward vertical handoff;
-
(iv)
strategy 4: take-back upward and downward vertical handoff,
where the take-back vertical handoff means that the vertical handoff traffics, which have been connected to the CDMA (or WLAN) as overflow, are taken back to a WLAN (or CDMA) of the appropriate layer as soon as the traffic channels become available. This capability has the effect that the number of MSs with different speeds is minimized in the considered cell layer. In general, the slow MS is connected to the WLAN according to the network selection algorithm. If no other AP is available, the slow MS first is connected to the CDMA cell. Next, if an AP becomes available, the slow MS is back to the WLAN. The four strategies enable the network to clear the handoff target cell depending on the user's mobility. The four strategies can be used to estimate the velocity threshold ( ) for various handoff admission controls.
) for various handoff admission controls.
In this paper, all WLANs of the lower layer are treated equally to simplify the overflow. We present analytical results for the proposed system. As stated, our objective is to focus on simple and tractable mechanisms for which analytical results can give an insight into the handoff mechanism between different networks. According to the velocity threshold, all the mobile users are divided into two groups: slower moving users ( ) and fast moving users (
) and fast moving users ( ). In order to determine the optimal threshold velocity, which is one of the main goals of this study, a few assumptions related to mobility characteristics are made in the system model.
). In order to determine the optimal threshold velocity, which is one of the main goals of this study, a few assumptions related to mobility characteristics are made in the system model.
The assumptions we employ in the mobility models are taken from [22] as cells are circular with radius  , mobiles are uniformly distributed in the system, mobiles making new calls in WLAN move along a straight line with a direction uniformly distributed between
, mobiles are uniformly distributed in the system, mobiles making new calls in WLAN move along a straight line with a direction uniformly distributed between  , and mobiles crossing cell boundary enter a neighbor cell with the incident angle
, and mobiles crossing cell boundary enter a neighbor cell with the incident angle  which assumes the distribution:
which assumes the distribution:  .
.
WLAN cells assume two types of new call traffics, represented by the call arrival rates  and
and  , respectively, and modeled by the Markov-modulated Poisson process (M/M/k/k, in voice traffic model) [23]. Let random variables
, respectively, and modeled by the Markov-modulated Poisson process (M/M/k/k, in voice traffic model) [23]. Let random variables  and
and  denote the straight mobile paths for new calls and handoff calls, respectively. With the assumption of unique WLAN cell size and the same speed for the MSs, WLAN cell boundary crossing rate per call (
denote the straight mobile paths for new calls and handoff calls, respectively. With the assumption of unique WLAN cell size and the same speed for the MSs, WLAN cell boundary crossing rate per call ( ), provided that no handoff failure occurs [22], is
), provided that no handoff failure occurs [22], is  . New calls are assumed to finish within the average call duration time,
. New calls are assumed to finish within the average call duration time,  , or the call handoffs to an adjacent cell. The proportion of the channels returned by the handoff is
, or the call handoffs to an adjacent cell. The proportion of the channels returned by the handoff is  [22]. In other words, the rate of channel release and that of the call completion due to handoff are
[22]. In other words, the rate of channel release and that of the call completion due to handoff are  and
and  , respectively.
, respectively.
4.1. Handoff Strategy-1: No Vertical Handoff
In this strategy, we consider the reference system in which each layer in the overlaid WLAN/CDMA network is kept completely independent. Slow mobile users are traversing only in the WLAN and fast mobile users are traversing in the CDMA system. Horizontal handoff is allowed but vertical handoff is not allowed in this strategy.
We denote the blocking probability of calls from the CDMA system and WLAN by  and
and  , respectively. The handoff traffic from slow and fast mobiles is denoted as follows.
, respectively. The handoff traffic from slow and fast mobiles is denoted as follows.  and
and  are the rates of fast and slow mobile handoff traffic in a CDMA system, respectively.
are the rates of fast and slow mobile handoff traffic in a CDMA system, respectively.  and
and  are the rates of fast and slow mobile handoff traffic in a WLAN, respectively.
are the rates of fast and slow mobile handoff traffic in a WLAN, respectively.
4.1.1. The New Call Blocking Probability
The Call Blocking Probability in WLAN
The total traffic rate into the WLAN due to a slow MS is computed as follows:

where the superscript  denotes the slow MS. The subscript 1 is for WLAN. The subscripts
denotes the slow MS. The subscript 1 is for WLAN. The subscripts  and
and  denote the new call and the handoff call, respectively.
denote the new call and the handoff call, respectively.
The generation rate of the handoff traffic of a slow mobile station in a WLAN is given by

The offered load in a WLAN is  . The Erlang-B formula calculates the blocking probability of WLAN with the traffic
. The Erlang-B formula calculates the blocking probability of WLAN with the traffic  and the number of channels
and the number of channels  as
as

This result can be easily extended to Erlang-C or M/M/k/k queue models.
The Call Blocking Probability in CDMA System
The total traffic rate into the CDMA cellular system due to a fast MS is computed as follows

The generation rate of the handoff traffic of a fast mobile station in a CDMA system is given by

The offered load to a CDMA system is calculated as  . Similar to the new call blocking probability of WLAN, the CDMA system's blocking probability can be expressed as
. Similar to the new call blocking probability of WLAN, the CDMA system's blocking probability can be expressed as

4.1.2. The Handoff Call Dropping Probability
The Handoff Call Dropping Probability in WLAN
Slow MS users are supposed to use WLAN channels. The probability of handoff call drop in WLAN can be calculated as follows.  is defined in such a way that the
is defined in such a way that the  th handoff request is successful but the
th handoff request is successful but the  th request is dropped:
th request is dropped:

where  and
and  . The variable
. The variable  describes the probability that the handoff fails due to the channel shortage, and
describes the probability that the handoff fails due to the channel shortage, and  is the probability of successful handoff.
is the probability of successful handoff.
The Handoff Call Dropping Probability in the CDMA System
Similar to the call dropping probability of WLAN, the probability of call dropping in CDMA systems can be calculated as follows:

The overall probability of either dropping or handoff failure can be expressed as follows:

where  and
and  are the fractions of slow and fast MSs, respectively.
are the fractions of slow and fast MSs, respectively.
4.2. Handoff Strategy-2: Upward Vertical Handoff
The system in this strategy allows upward vertical handoff from the WLAN to the CDMA system. Only upward vertical handoff of new MS and handoff traffic for a slow MS to the CDMA system is allowed.
4.2.1. The New Call Blocking Probability
The New Call Blocking Probability in WLAN
The total traffic rate in WLAN due to a slow MS is the same as (4), where  is the new call generation rate in WLAN due to a slow MS, and
is the new call generation rate in WLAN due to a slow MS, and  is the rate of handoff call in a WLAN of a slow MS. Notice also that the generation rate of the handoff traffic of a slow mobile station in a WLAN is the same as (5).
is the rate of handoff call in a WLAN of a slow MS. Notice also that the generation rate of the handoff traffic of a slow mobile station in a WLAN is the same as (5).
The offered load in a WLAN is  . The Erlang-B formula (6) calculates the blocking probability of WLAN with the traffic
. The Erlang-B formula (6) calculates the blocking probability of WLAN with the traffic  and the number of channels
and the number of channels  .
.
The New Call Blocking Probability in the CDMA System
The total traffic rate in the CDMA cellular system due to a fast MS assumes the same expression as in (7). The total traffic rate into a CDMA system due to a slow MS is given by

where  denotes the number of WLANs in an overlay CDMA cellular system. The generation rate of the handoff traffic of a fast mobile station in a CDMA system assumes the same expression as in (8). The generation rate of the handoff traffic of a slow mobile station in a CDMA system is given by
denotes the number of WLANs in an overlay CDMA cellular system. The generation rate of the handoff traffic of a fast mobile station in a CDMA system assumes the same expression as in (8). The generation rate of the handoff traffic of a slow mobile station in a CDMA system is given by

The offered load to a CDMA system is calculated as  . Finally, the blocking probability of the CDMA system can be expressed as in (9).
. Finally, the blocking probability of the CDMA system can be expressed as in (9).
4.2.2. The Handoff Call Dropping Probability
The Handoff Call Dropping Probability in the WLAN
The probability of handoff call drop in the WLAN can be calculated as follows:

The notation  denotes the probability that a slow MS fails to be handed over to a near WLAN, and to be handed over to the overlaying CDMA system. The notation
denotes the probability that a slow MS fails to be handed over to a near WLAN, and to be handed over to the overlaying CDMA system. The notation  denotes the probability that a slow MS fails to be handed over to the CDMA system during a call.
denotes the probability that a slow MS fails to be handed over to the CDMA system during a call.
The notation  is defined in such a way that the
is defined in such a way that the  th handoff request is successful but the
th handoff request is successful but the  th request is dropped:
th request is dropped:

 is calculated as follows:
is calculated as follows:

The Handoff Call Dropping Probability in the CDMA System
The probability of call dropping of a fast mobile station in the CDMA system is the same as (11). The overall probability of dropping is the same as (12).
4.3. Handoff Strategy-3: Upward and Downward Vertical Handoffs
In this subsection, we describe the performance analysis of strategy-3. In strategy-3, we consider upward and downward vertical handoffs between WLAN and the CDMA system.
4.3.1. The New Call Blocking Probability
The New Call Blocking Probability in the WLAN
The total traffic rate into the WLAN due to a slow MS is the same as (4). The total traffic rate into the WLAN due to a fast MS is expressed as

The generation rate of the handoff traffic of a slow MS in a WLAN is the same as (5). The generation rate of the handoff traffic of a fast moving MS in a WLAN is characterized by

The parameter  is the actual offered load to a WLAN from the new call arrival and the handoff call arrival. Invoking this important property, we can use
is the actual offered load to a WLAN from the new call arrival and the handoff call arrival. Invoking this important property, we can use  as the offered load to WLAN. The Erlang-B formula (6) can be used then to calculate the blocking probability with the traffic
as the offered load to WLAN. The Erlang-B formula (6) can be used then to calculate the blocking probability with the traffic  and the number of channels
and the number of channels  [22].
[22].
The New Call Blocking Probability in the CDMA System
The total traffic rate into the CDMA system due to a fast MS is the same as (7). The total traffic rate into the CDMA due to slow MS is expressed as (13). The total traffic rate into the CDMA system due to a fast MS is the same as (8). The generation rate of the handoff traffic of a fast MS in the CDMA system is calculated as

The generation rate of the handoff traffic of a slow MS in the CDMA system is computed as (14). The probability of call blocking is given by the Erlang-B formula because it does not depend on the distribution of the session time. Invoking this important property, we can use  as the offered load to the CDMA system, and the blocking probability can be expressed as in (9).
as the offered load to the CDMA system, and the blocking probability can be expressed as in (9).
4.3.2. The Handoff Call Dropping Probability
The Handoff Call Dropping Probability in WLAN
Slow MSs are supposed to use WLAN channels. However, since the handoff to the CDMA system is also allowed, the probability of handoff call drop in WLAN can be calculated as follows. Let  denote the probability that a slow MS fails to be handed over to a near WLAN. The probability of calls in a WLAN,
denote the probability that a slow MS fails to be handed over to a near WLAN. The probability of calls in a WLAN,  , denotes the probability of failed upward vertical handoffs to the overlaying CDMA system due to channel shortages. Then the handoff call dropping probability can be expressed as (15).
, denotes the probability of failed upward vertical handoffs to the overlaying CDMA system due to channel shortages. Then the handoff call dropping probability can be expressed as (15).
The Handoff Call Dropping Probability in the CDMA System
The probability of call droppings of a fast mobile station in the CDMA system can be approximated by

The overall probability of dropping is the same as (12).
4.4. Handoff Strategy-4: Take-Back Vertical Handoff
In this subsection, we describe the performance analysis of strategy-4. In strategy-4, we consider take-back vertical handoff between the WLAN and the CDMA system.
4.4.1. New Call Blocking Probability
New Call Blocking Probability in the WLAN
We denote the take-back traffic rates to the CDMA system and WLAN by  and
and  , respectively. The notations
, respectively. The notations  and
and  denote the take-back probabilities from the CDMA system and the WLAN, respectively.
denote the take-back probabilities from the CDMA system and the WLAN, respectively.
The total traffic rate into the WLAN due to a slow MS is computed as follows:

where the take-back traffic rate component is given by

The total traffic rate into the WLAN due to a fast MS is expressed as

The generation rate of the handoff traffic of a slow MS in a WLAN is given by

The generation rate of the handoff traffic of a fast moving MS in a WLAN is characterized by

The parameter  is the actual offered load to a WLAN from the new call arrival and the handoff call arrival. Invoking this important property, we can use
is the actual offered load to a WLAN from the new call arrival and the handoff call arrival. Invoking this important property, we can use  as the offered load to the WLAN. Notice that the Erlang-B formula (6) calculates the blocking probability with the traffic
as the offered load to the WLAN. Notice that the Erlang-B formula (6) calculates the blocking probability with the traffic  and the number of channels
and the number of channels  .
.
The New Call Blocking Probability in the CDMA System
The total traffic rate into the CDMA system due to a fast MS is computed as follows:

Here, the take-back traffic rate component takes the expression

Thus the total traffic rate into the CDMA system due to a slow MS is given by

The generation rate of the handoff traffic of a fast MS in the CDMA system is

The generation rate of the handoff traffic of a slow MS in the CDMA system is computed as

The probability of call blocking is given by the Erlang-B formula because it does not depend on the distribution of the session time. Invoking this important property, we can use  as the offered load to the CDMA system, and the blocking probability can be expressed as in (9).
as the offered load to the CDMA system, and the blocking probability can be expressed as in (9).
4.4.2. The Handoff Call Dropping Probability
The handoff call dropping probability in WLAN
Slow MSs are supposed to use WLAN channels. However, since handoff to the CDMA system is also allowed, the probability of handoff call drop in WLAN can be calculated as follows. The handoff call dropping probability is the same as (15).
The handoff call dropping probability in the CDMA system
The probability of call dropping probability of a fast mobile station in the CDMA system can be calculated as follows:

The overall probability of either dropping or handoff failure is given by (12).
4.5. The Number of Handoffs and Grade of Service
We will use the term handoff rate to refer to the mean number of handoffs per call. We use geometric models to predict handoff rates per call as the cell shapes and sizes are varied. Approximating the cell as a circle with radius  and the speed of the mobile station with
and the speed of the mobile station with  , the expected mean sojourn time in the call initiated cell and in an arbitrary cell can be found [22], and are given, respectively, by
, the expected mean sojourn time in the call initiated cell and in an arbitrary cell can be found [22], and are given, respectively, by

A user will experience a handoff if he moves out of the radio coverage of the base station with which he/she currently communicates. The faster the user travel, probably the more handoffs he/she will experience. Using a result from renewal theory, the expected number of handoffs given the speed of the user can be found [22]:

Among many system performance measures, GoS is the most widely used. In fact, users complain much more for call droppings than for call blockings. GoS is evaluated using the prespecified weights  and
and  [22]:
[22]:

where  and
and  represent the blocking and dropping probabilities of the involved systems, respectively. The weight
represent the blocking and dropping probabilities of the involved systems, respectively. The weight  emphasizes the dropping effect with its value in general larger than one half. In this paper, we use
emphasizes the dropping effect with its value in general larger than one half. In this paper, we use  due to the fact that the dropping effect is more critical for calling users.
due to the fact that the dropping effect is more critical for calling users.
5. Numerical Examples
The proposed procedure is tested using several numerical examples for the overlaid structure. The test system consists of 10 WLANs in the CDMA system. The total traffic is  , where
, where  and
and  stand for the new call arrival rates for the CDMA system and WLAN, respectively. The radii of WLAN and the CDMA system are assumed 300 m and 1000 m, respectively. The average call duration is
stand for the new call arrival rates for the CDMA system and WLAN, respectively. The radii of WLAN and the CDMA system are assumed 300 m and 1000 m, respectively. The average call duration is  seconds. The number of channels in each CDMA system and WLAN is
seconds. The number of channels in each CDMA system and WLAN is  and
and  , respectively, for the total
, respectively, for the total  Erlang. Assume the traffic mobility distribution is the same as [22].
Erlang. Assume the traffic mobility distribution is the same as [22].
During the operation phase, one can draw a histogram to estimate  , and the expected value of the mobile speed can be calculated by averaging the mobile speeds monitored by the system. Analytically, we can obtain
, and the expected value of the mobile speed can be calculated by averaging the mobile speeds monitored by the system. Analytically, we can obtain  for such a simple hypothetical velocity distribution [12], as it is shown in Figure 6.
for such a simple hypothetical velocity distribution [12], as it is shown in Figure 6.
Assume there are three types of traffic mobility distributions as displayed in Figure 6 for the given total traffic. Type 1 is the case when slower moving users are present in a larger number (prevalent), whereas the type 3 is the reverse case. Type 2 is the case when medium moving users represent the largest number.
Figure 7 shows the GoS for three different mobility distributions of the mobiles in the system. The vertical arrows in the figure show the range of the possible velocity thresholds at a certain load level. A fictitious traffic type 3 in which the number of fast moving mobiles is larger than those of slow moving mobiles is also considered, and the optimal value lies in the high-value region.
Four handoff strategies are considered for comparison, as depicted below. In this point analysis, we use Type 2.
-
(i)
No vertical handoff: a reference system where the two layers are kept completely independent.
-
(ii)
Upward vertical handoff: a system where only upward vertical handoff traffic for a slow MS to the CDMA system is allowed.
-
(iii)
Upward and downward vertical handoffs: a system where upward and downward vertical handoffs traffic for both slow and fast MS is allowed.
-
(iv)
Take-back vertical handoff: take-back vertical handoff traffic of both slow and fast MS to their appropriate layers.
The probability of blocking and call dropping versus velocity threshold are given in Figures 8-9. As shown in Figure 8, the probability of a new call blocking is almost unchanged, but it increases as  is minimized. If
is minimized. If  increases, the number of users being serviced in the CDMA system also increases. Thus
increases, the number of users being serviced in the CDMA system also increases. Thus  of the CDMA system increases, while
of the CDMA system increases, while  of WLAN decreases. Also, the overall probability of call droppings diminishes.
of WLAN decreases. Also, the overall probability of call droppings diminishes.
Figure 10 shows the plot of (45) for the mobility distributions of the MS in the system. As the velocity threshold increases, the number of handoff attempts in the system also increases. To achieve the goal of minimizing  , we want to place more users in the CDMA system because crossing the boundaries of large cells becomes less frequent. However, this may overload the CDMA system. Many calls may be blocked due to the lack of channels and have to be handed down to the WLAN. This imposes an extra cost. Therefore, it is desirable to maintain a GoS in the system.
, we want to place more users in the CDMA system because crossing the boundaries of large cells becomes less frequent. However, this may overload the CDMA system. Many calls may be blocked due to the lack of channels and have to be handed down to the WLAN. This imposes an extra cost. Therefore, it is desirable to maintain a GoS in the system.
We investigate next the GoS, which is a function of both the traffic load and mobility distribution. Figure 11 shows the plot of (46) for the mobility distributions of MS in the system. The vertical arrows in the figure show the range of possible velocity thresholds at a certain load level. The lowest point in the range corresponds to the maximum allowable and optimal velocity threshold. The optimal  is 12 m/sec, 14 m/sec, 13 m/sec, 12 m/sec for cases (a), (b), (c), and (d), respectively. Here, the GoS of cases (c) and (d) present minima of nearly equal values, but
is 12 m/sec, 14 m/sec, 13 m/sec, 12 m/sec for cases (a), (b), (c), and (d), respectively. Here, the GoS of cases (c) and (d) present minima of nearly equal values, but  assumes different values. Case (d) is favorable (see Figure 11) since
assumes different values. Case (d) is favorable (see Figure 11) since  in the case (d) is smaller than that of case (c) and thus more users are serviced in the CDMA system while WLAN serves fewer users. Also, the optimal threshold value which presents the minimum handoff rate assumes 12 m/sec or 13 m/sec (see Figure 10). The smaller threshold value assumes smaller handoff rates, and these values then achieve optimal values. As a result, WLAN will give rise to a higher number of handoff requests for high-mobility users, and the corresponding number of handoff requests of the calls in progress may cause an excessive processing load in the network. If the GoS value is given by
in the case (d) is smaller than that of case (c) and thus more users are serviced in the CDMA system while WLAN serves fewer users. Also, the optimal threshold value which presents the minimum handoff rate assumes 12 m/sec or 13 m/sec (see Figure 10). The smaller threshold value assumes smaller handoff rates, and these values then achieve optimal values. As a result, WLAN will give rise to a higher number of handoff requests for high-mobility users, and the corresponding number of handoff requests of the calls in progress may cause an excessive processing load in the network. If the GoS value is given by  , the range of the optimal threshold value (
, the range of the optimal threshold value ( ) becomes 9 m/sec to 20 m/sec, 9 m/sec to 20 m/sec, 11 m/sec to 20 m/sec, about 12 m/sec for cases (a), (b), (c), and (d), respectively.
) becomes 9 m/sec to 20 m/sec, 9 m/sec to 20 m/sec, 11 m/sec to 20 m/sec, about 12 m/sec for cases (a), (b), (c), and (d), respectively.
For the range exceeding the threshold, as  is smaller, more traffic can be accommodated for the increased
is smaller, more traffic can be accommodated for the increased  , and more traffic is allocated to the WLAN. As the traffic increases,
, and more traffic is allocated to the WLAN. As the traffic increases,  corresponding to the minimum
corresponding to the minimum  becomes higher. Thus more traffic should be assigned to WLAN. For example, if the number of fast-moving MSs is larger than the number of slow-moving MSs, the optimal
becomes higher. Thus more traffic should be assigned to WLAN. For example, if the number of fast-moving MSs is larger than the number of slow-moving MSs, the optimal  (in terms of GoS) lies in the relatively higher position of the region.
(in terms of GoS) lies in the relatively higher position of the region.
We make a comparison of the performance according to a variety of offered loads (Erlang value). The performance of GoS according to the offered load is shown in Figure 12. As the offered load increases, the performance of GoS becomes worse. As GoS, according to the offered load, is minimized, the velocity threshold value will be changed. Therefore, the velocity threshold value for which GoS is minimized is dependent on the offered load, velocity distribution, and handoff strategy. As showed previously in this research, we have corroborated that the velocity threshold is a function of a variety of factors.
In the case of handoff triggering using both RSS and distance information, GoS is showed in Figure 13. After handoff triggering, the network selection process is performed. The figure presents the performance graphs based on strategy-3 that is considered in both the upward and downward vertical handoffs. The probability of handoff is reduced with an average of 10% [19]. As the figure indicates, handoff triggering using both RSS and distance information exhibits better performance, compared with that using only RSS. Due to this aspect, the triggering method that exploits RSS and distance information may avoid unnecessary handoffs.
With all the observations in mind, the strategy we proposed exhibits some desirable features, that is, finding the optimal velocity threshold value GoS and the handoff rate.
6. Conclusions
This paper proposed a handoff decision process with network selection that decides the optimal velocity threshold in order to improve GoS and minimize the number of handoff attempts with a given traffic volume in a WLAN-CDMA integrated network. The simulation results show the dependency of the system performance upon the velocity threshold  . The velocity threshold has been shown to be an important system parameter that the system provider should determine to produce better GoS and lower handoff rates. From the simulation results, we were able to validate the procedures determining the optimal
. The velocity threshold has been shown to be an important system parameter that the system provider should determine to produce better GoS and lower handoff rates. From the simulation results, we were able to validate the procedures determining the optimal  , which depends upon GoS as well as the number of handoff attempts. Finally, we would like to mention that due to lack of space the results presented in our preliminary conference paper [24] address only a general decision process (based on received signal strength) and a simple handoff algorithm (take-back handoff). The work presented herein represents a significant extension of the results reported in [24] in the following aspects. The present paper proposes novel decision making schemes (based on the received signal strength, and the combination between signal strength and distance), novel network selection algorithms (based on velocity and GoS, and the number of competing terminals with throughput), as well as additional novel network selection algorithms (based on (a) no vertical handoff; (b) upward vertical handoff; (c) upward/downward vertical handoff; and (d) take-back handoff).
, which depends upon GoS as well as the number of handoff attempts. Finally, we would like to mention that due to lack of space the results presented in our preliminary conference paper [24] address only a general decision process (based on received signal strength) and a simple handoff algorithm (take-back handoff). The work presented herein represents a significant extension of the results reported in [24] in the following aspects. The present paper proposes novel decision making schemes (based on the received signal strength, and the combination between signal strength and distance), novel network selection algorithms (based on velocity and GoS, and the number of competing terminals with throughput), as well as additional novel network selection algorithms (based on (a) no vertical handoff; (b) upward vertical handoff; (c) upward/downward vertical handoff; and (d) take-back handoff).
References
Salkintzis AK, Fors C, Pazhyannur R: WlAN-GPRS integration for next-generation mobile data networks. IEEE Wireless Communications 2002, 9(5):112-124. 10.1109/MWC.2002.1043861
Ahmavaara K, Haverinen H, Pichna R: Interworking Architecture between 3GPP and WLAN Systems. IEEE Communications Magazine 2003, 41(11):74-81. 10.1109/MCOM.2003.1244926
ETSI : Requirements and architectures for interworking between HIPERLAN/3 and 3rd generation cellular system. European Telecommunications Standards Institute, Sophia Antipolis, France; 2001.
3GPP system to WLAN interworking: functional and architectural definition 3GPP, Valbonne, France; 2002.
Buddhikot MM, Chandranmenon G, Han S, Lee Y-W, Miller S, Salgarelli L: Design and implementation of a WLAN/CDMA2000 interworking architecture. IEEE Communications Magazine 2003, 41(11):90-100. 10.1109/MCOM.2003.1244928
Luo H, Jiang Z, Kim B-J, Shankaranarayanan NK, Henry P: Integrating wireless LAN and cellular data for the enterprise. IEEE Internet Computing 2003, 7(2):25-33. 10.1109/MIC.2003.1189186
Feasibility study on 3GPP system to wireless local area network (WLAN) interworking 3GPP, Valbonne, France; 2002.
cdma2000 high rate packet data air interface specification 3GPP2; 2001.
Akyildiz LF, McNair J, Ho J, Uzunalioglu H, Wang W: Mobility management in current and future communications networks. IEEE Network 1998, 12(4):39-49. 10.1109/65.713355
Liang B, Haas ZJ: Predictive distance-based mobility management for multidimensional PCS networks. IEEE/ACM Transactions on Networking 2003, 11(5):718-732. 10.1109/TNET.2003.815301
Zhang Q, Guo C, Guo Z, Zhu W: Efficient mobility management for vertical handoff between WWAN and WLAN. IEEE Communications Magazine 2003, 41(11):102-108. 10.1109/MCOM.2003.1244929
Wang HJ, Katz RH, Giese J: Policy-enabled handoffs across heterogeneous wireless networks. Proceedings of the 2nd IEEE Workshop on Mobile Computing Systems and Applications (WMCSA '99), February 1999, New Orleans, La, USA 51-60.
Chen L-J, Sun T, Chen B, Rajendran V, Gerla M: A smart decision model for vertical handoff. Proceedings of the 4th ANWIRE International Workshop on Wireless Internet and Reconfigurability (ANWIRE '04), January 2004, Athens, Greece
Balasubramaniam S, Indulska J: Vertical handover supporting pervasive computing in future wireless networks. Computer Communications 2004, 27(8):708-719. 10.1016/j.comcom.2003.10.010
Saaty TL: How to make a decision: the analytic hierarchy process. European Journal of Operational Research 1990, 48(1):9-26. 10.1016/0377-2217(90)90057-I
Nkansah-Gyekye Y, Agbinya JI: Vertical handoff decision algorithm for UMTS-WLAN. Proceedings of the 2nd International Conference on Wireless Broadband and Ultra Wideband Communications (AusWireless '07), August 2007, Sydney, Australia 37.
Liao H, Tie L, Du Z: A vertical handover decision algorithm based on fuzzy control theory. Proceeding of the 1st IEEE International Multi-Symposiums on Computer and Computa-tional Sciences (IMSCCS '06), June 2006, Hangzhou, China 309-313.
Majlesi A, Khalaj BH: An adaptive fuzzy logic based handoff algorithm for hybrid networks. Proceedings of the 6th International Conference on Signal Processing (ICSP '02), August 2002, Beijing, China 2: 1223-1228.
Bing H, He C, Jiang L: Performance analysis of vertical handover in a UMTS-WLAN integrated network. Proceedings of the 14th IEEE International Symposium on Personal, Indoor and Mobile Radio Communication (PIMRC '03), September 2003, Beijing, China 1: 187-191.
Bianchi G, Tinnirello I: Kalman filter estimation of the number of competing terminals in an IEEE 802.11 network. Proceedings of the 22nd Annual Joint Conference of the IEEE Computer and Communications Societies (INFOCOM '03), March-April 2003, San Franciso, Calif, USA 2: 844-852.
Onvural RO: Asynchronous Transfer Mode Networks: Performance Issues. Artech House, Norwood, Mass, USA; 1994.
Yeung KL, Nanda S: Channel management in microcell/macrocell cellular radio systems. IEEE Transactions on Vehicular Technologies 1996, 45(4):601-612. 10.1109/25.543716
Fischer W, Meier-Hellstern K: The Markov-modulated Poisson process (MMPP) cookbook. Performance Evaluation 1992, 18(2):149-171.
Kim J-S, Chung M-Y, Shin D-R: A vertical handoff decision process and algorithm based on context information in CDMA-WLAN interworking. In Proceedings of the 5th International Conference Computational Science (ICCS '05), May 2005, Atlanta, Ga, USA, Lecture Notes in Computer Science. Volume 3515. Emory University; 601-609.
Acknowledgments
This work was supported in part by the Korea Research Foundation and Qatar National Research Foundation (QNRF) through an NPRP grant.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Kim, JS., Serpedin, E., Shin, DR. et al. Handoff Triggering and Network Selection Algorithms for Load-Balancing Handoff in CDMA-WLAN Integrated Networks. J Wireless Com Network 2008, 136939 (2008). https://doi.org/10.1155/2008/136939
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2008/136939
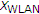 : predefined threshold value when the handoff is in WLAN;
: predefined threshold value when the handoff is in WLAN;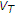 : velocity threshold whether a fast mobile station (MS) or a slow MS.
: velocity threshold whether a fast mobile station (MS) or a slow MS.

 : predefined signal strength thresholds for the handoff in the CDMA network and WLAN, respectively;
: predefined signal strength thresholds for the handoff in the CDMA network and WLAN, respectively; : predefined distance thresholds for the CDMA network and WLAN, respectively;
: predefined distance thresholds for the CDMA network and WLAN, respectively;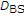 : current measured distance between BS and MS.
: current measured distance between BS and MS.









