- Research Article
- Open access
- Published:
Cores of Cooperative Games in Information Theory
EURASIP Journal on Wireless Communications and Networking volume 2008, Article number: 318704 (2008)
Abstract
Cores of cooperative games are ubiquitous in information theory and arise most frequently in the characterization of fundamental limits in various scenarios involving multiple users. Examples include classical settings in network information theory such as Slepian-Wolf source coding and multiple access channels, classical settings in statistics such as robust hypothesis testing, and new settings at the intersection of networking and statistics such as distributed estimation problems for sensor networks. Cooperative game theory allows one to understand aspects of all these problems from a fresh and unifying perspective that treats users as players in a game, sometimes leading to new insights. At the heart of these analyses are fundamental dualities that have been long studied in the context of cooperative games; for information theoretic purposes, these are dualities between information inequalities on the one hand and properties of rate, capacity, or other resource allocation regions on the other.
1. Introduction
A central problem in information theory is the determination of rate regions in data compression problems and that of capacity regions in communication problems. Although single-letter characterizations of these regions were given for lossless data compression of one source and for communication from one transmitter to one receiver by Shannon himself, more elaborate scenarios involving data compression from many correlated sources or communication between a network of users remain of great theoretical and practical interest, with many key problems remaining open. In these multiuser scenarios, rate and capacity regions are subsets of some Euclidean space whose dimension depends on the number of users. The search for an "optimal" rate point is no longer trivial, even if the rate region is known, because of the fact that there is no natural total ordering on points of Euclidean space. Indeed, it is important to ask in the first place what optimality means in the multiuser context–-typical criteria for optimality, depending on the scenario of interest, would derive from considerations of fairness, net efficiency, extraneous costs, or robustness to various kinds of network failures.
Our primary goal in this paper is to point out that notions from cooperative game theory arise in a very natural way in connection with the study of rate and capacity regions for several important problems. Examples of these problems include Slepian-Wolf source coding, multiple access channels, and certain distributed estimation problems for sensor networks. Using notions from cooperative game theory, certain properties of the rate regions follow from appropriate information inequalities. In the case of Slepian-Wolf coding and multiple access channels, these results are very well known; perhaps some of the interpretations are unusual, but the experts will not find them surprising. In the case of the distributed estimation setting, the results are recent and the interpretation is new. We supplement the analysis of these rate regions by pointing out that the classical capacity-based theory of composite hypothesis testing pioneered by Huber and Strassen also has a game-theoretic interpretation, but in terms of games with an uncountable infinity of players. Since most of our results concern new interpretations of known facts, we label them as Translations.
The paper is organized as follows. In Section 2, some basic facts from the theory of cooperative games are reviewed. Section 3 treats using the game-theoretic framework the distributed compression problem solved by Slepian and Wolf. The extreme points of the Slepian-Wolf rate region are interpreted in terms of robustness to certain kinds of network failures, and allocations of rates to users that are "fair" or "tolerable" are also discussed. Section 4 considers various classes of multiple access channels. An interesting special case is the Gaussian multiple access channel, where the game associated with the standard setting has significantly nicer structure than the game studied by La and Anantharam [1] associated with an arbitrarily varying setting. Section 5 describes a model for distributed estimation using sensor networks and studies a game associated with allocation of risks for this model. Section 6 looks at various games involving the entropies and entropy powers of sums. These do not seem to have an operational interpretation but are related to recently developed information inequalities. Section 7 discusses connections of the game-theoretic framework with the theory of robust hypothesis testing. Finally, Section 8 contains some concluding remarks.
2. A Review of Cooperative Game Theory
The theory of cooperative games is classical in the economics and game theory literature and has been extensively developed. The basic setting of such a game consists of  players, who can form arbitrary coalitions
players, who can form arbitrary coalitions  , where
, where  denotes the set
denotes the set  of players. A game is specified by the set
of players. A game is specified by the set  of players, and a value function
of players, and a value function  , where
, where  is the nonnegative real numbers, and it is always assumed that
is the nonnegative real numbers, and it is always assumed that  . The value of a coalition
. The value of a coalition  is equal to
is equal to  .
.
We will usually interpret the cooperative game (in its standard form) as the setting for a cost allocation problem. Suppose that player  contributes an amount of
contributes an amount of  . Since the game is assumed to involve (linearly) transferable utility, the cumulative cost to the players in the coalition
. Since the game is assumed to involve (linearly) transferable utility, the cumulative cost to the players in the coalition  is simply
is simply  . Since each coalition must pay its due of
. Since each coalition must pay its due of  , the individual costs
, the individual costs  must satisfy
must satisfy  for every
for every  . This set of cost vectors, namely
. This set of cost vectors, namely

is the set of aspirations of the game, in the sense that this set defines what the players can aspire to. The goal of the game is to minimize social cost, that is, the total sum of the costs  . Clearly this minimum is achieved when
. Clearly this minimum is achieved when  . This leads to the definition of the core of a game.
. This leads to the definition of the core of a game.
Definition 1.
The core of a game  is the set of aspiration vectors
is the set of aspiration vectors  such that
such that  .
.
One may think of the core of an arbitrary game as the intersection of the set of aspirations  and the "efficiency hyperplane":
and the "efficiency hyperplane":

The core can be equivalently defined as the set of undominated imputations; see, for example, Owen's book [2] for this approach, and a proof of the equivalence. In this paper, we will not consider the question of where the value function of a game comes from but rather take the value function as given and study the corresponding game using structural results from game theory. However, in the original economic interpretation, one should think of  as the amount of utility that the members of
as the amount of utility that the members of  can obtain from the game whatever the remaining players may do. Then, one can interpret
can obtain from the game whatever the remaining players may do. Then, one can interpret  as the payoff to the
as the payoff to the  th player and
th player and  as the minimum net payoff to the members of the coalition
as the minimum net payoff to the members of the coalition  that they will accept. This gives the aspiration set a slightly different interpretation. Indeed, the aspiration set can be thought of as the set of payoff vectors to players that no coalition would block as being inadequate. For the purposes of this paper, one may think of a cooperative game either in terms of payoffs as discussed in this paragraph or in terms of cost allocation as described earlier.
that they will accept. This gives the aspiration set a slightly different interpretation. Indeed, the aspiration set can be thought of as the set of payoff vectors to players that no coalition would block as being inadequate. For the purposes of this paper, one may think of a cooperative game either in terms of payoffs as discussed in this paragraph or in terms of cost allocation as described earlier.
A pathbreaking result in the theory of transferable utility games was the Bondareva-Shapley theorem characterizing whether the core of the game is empty. First, we need to define the notion of a balanced game.
Definition 2.
Given a collection  of subsets of
of subsets of  , a function
, a function  is a fractional partition if for each
is a fractional partition if for each  , we have
, we have  . A game is balanced if
. A game is balanced if

for any fractional partition  for any collection
for any collection  .
.
Actually, to check that a game is balanced, one does not need to show the inequality (3) for all fractional partitions for all collections  . It is sufficient to check (3) for "minimal balanced collections" (and these collections turn out to yield a unique fractional partition). Details may be found, for example, in Owen [2].
. It is sufficient to check (3) for "minimal balanced collections" (and these collections turn out to yield a unique fractional partition). Details may be found, for example, in Owen [2].
We now state the Bondareva-Shapley theorem [3, 4].
Fact 1.
The core of a game is nonempty if and only if the game is balanced.
Proof.
Consider the linear program:

The dual problem is easily obtained

If  and
and  denote the primal and dual optimal values, duality theory tells us that
denote the primal and dual optimal values, duality theory tells us that  . Also, the game being balanced means
. Also, the game being balanced means  , while the core being nonempty means that
, while the core being nonempty means that  . (Note that by setting
. (Note that by setting  for some subsets
for some subsets  , fractional partitions using arbitrary collections of sets can be thought of as fractional partitions using the full power set
, fractional partitions using arbitrary collections of sets can be thought of as fractional partitions using the full power set  .) Thus, the game having a nonempty core is equivalent to its being balanced.
.) Thus, the game having a nonempty core is equivalent to its being balanced.
An important class of games is that of convex games.
Definition 3.
A game is convex if

for any sets  and
and  . (In this case, the set function
. (In this case, the set function  is also said to be supermodular.)
is also said to be supermodular.)
The connection between convexity and balancedness goes back to Shapley.
Fact 2.
A convex game is balanced and has nonempty core; the converse need not hold.
Proof.
Shapley [5] showed that convex games have nonempty core, hence they must be balanced by Fact 1. A direct proof by induction of the fact that convexity implies fractional superadditivity inequalities (which include balancedness) is given in [6].
Incidentally, Maschler et al. [7] (cf., Edmonds [8]) noticed that the dimension of the core of a convex game was determined by the decomposability of the game, which is a measure of how much "additivity" (as opposed to the kind of superadditivity imposed by convexity) there is in the value function of the game.
There are various alternative characterizations of convex games that are of interest. For any game  and any ordering (permutation)
and any ordering (permutation)  on
on  , the marginal worth vector
, the marginal worth vector  is defined by
is defined by

for each  , and
, and  . The convex hull of all the marginal vectors is called the Weber set . Weber [9] showed that the Weber set of any game contains its core. The Shapley-Ichiishi theorem [5, 10] says that the Weber set is identical to the core if and only if the game is convex. In particular, the extreme points of the core of a convex game are precisely the marginal vectors.
. The convex hull of all the marginal vectors is called the Weber set . Weber [9] showed that the Weber set of any game contains its core. The Shapley-Ichiishi theorem [5, 10] says that the Weber set is identical to the core if and only if the game is convex. In particular, the extreme points of the core of a convex game are precisely the marginal vectors.
This characterization of convex games is obviously useful from an optimization point of view, as studied deeply by Edmonds [8] in the closely related theory of polymatroids. Indeed, polymatroids (strictly speaking, contra-polymatroids) may simply be thought of as the aspiration sets of convex games. Note that in the presence of the convexity condition, the assumption that  takes only nonnegative values is equivalent to the nondecreasing condition
takes only nonnegative values is equivalent to the nondecreasing condition  if
if  . Since a linear program is solved at extreme points, the results of Edmonds (stated in the language of polymatroids) and Shapley (stated in the language of convex games) imply that any linear function defined on the core of a convex game (or the dominant face of a polymatroid) must be extremized at a marginal vector. Edmonds [8] uses this to develop greedy methods for such optimization problems. Historically speaking, the two parallel theories of polymatroids and convex games were developed around the same time in the mid-1960s with awareness of and stimulated by each other (as evidenced by a footnote in [5]); however, in information theory, this parallelism does not seem to be part of the folklore, and the game interpretation of rate or capacity regions has only been used to the author's knowledge in the important paper of La and Anantharam [1].
. Since a linear program is solved at extreme points, the results of Edmonds (stated in the language of polymatroids) and Shapley (stated in the language of convex games) imply that any linear function defined on the core of a convex game (or the dominant face of a polymatroid) must be extremized at a marginal vector. Edmonds [8] uses this to develop greedy methods for such optimization problems. Historically speaking, the two parallel theories of polymatroids and convex games were developed around the same time in the mid-1960s with awareness of and stimulated by each other (as evidenced by a footnote in [5]); however, in information theory, this parallelism does not seem to be part of the folklore, and the game interpretation of rate or capacity regions has only been used to the author's knowledge in the important paper of La and Anantharam [1].
The Shapley value of a game  is the centroid of the marginal vectors:
is the centroid of the marginal vectors:

where  is the symmetric group consisting of all permutations. As shown by Shapley [11], its components are given by
is the symmetric group consisting of all permutations. As shown by Shapley [11], its components are given by

and it is the unique vector satisfying the following axioms: (a)  lies in the efficiency hyperplane
lies in the efficiency hyperplane  , (b) it is invariant under permutation of players, and (c) if
, (b) it is invariant under permutation of players, and (c) if  and
and  are two games, then
are two games, then  . Clearly, the Shapley value gives one possible formalization of the notion of a "fair allocation" to the players in the game.
. Clearly, the Shapley value gives one possible formalization of the notion of a "fair allocation" to the players in the game.
Fact 3.
For a convex game, the Shapley value is in the core.
Proof.
As pointed out by Shapley [5], this simply follows from the representation of the Shapley value as a convex combination of marginal vectors and the fact that the core of a convex game contains its Weber set.
For a cooperative game, convexity is quite a strong property. It implies, in particular, both that the game is exact and that it has a large core; we describe these notions below.
If  for each
for each  , does there exist
, does there exist  in the core such that
in the core such that  (component-wise)? If so, the core is said to be large. Sharkey [12] showed that not all balanced games have large cores, and that not all games with large cores are convex. However, [12] also showed the following fact.
(component-wise)? If so, the core is said to be large. Sharkey [12] showed that not all balanced games have large cores, and that not all games with large cores are convex. However, [12] also showed the following fact.
Fact 4.
A convex game has a large core.
A game with value function  is said to be exact if for every set
is said to be exact if for every set  , there exists a cost vector
, there exists a cost vector  in the core of the game such that
in the core of the game such that

Since for any point in the core, the net cost to the members of  is at least
is at least  , a game is exact if and only if
, a game is exact if and only if

The exactness and large core properties are not comparable (counterexamples can be found in [12] and Biswas et al. [13]). However, Schmeidler [14] showed the following fact.
Fact 5.
A convex game is exact.
Interestingly, Rabie [15] showed that the Shapley value of an exact game need not be in its core.
One may define, in an exactly complementary way to the above development, cooperative games that deal with resource allocation rather than cost allocation. The set of aspirations for a resource allocation game is

and the core is the intersection of this set with the efficiency hyperplane  defined in (2), which represents the maximum achievable resource for the grand coalition of all players, and thus a public good. A resource allocation game is concave if
defined in (2), which represents the maximum achievable resource for the grand coalition of all players, and thus a public good. A resource allocation game is concave if

for any sets  and
and  . The concavity of a game can be thought of as the "decreasing marginal returns" property of the value function, which is well motivated by economics.
. The concavity of a game can be thought of as the "decreasing marginal returns" property of the value function, which is well motivated by economics.
One can easily formulate equivalent versions of Facts 1, 2, 3, 4, and 5 for resource allocation games. For instance, the analogue of Fact 1 is that the core of a resource allocation game is nonempty if and only if

for each fractional partition  for any collection of subsets
for any collection of subsets  (we call this property also balancedness, with some slight abuse of terminology). This follows from the fact that the duality used to prove Fact 1 remains unchanged if we simultaneously change the signs of
(we call this property also balancedness, with some slight abuse of terminology). This follows from the fact that the duality used to prove Fact 1 remains unchanged if we simultaneously change the signs of  and
and  , and reverse relevant inequalities.
, and reverse relevant inequalities.
Notions from cooperative game theory also appear in the more recently developed theory of combinatorial auctions. In combinatorial auction theory, the interpretation is slightly different, but it remains an economic interpretation, and so we discuss it briefly to prepare the ground for some additional insights that we will obtain from it. Consider a resource allocation game  , where
, where  indexes the items available on auction. Think of
indexes the items available on auction. Think of  as the amount that a bidder in an auction is willing to pay for the particular bundle of items indexed by
as the amount that a bidder in an auction is willing to pay for the particular bundle of items indexed by  . In designing the rules of an auction, one has to take into account all the received bids, represented by a number of such set functions or "valuations"
. In designing the rules of an auction, one has to take into account all the received bids, represented by a number of such set functions or "valuations"  . The auction design then determines how to make an allocation of items to bidders, and computational concerns often play a major role.
. The auction design then determines how to make an allocation of items to bidders, and computational concerns often play a major role.
We wish to highlight a fact that has emerged from combinatorial auction theory; first we need a definition introduced by Lehmann et al. [16].
Definition 4.
A set function  is additive if there exist nonnegative real numbers
is additive if there exist nonnegative real numbers  such that
such that  for each
for each  . A set function
. A set function  is XOS, if there are additive value functions
is XOS, if there are additive value functions  for some positive integer
for some positive integer  such that
such that

The terminology XOS emerged as an abbreviation for "XOR of OR of singletons" and was motivated by the need to represent value functions efficiently (without storing all  values) in the computer science literature. Feige [17] proves the following fact, by a modification of the argument for the Bondareva-Shapley theorem.
values) in the computer science literature. Feige [17] proves the following fact, by a modification of the argument for the Bondareva-Shapley theorem.
Fact 6.
A game has an XOS value function if and only if the game is balanced.
By analogy with the definition of exactness for cost allocation games, a resource allocation game is exact if and only if

In other words, for an exact game, the additive value functions in the XOS representation of the game can be taken to be those corresponding to the elements of the core (if we allow maximizing over a potentially infinite set of additive value functions).
Some of the concepts elaborated in this section can be extended to games with infinitely many players, although many new technicalities arise. Indeed, there is a whole theory of so-called "nonatomic games" in the economics literature. This is briefly alluded to in Section 7, where we discuss an example of an infinite game.
3. The Slepian-Wolf Game
The Slepian-Wolf problem refers to the problem of losslessly compressing data from two correlated sources in a distributed manner. Let  denote the joint probability mass function of the sources
denote the joint probability mass function of the sources  , which take values in discrete alphabets. When the sources are coded in a centralized manner, any rate
, which take values in discrete alphabets. When the sources are coded in a centralized manner, any rate  (in bits per symbol) is sufficient, where
(in bits per symbol) is sufficient, where  denotes the joint entropy, that is,
denotes the joint entropy, that is,  . What rates are achievable when the sources must be coded separately? This problem was solved for i.i.d sources by Slepian and Wolf [18] and extended to jointly ergodic sources using a binning argument by Cover [19].
. What rates are achievable when the sources must be coded separately? This problem was solved for i.i.d sources by Slepian and Wolf [18] and extended to jointly ergodic sources using a binning argument by Cover [19].
Fact 7.
Correlated sources  can be described separately at rates
can be described separately at rates  and recovered with arbitrarily low error probability by a common decoder if and only if
and recovered with arbitrarily low error probability by a common decoder if and only if

for each  . In other words, the Slepian-Wolf rate region is the set of aspirations of the cooperative game
. In other words, the Slepian-Wolf rate region is the set of aspirations of the cooperative game  , which we call the Slepian-Wolf game.
, which we call the Slepian-Wolf game.
A key consequence is that using only knowledge of the joint distribution of the data, one can achieve a compression rate equal to the joint entropy of the users (i.e., there is no loss from the incapability to communicate). However, this is not automatic from the characterization of the rate region above; one needs to check that the Slepian-Wolf game is balanced. The balancedness of the Slepian-Wolf game is precisely the content of the lower bound in the following inequality of Madiman and Tetali [6]: for any fractional partition  using
using  ,
,

This weak fractional form of the joint entropy inequalities in [6] coupled with Fact 1 proves that the joint entropy is an achievable sum rate even for distributed compression. In fact, the Slepian-Wolf game is much nicer.
Translation 1.
The Slepian-Wolf game is a convex game.
Proof.
To show that the Slepian-Wolf game is convex, we need to show that  is supermodular. This fact was first explicitly pointed out by Fujishige [20].
is supermodular. This fact was first explicitly pointed out by Fujishige [20].
By applying Fact 2, the core is nonempty since the game is convex, which means that there exists a rate point satisfying

This recovers the fact that a sum rate of  is achievable. Note that, combined with Fact 1, this observation in turn gives an immediate proof of the inequality (18).
is achievable. Note that, combined with Fact 1, this observation in turn gives an immediate proof of the inequality (18).
We now look at how robust this situation is to network degradation because some users drop out. First note that by Fact 5, the Slepian-Wolf game is exact. Hence, for any subset  of users, there exists a vector
of users, there exists a vector  that is sum-rate optimal for the grand coalition of all users, which is also sum-rate optimal for the users in
that is sum-rate optimal for the grand coalition of all users, which is also sum-rate optimal for the users in  , that is,
, that is,  . However, in general, it is not possible to find a rate vector that is simultaneously sum-rate optimal for multiple proper subsets of users. Below, we observe that finding such a rate vector is possible if the subsets of interest arise from users potentially dropping out in a certain order.
. However, in general, it is not possible to find a rate vector that is simultaneously sum-rate optimal for multiple proper subsets of users. Below, we observe that finding such a rate vector is possible if the subsets of interest arise from users potentially dropping out in a certain order.
Translation 2 (Robust Slepian-Wolf coding).
Suppose the users can only drop out in a certain order, which without loss of generality we can take to be the natural decreasing order on  (i.e., we assume that the first user to potentially drop out would be user
(i.e., we assume that the first user to potentially drop out would be user  , followed by user
, followed by user  , etc.). Then, there exists a rate point for Slepian-Wolf coding which is feasible and optimal irrespective of the number of users that have dropped out.
, etc.). Then, there exists a rate point for Slepian-Wolf coding which is feasible and optimal irrespective of the number of users that have dropped out.
Proof.
The solution to this problem is related to a modified Slepian-Wolf game, given by the utility function:

where  . Indeed, if this game is shown to have a nonempty core, then there exists a rate point which is simultaneously in the Slepian-Wolf rate region of every
. Indeed, if this game is shown to have a nonempty core, then there exists a rate point which is simultaneously in the Slepian-Wolf rate region of every  , for
, for  . However, the nonemptiness of the core is equivalent to the balancedness of
. However, the nonemptiness of the core is equivalent to the balancedness of  , which follows from the inequality
, which follows from the inequality

where  is any fractional partition using
is any fractional partition using  , which was proved by Madiman and Tetali [6]. To see that the core of this modified game actually contains an optimal point (i.e., a point in the core of the subgame corresponding to the first
, which was proved by Madiman and Tetali [6]. To see that the core of this modified game actually contains an optimal point (i.e., a point in the core of the subgame corresponding to the first  users) for each
users) for each  , simply note that the marginal vector corresponding to the natural order on
, simply note that the marginal vector corresponding to the natural order on  gives a constructive example.
gives a constructive example.
The main idea here is known in the literature, although not interpreted or proved in this fashion. Indeed, other interpretations and uses of the extreme points of the Slepian-Wolf rate region are discussed, for example, in Coleman et al. [21], Cristescu et al. [22], and Ramamoorthy [23].
It is interesting to interpret some of the game-theoretic facts described in Section 2 for the Slepian-Wolf game. This is particularly useful when there is no natural ordering on the set of players, but rather our goal is to identify a permutation-invariant (and more generally, a "fair") rate point. By Fact 3, we have the following translation.
Translation 3.
The Shapley value of the Slepian-Wolf game satisfies the following properties. (a) It is in the core of the Slepian-Wolf game, and hence is sum-rate optimal. (b) It is a fair allocation of compression rates to users because it is permutation-invariant. (c) Suppose an additional set of  sources, independent of the first
sources, independent of the first  , is introduced. Suppose the Shapley values of the Slepian-Wolf games for the first set of sources is
, is introduced. Suppose the Shapley values of the Slepian-Wolf games for the first set of sources is  , and for the second set of sources is
, and for the second set of sources is  . If each source from the first set is paired with a distinct source from the second set, then the Shapley value for the Slepian-Wolf game played by the set of pairs is
. If each source from the first set is paired with a distinct source from the second set, then the Shapley value for the Slepian-Wolf game played by the set of pairs is  . (In other words, the "fair" allocation for the pair can be "fairly" split up among the partners in the pair.)
. (In other words, the "fair" allocation for the pair can be "fairly" split up among the partners in the pair.)
It is pertinent to note, moreover, that implementing Slepian-Wolf coding at any point in the core is practically implementable. While it has been noticed for some time that one can efficiently construct codebooks that nearly achieve the rates at an extreme point of the core, Coleman et al. [21], building on work of Rimoldi and Urbanke [24] in the multiple access channel setting, show a practical approach to efficient coding for any rate point in the core (based on viewing any such rate point as an extreme point of the core of a Slepian-Wolf game for a larger set of sources).
Fact 4 says that the Slepian-Wolf game has a large core, which may be interpreted as follows.
Translation 4.
Suppose, for each  ,
,  is the maximum compression rate that user
is the maximum compression rate that user  is willing to tolerate. A tolerance vector
is willing to tolerate. A tolerance vector  is said to be feasible if
is said to be feasible if

for each  . Then, for any feasible tolerance vector
. Then, for any feasible tolerance vector  , it is always possible to find a rate point
, it is always possible to find a rate point  in the core so that
in the core so that  (i.e., the rate point is tolerable to all users).
(i.e., the rate point is tolerable to all users).
4. Multiple Access Channels and Games
A multiple access channel (MAC) refers to a channel between multiple independent senders (the data sent by the  th sender is typically denoted
th sender is typically denoted  ) and one receiver (the received data is typically denoted
) and one receiver (the received data is typically denoted  ). The channel characteristics, defined for each transmission by a probability transition
). The channel characteristics, defined for each transmission by a probability transition  , is assumed to be known. We will further restrict our discussion to the case of memoryless channels, where each transmission is assumed to occur independently according to the channel transition probability.
, is assumed to be known. We will further restrict our discussion to the case of memoryless channels, where each transmission is assumed to occur independently according to the channel transition probability.
Even within the class of memoryless multiple access channels, there are several notable special cases of interest. The first is the discrete memoryless multiple access channel (DM-MAC), where all random variables take values in possibly different finite alphabets, but the channel transition matrix is otherwise unrestricted. The second is the Gaussian memoryless multiple access channel (G-MAC); here each sender has a power constraint  , and the noise introduced to the superposition of the data from the sources is additive Gaussian noise with variance
, and the noise introduced to the superposition of the data from the sources is additive Gaussian noise with variance  . In other words,
. In other words,

where  are the independent sources, and
are the independent sources, and  is a mean-zero, variance
is a mean-zero, variance  is normal independent of the sources. Note that although the power constraints are an additional wrinkle to the problem compared to the DM-MAC, the G-MAC is in a sense more special because of the strong assumption; it makes on the nature of the channel. A third interesting special case is the Poisson memoryless multiple access channel (P-MAC), which models optical communication from many senders to one receiver and operates in continuous time. Here, the channel takes in as inputs data from the
is normal independent of the sources. Note that although the power constraints are an additional wrinkle to the problem compared to the DM-MAC, the G-MAC is in a sense more special because of the strong assumption; it makes on the nature of the channel. A third interesting special case is the Poisson memoryless multiple access channel (P-MAC), which models optical communication from many senders to one receiver and operates in continuous time. Here, the channel takes in as inputs data from the  sources in the form of waveforms
sources in the form of waveforms  , whose peak powers are constrained by some number
, whose peak powers are constrained by some number  ; in other words, for each sender
; in other words, for each sender  ,
,  . The output of the channel is a Poisson process of rate:
. The output of the channel is a Poisson process of rate:

where the nonnegative constant  represents the rate of a homogeneous Poisson process (noise) called the dark current. For further details, one may consult the references cited below.
represents the rate of a homogeneous Poisson process (noise) called the dark current. For further details, one may consult the references cited below.
The capacity region of the DM-MAC was first found by Ahlswede [25] (see also Liao [26] and Slepian and Wolf [27]). Han [28] developed a clear approach to an even more general problem; he used in a fundamental way the polymatroidal properties of entropic quantities, and thus it is no surprise that the problem is closely connected to cooperative games. Below  denotes mutual information (see, e.g., [29]); for notational convenience, we suppress the dependence of the mutual information on the joint distribution.
denotes mutual information (see, e.g., [29]); for notational convenience, we suppress the dependence of the mutual information on the joint distribution.
Fact 8.
Let  be the class of joint distributions on
be the class of joint distributions on  for which the marginal on
for which the marginal on  is a product distribution, and the conditional distribution of
is a product distribution, and the conditional distribution of  given
given  is fixed by the channel characteristics. For
is fixed by the channel characteristics. For  , let
, let  be the set of capacity vectors
be the set of capacity vectors  satisfying
satisfying

for each  . The capacity region of the
. The capacity region of the  -user DM-MAC is the closure of the convex hull of the union
-user DM-MAC is the closure of the convex hull of the union  .
.
This rate region is more complex than the Slepian-Wolf rate region because it is the closed convex hull of the union of the aspiration sets of many cooperative games, each corresponding to a product distribution on  . Yet the analogous result turns out to hold. More specifically, even though the different senders have to code in a distributed manner, a sum capacity can be achieved that may be interpreted as the capacity of a single channel from the combined set of sources (coded together).
. Yet the analogous result turns out to hold. More specifically, even though the different senders have to code in a distributed manner, a sum capacity can be achieved that may be interpreted as the capacity of a single channel from the combined set of sources (coded together).
Translation 5.
The DM-MAC capacity region is the union of the aspiration sets of a class of concave games. In particular, a sum capacity of  is achievable, where the supremum is taken over all joint distributions on
is achievable, where the supremum is taken over all joint distributions on  that lie in
that lie in  .
.
Proof.
Let  denote the set of all conditional mutual information vectors (in the Euclidean space of dimension
denote the set of all conditional mutual information vectors (in the Euclidean space of dimension  ) corresponding to the discrete distributions on
) corresponding to the discrete distributions on  that lie in
that lie in  . More precisely, corresponding to any joint distribution in
. More precisely, corresponding to any joint distribution in  is a point
is a point  defined by
defined by

for each  . Han [28] showed that for any joint distribution in
. Han [28] showed that for any joint distribution in  ,
,  is a submodular set function. In other words, each point
is a submodular set function. In other words, each point  defines a concave game.
defines a concave game.
As shown in [28], the DM-MAC capacity region may also be characterized as the union of the aspiration sets of games from  , where
, where  is the closure of the convex hull of
is the closure of the convex hull of  . It remains to check that each point in
. It remains to check that each point in  corresponds to a concave game, and this follows from the easily verifiable facts that a convex combination of concave games is concave, and that a limit of concave games is concave.
corresponds to a concave game, and this follows from the easily verifiable facts that a convex combination of concave games is concave, and that a limit of concave games is concave.
For the second assertion, note that for any  , a sum capacity of
, a sum capacity of  is achievable by Fact 2 (applied to resource allocation games). Combining this with the above characterization of the capacity region and the fact that
is achievable by Fact 2 (applied to resource allocation games). Combining this with the above characterization of the capacity region and the fact that  for
for  completes the argument.
completes the argument.
We now take up the G-MAC. The additive nature of the G-MAC is reflected in a simpler game-theoretic description of its capacity region.
Fact 9.
The capacity region of the  -user G-MAC is the set of capacity allocations
-user G-MAC is the set of capacity allocations  that satisfy
that satisfy

for each  , where
, where  . In other words, the capacity region of the G-MAC is the aspiration set of the game defined by
. In other words, the capacity region of the G-MAC is the aspiration set of the game defined by  , which we may call the G-MAC game.
, which we may call the G-MAC game.
Translation 6.
The G-MAC game is a concave game. In particular, its core is nonempty, and a sum capacity of  is achievable.
is achievable.
As in the previous section, we may ask whether this is robust to network degradation in the form of users dropping out, at least in some order; the answer is obtained in an exactly analogous fashion.
Translation 7 (Robust coding for the G-MAC).
Suppose the senders can only drop out in a certain order, which without loss of generality we can take to be the natural decreasing order on  (i.e., we assume that the first user to potentially drop out would be sender
(i.e., we assume that the first user to potentially drop out would be sender  , followed by sender
, followed by sender  , etc.). Then, there exists a capacity allocation to senders for the G-MAC which is feasible and optimal irrespective of the number of users that have dropped out.
, etc.). Then, there exists a capacity allocation to senders for the G-MAC which is feasible and optimal irrespective of the number of users that have dropped out.
Furthermore, just as for the Slepian-Wolf game, Fact 4 has an interpretation in terms of tolerance vectors analogous to Translation 4. When there is no natural ordering of senders, Fact 3 suggests that the Shapley value is a good choice of capacity allocation for the G-MAC game. Practical implementation of an arbitrary capacity allocation point in the core is discussed by Rimoldi and Urbanke [24] and Yeh [30].
While the ground for the study of the geometry of the G-MAC capacity region using the theory of polymatroids was laid by Han, such a study and its implications were further developed, and in the more general setting of fading that allows the modeling of wireless channels, by Tse and Hanly [31] (see also [30]). Clearly statements like Translation 7 can be carried over to the more general setting of fading channels by building on the observations made in [31].
La and Anantharam [1] provide an elegant analysis of capacity allocation for a different Gaussian MAC model using cooperative game theoretic ideas. We briefly review their results in the context of the preceding discussion.
Consider an Gaussian multiple access channel that is arbitrarily varying, in the sense that the users are potentially hostile, aware of each others' codebooks, and are capable of forming "jamming coalitions". A jamming coalition is a set of users, say  , who decide not to communicate but instead get together and jam the channel for the remaining users, who constitute the communicating coalition
, who decide not to communicate but instead get together and jam the channel for the remaining users, who constitute the communicating coalition  . As before, each user has a power constraint; the
. As before, each user has a power constraint; the  th sender cannot use power greater than
th sender cannot use power greater than  whether it wishes to communicate or jam. It is still a Gaussian MAC because the received signal is the superposition of the inputs provided by all the senders, plus additive Gaussian noise of variance
whether it wishes to communicate or jam. It is still a Gaussian MAC because the received signal is the superposition of the inputs provided by all the senders, plus additive Gaussian noise of variance  . In [1], the value function
. In [1], the value function  for the game corresponding to this channel is derived; the value for a coalition
for the game corresponding to this channel is derived; the value for a coalition  is the capacity achievable by the users in
is the capacity achievable by the users in  even when the users in
even when the users in  coherently combine to jam the channel.
coherently combine to jam the channel.
Fact 10.
The capacity region of the arbitrarily varying Gaussian MAC with potentially hostile senders is the aspiration set of the La-Anantharam game, defined by

where  ,
,  , and
, and  .
.
Note that two things have changed relative to the naive G-MAC game; the power available for transmission (appearing in the numerator of the argument of the  function) is reduced because some senders are rendered incapable of communicating by the jammers, and the noise term (appearing in the denominator) is no longer constant for all coalitions but is augmented by the power of the jammers. This tightening of the aspiration set of the La-Anantharam game versus the G-MAC game causes the concavity property to be lost.
function) is reduced because some senders are rendered incapable of communicating by the jammers, and the noise term (appearing in the denominator) is no longer constant for all coalitions but is augmented by the power of the jammers. This tightening of the aspiration set of the La-Anantharam game versus the G-MAC game causes the concavity property to be lost.
Translation 8.
The La-Anantharam game is not a concave game, but it has a nonempty core. In particular, a sum capacity of  is achievable.
is achievable.
Proof.
La and Anantharam [1] show that the Shapley value need not lie in the core of their game, but they demonstrate the existence of another distinguished point in the core. By the analogue of Fact 3 for resource allocation games, the La-Anantharam game cannot be concave.
Although [1] shows that the Shapley value may not lie in the core, they demonstrate the existence of a unique capacity point that satisfies three desirable axioms: (a) efficiency, (b) invariance to permutation, and (c) envy-freeness. While the first two are also among the Shapley value axioms, [1] provides justification for envy-freeness as an appropriate axiom from the point of view of applications.
We mention here a natural question that we leave for the reader to ponder: given that the La-Anantharam game is balanced but not concave, is it exact? Note that the fact that the Shapley value does not lie in the core is not incompatible with exactness, as shown by Rabie [15].
Finally, we turn to the P-MAC. Lapidoth and Shamai [32] performed a detailed study of this communication problem and showed in particular that the capacity region when all users have the same peak power constraint is given as the closed convex hull of the union of aspiration sets of certain games, just as in the case of the DM-MAC. As in that case, one may check that the capacity region is in fact the union of aspiration sets of a class of concave games, and in particular, as shown in [32], the maximum throughput that one may hope for is achievable.
Of course, there is much more to the well-developed theory of multiple access channels than the memoryless scenarios (discrete, Gaussian and Poisson) discussed above. For instance, there is much recent work on multiuser channels with memory and also with feedback (see, e.g., Tatikonda [33] for a deep treatment of such problems at the intersection of communication and control). We do not discuss these works further, except to make the observation that things can change considerably in these more general scenarios. Indeed, it is quite conceivable that the appropriate games for these scenarios are not convex or concave, and it is even conceivable that such games may not be balanced, which may mean that there are unexpected limitations to achieving the sum rate or sum capacity that one may hope for at first sight.
5. A Distributed Estimation Game
In the nascent theory of distributed estimation using sensor networks, one wishes to characterize the fundamental limits of performing statistical tasks such as parameter estimation using a sensor network and apply such characterizations to problems of cost or resource allocation. We discuss one such question for a toy model for distributed estimation introduced by Madiman et al. [34]. By ignoring communication, computation, and other constraints, this model allows one to study the central question of fundamental statistical limits without obfuscation.
The model we consider is as follows. The goal is to estimate a parameter  , which is some unknown real number. Consider a class of sensors, all of which have estimating
, which is some unknown real number. Consider a class of sensors, all of which have estimating  as their goal. However, the sensors cannot measure
as their goal. However, the sensors cannot measure  directly; they are immersed in a field of sources (that do not depend on
directly; they are immersed in a field of sources (that do not depend on  and may be considered as producers of noise for the purposes of estimating
and may be considered as producers of noise for the purposes of estimating  ). More specifically, suppose there are
). More specifically, suppose there are  sources, with each source producing a data sample of size
sources, with each source producing a data sample of size  according to some known probability distribution. Let us say that source
according to some known probability distribution. Let us say that source  generates
generates  . The class of sensors available corresponds to a class
. The class of sensors available corresponds to a class  of subsets of
of subsets of  , which indexes the set of sources. Owing to the geographical placement of the sensors or for other reasons, each sensor only sees certain aggregate data; indeed, the sensor corresponding to a subset
, which indexes the set of sources. Owing to the geographical placement of the sensors or for other reasons, each sensor only sees certain aggregate data; indeed, the sensor corresponding to a subset  , known as the
, known as the  -sensor, only sees at any given time the sum of
-sensor, only sees at any given time the sum of  and the data coming from the sources in the set
and the data coming from the sources in the set  . In other words, the
. In other words, the  -sensor has access to the observations
-sensor has access to the observations  , where
, where

Clearly,  shows up as a common location parameter for the observations seen by any sensor.
shows up as a common location parameter for the observations seen by any sensor.
From the observations  that are available to it, the
that are available to it, the  -sensor constructs an estimator
-sensor constructs an estimator  of the unknown parameter
of the unknown parameter  . The goodness of an estimator is measured by comparing to the "best possible estimator in the worst case", that is, by comparing the risk of the given estimator with the minimax risk. If the risk is measured in terms of mean squared error, then the minimax risk achievable by the
. The goodness of an estimator is measured by comparing to the "best possible estimator in the worst case", that is, by comparing the risk of the given estimator with the minimax risk. If the risk is measured in terms of mean squared error, then the minimax risk achievable by the  -sensor is
-sensor is

(For location parameters, Girshick and Savage [35] showed that there exists an estimator that achieves this minimax risk.)
The cost measure of interest in this scenario is error variance. Suppose we can give variance permissions for each source, that is, the
for each source, that is, the  -sensor is only allowed an unbiased estimator with variance not more than
-sensor is only allowed an unbiased estimator with variance not more than  , or more generally, an estimator with mean squared risk not more than this number. For the variance permission vector
, or more generally, an estimator with mean squared risk not more than this number. For the variance permission vector  to be feasible with respect to an arbitrary sensor configuration (i.e., for there to exist an estimator for the
to be feasible with respect to an arbitrary sensor configuration (i.e., for there to exist an estimator for the  -user with worst-case risk bounded by
-user with worst-case risk bounded by  , for every
, for every  ), we need that
), we need that

for each  . Thus, we have the following fact.
. Thus, we have the following fact.
Fact 11.
The set of feasible variance permission vectors is the aspiration set of the cost allocation game

which we call the distributed estimation game.
The natural question is the following. Is it possible to allot variance permissions in such a way that there is no wasted total variance, that is,  , and the allotment is feasible for arbitrary sensor configurations? The affirmative answer is the content of the following result.
, and the allotment is feasible for arbitrary sensor configurations? The affirmative answer is the content of the following result.
Translation 9.
Assuming that all sources have finite variance, the distributed estimation game is balanced. Consequently, there exists a feasible variance allotment  to sources in
to sources in  such that the
such that the  -sensor cannot waste any of the variance allotted to it.
-sensor cannot waste any of the variance allotted to it.
Proof.
The main result of Madiman et al. [34] is the following inequality relating the minimax risks achievable by the  -users from the class
-users from the class  to the minimax risk achievable by the
to the minimax risk achievable by the  -user, that is, one who only sees observations of
-user, that is, one who only sees observations of  corrupted by all the sources. Under the finite variance assumption, for any sample size
corrupted by all the sources. Under the finite variance assumption, for any sample size  ,
,

holds for any fractional partition  using any collection of subsets
using any collection of subsets  . In other words, the game
. In other words, the game  is balanced. Fact 1 now implies that the core is nonempty, that is, a total variance as low as
is balanced. Fact 1 now implies that the core is nonempty, that is, a total variance as low as  is achievable.
is achievable.
Translation 9 implies that the optimal sum of variance permissions that can be achieved in a distributed fashion using a sensor network is the same as the best variance that can be achieved using a single centralized sensor that sees all the sources.
Other interesting questions relating to sensor networks can be answered using the inequality (33). For instance, it suggests that using a sensor configuration corresponding to the class  of all singleton sets is better than using a sensor configuration corresponding to the class
of all singleton sets is better than using a sensor configuration corresponding to the class  of all sets of size 2. We refer the reader to [34] for details. An interesting open problem is the determination of whether this distributed estimation game has a large core.
of all sets of size 2. We refer the reader to [34] for details. An interesting open problem is the determination of whether this distributed estimation game has a large core.
6. An Entropy Power Game
The entropy power of a continuous random vector  is
is  , where
, where  denotes differential entropy. Entropy power plays a key role in several problems of multiuser information theory, and entropy power inequalities have been key to the determination of some capacity and rate regions. (Such uses of entropy power inequalities may be found, e.g., in Shannon [36], Bergmans [37], Ozarow [38], Costa [39], and Oohama [40].) Furthermore, rate regions for several multiuser problems, as discussed already, involve subset sum constraints. Thus, it is conceivable that there exists an interpretation of the discussion below in terms of a multiuser communication problem, but we do not know of one.
denotes differential entropy. Entropy power plays a key role in several problems of multiuser information theory, and entropy power inequalities have been key to the determination of some capacity and rate regions. (Such uses of entropy power inequalities may be found, e.g., in Shannon [36], Bergmans [37], Ozarow [38], Costa [39], and Oohama [40].) Furthermore, rate regions for several multiuser problems, as discussed already, involve subset sum constraints. Thus, it is conceivable that there exists an interpretation of the discussion below in terms of a multiuser communication problem, but we do not know of one.
We make the following conjecture.
Conjecture 1.
Let  be independent
be independent  -valued random vectors with densities and finite covariance matrices. Suppose the region of interest is the set of points
-valued random vectors with densities and finite covariance matrices. Suppose the region of interest is the set of points  satisfying
satisfying

for each  . Then, there exists a point in this region such that the total sum
. Then, there exists a point in this region such that the total sum  .
.
By Fact 1, the following conjecture, implicitly proposed by Madiman and Barron [41], is equivalent.
Conjecture 2.
Let  be independent
be independent  -valued random vectors with densities and finite covariance matrices. For any collection
-valued random vectors with densities and finite covariance matrices. For any collection  of subsets of
of subsets of  , let
, let  be a fractional partition. Then,
be a fractional partition. Then,

Equality holds if and only if all the  are normal with proportional covariance matrices.
are normal with proportional covariance matrices.
Note that Conjecture 2 simply states that the "entropy power game" defined by  is balanced. Define the maximum degree in
is balanced. Define the maximum degree in  as
as  , where the degree
, where the degree of
of  in
in  is the number of sets in
is the number of sets in  that contain
that contain  . Madiman and Barron [41] showed that Conjecture 2 is true if
. Madiman and Barron [41] showed that Conjecture 2 is true if  is replaced by
is replaced by  , where
, where  is the maximum degree in
is the maximum degree in  . When every index
. When every index  has the same degree,
has the same degree,  is indeed a fractional partition.
is indeed a fractional partition.
The equivalence of Conjectures 1 and 2 serves to underscore the fact that the balancedness inequality of Conjecture 2 may be regarded as a more fundamental property (if true) than the generalized entropy power inequalities in [41] and is therefore worthy of attention. The interested reader may also wish to consult [42], where we give some further evidence towards its validity. Of course, if the entropy power game above turns out to be balanced, a natural next question would be whether it is exact or even convex.
While on the topic of games involving the entropy of sums, it is worth mentioning that much more is known about the game with value function:

where  denotes discrete entropy, and
denotes discrete entropy, and  are independent discrete random variables. Indeed, as shown by the author in [42], this game is concave, and in particular, has a nonempty core which is the convex hull of its marginal vectors.
are independent discrete random variables. Indeed, as shown by the author in [42], this game is concave, and in particular, has a nonempty core which is the convex hull of its marginal vectors.
For independent continuous random vectors, the set function

where  denotes differential entropy, is submodular as in the discrete case. However, this set function does not define a game; indeed, the appropriate convention for
denotes differential entropy, is submodular as in the discrete case. However, this set function does not define a game; indeed, the appropriate convention for  is that
is that  , since the null set corresponds to looking at the differential entropy of a constant (say, zero), which is
, since the null set corresponds to looking at the differential entropy of a constant (say, zero), which is  . Because of the fact that the set function
. Because of the fact that the set function  is not real-valued, the submodularity of
is not real-valued, the submodularity of  does not imply that it is even subadditive (and thus
does not imply that it is even subadditive (and thus  certainly does not satisfy the inequalities that define balancedness). On the other hand, if
certainly does not satisfy the inequalities that define balancedness). On the other hand, if  is a continuous random vector independent of
is a continuous random vector independent of  , and with differentiall entropy
, and with differentiall entropy  , then the modified set function
, then the modified set function

is indeed the value function of a balanced cooperative game; see [42] for details and further discussion.
7. Games in Composite Hypothesis Testing
Interestingly, similar notions also come up in the study of composite hypothesis testing but in the setting of a cooperative resource allocation game for infinitely many users. Let  be a Polish space with its Borel
be a Polish space with its Borel  -lgebra, and let
-lgebra, and let  be the space of probability measures on
be the space of probability measures on  . We may think of
. We may think of  as a set of infinitely many "microscopic players", namely
as a set of infinitely many "microscopic players", namely  . The allowed coalitions of microscopic users are the Borel sets. For our purposes, we specify an infinite cooperative game using a value function
. The allowed coalitions of microscopic users are the Borel sets. For our purposes, we specify an infinite cooperative game using a value function  that satisfies the following conditions:
that satisfies the following conditions:
-
(1)
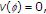 and
and 
-
(2)
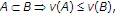
-
(3)
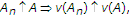
-
(4)
for closed sets
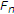 with
with 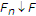 ,
,  .
.
The continuity conditions are necessary regularity conditions in the context of infinitely many players. The normalization  (which is also sometimes imposed in the study of finite games) is also useful. In the mathematics literature, a value function satisfying the itemized conditions is called a capacity , while in the economics literature, it is a (0,1)-normalized nonatomic game (usually additional conditions are imposed for the latter). There are many subtle analytical issues that emerge in the study of capacities and nonatomic games. We avoid these and simply mention some infinite analogues of already stated facts.
(which is also sometimes imposed in the study of finite games) is also useful. In the mathematics literature, a value function satisfying the itemized conditions is called a capacity , while in the economics literature, it is a (0,1)-normalized nonatomic game (usually additional conditions are imposed for the latter). There are many subtle analytical issues that emerge in the study of capacities and nonatomic games. We avoid these and simply mention some infinite analogues of already stated facts.
For any capacity  , one may define the family of probability measures
, one may define the family of probability measures

The set  may be thought of as the core of the game
may be thought of as the core of the game  . Indeed, the additivity of a measure on disjoint sets is the continuous formulation of the transferable utility assumption that earlier caused us to consider sums of resource allocations, while the restriction to probability measures ensures efficiency, that is, the maximum possible allocation for the full set.
. Indeed, the additivity of a measure on disjoint sets is the continuous formulation of the transferable utility assumption that earlier caused us to consider sums of resource allocations, while the restriction to probability measures ensures efficiency, that is, the maximum possible allocation for the full set.
Let  be a family of probability measures on
be a family of probability measures on  . The set function
. The set function

is called the upper envelope of  , and it is a capacity if
, and it is a capacity if  is weakly compact. Note that such upper envelopes are just the analogue of the XOS valuations defined in Section 2 for the finite setting. By an extension of Fact 6 to infinite games, one can deduce that the core
is weakly compact. Note that such upper envelopes are just the analogue of the XOS valuations defined in Section 2 for the finite setting. By an extension of Fact 6 to infinite games, one can deduce that the core  is nonempty when
is nonempty when  is the upper envelope game for a weakly compact family
is the upper envelope game for a weakly compact family  of probability measures.
of probability measures.
We say that the infinite game  is concave if, for all measurable sets
is concave if, for all measurable sets  and
and  ,
,

In the mathematics literature, the value function of a concave infinite game is often called a 2-alternating capacity, following Choquet's seminal work [43]. When  defines a concave infinite game,
defines a concave infinite game,  is nonempty; this is an analog of Fact 2. Furthermore, by the analog of Fact 5,
is nonempty; this is an analog of Fact 2. Furthermore, by the analog of Fact 5,  is an exact game since it is concave, and as in the remarks after Fact 6, it follows that
is an exact game since it is concave, and as in the remarks after Fact 6, it follows that  is just the upper envelope of
is just the upper envelope of  .
.
Concave infinite games  are not just of abstract interest; the families of probability measures
are not just of abstract interest; the families of probability measures  that are their cores include important classes of families such as total variation neighborhoods and contamination neighborhoods, as discussed in the references cited below.
that are their cores include important classes of families such as total variation neighborhoods and contamination neighborhoods, as discussed in the references cited below.
A famous, classical result of Huber and Strassen [44] can be stated in the language of infinite cooperative games. Suppose one wishes to test between the composite hypotheses  and
and  , where
, where  and
and  define infinite games. The criterion that one wishes to minimize is the decay rate of the probability of one type of error in the worst case (i.e., for the worst pair of sources in the two classes), given that the error probability of the other kind is kept below some small constant; in other words, one is using the minimax criterion in the Neyman-Pearson framework. Note that the selection of a critical region for testing is, in the game language, the selection of a coalition. In the setting of simple hypotheses, the optimal coalition is obtained as the set for which the Radon-Nikodym derivative between the two probability measures corresponding to the two hypotheses exceeds a threshold. Although there is no obvious notion of Radon-Nikodym derivative between two composite hypotheses, [44] demonstrates that a likelihood ratio test continues to be optimal for testing between composite hypotheses under some conditions on the games
define infinite games. The criterion that one wishes to minimize is the decay rate of the probability of one type of error in the worst case (i.e., for the worst pair of sources in the two classes), given that the error probability of the other kind is kept below some small constant; in other words, one is using the minimax criterion in the Neyman-Pearson framework. Note that the selection of a critical region for testing is, in the game language, the selection of a coalition. In the setting of simple hypotheses, the optimal coalition is obtained as the set for which the Radon-Nikodym derivative between the two probability measures corresponding to the two hypotheses exceeds a threshold. Although there is no obvious notion of Radon-Nikodym derivative between two composite hypotheses, [44] demonstrates that a likelihood ratio test continues to be optimal for testing between composite hypotheses under some conditions on the games  and
and  .
.
Translation 10.
For concave infinite games  and
and  , consider the composite hypotheses
, consider the composite hypotheses  and
and  that are their cores. Then, a minimax Neyman-Pearson test between the
that are their cores. Then, a minimax Neyman-Pearson test between the  and
and  can be constructed as the likelihood ratio test between an element of
can be constructed as the likelihood ratio test between an element of  and one of
and one of  ; in this case, the representative elements minimize the Kullback divergence between the two families.
; in this case, the representative elements minimize the Kullback divergence between the two families.
In a certain sense, a converse statement can also be shown to hold. We refer to Huber and Strassen [44] for proofs and to Veeravalli et al. [45] for context, further results, and applications. Related results for minimax linear smoothing and rate distortion theory on classes of sources were given by Poor [46, 47] and to channel coding with model uncertainty were given by Geraniotis [48, 49].
8. Discussion
The general approach to using cooperative game theory to understand rate or capacity regions involves the following steps. (i) Formulate the region of interest as the aspiration set of a cooperative game. This is frequently the right kind of formulation for multiuser problems. (ii) Study the properties of the value function of the game, starting with checking if it is balanced, if it is exact, if it has a large core, and ultimately by checking convexity or concavity. (iii) Interpret the properties of the game that follow from the discovered properties of the value function. For instance, balancedness implies a nonempty core, while convexity implies a host of results, including nice properties of the Shapley value. These are structural results, and their game-theoretic interpretation has the potential to provide some additional intuition.
There are numerous other papers which make use of cooperative game theory in communications, although with different emphases and applications in mind. See, for example, van den Nouweland et al. [50], Han and Poor [51], Jiang and Baras [52], and Yaïche et al. [53]. However, we have pointed out a very fundamental connection between the two fields—arising from the fact that rate and capacity regions are often closely related to the aspiration sets of cooperative games. In several exemplary scenarios, both classical and relatively new, we have reinterpreted known results in terms of game-theoretic intuition and also pointed out a number of open problems. We expect that the cooperative game theoretic point of view will find utility in other scenarios in network information theory, distributed inference, and robust statistics.
References
La RJ, Anantharam V: A game-theoretic look at the Gaussian multiaccess channel. DIMACS Series in Discrete Mathematics and Theoretical Computer Science 2002.
Owen G: Game Theory. 3rd edition. Academic Press, Boston, Mass, USA; 2001.
Bondareva ON: Some applications of the methods of linear programming to the theory of cooperative games. Problemy Kibernetiki 1963, (Russian), 10: 119-139.
Shapley LS: On balanced sets and cores. Naval Research Logistics Quarterly 1967, 14(4):453-560. 10.1002/nav.3800140404
Shapley LS: Cores of convex games. International Journal of Game Theory 1971, 1(1):11-26. 10.1007/BF01753431
Madiman M, Tetali P: Information inequalities for joint distributions, with interpretations and applications. Tentatively accepted to IEEE Transactions on Information Theory, 2008
Maschler M, Peleg B, Shapley LS: The kernel and bargaining set for convex games. International Journal of Game Theory 1972, 2: 73-93.
Edmonds J: Submodular functions, matroids and certain polyhedra. In Proceedings of the Calgary International Conference on Combinatorial Structures and Their Applications, June 1969, Calgary, Canada. Gordon and Breach;
Weber RJ: Probabilistic values for games. In The Shapley Value. Cambridge University Press, Cambridge, UK; 1988:101-119.
Ichiishi T: Super-modularity: applications to convex games and to the greedy algorithm for LP . Journal of Economic Theory 1981, 25(2):283-286. 10.1016/0022-0531(81)90007-7
Shapley LS: A value for n-person games. Annals of Mathematics Study 1953, 28: 307-317.
Sharkey WW: Cooperative games with large cores. International Journal of Game Theory 1982, 11(3-4):175-182. 10.1007/BF01755727
Biswas AK, Parthasarathy T, Potters JAM, Voorneveld M: Large cores and exactness. Games and Economic Behavior 1999, 28(1):1-12. 10.1006/game.1998.0686
Schmeidler D: Cores of exact games, I. Journal of Mathematical Analysis and Applications 1972, 40(1):214-225. 10.1016/0022-247X(72)90045-5
Rabie MA: A note on the exact games. International Journal of Game Theory 1981, 10(3-4):131-132. 10.1007/BF01755958
Lehmann B, Lehmann D, Nisan N: Combinatorial auctions with decreasing marginal utilities. Proceedings of the 3rd ACM Conference on Electronic Commerce (EC '01), October 2001, Tampa, Fla, USA 18-28.
Feige U: On maximizing welfare when utility functions are subadditive. Proceedings of the 38th Annual ACM Symposium on Theory of Computing (STOC '06), May 2006, Seattle, Wash, USA 41-50.
Slepian D, Wolf JK: Noiseless coding of correlated information sources. IEEE Transactions on Information Theory 1973, 19(4):471-480. 10.1109/TIT.1973.1055037
Cover TM: A proof of the data compression theorem of Slepian and Wolf for ergodic sources. IEEE Transactions on Information Theory 1975, 21(2):226-228. 10.1109/TIT.1975.1055356
Fujishige S: Polymatroidal dependence structure of a set of random variables. Information and Control 1978, 39(1):55-72. 10.1016/S0019-9958(78)91063-X
Coleman TP, Lee AH, Médard M, Effros M: Low-complexity approaches to Slepian-Wolf near-lossless distributed data compression. IEEE Transactions on Information Theory 2006, 52(8):3546-3561.
Cristescu R, Beferull-Lozano B, Vetterli M: Networked Slepian-Wolf: theory, algorithms, and scaling laws. IEEE Transactions on Information Theory 2005, 51(12):4057-4073. 10.1109/TIT.2005.858980
Ramamoorthy A: Minimum cost distributed source coding over a network. Proceedings of IEEE International Symposium on Information Theory (ISIT '07), June 2007, Nice, France
Rimoldi B, Urbanke R: A rate-splitting approach to the Gaussian multiple-access channel. IEEE Transactions on Information Theory 1996, 42(2):364-375. 10.1109/18.485709
Ahlswede R: Multi-way communication channels. In Proceedings of the 2nd International Symposium on Information Theory (ISIT '71), September 1971, Tsahkadsor, Armenia. Hungarian Academy of Sciences;
Liao H: A coding theorem for multiple access communication. Proceedings of IEEE International Symposium on Information Theory (ISIT '72), January 1972, Asilomar, Calif, USA
Slepian D, Wolf JK: A coding theorem for multiple access channels with correlated sources. Bell System Technical Journal 1973, 52(7):1037-1076.
Han TS: The capacity region of general multiple-access channel with certain correlated sources. Information and Control 1979, 40(1):37-60. 10.1016/S0019-9958(79)90337-1
Cover TM, Thomas JA: Elements of Information Theory. John Wiley & Sons, New York, NY, USA; 1991.
Yeh EM: Multiaccess and fading in communication networks, Ph.D. thesis. Massachusetts Institute of Technology, Cambridge, Mass, USA; 2001.
Tse DNC, Hanly SV: Multiaccess fading channels. I. Polymatroid structure, optimal resource allocation and throughput capacities. IEEE Transactions on Information Theory 1998, 44(7):2796-2815. 10.1109/18.737513
Lapidoth A, Shamai S: The Poisson multiple-access channel. IEEE Transactions on Information Theory 1998, 44(2):488-501. 10.1109/18.661499
Tatikonda SC: Control under communication constraints, Ph.D. thesis. Massachusetts Institute of Technology, Cambridge, Mass, USA; 2000.
Madiman M, Barron AR, Kagan AM, Yu T: Minimax risks for distributed estimation of the background in a field of noise sources. Proceedings of the 2nd International Workshop on Information Theory for Sensor Networks (WITS '08), June 2008, Santorini Island, Greece preprint
Girshick MA, Savage LJ: Bayes and minimax estimates for quadratic loss functions. In Proceedings of the 2nd Berkeley Symposium on Mathematical Statistics and Probability, July-August 1951, Berkeley, Calif, USA. University of California Press; 53-73.
Shannon CE: A mathematical theory of communication. Bell System Technical Journal 1948, 27: 379-423.
Bergmans P: A simple converse for broadcast channels with additive white Gaussian noise. IEEE Transactions on Information Theory 1974, 20(2):279-280. 10.1109/TIT.1974.1055184
Ozarow L: On a source-coding problem with two channels and three receivers. Bell System Technical Journal 1980, 59(10):1909-1921.
Costa M: On the Gaussian interference channel. IEEE Transactions on Information Theory 1985, 31(5):607-615. 10.1109/TIT.1985.1057085
Oohama Y: The rate-distortion function for the quadratic Gaussian CEO problem. IEEE Transactions on Information Theory 1998, 44(3):1057-1070. 10.1109/18.669162
Madiman M, Barron A: Generalized entropy power inequalities and monotonicity properties of information. IEEE Transactions on Information Theory 2007, 53(7):2317-2329.
Madiman M: On the entropy of sums. Proceedings of IEEE Information Theory Workshop (ITW '08), May 2008, Porto, Portugal
Choquet G: Theory of capacities. Annales de L'institut Fourier 1954, 5: 131-295.
Huber PJ, Strassen V: Minimax tests and the Neyman-Pearson lemma for capacities. Annals of Statistics 1973, 1(2):251-263. 10.1214/aos/1176342363
Veeravalli VV, Basar T, Poor HV: Minimax robust decentralized detection. IEEE Transactions on Information Theory 1994, 40(1):35-40. 10.1109/18.272453
Poor HV: The rate-distortion function on classes of sources determined by spectral capacities. IEEE Transactions on Information Theory 1982, 28(1):19-26. 10.1109/TIT.1982.1056450
Poor HV: Minimax linear smoothing for capacities. Annals of Probability 1982, 10(2):504-507. 10.1214/aop/1176993874
Geraniotis E: Minimax robust coding for channels with uncertainty statistics. IEEE Transactions on Information Theory 1985, 31(6):802-811. 10.1109/TIT.1985.1057111
Geraniotis E: Robust coding for multiple-access channels. IEEE Transactions on Information Theory 1986, 32(4):550-560. 10.1109/TIT.1986.1057196
van den Nouweland A, Borm P, van Golstein Brouwers W, Groot Bruinderink R, Tijs S: A game theoretic approach to problems in telecommunication. Management Science 1996, 42(2):294-303. 10.1287/mnsc.42.2.294
Han Z, Poor HV: Coalition games with cooperative transmission: a cure for the curse of boundary nodes in selfish packet-forwarding wireless networks. Proceedings of the 5th International Symposium on Modeling and Optimization in Mobile, Ad Hoc,and Wireless Networks (WiOpt '07), April 2007, Limassol, Cyprus
Jiang T, Baras JS: Fundamental tradeoffs and constrained coalitional games in autonomic wireless networks. Proceedings of the 5th International Symposium on Modeling and Optimization in Mobile, Ad Hoc,and Wireless Networks (WiOpt '07), April 2007, Limassol, Cyprus
Yaïche H, Mazumdar RR, Rosenberg C: A game theoretic framework for bandwidth allocation and pricing in broadband networks. IEEE/ACM Transactions on Networking 2000, 8(5):667-678. 10.1109/90.879352
Acknowledgments
I am indebted to Rajesh Sundaresan for a detailed discussion that clarified my understanding of some of the literature, and the identification of an error in the first version of this paper. I am grateful to Sekhar Tatikonda and Edmund Yeh for useful conversations and help with references, and to A. R. Barron, A. M. Kagan, P. Tetali, and T. Yu for being collaborators on related work. Part of this work was done while I was a Visiting Fellow in the School of Technology and Computer Science at the Tata Institute of Fundamental Research, Mumbai, India, and I thank Vivek Borkar in particular for providing a stimulating environment.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Madiman, M. Cores of Cooperative Games in Information Theory. J Wireless Com Network 2008, 318704 (2008). https://doi.org/10.1155/2008/318704
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2008/318704
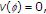 and
and 
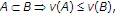
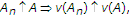
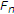 with
with 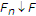 ,
,  .
.