- Research Article
- Open access
- Published:
A Low-Complexity UEP Methodology Demonstrated on a Turbo-Encoded Wavelet Image Satellite Downlink
EURASIP Journal on Wireless Communications and Networking volume 2008, Article number: 342415 (2007)
Abstract
Realizing high-quality digital image transmission via a satellite link, while optimizing resource distribution and minimizing battery consumption, is a challenging task. This paper describes a methodology to optimize a turbo-encoded wavelet-based satellite downlink progressive image transmission system with unequal error protection (UEP) techniques. To achieve that goal, we instantiate a generic UEP methodology onto the system, and demonstrate that the proposed solution has little impact on the average performance, while greatly reducing the run-time complexity. Based on a simple design-time distortion model and a low-complexity run-time algorithm, the provided solution can dynamically tune the system's configuration to any bitrate constraint or channel condition. The resulting system outperforms in terms of peak signal-to-noise ratio (PSNR), a state-of-the-art, fine-tuned equal error protection (EEP) solution by as much as 2 dB.
1. Introduction
This paper focuses on an existing satellite transmission system based on a state-of-the-art joint source-channel coding solution, transmitting images from an orbital space module to an earth ground station through a classical DVB-S2 (digital video broadcast for satellite) channel. In this system, the FlexWave-II core [1–4] is the wavelet-based image coder providing embedded scalability and low computational complexity. In addition, the T@mpo [5, 6] provides an efficient low-latency low-power turbo coder enabling close-to-capacity performance.
Our purpose is to jointly optimize the source and channel cores to offer a reliable delivery of high-quality digital images. In order to maximize the end-user quality, the system should be flexible and able to dynamically select an optimal protection scheme, while meeting the bandwidth constraint and adapting to the varying channel conditions. Source scalability induces a sequential dependency and a natural unequal error sensitivity among the compressed source symbols. This phenomenon naturally calls for an unequal error protection (UEP) scheme allowing a gradual protection leveling as we move from important to unimportant symbols. UEP [7–12] improves the system by protecting more the more important bits, and protecting less the less important bits, thus improving the average performance of the system with the same amount of resources.
Impairments occurring on transmission channels usually results in data erasure or data corruption. Corruption means that data may be received with errors, while erasure means that data is not received at all. A system transmitting data directly on the channel would likely undergo corruption. More complex system including an IP stack would internally handle the detection of errors, resulting in data erasure.
For erasure channels, techniques like priority encoding transmission (PET) [13] are generally used. The PET framework allows for an optimal distribution of the transmission bit budget  . Initially, many solutions were initially developed, based on dynamic programming (DP) algorithms [14–17]. Recent solutions using an initial rate-optimal optimization followed by a fast local search distortion-optimal or Lagrangian techniques [18–21] were developed to bring down the complexity to a linear
. Initially, many solutions were initially developed, based on dynamic programming (DP) algorithms [14–17]. Recent solutions using an initial rate-optimal optimization followed by a fast local search distortion-optimal or Lagrangian techniques [18–21] were developed to bring down the complexity to a linear  order.
order.
However, corruption channels require an error-detection step before the source decoder, in order to prevent error propagation. Classically, the source decoding is stopped after the first detected errors, resulting in some parts of the transmitted content to be considered undecodable. Applied to the problem of joint source-channel optimization, various techniques like concatenated coding [22, 23], dynamic programming [23–25], exhaustive search [22], and gradient-based optimization [26, 27] are employed to solve different variants of the problem.
We note that all aforementioned techniques suppose that the source coder is not able to handle bitstream corruption, and somehow eliminate residual errors in order to feed the source decoding stage with uncorrupted data by either inserting an error detection stage, or by using packet-based transmission where the network itself suppresses residual errors by discarding data packets. This is suboptimal as recent coders have the possibility to efficiently use part of the data that was discarded. More specifically, by letting corrupted data enter the decoding stage, and building specific distortion models that evaluate the impact of corruption, we can optimize the system and exploit previously unused data.
As an example, we can see in Figure 1 the performance of FlexWave-II when the data is either truncated or corrupted at different locations in the bitstream. The  -axis represents the bitstream location on a bit per pixel scale, while the
-axis represents the bitstream location on a bit per pixel scale, while the  -axis represents the PSNR quality obtained after decoding. The plain curve shows the PSNR quality when the bitstream is truncated. Each cross shows the PSNR quality when a single bit error is inserted, leaving the rest of the bitstream untouched. We can see that the distortion resulting from a bit error at any location in the bitstream is always smaller than the distortion resulting from a truncation at the same location. This means that the source decoder can efficiently use the data beyond the corruption point to reduce the distortion.
-axis represents the PSNR quality obtained after decoding. The plain curve shows the PSNR quality when the bitstream is truncated. Each cross shows the PSNR quality when a single bit error is inserted, leaving the rest of the bitstream untouched. We can see that the distortion resulting from a bit error at any location in the bitstream is always smaller than the distortion resulting from a truncation at the same location. This means that the source decoder can efficiently use the data beyond the corruption point to reduce the distortion.
Our UEP methodology [28] proposes a novel, generic, and pragmatic approach to solve the source-channel allocation problem. It is based on a joint source-channel model that is steered at runtime by a low-complexity algorithm. This joint model is merging different models, respectively, characterizing the different components of the system (source, source coder, channel coder, and channel), and is enabled by a set of well-defined simplifying assumptions. These assumptions greatly reduce the complexity of the model. This joint source-channel model is actually very flexible, and is able to dynamically provide the rate-distortion characteristics of the system depending on parameters such as the global bit budget or the channel conditions. At runtime, these rate-distortion characteristics are exploited by a low-complexity algorithm that optimizes the code rate allocation. This paper focuses on the instantiation of our solution for the satellite communication system described before.
Because of complexity constraints, the source model is source-independent and only represents a statistical expectation of the rate-distortion behavior over a training set of satellite images. Hence, it is a priori suboptimal. Previous work [29] has demonstrated that the source-independent model had no significant impact on the end-to-end rate-distortion performance of our methodology.
In this paper, the UEP controller performance will be compared with a classical equal error protection (EEP) solution that simply utilizes the incoming order of the FlexWave-II bitstream as prioritarization information. We will prove that the proposed UEP solution can dynamically adapt to varying transmission conditions, and outperforms the EEP scheme in the working range of channel conditions.
Section 2 gives an overview of our UEP methodology. Section 3 describes the general setup of the satellite communication system and derives the characteristics of the rate-distortion model. Section 4 shows the simulation results. Section 5 compares the simulated results to the performance of the hardware implementation. Section 6 concludes the paper.
2. UEP Methodology
The proposed generic UEP methodology can be incorporated in any system offering UEP capabilities. In previous work [28], this methodology has been successfully applied to a JPEG2000-based system. The goal of this paper is to apply the same methodology to a satellite compression system, and to demonstrate its performance.
Section 2.1 recalls the general problem statement. Section 2.2 deals with the joint modeling of the channel and source components. Sections 2.3 and 2.4, respectively, explain how the separate models are combined at run-time and how the resulting rate-distortion characteristics are exploited to derive the final protection allocation.
2.1. Problem Statement
We consider the transmission of a scalable bitstream embedding  substreams. We have
substreams. We have  discrete protection levels, including the possibility of transmitting a substream without protection or not transmitting it at all. Protection levels are indexed from
discrete protection levels, including the possibility of transmitting a substream without protection or not transmitting it at all. Protection levels are indexed from  to
to  , where
, where  corresponds to the untransmitted case (cut substream), and
corresponds to the untransmitted case (cut substream), and  corresponds to the unprotected case (uncoded substream). A global bit budget
corresponds to the unprotected case (uncoded substream). A global bit budget  is available to transmit the data and is shared among these substreams. Our objective is to maximize the expected quality of the received data, or to minimize the expected distortion
is available to transmit the data and is shared among these substreams. Our objective is to maximize the expected quality of the received data, or to minimize the expected distortion  . Concerning the protection allocation, three important remarks have to be made.
. Concerning the protection allocation, three important remarks have to be made.
The first remark is that the system allows residual bit errors in the transmitted substreams. This means that all substreams are effectively used by the source decoder, with a possibility to quality degradation when the source is reconstructed. The second remark is that each substream is considered as an independently decodable unit. This means that the amount of protection allocated to each substream (related to the amount of residual errors) can be independently and arbitrarily chosen. In other words, we are not constraining the resource distribution to be monotonically decreasing, as would be done in the case of a progressive bitstream [22, 30].
It could be argued that even though a scalable bitstream is not necessarily progressive, decoding dependencies may subsist in the bitstream. Actually, this decoding dependency is the cause of the unequal error sensitivity observed in a scalable bitstream. Additionally, the proposed solution measures this error sensitivity through a model and unequally distributes the protection accordingly. Therefore, the joint source-channel model is a central tool that allows the algorithm to gradually match the protection level to the error sensitivity and thus taking into account the possible decoding dependencies.
We assume the total expected image distortion  to be the sum of the expected distortion for each image substream [31]. This is expressed by the following equation:
to be the sum of the expected distortion for each image substream [31]. This is expressed by the following equation:

where  represents the
represents the  -tuple
-tuple  of protection levels applied, respectively, to the
of protection levels applied, respectively, to the  substreams; and
substreams; and  is the distortion contribution of substream
is the distortion contribution of substream  associated with protection level
associated with protection level  . Given a protection set
. Given a protection set  we compute the global rate required:
we compute the global rate required:

where  is the length of substream
is the length of substream  and
and  is the channel coding rate for the protection
is the channel coding rate for the protection  . Smaller coding rates give better protection levels and increase the corresponding rate expense. Protection
. Smaller coding rates give better protection levels and increase the corresponding rate expense. Protection  incurs no rate expense since the corresponding substream data will not be transmitted. The problem is solved by finding the optimal protection set
incurs no rate expense since the corresponding substream data will not be transmitted. The problem is solved by finding the optimal protection set  that minimizes the global distortion
that minimizes the global distortion  , while meeting the global rate constraint
, while meeting the global rate constraint  :
:

This additive distortion model allows for an independent optimization of the protection levels for each substream, and thus greatly simplifies the task of the runtime optimization. In the following, we give more details about the distortion model.
2.2. Joint Source-Channel Distortion Model
The joint source-channel distortion model is actually a combination of two simpler models which individually estimate the characteristics of the source coder and the different protection modes of the channel coder. This section describes the computation of the individual source and channel models, and explains how they are combined into the joint source-channel model.
2.2.1. Source Model
The source model evaluates the distortion induced by cutting or corrupting individual substreams. This is done in two steps.
-
(i)
First, we compute the
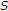 values
values 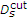 , which represent the MSE distortion resulting after cutting the substream
, which represent the MSE distortion resulting after cutting the substream  out of the bitstream while leaving other substreams untouched. It should be noted that cutting substream
out of the bitstream while leaving other substreams untouched. It should be noted that cutting substream  means that protection level
means that protection level 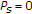 has been assigned to substream
has been assigned to substream  .
. -
(ii)Secondly,
we compute the
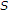 values
values 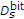 which estimate the average MSE distortion per erroneous bit in the substream
which estimate the average MSE distortion per erroneous bit in the substream  . This is obtained by inserting individual bit errors in the substream, while leaving remaining bits uncorrupted.
. This is obtained by inserting individual bit errors in the substream, while leaving remaining bits uncorrupted.
2.2.2. Channel Model
The channel coder offers  distinct protection levels. Depending on the channel quality
distinct protection levels. Depending on the channel quality  and the protection level
and the protection level  , the channel model provides an average estimation of the bit error rate (BER), which we will denote
, the channel model provides an average estimation of the bit error rate (BER), which we will denote  .
.
2.2.3. Joint Source-Channel Model
Considering a fixed channel quality  , the joint source-channel model estimates the expected MSE distortion
, the joint source-channel model estimates the expected MSE distortion  inside substream, depending on the protection level
inside substream, depending on the protection level  . Since residual errors are considered independent, we can simply estimate the distortion
. Since residual errors are considered independent, we can simply estimate the distortion  in function of the estimated residual BER
in function of the estimated residual BER  . To obtain a usable model, we estimate the expected MSE distortion
. To obtain a usable model, we estimate the expected MSE distortion  on the range of possible BER values
on the range of possible BER values  between
between  and
and  . To achieve that, we simply measure
. To achieve that, we simply measure  on a discrete set of BER values, relying on a linear extrapolation for intermediate values.
on a discrete set of BER values, relying on a linear extrapolation for intermediate values.
It should be noted that when the residual BER within substream  is equal to
is equal to  , the average number of errors is equal to
, the average number of errors is equal to  , and the expected MSE distortion
, and the expected MSE distortion  is matching the average bit distortion
is matching the average bit distortion  . Eventually, we are able to estimate the expected distortion within substream
. Eventually, we are able to estimate the expected distortion within substream  , undergoing loss or corruption according to the following equations:
, undergoing loss or corruption according to the following equations:

2.3. Rate-Distortion Curves
Consider the transmission of a bitstream with protection  . Assuming the substream,
. Assuming the substream,  has its protection level upgraded from
has its protection level upgraded from  to
to  , we express the distortion reduction
, we express the distortion reduction  as
as

Hence, the distortion reduction has been evaluated as if the substream with protection  was cut from the bitstream and added again with protection
was cut from the bitstream and added again with protection  . Rewriting (5) for the case when the substream
. Rewriting (5) for the case when the substream  is simply added to the bitstream delivers
is simply added to the bitstream delivers

Furthermore, we define the importance value  as the ratio between the distortion decrease and the bitrate increase induced by upgrading the protection level of the substream
as the ratio between the distortion decrease and the bitrate increase induced by upgrading the protection level of the substream  from
from  to
to  :
:

Actually, the set of importance values  matches exactly the slope values of the rate-distortion curve for substream
matches exactly the slope values of the rate-distortion curve for substream  . We assume here that the obtained rate-distortion curve is convex. However, if this is not the case, we can prune out protection levels for a specific substream so that the
. We assume here that the obtained rate-distortion curve is convex. However, if this is not the case, we can prune out protection levels for a specific substream so that the  slope series is monotonically decreasing. At most,
slope series is monotonically decreasing. At most,  values must be computed for all possible protection levels
values must be computed for all possible protection levels  from
from  to
to  and for all substreams
and for all substreams  from
from  to
to  . It yields a maximum number of
. It yields a maximum number of  importance values.
importance values.
2.4. Proposed Runtime Algorithm
According to (7), we have at most  importance values
importance values  , with
, with  and
and  .
.  represents the relative importance or quality improvement that would be observed if the protection level of substream
represents the relative importance or quality improvement that would be observed if the protection level of substream  would be upgraded to
would be upgraded to  . This actually means that these importance values represent the slopes of the rate-distortion curves associated to each associated to the
. This actually means that these importance values represent the slopes of the rate-distortion curves associated to each associated to the  substreams.
substreams.
These  values are now sorted in decreasing order and the corresponding indices are arranged in two series
values are now sorted in decreasing order and the corresponding indices are arranged in two series  and
and  . The allocation is done with an iterative process over the
. The allocation is done with an iterative process over the  stages. At stage
stages. At stage  , all substreams are initialized to
, all substreams are initialized to  . At each stage
. At each stage  , the substream
, the substream  is upgraded to protection level
is upgraded to protection level  until we reach stage
until we reach stage  , where all substreams are maximally protected with protection level
, where all substreams are maximally protected with protection level  .
.
As an example, in Figure 2 we have  substreams,
substreams,  protection levels, and
protection levels, and  importance values. We see that the importance values are sorted in the following decreasing order:
importance values. We see that the importance values are sorted in the following decreasing order:  ,
,  ,
,  ,
,  ,
,  and
and  . Table 1 shows how the proposed UEP algorithm attributes the protection levels to the 2 substreams in a 6-stage allocation.
. Table 1 shows how the proposed UEP algorithm attributes the protection levels to the 2 substreams in a 6-stage allocation.
During the algorithm, we also form the series of protection set  and rate expense
and rate expense  .
.  is the protection set where all substreams are cut.
is the protection set where all substreams are cut.  is therefore equal to
is therefore equal to  since no substream is transmitted.
since no substream is transmitted.  is defined follows:
is defined follows:

where  is the protection level associated with substream
is the protection level associated with substream  at stage
at stage  . We derive
. We derive  from
from  by upgrading the protection level of substream
by upgrading the protection level of substream  to
to  . Therefore,
. Therefore,  is identical to
is identical to  except for its
except for its  th element, which is equal to
th element, which is equal to  . Accordingly, we derive
. Accordingly, we derive  from
from  by adding the extra rate incurred by protection
by adding the extra rate incurred by protection  on substream
on substream  . Using (2), we define the global rate
. Using (2), we define the global rate  :
:

We eventually obtain the rate sets  and the corresponding optimal protection sets
and the corresponding optimal protection sets  . Thanks to the reordering operation, the global optimization is achieved by selecting the highest
. Thanks to the reordering operation, the global optimization is achieved by selecting the highest  being smaller than the target rate
being smaller than the target rate  . After the global optimization step, the two series
. After the global optimization step, the two series  and
and  enable the system to reach an optimal protection set for any rate constraint. This means that our low-complexity algorithm is very dynamic and can adapt to any rate condition with a simple search, without loss of optimality in the specific case of convex rate-distortion characteristics.
enable the system to reach an optimal protection set for any rate constraint. This means that our low-complexity algorithm is very dynamic and can adapt to any rate condition with a simple search, without loss of optimality in the specific case of convex rate-distortion characteristics.
2.5. Complexity Evaluation
The computation of the importance values  in (7) requires
in (7) requires  multiplications and
multiplications and  additions, according to (7), and (4). The sorting costs an expected
additions, according to (7), and (4). The sorting costs an expected  comparisons. The
comparisons. The  series computation do not require any computation. According to (9), each
series computation do not require any computation. According to (9), each  computation needs
computation needs  multiplication and
multiplication and  additions for a total of
additions for a total of  multiplications and
multiplications and  additions. The selection of the optimal
additions. The selection of the optimal  is performed by a bisection search and requires an expected
is performed by a bisection search and requires an expected  comparisons in order to find the optimal
comparisons in order to find the optimal  . If we consider that the multiplication is the dominant term, the proposed algorithm has a complexity of order
. If we consider that the multiplication is the dominant term, the proposed algorithm has a complexity of order  , which is linear with respect to the number of substreams
, which is linear with respect to the number of substreams  and the number of protection levels
and the number of protection levels  . Given that the number of protection levels can be limited to
. Given that the number of protection levels can be limited to  , the proposed runtime algorithm has a very low complexity.
, the proposed runtime algorithm has a very low complexity.
3. System Setup
The transmission of the data from the satellite to the ground station is performed over a DVB-S2 channel. Basically, the FlexWave-II still image encoder produces a progressive bitstream by outputting a series of data substreams that holds a varying number of bytes. These substreams are forwarded to the T@mpo encoder that adds a certain number of parity symbols depending on the selected protection mode. The protected substreams are then sent directly on the transmission channel and received by the T@mpo decoder. The decoded substreams are then fed to the FlexWave-II decoder, which subsequently decodes the image.
3.1. Source
Since satellite imaging is targeted, it is therefore necessary to optimize the source model for this application. To this end, we chose the black and white version of the Toulouse image represented in Figure 3.
The main advantage of the methodology [28] is the separation of the design-time modeling phase and the runtime optimization phase. In the ideal case, the source model is perfectly matching the distortion characteristic of the transmitted image. However, this can only be obtained by computing the model at runtime, which is unpractical given the high complexity of the modeling process. A real-life transmission system will therefore utilize a model calculated offline based on a training set of images, which we address as the source-independent model. When a communication system is transmitting a specific class of images like space imagery as our satellite data, the source-independent model will be statistically close to the type of images that are being transmitted, as proved in the next paragraph.
The distortion characteristics of the source-independent model are based on a training set of  images: we first compute the
images: we first compute the  components
components  ,
,  and
and  as described in Section 2, which correspond to the
as described in Section 2, which correspond to the  individual source models for each training image. We obtain the
individual source models for each training image. We obtain the  source-independent model components
source-independent model components  ,
,  and
and  by averaging the individual models over the training set.
by averaging the individual models over the training set.
Two source models are computed. The reference source model is directly computed from the Toulouse image itself. The source-independent model training set contains 12 images that were taken from the USC-SIPI free image database [32]. It represents an average source model for satellite image class. Further on in this document, we refer, respectively, to these models as Toulouse and Sipi models.
From the series of  values, it is natural to sort the substreams by decreasing distortion values. Conceptually, the bitstream order is a property, which is only dependent on the characteristics of the source coder and, therefore, we only use the cut distortion values
values, it is natural to sort the substreams by decreasing distortion values. Conceptually, the bitstream order is a property, which is only dependent on the characteristics of the source coder and, therefore, we only use the cut distortion values  . As we averaged the distortions characteristics of each substream over a set of training images, we obtain a probabilistic importance order of the substreams, which we call the source-independent bitstream order.
. As we averaged the distortions characteristics of each substream over a set of training images, we obtain a probabilistic importance order of the substreams, which we call the source-independent bitstream order.
Figures 4 and 5 show a comparison of the distortion characteristics between the Toulouse model and the Sipi model. On both curves, the  -axis is the substream index, following the source-independent bitstream order, and the
-axis is the substream index, following the source-independent bitstream order, and the  -axis represents the MSE distortion. The plain curve represents the Sipi model. The dashed curve follows the Toulouse model profile. The Sipi model matches well the Toulouse model, apart from some local deviations. This is a logical conclusion since the Sipi model is based on a training set of images that represent specifically the class of images to which Toulouse belongs.
-axis represents the MSE distortion. The plain curve represents the Sipi model. The dashed curve follows the Toulouse model profile. The Sipi model matches well the Toulouse model, apart from some local deviations. This is a logical conclusion since the Sipi model is based on a training set of images that represent specifically the class of images to which Toulouse belongs.
3.2. Source Coder
The source coder used in this satellite system is based on the FlexWave-II architecture. This architecture has been specifically designed as a dedicated compression component for space-born applications. It is based on a  wavelet decomposition, which is also used by similar state-of-art source coders like SPIHT [33] and JPEG2000 [34]. However, the SPIHT and JPEG2000 are fully featured source coders that are too complex to implement in a low-power cost-efficient application specific integrated circuit (ASIC) realization for space applications. Therefore, specific algorithmic simplifications have been brought to the FlexWave-II core in order to reduce the complexity of the solution at the cost of a slight compression performance decrease. On a field-programmable gate array (FPGA) implementation of the FlexWave-II, clocked at 41 MHz, a processing performance of up to 10 Mpixels/s was measured. For this paper, we configured the FlexWave-II core for a 4-level wavelet decomposition depth, which outputs a total of
wavelet decomposition, which is also used by similar state-of-art source coders like SPIHT [33] and JPEG2000 [34]. However, the SPIHT and JPEG2000 are fully featured source coders that are too complex to implement in a low-power cost-efficient application specific integrated circuit (ASIC) realization for space applications. Therefore, specific algorithmic simplifications have been brought to the FlexWave-II core in order to reduce the complexity of the solution at the cost of a slight compression performance decrease. On a field-programmable gate array (FPGA) implementation of the FlexWave-II, clocked at 41 MHz, a processing performance of up to 10 Mpixels/s was measured. For this paper, we configured the FlexWave-II core for a 4-level wavelet decomposition depth, which outputs a total of  substreams.
substreams.
3.3. Channel
Typically, the quality of service offered over a DVB-S2 channel is subject to tropospheric phenomena, such as rain and clouds, as well as the influence of atmospheric gas. Both can severely degrade the quality of the transmission channel. These effects can have an influence on the long-term distribution of the channel attenuation statistics.
Figure 6 represents a simulated time series of  samples for a typical DVB-S2 channel. The channel simulator is outputting correlated channel coefficients at a basic frequency
samples for a typical DVB-S2 channel. The channel simulator is outputting correlated channel coefficients at a basic frequency  Hz, so that the channel series spans over 1 hour. The actual datarate of the system is
Hz, so that the channel series spans over 1 hour. The actual datarate of the system is  Mbit/s. Therefore, we can insert approximately 2.8 Mbytes of data between 2 consecutive samples. Considering a standard size compressed picture to be sent on this channel, we see that it will be entirely contained between two consecutive coefficients. Moreover, due to the time-domain correlation, two consecutive samples will have similar amplitudes (see Figure 6). As a consequence, we can already anticipate that the system will exclusively work in slow fading mode. This means that the protection allocation optimizer can safely consider the channel as a constant additive white Gaussian noise (AWGN) channel with a specific signal-to-noise ratio for the complete transmission of an image corresponding to the current attenuation of the DVB-S2 channel.
Mbit/s. Therefore, we can insert approximately 2.8 Mbytes of data between 2 consecutive samples. Considering a standard size compressed picture to be sent on this channel, we see that it will be entirely contained between two consecutive coefficients. Moreover, due to the time-domain correlation, two consecutive samples will have similar amplitudes (see Figure 6). As a consequence, we can already anticipate that the system will exclusively work in slow fading mode. This means that the protection allocation optimizer can safely consider the channel as a constant additive white Gaussian noise (AWGN) channel with a specific signal-to-noise ratio for the complete transmission of an image corresponding to the current attenuation of the DVB-S2 channel.
In the remainder of the document, we will therefore focus on the end-to-end performance of the system over an AWGN channel. The derivation of the performance over the DVB-S2 channel is simply performed by a convolution between an AWGN performance curve and the modeled DVB-S2 channel statistic profile.
3.4. Channel Coder
The channel coder used in the T@mpo system is an efficient implementation of a low-latency low-power turbo coder/decoder based on parallel concatenated convolutional turbo codes (PCCC). The T@mpo coder has 4 protection modes allowing the system to adapt the degree of protection against errors. The protection levels are described by their respective coderates in Table 2.
Under independent channel errors assumption [28], the BER after decoding is taken as the only parameter to characterize the occurrence of errors in the system. In Section 3.3 we considered that computing the performance of the system transmitting over AWGN channels was sufficient to accurately derive the performance of the system over the considered DVB-S2 satellite channel. Figure 7 gives an overview of the performance of the T@mpo channel coder over an AWGN channel. The  -axis represents the signal-to-noise ratio
-axis represents the signal-to-noise ratio  , while the
, while the  -axis represents the BER at the output of the channel decoder. Plain curves represents the performance of the 4 modes of the T@mpo coder as presented in Section 3.4. The dashed curve represents the classical noncoded performance on an AWGN channel.
-axis represents the BER at the output of the channel decoder. Plain curves represents the performance of the 4 modes of the T@mpo coder as presented in Section 3.4. The dashed curve represents the classical noncoded performance on an AWGN channel.
4. Simulations
In this section, we compare the performance of the full UEP controller with an EEP controller that would equally protect the bitstream with a single average protection level. As introduced in Section 2, a predictive model of the end-to-end distortion propagation is required by the full UEP controller in order to optimize the protection allocation. This predictive model is based on the assumption that the distortion caused by transmission errors is additive at the substream level. This approximation is required to enable the low-complexity optimization described in Section 2.4, but may introduce a mismatch between the estimated distortion during the optimization of the protection allocation and the actual distortion observed at the receiver. Depending on the amount of mismatch, the performance of the UEP allocation may be deteriorated.
Though, the parameters of the simulations have been previously introduced in Section 3, they are briefly recalled hereafter. The number of encoded substreams is  and corresponds to a
and corresponds to a  -level wavelet decomposition. The number of protection levels is equal to
-level wavelet decomposition. The number of protection levels is equal to  , and accounts for the
, and accounts for the  T@mpo protection modes (see Table 2) plus the additional unprotected and nontransmitted modes. It was shown in the literature [35] that three protection levels are usually sufficient to obtain most UEP gains for binary symmetric channels with error probabilities inferior to
T@mpo protection modes (see Table 2) plus the additional unprotected and nontransmitted modes. It was shown in the literature [35] that three protection levels are usually sufficient to obtain most UEP gains for binary symmetric channels with error probabilities inferior to  . Therefore, our system used a sufficiently high number of protection levels.
. Therefore, our system used a sufficiently high number of protection levels.
In what follows, we compare the simulated end-to-end performance of our solution with a state-of-the-art EEP solution and assess the impact of the additivity assumption on the end-to-end performance.
4.1. End-to-End Performance
In this section, we compare the end-to-end-performance of the proposed UEP controller with that of an advanced EEP system. A general EEP algorithm simply utilizes the order of the embedded substreams as prioritarization information. The image is encoded by the source coder, which subsequently outputs an ordered sequence of substreams. The substreams are further protected by the channel coder with a single error correcting code until the bit budget is exhausted. The remaining part of the bitstream is discarded and therefore not transmitted. Note that such an EEP solution relies already on a progressive bitstream, which can be cut at any place and is provided in a rate-distortion optimized order.
Figure 8 compares the performance of the EEP and UEP controllers for a global budget corresponding to the size of the Toulouse source bitstream. The plain curve shows the performance of the UEP controller, while the dashed curve shows the PSNR performance of the EEP controller. In a classical EEP system, the protection level is fixed for the whole range of channel conditions. In this simulation, the EEP performance is actually derived from the hull of all possible EEP optimization, given the number of protection levels available in the system. Therefore, the EEP performance of Figure 8 corresponds to an EEP controller that would choose the optimal protection mode according to the channel condition. It should be noted that a classical EEP system cannot achieve such an optimization since the protection level is fixed. However, for the UEP controller, the allocation is based on a predictive model, which is directly dependent on the channel condition. Therefore, the protection levels are automatically adapted prior to transmission.
The bottom  -axis represents the signal-to-noise ratio
-axis represents the signal-to-noise ratio  , while the top
, while the top  -axis represent the equivalent uncoded BER on an AWGN with binary phase-shift keying (BPSK) modulation. For low and high
-axis represent the equivalent uncoded BER on an AWGN with binary phase-shift keying (BPSK) modulation. For low and high  , the performance of both the EEP and the UEP controller are closely matched. This is explained by the fact that for
, the performance of both the EEP and the UEP controller are closely matched. This is explained by the fact that for  below −3 dB and above 12 dB, single protection modes are selected by both algorithms. Looking at Figure 7, we see that for bad channel conditions (
below −3 dB and above 12 dB, single protection modes are selected by both algorithms. Looking at Figure 7, we see that for bad channel conditions ( dB), the best T@mpo mode (1/3 rate) gives a BER of
dB), the best T@mpo mode (1/3 rate) gives a BER of  while the next best mode (1/2 rate) gives a BER above
while the next best mode (1/2 rate) gives a BER above  . Both algorithms decide to transmit 1/3 of the bitstream with the best T@mpo mode. Similarly, for very good channel conditions (
. Both algorithms decide to transmit 1/3 of the bitstream with the best T@mpo mode. Similarly, for very good channel conditions ( dB), the unprotected mode is subject to a sufficiently low BER to deliver the whole bitstream without any protection. For intermediate channel conditions (
dB), the unprotected mode is subject to a sufficiently low BER to deliver the whole bitstream without any protection. For intermediate channel conditions ( between −2 dB and 12 dB), the image reconstruction quality is acceptable, with a PSNR above 30 dB and the UEP controller outperforms the EEP controller by as much as 2 dB.
between −2 dB and 12 dB), the image reconstruction quality is acceptable, with a PSNR above 30 dB and the UEP controller outperforms the EEP controller by as much as 2 dB.
It should be noted that for both controllers, the reconstructed quality has a staircase effect. This effect is clearly visible on the EEP performance curve. The different switching points actually correspond to the channel conditions where the EEP controller decides to switch to the next protection mode. This effect is mainly due to the fact that the number of protection levels is limited. Indeed, for each protection level, only one bitstream truncation point is possible in order to fit the available budget. Between consecutive switching points, the amount of source data will therefore be constant and correspond to a quality plateau. At the next protection mode switch, the truncation point jumps further along the bitstream. Looking at the UEP controller performance, we remark that the staircase effect is less visible, giving a smoother transition between the switching points. This is explained by the fact that the UEP controller can allocate multiple protection rates across the substreams and trade more precisely source and channel resources for a given channel condition. It should be stressed that the UEP controller automatically adapts the number of protection levels used and their distribution across the substreams according to the algorithm described in Section 2.4.
4.2. Impact of Additivity Mismatch
The additivity assumption is central to the optimization algorithms proposed in [28] and in Section 2. It allows the use of a low-complexity algorithm for the UEP global optimization. First, we characterize the amplitude of the mismatch with large parameters  and
and  in order to characterize the deviation for the system setup described in Section 3. In a second step, we evaluate the end-to-end performance and the mismatch for small parameters
in order to characterize the deviation for the system setup described in Section 3. In a second step, we evaluate the end-to-end performance and the mismatch for small parameters  and
and  . The impact of the deviation on the end-to-end is actually checked against a reference full-search algorithm, which is only feasible when the parameters are small. Since the deviation has no impact when parameters are small, and that deviation characteristics are similar whether we use small or large parameters, we suppose that the system will keep good performance with large parameters. Details of the simulations are given hereafter.
. The impact of the deviation on the end-to-end is actually checked against a reference full-search algorithm, which is only feasible when the parameters are small. Since the deviation has no impact when parameters are small, and that deviation characteristics are similar whether we use small or large parameters, we suppose that the system will keep good performance with large parameters. Details of the simulations are given hereafter.
Uniform BERs ranging from  to
to  are applied on the different substreams. For each BER, 100 simulations are run to obtain a reasonable averaging of the MSE and the peak signal-to-noise ratio (PSNR) measurements. First we jointly corrupt all substreams with a fixed BER and compute the output distortion
are applied on the different substreams. For each BER, 100 simulations are run to obtain a reasonable averaging of the MSE and the peak signal-to-noise ratio (PSNR) measurements. First we jointly corrupt all substreams with a fixed BER and compute the output distortion  . Secondly, we corrupt each of the
. Secondly, we corrupt each of the  substreams with a fixed BER
substreams with a fixed BER  while leaving other substreams uncorrupted, and compute the
while leaving other substreams uncorrupted, and compute the  individual distortions
individual distortions  , where
, where  . Figure 9 shows the additivity mismatch defined as
. Figure 9 shows the additivity mismatch defined as

which happens to be strictly positive. This confirms that the additivity-based distortion estimation overestimates the real joint distortion. The mismatch starts off with less than 10% mismatch at a BER of  and reaches a plateau at 100% for a BER of
and reaches a plateau at 100% for a BER of  before reaching a peak at 200% for a BER of
before reaching a peak at 200% for a BER of  . Clearly additivity is not respected within FlexWave-II and exhibits a large additivity deviation. However, it should be stressed that a model mismatch does not necessarily lead to a wrong decision during the optimization phase or a decrease in the end-to-end performance of the system.
. Clearly additivity is not respected within FlexWave-II and exhibits a large additivity deviation. However, it should be stressed that a model mismatch does not necessarily lead to a wrong decision during the optimization phase or a decrease in the end-to-end performance of the system.
To assess the impact of the additive model deviation on the end-to-end performance, we compared the output optimization decision with a full-search algorithm. A full-search algorithm basically computed the expected distortion of all possible protection allocations prior to the transmission, and picked the best allocation based on the lowest distortion value. The full-search algorithm is not realizable with the large parameters  and
and  used in Section 4.1. However, with
used in Section 4.1. However, with  and
and  , we found that the protection allocation performed by the system with the additive model was identical to that of the full-search algorithm, while having similar mismatch amplitudes. Therefore, we assume that the behavior of our low-complexity solution will remain optimal with increasing parameters.
, we found that the protection allocation performed by the system with the additive model was identical to that of the full-search algorithm, while having similar mismatch amplitudes. Therefore, we assume that the behavior of our low-complexity solution will remain optimal with increasing parameters.
As a final comment, we have to state that the UEP algorithms optimally match the protection levels to the importance of each substream. By increasing the protection of important substreams, we expect to reduce their large contribution to the distortion. Hence, we expect UEP to mitigate the masking effect [31] when the parameters  and
and  are increased, which is one of the main cause for the additivity mismatch, as dominant substreams will be heavily protected.
are increased, which is one of the main cause for the additivity mismatch, as dominant substreams will be heavily protected.
5. Hardware Implementation
During the development of the satellite communication system, a hardware implementation of the UEP-optimized system has been realized. This section briefly describes the hardware setup that was designed. The hardware platform has been realized on a PICARD system http://www.imec.be/wireless/picard. The PICARD system consists of a PC in an industrial 19-inch rack. The backplane of the rack exposes a compact PCI (C-PCI) backplane. On this backplane, boards containing IP cores can be plugged. The T@mpo, FlexWave-II and AWGN channel are all integrated on such a circuit board. The board is built around as central FPGA that interconnects all the IP cores.
Figure 10 shows the comparison between the software version of the system presented in Section 4.1, and the hardware platform that has been instantiated. The transmission scenario described in Section 4 is used. The plain curve of Figure 10 is therefore identical to the plain curve of Figure 8, showing the performance of the UEP controller. The starred curve shows the performance of the Hardware implementation. As we can see, there is an almost perfect match between the two curves. This validates the hardware implementation of the FlexWave-II and T@mpo cores compared to their software versions. A processing performance of up to 10 Mpixels/s was measured on the final platform.
6. Conclusions
We have shown that joint source-channel optimization is a promising technique for the future of satellite imaging. By combining the embedded scalability offered by state-of-the-art wavelet-based source coders and recent channel coding techniques that are providing a flexible range of protection levels, and applying a generic UEP methodology on the combined system, we have developed an efficient satellite image transmission system. The proposed UEP solution outperforms an optimized state-of-the-art EEP solution by as much as 2 dB in the working range of channel conditions, and is able to adapt to any bitrate and any channel condition. The inherent low complexity of the resulting solution, enabled by an efficient joint source-channel modeling of the system, allowed the practical implementation of the complete system on an hardware platform and proved to have a rate-distortion performance very close to the software platform.
References
Nachtergaele L, Bormans J, Lafruit G, Vanhoof B, Bolsens I: Methodological reduction of memory requirements for a vlsi spaceborne wavelet compression engine. Proceedings of the 6th International Workshop on Digital Signal Processing Techniques for Space Applications (DSP '98), September 1998, Noordwijk, The Netherlands 3-4.
Schelkens p, Lafruit G, Decroos F, Cornelis J, Catthoor F: Power exploration for embedded zero-tree wavelet encoding. Proceedings of International Symposium on Low Power Electronics and Design (ISLPED '99), August 1999, San Diego, Calif, USA
Masschelein B, Bormans JG, Lafruit G: The local wavelet transform: a cost-efficient custom processor for space image compression. Applications of Digital Image Processing XXV, July 2002, Seattle, Wash, USA, Proceedings of SPIE 4790: 334-345.
Vanhoof B, Massachelein B, Chirila-Rus A, Osorio R: The FlexWave-II: a wavelet-based compression engine. European Space Components Conference (ESCCON '02), December 2002, Toulouse, France 301-308.
Giulietti A, Bougard B, Derudder V, Dupont S, Weijers J-W, Van der Perre L: A 80 Mb/s low-power scalable turbo codec core. Proceedings of the Custom Integrated Circuits Conference, May 2002, Orlando, Fla, USA 389-392.
Bougard B, Giulietti A, Derudder V, et al.: A scalable 8.7nJ/bit 75.6Mb/s parallel concatenated convolutional (turbo) codec. IEEE International Solid-State Circuits Conference, Digest of Technical Papers (ISSCC '03), February 2003, San Francisco, Calif, USA 1: 152-484.
Hamzaoui R, Stanković V, Xiong Z: Fast joint source-channel coding algorithms for internet/wireless multimedia. Proceedings of International Joint Conference on Neural Networks (IJCNN '02), May 2002, Honolulu, Hawaii, USA 3: 2108-2113.
Natu A, Taubman D: Unequal protection of JPEG2000 code-streams in wireless channels. Proceedings of IEEE Global Telecommunications Conference (GLOBECOM '02), November 2002, Taipei, Taiwan 1: 534-538.
Joohee K, Mersereau RM, Altunbasak Y: Error-resilient image and video transmission over the Internet using unequal error protection. IEEE Transactions on Image Processing 2003, 12(2):121-131. 10.1109/TIP.2003.809006
Cai H, Zeng B, Shen G, Li S: Error-resilient unequal protection of fine granularity scalable video bitstreams. Proceedings of the IEEE International Conference on Communications (ICC '04), June 2004, Paris, France 3: 1303-1307.
Wu Z, Bilgin A, Marcellin MW: Joint source/channel coding for image transmission with JPEG2000 over memoryless channels. IEEE Transactions on Image Processing 2005, 14(8):1020-1032.
Liu Z, Zhao M, Xiong Z: Efficient rate allocation for progressive image transmission via unequal error protection over finite-state Markov channels. IEEE Transactions on Signal Processing 2005, 53(11):4330-4338.
Albanese A, Blomer J, Edmonds J, Luby M, Sudan M: Priority encoding transmission. IEEE Transactions on Information Theory 1996, 42(6):1737-1744. 10.1109/18.556670
Puri R, Ramchandran K: Multiple description source coding using forward error correction codes. Proceedings of the 33rd Asilomar Conference on Signals, Systems, and Computers, October 1999, Pacific Grove, Calif, USA 1: 342-346.
Mohr AE, Riskin EA, Ladner RE: Approximately optimal assignment for unequal loss protection. Proceedings of International Conference on Image Processing (ICIP '00), September 2000, Vancouver, BC, Canada 1: 367-370.
Stockhammer T, Buchner C: Progressive texture video streaming for lossy packet networks. Proceeding of the 11th International Packet Video Workshop (PV '01), May 2004, Kyongju, Korea 57.
Dumitrescu S, Wu X, Wang Z: Globally optimal uneven error-protected packetization of scalable code streams. IEEE Transactions on Multimedia 2004, 6(2):230-239. 10.1109/TMM.2003.822793
Puri R, Lee K-W, Ramchandran K, Bharghavan V: An integrated source transcoding and congestion control paradigm for video streaming in the internet. IEEE Transactions on Multimedia 2001, 3(1):18-32. 10.1109/6046.909591
Stanković VM, Hamzaoui R, Charfi Y, Xiong Z: Real-Time unequal error protection algorithms for progressive image transmission. IEEE Journal on Selected Areas in Communications 2003, 21(10):1526-1535. 10.1109/JSAC.2003.816455
Hamzaoui R, Stanković V, Xiong Z: Optimized error protection of scalable image bit streams. IEEE Signal Processing Magazine 2005, 22(6):91-107.
Dumitrescu S, Wu X, Wang Z: Efficient algorithm for globally optimal uneven erasure-protected packetization of scalable code streams. Proceedings of IEEE International Conference on Multimedia and Expo (ICME '06), July 2006, Toronto, ON, Canada 2006: 605-608.
Sherwood PG, Zeger K: Progressive image coding for noisy channels. IEEE Signal Processing Letters 1997, 4(7):189-191. 10.1109/97.596882
Banister BA, Belzer B, Fischer TR: Robust image transmission using JPEG2000 and turbo-codes. IEEE Signal Processing Letters 2002, 9(4):117-119. 10.1109/97.1001646
Chande V, Farvardin N, Jafarkhani H: Image communication over noisy channels with feedback. Proceedings of IEEE International Conference on Image Processing (ICIP '99), October 1999, Kobe, Japan 2: 540-544.
Chande V, Farvardin N: Progressive transmission of images over memoryless noisy channels. IEEE Journal on Selected Areas in Communications 2000, 18(6):850-860. 10.1109/49.848239
Appadwedula S, Jones DL, Ramchandran K, Konzintsev I: Joint source channel matching for a wireless communications link. Proceedings of the IEEE International Conference on Communications (ICC '98), June 1998, Atlanta, Ga, USA 1: 482-486.
Etemadi F, Yousefi'zadeh H, Jafarkhani H: Progressive bitstream transmission over tandem channels. Proceedings of IEEE International Conference on Image Processing (ICIP '05), September 2005, Genova, Italy 1: 765-768.
Salemi E, Desset C, Dejonghe A, Cornelis J, Schelkens P: A low-complexity methodology for unequal error protection of scalable images. Proceedings of IEEE Global Telecommunications Conference (Globecom '06), November-December 2007, San Francisco, Calif, USA 1-5.
Salemi E, Desset C, Dejonghe A, Cornelis J, Schelkens P: Impact of source-independent modeling on unequal error protection for JPEG2000 images. Wavelet Applications in Industrial Processing IV, October 2006, San Jose, Calif, USA, Proceedings of SPIE 6383: 1-8.
Nosratinia A, Lu J, Aazhang B: Source-channel rate allocation for progressive transmission of images. IEEE Transactions on Communications 2003, 51(2):186-196. 10.1109/TCOMM.2003.809256
Salemi E, Desset C, Cornells J, Schelkens P: Additive distortion modeling for unequal error protection of scalable multimedia content. Proceedings of IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP '05), March 2005, Philadelphia, Pa, USA 2: 269-272.
USC-SIPI image database, available at http://sipi.usc.edu/database
Said A, Pearlman WA: A new, fast, and efficient image codec based on set partitioning in hierarchical trees. IEEE Transactions on Circuits and Systems for Video Technology 1996, 6(3):243-250. 10.1109/76.499834
Taubman SD: JPEG2000: Image Compression Fundamentals, Standards and Practice. Kluwer Academic Publishers, Norwell, Mass, USA; 2001.
Zhao M, Akansu AN: Optimization of dynamic UEP schemes for embedded image sources in noisy channels. Proceedings of IEEE International Conference on Image Processing (ICIP '00), September 2000, Vancouver, BC, Canada 1: 383-386.
Acknowledgments
The authors would like to thank the IMEC TOTEM team for the development of the software and hardware platform as well as for the majority of the results produced for this paper. Peter Schelkens was supported by a postdoctoral mandate of the Fund for Scientific Research—Flanders (FWO). This work has been funded and supported by the European Space Agency (ESA) through the Tandem Optimized Turbo Encoded Multimedia (TOTEM) project.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Salemi, E., Desset, C., Dejonghe, A. et al. A Low-Complexity UEP Methodology Demonstrated on a Turbo-Encoded Wavelet Image Satellite Downlink. J Wireless Com Network 2008, 342415 (2007). https://doi.org/10.1155/2008/342415
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2008/342415

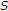 values
values 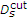 , which represent the MSE distortion resulting after cutting the substream
, which represent the MSE distortion resulting after cutting the substream  out of the bitstream while leaving other substreams untouched. It should be noted that cutting substream
out of the bitstream while leaving other substreams untouched. It should be noted that cutting substream  means that protection level
means that protection level 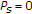 has been assigned to substream
has been assigned to substream  .
.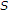 values
values 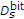 which estimate the average MSE distortion per erroneous bit in the substream
which estimate the average MSE distortion per erroneous bit in the substream  . This is obtained by inserting individual bit errors in the substream, while leaving remaining bits uncorrupted.
. This is obtained by inserting individual bit errors in the substream, while leaving remaining bits uncorrupted.


 and Sipi
and Sipi  source model distortion profile.
source model distortion profile.
 and Sipi
and Sipi  source model distortion profile.
source model distortion profile.



