- Research Article
- Open access
- Published:
Differentially Encoded LDPC Codes—Part II: General Case and Code Optimization
EURASIP Journal on Wireless Communications and Networking volume 2008, Article number: 367287 (2008)
Abstract
This two-part series of papers studies the theory and practice of differentially encoded low-density parity-check (DE-LDPC) codes, especially in the context of noncoherent detection. Part I showed that a special class of DE-LDPC codes, product accumulate codes, perform very well with both coherent and noncoherent detections. The analysis here reveals that a conventional LDPC code, however, is not fitful for differential coding and does not, in general, deliver a desirable performance when detected noncoherently. Through extrinsic information transfer (EXIT) analysis and a modified "convergence-constraint" density evolution (DE) method developed here, we provide a characterization of the type of LDPC degree profiles that work in harmony with differential detection (or a recursive inner code in general), and demonstrate how to optimize these LDPC codes. The convergence-constraint method provides a useful extension to the conventional "threshold-constraint" method, and can match an outer LDPC code to any given inner code with the imperfectness of the inner decoder taken into consideration.
1. Introduction
With an increasingly mature status of the sparse-graph coding technology in a theoretical context, the very pervasive scope of their well-proven practical applications, and the wide-scale availability of software radio, low-density parity-check (LDPC) codes have become and continue to be a favorable coding strategy for researchers and practitioners. Their superb performance on various channel models and with various modulation schemes have been documented in many papers. While the existing literature has shed great light on the theory and practice of LDPC codes, investigation was largely carried out from a pure coding perspective, where the prevailing assumption is that the synchronization and channel estimation are handled perfectly by the front-end receiver.
In wireless communications, accurate phase estimation may in many cases be very expensive or infeasible, which calls for noncoherent detection. Practical noncoherent detection is generally performed in one of the two ways: inserting pilot symbols directly in the coded and modulated sequence to help track the channel (it is possible to insert either pilot tones or pilot symbols, but the latter is found to be more effective and is what of relevance to this paper), and employing differential coding. Considering that the former may result in a nontrivial expansion of bandwidth especially on fast-changing channels, many wireless systems adopt the latter, including satellite and radio-relay communications.
The problem we wish to investigate is: LDPC codes perform remarkably well with coherent detection, but how about their performance with noncoherent detection and noncoherent differential detection in particular? This series of two-part papers aim to generate useful insight and engineering rules. In Part I of the series [1], we considered a special class of differentially encoded LDPC (DE-LDPC) codes, product accumulate (PA) codes [2]. The outer code of a  PA code is a simple, structured LDPC code with left (variable) degree profile
PA code is a simple, structured LDPC code with left (variable) degree profile  and right (check) degree profile
and right (check) degree profile  ; and the inner code is a differential encoder
; and the inner code is a differential encoder  . We showed that, despite their simplicity, PA codes perform quite well with coherent detection as well as noncoherent differential detection [1]. This motivates us, in Part II of this series of papers, to study the general case of differentially encoded LDPC codes. The question of how LDPC codes perform with differential coding is a worthy one [3–6], and directly relates to other interesting problems. For example, what is the best strategy to apply LDPC codes in noncoherent detection–-should differential coding be used or not? Modulation schemes such as the minimum phase shift keying (MPSK) have equivalent realizations in recursive and non-recursive forms; is one form preferred over the other in the context of LDPC coding? What other DE-LDPC configurations, besides PA codes, are good for differential coding, and how to find them?
. We showed that, despite their simplicity, PA codes perform quite well with coherent detection as well as noncoherent differential detection [1]. This motivates us, in Part II of this series of papers, to study the general case of differentially encoded LDPC codes. The question of how LDPC codes perform with differential coding is a worthy one [3–6], and directly relates to other interesting problems. For example, what is the best strategy to apply LDPC codes in noncoherent detection–-should differential coding be used or not? Modulation schemes such as the minimum phase shift keying (MPSK) have equivalent realizations in recursive and non-recursive forms; is one form preferred over the other in the context of LDPC coding? What other DE-LDPC configurations, besides PA codes, are good for differential coding, and how to find them?
Since the conventional differential detector (CDD) operating on two symbol intervals incurs a nontrivial performance loss [7], and since multiple symbol differential detectors (MSDD) [8] have a rather high complexity that increases exponentially with the window size, we developed, in Part I of this series of papers, a simple iterative differential detection and decoding (IDDD) receiver, whose structure is shown in [1, Figure 6]. The IDDD receiver comprises a CDD with 2-symbol observation window (the current and the previous), a phase-tracking Wiener filter, a message-passing decoder for the accumulator  [2], and a message-passing decoder configured for the (outer) LDPC code. The CDD, coupled with the phase-tracking unit and the
[2], and a message-passing decoder configured for the (outer) LDPC code. The CDD, coupled with the phase-tracking unit and the  decoder, acts as the front-end, or, the inner decoder of the serially concatenated system, and the succeeding LDPC decoder acts as the outer decoder. Soft reliability information in the form of log-likelihood ratio (LLR) is exchanged between the inner and the outer decoders to successively refine the decision. In the sequel, unless otherwise stated, we take the IDDD receiver as the default noncoherent receiver in our discussion of DE-LDPC codes.
decoder, acts as the front-end, or, the inner decoder of the serially concatenated system, and the succeeding LDPC decoder acts as the outer decoder. Soft reliability information in the form of log-likelihood ratio (LLR) is exchanged between the inner and the outer decoders to successively refine the decision. In the sequel, unless otherwise stated, we take the IDDD receiver as the default noncoherent receiver in our discussion of DE-LDPC codes.
We study the convergence property of IDDD for a general DE-LDPC code, through extrinsic information transfer (EXIT) charts [9, 10]. A somewhat unexpected finding is that, while a high-rate PA code yields desirable performance with noncoherent (differential) detection, a general DE-LDPC code does not. We attribute the reason to the mismatch of the convergence behavior between a conventional LDPC code and a differential decoder. This suggests that conventional LDPC codes, while an excellent choice for coherent detection, are not as desirable for noncoherent detection. It also gives rise to the question of what special LDPC codes, possibly performing poorly in the conventional scenario (such as the outer code of the PA code), may turn out right for differential modulation and detection?
One remarkable property of LDPC codes is the possibility to design their degree profiles, through density evolution [11], to match to a specific channel or a specific inner code [12–15]. To make LDPC codes work in harmony with the noncoherent differential decoder of interest, here we develop a convergence-constraint density evolution method. The conventional threshold-constraint method [11, 16] targets the best asymptotic threshold, and the new method effectively captures the interaction and convergence between the inner and the outer EXIT curves through a set of "sample points." In that, it makes it possible to optimize LDPC codes to match to an (arbitrary) inner code/modulation with the imperfectness of the inner decoder/demodulator taken into account. Our study reveals that LDPC codes may be divided in two groups. Those having minimum left degree of ≥2 are generally suitable for a nonrecursive inner code/modulator but not for a differential detector or any recursive inner code. On the other hand, the LDPC codes that perform well with a recursive receiver always have degree-1 (and degree-2) variable nodes. Further, when the code rate is high, these degree-1 and -2 nodes become dominant. This also explains why high-rate PA codes, whose outer code has degree-1 and degree-2 nodes only, perform remarkably with (noncoherent) differential detection [1].
The channel model of interest here is flat Rayleigh fading channels with additive white Gaussian noise (AWGN), the same as discussed in Part I [1]. Let  be the noisy signal at the receiver, let
be the noisy signal at the receiver, let  be the binary phase shift keying (BPSK) modulated signal at the transmitter, let
be the binary phase shift keying (BPSK) modulated signal at the transmitter, let  be the i.i.d. complex AWGN with zero mean and variance
be the i.i.d. complex AWGN with zero mean and variance  in each dimension, and let
in each dimension, and let  be the fading coefficient with Rayleigh distributed amplitude
be the fading coefficient with Rayleigh distributed amplitude  and uniformly distributed phase
and uniformly distributed phase  . We have
. We have  . Throughout the paper,
. Throughout the paper,  is assumed known perfectly to the receiver/decoder in the coherent detection case, and unknown (and needs to be worked around) in the noncoherent detection case. Further, the receiver is said to have channel state information (CSI) if
is assumed known perfectly to the receiver/decoder in the coherent detection case, and unknown (and needs to be worked around) in the noncoherent detection case. Further, the receiver is said to have channel state information (CSI) if  known (irrespective of
known (irrespective of  ), and no CSI otherwise.
), and no CSI otherwise.
We consider correlated channel fading coefficients (so that noncoherent detection is possible). Applying Jakes' isotropic scattering land mobile Rayleigh channel model, the autocorrelation of  is characterized by the 0th-order Bessel function of the first kind
is characterized by the 0th-order Bessel function of the first kind

and the power spectrum density (PSD) is given by

where  is the normalized Doppler spread,
is the normalized Doppler spread,  is the frequency band,
is the frequency band,  is the lag parameter, and
is the lag parameter, and  is a constant that is dependent on the average received power given a specific antenna and the distribution of the angles of the incoming power.
is a constant that is dependent on the average received power given a specific antenna and the distribution of the angles of the incoming power.
The rest of the paper is organized as follows. Section 2 evaluates the performance of a conventional LDPC code with noncoherent detection, and compare it with that of PA codes. Section 3 proposes the convergence-constraint method to optimize LDPC codes to match to a given inner code and particular a differential detector. Section 4 concludes the paper.
2. Codes Matched to Differential Coding
Part I showed that PA codes, a special class of DE-LDPC codes, perform quite well with coherent detection as well as noncoherent detection [1]. This section reveals whether or not this also holds for general DE-LDPC codes, and the far subtly why.
The analysis makes essential use of the EXIT charts [9, 10], which are obtained through a repeated application of density evolution at different decoding stages. Although they were initially proposed solely as a visualization tool, recent studies have revealed surprisingly elegant and useful properties of EXIT charts. Specifically, the convergence property states that, in order for the iterative decoder to converge successfully, the outer EXIT curve should stay strictly below the inner EXIT curve, leaving an open tunnel between the two curves. The area property states that the area under the EXIT curve,  , corresponds to the rate of the code [10], where
, corresponds to the rate of the code [10], where  and
and  denote the a priori (input) mutual information to and the extrinsic (output) mutual information from a particularly subdecoder, respectively. When the auxiliary channel is an erasure channel and the subdecoder is an optimal one, the relation is exact; otherwise, it is a good approximation [10]. The immediate implication of these properties is that, to fully harness the capacity (achievable rate) provided by the (noncoherent) inner differential decoder, the outer code must have an EXIT curve closely matched in shape and in position to that of the inner code.
denote the a priori (input) mutual information to and the extrinsic (output) mutual information from a particularly subdecoder, respectively. When the auxiliary channel is an erasure channel and the subdecoder is an optimal one, the relation is exact; otherwise, it is a good approximation [10]. The immediate implication of these properties is that, to fully harness the capacity (achievable rate) provided by the (noncoherent) inner differential decoder, the outer code must have an EXIT curve closely matched in shape and in position to that of the inner code.
With this in mind, we evaluate a few examples of (DE-)LDPC codes. (The computation of EXIT charts specific to DE-LDPC codes with IDDD receiver is discussed in [1].) We consider two configurations of the inner code:
-
(1)
a differential decoder for
 ; and
; and -
(2)
a direct detector, that is, a BPSK detector;
and three configurations of the outer code:
-
(1)
the outer code of a PA code, which has degree profile:
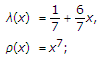 (3)
(3)
-
(2)
a (3,12)-regular LDPC code; and
-
(3)
an optimized irregular LDPC code reported in [17], whose threshold is
 –-about
–-about  dB away from the AWGN capacity–-and whose degree profile is
dB away from the AWGN capacity–-and whose degree profile is 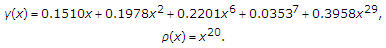 (4)
(4)
All three outer codes have rate 3/4, and the channel is a correlated Rayleigh fading channel with AWGN and normalized Doppler rate of  .
.
The EXIT curves, plotted in Figure 1, demonstrate that the outer code of the PA code and the differential decoder match quite well, but a conventional LDPC code, regular or irregular, will either intersect with the differential decoder, causing decoder failure, or leave a huge area between the curves, causing a capacity loss. On the other hand, LDPC codes, especially the (optimized) irregular ones, agree very well with the direct detector. This suggests that (conventional) LDPC codes perform better as a single code than being concatenated with a recursive inner code. Put it another way, an LDPC code that is optimal in the usual sense, for example, BPSK modulation and memoryless channels, may become quite suboptimal when operated together with a recursive inner code or a recursive modulation, such as a differential encoder. On the other hand, not using differential coding generally requires more pilot symbols in order to track the channel well, especially on fast-fading environments. Hence, it is fair to say that (conventional) LDPC codes that boast outstanding performance under coherent detection may not be nearly as advantageous under noncoherent detection, since they either suffer from performance loss (with differential encoding) or incur a large bandwidth expansion (without differential encoding). In comparison, PA codes can make use of the (intrinsic) differential code for noncoherent detection, and therefore present a better choice for bandwidth-limited wireless applications.
Before providing simulations to confirm our findings, we note that the EXIT curves of both inner codes in Figure 1 are computed using perfect knowledge of the fading coefficients. We used this genie-aided case in the discussion, to rid off the artifact of coarse channel estimation and better contrast the differences between the recursive differential detector and the nonrecursive direct detector. If the amplitude and phase information is to be estimated and handled by the inner code as in actual noncoherent detection, then the EXIT curve of the direct detector will show a small rising slope at the left end instead of being a flat straight line all the way through, and the EXIT curve of the differential decoder will also exhibit a deeper slope at the left end.
Figure 2 plots the BER performance curves of the same three codes specified in Figure 1 on Rayleigh channels with noncoherent detection. All the codes have data block size  K and code rate 3/4. Soft feedback is used in IDDD, the normalized Doppler spread is 0.01, and
K and code rate 3/4. Soft feedback is used in IDDD, the normalized Doppler spread is 0.01, and  or
or  pilot symbols are inserted to help track the channel. The two LDPC codes are evaluated either with or without a differential inner code. From the most power efficient to the least power efficient, the curves shown are (i) PA code with
pilot symbols are inserted to help track the channel. The two LDPC codes are evaluated either with or without a differential inner code. From the most power efficient to the least power efficient, the curves shown are (i) PA code with  of pilot symbols, (ii) PA code with
of pilot symbols, (ii) PA code with  of pilot symbols, (iii) BPSK-coded irregular LDPC code with
of pilot symbols, (iii) BPSK-coded irregular LDPC code with  of pilot symbols, (iv) BPSK-coded regular LDPC code with
of pilot symbols, (iv) BPSK-coded regular LDPC code with  of pilot symbols, (v) BPSK-coded irregular LDPC code with
of pilot symbols, (v) BPSK-coded irregular LDPC code with  of pilot symbols, (vi) differentially encoded irregular LDPC code with
of pilot symbols, (vi) differentially encoded irregular LDPC code with  of pilot symbols. It is evident that (conventional) LDPC codes suffer from a differential inner code. For example, with
of pilot symbols. It is evident that (conventional) LDPC codes suffer from a differential inner code. For example, with  of bandwidth expansion, BPSK-coded irregular and regular LDPC codes perform about 0.5 and 1 dB worse than PA codes at BER of
of bandwidth expansion, BPSK-coded irregular and regular LDPC codes perform about 0.5 and 1 dB worse than PA codes at BER of  , respectively, but the differentially encoded irregular LDPC code falls short by more than 2.2 dB. Further, while the irregular LDPC code (not differentially coded) is moderately (0.5 dB) behind the PA code with
, respectively, but the differentially encoded irregular LDPC code falls short by more than 2.2 dB. Further, while the irregular LDPC code (not differentially coded) is moderately (0.5 dB) behind the PA code with  of pilot symbols, the gap becomes much more significant when pilot symbols are reduced in half. For PA codes,
of pilot symbols, the gap becomes much more significant when pilot symbols are reduced in half. For PA codes,  of pilot symbols remain adequate to support a desirable performance, but they become insufficient to track the channel for nondifferentially encoded LDPC codes, causing a considerable performance loss and an error floor as high as BER of
of pilot symbols remain adequate to support a desirable performance, but they become insufficient to track the channel for nondifferentially encoded LDPC codes, causing a considerable performance loss and an error floor as high as BER of  . Thus, the advantages of PA codes over (conventional) LDPC codes are rather apparent, especially in cases when noncoherent detection is required and when only limited bandwidth expansion is allowed.
. Thus, the advantages of PA codes over (conventional) LDPC codes are rather apparent, especially in cases when noncoherent detection is required and when only limited bandwidth expansion is allowed.
Comparison of PA codes and LDPC codes on fast-fading Rayleigh channels with noncoherent detection and decoding. Solid line: PA codes, dashed lines: LDPC codes. Code rate 0.75, data block size 1 K, filter length 65, normalized Doppler spread 0.01, 10 global iterations, and 4 (local) iterations within LDPC codes or the outer code of PA codes inside each global iteration.
3. Code Design from the Convergence Property
3.1. Problem Formulation
EXIT analysis and computer simulations in the previous section show that a conventional LDPC code does not fit differential coding, but special cases such as the the outer code of PA codes do. This raises more interesting questions: what other (special) LDPC codes are also in harmony with differential encoding? What degree profiles do they have? Is it possible to characterize and optimize the degree profiles, and how?
The fundamental tool to solve these questions lies in convex optimization. In [11], the optimization problem of the irregular LDPC degree profiles on AWGN channels was formulated as a duality-based convex optimization problem, and an iterative method termed density evolution was proposed to solve the problem. In [16], a Gaussian approximation was applied to the density evolution method, which reduces the problem to be a linear optimization problem. Density evolution has since been exploited, in different flavors and possibly combined with differential evolution [18], to design good LDPC ensembles for a variety of communication channels and modulation schemes, see, for example [12–15] and the references therein. The results reported in these previous papers are excellent, but they almost exclusively aimed at the asymptotic threshold, namely, their cost functions were set to minimize the SNR threshold for a target code rate, or, equivalently, to maximize the code rate for a target SNR threshold. This is well justified, since in these papers, the primary involvement of the channel is to provide the initial LLR information to trigger the start of the density evolution process.
However, the problem we consider here is somewhat different. Our goal is to design codes that can fully achieve the capacity provided by the given inner receiver, and the noncoherent differential decoder in particular. Considering that the inner receiver, due to the lack of channel knowledge or other practical constraints, may not be an optimal receiver, it is of paramount importance to control the interaction between the inner and the outer code, or, the convergence behavior as reflected in the matching of shape and position of the corresponding EXIT curves. To emphasize the difference, we thereafter refer to the conventional density evolution method as the "threshold-constraint" method, and propose a "convergence-constraint" method as a useful extension to the conventional method.
The key idea of the proposed method is to sample the inner EXIT curve and design an (outer) EXIT curve that matches with these sample points, or, "control points." Suppose we choose a set of  control points in the EXIT plane, denoted as
control points in the EXIT plane, denoted as  ,
,  . Let
. Let  be the input-output mutual information transfer function of the outer LDPC code (whose exact expression of
be the input-output mutual information transfer function of the outer LDPC code (whose exact expression of  will be defined later in (17)), the optimization problem is formulated as
will be defined later in (17)), the optimization problem is formulated as

where  denotes the code rate of the outer LDPC code, and
denotes the code rate of the outer LDPC code, and  and
and  denote the fraction of edges that connect to variable nodes and check nodes of degree
denote the fraction of edges that connect to variable nodes and check nodes of degree  , respectively.
, respectively.
The formulation in (5) assumes that the LLR messages at the input of the inner and the outer decoder are Gaussian distributed, and that the output extrinsic mutual information (MI) of an irregular LDPC code corresponds to a linear combination of the extrinsic MI from a set of regular codes. As reported in literature, the Gaussian assumption for LLR messages is less not far from reality on AWGN channels but less accurate on Rayleigh fading channels [12]. Nevertheless, Gaussian assumption is used for several reasons. The first reason is simplicity and tractability. Tracking and optimizing the exact message pdf's involves tedious computation, which is exacerbated by the fact the proposed new method is governed by a set of control points, rather than a single control point as in the conventional method. Second, recall that to compute EXIT curves inevitably uses the Gaussian approximation. Thus, it seems well acceptable to adopt the same approximation when shaping and positioning an EXIT curve. Finally, characterizing and representing EXIT curves using mutual information help stabilize the process and alleviate the inaccuracy caused by Gaussian approximation and other factors. As confirmed by many previous papers as well as this one, the optimization generates very good results in spite of the use of the Gaussian approximation.
3.2. The Optimization Method
Below we detail the convergence-constraint design method formulated in (5). We conform to the notations and the graphic framework presented in [16]. Let  and
and  be the degree profiles from the edge perspective, where
be the degree profiles from the edge perspective, where  and
and  are the maximum variable node and check node degrees, and
are the maximum variable node and check node degrees, and  and
and  are the fraction of edges incident to variable nodes and check nodes of degree
are the fraction of edges incident to variable nodes and check nodes of degree  . Similarly, let
. Similarly, let  and
and  be the degree profiles from the node perspective. Let
be the degree profiles from the node perspective. Let  be the code rate. The following relation holds:
be the code rate. The following relation holds:

Let superscript  denote the
denote the  th LDPC decoding iteration, and subscript
th LDPC decoding iteration, and subscript  and
and  denote the quantities pertaining to variable nodes and check nodes, respectively. Further, define two functions that will be useful in the discussion
denote the quantities pertaining to variable nodes and check nodes, respectively. Further, define two functions that will be useful in the discussion


Function  maps the message mean
maps the message mean  to the corresponding mutual information (under Gaussian assumption), and
to the corresponding mutual information (under Gaussian assumption), and  helps describe how the message mean evolves in
helps describe how the message mean evolves in  operation, where
operation, where  follows a Gaussian distribution with mean
follows a Gaussian distribution with mean  and variance
and variance  .
.
The complete design process takes a dual constraint optimization process that progressively optimizes variable node degree profile  and check node degree profile
and check node degree profile  based on each other. Despite the duality in the formulation and the steps, optimizing
based on each other. Despite the duality in the formulation and the steps, optimizing  is far more critical to the code performance than optimizing
is far more critical to the code performance than optimizing  , largely because the optimal check node degree profile are shown to follow the concentration rule [16]:
, largely because the optimal check node degree profile are shown to follow the concentration rule [16]:

It is therefore a common practice to preset  according to (9) and code rate
according to (9) and code rate  , and optimize
, and optimize  only. For this reason, below we focus our discussion on optimizing
only. For this reason, below we focus our discussion on optimizing  for a given
for a given  . Interested readers can formulate the optimization of
. Interested readers can formulate the optimization of  in a similar way.
in a similar way.
3.2.1. Threshold-Constraint Method (Optimizing  )
)
Under the assumption that the messages passed along all the edges are i.i.d. and Gaussian distributed, the average messages variable nodes receive from their neighboring check nodes follow a mixed Gaussian distribution. From  th iteration to
th iteration to  th local iteration (in the LDPC decoder), the mean of the messages associated with the variable node,
th local iteration (in the LDPC decoder), the mean of the messages associated with the variable node,  , evolves as
, evolves as


where  denotes the mean of the initial messages received from the inner code (or the channel). Let us define
denotes the mean of the initial messages received from the inner code (or the channel). Let us define

Then (11) can be rewritten as

The conventional threshold-constraint density evolution guarantees that the degree profile converges asymptotically to the zero-error state at the given initial message mean  . This is achieved by enforcing [16]
. This is achieved by enforcing [16]

Viewed from the EXIT chart, the threshold-constraint method has implicitly used a control point  , such that the resultant EXIT curve will stay below it.
, such that the resultant EXIT curve will stay below it.
3.2.2. Convergence-Constraint Method (Optimizing 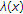 )
)
The proposed convergence-constraint method extends the conventional threshold-constraint method by introducing a set of control points, which may be placed in arbitrary positions in the EXIT plane, to control the shape and the position of the EXIT cure. Each control point  ensures that the EXIT curve will, at the input a priori mutual information
ensures that the EXIT curve will, at the input a priori mutual information  , produce extrinsic mutual information greater than
, produce extrinsic mutual information greater than  . This is reflected in the optimization process by changing (14) to
. This is reflected in the optimization process by changing (14) to

where  is the threshold value that satisfies
is the threshold value that satisfies  . We can reformulate the problem as follows: for a given check node degree profile
. We can reformulate the problem as follows: for a given check node degree profile  and a control point (
and a control point ( ) in the EXIT chart, where
) in the EXIT chart, where  ,
,

where  and
and  satisfies
satisfies

Apparently, when  , we get
, we get  , and the case reduces to that of the conventional threshold-constraint design.
, and the case reduces to that of the conventional threshold-constraint design.
Hence, given a set of  control points,
control points,  ,
,  , where
, where  and
and  , one can combine the constraints associated with each individual control point and perform joint optimization, to control the shape and the position of the resulting EXIT curve. Specifically, when the set of control points are proper samples from the inner EXIT curve, the resultant EXIT curve represents an optimized LDPC ensemble that matches to the inner code.
, one can combine the constraints associated with each individual control point and perform joint optimization, to control the shape and the position of the resulting EXIT curve. Specifically, when the set of control points are proper samples from the inner EXIT curve, the resultant EXIT curve represents an optimized LDPC ensemble that matches to the inner code.
3.2.3. Linear Programming
The basic idea of convergence-constraint design, as discussed before, is simple. Complication arises from the fact that constraint (ii) in (16) is a nonlinear function of  's. Furthermore, observe that the determination of the optimization range, or, the computation of
's. Furthermore, observe that the determination of the optimization range, or, the computation of  from (17), requires the knowledge of
from (17), requires the knowledge of  , which is yet to be optimized. One possible approach to overcome this chicken-and-egg dilemma is to attempt an approximated
, which is yet to be optimized. One possible approach to overcome this chicken-and-egg dilemma is to attempt an approximated  in (17) to compute
in (17) to compute  . Specifically, we propose accounting for the two lowest degree variable nodes
. Specifically, we propose accounting for the two lowest degree variable nodes  and
and  , and approximating the degree profile as
, and approximating the degree profile as

in (17). First, this approximated  is only used in (17) to tentatively determine
is only used in (17) to tentatively determine  , so that the optimization process can get started. The exact
, so that the optimization process can get started. The exact  in (16), (i) and (ii), is to be optimized. Second, the value of
in (16), (i) and (ii), is to be optimized. Second, the value of  and
and  (or
(or  ) in the approximated
) in the approximated  is calculated in one of the following two ways.
is calculated in one of the following two ways.
Case 1.
A conventional LDPC ensemble has  , that is, no degree-1 variable nodes. This is because the outbound messages from degree-1 variable nodes do not improve over the message-passing process. In that case, we consider only degree-2 and 3 nodes (
, that is, no degree-1 variable nodes. This is because the outbound messages from degree-1 variable nodes do not improve over the message-passing process. In that case, we consider only degree-2 and 3 nodes ( and
and  ), upper bound the percentage of degree-2 nodes with
), upper bound the percentage of degree-2 nodes with  , and treat all the rest as degree-3 nodes. The stability condition [11, 16] states that there exists a value
, and treat all the rest as degree-3 nodes. The stability condition [11, 16] states that there exists a value  such that, given an initial symmetric message density
such that, given an initial symmetric message density  satisfying
satisfying  , then the necessary and sufficient condition for the density evolution to converge to the zero-error state is
, then the necessary and sufficient condition for the density evolution to converge to the zero-error state is  , where
, where  . Applying the stability condition on Gaussian messages with initial mean value
. Applying the stability condition on Gaussian messages with initial mean value  , we get
, we get  and
and  , or equivalently,
, or equivalently,

It should be noted that not all values of  from the
from the  preselected control points are suitable for (19) in computing
preselected control points are suitable for (19) in computing  . Since the stability condition ensures the asymptotic convergence to the zero-error state for a given input messages,
. Since the stability condition ensures the asymptotic convergence to the zero-error state for a given input messages,  is valid and required only when the output mutual information will approach 1 at the input mutual information
is valid and required only when the output mutual information will approach 1 at the input mutual information  . What this implies in sampling the inner EXIT curve is that, at least one control point, say, the rightmost point
. What this implies in sampling the inner EXIT curve is that, at least one control point, say, the rightmost point  , should roughly satisfy the requirement:
, should roughly satisfy the requirement:  . This value of
. This value of  is then used in (19) to compute
is then used in (19) to compute  , which is subsequently used in
, which is subsequently used in  to compute
to compute  from (17).
from (17).  will then be applied to all the control points from 1 to
will then be applied to all the control points from 1 to  .
.
It is also worth mentioning that when a Gaussian approximation is used on the message pdf's, the stability condition reduces to

which is a weaker condition than (19). Since we use Gaussian approximation primarily for the purpose of complexity reduction, unnecessary application is therefore avoided. Thus (19) rather than (20) is used in our design process.
Case 2.
Consider the case when an LDPC code is iteratively decoded together with a differential encoder, or, other recursive inner code or modulation with memory. Since the inner code imposes another level of checks on all the variable nodes, degree-1 variable nodes in the outer LDPC code will get extrinsic information from the inner code, and their estimates will improve with decoding iterations. Thus, without loss of generality, we let the first and the second nonzero  's be
's be  and
and  . No analytical bounds on
. No analytical bounds on  or
or  were reported in literature for this case. We propose to bound
were reported in literature for this case. We propose to bound  by
by  , where
, where  is the code rate (the exact code rate is dependent on the optimization result, and may be slightly different from the target code rate). The rational is that, if
is the code rate (the exact code rate is dependent on the optimization result, and may be slightly different from the target code rate). The rational is that, if  , then there exist at least two degree-1 variable nodes, say the
, then there exist at least two degree-1 variable nodes, say the  th node and the
th node and the  th node, which connect to the same check. When the LDPC code operates alone, these two variable nodes are apparently useless and wasteful, and can be removed altogether. When the LDPC code is combined with an inner recursive code, as shown in Figure 3, these two degree-1 variable nodes will cause a minimum distance of
th node, which connect to the same check. When the LDPC code operates alone, these two variable nodes are apparently useless and wasteful, and can be removed altogether. When the LDPC code is combined with an inner recursive code, as shown in Figure 3, these two degree-1 variable nodes will cause a minimum distance of  for the entire codeword, irrespective of the code length. Using this empirical bound on
for the entire codeword, irrespective of the code length. Using this empirical bound on  , we can employ the approximation
, we can employ the approximation  in (17), which leads to the computation of (a lower bound for)
in (17), which leads to the computation of (a lower bound for)  . Code optimization as formulated by the convergence-constraint method can thus be solved using linear programming.
. Code optimization as formulated by the convergence-constraint method can thus be solved using linear programming.
It is rather expected that the choice of the control points directly affects the optimization results. The set of control points need not be large–-in fact, an excessive number of control points actually makes the optimization process converge slow and at times converge poor. We suggest choosing 3 to 5 control points that can reasonably characterize the shape of the inner EXIT curve. Our experiments show that the proposed method generates EXIT curves with a shape matching very well to what we desire, but the position is slightly lower, indicating that the resultant code rate is slightly pessimistic. This can be compensated by presetting the control points slightly higher than we actually want them to be.
3.3. Optimization Results and Useful Findings
For complexity concerns, instead of performing dual optimization, we apply the concentration theorem in (9) and preselect  that will make the the average column weight to be approximately 3. The left degree profile
that will make the the average column weight to be approximately 3. The left degree profile  is optimized through the convergence-constraint method discussed in the previous subsection. We now discuss some observations and findings from our optimization experiments.
is optimized through the convergence-constraint method discussed in the previous subsection. We now discuss some observations and findings from our optimization experiments.
First, the LDPC ensemble optimal for differential coding always contains degree-1 and degree-2 variable nodes. For high rate codes above 0.75, these nodes are dominant, and in some cases, are the the only types of variable nodes in the degree profile. For medium rates around 0.5, there exist also a good portion of high-degree variable nodes. Considering that the outer code of a PA code has only degree-1 and degree-2 variable nodes,  , where
, where  is the code rate, it is fair to say that PA are (near-)optimal at high rates, but less optimal at medium rates (the optimized LDPC ensemble contains slightly different degree distribution than that of the PA code, the difference is very small in either asymptotic thresholds or finite length simulations). This is actually well reflected in the EXIT charts. As rate 3/4 (see Figure 1), the area between the outer code of the PA code and the inner differential code is very small, leaving not much room for improvement. In comparison, at rate around 0.5 (see Figure 4), the area becomes much bigger, indicating that an optimized outer code could acquire more information rate for the same SNR threshold, or, for the same information rate, achieve a better SNR threshold.
is the code rate, it is fair to say that PA are (near-)optimal at high rates, but less optimal at medium rates (the optimized LDPC ensemble contains slightly different degree distribution than that of the PA code, the difference is very small in either asymptotic thresholds or finite length simulations). This is actually well reflected in the EXIT charts. As rate 3/4 (see Figure 1), the area between the outer code of the PA code and the inner differential code is very small, leaving not much room for improvement. In comparison, at rate around 0.5 (see Figure 4), the area becomes much bigger, indicating that an optimized outer code could acquire more information rate for the same SNR threshold, or, for the same information rate, achieve a better SNR threshold.
The optimization result of a target rate 0.5 is shown in Figure 4. We consider an inner differential code, operating at  dB on a
dB on a  Rayleigh fading channel, and decoded using the noncoherent IDDD receiver with the help of using
Rayleigh fading channel, and decoded using the noncoherent IDDD receiver with the help of using  pilot symbols. The optimzed LDPC ensemble has code rate
pilot symbols. The optimzed LDPC ensemble has code rate  and degree profile
and degree profile

We see that the two EXIT curves match very well with each other. Here the inner EXIT curve is computed through Monte Carlo simulations, when the sequences are taken in blocks of  bits, and the power penalty due to the pilot symbols is also compensated for.
bits, and the power penalty due to the pilot symbols is also compensated for.
The optimized LDPC ensemble requires  dB asymptotically, in order for the iterative process to converge successfully. Compared to a rate 0.50 PA code which requires
dB asymptotically, in order for the iterative process to converge successfully. Compared to a rate 0.50 PA code which requires  dB (Figure 4), the optimized LDPC ensemble is about 1.04 dB better asymptotically. However, as the tunnel between the inner and the outer EXIT curves becomes more narrow, the message-passing decoder takes a larger number of iterations to arrive at the zero-error state. The increased computing complexity and processing time are the price we pay for reaching out to the limit.
dB (Figure 4), the optimized LDPC ensemble is about 1.04 dB better asymptotically. However, as the tunnel between the inner and the outer EXIT curves becomes more narrow, the message-passing decoder takes a larger number of iterations to arrive at the zero-error state. The increased computing complexity and processing time are the price we pay for reaching out to the limit.
The optimized LDPC ensemble is good in the asymptotic sense, that is, with infinite or very long code lengths. In practice, we are also concerned with finite-length implementation or individual code realization. According to the concentration rule, at long lengths, all code realizations perform close to each other, and they all tend to converge to the asymptotic threshold as length increases with bound. At short lengths, however, the concentration rule fails and the performance may vary rather noticeably from one code realization to another. Good realizations have improved neighborhood condition than others, including a larger girth (achieved, e.g., through the edge progressive growth algorithm), a smaller number of short cycles, or a smaller trapping set.
Figure 5 simulates the optimized rate-0.5037 LDPC code with differential encoding and noncoherent differential decoding. The Rayleigh channel and the inner differential decoder (the IDDD receiver) are the same as discussed in Figure 4. We chose a long codeword length of  K to test how well the simulation agrees with the analytical threshold. As mentioned before, a large number of iterations (e.g., 100 iterations) is preferred to fully harness the code gain, but considering the complexity and delay affordable in a practical system, we simulated only 15 iterations. In the figure, the leftmost curve corresponds to the optimized DE-LDPC code using ideal detection (perfect knowledge on the fading phases and amplitudes), but with
K to test how well the simulation agrees with the analytical threshold. As mentioned before, a large number of iterations (e.g., 100 iterations) is preferred to fully harness the code gain, but considering the complexity and delay affordable in a practical system, we simulated only 15 iterations. In the figure, the leftmost curve corresponds to the optimized DE-LDPC code using ideal detection (perfect knowledge on the fading phases and amplitudes), but with  pilot symbols. These wasteful pilot symbols are included in this coherent detection case to offset the curve, and to compare fairly with all the other noncoherently detected curves with
pilot symbols. These wasteful pilot symbols are included in this coherent detection case to offset the curve, and to compare fairly with all the other noncoherently detected curves with  of pilot insertion. The three circled curves to the right of this ideal detection curve correspond to the noncoherent performance using iterative differential detection and decoding at the 5th, 10th, and 15th iteration. We see that the performance of the optimized differentially encoded LDPC code performs only about 0.3 dB worse than the coherent detection, which is very encouraging. Further, the simulated performance is only 0.75 dB away from the asymptotic threshold of
of pilot insertion. The three circled curves to the right of this ideal detection curve correspond to the noncoherent performance using iterative differential detection and decoding at the 5th, 10th, and 15th iteration. We see that the performance of the optimized differentially encoded LDPC code performs only about 0.3 dB worse than the coherent detection, which is very encouraging. Further, the simulated performance is only 0.75 dB away from the asymptotic threshold of  dB (discussed before), showing a good theory-practice agreement.
dB (discussed before), showing a good theory-practice agreement.
For reference, we also plot in Figure 5 the performance of a PA code and a conventional LDPC code without differential coding (recall that conventional LDPC codes perform worse with differential coding than without), both having code rate around 0.5 and both noncoherently detected. We see that the PA code outperforms the conventional LDPC code by 1.5 dB, but the optimized DE-LDPC code outperforms the PA code by another 1.4 dB!
4. Conclusion
Part I of this two-part series of papers [1] studied product accumulate codes, a special case of differentially encoded LDPC codes, with coherent detection and especially noncoherent detection. It showed that PA codes perform very well in both cases. Here in Part II, we generalize the study from PA codes to an arbitrary differentially encoded LDPC code.
The remarkable performance of LDPC codes with coherent detection has been extensively studied, but much less work has been carried out on noncoherently detected LDPC codes. In general, a noncoherently detected system may or may not employ differential encoding. The former leads to a differential encoding and noncoherent differential detection architecture, and the latter requires the insertion of (many) pilot symbols in order to track the (fast-changing) channel well. A rather unexpected finding here is that a conventional LDPC code actually suffers in either case: in the former it was because of an EXIT mismatch between the (outer) LDPC code and the (inner) differential code, and in the latter it was because of the large bandwidth expansion. Here by conventional we mean the LDPC code that delivers a superb performance in the usual setting with coherent detection and possibly channel state information.
Further investigation shows that it is not only possible, but highly beneficial, to optimize an LDPC code to match to a differential decoder. The optimization is achieved through a new convergence-constraint density evolution method developed here. The resultant optimized degree profiles are rather nonconventional, as they contain (many) degree-1 and -2 variable nodes. This is in sharp contrast to the conventional LDPC case (i.e., coherent detection) where degree-1 variable nodes are deemed highly undesirable.
The effectiveness of the new DE method is confirmed by the fact that the optimized DE-LDPC code brings an additional 1.4 dB and 2.9 dB, respectively, over the existing PA code and the conventional LDPC code (when noncoherent detection is used). The proposed DE optimization procedure is very useful. It provides a practical way to tune the shape and the position of an EXIT curve, and can therefore match an LDPC code to virtually any front-end processor, with the imperfectness of the processor taken into explicit consideration.
We conclude by stating that LDPC codes can after all perform very well with differential encoding (or any other recursive inner code or modulation), but the degree profiles need to be carefully (re)designed, using, for example, the convergence-constraint density evolution developed here, and one should expect the optimized degree profile to contain many degree-1 (and degree-2) variable nodes.
References
Li J: Differentially-encoded LDPC codes: part I—special case of product accumulate codes. to appear in EURASIP Journal on Wireless Communications and Networking
Li J, Narayanan KR, Georghiades CN: Product accumulate codes: a class of codes with near-capacity performance and low decoding complexity. IEEE Transactions on Information Theory 2004, 50(1):31-46. 10.1109/TIT.2003.821995
Nam VT, Kam P-Y, Xin Y: LDPC codes with BDPSK and differential detection over flat Rayleigh fading channels. Proceedings of the 50th IEEE Global Telecommunications Conference (GLOBECOM '07), November 2007, Washington, DC, USA 3245-3249.
Tatsunami H, Ishibashi K, Ochiai H: On the performance of LDPC codes with differential detection over Rayleigh fading channels. Proceedings of the 63rd IEEE Vehicular Technology Conference (VTC '06), May 2006, Melbourne, Victoria, Australia 5: 2388-2392.
Franceschini M, Ferrari G, Raheli R, Curtoni A: Serial concatenation of LDPC codes and differential modulations. IEEE Journal on Selected Areas in Communications 2005, 23(9):1758-1768.
Mitra J, Lampe L: Simple concatenated codes using differential PSK. Proceedings of the 49th IEEE Global Telecommunications Conference (GLOBECOM '06), November 2006, San Francisco, Calif, USA 1-6.
Valenti MC, Woerner BD: Iterative channel estimation and decoding of pilot symbol assisted turbo codes over flat-fading channels. IEEE Journal on Selected Areas in Communications 2001, 19(9):1697-1705. 10.1109/49.947034
Peleg M, Shamai S: Iterative decoding of coded and interleaved noncoherent multiple symbol detected DPSK. Electronics Letters 1997, 33(12):1018-1020. 10.1049/el:19970697
ten Brink S: Convergence behavior of iteratively decoded parallel concatenated codes. IEEE Transactions on Communications 2001, 49(10):1727-1737. 10.1109/26.957394
Ashikhmin A, Kramer G, ten Brink S: Extrinsic information transfer functions: model and erasure channel properties. IEEE Transactions on Information Theory 2004, 50(11):2657-2673. 10.1109/TIT.2004.836693
Richardson TJ, Shokrollahi MA, Urbanke RL: Design of capacity-approaching irregular low-density parity-check codes. IEEE Transactions on Information Theory 2001, 47(2):619-637. 10.1109/18.910578
Hou J, Siegel PH, Milstein LB: Performance analysis and code optimization of low density parity-check codes on Rayleigh fading channels. IEEE Journal on Selected Areas in Communications 2001, 19(5):924-934. 10.1109/49.924876
Shokrollahi A, Storn R: Design of efficient erasure codes with differential evolution. Proceedings of the IEEE International Symposium on Information Theory, June 2000, Sorrento, Italy 5.
ten Brink S, Kramer G, Ashikhmin A: Design of low-density parity-check codes for modulation and detection. IEEE Transactions on Communications 2004, 52(4):670-678. 10.1109/TCOMM.2004.826370
Chen R-R, Koetter R, Madhow U, Agrawal D: Joint noncoherent demodulation and decoding for the block fading channel: a practical framework for approaching Shannon capacity. IEEE Transactions on Communications 2003, 51(10):1676-1689. 10.1109/TCOMM.2003.818087
Chung S-Y, Richardson TJ, Urbanke RL: Analysis of sum-product decoding of low-density parity-check codes using a Gaussian approximation. IEEE Transactions on Information Theory 2001, 47(2):657-670. 10.1109/18.910580
Storn R, Price K: Differential evolution—a simple and efficient heuristic for global optimization over continuous spaces. Journal of Global Optimization 1997, 11(4):341-359. 10.1023/A:1008202821328
Acknowledgments
This research work supported in part by the National Science Foundation under Grant no. CCF-0430634 and CCF-0635199, and by the Commonwealth of Pennsylvania through the Pennsylvania Infrastructure Technology Alliance (PITA).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Li (Tiffany), J. Differentially Encoded LDPC Codes—Part II: General Case and Code Optimization. J Wireless Com Network 2008, 367287 (2008). https://doi.org/10.1155/2008/367287
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2008/367287
 ; and
; and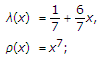
 –-about
–-about  dB away from the AWGN capacity–-and whose degree profile is
dB away from the AWGN capacity–-and whose degree profile is 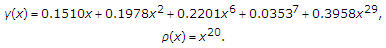

 dB, code rate 3/4,
dB, code rate 3/4,  -regular LDPC code, and optimized irregular LDPC code with
-regular LDPC code, and optimized irregular LDPC code with  and
and  .
.
 )
) )
)
 . When the four bits associated with the solid circles flip altogether, another valid codeword results, and the decoder is unable to tell (undetectable error).
. When the four bits associated with the solid circles flip altogether, another valid codeword results, and the decoder is unable to tell (undetectable error).
 of pilot symbols are assumed to assist noncoherent differential detection. Degree profile of the optimized LDPC ensemble:
of pilot symbols are assumed to assist noncoherent differential detection. Degree profile of the optimized LDPC ensemble: 









 pilot insertion, degree profile
pilot insertion, degree profile 







 and
and  , 15 (global) iterations each with 6 (local) iterations in the outer LDPC decoding.
, 15 (global) iterations each with 6 (local) iterations in the outer LDPC decoding.