- Research Article
- Open access
- Published:
Hybrid Polling Method for Direct Link Communication for IEEE 802.11 Wireless LANs
EURASIP Journal on Wireless Communications and Networking volume 2008, Article number: 598038 (2008)
Abstract
The direct link communication between STAtions (STAs) is one of the techniques to improve the MAC performance of IEEE 802.11 infrastructure networks. For the efficient direct link communication, in the literature, the simultaneous polling method was proposed to allow the multiple direct data communication to be performed simultaneously. However, the efficiency of the simultaneous polling method is affected by the interference condition. To alleviate the problem of the lower polling efficiency with the larger interference range, the hybrid polling method is proposed for the direct link communication between STAs in IEEE 802.11 infrastructure networks. By the proposed polling method, we can integrate the sequential and simultaneous polling methods properly according to the interference condition. Numerical examples are also presented to show the medium access control (MAC) performance improvement by the proposed polling method.
1. Introduction
The fundamental IEEE 802.11 wireless LAN technology was developed to support two PHY data rates of 1 and 2 Mbps in the industrial, science, and medical (ISM) frequency band at 2.4 GHz [1]. Three PHY variants of IEEE 802.11a, IEEE 802.11b, and IEEE 802.11g technologies support the maximum PHY data rates of 54 Mbps, 11 Mbps, and 54 Mbps, respectively [2–4]. All these PHY variants of IEEE 802.11 wireless LAN technologies employ the distributed coordination function (DCF) and point coordination function (PCF) for the medium access control (MAC) protocol [1]. The DCF protocol based on carrier sense multiple access with collision avoidance (CSMA/CA) was designed to support the best-effort services in the wireless LAN service environment, and the PCF protocol based on a polling method was designed for the real-time services such as voice over internet protocol (VoIP).
IEEE 802.11 wireless LAN technology can support both infrastructure and ad hoc networks. In an IEEE 802.11 ad hoc network consisting of a set of STAtions (STAs), the STAs can transmit their data frames directly to the recipients. In an IEEE 802.11 infrastructure network consisting of a set of STAs and an access point (AP), the AP relays the data frames from the STAs to an external network or to the recipients in the same network. The STAs cannot directly communicate with each other in the infrastructure network [1]. For this reason, two data transmissions from an STA and the AP are needed for a data transmission between STAs in the same infrastructure network and the delay performance and the efficiency of the radio bandwidth can be degraded in the infrastructure network.
To enable the direct link communication between STAs in infrastructure-based wireless networks, the researches have been carried out in [5–7]. Before the actual direct link communication between STAs is activated, the direct link connection should be established based on the connectivity information. The MAC protocol proposed in [6] assumes that the AP maintains a database for the geographical locations of the STAs and the connectivity information among the STAs can be derived from this database. The hybrid coordination function (HCF) protocol in [5] proposes the four-step process of establishing the direct link connection, but the method for obtaining the connectivity information is not specified in [5]. Our previous work in [7] proposes the efficient method for the APs collecting the connectivity and interference information among the STAs, and the simultaneous polling method to allow the multiple direct data communication to be performed simultaneously.
The efficiency of the simultaneous polling method in [7] depends on the interference condition among the STAs. The larger interference range allows less direct data communication to be simultaneously performed without interference. When the interference range is large enough for the data transmission of each STA to interfere with the data receptions of all other STAs in the same wireless LAN, the simultaneous direct data communication is impossible, and the efficiency of the simultaneous polling method will be the same as that of the conventional PCF protocol. Therefore, the simultaneous polling method needs to be enhanced to alleviate this problem of the lower polling efficiency with the larger interference range.
In this paper, the hybrid polling method is proposed for the direct link communication between STAs in IEEE 802.11 infrastructure networks. By the proposed polling method, we can integrate the sequential polling method in [8], which was originally developed to support the uplink data transmission from the STAs to the AP, and the simultaneous polling method in [7] properly according to the interference condition. In cases where the simultaneous polling method is not effective because of severe interference, the proposed polling method can employ the sequential polling method to complement the simultaneous polling method.
This paper is organized as follows. In Section 2, we briefly review the simultaneous polling method in [7]. In Sections 3 and 4, our hybrid polling method and the scheduling algorithms applicable to our proposed polling method are explained in detail for the direct link communication between STAs in IEEE 802.11 infrastructure networks. The simulation results are presented to show the MAC performance improvement by the proposed polling method in Section 5. Finally, we conclude in Section 6.
2. Review of Simultaneous Polling Method
2.1. PCF Protocol
The AP transmits the polling frames to grant the transmission opportunities to the STAs. After the beacon frame, the AP waits for one Short InterFrame Space (SIFS) period, and then transmits to an STA a polling frame on which a data frame destined for the STA can be piggybacked. The STA should respond to the polling frame by transmitting to the AP its data frame on which the ACK frame corresponding to the data frame transmitted by the AP can be piggybacked. After the reception of the data frame transmitted by the STA, the AP transmits to another STA a polling frame on which a data frame and the ACK frame corresponding to the previous data frame transmitted by the STA can be piggybacked. The STA responds to the polling frame by transmitting its data frame on which the ACK frame can be piggybacked. The STAs can respond to the polling frames by transmitting the null frames if the STAs do not have the data frames to transmit. If the STAs fail to respond to the polling frames within one SIFS period following the transmissions of the AP, for the error recovery, the AP transmits a polling frame to another STA after one PCF InterFrame Space (PIFS) period from the end of the previous transmission. In this manner, the process of the AP's polling and the STAs' responding continues until the contention-free period (CFP) ends.
2.2. CFP Structure
According to the superframe structure in [1], a CFP during which the PCF polls the STAs to grant the transmission opportunities alternates with a contention period (CP) during which the DCF controls the data transfer. S will represent the set of the STAs to which the transmission opportunities should be granted during a CFP. To support the simultaneous polling method in [7], the original IEEE 802.11 CFP structure was modified so that each CFP is divided into the multiple subperiods (SPs), each of which is composed of a polling interval (PI) and a direct communication polling interval (DCPI) as shown in Figure 1. In the PI, similarly to the PCF protocol, the AP grants the transmission opportunities to the STAs by transmitting the polling frames to the STAs in an order. In the DCPI, the direct link communication is actually performed using the simultaneous polling method. If one or more direct data transmission opportunities are actually granted in the DCPI, only one transmission opportunity is granted to each transmitting STA of the direct link communication and two transmission opportunities are granted each to the other STAs in the PI of the next SP. This is for providing a fair allocation of the wireless medium to the STAs.
Modified CFP structure in [ 7 ].
2.3. Connectivity and Interference Information
The simultaneous polling method is based on the connectivity and interference information among the STAs. We want to explain briefly the method for the APs collecting the connectivity and interference information among the STAs in the PI. Each STA  maintains the sets,
maintains the sets,  and
and  which are the sets of STAs of which the transmission signal can be heard by STA
which are the sets of STAs of which the transmission signal can be heard by STA  , and can interfere with the data reception of STA
, and can interfere with the data reception of STA  , respectively. STA
, respectively. STA  can obtain the MAC address of STA
can obtain the MAC address of STA  (
( ) from the polling frame transmitted by the AP before the transmission of STA
) from the polling frame transmitted by the AP before the transmission of STA  . For this purpose, the polling frames should be received by the STAs. When STA
. For this purpose, the polling frames should be received by the STAs. When STA  hears the transmission signal of other STA
hears the transmission signal of other STA  not in
not in  , STA
, STA  adds STA
adds STA  to
to  . When STA
. When STA  has not heard the transmission signal of other STA
has not heard the transmission signal of other STA  in
in  during recent three PIs, STA
during recent three PIs, STA  deletes STA
deletes STA  from
from  . In this manner, each STA can maintain the set,
. In this manner, each STA can maintain the set,  . STA
. STA  can also maintain the set,
can also maintain the set,  as follows. When STA
as follows. When STA  finds the reception power level of the transmission signal of other STA
finds the reception power level of the transmission signal of other STA  not in
not in  to be above that of the background noise, STA
to be above that of the background noise, STA  adds STA
adds STA  to
to  . When STA
. When STA  has not found the power level of the transmission signal of other STA
has not found the power level of the transmission signal of other STA  in
in  to be above that of the background noise during recent three PIs, STA
to be above that of the background noise during recent three PIs, STA  deletes STA
deletes STA  from
from  . Actually, each STA
. Actually, each STA  can piggyback the MAC addresses of the STAs that are deleted from or added to
can piggyback the MAC addresses of the STAs that are deleted from or added to  and
and  on the response null or data frames transmitted to the AP. Considering the case when transmission errors occur, we modified the method in [7] for the APs collecting the connectivity and interference information to wait for three PIs before deleting STA
on the response null or data frames transmitted to the AP. Considering the case when transmission errors occur, we modified the method in [7] for the APs collecting the connectivity and interference information to wait for three PIs before deleting STA  from
from  or
or  .
.
With the asymmetric connectivity and interference condition, the AP needs two PIs to collect the connectivity and interference information among the STAs when no transmission error occurs. In order for STA  to obtain the connectivity and interference information between STA
to obtain the connectivity and interference information between STA  and STA
and STA  (
( ), the following two events should sequentially occur in a PI:
), the following two events should sequentially occur in a PI:
-
(i)
the polling frame destined for STA
 is successfully received by STA
is successfully received by STA 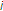 and STA
and STA 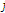 ;
; -
(ii)
the response frame transmitted by STA
 is successfully received by STA
is successfully received by STA  when STA
when STA  is within the transmission range of STA
is within the transmission range of STA  . STA
. STA 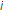 can detect the interference by the reception power level of the response frame transmitted by STA
can detect the interference by the reception power level of the response frame transmitted by STA  when STA
when STA 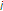 is within the interference range of STA
is within the interference range of STA  .
.
Denoting the probabilities that the two events occur in a PI by  and
and  , we can compute the probability that STA
, we can compute the probability that STA  can successfully obtain the connectivity and interference information between STA
can successfully obtain the connectivity and interference information between STA  and STA
and STA  within three PIs as
within three PIs as  . When the failure probabilities of the two events are less than or equal to 0.05, that is,
. When the failure probabilities of the two events are less than or equal to 0.05, that is,  and
and  ,
,  , therefore, we can infer that it is quite reasonable to wait for three PIs before deleting STA
, therefore, we can infer that it is quite reasonable to wait for three PIs before deleting STA  from
from  or
or  .
.
In the PI, after the four-step process of establishing the direct link connection in [5], each STA can request at most one direct data transmission opportunity by piggybacking the MAC address of the recipient of the direct data transmission on the response null or data frames transmitted to the AP. Based on the connectivity information, the AP can determine whether the direct link connection can be established to serve the direct link communication. After the successful four-step connection establishment process, each STA can optionally transmit its data frame directly to the recipient by writing the MAC address of the recipient in the recipient address (RA) field of the MAC header of the data frame transmitted when it is granted the transmission opportunity in the PI. The constants,  and
and  for
for  and
and  , and
, and  and
and  for
for  , which are collected in the PI to specify the connectivity and interference information, and the information of the STAs' requests for the direct link communication, respectively, are defined as follows:
, which are collected in the PI to specify the connectivity and interference information, and the information of the STAs' requests for the direct link communication, respectively, are defined as follows:
-
(i)
 if STA
if STA  . Otherwise,
. Otherwise, 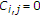 ;
; -
(ii)
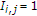 if STA
if STA  . Otherwise,
. Otherwise,  ;
; -
(iii)
 : the MAC address of the recipient of the direct data transmission that STA
: the MAC address of the recipient of the direct data transmission that STA  requested on a packet basis in the recent PI. If STA
requested on a packet basis in the recent PI. If STA 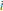 did not request the direct data transmission,
did not request the direct data transmission,  .
.
2.4. Simultaneous Polling Method
The simultaneous polling method is the multipolling method that allows the AP to poll a group of STAs by transmitting a single multipolling frame, where the MAC addresses of the STAs are indicated. With the simultaneous polling method, STA  , STA
, STA  and STA
and STA  in the group
in the group  attempt to transmit their frames simultaneously to the recipients, STA
attempt to transmit their frames simultaneously to the recipients, STA  , STA
, STA  and STA
and STA  , respectively, an SIFS period after receiving the multipolling frame. For the simultaneous transmissions to be performed properly without interference, STA
, respectively, an SIFS period after receiving the multipolling frame. For the simultaneous transmissions to be performed properly without interference, STA  should hear the transmission of STA
should hear the transmission of STA  for
for  , and the interference among the transmissions should be ignorable. Therefore, we need the following connectivity and interference condition:
, and the interference among the transmissions should be ignorable. Therefore, we need the following connectivity and interference condition:

The efficiency (or the number of simultaneous direct transmissions) of the simultaneous polling method depends on the interference range of STAs. In cases where the simultaneous polling method is not effective due to the large interference range, the simultaneous polling method needs to be enhanced to alleviate the problem of the lower polling efficiency with the larger interference range.
3. Hybrid Polling Method
The real-time services such as VoIP do not usually require the ACK frame transmission. We assume that the ACK frame transmission can be omitted. When an STA, having one or more established direct link connections, malfunctions, is just switched off or moves out of the transmission range, without the ACK transmission, the AP can detect that the direct link connections are broken using the connectivity information that will be collected in the next PIs. With the proposed polling method that is used to grant the requested direct transmission opportunities to the STAs in the DCPI, the AP transmits a multipolling frame to the STAs in the sequence  STA
STA  , STA
, STA  STA
STA  and the group
and the group  STA
STA  , STA
, STA  STA
STA  . The STAs in the sequence
. The STAs in the sequence  transmit their frames sequentially after the multipolling frame is received. An SIFS period after receiving the multipolling frame, STA
transmit their frames sequentially after the multipolling frame is received. An SIFS period after receiving the multipolling frame, STA  first attempts to transmit its frame. An SIFS period after sensing the end of the transmission of STA
first attempts to transmit its frame. An SIFS period after sensing the end of the transmission of STA  , STA
, STA  attempts to transmit its frame. STA
attempts to transmit its frame. STA  attempts to transmit its frame an SIFS period after sensing the end of the transmission of STA
attempts to transmit its frame an SIFS period after sensing the end of the transmission of STA  . In this manner, the STAs transmit their frames sequentially. An SIFS period after sensing the end of the transmission of STA
. In this manner, the STAs transmit their frames sequentially. An SIFS period after sensing the end of the transmission of STA  , the STAs in the group
, the STAs in the group  transmit their frames simultaneously. In order for the sequential transmissions to be performed properly, STA
transmit their frames simultaneously. In order for the sequential transmissions to be performed properly, STA  , which is the recipient for STA
, which is the recipient for STA  , should hear the transmission of STA
, should hear the transmission of STA  for
for  , and STA
, and STA  should sense the end of the transmission of STA
should sense the end of the transmission of STA  for
for  . The STAs in the group
. The STAs in the group  should sense the end of the transmission of STA
should sense the end of the transmission of STA  . Therefore, in addition to the conditions of (1), the following connectivity condition should be satisfied for the proposed polling method:
. Therefore, in addition to the conditions of (1), the following connectivity condition should be satisfied for the proposed polling method:

If an STA in  fails to respond to the multipolling frame or the transmission of the previous STA in the sequence within an SIFS period following the transmission of the AP or the previous STA, for the error recovery the AP will transmit the multipolling frame to repoll the next STAs in the sequence
fails to respond to the multipolling frame or the transmission of the previous STA in the sequence within an SIFS period following the transmission of the AP or the previous STA, for the error recovery the AP will transmit the multipolling frame to repoll the next STAs in the sequence  and the group
and the group  after a PIFS period, which is an SIFS period plus a slot time, from the end of the previous transmission. The format of the multipolling frame is shown in Figure 2.
after a PIFS period, which is an SIFS period plus a slot time, from the end of the previous transmission. The format of the multipolling frame is shown in Figure 2.
In Figure 2,  and
and  indicate the MAC addresses of the STAs in the sequence
indicate the MAC addresses of the STAs in the sequence  ,
,  and
and  the MAC addresses of the STAs in the group
the MAC addresses of the STAs in the group  , and
, and  and
and  are the numbers of the STAs in the sequence
are the numbers of the STAs in the sequence  and the group
and the group  , respectively. The other fields are from [1]. We can omit
, respectively. The other fields are from [1]. We can omit  or
or  . When
. When  (or
(or  ) is omitted in the multipolling frame, the simultaneous (or sequential) polling method is only specified.
) is omitted in the multipolling frame, the simultaneous (or sequential) polling method is only specified.
When all direct data transmission opportunities are granted, the AP initiates the next PI by transmitting a polling frame to an STA an SIFS period after the response transmissions from the STAs are completed or can initiate the next PI after the wireless medium is determined to be idle during a PIFS period.
4. Scheduling Algorithms
In this section, we propose two scheduling algorithms applicable to the hybrid polling method: the packet-level and the connection-level scheduling algorithms. By performing the packet-level scheduling algorithm at the beginning of DCPIs, the AP can schedule efficiently the direct data transmissions requested on a packet basis. The connection-level scheduling algorithm derives the polling sequence for granting the transmission opportunities to the transmitting STAs of all existing established direct link connections. When polling the STAs in DCPIs, by a simple method, the AP modifies the polling sequence derived by the connection-level scheduling algorithm considering the information of the STAs' requests for the direct link communication. The connection-level scheduling algorithm is suitable for the case when the AP cannot perform the packet-level scheduling algorithm quickly enough to reflect exactly the STAs' new requests for the direct link communication in the next DCPI. However, in the cases where the connectivity and interference information and the information of the STAs' requests for the direct link communication do not change for a period of time during which the AP can derive the polling sequence by the packet-level scheduling algorithm or a small number of STAs actually request the direct link communication, the packet-level scheduling algorithm should be applied for the efficient use of the wireless bandwidth. Note that when no STA requests the direct link communication, the next DCPI will be skipped.
4.1. Packet-Level Scheduling Algorithm
In the DCPI, the AP needs to schedule efficiently the requested direct data transmissions based on the connectivity and interference information among the STAs and the information of the STAs' requests for the direct link communication. Let  be the set of STAs that requested the direct data transmissions, which are determined to be feasible using the connectivity information, in the recent PI. Then
be the set of STAs that requested the direct data transmissions, which are determined to be feasible using the connectivity information, in the recent PI. Then  can be obtained as follows:
can be obtained as follows:

We propose a two-phase scheduling algorithm for granting the direct transmission opportunities to the STAs in  using the proposed polling method.
using the proposed polling method.
In the first phase of the algorithm, we handle the problem of grouping the STAs in  with as few groups as possible in such a way that no two STAs,
with as few groups as possible in such a way that no two STAs,  and
and  with
with  or
or  , are in the same group. Note that the connectivity and interference conditions as shown in (1) are satisfied for each group. Therefore, the AP can grant the simultaneous direct transmission opportunities to the STAs in each group using the simultaneous polling method. This grouping problem can be formulated as graph coloring problem (GCP), where the STAs in
, are in the same group. Note that the connectivity and interference conditions as shown in (1) are satisfied for each group. Therefore, the AP can grant the simultaneous direct transmission opportunities to the STAs in each group using the simultaneous polling method. This grouping problem can be formulated as graph coloring problem (GCP), where the STAs in  are vertices and two STAs,
are vertices and two STAs,  and
and  in
in  , are connected only when
, are connected only when  or
or  . We can use the simple heuristic for GCP, which is based on the degree-descending order of the vertices [9, page 14]. The set of the groups obtained by the heuristic is denoted by
. We can use the simple heuristic for GCP, which is based on the degree-descending order of the vertices [9, page 14]. The set of the groups obtained by the heuristic is denoted by  for
for  [9, page 14]. We need
[9, page 14]. We need  polling frame transmissions to poll the STAs in the groups in
polling frame transmissions to poll the STAs in the groups in  using the simultaneous polling method. The first phase of the algorithm was considered in the simultaneous polling method in [7].
using the simultaneous polling method. The first phase of the algorithm was considered in the simultaneous polling method in [7].
In the second phase of the algorithm, we try to further reduce the number of polling frame transmissions by applying the sequential polling method to the groups in  . The AP can poll the STAs in the groups in the sequence
. The AP can poll the STAs in the groups in the sequence  with
with  for
for  by transmitting a multipolling frame, the format of which is as shown in Figure 2, to the STAs when only one STA exists in
by transmitting a multipolling frame, the format of which is as shown in Figure 2, to the STAs when only one STA exists in  for
for  , and the following connectivity condition is satisfied:
, and the following connectivity condition is satisfied:

where  indicates that the STAs in
indicates that the STAs in  can hear the transmission of the STA in
can hear the transmission of the STA in  . We will call such a polling sequence satisfying the condition of (4) sequentially connected. For convenience of explanation, we will also call the sequence H having only one group sequentially connected.
. We will call such a polling sequence satisfying the condition of (4) sequentially connected. For convenience of explanation, we will also call the sequence H having only one group sequentially connected.
When some of the groups in  have only one STA, that is, the simultaneous polling method cannot be actually applied to some of the groups, we can further reduce the number of polling frame transmissions by finding the sequentially connected polling sequences and applying the proposed polling method to the sequentially connected polling sequences. The problem of finding the optimal polling sequence of the groups in
have only one STA, that is, the simultaneous polling method cannot be actually applied to some of the groups, we can further reduce the number of polling frame transmissions by finding the sequentially connected polling sequences and applying the proposed polling method to the sequentially connected polling sequences. The problem of finding the optimal polling sequence of the groups in  that minimizes the multipolling frame transmissions can be formulated as the asymmetric traveling salesman problem (TSP), where the groups in
that minimizes the multipolling frame transmissions can be formulated as the asymmetric traveling salesman problem (TSP), where the groups in  are
are  cities, and the distance,
cities, and the distance,  from
from  to
to  , is binary valued:
, is binary valued:

Let us denote the sequence as a solution of the TSP by  , and the corresponding total distance by
, and the corresponding total distance by  . If
. If  , that is,
, that is,  is sequentially connected, only one multipolling frame transmission is sufficient to grant the direct transmission opportunities to the STAs in the groups in
is sequentially connected, only one multipolling frame transmission is sufficient to grant the direct transmission opportunities to the STAs in the groups in  . If
. If  , we can cyclically reorder the groups in
, we can cyclically reorder the groups in  to obtain the sequentially connected polling sequence,
to obtain the sequentially connected polling sequence,  , and only one multipolling frame transmission is sufficient to poll the STAs in the groups in
, and only one multipolling frame transmission is sufficient to poll the STAs in the groups in  . If
. If  , we can cyclically reorder the groups in
, we can cyclically reorder the groups in  to obtain two sequentially connected polling sequences,
to obtain two sequentially connected polling sequences,  and
and  . (For instance, let
. (For instance, let  ,
, 
 ,
,  , and
, and  . Then we can reorder
. Then we can reorder  to obtain two sequentially connected polling sequences as
to obtain two sequentially connected polling sequences as  ,
,  .) Generally, if
.) Generally, if  , we can cyclically reorder
, we can cyclically reorder  to obtain
to obtain  sequentially connected polling sequences,
sequentially connected polling sequences,  and
and  , and
, and  multipolling frame transmissions are sufficient to grant the direct transmission opportunities to the STAs in the groups in
multipolling frame transmissions are sufficient to grant the direct transmission opportunities to the STAs in the groups in  .
.
To solve the asymmetric TSP, we can use the following dynamic search algorithm.
Algorithm (DYNAMIC_SEARCH (Time_Limit =  )).
)).
Step 1. Set Bounding_Cost =  (the number of the groups having two or more STAs in
(the number of the groups having two or more STAs in  ).
).
Step 2. Start to search the enumeration tree with Bounding_Cost.
Step 3. If a solution with the cost less than or equal to Bounding_Cost is found using the branch and bound technique based on the depth-first search method within Time_Limit, the solution is the result of the algorithm and the algorithm is terminated. Otherwise, update Bounding_Cost : Bounding_Cost  Bounding_Cost + 1, and go to Step 2.
Bounding_Cost + 1, and go to Step 2.
When  is the number of the groups having two or more STAs in
is the number of the groups having two or more STAs in  , at least
, at least  multipolling frame transmissions are needed to poll the STAs in the groups in
multipolling frame transmissions are needed to poll the STAs in the groups in  . The preceding algorithm first tries to obtain the solution with
. The preceding algorithm first tries to obtain the solution with  . If the algorithm does not succeed to get the solution within time of Time_Limit, the algorithm relaxes the constraint for the cost of the solution by increasing Bounding_Cost by 1 and tries to get the solution with
. If the algorithm does not succeed to get the solution within time of Time_Limit, the algorithm relaxes the constraint for the cost of the solution by increasing Bounding_Cost by 1 and tries to get the solution with  . If the algorithm fails again, the algorithm again increases Bounding_Cost by 1 and tries to get the solution with
. If the algorithm fails again, the algorithm again increases Bounding_Cost by 1 and tries to get the solution with  . In this manner, the algorithm continues until the solution with
. In this manner, the algorithm continues until the solution with  Bounding_Cost is obtained. By the branch and bound techniques, if a part of tour has a cost higher than or equal to the current optimal cost or higher than Bounding_Cost, all tours including this part of tour are skipped.
Bounding_Cost is obtained. By the branch and bound techniques, if a part of tour has a cost higher than or equal to the current optimal cost or higher than Bounding_Cost, all tours including this part of tour are skipped.
4.2. Connection-Level Scheduling Algorithm
Let  be the set of existing simplex direct link connections. A duplex connection can be realized by two simplex connections. We propose a two-phase scheduling algorithm for granting the direct transmission opportunities to the transmitting STAs of the direct link connections in
be the set of existing simplex direct link connections. A duplex connection can be realized by two simplex connections. We propose a two-phase scheduling algorithm for granting the direct transmission opportunities to the transmitting STAs of the direct link connections in  . We will denote the transmitting and receiving STAs of direct link connection,
. We will denote the transmitting and receiving STAs of direct link connection,  in
in  by
by  and
and  , respectively.
, respectively.
In the first phase of the algorithm, we handle the problem of grouping the connections in  with as few groups as possible in such a way that no two connections,
with as few groups as possible in such a way that no two connections,  and
and  with
with  or
or  , are in the same group. This grouping problem can be also formulated as GCP, where the connections in
, are in the same group. This grouping problem can be also formulated as GCP, where the connections in  are vertices and two connections,
are vertices and two connections,  and
and  in
in  , are connected only when
, are connected only when  or
or  . We can use the simple heuristic for GCP, which is based on the degree-descending order of the vertices [9, page 14]. The simultaneous polling method can be actually applied to the groups with two or more connections [9, page 14]. We will call such groups with two or more connections and the groups with only one connection the simultaneous polling groups and the nonsimultaneous polling groups, respectively.
. We can use the simple heuristic for GCP, which is based on the degree-descending order of the vertices [9, page 14]. The simultaneous polling method can be actually applied to the groups with two or more connections [9, page 14]. We will call such groups with two or more connections and the groups with only one connection the simultaneous polling groups and the nonsimultaneous polling groups, respectively.
Generally, a transmitting STA can have two or more established direct link connections. However, we want to grant at most one direct transmission opportunity to each STA. For this purpose, when a nonsimultaneous polling group obtained by the heuristic consists of a connection with a transmitting STA, we need to remove the other connections with the transmitting STA from other groups before we go to the second phase of the algorithm. Generally, we can say that the connections with a transmitting STA cannot be in the same simultaneous polling group due to the interference. Actually, we want to avoid the case that two or more connections with a transmitting STA are separately in the nonsimultaneous polling groups, and the case that two or more connections with a transmitting STA are scattered in both the simultaneous and nonsimultaneous polling groups. Note that we allow the case that two or more connections with a transmitting STA are individually in the different simultaneous polling groups. When two or more connections with a transmitting STA are individually in the different simultaneous polling groups, the STA should choose only one connection to transmit its direct data frame when polled by the AP. The set of the groups obtained by the first phase of the algorithm is denoted by  for
for  . We need
. We need  polling frame transmissions to poll the transmitting STAs of the connections in the groups in
polling frame transmissions to poll the transmitting STAs of the connections in the groups in  using the simultaneous polling method.
using the simultaneous polling method.
In the second phase of the algorithm, we try to further reduce the number of polling frame transmissions by applying the sequential polling method to the groups in  . The AP can poll the transmitting STAs of the connections in the groups in the sequence
. The AP can poll the transmitting STAs of the connections in the groups in the sequence  with
with  for
for  by transmitting a multipolling frame, the format of which is as shown in Figure 2, to the STAs when only one connection exists in
by transmitting a multipolling frame, the format of which is as shown in Figure 2, to the STAs when only one connection exists in  for
for  , and the following connectivity condition is satisfied:
, and the following connectivity condition is satisfied:

where  indicates that the transmitting STAs of the connections in
indicates that the transmitting STAs of the connections in  can hear the transmission of the transmitting STA of the connection in
can hear the transmission of the transmitting STA of the connection in  . We will call such a polling sequence satisfying the condition of (6) sequentially connected.
. We will call such a polling sequence satisfying the condition of (6) sequentially connected.
When some of the groups in  have only one connection, that is, the simultaneous polling method cannot be actually applied to some of the groups, we can further reduce the number of polling frame transmissions by finding the sequentially connected polling sequences and applying the proposed polling method to the sequentially connected polling sequences. The problem of finding the optimal polling sequence of the groups in
have only one connection, that is, the simultaneous polling method cannot be actually applied to some of the groups, we can further reduce the number of polling frame transmissions by finding the sequentially connected polling sequences and applying the proposed polling method to the sequentially connected polling sequences. The problem of finding the optimal polling sequence of the groups in  that minimizes the multipolling frame transmissions can be also formulated as the asymmetric TSP, where the groups in
that minimizes the multipolling frame transmissions can be also formulated as the asymmetric TSP, where the groups in  are
are  cities, and the distance,
cities, and the distance,  from
from  to
to  , is binary valued:
, is binary valued:

Let us denote the sequence as a solution of the TSP by  , and the corresponding total distance by
, and the corresponding total distance by  . If
. If  , that is,
, that is,  is sequentially connected, only one multipolling frame transmission is sufficient to grant the direct transmission opportunities to the transmitting STAs of the connections in the groups in
is sequentially connected, only one multipolling frame transmission is sufficient to grant the direct transmission opportunities to the transmitting STAs of the connections in the groups in  . If
. If  , we can cyclically reorder
, we can cyclically reorder  to obtain
to obtain  sequentially connected polling sequences,
sequentially connected polling sequences,  and
and  , and
, and  multipolling frame transmissions are sufficient to grant the direct transmission opportunities to the transmitting STAs of the connections in the groups in
multipolling frame transmissions are sufficient to grant the direct transmission opportunities to the transmitting STAs of the connections in the groups in  . To solve the asymmetric TSP, we can employ a dynamic search algorithm similar to the one of the packet-level scheduling algorithm with Time_Limit of 10 seconds.
. To solve the asymmetric TSP, we can employ a dynamic search algorithm similar to the one of the packet-level scheduling algorithm with Time_Limit of 10 seconds.
When a group in  consists of a single connection, the transmitting STA of the connection can transmit its direct data frame to any receiving STA of the established direct link connections in its transmission range when polled by the AP. When the transmitting STA of the connection has no direct data frame to transmit, the STA should use the granted transmission opportunity to transmit its null or data frame to the AP when polled by the AP. The AP can optionally modify the derived polling sequence to insert the AP's polling frame transmissions before the transmissions of the nonsimultaneous polling groups when the AP has the data frames, which are actually piggybacked on the polling frames, destined for the nonsimultaneous polling groups. When no direct link communication through the connections in a simultaneous polling group in
consists of a single connection, the transmitting STA of the connection can transmit its direct data frame to any receiving STA of the established direct link connections in its transmission range when polled by the AP. When the transmitting STA of the connection has no direct data frame to transmit, the STA should use the granted transmission opportunity to transmit its null or data frame to the AP when polled by the AP. The AP can optionally modify the derived polling sequence to insert the AP's polling frame transmissions before the transmissions of the nonsimultaneous polling groups when the AP has the data frames, which are actually piggybacked on the polling frames, destined for the nonsimultaneous polling groups. When no direct link communication through the connections in a simultaneous polling group in  was requested, the AP will modify the derived polling sequence to remove the group from the polling sequence that is actually delivered to the STAs. This is for avoiding wasting the wireless bandwidth. When all connections with a transmitting STA are separately in the different simultaneous polling groups, the STA can choose only one connection to transmit its direct data frame when polled by the AP. Note that the first phase of the algorithm avoided the case that two or more connections with a transmitting STA are separately in the nonsimultaneous polling groups, and the case that two or more connections with a transmitting STA are scattered in both the simultaneous and nonsimultaneous polling groups.
was requested, the AP will modify the derived polling sequence to remove the group from the polling sequence that is actually delivered to the STAs. This is for avoiding wasting the wireless bandwidth. When all connections with a transmitting STA are separately in the different simultaneous polling groups, the STA can choose only one connection to transmit its direct data frame when polled by the AP. Note that the first phase of the algorithm avoided the case that two or more connections with a transmitting STA are separately in the nonsimultaneous polling groups, and the case that two or more connections with a transmitting STA are scattered in both the simultaneous and nonsimultaneous polling groups.
5. Simulation Results
To show the MAC performance improvement by the proposed hybrid polling method, for each number of STAs,  , and 40, we generated ten IEEE 802.11a wireless LANs, where the APs are located at the centers of the circular service areas, and twenty, thirty, or forty STAs are randomly located in the service areas, including the one consisting of one AP and thirty STAs in Figure 3. Each wireless LAN serves one or more simultaneous full-duplex VoIP traffic streams between STA
, and 40, we generated ten IEEE 802.11a wireless LANs, where the APs are located at the centers of the circular service areas, and twenty, thirty, or forty STAs are randomly located in the service areas, including the one consisting of one AP and thirty STAs in Figure 3. Each wireless LAN serves one or more simultaneous full-duplex VoIP traffic streams between STA  and STA
and STA  .
.  will denote the number of simultaneous full-duplex VoIP traffic streams between two STAs of each pair. The STAs perform a good uplink power control in PIs so that the null or data frames transmitted by each STA can be received by the STAs including the AP in the circular transmission range with the radius
will denote the number of simultaneous full-duplex VoIP traffic streams between two STAs of each pair. The STAs perform a good uplink power control in PIs so that the null or data frames transmitted by each STA can be received by the STAs including the AP in the circular transmission range with the radius  of the distance between the STA and the AP, and the STAs out of the transmission range cannot hear the transmission signal of the STA.
of the distance between the STA and the AP, and the STAs out of the transmission range cannot hear the transmission signal of the STA.
In Figure 3, the eleven STAs indicated by the shaded circles can transmit the VoIP traffic streams directly to their recipients, and the other STAs should transmit the VoIP traffic streams indirectly to the recipients via the AP.
From the uplink power control, we can obtain the connectivity information among the STAs. The transmission and interference ranges are mainly determined by transmission power, radio propagation properties, and signal-to-noise ratio (SNR) threshold. In practice, the interference range is larger than the transmission range. We consider five cases of the interference range with the radius  in each wireless LAN [10]. The connectivity information remains the same in all five cases. In the first case,
in each wireless LAN [10]. The connectivity information remains the same in all five cases. In the first case,  , that is, the interference ranges are set to the same as the transmission ranges.
, that is, the interference ranges are set to the same as the transmission ranges.  is set to 1.3
is set to 1.3  , 1.5
, 1.5  , and 1.8
, and 1.8  in the second, third, and fourth cases, respectively. According to [10], the corresponding SNR threshold values of the second, third, and fourth cases are approximately 2.9, 5.1, and 10.5, respectively. Finally, the interference ranges are set to be large enough for the data transmission of each STA to interfere with the data receptions of all other STAs in the last case.
in the second, third, and fourth cases, respectively. According to [10], the corresponding SNR threshold values of the second, third, and fourth cases are approximately 2.9, 5.1, and 10.5, respectively. Finally, the interference ranges are set to be large enough for the data transmission of each STA to interfere with the data receptions of all other STAs in the last case.
For convenience of simulation analysis, we assume that the connectivity and interference information do not change over time. When the connectivity and interference information change, only the change of the connectivity and interference information is actually delivered to the AP. For example, if five MAC addresses per second, which are actually piggybacked on the response null or data frames transmitted to the AP, need to be delivered to report the change of the connectivity and interference information among the STAs, only the data rate of  bytes/second = 240 bps is required for this overhead.
bytes/second = 240 bps is required for this overhead.
As the result of the first phase of the packet-level and the connection-level scheduling algorithms applied to the five cases when the eleven STAs, 1, 4, 7, 8, 14, 15, 16, 23, 25, 27, and 30 request the direct data transmission opportunity on a packet basis, we obtained the following groups, each of which consists of the STAs that can be simultaneously polled using the simultaneous polling method:
-
(i)
 : (STAs 4 and 25), (STAs 27 and 14), (STAs 7, 15 and 1), (STAs 8 and 30), and (STAs 16 and 23);
: (STAs 4 and 25), (STAs 27 and 14), (STAs 7, 15 and 1), (STAs 8 and 30), and (STAs 16 and 23); -
(ii)
 : (STAs 4 and 30), (STAs 7 and 25), (STAs 14 and 15), (STAs 8 and 1), (STA 23), (STA 27), and (STA 16);
: (STAs 4 and 30), (STAs 7 and 25), (STAs 14 and 15), (STAs 8 and 1), (STA 23), (STA 27), and (STA 16); -
(iii)
 : (STA 7), (STA 8), (STA 14), (STAs 15 and 1), (STAs 16 and 30), (STAs 25 and 23), (STA 4), and (STA 27);
: (STA 7), (STA 8), (STA 14), (STAs 15 and 1), (STAs 16 and 30), (STAs 25 and 23), (STA 4), and (STA 27); -
(iv)
 : (STA 4), (STA 7), (STA 25), (STA 8), (STA 16), (STA 15), (STA 14), (STAs 23 and 30), and (STAs 1 and 27);
: (STA 4), (STA 7), (STA 25), (STA 8), (STA 16), (STA 15), (STA 14), (STAs 23 and 30), and (STAs 1 and 27); -
(v)
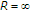 : (STA 30), (STA 27), (STA 25), (STA 23), (STA 16), (STA 15), (STA 14), (STA 8), (STA 7), (STA 4), and (STA 1).
: (STA 30), (STA 27), (STA 25), (STA 23), (STA 16), (STA 15), (STA 14), (STA 8), (STA 7), (STA 4), and (STA 1).
We could obtain each of the following hybrid polling sequences within 1 microsecond by applying the second phase of the packet-level and the connection-level scheduling algorithms to the proceeding groups in a computer with 3.0 GHz CPU:
-
(i)
 : (STAs 4 and 25), (STAs 27 and 14), (STAs 7, 15 and 1), (STAs 8 and 30), and (STAs 16 and 23);
: (STAs 4 and 25), (STAs 27 and 14), (STAs 7, 15 and 1), (STAs 8 and 30), and (STAs 16 and 23); -
(ii)
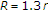 : [STA 23, STA 27], (STA 16), (STAs 4 and 30), (STAs 7 and 25), (STAs 14 and 15), and (STAs 8 and 1);
: [STA 23, STA 27], (STA 16), (STAs 4 and 30), (STAs 7 and 25), (STAs 14 and 15), and (STAs 8 and 1); -
(iii)
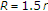 : [STA 8, STA 4, STA 27], (STA 14), (STAs 15 and 1), (STAs 16 and 30), (STAs 25 and 23), and (STA 7);
: [STA 8, STA 4, STA 27], (STA 14), (STAs 15 and 1), (STAs 16 and 30), (STAs 25 and 23), and (STA 7); -
(iv)
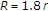 : [STA 25, STA 14], (STAs 23 and 30), (STAs 1 and 27), [STA 8, STA 16, STA 15, STA 4], and (STA 7);
: [STA 25, STA 14], (STAs 23 and 30), (STAs 1 and 27), [STA 8, STA 16, STA 15, STA 4], and (STA 7); -
(v)
 : [STA 27, STA 23, STA 8, STA 16, STA 15, STA 4], [STA 7, STA 1, STA 25, STA 14, STA 30].
: [STA 27, STA 23, STA 8, STA 16, STA 15, STA 4], [STA 7, STA 1, STA 25, STA 14, STA 30].
In the preceding polling sequences, the STAs in (·) can be simultaneously polled using the simultaneous polling method, and the STAs in [·] can be sequentially polled by a single hybrid polling frame transmission.
Applying the packet-level scheduling algorithm, which is based on the information of the STAs' requests for the direct link communication on a packet basis, to the total of thirty wireless LANs, each with the five interference conditions and three selected values of  , we could obtain each hybrid polling sequence for 414 combinations of wireless LANs, interference conditions, and selected values of
, we could obtain each hybrid polling sequence for 414 combinations of wireless LANs, interference conditions, and selected values of  out of 450 = 30 (wireless LANs)
out of 450 = 30 (wireless LANs)  (interference conditions)
(interference conditions)  (selected values of
(selected values of  ) combinations within 1 microsecond. The three selected values of
) combinations within 1 microsecond. The three selected values of  represent the light, medium, and heavy traffic loads carried on wireless LAN. We applied the connection-level scheduling algorithm to the remaining 36 combinations, and could obtain each hybrid polling sequence for 33 combinations within 10 seconds. The connection-level polling scheduling algorithm took about 117 seconds to derive each hybrid polling sequence for 3 combinations of a wireless LAN with 40 STAs and the interference condition of
represent the light, medium, and heavy traffic loads carried on wireless LAN. We applied the connection-level scheduling algorithm to the remaining 36 combinations, and could obtain each hybrid polling sequence for 33 combinations within 10 seconds. The connection-level polling scheduling algorithm took about 117 seconds to derive each hybrid polling sequence for 3 combinations of a wireless LAN with 40 STAs and the interference condition of  . From these observations, it was determined that we can perform the simulation analysis of the performance of our proposed polling method applying the packet-level and the connection-level scheduling algorithms to the 414 and 36 combinations, respectively.
. From these observations, it was determined that we can perform the simulation analysis of the performance of our proposed polling method applying the packet-level and the connection-level scheduling algorithms to the 414 and 36 combinations, respectively.
For convenience of simulation analysis, we assume that the CP does not exist, and only the CFP exists. The burst and idle periods of each VoIP traffic stream are 1.5 seconds and 1 second, respectively. The length of the user payload of each VoIP data frame is 88 bits [11]. When the improved multiband excitation (IMBE) speech coder is used, the total number of VoIP data frames generated in a burst period by each VoIP traffic stream is 4.8 Kbps 1.5 seconds/88 bits = 82, where 4.8 Kbps is the speech coding rate of the IMBE speech coder [11]. A VoIP data frame consists of the user datagram protocol (UDP), internet protocol (IP) and MAC layer headers, and the user payload. The lengths of the UDP, IP, and MAC layer headers are 16 bits, 224 bits, and 224 bits, respectively [1, 11]. One SIFS period of 16 microseconds, one PIFS period of 25 microseconds, and the physical layer header transmission time of 24 microseconds are used [1, 2]. We assume that all data, polling and multipolling frames are transmitted with the peak rate, 54 Mbps. It is assumed that the ACK frame transmission for the VoIP traffic streams can be omitted. We also assume that a PCF polling frame and a polling frame transmitted in PIs can optionally have two recipient MAC addresses, one indicating the polled STA and one indicating the recipient of the data frame piggybacked on the polling frame. When the polled STA and the recipient of the piggybacked data frame are the same, the polling frame will have only one recipient MAC address.
1.5 seconds/88 bits = 82, where 4.8 Kbps is the speech coding rate of the IMBE speech coder [11]. A VoIP data frame consists of the user datagram protocol (UDP), internet protocol (IP) and MAC layer headers, and the user payload. The lengths of the UDP, IP, and MAC layer headers are 16 bits, 224 bits, and 224 bits, respectively [1, 11]. One SIFS period of 16 microseconds, one PIFS period of 25 microseconds, and the physical layer header transmission time of 24 microseconds are used [1, 2]. We assume that all data, polling and multipolling frames are transmitted with the peak rate, 54 Mbps. It is assumed that the ACK frame transmission for the VoIP traffic streams can be omitted. We also assume that a PCF polling frame and a polling frame transmitted in PIs can optionally have two recipient MAC addresses, one indicating the polled STA and one indicating the recipient of the data frame piggybacked on the polling frame. When the polled STA and the recipient of the piggybacked data frame are the same, the polling frame will have only one recipient MAC address.
The maximum delay bound for each combination of wireless LANs, interference conditions, and traffic loads was obtained by computer simulation during about  time slots using the specialized simulator developed in
time slots using the specialized simulator developed in  code by the author. One slot time is 9 microseconds in IEEE 802.11a wireless LANs. In Figures 4, 5, 6, 7, 8, 9, 10, 11, and 12, we present the simulation results of the maximum delay bounds of IEEE 802.11a wireless LAN with the conventional PCF polling method with the direct link communication technique in [5], the simultaneous polling method in [7], and the hybrid polling method in Section 3. The results of the mean delay bounds, which are encountered by at least 99% of the VoIP data frames transmitted in wireless LAN, were obtained for the five interference conditions, the three traffic loads and the three numbers of STAs in a wireless LAN. It is assumed that the VoIP data or polling frames are transmitted erroneously with probability of 0.001.
code by the author. One slot time is 9 microseconds in IEEE 802.11a wireless LANs. In Figures 4, 5, 6, 7, 8, 9, 10, 11, and 12, we present the simulation results of the maximum delay bounds of IEEE 802.11a wireless LAN with the conventional PCF polling method with the direct link communication technique in [5], the simultaneous polling method in [7], and the hybrid polling method in Section 3. The results of the mean delay bounds, which are encountered by at least 99% of the VoIP data frames transmitted in wireless LAN, were obtained for the five interference conditions, the three traffic loads and the three numbers of STAs in a wireless LAN. It is assumed that the VoIP data or polling frames are transmitted erroneously with probability of 0.001.
As can be seen in Figures 4 to 12, the increase of the interference range negatively influences the performances of the simultaneous polling method and the hybrid polling method. Note that the interference range does not influence the performance of the PCF polling method. Comparing the results of the simultaneous polling method and the proposed polling method, we can see that the hybrid polling method copes with the increase of the interference range better than the simultaneous polling method. The performance of the simultaneous polling method decreases sharply after the interference condition of  , and becomes the same as that of the PCF polling method under the severe interference condition of
, and becomes the same as that of the PCF polling method under the severe interference condition of  . However, with the hybrid polling method, the decrease in the MAC performance is relatively small even in the interference conditions of
. However, with the hybrid polling method, the decrease in the MAC performance is relatively small even in the interference conditions of  and
and  . Compared with the simultaneous polling method, the hybrid polling method decreases the mean delay bound by about 7.6%, 11.0%, 18.5%, 27.8%, and 40.5% under the interference conditions of
. Compared with the simultaneous polling method, the hybrid polling method decreases the mean delay bound by about 7.6%, 11.0%, 18.5%, 27.8%, and 40.5% under the interference conditions of  , and
, and  , respectively. Compared with the PCF polling method, the hybrid polling method decreases the mean delay bound by about 58.8%, 45.1%, 39.1%, 38.0%, and 38.9% under the interference conditions of
, respectively. Compared with the PCF polling method, the hybrid polling method decreases the mean delay bound by about 58.8%, 45.1%, 39.1%, 38.0%, and 38.9% under the interference conditions of  , and
, and  , respectively. From the simulation results, we can see that the hybrid polling method outperforms both the PCF protocol and the simultaneous polling method in maximum delay especially under the severe interference condition.
, respectively. From the simulation results, we can see that the hybrid polling method outperforms both the PCF protocol and the simultaneous polling method in maximum delay especially under the severe interference condition.
For a bandwidth-efficient direct link communication, we need to reduce the number of polling frame transmissions in DCPIs because the transmissions of the polling frames on which the data frames are not usually piggybacked for the direct link communication are the scheduling overhead in the simultaneous and hybrid polling methods. While with the simultaneous polling method the AP should transmit the separate polling frames to poll the STAs for the direct link communication under the severe interference condition, with the hybrid polling method, the AP can reduce significantly the number of polling frame transmissions using the connectivity among the STAs. The hybrid polling method can improve the MAC performance by reducing the scheduling overhead.
6. Conclusions
In this paper, we proposed the hybrid polling method for supporting direct link communication between STAs in IEEE 802.11 wireless LANs. Compared with the simultaneous polling method proposed in the literature, the proposed polling method can improve the MAC performance by reducing the number of polling frame transmissions using the connectivity among the STAs. Simulation results show that the proposed polling method is useful especially when the interference range is large.
References
IEEE Std 802.11 : Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications. 1999
IEEE Std 802.11a : Wireless LAN Medium Access Control (MAC) and Physical Layer Specifications: High Speed Physical Layer in the 5 GHz Band. 1999
IEEE Std 802.11b : Wireless LAN Medium Access Control (MAC) and Physical Layer Specifications: Higher Speed Physical Layer (PHY) Extension in the 2.4 GHz Band. 1999
IEEE Std 802.11g : Wireless LAN Medium Access Control (MAC) and Physical Layer Specifications: Higher Speed Physical Layer (PHY) Extension in the 2.4 GHz Band. 2003
IEEE 802.11e : Wireless LAN Medium Access Control (MAC) and Physical Layer Specifications: Medium Access Control (MAC) Quality of Service (QoS) Enhancements. 2005
Naraghi-Pour M, Hegde M, Pallapotu R: Peer-to-peer communication in wireless local area networks. Proceedings of the 7th International Conference on Computer Communications and Networks (ICCCN '98), October 1998, Lafayette, La, USA 432-439.
Choi W-Y: Efficient direct link communication protocol for infrastructure mode IEEE 802.11 wireless LANs. Frequenz 2007, 61(7-8):166-171. 10.1515/FREQ.2007.61.7-8.166
Choi W-Y: An efficient polling scheme for enhancing IEEE 802.11 PCF protocol. Frequenz 2005, 59(11-12):268-271. 10.1515/FREQ.2005.59.11-12.268
Falkenauer E: Genetic Algorithms and Grouping Problems. John Wiley & Sons, New York, NY, USA; 1998.
Xu K, Gerla M, Bae S: How effective is the IEEE 802.11 RTS/CTS handshake in ad hoc networks? Proceedings of the IEEE Global Telecommunications Conference (GLOBECOM '02), November 2002, Taipei, Taiwan 1: 72-76.
Zahedi A, Pahlavan K: Capacity of a wireless LAN with voice and data services. IEEE Transactions on Communications 2000, 48(7):1160-1170. 10.1109/26.855523
Acknowledgments
The author would like to thank the anonymous reviewers for the valuable comments, which are very helpful to improve the paper. The author also would like to thank Professor Christian Hartmann for coordinating the review process. This study was supported by research funds from Dong-A University.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Choi, WY. Hybrid Polling Method for Direct Link Communication for IEEE 802.11 Wireless LANs. J Wireless Com Network 2008, 598038 (2008). https://doi.org/10.1155/2008/598038
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2008/598038

 is successfully received by STA
is successfully received by STA 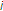 and STA
and STA 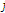 ;
; is successfully received by STA
is successfully received by STA  when STA
when STA  is within the transmission range of STA
is within the transmission range of STA  . STA
. STA 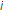 can detect the interference by the reception power level of the response frame transmitted by STA
can detect the interference by the reception power level of the response frame transmitted by STA  when STA
when STA 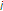 is within the interference range of STA
is within the interference range of STA  .
. if STA
if STA  . Otherwise,
. Otherwise, 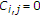 ;
;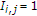 if STA
if STA  . Otherwise,
. Otherwise,  ;
; : the MAC address of the recipient of the direct data transmission that STA
: the MAC address of the recipient of the direct data transmission that STA  requested on a packet basis in the recent PI. If STA
requested on a packet basis in the recent PI. If STA 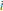 did not request the direct data transmission,
did not request the direct data transmission,  .
.

 : (STAs 4 and 25), (STAs 27 and 14), (STAs 7, 15 and 1), (STAs 8 and 30), and (STAs 16 and 23);
: (STAs 4 and 25), (STAs 27 and 14), (STAs 7, 15 and 1), (STAs 8 and 30), and (STAs 16 and 23); : (STAs 4 and 30), (STAs 7 and 25), (STAs 14 and 15), (STAs 8 and 1), (STA 23), (STA 27), and (STA 16);
: (STAs 4 and 30), (STAs 7 and 25), (STAs 14 and 15), (STAs 8 and 1), (STA 23), (STA 27), and (STA 16); : (STA 7), (STA 8), (STA 14), (STAs 15 and 1), (STAs 16 and 30), (STAs 25 and 23), (STA 4), and (STA 27);
: (STA 7), (STA 8), (STA 14), (STAs 15 and 1), (STAs 16 and 30), (STAs 25 and 23), (STA 4), and (STA 27); : (STA 4), (STA 7), (STA 25), (STA 8), (STA 16), (STA 15), (STA 14), (STAs 23 and 30), and (STAs 1 and 27);
: (STA 4), (STA 7), (STA 25), (STA 8), (STA 16), (STA 15), (STA 14), (STAs 23 and 30), and (STAs 1 and 27);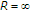 : (STA 30), (STA 27), (STA 25), (STA 23), (STA 16), (STA 15), (STA 14), (STA 8), (STA 7), (STA 4), and (STA 1).
: (STA 30), (STA 27), (STA 25), (STA 23), (STA 16), (STA 15), (STA 14), (STA 8), (STA 7), (STA 4), and (STA 1). : (STAs 4 and 25), (STAs 27 and 14), (STAs 7, 15 and 1), (STAs 8 and 30), and (STAs 16 and 23);
: (STAs 4 and 25), (STAs 27 and 14), (STAs 7, 15 and 1), (STAs 8 and 30), and (STAs 16 and 23);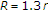 : [STA 23, STA 27], (STA 16), (STAs 4 and 30), (STAs 7 and 25), (STAs 14 and 15), and (STAs 8 and 1);
: [STA 23, STA 27], (STA 16), (STAs 4 and 30), (STAs 7 and 25), (STAs 14 and 15), and (STAs 8 and 1);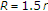 : [STA 8, STA 4, STA 27], (STA 14), (STAs 15 and 1), (STAs 16 and 30), (STAs 25 and 23), and (STA 7);
: [STA 8, STA 4, STA 27], (STA 14), (STAs 15 and 1), (STAs 16 and 30), (STAs 25 and 23), and (STA 7);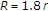 : [STA 25, STA 14], (STAs 23 and 30), (STAs 1 and 27), [STA 8, STA 16, STA 15, STA 4], and (STA 7);
: [STA 25, STA 14], (STAs 23 and 30), (STAs 1 and 27), [STA 8, STA 16, STA 15, STA 4], and (STA 7);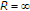 : [STA 27, STA 23, STA 8, STA 16, STA 15, STA 4], [STA 7, STA 1, STA 25, STA 14, STA 30].
: [STA 27, STA 23, STA 8, STA 16, STA 15, STA 4], [STA 7, STA 1, STA 25, STA 14, STA 30].
 ) is imposed on IEEE 802. 11a wireless LAN with 20 STAs.
) is imposed on IEEE 802. 11a wireless LAN with 20 STAs.
 ) is imposed on IEEE 802. 11a wireless LAN with 20 STAs.
) is imposed on IEEE 802. 11a wireless LAN with 20 STAs.
 ) is imposed on IEEE 802. 11a wireless LAN with 20 STAs.
) is imposed on IEEE 802. 11a wireless LAN with 20 STAs.
 ) is imposed on IEEE 802. 11a wireless LAN with 30 STAs.
) is imposed on IEEE 802. 11a wireless LAN with 30 STAs.
 ) is imposed on IEEE 802. 11a wireless LAN with 30 STAs.
) is imposed on IEEE 802. 11a wireless LAN with 30 STAs.
 ) is imposed on IEEE 802. 11a wireless LAN with 30 STAs.
) is imposed on IEEE 802. 11a wireless LAN with 30 STAs.
 ) is imposed on IEEE 802. 11a wireless LAN with 40 STAs.
) is imposed on IEEE 802. 11a wireless LAN with 40 STAs.
 ) is imposed on IEEE 802. 11a wireless LAN with 40 STAs.
) is imposed on IEEE 802. 11a wireless LAN with 40 STAs.
 ) is imposed on IEEE 802. 11a wireless LAN with 40 STAs.
) is imposed on IEEE 802. 11a wireless LAN with 40 STAs.