- Research Article
- Open access
- Published:
DOA Estimation in the Uplink of Multicarrier CDMA Systems
EURASIP Journal on Wireless Communications and Networking volume 2008, Article number: 851726 (2007)
Abstract
We consider the uplink of a multicarrier code-division multiple-access (MC-CDMA) network and assume that the base station is endowed with a uniform linear array. Transmission takes place over a multipath channel and the goal is the estimation of the directions of arrival (DOAs) of the signal from the active users. In a multiuser scenario, difficulties are primarily due to the large number of parameters involved in the estimation of the DOAs which makes this problem much more challenging than in single-user transmissions. The solution we propose allows estimating the DOAs of different users independently, thereby leading to a significant reduction in the system complexity. In the presence of multipath propagation, however, estimating the DOAs of a given user through maximum-likelihood methods remains a formidable task since it involves a search over a multidimensional domain. Therefore, we look for simpler solutions and discuss two alternative schemes based on the SAGE and ESPRIT algorithms.
1. Introduction
Antenna arrays at the base station (BS) can dramatically improve the capacity of a communication system [1–3]. Actually, they can be exploited in various ways. First, to form retrodirective beams that select the desired signals and attenuate the interfering ones. Secondly, antenna arrays make it possible to implement space-time selective transmission in the downlink. Finally, they can provide accurate localization of the user terminals [4], which is of interest in advanced handover schemes, public safety services, and intelligent transportation systems. In all these applications, accurate estimation of the directions of arrival (DOAs) of the desired signals is required.
DOA estimation has received much attention in the past years and several solutions are available in the technical literature (see [5–9] and the references therein). In particular, the schemes discussed in [5, 6] have good performance but are only devised for single-user applications and cannot be directly used in the uplink of a multiuser system. A tutorial review of subspace-based methods for DOA estimation is provided in [7]. The main drawback of these algorithms is that they can only handle a limited number of users since the overall number of resolvable paths cannot exceed the number of sensors in the antenna array. For this reason their application to a scenario with tens of users and several paths per user (as envisioned in fourth generation wireless systems) seems hardly viable. Schemes for estimating the DOAs in a CDMA multiuser system have been recently proposed in [8, 9]. In particular, the method discussed in [9] concentrates on a single user's parameters and models the multiple-access interference (MAI) as colored Gaussian noise. This idea is effective as it splits the multiuser DOA estimation problem into a series of simpler tasks in which DOAs of different users are estimated independently instead of jointly. A possible shortcoming of this method is that it requires knowledge of the MAI covariance matrix, which must be estimated in some manner.
In the present paper, we consider the uplink of a multicarrier code-division multiple-access (MC-CDMA) network [10, 11] and propose a method for estimating the DOAs of each active user. Transmission takes place over a multipath time-varying channel in which several paths with possibly different DOAs are present for each user. In a multiuser scenario the main obstacle is the large number of parameters involved in the estimation of the DOAs which makes this problem much more challenging than in single-user transmissions. A practical solution to this problem consists of separating each user from the others before applying conventional DOA estimation schemes. For this purpose, we first estimate the channel response and the data symbols of each active user by resorting to the method discussed in [12]. Once channel estimates and data decisions are obtained, they are exploited to reconstruct the interfering signals, which are then subtracted from the received waveform. This produces an MAI-free signal which is finally used for DOA estimation. In this way the DOAs are estimated independently for each user but, contrarily to [9], no knowledge of the MAI statistics is required.
In spite of the significant simplification achieved by means of users' separation, estimating the DOAs of a given user through ML methods is still difficult as it involves a numerical search over a multidimensional domain. To reduce the system complexity we investigate two alternative schemes. The first is based on the space-alternating generalized expectation-maximization (SAGE) algorithm [13], in which the DOAs of a given user are estimated sequentially instead of jointly. This reduces the original multidimensional problem to a sequence of one-dimensional searches. The second scheme exploits the ESPRIT (Estimation of Signal Parameters by Rotational Invariance Techniques) algorithm [14] and estimates the DOAs in closed form.
The main contribution of this paper is a method for estimating the DOAs of all active users in an MC-CDMA scenario characterized by multiple resolvable paths. As mentioned previously, the major difficulty comes from the need of separating each user from the others before his DOAs can be estimated. Notice that conventional DOA estimation algorithms cannot be employed in such a scenario unless users' separation has been successfully completed, since otherwise the number of sensors in the antenna array should be prohibitively high (on the order of the total number of resolvable paths). To the best of the authors' knowledge, a similar problem has previously been addressed only in [15]. In particular, the solution proposed in [15] is tailored for the rate  space-time block code introduced by Tarokh in [16] and assumes a static channel with a single DOA for each user. Unfortunately, its extension to a time-varying multipath channel with possibly multiple DOAs for each user does not seem straightforward. A second contribution is a comparison between two popular schemes, namely, the SAGE and ESPRIT algorithms, both in terms of estimation accuracy and system complexity.
space-time block code introduced by Tarokh in [16] and assumes a static channel with a single DOA for each user. Unfortunately, its extension to a time-varying multipath channel with possibly multiple DOAs for each user does not seem straightforward. A second contribution is a comparison between two popular schemes, namely, the SAGE and ESPRIT algorithms, both in terms of estimation accuracy and system complexity.
The rest of the paper is organized as follows. Section 2 describes the signal model and introduces basic notation. In Section 3 we derive the methods for estimating the DOAs. Simulation results are discussed in Section 4 and some conclusions are offered in Section 5.
2. Signal Model
2.1. MC-CDMA System
We consider the uplink of an MC-CDMA network employing N subcarriers for the transmission of  data symbols. The
data symbols. The  modulated subcarriers are located in the middle of the signal bandwidth and are divided into smaller groups of Q elements [17]. The remaining
modulated subcarriers are located in the middle of the signal bandwidth and are divided into smaller groups of Q elements [17]. The remaining  subcarriers at the edges of the spectrum are not used to limit the out-of-band radiation (virtual carriers). The BS is equipped with P antennas and employs the subcarriers of a given group to communicate with K users that are separated through orthogonal Walsh-Hadamard (WH) codes of length
subcarriers at the edges of the spectrum are not used to limit the out-of-band radiation (virtual carriers). The BS is equipped with P antennas and employs the subcarriers of a given group to communicate with K users that are separated through orthogonal Walsh-Hadamard (WH) codes of length  . Without loss of generality, we concentrate on a single group and assume that the Q subcarriers are uniformly spread over the signal bandwidth so as to exploit the channel frequency diversity. We denote
. Without loss of generality, we concentrate on a single group and assume that the Q subcarriers are uniformly spread over the signal bandwidth so as to exploit the channel frequency diversity. We denote  the subcarrier indices in the group, with
the subcarrier indices in the group, with  .
.
The i th symbol  of the k th user is spread over Q chips using the code sequence
of the k th user is spread over Q chips using the code sequence  , where
, where  and the notation
and the notation  means transpose operation. The resulting vector
means transpose operation. The resulting vector  is then mapped onto Q subcarriers using an OFDM modulator. The channel is assumed static over an OFDM block (slow-fading) and an
is then mapped onto Q subcarriers using an OFDM modulator. The channel is assumed static over an OFDM block (slow-fading) and an  -point cyclic prefix (longer than the channel impulse response) is inserted to avoid interference between adjacent blocks.
-point cyclic prefix (longer than the channel impulse response) is inserted to avoid interference between adjacent blocks.
At the receiver side the incoming waveform is first filtered and then sampled with period  , where
, where  is the block duration. Next, the cyclic prefix is removed and the remaining samples are passed to an N-point discrete Fourier transform (DFT) unit. We concentrate on the m th MC-CDMA block and denote
is the block duration. Next, the cyclic prefix is removed and the remaining samples are passed to an N-point discrete Fourier transform (DFT) unit. We concentrate on the m th MC-CDMA block and denote  the demodulator outputs at the p th antenna corresponding to the Q subcarriers of the considered group. Also, we assume a quasisynchronous system in which each user is time-aligned to the BS reference in a way similar to that discussed in [18]. In these circumstances we have
the demodulator outputs at the p th antenna corresponding to the Q subcarriers of the considered group. Also, we assume a quasisynchronous system in which each user is time-aligned to the BS reference in a way similar to that discussed in [18]. In these circumstances we have

where  is a Q-dimensional vector with entries
is a Q-dimensional vector with entries

and  is the k th user's channel frequency response over the
is the k th user's channel frequency response over the  th subcarrier at the p th antenna. Also,
th subcarrier at the p th antenna. Also,  is thermal noise, which is modeled as a Gaussian vector with zero mean and covariance matrix
is thermal noise, which is modeled as a Gaussian vector with zero mean and covariance matrix  (we denote
(we denote  the identity matrix of order Q).
the identity matrix of order Q).
2.2. Channel Model
We assume that the P receive antennas are arranged in a uniform linear array with interelement spacing  . The signal transmitted by each user propagates through a multipath channel with L distinct paths. Thus, the k th baseband channel impulse response (CIR) at the p th antenna during the m th MC-CDMA block takes the form
. The signal transmitted by each user propagates through a multipath channel with L distinct paths. Thus, the k th baseband channel impulse response (CIR) at the p th antenna during the m th MC-CDMA block takes the form

where  is the convolution between the impulse responses of the transmit and receive filters,
is the convolution between the impulse responses of the transmit and receive filters,  is the delay of the
is the delay of the  -path and
-path and  the corresponding complex amplitude. Finally,
the corresponding complex amplitude. Finally,  is defined as
is defined as

where  is the free-space wavelength and
is the free-space wavelength and  is the DOA of the
is the DOA of the  -path. From (4) we see that measuring
-path. From (4) we see that measuring  is equivalent to measuring
is equivalent to measuring  since there is a one-to-one relation between these quantities provided that
since there is a one-to-one relation between these quantities provided that  is limited within
is limited within  and
and  . In the following we assume that the path delays and DOAs do not change significantly with time, that is, we set
. In the following we assume that the path delays and DOAs do not change significantly with time, that is, we set  and
and  . Vice versa, the path gains
. Vice versa, the path gains  are modeled as independent Gaussian random processes with zero-mean and average power
are modeled as independent Gaussian random processes with zero-mean and average power  .
.
The channel frequency response  is computed as the Fourier transform of
is computed as the Fourier transform of  at
at  and reads
and reads

where  is the duration of the useful part of the MC-CDMA block and
is the duration of the useful part of the MC-CDMA block and  is the frequency response of
is the frequency response of  at the
at the  th subcarrier. In the sequel, we assume that the
th subcarrier. In the sequel, we assume that the  modulated subcarriers are located within the flat region of
modulated subcarriers are located within the flat region of  . In these circumstances,
. In these circumstances,  reduces to
reduces to

where  has been set equal to unity without loss of generality.
has been set equal to unity without loss of generality.
Notice that our multiuser scenario assumes KL resolvable paths. In practice, KL may be so large to prevent the joint estimation of the DOAs of all active users. To overcome this obstacle, we propose to estimate the DOAs of each user separately. In doing so we first compute estimates of the channel responses and data symbols of all active users. Next we exploit these results to reconstruct the interfering signals and cancel them out from the DFT output, thereby isolating the signal of the desired user. The problem of channel estimation and data detection is accomplished using the method discussed in [12] which provides accurate results with limited complexity. For this purpose, we assume that the MC-CDMA blocks are organized in frames. As shown in Figure 1, each frame is composed by  data blocks preceded by
data blocks preceded by  training blocks that are exploited to get initial estimates of
training blocks that are exploited to get initial estimates of  (acquisition). Such estimates are then updated during the data section of the frame (tracking) by means of the least-mean-square (LMS) algorithm.
(acquisition). Such estimates are then updated during the data section of the frame (tracking) by means of the least-mean-square (LMS) algorithm.
3. DOA Estimation
In this section, we show how the channel estimates and data decisions are exploited to perform DOA estimation. To this end, we denote by  the data decisions and by
the data decisions and by  the estimates of the channel frequency responses. We begin by computing the following quantities during the m th received block:
the estimates of the channel frequency responses. We begin by computing the following quantities during the m th received block:

Substituting (1)-(2) into (7) and assuming  and
and  yields
yields

where we have set  which is valid for PSK constellations. Letting
which is valid for PSK constellations. Letting  , from (6) we see that
, from (6) we see that  can also be written as
can also be written as

It is worth noting that apart from thermal noise, only the contribution of the k th user is present in the right-hand side (RHS) of (9). This amounts to saying that the quantities  are MAI-free and, therefore, they can be used to estimate the DOAs of the k th user. In this way, DOA estimation is performed independently for each active user instead of jointly and the complexity of the overall estimation process is significantly reduced.
are MAI-free and, therefore, they can be used to estimate the DOAs of the k th user. In this way, DOA estimation is performed independently for each active user instead of jointly and the complexity of the overall estimation process is significantly reduced.
As mentioned in Section 2.2, measuring  is equivalent to measuring the DOA
is equivalent to measuring the DOA  . Without loss of generality, in this section we concentrate on the first user and aim at estimating
. Without loss of generality, in this section we concentrate on the first user and aim at estimating  based on the observation of
based on the observation of  . Since the ML estimation of
. Since the ML estimation of  is prohibitively complex as it involves a numerical search over a multidimensional domain, in the sequel we discuss two practical DOA estimators based on the SAGE and ESPRIT algorithms. For notational simplicity, we drop the subscript identifier for the first user.
is prohibitively complex as it involves a numerical search over a multidimensional domain, in the sequel we discuss two practical DOA estimators based on the SAGE and ESPRIT algorithms. For notational simplicity, we drop the subscript identifier for the first user.
3.1. ML Estimation
During the m th received block, the quantities  are arranged into P-dimensional vectors
are arranged into P-dimensional vectors

We assume slow channel variations so that  can be considered practically constant over
can be considered practically constant over  consecutive blocks. Then, we divide the data section of the frame into adjacent segments, each containing
consecutive blocks. Then, we divide the data section of the frame into adjacent segments, each containing  blocks, and compute the following average:
blocks, and compute the following average:

where r is the segment index and R denotes the number of segments within the frame (the number of data blocks in each frame is  ). Substituting (9) into (11), bearing in mind that
). Substituting (9) into (11), bearing in mind that  over the r th segment (i.e., for
over the r th segment (i.e., for  ), yields
), yields

where  ,
,  has entries
has entries  and
and  are statistically independent Gaussian vectors with zero-mean and covariance matrix
are statistically independent Gaussian vectors with zero-mean and covariance matrix  . Letting
. Letting 
 , we may rewrite (12) in the equivalent form
, we may rewrite (12) in the equivalent form

where  has entries
has entries  for
for  .
.
We now jointly estimate  and
and  based on the observation of
based on the observation of  for
for  and
and  . Dropping irrelevant terms and factors, the log-likelihood function for
. Dropping irrelevant terms and factors, the log-likelihood function for  and
and  takes the form
takes the form

where  and
and  are trial values of the unknown parameters while
are trial values of the unknown parameters while  denotes Euclidean norm. Keeping
denotes Euclidean norm. Keeping  fixed and letting
fixed and letting  vary, the minimum of (14) is achieved for
vary, the minimum of (14) is achieved for

Next, substituting (15) into (14) and maximizing with respect to  produce
produce

Unfortunately there is no closed form solution to the maximization of (16). The only possible approach is to perform a search over the L-dimensional space spanned by  . As the computational load would be too intense, in the next subsection we employ the SAGE algorithm to find an approximate solution of (16).
. As the computational load would be too intense, in the next subsection we employ the SAGE algorithm to find an approximate solution of (16).
Remark 1.
The ML estimators (15)-(16) have been derived using channel estimates given in (7). In principle, one can directly use the estimates provided by the LMS channel tracker, which are more or less correlated depending on the value of the step-size employed in the tracking algorithm. In contrast, assuming perfect interference cancellation, it is easily recognized that (7) provides uncorrelated channel estimates that facilitate the derivation of the joint ML estimator of  and
and  . Since the additional complexity involved by (7) is negligible, we have adopted the latter approach.
. Since the additional complexity involved by (7) is negligible, we have adopted the latter approach.
3.2. SAGE-Based Estimation
In a variety of ML estimation problems the maximization of the likelihood function is analytically unfeasible as it involves a numerical search over a huge number of parameters. In these cases the SAGE algorithm proves to be effective as it achieves the same final result with a comparatively simpler iterative procedure. Compared with the more familiar EM algorithm [19], the SAGE has a faster convergence rate. The reason is that the maximizations involved in the EM algorithm are performed with respect to all the unknown parameters simultaneously, which results in a slow process that requires searches over spaces with many dimensions. Vice versa, the maximizations in SAGE are performed varying small groups of parameters at a time. In the following, the SAGE algorithm is applied to our problem without further explanation. The reader is referred to [13] for details.
Returning to the joint estimation of  and
and  , we apply the SAGE algorithm in such a way that the parameters of a single path are updated at a time. This leads to the following procedure consisting of cycles and steps. A cycle is made of L steps and each step updates the parameters of a single path. In particular, the
, we apply the SAGE algorithm in such a way that the parameters of a single path are updated at a time. This leads to the following procedure consisting of cycles and steps. A cycle is made of L steps and each step updates the parameters of a single path. In particular, the  -step of the i th cycle looks for the minimum of
-step of the i th cycle looks for the minimum of

where  is defined as
is defined as

and  denotes the estimate of
denotes the estimate of  at the i th cycle. It is worth noting that
at the i th cycle. It is worth noting that  represents an expurgated version of
represents an expurgated version of  , in which the latest estimates of
, in which the latest estimates of  are exploited to cancel out the multipath interference. Minimizing (17) with respect to
are exploited to cancel out the multipath interference. Minimizing (17) with respect to  produces
produces


with

Note that only one-dimensional searches are involved in (19).
The following remarks are of interest.
-
(1)
The maximization in the RHS of (19) is pursued through a two-step procedure. The first (coarse search) computes
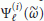 over a grid of
over a grid of 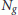 values, say
values, say 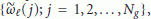 , and determines the location
, and determines the location 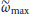 of the maximum. In the second step (fine search) the quantities
of the maximum. In the second step (fine search) the quantities 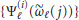 are interpolated and the local maximum nearest to
are interpolated and the local maximum nearest to  is found.
is found. -
(2)
From (21) it follows that
 is a periodic function of
is a periodic function of 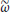 with period
with period 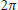 . Thus, the maximum of
. Thus, the maximum of  lies in the interval
lies in the interval 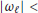 and, in consequence, the estimator (19) gives correct results provided that
and, in consequence, the estimator (19) gives correct results provided that 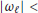 π. From (4) it is seen that this condition is easily met using an antenna array with interelement spacing less than half the free-space wavelength.
π. From (4) it is seen that this condition is easily met using an antenna array with interelement spacing less than half the free-space wavelength. -
(3)
In applying the SAGE we have implicitly assumed knowledge of the number L of paths. In practice L is unknown and must be established in some way. One possible way is to choose L large enough so that all the paths with significant energy are considered. Alternatively, an estimate of L can be obtained in the first cycle as follows. Physical reasons and simulation results indicate that in any cycle the multipath components are taken in a decreasing order of strength. On the other hand, if
 are the estimates of
are the estimates of 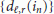 at the first cycle, an indication of the energy of the
at the first cycle, an indication of the energy of the 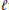 th path is
th path is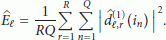 (22)
(22)Thus, the first cycle may be stopped at that step, say
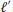 , where
, where 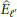 drops below a prefixed threshold and
drops below a prefixed threshold and  may be taken as an estimate of the number of significant paths.
may be taken as an estimate of the number of significant paths. -
(4)
The computational load of the SAGE is assessed as follows. Evaluating
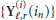 for
for 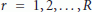 and
and  needs
needs 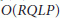 operations at each step. The complexity involved in the computation of
operations at each step. The complexity involved in the computation of 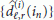 in (20) is
in (20) is 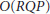 while
while  operations are required to compute the quantities
operations are required to compute the quantities  for
for 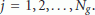 . Denoting
. Denoting  the number of cycles and bearing in mind that each cycle is made of L steps, it follows that the overall complexity of the SAGE is
the number of cycles and bearing in mind that each cycle is made of L steps, it follows that the overall complexity of the SAGE is  .
.
3.3. ESPRIT-Based Estimation
An alternative approach for estimating the DOAs relies on subspace-based methods like the \MUSIC (MUltiple Signal Classication) [20] or ESPRIT algorithms [14]. In the following we discuss DOA estimation based on ESPRIT. The reason is that this method provides estimates in closed form while a grid-search is needed with MUSIC.
To begin, we exploit vectors  in (10) to compute the sample correlation matrix
in (10) to compute the sample correlation matrix

Then, based on the forward-backward (FB) approach [21], we obtain the following modified sample correlation matrix

in which J is the exchange matrix with 1's on its antidiagonal and 0's elsewhere.
In the ESPRIT method, the eigenvectors associated with the L largest eigenvalues of  are arranged into a
are arranged into a  matrix
matrix  . Next, we consider the matrices
. Next, we consider the matrices  and
and  , where 0 is an L-dimensional column vector with zero entries. The estimate of
, where 0 is an L-dimensional column vector with zero entries. The estimate of  is eventually obtained as
is eventually obtained as

where  are the eigenvalues of
are the eigenvalues of

and  denotes the phase angle of
denotes the phase angle of  in the interval
in the interval  .
.
The following remarks are of interest.
-
(1)
A necessary condition for the existence of
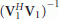 in RHS of (26) is that the number of rows in
in RHS of (26) is that the number of rows in 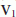 is greater than or equal to the number of columns. Since
is greater than or equal to the number of columns. Since 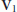 has dimension
has dimension 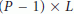 , the above condition implies that
, the above condition implies that  , that is, the number of antennas must be greater than the number of multipath components. We also observe that the inverse of
, that is, the number of antennas must be greater than the number of multipath components. We also observe that the inverse of 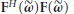 in the ML estimator (16) exists provided that
in the ML estimator (16) exists provided that 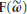 is full rank and
is full rank and 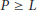 . Thus, DOA estimation with ESPRIT needs one more antenna compared with the ML estimator. It is worth noting that the minimum number of antennas required by both schemes is independent of the number K of contemporarily active users.
. Thus, DOA estimation with ESPRIT needs one more antenna compared with the ML estimator. It is worth noting that the minimum number of antennas required by both schemes is independent of the number K of contemporarily active users. -
(2)
The number of paths can be estimated using the minimum description length (MDL) criterion [22]. To this purpose, let
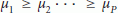 be the eigenvalues of the correlation matrix
be the eigenvalues of the correlation matrix 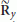 in (24) (arranged in a nonincreasing order of magnitude). Then, an estimate of L is computed as
in (24) (arranged in a nonincreasing order of magnitude). Then, an estimate of L is computed as (27)
(27)where
 is a trial value of L while
is a trial value of L while 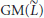 and
and 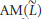 denote the geometric and arithmetic means of
denote the geometric and arithmetic means of  respectively, that is,
respectively, that is, (28)
(28) -
(3)
The complexity of the ESPRIT is assessed as follows. Evaluating
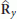 in (23) needs
in (23) needs 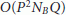 operations. Bearing in mind that inverting an
operations. Bearing in mind that inverting an 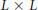 matrix requires
matrix requires  operations, it follows that the complexity involved in the computation of S in (26) is approximately
operations, it follows that the complexity involved in the computation of S in (26) is approximately 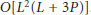 . Finally, computing the eigenvectors of S needs
. Finally, computing the eigenvectors of S needs 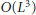 operations. In summary, the overall complexity of the ESPRIT is
operations. In summary, the overall complexity of the ESPRIT is  3P. In writing this figure we have ignored the operations required to compute
3P. In writing this figure we have ignored the operations required to compute  ,
, 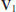 , and
, and  since these matrices are easily obtained from
since these matrices are easily obtained from 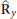 with negligible complexity.
with negligible complexity.
4. Simulation Results
4.1. System Parameters
We consider a cellular system operating over a typical urban area with a cell radius of 1 km. The transmitted symbols belong to a QPSK constellation and are obtained from the information bits through a Gray map. The number of modulated subcarriers is  and the DFT has dimension
and the DFT has dimension  . Walsh-Hadamard codes of length
. Walsh-Hadamard codes of length  are used for spreading purposes. The signal bandwidth is
are used for spreading purposes. The signal bandwidth is  MHz, so that the useful part of each MC-CDMA block has length
MHz, so that the useful part of each MC-CDMA block has length  microseconds. The sampling period is
microseconds. The sampling period is  microsecond and a cyclic prefix of
microsecond and a cyclic prefix of  microseconds is adopted to eliminate interblock interference. This corresponds to an extended block (including the cyclic prefix) of 10 microseconds. The users are synchronous within the cyclic prefix and have the same power. The carrier frequency is
microseconds is adopted to eliminate interblock interference. This corresponds to an extended block (including the cyclic prefix) of 10 microseconds. The users are synchronous within the cyclic prefix and have the same power. The carrier frequency is  GHz (corresponding to a wavelength
GHz (corresponding to a wavelength  cm) and the interelement spacing in the antenna array is
cm) and the interelement spacing in the antenna array is  . The channel impulse responses of the active users are generated as indicated in (3) with three paths (
. The channel impulse responses of the active users are generated as indicated in (3) with three paths ( ). Pulse
). Pulse  has a raised-cosine Fourier transform with roll-off 0.22 and duration
has a raised-cosine Fourier transform with roll-off 0.22 and duration  microsecond. The path delays and DOAs of the desired user are equal to (
microsecond. The path delays and DOAs of the desired user are equal to ( ), (
), ( ), and (
), and ( ). Vice versa, path delays and DOAs of the interfering users are uniformly distributed within [0, 1] microseconds and [
). Vice versa, path delays and DOAs of the interfering users are uniformly distributed within [0, 1] microseconds and [ ], respectively, and are kept constant over a frame. For all active users (including the desired one), the path gains have powers
], respectively, and are kept constant over a frame. For all active users (including the desired one), the path gains have powers

where  is chosen such that the channel energy is normalized to unity, that is,
is chosen such that the channel energy is normalized to unity, that is,  . Each path varies independently of the others within a frame and is generated by filtering a white Gaussian process in a third-order lowpass Butterworth filter. The 3-dB bandwidth of the filter is taken as a measure of the Doppler rate
. Each path varies independently of the others within a frame and is generated by filtering a white Gaussian process in a third-order lowpass Butterworth filter. The 3-dB bandwidth of the filter is taken as a measure of the Doppler rate  , where v denotes the speed of the mobile terminal and
, where v denotes the speed of the mobile terminal and  m/s is the speed of light.
m/s is the speed of light.
A simulation run begins with the generation of the channel responses of each user. Channel acquisition is performed using Walsh-Hadamard training sequences of length  while channel tracking is accomplished by exploiting data decisions provided by a parallel interference cancellation (PIC) receiver [12]. Throughout simulations the number of data blocks per frame is set to
while channel tracking is accomplished by exploiting data decisions provided by a parallel interference cancellation (PIC) receiver [12]. Throughout simulations the number of data blocks per frame is set to  . Once channel estimates and data decisions are obtained, they are passed to the proposed SAGE- or ESPRIT-based DOA estimators. The SAGE computes the function
. Once channel estimates and data decisions are obtained, they are passed to the proposed SAGE- or ESPRIT-based DOA estimators. The SAGE computes the function  over a grid of
over a grid of  values and it is stopped at the end of the second cycle (
values and it is stopped at the end of the second cycle ( ). Parameter
). Parameter  in (11) is fixed to 16, so that
in (11) is fixed to 16, so that  . The mobile velocity, the number of users, and the number of antennas are varied throughout simulations so as to assess their impact on the system performance.
. The mobile velocity, the number of users, and the number of antennas are varied throughout simulations so as to assess their impact on the system performance.
4.2. Performance Assessment
The system performance has been assessed in terms of root mean-square-error (RMSE) of the DOA estimates. For simplicity, the number L of paths is assumed perfectly known at the receiver.
Figure 2 illustrates the performance of the SAGE-based scheme versus  (
( is the average received energy per bit and
is the average received energy per bit and  is the two-sided noise power spectral density) for a half-loaded system (
is the two-sided noise power spectral density) for a half-loaded system ( ). The mobile speed is 10 m/s and the number of sensors in the array is
). The mobile speed is 10 m/s and the number of sensors in the array is  . Marks indicate simulation results while solid lines are drawn to ease the reading. We see that the curves exhibit a floor. In particular, the RMSE of the weakest path is approximately 15 degrees for
. Marks indicate simulation results while solid lines are drawn to ease the reading. We see that the curves exhibit a floor. In particular, the RMSE of the weakest path is approximately 15 degrees for  dB. The appearance of the floor can be explained as follows. Inspection of (19) and (21) reveals that at the first step of the first cycle, the SAGE looks for the maximum of the periodogram
dB. The appearance of the floor can be explained as follows. Inspection of (19) and (21) reveals that at the first step of the first cycle, the SAGE looks for the maximum of the periodogram  . Neglecting the effect of thermal noise, we expect that
. Neglecting the effect of thermal noise, we expect that  has three peaks located at the angular frequencies
has three peaks located at the angular frequencies  for
for  . As is known [21], in periodogram-based methods the width of the main lobe is approximately
. As is known [21], in periodogram-based methods the width of the main lobe is approximately  . It follows that if a pair of angular frequencies are separated by less than
. It follows that if a pair of angular frequencies are separated by less than  , then the corresponding peaks appear as a single broader peak (smearing effect). In these circumstances the two paths cannot be resolved and large estimation errors may occur even in the absence of noise. Note that in Figure 2 we have
, then the corresponding peaks appear as a single broader peak (smearing effect). In these circumstances the two paths cannot be resolved and large estimation errors may occur even in the absence of noise. Note that in Figure 2 we have  ,
,  and
and  , so that the separation between the first and second paths is close to the resolution limit
, so that the separation between the first and second paths is close to the resolution limit  . Extensive simulations (not shown for space limitations) indicate that the floor of the SAGE estimator becomes smaller and smaller as the difference between the powers of the first and second path increases. The reason is that in these circumstances the smearing effect reduces and the parameters of the strongest path can be accurately estimated and canceled out from
. Extensive simulations (not shown for space limitations) indicate that the floor of the SAGE estimator becomes smaller and smaller as the difference between the powers of the first and second path increases. The reason is that in these circumstances the smearing effect reduces and the parameters of the strongest path can be accurately estimated and canceled out from  (see (18)).
(see (18)).
Figure 3 shows simulation results as obtained with the ESPRIT estimator in the same operating conditions of Figure 2. As we see, the RMSE curves have no floor. The reason is that ESPRIT is a high-resolution technique, meaning that it can resolve angular frequencies separated by less than  . Comparing to Figure 2, however, it turns out that the SAGE estimator performs better than the ESPRIT at low signal-to-noise ratios (SNRs).
. Comparing to Figure 2, however, it turns out that the SAGE estimator performs better than the ESPRIT at low signal-to-noise ratios (SNRs).
Figure 4 shows the performance of the SAGE scheme with  ,
,  m/s, and
m/s, and  1, 2, 4, or 8. In order not to overcrowd the figure, only the RMSE of the strongest path is shown. It turns out that the number of active users has little impact on the accuracy of the SAGE-based estimator. In particular, the comparison with the single-user case (
1, 2, 4, or 8. In order not to overcrowd the figure, only the RMSE of the strongest path is shown. It turns out that the number of active users has little impact on the accuracy of the SAGE-based estimator. In particular, the comparison with the single-user case ( 1) demonstrates the effectiveness of the proposed cancellation scheme in combating the multiple-access interference.
1) demonstrates the effectiveness of the proposed cancellation scheme in combating the multiple-access interference.
The same conclusions hold for the ESPRIT-based estimator, as shown by the simulation results reported in Figure 5.
The dependence of the system performance on the number of antennas is shown in Figure 6. As expected, the estimation accuracy improves as P increases. In particular, the floor in the SAGE algorithm is approximately 1.8 degrees when  and reduces to 0.75 degrees with
and reduces to 0.75 degrees with  . This can be explained bearing in mind that the resolution capability of the SAGE estimator increases with P.
. This can be explained bearing in mind that the resolution capability of the SAGE estimator increases with P.
Figure 7 illustrates the performance of the proposed schemes for several mobile speeds. The system is half-loaded and the number of antennas is  . For simplicity, only the RMSE of the strongest path is shown. At first sight the results of this figure look strange in that the system performance improves as the mobile speed increases. The explanation is that the channel variations provide the system with time diversity. Actually, the DOA estimate of a weak multipath component improves if the path strength varies over the frame duration.
. For simplicity, only the RMSE of the strongest path is shown. At first sight the results of this figure look strange in that the system performance improves as the mobile speed increases. The explanation is that the channel variations provide the system with time diversity. Actually, the DOA estimate of a weak multipath component improves if the path strength varies over the frame duration.
Figure 8 shows the complexity of the proposed DOA estimation schemes as a function of the observation length (expressed in number of data blocks per frame). The curves are computed setting  while the other system parameters are chosen as indicated in Section 4.1. The number of iterations with SAGE is either
while the other system parameters are chosen as indicated in Section 4.1. The number of iterations with SAGE is either  or
or  . We see that ESPRIT affords substantial computational saving with respect to the SAGE estimator. For
. We see that ESPRIT affords substantial computational saving with respect to the SAGE estimator. For  , the latter requires approximately
, the latter requires approximately  operations while the ESPRIT allows a reduction of the system complexity by a factor 5.
operations while the ESPRIT allows a reduction of the system complexity by a factor 5.
5. Conclusions
We have discussed a method for estimating the DOAs of the active users in the uplink of an MC-CDMA network. Conventional DOA estimation schemes cannot be directly applied in a multiuser scenario due to the large number of parameters involved in the estimation process. Our solution exploits channel estimates and data decisions to isolate the contribution of each user from the received signal. In this way, DOA estimation is performed independently for each user employing either SAGE or ESPRIT algorithms.
Comparisons between the proposed schemes are not simple because of the different weights that may be given to the various performance indicators, that is, estimation accuracy and computational complexity. It is likely that the choice will depend on the specific application. For example, the ESPRIT is simpler and has good accuracy. On the other hand, the SAGE outperforms ESPRIT at low SNR values but has limited resolution. Using more antenna elements can alleviate this problem at the cost of an increased complexity. Computer simulations indicate that both schemes are robust against multiuser interference and channel variations.
References
Godara LC: Application of antenna arrays to mobile communications—part I: performance improvement, feasibility, and system considerations. Proceedings of the IEEE 1997, 85: 1029-1060.
Naguib AF, Paulraj A, Kailath T: Capacity improvement with base-station antenna arrays in cellular CDMA. IEEE Transactions on Vehicular Technology 1994, 43(3, part 2):691-698. 10.1109/25.312780
Liberti JC Jr., Rappaport TS: Analytical results for capacity improvements in CDMA. IEEE Transactions on Vehicular Technology 1994, 43(3, part 2):680-690. 10.1109/25.312781
Caffery JJ, Stüber GL: Overview of radiolocation in CDMA cellular systems. IEEE Communications Magazine 1998, 36(4):38-45. 10.1109/35.667411
Wax M, Leshem A: Joint estimation of time delays and directions of arrival of multiple reflections of a known signal. IEEE Transactions on Signal Processing 1997, 45(10):2477-2484. 10.1109/78.640713
van der Veen A-J, Vanderveen MC, Paulraj A: Joint angle and delay estimation using shift-invariance techniques. IEEE Transactions on Signal Processing 1998, 46(2):405-418. 10.1109/78.655425
Godara LC: Application of antenna arrays to mobile communications—part II: beam-forming and direction-of-arrival considerations. Proceedings of the IEEE 1997, 85(8):1195-1245. 10.1109/5.622504
Lei Z, Lim TJ: Estimation of directions of arrival of multipath signals in CDMA systems. IEEE Transactions on Communications 2000, 48(6):1022-1028. 10.1109/26.848564
D'Amico AA, Mengali U, Morelli M: DOA and channel parameter estimation for wideband CDMA systems. IEEE Transactions on Wireless Communications 2004, 3(6):1942-1947. 10.1109/TWC.2004.837446
Fazel K: Performance of CDMA/OFDM for mobile communication system. Proceedings of the 2nd International Conference on Universal Personal Communications (ICUPC '93), October 1993, Ottawa, Ontario, Canada 2: 975-979.
Hara S, Prasad R: Overview of multicarrier CDMA. IEEE Communications Magazine 1997, 35(12):126-133. 10.1109/35.642841
Sanguinetti L, Morelli M: Channel acquisition and tracking for MC-CDMA uplink transmissions. IEEE Transactions on Vehicular Technology 2006, 55(3):956-967. 10.1109/TVT.2005.863354
Fessler JA, Hero AO: Space-alternating generalized expectation-maximization algorithm. IEEE Transactions on Signal Processing 1994, 42(10):2664-2677. 10.1109/78.324732
Roy R, Kailath T: ESPRIT-estimation of signal parameters via rotational invariance techniques. IEEE Transactions on Acoustics, Speech, and Signal Processing 1989, 37(7):984-995. 10.1109/29.32276
Deng K, Yin Q, Luo M, Zeng Y: Blind uplink channel and DOA estimator for space-time block coded MC-CDMA system with uniform linear array. Proceedings of the 59th IEEE Vehicular Technology Conference (VTC '04), May 2004, Milan, Italy 1: 69-73.
Tarokh V, Jafarkhani H, Calderbank AR: Space-time block codes from orthogonal designs. IEEE Transactions on Information Theory 1999, 45(5):1456-1467. 10.1109/18.771146
Kaiser S: Multi-carrier CDMA mobile radio systems—analysis and optimization of detection, decoding, and channel estimation, M.S. thesis. VDI-Verlag, Fortschittberichte VDI, University of Kaiserslautern, Dusseldorf, Germany; 1998.
Morelli M: Timing and frequency synchronization for the uplink of an OFDMA system. IEEE Transactions on Communications 2004, 52(2):296-306. 10.1109/TCOMM.2003.822699
Dempster AP, Laird NM, Rubin DB: Maximum likelihood from incomplete data via the EM algorithm. Journal of the Royal Statistical Society 1977, 39(1):1-38.
Schmidt R: Multiple emitter location and signal parameter estimation. Proceedings of the 2nd RADC Spectrum Estimation Workshop, October 1979, Rome, NY, USA 243-258.
Stoica P, Moses R: Introduction to Spectral Analysis. Prentice-Hall, Englewood Cliffs, NJ, USA; 1997.
Wax M, Kailath T: Detection of signals by information theoretic criteria. IEEE Transactions on Acoustics, Speech, and Signal Processing 1985, 33(2):387-392. 10.1109/TASSP.1985.1164557
Acknowledgment
This work has been partly presented to the 6th International Workshop on Multi-Carrier Spread Spectrum (MC-SS 2007), Herrsching, Germany, 2007.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
D'Amico, A.A., Morelli, M. & Sanguinetti, L. DOA Estimation in the Uplink of Multicarrier CDMA Systems. J Wireless Com Network 2008, 851726 (2007). https://doi.org/10.1155/2008/851726
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2008/851726

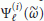 over a grid of
over a grid of 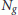 values, say
values, say 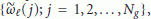 , and determines the location
, and determines the location 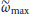 of the maximum. In the second step (fine search) the quantities
of the maximum. In the second step (fine search) the quantities 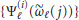 are interpolated and the local maximum nearest to
are interpolated and the local maximum nearest to  is found.
is found. is a periodic function of
is a periodic function of 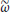 with period
with period 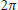 . Thus, the maximum of
. Thus, the maximum of  lies in the interval
lies in the interval 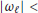 and, in consequence, the estimator (19) gives correct results provided that
and, in consequence, the estimator (19) gives correct results provided that 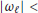 π. From (4) it is seen that this condition is easily met using an antenna array with interelement spacing less than half the free-space wavelength.
π. From (4) it is seen that this condition is easily met using an antenna array with interelement spacing less than half the free-space wavelength. are the estimates of
are the estimates of 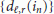 at the first cycle, an indication of the energy of the
at the first cycle, an indication of the energy of the 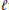 th path is
th path is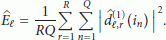
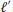 , where
, where 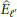 drops below a prefixed threshold and
drops below a prefixed threshold and  may be taken as an estimate of the number of significant paths.
may be taken as an estimate of the number of significant paths.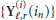 for
for 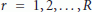 and
and  needs
needs 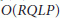 operations at each step. The complexity involved in the computation of
operations at each step. The complexity involved in the computation of 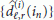 in (20) is
in (20) is 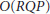 while
while  operations are required to compute the quantities
operations are required to compute the quantities  for
for 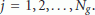 . Denoting
. Denoting  the number of cycles and bearing in mind that each cycle is made of L steps, it follows that the overall complexity of the SAGE is
the number of cycles and bearing in mind that each cycle is made of L steps, it follows that the overall complexity of the SAGE is  .
.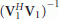 in RHS of (26) is that the number of rows in
in RHS of (26) is that the number of rows in 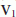 is greater than or equal to the number of columns. Since
is greater than or equal to the number of columns. Since 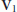 has dimension
has dimension 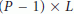 , the above condition implies that
, the above condition implies that  , that is, the number of antennas must be greater than the number of multipath components. We also observe that the inverse of
, that is, the number of antennas must be greater than the number of multipath components. We also observe that the inverse of 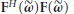 in the ML estimator (16) exists provided that
in the ML estimator (16) exists provided that 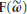 is full rank and
is full rank and 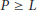 . Thus, DOA estimation with ESPRIT needs one more antenna compared with the ML estimator. It is worth noting that the minimum number of antennas required by both schemes is independent of the number K of contemporarily active users.
. Thus, DOA estimation with ESPRIT needs one more antenna compared with the ML estimator. It is worth noting that the minimum number of antennas required by both schemes is independent of the number K of contemporarily active users.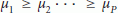 be the eigenvalues of the correlation matrix
be the eigenvalues of the correlation matrix 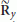 in (24) (arranged in a nonincreasing order of magnitude). Then, an estimate of L is computed as
in (24) (arranged in a nonincreasing order of magnitude). Then, an estimate of L is computed as
 is a trial value of L while
is a trial value of L while 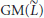 and
and 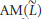 denote the geometric and arithmetic means of
denote the geometric and arithmetic means of  respectively, that is,
respectively, that is,
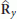 in (23) needs
in (23) needs 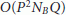 operations. Bearing in mind that inverting an
operations. Bearing in mind that inverting an 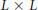 matrix requires
matrix requires  operations, it follows that the complexity involved in the computation of S in (26) is approximately
operations, it follows that the complexity involved in the computation of S in (26) is approximately 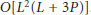 . Finally, computing the eigenvectors of S needs
. Finally, computing the eigenvectors of S needs 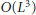 operations. In summary, the overall complexity of the ESPRIT is
operations. In summary, the overall complexity of the ESPRIT is  3P. In writing this figure we have ignored the operations required to compute
3P. In writing this figure we have ignored the operations required to compute  ,
,  , and
, and  since these matrices are easily obtained from
since these matrices are easily obtained from  with negligible complexity.
with negligible complexity.
 , and
, and  m/s.
m/s.
 ,
,  and
and  m/s.
m/s.
 ,
,  m/s, and some values of K
m/s, and some values of K
 ,
,  m/s, and some values of K
m/s, and some values of K 
 ,
,  m/s, and
m/s, and  or 8
or 8
 ,
,  and some mobile speeds.
and some mobile speeds.
 .
.