- Research Article
- Open access
- Published:
Resource Partitioning with Beamforming for the Decode-Forward Relay Networks
EURASIP Journal on Wireless Communications and Networking volume 2008, Article number: 853164 (2007)
Abstract
A joint power and time slot partitioning scheme based on the channel status information (CSI) is proposed for networks of multiple relays using decode and forward (DF) protocol. A set of power constraints for the famous water pouring method is presented depending on the time slot partitioning and CSI. Optimizing the timing and the power distributions enhances the network throughput in addition to the diversity advantage well known for the open loop relay protocols. Beamforming techniques for the source or destination with multiple antennas are also proposed and utilized in the partitioning process.
1. Introduction
Due to the cost and size of mobile user terminals, the number of multiple antennas that can be mounted on them is limited in practice. Distributed antenna systems or user cooperation techniques (see [1–6]) have been proposed as an alternative or supplementary technology to enhance existing wireless links without multiple antennas on each terminal. The diversity enhancement capability of cooperative relaying has been the main concern of the research community for the last few years (see [2–6]). In support of this approach, the popular amplify-forward (AF) and DF protocols were introduced in [3].
Because of the half duplex constraint, it is anticipated that a loss in the throughput of a relay network is inevitable compared to the direct transmission. (The source uses only the half of its transmission time.) This is demonstrated in the diversity-multiplexing tradeoff (DMT) analysis of relaying protocols [2], where the diversity is shown to be acquired at the expense of throughput loss. Azarian et al. propose the dynamic decode-forward (DDF) protocol to recover the throughput loss in DF protocol [7] by allowing the size of relay cooperation phase to vary adaptively depending on the channel status information (CSI) of the source-to-relay channel.
When the CSI is available at the transmitter in the closed loop systems, we can further optimize resources of the relaying networks to enhance not only the diversity but also the throughput. (In practice, only quantized CSI is available at the transmitter due to the bandwidth limitation of feedback channels. Thus, the full CSI assumption is the limiting case when the feedback channels expand their bandwidth to infinity. In [8], it is shown that the performance of AF relay power control with full CSI can be approached with small amount of feedback information. We leave the analysis of finite feedback effect in DF resource partitioning for future work.) In [8], a set of power allocation techniques for the AF relaying is considered for the full and finite feedback strategies. Optimization of power distribution in the symbol error sense is considered for the AF relay networks [9] and DF relay [5] networks, respectively. The authors in [10] present power allocation techniques for the relay protocols based on the long-term statistics of CSI. Instant CSI-based approach is taken in [11], where the power and the time slot are jointly optimized for the DF relays.
As shown in [7], the time slot partitioning based on CSI is crucial in targeting the throughput enhancement. In this paper, we try to show that appropriate partitioning of the resources (power and time slots) enhances the diversity and the throughput of DF relaying system at the same time. Contrary to [11], where only the relay-to-destination link is considered, we consider the combined link of source-to-destination and relay-to-destination links. Consequently, the resulting optimization applies the famous water pouring method with different power constraints depending on the time slot division and CSI. The best time slot division with the maximum mutual information is searched along with the power allocation for that specific time division. As a way to quantify the throughput enhancement by the resource partitioning, the probability of choosing relay cooperation over the direct transmission is analyzed and compared to that of DDF protocol in [7]. To cover more general settings, we consider the multiple relay case and the multiple antenna case as well. For the multiple relay case, it is shown that the resource partitioning based on relay selection is enough to find the best relaying configuration. When multiple antennas are used at the source, we propose a way to combine beamforming with the resource partitioning proposed.
After introducing system model in Section 2, resource partitioning with multiple relays and analysis of the relaying probability are presented in Section 3. The method to combine beamforming with the resource partitioning is presented in Section 4. We analyze and present the simulation results in Section 5. Section 6 concludes this paper.
2. System Model
The system model and channel gains ( ) of the relay network are shown in Figure 1. In the DF protocol, the source sends the information toward the destination with power
) of the relay network are shown in Figure 1. In the DF protocol, the source sends the information toward the destination with power  during the first time slot (
during the first time slot ( ). The th relay overhears this transmission. If it succeeds in decoding the message, it then re-encode the message with an independent code-book and transmits with power
). The th relay overhears this transmission. If it succeeds in decoding the message, it then re-encode the message with an independent code-book and transmits with power  during the second time slot (
during the second time slot ( ). Otherwise, the relay remains silent. Note time slot
). Otherwise, the relay remains silent. Note time slot  is divided such that
is divided such that  to support the source and relay transmissions. The destination leverages the observations from the two time slots to make the final decision of the
to support the source and relay transmissions. The destination leverages the observations from the two time slots to make the final decision of the  bits of information sent.
bits of information sent.
Let us denote the distance of each link by  . The channel gains are assumed to be Rayleigh distributed with
. The channel gains are assumed to be Rayleigh distributed with  . (The exponent
. (The exponent  denotes the path loss exponent. This is set to 2 in the simulations in Section 5.) The power of the additive noise at the relay and destination is assumed to be 1.
denotes the path loss exponent. This is set to 2 in the simulations in Section 5.) The power of the additive noise at the relay and destination is assumed to be 1.
3. Resource Partitioning and Relaying Probability
With full CSI at hand and  DF relays, we have an event space
DF relays, we have an event space  of
of  non overlapping elements, that is, 0th event corresponds to direct transmission with no relay cooperation and
non overlapping elements, that is, 0th event corresponds to direct transmission with no relay cooperation and  th event corresponds to full cooperation with
th event corresponds to full cooperation with  relays. Finding the optimum resource partitioning in each event and selecting the best choice among these event set gives the optimum resource allocation. We will see that this
relays. Finding the optimum resource partitioning in each event and selecting the best choice among these event set gives the optimum resource allocation. We will see that this  search space can be reduced to
search space can be reduced to  . The outage is defined to be the event when the mutual information from the source to the destination falls below the given rate. With the power constrain
. The outage is defined to be the event when the mutual information from the source to the destination falls below the given rate. With the power constrain  , we find the resource partitioning which minimizes the outage probability at the given rate
, we find the resource partitioning which minimizes the outage probability at the given rate  .
.
3.1. Resource Partitioning
Let  denotes the set of active relays in the th event (
denotes the set of active relays in the th event ( ). If
). If  and
and  , then the
, then the  th event is supported when all the links from the source to the relays in
th event is supported when all the links from the source to the relays in  have the mutual information greater than
have the mutual information greater than  . Otherwise, this event is discarded from further consideration. This condition is described mathematically as
. Otherwise, this event is discarded from further consideration. This condition is described mathematically as

where  and the source power
and the source power  and
and  for the
for the  th event will be determined later. Note that
th event will be determined later. Note that  is the condition when the
is the condition when the  th event is discarded from the consideration.
th event is discarded from the consideration.
Suppose the relays in  are not in outage, then the mutual information from the source to the destination is
are not in outage, then the mutual information from the source to the destination is

where  . (Authors in [2] used orthogonal space-time block coding among the relays in the set
. (Authors in [2] used orthogonal space-time block coding among the relays in the set  so that the multipaths from the relays can be coherently combined at the destination, which results in the mutual information of MISO channels as in the last logarithm expression of (2). Note the coherent combining of the MISO channel multipaths can also be done by precoding.) The last term in (2) can be maximized by allocationg all the relay power
so that the multipaths from the relays can be coherently combined at the destination, which results in the mutual information of MISO channels as in the last logarithm expression of (2). Note the coherent combining of the MISO channel multipaths can also be done by precoding.) The last term in (2) can be maximized by allocationg all the relay power  to the one with the best link to the destination (
to the one with the best link to the destination ( ). Thanks to this condition, we care for only the link toward this relay from the source not to be in outage and do not mind the links toward other relays in
). Thanks to this condition, we care for only the link toward this relay from the source not to be in outage and do not mind the links toward other relays in  . Thus, the search over
. Thus, the search over  event space can be reduced to the size
event space can be reduced to the size  space if we consider the events with only one relay helping the source. For each event, we find the resource distributions which maximize the throughput.
space if we consider the events with only one relay helping the source. For each event, we find the resource distributions which maximize the throughput.
Let  be the event when the
be the event when the  th relay is helping the source transmission and
th relay is helping the source transmission and  be the event no relay is helping the source transmission. Then, we have
be the event no relay is helping the source transmission. Then, we have

Note that in  ,
,  and
and  . Given
. Given  with the power constraints (1) and
with the power constraints (1) and  , (3) is known to be maximized by water pouring method. Thus, the optimal power distribution when
, (3) is known to be maximized by water pouring method. Thus, the optimal power distribution when  is
is

where  is the Lagrange multiplier and
is the Lagrange multiplier and  . By substituting
. By substituting  into the power constraint
into the power constraint  , we have
, we have

which leads to the following power distribution

The channel condition and  determines which combination of thresholds (
determines which combination of thresholds ( and
and  ) in (4) is applied. Depending on these combinations and CSI, we divide the power distribution scenario into the following four cases.
) in (4) is applied. Depending on these combinations and CSI, we divide the power distribution scenario into the following four cases.
-
(1)
When
 (i.e.,
(i.e., 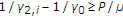 ), then it is forced to be
), then it is forced to be 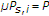 . The maximum mutual information is
. The maximum mutual information is 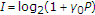 when
when 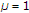 . This case is equivalent to the 0th event and is dismissed from further consideration.
. This case is equivalent to the 0th event and is dismissed from further consideration. -
(2)
When
 (i.e.,
(i.e., 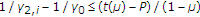 ) and
) and  , the mutual information is given as
, the mutual information is given as  (7)
(7)
-
(3)
When both
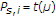 and
and 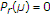 are satisfied at the same time (i.e.,
are satisfied at the same time (i.e., 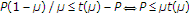 ), then the condition
), then the condition  dominates the condition
dominates the condition  . Hence,
. Hence, 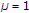 is forced and the case is dismissed as in the first case.
is forced and the case is dismissed as in the first case. -
(4)
Otherwise, the mutual information is
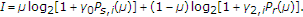 (8)
(8)
With the third case, the interval  of
of  is divided into two sections
is divided into two sections  and
and  with
with  ; the first section, where the condition
; the first section, where the condition  is met, is discarded. The condition for the first case also divides the interval into two sections
is met, is discarded. The condition for the first case also divides the interval into two sections  and
and  with
with  ; the second section is the region discarded this time. The condition
; the second section is the region discarded this time. The condition  makes all the values of
makes all the values of  to be trapped in the first or the third case and the event
to be trapped in the first or the third case and the event  is dismissed. Otherwise, the condition for the second case divides the remaining interval into two sections
is dismissed. Otherwise, the condition for the second case divides the remaining interval into two sections  and
and  with
with  ; (7) is used for
; (7) is used for  and (8) is used for
and (8) is used for  to find
to find  that maximizes the mutual information for the event
that maximizes the mutual information for the event  . This process is repeated for all
. This process is repeated for all  and the best resource partitioning among the
and the best resource partitioning among the  events is found. If the maximum mutual information does not support the rate
events is found. If the maximum mutual information does not support the rate  with the power constraint
with the power constraint  , then the channel is in outage. As a baseline system, we consider the case where
, then the channel is in outage. As a baseline system, we consider the case where  is confined to be in the set
is confined to be in the set  .
.
3.2. Relaying Probability
While open loop DF protocol trades the throughput with the diversity gain (see [2]), the DMT analysis of DDF protocol in [7] shows that it achieves the diversity without much throughput loss compared to DF protocol. Hence in this subsection, we compare the proposed scheme with DDF in throughput aspect.
The DDF protocol tries to control the cooperation phase without power control, hence it seems that the DDF performs worse than the proposed scheme in this paper. But, the source in the DDF protocol continues the transmission during the time the relays cooperate, which is an advantage over the proposed system. Since the proposed system outperforms both the source-to-destination direct link and the conventional DF protocol where  is fixed to
is fixed to  , the union of DMT curves of these protocols lower bound that of the proposed system. On the other hand, it is obvious that the proposed scheme performs worse than MISO or SIMO links with
, the union of DMT curves of these protocols lower bound that of the proposed system. On the other hand, it is obvious that the proposed scheme performs worse than MISO or SIMO links with  antennas since these correspond to perfect source-to-relay channels or relay-to-destination channels respectively. Thus, DMT curves of these links upper bound that of the proposed scheme. From this observation, we can conclude that the proposed joint time slot and power partitioning introduces the diversity advantage without sacrificing the throughput.
antennas since these correspond to perfect source-to-relay channels or relay-to-destination channels respectively. Thus, DMT curves of these links upper bound that of the proposed scheme. From this observation, we can conclude that the proposed joint time slot and power partitioning introduces the diversity advantage without sacrificing the throughput.
In another view, the probability that  are selected quantifies how much the relaying contributes to this throughput enhancement. In Section 3, it is shown that a relay cooperates when two independent events
are selected quantifies how much the relaying contributes to this throughput enhancement. In Section 3, it is shown that a relay cooperates when two independent events  occur at the same time. The probability that at least a relay among
occur at the same time. The probability that at least a relay among  relays cooperates with the time slot partitioning
relays cooperates with the time slot partitioning  is
is

Supposing that  and
and  are Chi-square distributed with degree 2 and
are Chi-square distributed with degree 2 and  being the statistical average of
being the statistical average of  , then we have the following lower bound:
, then we have the following lower bound:

where we used the two tangential lines of  at
at  and
and  for the lower bounding. The approximation holds at high SNR. Sending
for the lower bounding. The approximation holds at high SNR. Sending  allows us to send
allows us to send  , the minimum value of
, the minimum value of  in the saved section, to
in the saved section, to  . Then,
. Then,  and
and  send (10) to
send (10) to

Consider the DDF protocol [7], where the source and relay power are fixed as  and the system controls
and the system controls  for the minimum outage transmission. In this case, the cooperation of the
for the minimum outage transmission. In this case, the cooperation of the  th relay is selected if the conditions
th relay is selected if the conditions  and
and  occur at the same time with
occur at the same time with  . Then, we have
. Then, we have

Comparing this to (11) and assuming  , (11) is much closer to 1 than (12).
, (11) is much closer to 1 than (12).
Compared to the fixed time slot case where  is confined to be in the set
is confined to be in the set  , we can certainly find better
, we can certainly find better  with larger cooperation probability than
with larger cooperation probability than  . These analysis show that the joint partitioning of time slot and power has larger cooperation probability than the partitioning of individual resource only, thus contributes to the throughput enhancement.
. These analysis show that the joint partitioning of time slot and power has larger cooperation probability than the partitioning of individual resource only, thus contributes to the throughput enhancement.
4. Beamforming
Recent developments show that multiple antenna technology is the key ingredient in enhancing the wireless communication performance. Therefore, we expect further enhancement of relaying networks by exploiting the beamforming gain from multiple antennas. In this section, we propose methods to combine beamforming and resource partitioning in Section 3 when multiple transmit antennas are used at the source or at the destination. First, we assume  transmit antennas at the source and single antenna for the relays and the destination. The channel gains
transmit antennas at the source and single antenna for the relays and the destination. The channel gains  are
are  -dimensional vectors and
-dimensional vectors and  are scalars.
are scalars.
Suppose  is the beamforming vector applied at the source and
is the beamforming vector applied at the source and  is the event being considered. We have
is the event being considered. We have  , where
, where  when
when  . The mutual information for this event is given as
. The mutual information for this event is given as

From the condition for the third case in Section 3, it is easy to see that  is decreased if
is decreased if  increased. Since
increased. Since  is the interval with a weakest constraint, we can, obviously, expect better outage performance with a wide second section. Also, increasing
is the interval with a weakest constraint, we can, obviously, expect better outage performance with a wide second section. Also, increasing  contributes for the better mutual information in (8). Thus,
contributes for the better mutual information in (8). Thus,  should be jointly matched to
should be jointly matched to  and
and  .
.
The vector  can be decomposed as
can be decomposed as

where  is perpendicular to
is perpendicular to  . If we set
. If we set  , the vector
, the vector  is positioned between vector
is positioned between vector  and vector
and vector  as shown in Figure 2 and we have
as shown in Figure 2 and we have  and
and  . This parametrization gives
. This parametrization gives  and
and

Optimum point in the parameter space determined by  and
and  is to be searched with the four cases as in Section 3 depending on these parameter values.
is to be searched with the four cases as in Section 3 depending on these parameter values.
When there are  receive antennas at the destination and single antenna for the relays and the source, the channel gains
receive antennas at the destination and single antenna for the relays and the source, the channel gains  are
are  -dimensional vectors and
-dimensional vectors and  are scalars. Since the source and relay transmissions use orthogonal channels in time, we can apply different receive beamforming vectors (
are scalars. Since the source and relay transmissions use orthogonal channels in time, we can apply different receive beamforming vectors ( ) for these transmissions. In the event
) for these transmissions. In the event  ,
,  is applied for the source transmission and
is applied for the source transmission and  is applied for the relay transmission.
is applied for the relay transmission.
5. Simulation
In Figure 3, the cumulative distributions of mutual information corresponding to different resource partitioning schemes are plotted. The signal to noise ratio ( ) is set to 10 dB. For the time slot partitioning, we quantize
) is set to 10 dB. For the time slot partitioning, we quantize  into
into  uniform length regions, the quantized values of which are tested for the maximum mutual information with appropriate power allocation as in Section 3. For the beamforming, the angle
uniform length regions, the quantized values of which are tested for the maximum mutual information with appropriate power allocation as in Section 3. For the beamforming, the angle  is quantized into 4 uniform regions. Hence,
is quantized into 4 uniform regions. Hence,  quantized regions are tested for the set of
quantized regions are tested for the set of  and
and  . Note the power only control case corresponds to 2-level quantization, hence is different from open loop scheme because it relies on CSI and chooses
. Note the power only control case corresponds to 2-level quantization, hence is different from open loop scheme because it relies on CSI and chooses  , that is, the direct source-to-destination link, according to the conditions in Section 3. With power allocation only, more than three-fold increase in the rate is observed with
, that is, the direct source-to-destination link, according to the conditions in Section 3. With power allocation only, more than three-fold increase in the rate is observed with  outage probability. Joint power and time slot partitioning gives additional
outage probability. Joint power and time slot partitioning gives additional  and the beamforming gives another
and the beamforming gives another  at the same outage probability.
at the same outage probability.
The outage probabilities of different schemes against the SNR ( ) are plotted in Figure 4. Besides that the number of relays is one, all the conditions are the same as in Figure 3. The slopes of the curves represent the diversity order enhancement from the relaying. As shown in Figure 4(a), the resource partitioning schemes give additional power gain over the transmission scheme without relay. As the rate (
) are plotted in Figure 4. Besides that the number of relays is one, all the conditions are the same as in Figure 3. The slopes of the curves represent the diversity order enhancement from the relaying. As shown in Figure 4(a), the resource partitioning schemes give additional power gain over the transmission scheme without relay. As the rate ( ) increases from
) increases from  to
to  , the benefit of partitioning time slot becomes prominent.
, the benefit of partitioning time slot becomes prominent.
6. Conclusion
We present a joint time slot and power partitioning scheme along with a beamforming strategy for the network with multiple DF relays possibly with multiple antennas at the source or destination. Based on the CSI information, the proposed scheme further enhances the throughput as well as the diversity advantage known in open loop relay networks. The analysis of relaying probability indicates the enhancement from the resource partitioning. Supporting simulation results are presented.
References
Sendonaris A, Erkip E, Aazhang B: User cooperation diversity. Part I. System description. IEEE Transactions on Communications 2003, 51(11):1927-1938. 10.1109/TCOMM.2003.818096
Laneman JN, Wornell GW: Distributed space-time coded protocols for exploiting cooperative diversity in wireless networks. IEEE Transactions on Information Theory 2003, 49(10):2415-2425. 10.1109/TIT.2003.817829
Laneman JN, Tse DNC, Wornell GW: Cooperative diversity in wireless networks: efficient protocols and outage behavior. IEEE Transactions on Information Theory 2004, 50(12):3062-3080. 10.1109/TIT.2004.838089
Janani M, Hedayat A, Hunter TE, Nosratinia A: Coded cooperation in wireless communications: space-time transmission and iterative decoding. IEEE Transactions on Signal Processing 2004, 52(2):362-371. 10.1109/TSP.2003.821100
Scutari G, Barbarossa S: Distributed space-time coding for regenerative relay networks. IEEE Transactions on Wireless Communications 2005, 4(5):2387-2399.
Stefanov A, Erkip E: Cooperative coding for wireless networks. IEEE Transactions on Communications 2004, 52(9):1470-1476. 10.1109/TCOMM.2004.833070
Azarian K, El Gamal H, Schniter P: On the achievable diversity-multiplexing tradeoff in half-duplex cooperative channels. IEEE Transactions on Information Theory 2005, 51(12):4152-4172. 10.1109/TIT.2005.858920
Ahmed N, Khojastepour MA, Sabharwal A, Aazhang B: Outage minimization with limited feedback for the fading relay channel. IEEE Transactions on Communications 2006, 54(4):659-669.
Anghel PA, Kaveh M: On the performance of distributed space-time coding systems with one and two non-regenerative relays. IEEE Transactions on Wireless Communications 2006, 5(3):682-692.
Annavajjala R, Cosman PC, Milstein LB: Statistical channel knowledge-based optimum power allocation for relaying protocols in the high SNR regime. IEEE Journal on Selected Areas in Communications 2007, 25(2):292-305.
Larsson EG, Cao Y: Collaborative transmit diversity with adaptive radio resource and power allocation. IEEE Communications Letters 2005, 9(6):511-513. 10.1109/LCOMM.2005.1437354
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Hwang, D., Kim, J. & Kim, S. Resource Partitioning with Beamforming for the Decode-Forward Relay Networks. J Wireless Com Network 2008, 853164 (2007). https://doi.org/10.1155/2008/853164
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2008/853164

 (i.e.,
(i.e., 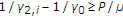 ), then it is forced to be
), then it is forced to be 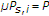 . The maximum mutual information is
. The maximum mutual information is 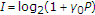 when
when 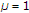 . This case is equivalent to the 0th event and is dismissed from further consideration.
. This case is equivalent to the 0th event and is dismissed from further consideration. (i.e.,
(i.e., 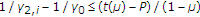 ) and
) and  , the mutual information is given as
, the mutual information is given as 
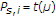 and
and 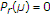 are satisfied at the same time (i.e.,
are satisfied at the same time (i.e., 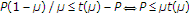 ), then the condition
), then the condition  dominates the condition
dominates the condition  . Hence,
. Hence, 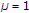 is forced and the case is dismissed as in the first case.
is forced and the case is dismissed as in the first case.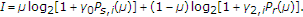

 , and
, and  vectors.
vectors.

 , (b) when
, (b) when  ; one relay is used.
; one relay is used.