- Research Article
- Open access
- Published:
Stochastic Resource Allocation for Energy-Constrained Systems
EURASIP Journal on Wireless Communications and Networking volume 2009, Article number: 246439 (2009)
Abstract
Battery-powered wireless systems running media applications have tight constraints on energy, CPU, and network capacity, and therefore require the careful allocation of these limited resources to maximize the system's performance while avoiding resource overruns. Usually, resource-allocation problems are solved using standard knapsack-solving techniques. However, when allocating conservable resources like energy (which unlike CPU and network remain available for later use if they are not used immediately) knapsack solutions suffer from excessive computational complexity, leading to the use of suboptimal heuristics. We show that use of Lagrangian optimization provides a fast, elegant, and, for convex problems, optimal solution to the allocation of energy across applications as they enter and leave the system, even if the exact sequence and timing of their entrances and exits is not known. This permits significant increases in achieved utility compared to heuristics in common use. As our framework requires only a stochastic description of future workloads, and not a full schedule, we also significantly expand the scope of systems that can be optimized.
1. Introduction
The goal of resource allocation is to assign a system's resources to applications in the way that maximizes the system's utility to the user. Resource allocation is in general a difficult problem, and as a result the allocation of resources to multiple applications in a multimedia system has seen considerable research. Ideally, we would be able to allocate resources—CPU time, network bandwidth, energy—in a way that best reflects the user's needs and hence maximizes the utility achieved by the user.
We specifically consider the case of a mobile system that performs several simultaneous tasks, each of which can be reconfigured in several modes with a variety of different CPU and network utilizations. Each of the modes is associated with a specific utility value that represents the quality of service in some way that is meaningful to the user.
In the traditional problem setup, allocation is done by assuming that the same tasks will run from startup until a specified future time [1]. If this is the case, the energy constraint and runtime constraint can be converted into a single constraint on power consumption, and the allocation problem can then be converted into an ordinary knapsack problem, subject to the constraints on network load, CPU load, and system power. Although the resulting allocation problem is an NP-hard knapsack problem, it is usually small enough to be computationally tractable and also tends to be amenable to fast heuristic solutions [2, 3].
In the context of unvarying workloads, the available energy and requested runtime are converted into a power constraint, and the resulting allocation is optimal if the system is allowed to run until the battery is exhausted. However, the runtime may be longer than requested due to the discrete selection of available application configurations.
The allocation problem where all workloads vary, but are all known in advance, can be solved using a straightforward extension of the techniques used for a single workload: the conversion to a knapsack problem by simultaneously considering all sets of applications. In this form, the energy constraint would be left unconverted, and the knapsack problem would optimize utility over all sets of applications that run during the battey's lifetime. In this case, there is a set of four constraints: CPU time, network bandwidth, desired runtime, and total energy available. However, this optimization problem is particularly complex as it requires the evaluation of a cross product of all configurations for each set of applications that will run during the entire running time of the system.
Due to the complexity of this optimization problem, various simplifications have been proposed. One approach to solve the energy-allocation problem involves creating a list of applications that will run in the future, and allocating energy to each of these applications in priority order [4]. Although this greedy heuristic can approach optimality if applications are being admitted only and do not have variable utility, it does not support applications with multiple possible utility levels and does not always have a clear ordering when multiple resources are considered. Another approach involves the use of various suboptimal optimization strategies, including the integer programming techniques described by Lee [3] and a fast heuristic solution to the underlying multidimensional multichoice knapsack described by Moser [2].
There is also an important class of problems in this family that have not been addressed in the literature; cases where the workload schedule is not known in advance, and instead only a probability distribution of workloads is known.
The theory of Lagrangian optimization [5] offers a framework in which we can optimally allocate resources under relatively weak convexity assumptions, and hence provides an approach we can take to solve this entire class of allocation problems without needing to solve a full NP-hard optimization problem. In addition to providing a direct solution to the scheduling of multiple workloads known in advance, the Lagrangian approach also allows us to solve the allocation problem stochastically, permitting statisically optimal allocations to be made even if we have only a probability distribution of the workloads that are to be run. In other words, through the use of the Lagrangian framework, we must know only what might run, and not necessarily if or when.
2. Stochastic Allocation Problem
Consider a battery-powered wireless security monitor system consisting of a controller and multiple cameras, placed to monitor an area for specified period of time. For much of the time, the area it is monitoring shows nothing of interest, and the utility gained by providing a high-quality representation of the area is low. Sometimes we may know when interesting events (such as a person appearing within the view of the camera) will occur; for example, when the facility being monitored opens and closes. But also consider the case where, while , for example, we may know from prior experience that  of the time, events of interest will occur, we do not know in advance exactly when these events will occur or which camera or cameras will see them. In either case, it is important that all of the cameras operate for the entire requested interval, and that when events of interest occur we get high-quality video from all of the cameras that have views of the events. This setup describes a stochastic allocation problem, which we analyze as a variant of the prescheduled workload problem described in [4]. Unlike the setup in [4], instead of having a list of workloads and the time periods that they are active, we have a list of potential or representative workloads, and probabilities that they are active at any given time instant.
of the time, events of interest will occur, we do not know in advance exactly when these events will occur or which camera or cameras will see them. In either case, it is important that all of the cameras operate for the entire requested interval, and that when events of interest occur we get high-quality video from all of the cameras that have views of the events. This setup describes a stochastic allocation problem, which we analyze as a variant of the prescheduled workload problem described in [4]. Unlike the setup in [4], instead of having a list of workloads and the time periods that they are active, we have a list of potential or representative workloads, and probabilities that they are active at any given time instant.
This setup describes a stochastic allocation problem that differs from problems previously solved in the literature in that not only are applications entering and exiting the system, but they are doing so in an unscheduled and unpredictable way. We know in advance only that the tasks may appear with a certain probability, not when or even if they will.
2.1. Utility Model
The utility model we use is that each application configuration is assigned a "utility rate" that is additive across applications and time. In other words, if we select a particular application configuration, we credit the system with its corresponding utility for as long as that configuration is active. We further assume that the utility of the application configurations increases as the resource utilization increases, and that the utility/energy curve of the applications being optimized is convex or nearly so, which implies a diminishing return in utility as more energy is expended.
For our experiments, we assigned increasing utility rates to application configurations as the frame rate and number of quantizer steps are increased. However, our utility model is general enough to permit the replacement of these assigned utilities with values that better reflect the actual utility of the tasks, for example, by assigning utility based on perceptual values of video quality derived from human trials.
2.2. Problem Formulation
Inputs to this optimization problem are an application list and the state of the system. Each application entry includes data providing estimates of the CPU utilization, network utilization, and utility associated with each configuration for the application. Network and CPU constraints are implemented using these utilization values, which represent a fraction of the total network and CPU time available used for a particular application. To avoid overloading the resource, the total utilization of both the CPU and the network must be less than or equal to 1.
Each application is represented with a unique ID  ;
;  represents the CPU operating frequency for a particular application, and
represents the CPU operating frequency for a particular application, and  is the selected configuration ID for the application. Applications entering and leaving the system result in a switch to a new workload. The utility of a particular workload is equal to the sum of the selected configurations of all applications running in a particular workload. The objective of the optimization is to maximize the integral of the sum of instant utilities of all running applications over the desired system runtime, such that at no point the CPU and network bounds are exceeded and the total energy consumed over the specified runtime
is the selected configuration ID for the application. Applications entering and leaving the system result in a switch to a new workload. The utility of a particular workload is equal to the sum of the selected configurations of all applications running in a particular workload. The objective of the optimization is to maximize the integral of the sum of instant utilities of all running applications over the desired system runtime, such that at no point the CPU and network bounds are exceeded and the total energy consumed over the specified runtime  is less than or equal to the starting battery energy
is less than or equal to the starting battery energy  .
.
We define the term  to be the probability of workload
to be the probability of workload  —that is, a combination of applications we index using
—that is, a combination of applications we index using  —being active at any given time instant. In other words, it is the probability that the system is running that particular combination of applications. We further assume independence of applications running at different times. While this assumption is generally false, if battery lifetime is long enough, the actual distribution of applications running during the lifetime of the battery will be close to the a priori probabilities.
—being active at any given time instant. In other words, it is the probability that the system is running that particular combination of applications. We further assume independence of applications running at different times. While this assumption is generally false, if battery lifetime is long enough, the actual distribution of applications running during the lifetime of the battery will be close to the a priori probabilities.  is computed as:
is computed as:

With these assumptions, the stochastic resource allocation problem can be stated as

where
-
(i)
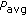 : average total system power (in Watts);
: average total system power (in Watts); -
(ii)
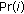 : probability of workload
: probability of workload  being active at any given time instant;
being active at any given time instant; -
(iii)
 : average utility (integrated over time);
: average utility (integrated over time); -
(iv)
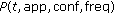 : average power in Watts;
: average power in Watts; -
(v)
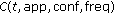 : normalized CPU utilization (
: normalized CPU utilization ( to
to  );
); -
(vi)
 : normalized network utilization (
: normalized network utilization ( to
to 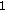 ).
).
Note that in this context, the energy constraint, and hence the average power constraint, is special because it extends across all workloads in the system. If a particular workload uses less energy than the average, another workload can use more. This is because energy that is not used is conserved for later use. The conservability of energy means that energy and power must be treated differently when solving the optimization problem, and it causes a dependency across workloads when finding optimal application configurations.
2.3. Naive Solution
Because the average power is added across different workloads in the stochastic allocation problem above, the allocation algorithm is equivalent to solving one instance of the NP-hard multidimensional multichoice knapsack problem (formally defined in [2]) which optimizes over every application and workload, choosing exactly one configuration for each application in every workload. Although the CPU and network constraint is affected only by application configurations selected in the current workload, the average power constraint depends on the configurations chosen for all applications in every workload that may potentially execute on the system. This means that the knapsack optimizer must evaluate all configurations for all applications across all workloads, which rapidly becomes computationally prohibitive as the number of applications and potential workloads increases. Suboptimal solutions such as the approximation algorithm presented in [2] can reduce the required computation, but even the use of these suboptimal approximations still leaves a large computationally complex problem.
3. Lagrangian Optimization
Solving a constrained problem is generally difficult. Specifically, the direct solution to a constrained optimization problem described in the previous section is equivalent to solving an NP-hard knapsack, where the knapsack represents the energy contained in the battery and the items that can be placed in the knapsack represent the various configurations of the tasks that run during the lifetime of the battery. To make matters worse, because tasks can enter and leave the system, it is not optimal to simply optimize for the current workload (as is done in [1]); if low-utility tasks enter the system early, they will "soak up" more than their share of energy from the battery, leaving little energy for high-utility tasks that arrive later. As a result, we cannot simply optimize for the tasks that are available now; we must optimize over the entire schedule of tasks that will arrive between the system's startup time and the time the battery is exhausted.
Because the underlying knapsack problem is nonpolynomial in complexity, this is a combinatorial explosion. To optimize over two different workloads that appear at different times, we must (in the worst case) evaluate every combination of application configurations in the first workload and every combination of application configurations in the second workload pairwise. In other words, the computational time required increases exponentially as the number of different workloads increases.
Because the combinatorial explosion that results when we must jointly optimize across varying workloads, we wanted to find a way to optimize the performance of a battery-operated system while keeping the optimization "local" to a particular workload and therefore tractable. One tool that can be used to do this is Lagrangian optimization.
3.1. Lagrangian Construction
The core idea of the Lagrangian approach to optimization [5] is that the constraints in a constrained optimization problem can be replaced with a Lagrange multiplier  by rewriting a constrained problem in the form of
by rewriting a constrained problem in the form of

using the form

Instead of having the constraint  inside a maximization operator, we have only a linear combination of the utility analog
inside a maximization operator, we have only a linear combination of the utility analog  and the constrained functions
and the constrained functions  . The constraint
. The constraint  has been removed; it will be used to pick a particular value of
has been removed; it will be used to pick a particular value of  but does not directly affect the minimization.
but does not directly affect the minimization.
In this construction, the Lagrange multiplier  represents a particular tradeoff between the term being maximized
represents a particular tradeoff between the term being maximized  and the constrained term
and the constrained term  . This formulation can in fact be generalized to an arbitrary number of constraints by introducing a separate Lagrange multiplier
. This formulation can in fact be generalized to an arbitrary number of constraints by introducing a separate Lagrange multiplier  for each constraint to be eliminated.
for each constraint to be eliminated.
3.2. Lagrangian Optimization of Independent Cells
The Lagrangian form of the optimization problem is ideally suited for the particular case where the functions  and
and  in (3) can be split into independent "cells" [5] that can be summed to calculate the value of
in (3) can be split into independent "cells" [5] that can be summed to calculate the value of  . For this special case, the original optimization problem takes the specific form
. For this special case, the original optimization problem takes the specific form

If the optimization problem takes this form, then when the original problem is reformulated as a Lagrangian it becomes

The summation and the minimization in (6) can be swapped, leaving

and reducing the problem from a joint maximization over the set of all  to a set of
to a set of  optimizations over a single variable
optimizations over a single variable  .
.
3.3. Optimality of the Lagrangian Formulation
Before the Lagrangian reformulation is used to solve an optimization problem, it is important to understand when and why it is equivalent to directly solving the original constrained optimization problem. This equivalence was shown for the general case with multiple Lagrange multipliers by Everett [5]; for clarity I summarize his argument for the multiple-cell, single- case of (7) here.
case of (7) here.
Theorem 1.
For any nonnegative real number  , if
, if  minimizes the function
minimizes the function  ,
,  maximizes
maximizes  over all
over all  such that
such that  .
.
Proof.
Because  minimizes
minimizes  ,
,

Since parameter set  must not use the resource
must not use the resource  more than parameter set
more than parameter set  ,
,

and thus the number in brackets is less than or equal to zero. Since  , we can remove it from the inequality, leaving
, we can remove it from the inequality, leaving

and therefore  satisfies the original optimization problem. In other words, if we solve the reformulated problem for some
satisfies the original optimization problem. In other words, if we solve the reformulated problem for some  and get back a configuration for which
and get back a configuration for which  is
is  , for that particular
, for that particular  and
and  the solutions of the constrained and unconstrained optimization problems are identical.
the solutions of the constrained and unconstrained optimization problems are identical.
3.4. Completeness: Can We Find  Matching
Matching 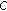 ?
?
Although we have proven that any solution found using the unconstrained Lagrangian form is in fact a solution to the original constrained optimization problem, we have not proven that we can find a solution corresponding to a particular value for  . In fact, not all values of
. In fact, not all values of  that can be reached with equality in the constrained form of the optimization can be achieved in the Lagrangian form; specifically, a particular value for
that can be reached with equality in the constrained form of the optimization can be achieved in the Lagrangian form; specifically, a particular value for  can be "found" by the Lagrangian optimization if it lies on a convex portion of the payoff verses resource use curve [5]. In other words, if a scatter plot is built using the resource consumption
can be "found" by the Lagrangian optimization if it lies on a convex portion of the payoff verses resource use curve [5]. In other words, if a scatter plot is built using the resource consumption  on the x-axis and the payoff
on the x-axis and the payoff  on the y-axis for all possible configuration sets
on the y-axis for all possible configuration sets  , the Lagrangian optimizer will be able to match any values of
, the Lagrangian optimizer will be able to match any values of  that correspond to points on the convex hull of this scatter plot.
that correspond to points on the convex hull of this scatter plot.
If the desired value of  does not correspond to a point on the convex hull of the resource-payoff scatter plot, when we search for an appropriate value of
does not correspond to a point on the convex hull of the resource-payoff scatter plot, when we search for an appropriate value of  , we will locate the value of
, we will locate the value of  that selects the point on the convex hull that comes closest to consuming the desired amount of the resource. This selection is still "optimal" in the sense that no other configuration achieves a greater payoff for the same or lesser resource utilization; however, selection of another point could result in a higher total payoff by using more of the available resource.
that selects the point on the convex hull that comes closest to consuming the desired amount of the resource. This selection is still "optimal" in the sense that no other configuration achieves a greater payoff for the same or lesser resource utilization; however, selection of another point could result in a higher total payoff by using more of the available resource.
3.5. Finding 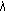 : Bisection Search Strategy
: Bisection Search Strategy
The convexity property of the Lagrangian optimization can also be used to create a fast strategy for finding a value for  that matches the actual resource consumption
that matches the actual resource consumption  against the desired resource consumption
against the desired resource consumption  .
.
Because of this convexity, increasing values of  will result in a monotonically increasing use of the constrained resource, so an efficient bisection search technique presented by Krongold [6] can be used to find the value of
will result in a monotonically increasing use of the constrained resource, so an efficient bisection search technique presented by Krongold [6] can be used to find the value of  corresponding to the desired constraint. This bisection search works by starting with low and high values of
corresponding to the desired constraint. This bisection search works by starting with low and high values of  ; initially, zero and a value of
; initially, zero and a value of  sufficiently high to dominate the
sufficiently high to dominate the  term are used, and
term are used, and  is calculated for each of these values. For each iteration, a new value of
is calculated for each of these values. For each iteration, a new value of  is set at the midpoint of these two values, and its corresponding
is set at the midpoint of these two values, and its corresponding  is computed. If the resource utilization realized from the new
is computed. If the resource utilization realized from the new  is greater than the goal constraint
is greater than the goal constraint  , the range is reduced to the new
, the range is reduced to the new  and the previous low value; if it is less, the new range is the new
and the previous low value; if it is less, the new range is the new  to the previous high value. This procedure is repeated until the resource utilizations of the new
to the previous high value. This procedure is repeated until the resource utilizations of the new  and the previous low
and the previous low  are equal.
are equal.
This bisection algorithm converges quickly; in its use to solve the DMT power allocation problem in [6], the optimal solution was found within 14 iterations with very conservative initial low and high values. Furthermore, nearly optimal solutions are found even if the search is terminated early; in [6],  of the optimal performance was achieved after only 8 iterations of the bisection search.
of the optimal performance was achieved after only 8 iterations of the bisection search.
4. Lagrangian Formulation of the Optimization Problem
We can apply the Lagrangian technique to the resource-allocation problem in (2) by realizing that we have a utility function analogous to the  shown in (3), and several resource constraint functions analogous to
shown in (3), and several resource constraint functions analogous to  . We can therefore transform this problem into a Lagrange form, and by finding suitable values for the Lagrange multipliers remove the constraints on the optimization, yielding an unconstrained problem.
. We can therefore transform this problem into a Lagrange form, and by finding suitable values for the Lagrange multipliers remove the constraints on the optimization, yielding an unconstrained problem.
Although the Lagrangian form can be used to transform multiple constraints into Lagrange multipliers, fast bisection searches for  are optimal only if a single Lagrange multiplier is used. (Bisection searches for
are optimal only if a single Lagrange multiplier is used. (Bisection searches for  are not known to be efficient or optimal if multiple Lagrange multipliers are used [5].) For this reason, we convert only the utility-energy tradeoff into a Lagrangian form and leave the CPU and network constraints in place. This results in a problem in the form of the single-resource multicell constrained optimization problem of (5).
are not known to be efficient or optimal if multiple Lagrange multipliers are used [5].) For this reason, we convert only the utility-energy tradeoff into a Lagrangian form and leave the CPU and network constraints in place. This results in a problem in the form of the single-resource multicell constrained optimization problem of (5).
Once reformulated to use a Lagrange multplier to optimally tradeoff utility and energy, the optimization problem can be stated as follows:

Because this transformation matches the Lagrangian form, the theoretical results shown in the previous section can be applied. Specifically, this means that we can optimize the system for a particular average power  by finding a value of
by finding a value of  that chooses configurations that meet this power constraint. If a particular value of
that chooses configurations that meet this power constraint. If a particular value of  results in the optimization choosing a set of application configurations that is equal to the desired power
results in the optimization choosing a set of application configurations that is equal to the desired power  , that set of application configurations maximizes the utility
, that set of application configurations maximizes the utility  for that power level. Furthermore, there exists a value of
for that power level. Furthermore, there exists a value of  that will match the average power consumed by every configuration on the convex hull of the utility/energy curve formed by the set of all possible applications and configurations weighted by the probability of the corresponding workloads.
that will match the average power consumed by every configuration on the convex hull of the utility/energy curve formed by the set of all possible applications and configurations weighted by the probability of the corresponding workloads.
The key benefit we get from the use of the Lagrangian technique is that it can be used to allocate energy across many different workloads while optimizing configurations across only one workload at a time. This is because each workload that may run forms a unique, independent "cell," linked only by the value of  chosen to optimize overall system utility. Consider the case where only one workload
chosen to optimize overall system utility. Consider the case where only one workload  exists and hence
exists and hence  . In this case, the maximization problem reduces to the form
. In this case, the maximization problem reduces to the form

subject to constraints on power, CPU, and network availability. This single-workload problem can be converted into a Lagrangian in the following form, subject to only the constraints on CPU and network

But because (11) fits the form of (6), we can interchange the order of summation and minimization and rewrite the stochastic Lagrangian optimization problem in terms of this single-workload Lagrange weight  :
:

Critically, in so doing we have eliminated the dependence of the optimization problem across workloads, and we can optimally allocate energy across workloads without considering the cross product of application configurations across all workloads.
Computing the value for  for a given value of
for a given value of  is equivalent to solving the problem of allocating resources to the applications running in a particular workload; other workloads are considered only in the effect that they have in the search for
is equivalent to solving the problem of allocating resources to the applications running in a particular workload; other workloads are considered only in the effect that they have in the search for  . In other words, after transforming the original optimization problem into the Lagrangian form, we can find an optimal set of configurations for a particular workload in the larger stochastic allocation problem without doing a search across configurations in other workloads.
. In other words, after transforming the original optimization problem into the Lagrangian form, we can find an optimal set of configurations for a particular workload in the larger stochastic allocation problem without doing a search across configurations in other workloads.
To find the value of  that maximizes the expected utility (to within a convex-hull approximation) while ensuring that the expected running time of the system is at least some fixed value, we simply do a search over
that maximizes the expected utility (to within a convex-hull approximation) while ensuring that the expected running time of the system is at least some fixed value, we simply do a search over  to find the value that minimizes
to find the value that minimizes  . Because
. Because  is expressed in terms of
is expressed in terms of  , this search does not require evaluating cross products of different workloads; each workload is only optimized once per value of
, this search does not require evaluating cross products of different workloads; each workload is only optimized once per value of  checked.
checked.
5. Properties of the Lagrangian Approach to Optimization
This section describes various properties of the Lagrangian optimation technique and uses these properties to analyze the behavior and performance of the Lagranian solution to the stochastic allocation algorithm.
5.1. Optimality
In Section 3.3, we showed that if a particular set of parameters  minimizes
minimizes  for a particular value of
for a particular value of  , the use of the resource
, the use of the resource  has been optimally allocated across the parameter set. Because our power allocation algorithm maps the average power parameter
has been optimally allocated across the parameter set. Because our power allocation algorithm maps the average power parameter  to the resource
to the resource  in the Lagrangian formulation, an argument analogous to the theorem presented there can be used to show that the configurations that minimize the Lagrangian
in the Lagrangian formulation, an argument analogous to the theorem presented there can be used to show that the configurations that minimize the Lagrangian  for a particular
for a particular  and the configurations that maximize the utility for the average power
and the configurations that maximize the utility for the average power  that corresponds to that
that corresponds to that  are the same. Furthermore, this is true even if the original utility-energy curve is not convex.
are the same. Furthermore, this is true even if the original utility-energy curve is not convex.
5.2. Computational Complexity
Even in the Lagrangian problem formulation, to compute  (and determine the optimal configurations for each application), we need to do an exhaustive search over the configurations of applications running at any given time, to ensure that the best possible use is made of the CPU and Network resources. In addition, the search for the value of
(and determine the optimal configurations for each application), we need to do an exhaustive search over the configurations of applications running at any given time, to ensure that the best possible use is made of the CPU and Network resources. In addition, the search for the value of  that maximizes utility while operating within the energy constraint adds complexity to the optimization problem, and as a result the Lagrange implementation requires more computation than the straight knapsack solver for a single application workload.
that maximizes utility while operating within the energy constraint adds complexity to the optimization problem, and as a result the Lagrange implementation requires more computation than the straight knapsack solver for a single application workload.
However, the amount of extra work required is limited. By nature  is a convex function of
is a convex function of  , so the search for
, so the search for  can be done using a fast bisection search that will converge within a small number of iterations [6, 7]. Our present implementation searches up to 18 points and finds
can be done using a fast bisection search that will converge within a small number of iterations [6, 7]. Our present implementation searches up to 18 points and finds  to precision of
to precision of  times the efficiency of the most efficient application configuration.
times the efficiency of the most efficient application configuration.
However, for the case where multiple workloads are considered, the search for  removes the need to jointly consider the application configurations across different workloads. This results in a reduction in the optimization complexity that is exponential in the number of workloads. For example, consider the case where there are two possible workloads, each consisting of two applications with 16 configurations each (like our Sensor workload). To optimize this system using the traditional approach, we must evaluate the 256 possible configurations of each of the two workloads pairwise, resulting in a total of 65536 combinations of configurations evaluated. Using the Lagrangian approach, however, we need to evaluate the constraints for each workload singly at up to 18 values of
removes the need to jointly consider the application configurations across different workloads. This results in a reduction in the optimization complexity that is exponential in the number of workloads. For example, consider the case where there are two possible workloads, each consisting of two applications with 16 configurations each (like our Sensor workload). To optimize this system using the traditional approach, we must evaluate the 256 possible configurations of each of the two workloads pairwise, resulting in a total of 65536 combinations of configurations evaluated. Using the Lagrangian approach, however, we need to evaluate the constraints for each workload singly at up to 18 values of  , resulting in only 9216 configurations evaluated. This is with only two workloads used; as the number of workloads increases, the benefit of evaluating workloads singly instead of jointly becomes larger and the computational workload of the joint optimization rapidly becomes infeasible.
, resulting in only 9216 configurations evaluated. This is with only two workloads used; as the number of workloads increases, the benefit of evaluating workloads singly instead of jointly becomes larger and the computational workload of the joint optimization rapidly becomes infeasible.
5.3. Interpretation: What Is  ?
?
Another key insight is the nature of the intermediate parameter  . Although the Lagrangian is a "synthesized" intermediate parameter, in many cases it has a real-world meaning. For example, in Frank Kelly's work on network pricing for elastic traffic [8], the Lagrangian values
. Although the Lagrangian is a "synthesized" intermediate parameter, in many cases it has a real-world meaning. For example, in Frank Kelly's work on network pricing for elastic traffic [8], the Lagrangian values  represent the marginal or "shadow" price of a unit of traffic on the corresponding network link. And in [9], the selected value for
represent the marginal or "shadow" price of a unit of traffic on the corresponding network link. And in [9], the selected value for  represents the tradeoff between the energy consumed by an equalizer filter tap and the amount of interference the filter tap can remove from the signal being received.
represents the tradeoff between the energy consumed by an equalizer filter tap and the amount of interference the filter tap can remove from the signal being received.
In the allocation problem we address here, the intermediate parameter  defines a tradeoff between the two optimization targets it connects—in this case, between utility and energy. A high
defines a tradeoff between the two optimization targets it connects—in this case, between utility and energy. A high  means that energy is at a premium, and that we should only use a configuration if it offers a particularly high utility in exchange for its energy consumption. A low
means that energy is at a premium, and that we should only use a configuration if it offers a particularly high utility in exchange for its energy consumption. A low  , on the other hand, means that power can be spent relatively freely in exchange for modest amounts of utility. In fact, due to the construction of
, on the other hand, means that power can be spent relatively freely in exchange for modest amounts of utility. In fact, due to the construction of  ,
,  is actually the minimum allowable slope between the selected point and the previous point on the utility-energy convex hull. ( This property is the key observation used to prove that there is a value of
is actually the minimum allowable slope between the selected point and the previous point on the utility-energy convex hull. ( This property is the key observation used to prove that there is a value of  corresponding to all convex-hull points in the scatter in [6]. ) This can be easily shown using an argument analagous to one presented by Ramchandran et al. in [7].
corresponding to all convex-hull points in the scatter in [6]. ) This can be easily shown using an argument analagous to one presented by Ramchandran et al. in [7].
Lemma 1.
 is the minimum permissible energy-utility slope (marginal utility for energy consumed) for the set of application configurations that minimizes
is the minimum permissible energy-utility slope (marginal utility for energy consumed) for the set of application configurations that minimizes  .
.
Proof.
Define

where  and
and  correspond to the total utility and power consumed by the configuration minimizing
correspond to the total utility and power consumed by the configuration minimizing  .
.
Because these values minimize  , perturbing
, perturbing  to
to  can only increase
can only increase  . Let
. Let  and
and  represent the utility and power consumed by a configuration minimizing
represent the utility and power consumed by a configuration minimizing  where
where  . Then
. Then

where slope is the slope of the utility-energy convex hull at the optimal operating point.
Even with the constraints, we can achieve any particular tradeoff between utility and power by only considering system configurations that have marginal efficiencies–-the change in utility over the change compared to the next lower-utility lower-energy point on the convex hull—greater than or equal to a fixed number  . (This observation also provides us with an indication of how we find the range over which we must search for
. (This observation also provides us with an indication of how we find the range over which we must search for  : it is sufficient to search from zero, which will permit any application configuration to run, to a number greater than the efficiency (utility over energy) of the efficient available application configuration in the system.) Furthermore, once we fix a value for
: it is sufficient to search from zero, which will permit any application configuration to run, to a number greater than the efficiency (utility over energy) of the efficient available application configuration in the system.) Furthermore, once we fix a value for  , we can continue to use it even if the applications running on the system change! The system will continue to run optimally with the same tradeoff between utility and energy, which means that if similar applications replace the currently running applications they will achieve a similar total runtime and utility. Moreover, if we replace the applications with new ones that offer more utility for energy spent, energy consumption will increase to take advantage of the better opportunities to gain utility for the user; likewise, if new applications are less efficient, energy use will be reduced to conserve energy for the future. The marginal efficiency metric
, we can continue to use it even if the applications running on the system change! The system will continue to run optimally with the same tradeoff between utility and energy, which means that if similar applications replace the currently running applications they will achieve a similar total runtime and utility. Moreover, if we replace the applications with new ones that offer more utility for energy spent, energy consumption will increase to take advantage of the better opportunities to gain utility for the user; likewise, if new applications are less efficient, energy use will be reduced to conserve energy for the future. The marginal efficiency metric  therefore provides a mechanism which permits the actual power consumption of the system to vary in response to the changing workloads in an optimal fashion.
therefore provides a mechanism which permits the actual power consumption of the system to vary in response to the changing workloads in an optimal fashion.
Because our constant as the workload changes is the efficiency metric  rather than power, energy, or utility, the system's power consumption can increase at one time to take advantage of the availability of high-efficiency tasks, and decrease at others if no high-efficiency tasks are available.
rather than power, energy, or utility, the system's power consumption can increase at one time to take advantage of the availability of high-efficiency tasks, and decrease at others if no high-efficiency tasks are available.
5.4. Optimality Properties
It is important that although our restated optimization problem remains an NP-hard knapsack problem, it shares important optimality properties with the Lagrangian approach.
First, a fixed  applies to all workloads and will correctly allocate energy to different applications, even as the workload changes. As long as the marginal utility remains constant, the allocation of energy to the various applications running at different times will achieve the optimal utility for the energy spent. In fact, if we use any fixed Lagrange multiplier
applies to all workloads and will correctly allocate energy to different applications, even as the workload changes. As long as the marginal utility remains constant, the allocation of energy to the various applications running at different times will achieve the optimal utility for the energy spent. In fact, if we use any fixed Lagrange multiplier  when we allocate utility and energy to the applications running on the system, the resulting system configurations will be optimal in that they will achieve the maximum possible utility for the amount of energy consumed.
when we allocate utility and energy to the applications running on the system, the resulting system configurations will be optimal in that they will achieve the maximum possible utility for the amount of energy consumed.
Second, as proven in the theorem of Section 3, for any value of  the returned solution is optimal in that no other solution has both a larger utility, and a smaller total energy consumption. Therefore the system using Lagrange optimization will always operate at an efficient operating point. And since an appropriate value of
the returned solution is optimal in that no other solution has both a larger utility, and a smaller total energy consumption. Therefore the system using Lagrange optimization will always operate at an efficient operating point. And since an appropriate value of  can be found to match any point on the convex hull utility-energy scatter plot, as long as the composite utility/energy curve is dense and nearly convex (which will be true for systems with a sufficiently large number of configurations), a value of
can be found to match any point on the convex hull utility-energy scatter plot, as long as the composite utility/energy curve is dense and nearly convex (which will be true for systems with a sufficiently large number of configurations), a value of  that consumes energy close to
that consumes energy close to  can be found.
can be found.
Although we are limited to points on the convex hull of the utility/energy scatter, in fact these points are "better" than points off the convex hull in the following sense: if we consider total (integrated over time) utility and we permit the system to achieve additional utility by slightly extending our runtime from the original goal, choosing convex hull points on the utility-energy curve will increase the total utility compared to a solution off the convex hull that comes closer to the desired lifetime. This directly follows from the optimality of the Lagrange (convex hull) solution for any runtime it finds.
Theorem 2.
Total utility (integrated over time) from a point on the utility-energy convex hull is higher than the net utility from a point off the convex hull that provides the same or greater utility.
Proof.
If we consider a point on the convex hull, and another point that provides more utility and is not on the convex hull, the efficiency (utility per unit energy) of the point on the convex hull will be greater than the efficiency of the point not on the convex hull. (Otherwise, the point not on the convex hull would also be on the convex hull, a contradiction.)
Therefore, as long as we can use any remaining energy to increase run time and achieve additional integrated utility, we will achieve more utility from the additional time than we would have by using the additional energy earlier. And as we accumulate more different workloads, the convex hull becomes denser and the extra utility we can achieve by using operating points not on the utility-energy convex hull diminishes.
5.5. Implementation Details
The complexity of the internal optimization operation is equal to the cross product of all the configurations of all applications running in a particular workload and each available CPU frequency. This represents a great reduction in computational complexity, because applications that are not active in a particular workload do not need to be considered.
Several effective but suboptimal simplifications can also be made. One is that the CPU frequency of all applications running at a particular time can be set to the same value. By doing so, we reduce the search space to only the cross product of the application configurations, times the number of CPU frequencies, with an increase in power consumption that is bounded by Jensen's inequality to the difference between two adjacent frequency steps.
Also, conventional fast search techniques for solving the multidimensional, multichoice knapsack problem can be applied to estimate  with reasonable results. This is especially valuable when the number of applications is high, as the complexity of a full search is higher and the suboptimality of doing a partial search is reduced.
with reasonable results. This is especially valuable when the number of applications is high, as the complexity of a full search is higher and the suboptimality of doing a partial search is reduced.
Because  is a convex function of
is a convex function of  , the search for
, the search for  can be done using a fast bisection search that will converge within a small number of iterations [7]; our present implementation searches up to 18 points and finds
can be done using a fast bisection search that will converge within a small number of iterations [7]; our present implementation searches up to 18 points and finds  to a precision of
to a precision of  times the efficiency of the most efficient application configuration.
times the efficiency of the most efficient application configuration.
The probability distribution of the workload is only used to select  to achieve the average system power and hence the runtime. Once the value of
to achieve the average system power and hence the runtime. Once the value of  is selected the probability distribution is not used again; more specifically, the probability distribution is not necessary to determine the configuration of the applications that is used at any particular time. This limits the effect of inaccuracies in workload probability estimates. Although an inaccurate estimate of the workloads' probability distribution will result in a runtime longer or shorter than desired, the system will still run efficiently.
is selected the probability distribution is not used again; more specifically, the probability distribution is not necessary to determine the configuration of the applications that is used at any particular time. This limits the effect of inaccuracies in workload probability estimates. Although an inaccurate estimate of the workloads' probability distribution will result in a runtime longer or shorter than desired, the system will still run efficiently.
Because  conveys all the information about how to select configurations to properly tradeoff between system lifetime and quality of service, it is also possible to design the system to allow the user to control
conveys all the information about how to select configurations to properly tradeoff between system lifetime and quality of service, it is also possible to design the system to allow the user to control  more directly. For example, the user can be presented with a slider selecting between optimizing for quality and system life. If this is done, the probability distribution can be used to provide an estimate of the resulting runtime for the value of
more directly. For example, the user can be presented with a slider selecting between optimizing for quality and system life. If this is done, the probability distribution can be used to provide an estimate of the resulting runtime for the value of  selected by the user.
selected by the user.
The optimal value of  depends only on the probability distribution of workloads that may run on the system; it does not depend on what applications are running at any particular time. Therefore, once an optimal
depends only on the probability distribution of workloads that may run on the system; it does not depend on what applications are running at any particular time. Therefore, once an optimal  is chosen, it can be used for a long time—until the desired runtime changes or the battery is replaced or charged, or until the probability distribution that was used to compute
is chosen, it can be used for a long time—until the desired runtime changes or the battery is replaced or charged, or until the probability distribution that was used to compute  is no longer valid. Even as the workload changes, the value of
is no longer valid. Even as the workload changes, the value of  we use to compute the optimal allocation of resources for any given workload stays the same, as it represents the optimal division of energy between the current workload and the future.
we use to compute the optimal allocation of resources for any given workload stays the same, as it represents the optimal division of energy between the current workload and the future.
The same Lagrangian approach used to solve the stochastic allocation problem can also be used to solve the related known-workload problem. For a single workload, simply setting  and
and  for the workload maps it into the stochastic framework and all the above proofs apply. The reservations proposed in [4] can also be accomodated by setting the probability associated with each workload to be the running time of that workload over the total running time of the system.
for the workload maps it into the stochastic framework and all the above proofs apply. The reservations proposed in [4] can also be accomodated by setting the probability associated with each workload to be the running time of that workload over the total running time of the system.
6. Optimality of the Energy-Greedy Heuristic
One important omission in the prior work by Yuan [1] is that it does not discuss the optimality of its allocation heuristics. The Lagrangian framework we use to solve the stochastic allocation problem can also be used to make statements about these types of heuristics. Because we compare the performance of the Lagrangian optimizer against the energy-greedy heuristic in Section 7, we digress briefly here to describe the conditions under which the "energy-greedy" heuristic described by Yuan is optimal.
The simplification made by the energy-greedy heuristic is that applications running when the allocation decision is made will continue to run until the system is shut down. Since this assumption describes a subproblem of the stochastic or varying-workload allocation problems, the energy-greedy heuristic is optimal if the applications in fact do not change, and is a good heuristic if the character of the applications running on the system stays roughly the same. However, if the utility or energy demands of the applications change dramatically over time, it may result in significantly suboptimal allocations.
Going back to our wireless camera example, this subproblem would assume that the data is equally "interesting" (and hence has an unvarying utility) for the entire running time of the system.
This unvarying-workload subproblem (and by extension the energy-greedy heuristic) is essentially a constant-power approach to the larger resource allocation problem; at all times it limits power consumption to a value that allows the required lifetime to be achieved given the current energy supply. (The power constraint can vary in response to current energy availability as the optimization is repeated.)
Theorem 3.
Given a dense set of application configurations, the energy-greedy heuristic results in a near-constant system power (The system power will vary by no more than the difference between the operating point and the next higher-power point on the utility/power curve. If operating points are closely spaced over the powers being optimized across, the utility/energy curve points will be close together and this difference is small.).
Proof.
To see that the energy-greedy approach attempts to equalize power consumption over time, we can consider its associated optimization problem. The energy-greedy heuristic maximizes the utility of the currently running applications subject to the power constraint

Utility is a monotonically increasing function of power, (although this is not true in general, any nonmonotonic points are always suboptimal and will therefore be ignored by the optimization process) and we will always choose to use as much power as possible to achieve the greatest possible utility. As a result, the energy consumption of the system will be as close as possible to  given the available application configurations. If the set of application configurations is dense, the actual power will be close to
given the available application configurations. If the set of application configurations is dense, the actual power will be close to  , and when the maximum allowable power is calculated again the result will be near (but perhaps slightly higher than)
, and when the maximum allowable power is calculated again the result will be near (but perhaps slightly higher than) .
.
7. Simulations
To evaluate the effectiveness of this Lagrangian resource allocation, we use a simulation of the GRACE framework [10, 11]. This simulation is described in more detail in [11]. It provides, earliest deadline first (EDF) scheduling of both the network and CPU, management of applications entering and leaving the system, and power modelling and estimation for both the network and CPU. The system runs a multimedia video encoder that is capable of operating at several utility levels (with varying image sizes, quantizer step sizes, and frame rates) and also permits compression efficiency to vary. The variable compression efficiency allows the system to save energy by reducing CPU demand at the expense of an increase in network-bandwidth utilization [12].
7.1. Simulation Environment
The network is modeled as having a bandwidth of 500 Kbyte/s and an active power of 0.5 W, corresponding to a per-byte energy cost of 1  J, a data rate and energy per byte similar to common 802.11 b wireless network interfaces. The network is assumed to be reliable as long as the bandwidth constraint is not exceeded, and no protocol or protocol overhead is assumed. Power estimates are generated by multiplying the active power of the network by the estimated or actual network utilization. The CPU energy and utilization estimates are based on the AMD Athlon XP-M 1700+ microprocessor, a model that incorporates voltage and frequency scaling; power is estimated by multiplying the CPU utilization by the power consumed when operating at the selected CPU frequency, ranging from 25 W at 1466 MHz to 6.4 W at 533 MHz.
J, a data rate and energy per byte similar to common 802.11 b wireless network interfaces. The network is assumed to be reliable as long as the bandwidth constraint is not exceeded, and no protocol or protocol overhead is assumed. Power estimates are generated by multiplying the active power of the network by the estimated or actual network utilization. The CPU energy and utilization estimates are based on the AMD Athlon XP-M 1700+ microprocessor, a model that incorporates voltage and frequency scaling; power is estimated by multiplying the CPU utilization by the power consumed when operating at the selected CPU frequency, ranging from 25 W at 1466 MHz to 6.4 W at 533 MHz.
The desired runtime is set to 600 seconds, and the starting energy of the battery is varied to simulate environments under tighter and looser power constraints. The simulation runs for 600 seconds or until the initial energy supply is exhausted, whichever comes first. Parasitic power demands (such as the display) are not considered; it is assumed that the provided initial energy excludes any parasitic power that would be consumed during the requested running time.
The simulation environment does not presently charge the Lagrange optimization for the processing time and energy spent doing its one-time search for the Lagrange multiplier. The run time for the current implementation of the Lagrange multiplier search is approximately 2 seconds at full processor speed for the "laptop" workload, so it would increase the total energy consumption for the Lagrangian case by about 50 J. We do not charge this energy because in practice it would be amortized over a much longer runtime than the 600 seconds used in these simulations.
7.1.1. Applications
For these simulations, we use the GRACE framework and adaptive encoder application described in [10], extended to add the ability to send uncoded as well as encoded macroblocks [11]. The application is run on input streams with two different image sizes, CIF ( ) and QCIF (
) and QCIF ( ). For each image size, the resource requirements can be reduced at the cost of decreasing utility by decreasing the frame rate from the base of 10 (CIF) or 15 (QCIF) fps. The system also supports reducing the quality by increasing the quantizer step size for CIF encoding, although these configurations are relatively inefficient (in terms of utility per unit power consumed) and are therefore not selected by the optimizer.
). For each image size, the resource requirements can be reduced at the cost of decreasing utility by decreasing the frame rate from the base of 10 (CIF) or 15 (QCIF) fps. The system also supports reducing the quality by increasing the quantizer step size for CIF encoding, although these configurations are relatively inefficient (in terms of utility per unit power consumed) and are therefore not selected by the optimizer.
Each operating mode allows application adaptation: 15 available compression modes when the quantizer step size Q is 6, and 6 modes when Q is 12.
The base utilities for every possible configuration of the encoder are shown in Table 1. These numbers are expressed as a rate, in terms of utility per second. Each second that the application is running and set to a given configuration, it accumulates the utility shown in the table.
Because choosing meaningful values for the base utility would require extensive human trials, values were instead assigned by hand. These particular values for utility were selected to ensure that the utility is a monotonic function of resource utilization and hence energy. They do not result in a convex energy/utility curve; this is intentional and intended to put the Lagrangian approach at a slight disadvantage.
In addition to the base utility, which is associated with the application itself, each time an application starts it is assigned a "weight" by the user. The weight connects the base utility of the application with the user's perception of its importance—it is a "utility mapping function." The implementation multiplies the weight assigned by the workload by the base utility rate of the application to find the actual utility rate for each potential application configuration. The higher the weight, the higher the resulting utility, and the more likely it will be that the application will be allocated enough energy, CPU time, and network bandwidth to operate at a high quality level.
7.2. Simulation Workloads
We implement these simulations by defining two different prototype workloads, consisting of the CIF and QCIF versions of our adaptive encoder application. The first "laptop" workload is intended to represent a reasonable variation in desired applications and utility; the second "sensor" workload is a favorable workload intended to highlight the improvements in total utility that can come from allocating energy only to the most beneficial applications.
The prototype workloads list the possible application sets, the weight for each application, and the probability that this application set is active. We then generate the actual workload by choosing a workload from the prototype according to the associated probability distribution for each 30-second slice of a 600-second simulation run. The input stream is a composite of several MPEG test sequences, treated as a circular array. As part of the workload creation process a starting position for each application invocation is chosen randomly (with a uniform distribution) from the frames in this composite stream.
In all cases, the original probability distribution from which the actual workloads are drawn is used along with composite statistics about the application's resource demands to compute the value for  used for the Lagrangian optimization.
used for the Lagrangian optimization.
It is important to note that the global allocator is permitted to refuse any offered jobs, and that each application can run at any one of several different quality/utility levels. This means that the actual energy consumption of an offered workload can vary down to zero, if none of the offered applications receives an energy allocation.
7.2.1. "Laptop" Workload
The "laptop" workload (Table 2) is intended to represent things a user could plausibly do with the computer. As we are limited by the fact that our adaptive application is an encoder, it is not particularly "laptop" in practice. However, unlike the "sensor" workload it has not been designed to provide the Lagrangian optimization approach with a large advantage. We therefore expect the utility improvement we achieve with this workload to be more representative of the general case.
One possible explanation for this type of workload is a laptop participating in a video teleconference. As the video conference progresses, various portions of the video (for instance, slides, the user, canned video, and animation) of varying importance start and end. This results in the entry and exit of different encoders with different frame sizes and importance.
7.2.2. "Sensor" Workload
The "sensor" workload (Table 3) is a realization of the problem outlined in the introduction. It represents a situation in which the Lagrangian optimization makes a large difference in the total utility of the system. It does not represent an upper bound (as the utility improvement given a suitably constructed workload availability is unbounded). It is instead intended to show that under certain circumstances, large utility improvements can be achieved.
This type of workload distribution could be found in a sensor network. The rare high-value operations occur when the sensor has detected something of interest and the operator is likely to be actively viewing the sensor's output; the common low-value operations occur when the system has not detected anything of interest and therefore is unlikely to be needed or monitored.
7.3. Simulation Results
We evaluate the performance of the Lagrange optimizer against the "Energy-greedy" heuristic described by Yuan et al. [1]. Figures 2 and 1 show the results of a simulation of the Lagrangian allocator. Each set of graphs includes five rows of three graphs. The first four rows represent the same sequence of workloads; each workload sequence consists of a list of workloads, drawn randomly from the "sensor" or "laptop" probability distributions of applications. New workloads are drawn for every 30-second slice, so there are 20 different workloads total represented in each graph. However, the system may shut down early and not run the last several workloads. The last row of graphs shows the average results across 10 realizations of the workload sequences, including the four shown as Workloads 1 through 4.
"Laptop" workload. The "Workload" graphs show specific results for four workload sequences; all points on the graph for each row come from the same sequence of applications entering and exiting. The "Average" graphs show average and min/max (indicated by error bars) results across 10 workloads. Dashed/lighter lines are from the energy-greedy heuristic, solid/dark lines are from the Lagrange optimizer. The left column shows the total (summed) utility, the middle column shows running time in seconds (limited to 600 seconds), and right column shows average ower in Watts.
"Sensor" workload. The "Workload" graphs show specific results for four workload sequences; all points on the graph for each row come from the same sequence of applications entering and exiting. The "Average" graphs show average and min/max (indicated by error bars) results across 10 workloads. Dashed/lighter lines are from the energy-greedy heuristic, solid/dark lines are from the Lagrange optimizer. The left column shows the total (summed) utility, the middle column shows running time in seconds (limited to 600 s), and right column shows average power in Watts.
The leftmost column of graphs shows the total realized utility—in other words, the sum of the utility values multiplied by the running time and the weight of each application—over the 600 seconds the system is allowed to run. The middle column shows the amount of time that the system runs before it shuts down, either due to running out of time or exhausting its energy. The rightmost column shows the total energy consumption of the system. None of these totals include the time and energy that would be spent finding the optimal value of  as it is assumed to have been computed offline. The overhead of allocating resources to each application entering and leaving the system is, however, included.
as it is assumed to have been computed offline. The overhead of allocating resources to each application entering and leaving the system is, however, included.
Each graph has a solid darker line representing the results for the Lagrangian optimization and a dashed lighter line representing the "energy-greedy" heuristic. The horizontal axis on all the graphs is the starting energy of the battery, expressed in terms of the average power permitted over the 600-second desired runtime; the starting energy in Joules is the value in Watts shown 600 times. The vertical axis on the "utility" graphs is utility units based on the application utility and weightings; on the "time" graphs it is seconds, and on the "energy" graphs it is once again in terms of power averaged over the desired runtime of 600 seconds. The performance is sampled across average power limits at every two Watts from 5 to 25 W.
The minimum and maximum values across all 10 workload sequences are shown as error bars on the "average" graphs. The darker error bars correspond to the Lagrangian optimizer, the lighter error bars correspond to the energy-greedy heuristic. Note that the minimum and maximum values for each starting energy are each selected independently and do not represent any single workload.
7.3.1. "Laptop" Workload
The results for the "laptop" workload are shown in Figure 1. We see that, on average, there is a significant increase in utility when the starting power is low, and no significant change in utility or energy consumption when the starting power is high. At an average power constraint of 5 W, we improve the average achieved utility by over  by pushing the power consumption from times that only low-utility tasks are running to other times when higher-utility tasks are available. However, once the starting energy is sufficient to allow the average power drain to exceed 15 W, there is no benefit from the use of the Lagrangian approach.
by pushing the power consumption from times that only low-utility tasks are running to other times when higher-utility tasks are available. However, once the starting energy is sufficient to allow the average power drain to exceed 15 W, there is no benefit from the use of the Lagrangian approach.
It can also be seen that in some cases, the total utility is reduced modestly. The worst loss of utility observed is  and occurs due to under-using energy; this case is shown as "Workload 3." Here, at an average power limit of 9 W, only
and occurs due to under-using energy; this case is shown as "Workload 3." Here, at an average power limit of 9 W, only  of the original energy is used at the end of the end of the 600-second desired runtime. This occurs when the actual application selections have a lower utility than the prototype distribution. Although the applications to be run are selected from the probability distribution provided to the code that computes the optimal Lagrange multiplier, the workload list is short enough that significant variations from the mean distribution can occur.
of the original energy is used at the end of the end of the 600-second desired runtime. This occurs when the actual application selections have a lower utility than the prototype distribution. Although the applications to be run are selected from the probability distribution provided to the code that computes the optimal Lagrange multiplier, the workload list is short enough that significant variations from the mean distribution can occur.
7.3.2. "Sensor" Workload
The results for the "sensor" workload are shown in Figure 2. Because this workload was constructed to show a large benefit from the Lagrangian optimization, we see an average improvement in utility of over  when the average power is limited to 5 W. (It is important to remember that a suitably constructed sequence could realize an arbitrarily large utility improvement.) As the average power increases, the benefit from the Lagrangian approach falls; at 13 W, the average improvement in utility is
when the average power is limited to 5 W. (It is important to remember that a suitably constructed sequence could realize an arbitrarily large utility improvement.) As the average power increases, the benefit from the Lagrangian approach falls; at 13 W, the average improvement in utility is  . Above 17 W, there is no improvement because the Lagrangian optimizer and the energy-greedy heuristic yield exactly the same configuration.
. Above 17 W, there is no improvement because the Lagrangian optimizer and the energy-greedy heuristic yield exactly the same configuration.
In fact, for several of the workloads, the utility curve is close to flat; for example, this is true of the second and fourth workloads shown in Figure 2. The flat utility curve is because, in these cases, there is enough energy to run all the high-utility tasks at full quality (achieving the highest utility), and the low-utility tasks do not contribute significantly to the total utility.
In our test system, the optimization process is driven entirely by estimates of the system loading and utility for the various available when the system first starts up. Since these estimates are by nature stochastic (they represent a "typical" operating condition rather than the specific operating condition that is actually encountered), inaccuracies in these estimates of energy and utility that go into choosing an appropriate  can result in the system behaving suboptimally.
can result in the system behaving suboptimally.
At the 15 W average power level, we see the effects of inaccuracy in the initial estimates resulting in a system outage quite clearly. It manifests as a dip in running time across all the workloads, which in some workloads results in a noticeable reduction in utility. This dip occurs because when we do the search for  , the system estimates that if all applications are run at their highest possible utility (i.e.,
, the system estimates that if all applications are run at their highest possible utility (i.e.,  is set to zero), the average power will be slightly less than 15 W. In reality, though, the power demand is slightly higher. Because the system uses more energy than is predicted as it actually runs, allowing the applications to all run at maximum utility does not conserve enough energy to run until the end of the run time. Therefore, if a high-utility task appears at the end of the sequence of workloads, it will not run and the system will be unable to achieve the maximum possible utility.
is set to zero), the average power will be slightly less than 15 W. In reality, though, the power demand is slightly higher. Because the system uses more energy than is predicted as it actually runs, allowing the applications to all run at maximum utility does not conserve enough energy to run until the end of the run time. Therefore, if a high-utility task appears at the end of the sequence of workloads, it will not run and the system will be unable to achieve the maximum possible utility.
This "dip" is partly, but not entirely, due to a systemic bias in the predictions: the power predictions made when  is calculated do not include energy used to allocate resources to applications as they enter and leave the system. There is also some systemic undercounting in the predicted cycle count, because the procedures used to create these tables do not accurately account for the per-application adaptation overhead. Although these systemic biases could have been corrected in the initial predictions, and various other techniques (such as implementing an energy reserve and recalculating
is calculated do not include energy used to allocate resources to applications as they enter and leave the system. There is also some systemic undercounting in the predicted cycle count, because the procedures used to create these tables do not accurately account for the per-application adaptation overhead. Although these systemic biases could have been corrected in the initial predictions, and various other techniques (such as implementing an energy reserve and recalculating  periodically based on actual system performance) could have been used to correct for stochastic variation, we felt that the resulting reduction in running time and loss of system utility was illustrative of the possibility of outage that results when stochastic techniques are used for optimization.
periodically based on actual system performance) could have been used to correct for stochastic variation, we felt that the resulting reduction in running time and loss of system utility was illustrative of the possibility of outage that results when stochastic techniques are used for optimization.
It is also possible for an outage to result because the workload has an atypically high occurrence of high-utility workloads—that is, more high-utility (and therefore energy-consuming) workloads appear than the probability distribution indicates. In these cases, the system may terminate early due to energy exhaustion. Because the 600 seconds lifetime we use in these experiments is relatively short, this effect can be easily seen in Workload 1, where the total utility is much higher than the other workloads, but the system shuts down early if the battery holds only enough energy for an average power of 5 W and fails to run a high-utility task. The probability of an outage this large would be diminished in practical implementations of systems using our stochastic allocation algorithm by longer total runtimes and more variation of the workload. Implementations could also recompute  periodically, which would also combat outages by forcing some of the high-utility tasks to run at a lower power level, helping to allow the system to achieve its required runtime. It is worth noting, however, that doing so would in general reduce the total utility achieved.
periodically, which would also combat outages by forcing some of the high-utility tasks to run at a lower power level, helping to allow the system to achieve its required runtime. It is worth noting, however, that doing so would in general reduce the total utility achieved.
8. Conclusions
Lagrangian optimization techniques can be productively applied to the problem of optimizing the allocation of a fixed pool of energy across multiple applications as they enter and leave a system. The Lagrangian approach to resource allocation requires only that the probabilities of various workloads to be known; foreknowledge of the actual schedule is not required. Compared to existing constant-power optimization algorithms, the Lagrangian procedure can provide significant improvements in achievable utility when energy is at a premium. Depending on workloads and energy availability, the Lagrangian allocation approach can increase total utility by a factor of two or more.
We have also shown problems that an actual implementation of this approach would encounter. The approach is sensitive to the accuracy of the probability distribution of the expected workload; the results show that mismatches result in consuming too much energy and terminating early, or consuming too little and achieving less than the best possible utility. By periodically recomputing the value of  taking into account changes in energy availability and probablility distribution, inaccuracies in the predictions can be corrected.
taking into account changes in energy availability and probablility distribution, inaccuracies in the predictions can be corrected.
References
Yuan W, Nahrstedt K, Adve SV, Jones DL, Kravets RH: Design and evaluation of a cross-layer adaptation framework for mobile multimedia systems. Multimedia Computing and Networking, January 2003, Proceedings of SPIE 5019: 1-13.
Moser M, Jokanovic D, Shiratori N: An algorithm for the multidimensional multiple-choice knapsack problem. IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences 1997, 80(3):582-589.
Lee C, Lehoczky J, Siewiorek D, Rajkumar R, Hansen J: A scalable solution to the multi-resource QoS problem. Proceedings of the 20th IEEE Real-Time Systems Symposium, December 1999 315-326.
Yuan W, Nahrstedt K: ReCalendar: calendaring and scheduling applications with CPU and energy resource guarantees for mobile devices. Proceedings of the IEEE Pervasive Computing and Communications (PerCom '03), March 2003
Everett H: Generalized Lagrange multiplier method for solving problems of optimum allocation of resources. Operations Research 1963, 11(3):399-418. 10.1287/opre.11.3.399
Krongold BS, Ramchandran K, Jones DL: Computationally efficient optimal power allocation algorithms for multicarrier communication systems. IEEE Transactions on Communications 2000, 48(1):23-27. 10.1109/26.818869
Ramchandran K, Vetterli M: Best wavelet packet bases in a rate-distortion sense. IEEE Transactions on Image Processing 1993, 2(2):160-175. 10.1109/83.217221
Kelly F: Charging and rate control for elastic traffic. European Transactions on Telecommunications 1997, 8(1):33-37. 10.1002/ett.4460080106
Goel M, Shanbhag NR: Dynamic algorithm transforms for low-power reconfigurable adaptive equalizers. IEEE Transactions on Signal Processing 1999, 47(10):2821-2832. 10.1109/78.790662
Vardhan V, et al.: Integrating fine-grained application adaptation with global adaptation for saving energy. Proceedings of the 2nd International Workshop on Power-Aware Real-Time Computing (PARC '05), September 2005, Jersey City, NJ, USA
Sachs DG: A new framework for hierarchical cross-layer adaptation, Ph.D. dissertation. University of Illinois at Urbana-Champaign, Urbana-Champaign, Ill, USA; May 2006.
Sachs DG, Adve SV, Jones DL: Cross-layer adaptive video coding to reduce energy on general-purpose processors. Proceedings of IEEE International Conference on Image Processing, September 2003, Barcelona, Spain 3: 109-112.
Acknowledgment
This material is based upon work supported in part by the National Science Foundation under Grant no. CCR-0205638.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Sachs, D., Jones, D.L. Stochastic Resource Allocation for Energy-Constrained Systems. J Wireless Com Network 2009, 246439 (2009). https://doi.org/10.1155/2009/246439
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/246439
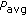 : average total system power (in Watts);
: average total system power (in Watts);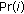 : probability of workload
: probability of workload  being active at any given time instant;
being active at any given time instant; : average utility (integrated over time);
: average utility (integrated over time);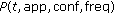 : average power in Watts;
: average power in Watts;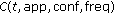 : normalized CPU utilization (
: normalized CPU utilization ( to
to  );
); : normalized network utilization (
: normalized network utilization ( to
to  ).
). Matching
Matching  ?
? : Bisection Search Strategy
: Bisection Search Strategy ?
?
