- Research Article
- Open access
- Published:
On Coverage and Capacity for Disaster Area Wireless Networks Using Mobile Relays
EURASIP Journal on Wireless Communications and Networking volume 2009, Article number: 251314 (2009)
Abstract
Public safety organizations increasingly rely on wireless technology to provide effective communications during emergency and disaster response operations. This paper presents a comprehensive study on dynamic placement of relay nodes (RNs) in a disaster area wireless network. It is based on our prior work of mobility model that characterizes the spatial movement of the first responders as mobile nodes (MNs) during their operations. We first investigate the COverage-oriented Relay Placement (CORP) problem that is to maximize the total number of MNs connected with the relays. Considering the network throughput, we then study the CApacity-oriented Relay Placement (CARP) problem that is to maximize the aggregated data rate of all MNs. For both coverage and capacity studies, we provide each the optimal and the greedy algorithms with computational complexity analysis. Furthermore, simulation results are presented to compare the performance between the greedy and the optimal solutions for the CORP and CARP problems, respectively. It is shown that the greedy algorithms can achieve near optimal performance but at significantly lower computational complexity.
1. Introduction
Public safety organizations increasingly rely on wireless technology to establish disaster area communication systems for first responder operations. The reason mainly lies in the fact that in catastrophe situations, wired network suffers from low sustainability, high expense, slow deployment, and being unadaptable to mobility. It is crucial for the replacement network to be highly dynamic in accordance with the mission-critical mobile users. Considering the first responders as mobile nodes (MNs), the communication range of each MN is often limited by its power constraint. Since MNs are highly mobile within the disaster area, using infrastructureless ad hoc networks would result in unexpected disconnection for some MNs and frequent rediscovery of routing paths. Therefore, mobile relay nodes (RNs) can be introduced to relay the communications between MNs and the base station. In this paper, we exemplify the movable RNs as vehicles loaded with wireless communication equipment. The RNs installed on wheeled vehicles move themselves to places where the first responders are actively working in the field. Although RNs form the backbone network, the number of users each RN can support is often limited, because each RN can only provide limited number of channels. Due to the abundance of available bandwidth in disaster area, we assume that each RN can set its bands at unused frequencies, so that they do not interfere with each other. With MNs and RNs defined, we term such a dynamic communication system as a disaster area wireless network (DAWN), shown in Figure 1.
In our prior work [1], we proposed a mobility model to describe the movement pattern of MNs within a large disaster area. Moreover, we studied the coverage problem with no capacity constraints on RNs. In this paper, we assume that each RN can support a limited number of users. Then the problem to be studied is formulated as finding the deployment of a given number of RNs such that:  most MNs can be covered;
most MNs can be covered;  the network throughput can be maximized.
the network throughput can be maximized.
We first study the COverage-oriented Relay Placement (CORP) problem of deploying a set of  RNs to cover a maximum number of MNs. As an initial setup, we consider the subproblem of Relay Assignment for COverage-oriented Relay Placement (RA-CORP) which is, for any given RNs' placement, to obtain the optimal associations between RNs and MNs using maximal matching method. Secondly, the Greedy Incremental COverage (GICO) algorithm is proposed to iteratively find the optimal location for the RN, one at each time. Thirdly, we put forward the constrained exhaustive search (CES) method to produce the optimal solution to the CORP problem as a benchmark for the GICO algorithm.
RNs to cover a maximum number of MNs. As an initial setup, we consider the subproblem of Relay Assignment for COverage-oriented Relay Placement (RA-CORP) which is, for any given RNs' placement, to obtain the optimal associations between RNs and MNs using maximal matching method. Secondly, the Greedy Incremental COverage (GICO) algorithm is proposed to iteratively find the optimal location for the RN, one at each time. Thirdly, we put forward the constrained exhaustive search (CES) method to produce the optimal solution to the CORP problem as a benchmark for the GICO algorithm.
We also investigate the CApacity-oriented Relay Placement (CARP) problem to maximize the total throughput of DAWN. In this case, the Relay Assignment for CApacity-oriented Relay Placement (RA-CARP) can be formulated as the assignment problem and solved by the Hungarian method [2]. Subsequently, we propose the Greedy Incremental Capacity (GICA) algorithm to find the RNs' positions one by one. In comparison, the optimal placement of all RNs can be obtained by solving a complicated binary integer programming problem but at very high computational complexity.
The rest of this paper is organized as follows. In Section 2, related work on disaster area networks, mobility model, and base station placement in wireless networks is summarized. In Section 3, we describe the mobility model of MNs within the disaster area; Section 4 presents the problem formulation of maximizing coverage for DAWN; Section 5 presents the technical approaches to solve the CORP problem. In Section 6, we present the problem formulation of maximizing aggregate throughput for DAWN. Subsequently, Section 7 presents the technical approaches to solve the CARP problem; simulation results are given in Section 8, followed by conclusions in Section 9.
2. Related Work
2.1. Disaster Area Wireless Network
Recently, many kinds of wireless networks have been proposed to be applied to disaster area relief operations. In [3], Hiroaki et al. propose and evaluate a mobile ad hoc network system to pursue the location and personal information of victims in occurrence of disaster. In [4], Kanchanasut et al. describe an emergency communication network platform designed for collaborative simultaneous emergency response operations using a combination of mobile ad hoc networking and a satellite IP network operating with conventional terrestrial internet. In [5], Malan et al. introduce a wireless infrastructure intended for emergency medical care, integrating low-power, wireless vital sign sensors, and PC-class systems. In addition, Zussman and Segall propose to construct an ad hoc network of wireless smart badges in order to acquire information from trapped survivors [6]. Besides, a novel ballooned wireless mesh network [7] has been proposed for emergency information system. All these works either assume the majority network nodes are static or mention little about their mobility model. Therefore, they fail in constructing the disaster area communication system to accommodate dynamic node configurations.
2.2. Macroscopic Mobility Model
In the recent years, several different macroscopic mobility models have been proposed and used for performance evaluation of networks. The fluid mobility model [8–10] conceptualizes traffic flow of users as the flow of a fluid, which models mobility in terms of the mean number of users crossing the boundary of a given area. Derived from transportation theory, these models give an aggregated description of the movement of several users, ranging from street scale and city scale [11–13] to national and international scales [12, 14]. Furthermore, two different event-driven role-based mobility models are designed for disaster area relief applications [15, 16]. However, these two models only apply in small area with specific disaster sites.
2.3. Base Station Placement
There have been extensive researches dedicated to base station placement problem in wireless sensor networks. In [17], a multiobjective metric is proposed for placing multiple base stations at the optimal positions in wireless sensor networks, including coverage, fault tolerance, energy consumption, and network delay. In [18], Shi and Hou propose a (1- ) optimal approximation algorithm to place base station so that the network lifetime could be maximized. In [19], a polynomial time heuristic is proposed for optimal base station selection within a wireless sensor network. In [20], Pan et al. study base station placement problem to maximize network lifetime. Most of existing base station placement schemes are designed for wireless networks with nodes at specific positions. Therefore, they are not suitable for the proposed mobile scenarios.
) optimal approximation algorithm to place base station so that the network lifetime could be maximized. In [19], a polynomial time heuristic is proposed for optimal base station selection within a wireless sensor network. In [20], Pan et al. study base station placement problem to maximize network lifetime. Most of existing base station placement schemes are designed for wireless networks with nodes at specific positions. Therefore, they are not suitable for the proposed mobile scenarios.
3. System Modeling and Applications
3.1. Mobility Model
As shown in Figure 2, we discretize the entire disaster area into squares, each square with a Catastrophic Intensity (CI) value to indicate the severity of damage. The squares that are yet to be cleared are called  . Those working-in-progress squares are also termed as
. Those working-in-progress squares are also termed as  . Both raw squares and busy squares are considered as
. Both raw squares and busy squares are considered as  . A square is said to be cleared if the CI value is reduced to zero. Faced with the mission of relieving such a large-scale disaster area, first responders ought to start from places near the boundary of the disaster area. The first responders do not stop working in the square until it is cleared. When first responders finish clearing a square, they split up and enter the adjacent uncleared squares. More specifically, the diversification is determined by the CI values and the current workforce in the neighboring squares. If obstacles and unreachable spots exist in the disaster area, as the stripe squares in Figure 2, first responders will make a detour according to our mobility model. As the first responders move deeper and broader spatially, they can finally clear the entire disaster area. The details of the mobility model can be referred to our prior work [1].
. A square is said to be cleared if the CI value is reduced to zero. Faced with the mission of relieving such a large-scale disaster area, first responders ought to start from places near the boundary of the disaster area. The first responders do not stop working in the square until it is cleared. When first responders finish clearing a square, they split up and enter the adjacent uncleared squares. More specifically, the diversification is determined by the CI values and the current workforce in the neighboring squares. If obstacles and unreachable spots exist in the disaster area, as the stripe squares in Figure 2, first responders will make a detour according to our mobility model. As the first responders move deeper and broader spatially, they can finally clear the entire disaster area. The details of the mobility model can be referred to our prior work [1].
3.2. Network Model
We consider a set of MNs moving within the disaster area following the mobility model described previously and assume that a fixed number of RNs are ready for deploying to connect all MNs to the backbone network. We assume that all MNs have small transmission range  . The transmission region of an MN is defined as the area in which all points are within distance
. The transmission region of an MN is defined as the area in which all points are within distance  from the MN. The
from the MN. The  th MN
th MN  can communicate bi-directionally with the
can communicate bi-directionally with the  th RN
th RN  if the distance between them
if the distance between them  . In other words,
. In other words,  is said to be covered by
is said to be covered by  if
if  is within the transmission region of
is within the transmission region of  . RNs are able to communicate with each other without distance constraints and they form the backbone network. We assume that the relay stations can be installed on vehicles and can quickly move to any locations in the disaster area. We assume each MN occupies one orthogonal channel associated with an RN for at least one time unit to communicate bi-directionally. Since the RN has a limited bandwidth, each RN can only support a certain number of MNs. As a note, no interference issues are considered in our network model due to abundant unoccupied spectrum in the disaster area.
. RNs are able to communicate with each other without distance constraints and they form the backbone network. We assume that the relay stations can be installed on vehicles and can quickly move to any locations in the disaster area. We assume each MN occupies one orthogonal channel associated with an RN for at least one time unit to communicate bi-directionally. Since the RN has a limited bandwidth, each RN can only support a certain number of MNs. As a note, no interference issues are considered in our network model due to abundant unoccupied spectrum in the disaster area.
4. Maximizing Node Coverage: Problem Formulation
We first provide the notation used in this section. Let  denote the set of four vertices of square
denote the set of four vertices of square  .
.  denotes the disk centering at
denotes the disk centering at  with radius as
with radius as  . A spot
. A spot  is said to be covered by
is said to be covered by  if
if  , denoted as
, denoted as  . A polygon
. A polygon  is said to be covered by
is said to be covered by  if for any point
if for any point  within
within  ,
,  , denoted as
, denoted as  .
.
For the CORP problem, RNs should be placed at positions to connect the maximum number of MNs. As MNs follow a macroscopic mobility model, we choose to cover the active (busy) squares instead of tracking the individual MNs. In other words, if a busy square is covered, then all MNs within the square are connected. We now claim Theorem 1 to show that a square can be covered by a circle if and only if its four vertices are within that circle.
Theorem 1 (covering a polygon).
Assume a polygon  , where
, where  and
and  denote the set of vertices and edges, respectively. If for all vertex
denote the set of vertices and edges, respectively. If for all vertex  ,
,  , then
, then  .
.
Proof.
First of all, we need to acknowledge the fact that if  ,
,  , then
, then  (
( denotes the edge connecting
denotes the edge connecting  and
and  ),
),  (it is obviously true since the edge is fully contained in one circle if the two terminals are within the same circle). For all
(it is obviously true since the edge is fully contained in one circle if the two terminals are within the same circle). For all  , we have
, we have  , where
, where  and
and  . Since for all
. Since for all  ,
,  , then
, then  and
and  . As a result,
. As a result,  , and
, and  .
.
Based on Theorem 1, the region where one RN should be placed to cover one busy square approximates to a circle (shown as Figure 3), which is defined as the feasible circle of each square. For every busy square in the DAWN, each has a corresponding feasible circle. These feasible circles may overlap each other and the intersected areas are referred as shared regions. As shown in Figure 4, three feasible circles are intersected and an RN placed in the shared region (shaded area) can cover all 3 squares at the same time. In a DAWN, these shared regions form a candidate set for RN placement. In this paper, our analysis and simulations are derived directly based on the concept of shared regions, instead of using traditional Cartesian coordinates.
The CORP problem is defined as follows. Given a set of busy squares, in which each contains some MNs inside with transmission range  , and
, and  RNs each with capability
RNs each with capability  , find the optimal placement of the RNs, such that the maximum number of MNs is covered.
, find the optimal placement of the RNs, such that the maximum number of MNs is covered.
5. Maximizing Node Coverage: Technical Approaches
In this section, we first present a maximal matching method to solve the RA-CORP problem if the RNs' positions are known. Secondly, we propose the GICO and CES algorithms to tackle the CORP problem. In addition, we conduct complexity analysis for both algorithms.
5.1. Relay Assignment for Fixed RN Positions (RA-CORP)
The RA-CORP problem tries to find the optimal association between MNs and RNs. We use a bipartite graph to represent the RA-CORP problem, and then use a sparse matrix-based algorithm to find the maximum-sized matching between the MNs and RNs.
Definition 1.
Denote the feasible circle of the  th busy square
th busy square  as
as  . Assume
. Assume  ,
,  have some area overlap, then the intersection area is defined as a shared region that only MNs within busy squares
have some area overlap, then the intersection area is defined as a shared region that only MNs within busy squares  (
( ) can access, denoted as
) can access, denoted as  , or simply as
, or simply as  .
.
At any time, MNs are distributed within a set of busy squares. The feasible circles of these busy squares intersect and yield a set of shared regions  where
where  denotes the cardinality of the set
denotes the cardinality of the set  . A fixed number of RNs
. A fixed number of RNs  are deployed at
are deployed at  ,
,  . Each RN can support at most
. Each RN can support at most  MNs within the squares covered by the RNs. Then the RA-CORP problem is formulated as
MNs within the squares covered by the RNs. Then the RA-CORP problem is formulated as

where  denotes that
denotes that  is connected with
is connected with  and 0 otherwise.
and 0 otherwise.  denotes the set of RNs that cover
denotes the set of RNs that cover  .
.  denotes the set of MNs that are covered by
denotes the set of MNs that are covered by  . The second constraint demands that each MN can at most connect to one RN. The third constraint shows that at most
. The second constraint demands that each MN can at most connect to one RN. The third constraint shows that at most  MNs can connect to one RN.
MNs can connect to one RN.
Given MNs placed within busy squares, and RNs deployed in some shared regions, the bipartite graph can be generated as in Figure 5, where  denotes the number of MNs. We prove that the maximal matching problem within a bipartite graph shown as Figure 5 is tantamount to the RA-CORP problem. In Figure 5, each MN can be assigned to any subband of an RN that covers the busy square where the MN is. Each line in Figure 5 shows that the corresponding MN can be connected to the RN with one channel. As each node of the bipartite graph can only be incident on one line, this bipartite graph correctly satisfies the second constraint in (1). Moreover, this bipartite graph extends each RN by
denotes the number of MNs. We prove that the maximal matching problem within a bipartite graph shown as Figure 5 is tantamount to the RA-CORP problem. In Figure 5, each MN can be assigned to any subband of an RN that covers the busy square where the MN is. Each line in Figure 5 shows that the corresponding MN can be connected to the RN with one channel. As each node of the bipartite graph can only be incident on one line, this bipartite graph correctly satisfies the second constraint in (1). Moreover, this bipartite graph extends each RN by  times to obtain the matchings between MNs and channels of RNs; this transformation successfully captures the third constraint in (1). Therefore, the RA-CORP problem is equivalent to the maximal-matching problem in a bipartite graph as shown in Figure 5.
times to obtain the matchings between MNs and channels of RNs; this transformation successfully captures the third constraint in (1). Therefore, the RA-CORP problem is equivalent to the maximal-matching problem in a bipartite graph as shown in Figure 5.
In this paper, we use a sparse matrix-based approach [21] to find the maximal matching between MNs and channels of RNs for each RN. This approach yields the optimal solution. The complexity of finding the maximal matching within a bipartite graph is  .
.
5.2. Relay Placement for Optimal Coverage (CORP)
We first claim Theorem 2 about complexity of the CORP problem.
Theorem 2.
The CORP problem is NP-complete.
Proof.
See Appendix .
Then we perform aggregation for all shared regions to reduce the solution space. Since the CORP problem is NP-complete, we introduce a heuristic approach GICO to solve the problem. To measure the performance of GICO, we also give the optimal solution by employing the CES algorithm.
5.2.1. Aggregation
The aggregation procedure aims to reduce the cardinality of the set of shared regions, thus greatly reduces the solution space. Given a set of shared regions  , the aggregation proceeds as in Algorithm 1. We say
, the aggregation proceeds as in Algorithm 1. We say  belongs to
belongs to  or
or  contains
contains  if
if  Let
Let  and
and  denote the set of all shared regions, and reduced set of shared regions, respectively.
denote the set of all shared regions, and reduced set of shared regions, respectively.  denotes the cardinality of the set
denotes the cardinality of the set  .
.
Algorithm 1: Aggregation procedure.
Aggregation( )
)
1 ;
;
-
2
for i=2 to

-
3
sign=0;
-
4
for j=1 to
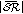
-
5
if
 belongs to
belongs to 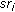
-
6
remove
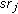 from
from 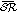 ;
; -
7
sign=1;
-
8
end if;
-
9
if
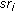 belongs to
belongs to 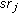
-
10
sign=2;
-
11
break;
-
12
end if;
-
13
end for;
-
14
if sign==0 or sign==1
-
15
add
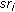 to
to 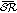 ;
; -
16
end if;
-
17
end for;
-
18
return
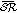 ;
;
The procedure reduces the cardinality of the set of shared regions by removing those that are contained by others. The procedure reduces the solution space without losing any coverage options. The reason is that RNs placed in  that contains
that contains  can cover busy squares
can cover busy squares  . Therefore, the set
. Therefore, the set  can contain all shared regions but with the minimal cardinality.
can contain all shared regions but with the minimal cardinality.
5.2.2. Greedy Incremental Coverage (GICO)
The GICO algorithm is based on the following idea. Although it is not computationally feasible to perform an exhaustive search for placing  RNs simultaneously, it is possible to choose an optimal position to place one RN at a time. When the RN is placed at each shared region, the optimal relay assignment can be obtained by utilizing the maximal matching method. The best shared region for placing one node can be found by exhaustively searching all shared regions in
RNs simultaneously, it is possible to choose an optimal position to place one RN at a time. When the RN is placed at each shared region, the optimal relay assignment can be obtained by utilizing the maximal matching method. The best shared region for placing one node can be found by exhaustively searching all shared regions in  . Once the location for this RN is fixed, the next RN can be placed following the same procedure. It should be noted that when placing next RN, those previously placed RNs should be jointly considered for relay assignment in order to compute the coverage values. In this approach, the RNs are placed one by one until all
. Once the location for this RN is fixed, the next RN can be placed following the same procedure. It should be noted that when placing next RN, those previously placed RNs should be jointly considered for relay assignment in order to compute the coverage values. In this approach, the RNs are placed one by one until all  RNs are deployed in the set
RNs are deployed in the set  .
.
As listed in Algorithm 2, GICO works as follows.  represents the shared regions that have been chosen to place RNs.
represents the shared regions that have been chosen to place RNs.  denotes the cardinality of
denotes the cardinality of  . It is possible that
. It is possible that  contains multiple same shared regions, which means that multiple RNs should be placed in that shared region. At line 4, each shared region in the set
contains multiple same shared regions, which means that multiple RNs should be placed in that shared region. At line 4, each shared region in the set  is added into the current set
is added into the current set  and the set
and the set  is obtained. The procedure at line 5 calculates and stores the maximal matching based on RNs' deployment according to the current
is obtained. The procedure at line 5 calculates and stores the maximal matching based on RNs' deployment according to the current  .
.  denotes the calculated optimal maximal matching while
denotes the calculated optimal maximal matching while  denotes the set of shared regions that each contains one RN. After executing the procedure of lines 4 and 5 for
denotes the set of shared regions that each contains one RN. After executing the procedure of lines 4 and 5 for  times, the best next shared region to place one RN is found (line 7) and added to the set
times, the best next shared region to place one RN is found (line 7) and added to the set  (line 8). Therefore, after greedily choosing RN placement one by one for
(line 8). Therefore, after greedily choosing RN placement one by one for  times, we can finally obtain the solution.
times, we can finally obtain the solution.
Algorithm 2: GICO.
GICO( )
)
-
1
1
 ;
; -
2
for i=1 to
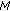
-
3
for j=1 to

-
4
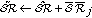
-
5
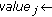 RA-CORP(
RA-CORP(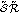 )
) -
6
end for;
-
7
[maximum, index]=Max(value);
-
8
 ;
;
9end for;
10 return ;
;
5.2.3. Constrained Exhaustive Search (CES)
In order to obtain the optimal solution as a benchmark for our GICO algorithm, we need to search all possible combinations of the shared regions. However, even after employing the aggregation procedure to reduce the size of solution space, the complexity for searching the optimal solution could still be as high as  Therefore, we resort to devising the CES algorithm to further reduce the solution space by adding one constraint to the combinations of shared regions. The constraint is that for each set of
Therefore, we resort to devising the CES algorithm to further reduce the solution space by adding one constraint to the combinations of shared regions. The constraint is that for each set of  RN placements, each RN should cover at least one MN based on the RA-CORP results. In particular, the number of RNs placed in one shared region times RNs' capability should not exceed the total number of MNs in those busy squares that are covered by the RNs by more than
RN placements, each RN should cover at least one MN based on the RA-CORP results. In particular, the number of RNs placed in one shared region times RNs' capability should not exceed the total number of MNs in those busy squares that are covered by the RNs by more than  , shown as
, shown as

where  denotes the number of RNs placed at
denotes the number of RNs placed at  and
and  denotes the number of MNs in the busy square
denotes the number of MNs in the busy square  .
.
5.3. Complexity Analysis
We first discuss the complexity of the aggregation procedure. Based on Algorithm 1, the procedure between line 5 to line 12 is iterated  times, and the procedure between line 14 to line 16 is iterated
times, and the procedure between line 14 to line 16 is iterated  times. As neither
times. As neither  nor
nor  is influenced by
is influenced by  , the complexity for the aggregation procedure is
, the complexity for the aggregation procedure is  .
.
Secondly, we analyze the complexity of GICO. Based on Algorithm 2, the complexity of the GICO algorithm is  , because the procedure from line 4 to line 5 is iterated
, because the procedure from line 4 to line 5 is iterated  times, and the worst case complexity for the maximal matching method is
times, and the worst case complexity for the maximal matching method is  .
.
For CES, the complexity analysis is more complicated. According to the constraint in (2), each shared region cannot host more than a limited number of RNs. Therefore, we assume on average each shared region can host  (
( ) RNs, as shown in
) RNs, as shown in

In other words, the list of shared regions can be extended to a longer one with length  , on which each shared region can host at most one RN. As the worst case complexity for the maximal matching method is
, on which each shared region can host at most one RN. As the worst case complexity for the maximal matching method is  , the computation complexity for CES can be stated as
, the computation complexity for CES can be stated as  . Now we claim that the complexity of the CES algorithm is higher than GICO, as shown in Theorem 3.
. Now we claim that the complexity of the CES algorithm is higher than GICO, as shown in Theorem 3.
Theorem 3 (complexity of GICO and CES).
The complexity of the GICO algorithm is lower than the complexity of the CES algorithm.
Proof.
As already explained, the complexity of GICO is  while the complexity for CES is
while the complexity for CES is  We can tell that
We can tell that  has little relation with
has little relation with  , while
, while  is roughly linearly related with
is roughly linearly related with  , that is,
, that is,  , because the more MNs, the more channels are required to access them to the backbone network. Then we can develop the ultimate form for the complexity of GICO as
, because the more MNs, the more channels are required to access them to the backbone network. Then we can develop the ultimate form for the complexity of GICO as

By substituting  in (5) with (3), the ultimate form for the complexity of CES is developed as
in (5) with (3), the ultimate form for the complexity of CES is developed as

Obviously, the term  . Therefore, the complexity for GICO is less than the complexity for CES.
. Therefore, the complexity for GICO is less than the complexity for CES.
6. Maximizing Aggregate Throughput: Problem Formulation
In Section 4, we formulate the CORP problem, which is aimed to maximize the number of MNs that can be connected to the backbone network. However, the objective of the CORP problem does not address the quality of service (QoS) requirements of individual links. In other words, the deployment of RNs has to consider not only the coverage but also the QoS performance with intelligent channel allocation. Therefore, we put forward the CARP problem in the interest of enhancing the QoS performance of DAWN.
To measure the throughput of individual links, we ought to set the positions of RNs as exact Cartesian coordinates. In particular, instead of defining the position of an RN as a region, we specify its position as the centroid point of the polygon, whose vertices are the intersection points of the arcs of a region in counterclockwise order. An example is shown in Figure 6. Let us denote the coordinates of the intersection points of  as
as  , the coordinates of the centroid point as
, the coordinates of the centroid point as  , where
, where  denotes the centroid point of
denotes the centroid point of  . Then the coordinates of the centroid point is calculated as
. Then the coordinates of the centroid point is calculated as

where  denotes the area of the polygon formed by connecting the intersection points in a counterclockwise order, which can be calculated using
denotes the area of the polygon formed by connecting the intersection points in a counterclockwise order, which can be calculated using

Based on Shannon formula, the channel capacity of a link can be expressed as (8) using path loss model

where  denotes the capacity of the channel,
denotes the capacity of the channel,  denotes the bandwidth of the channel,
denotes the bandwidth of the channel,  denotes the distance between the transmitter and receiver of the link,
denotes the distance between the transmitter and receiver of the link,  denotes the path loss coefficient,
denotes the path loss coefficient,  denotes the transmit power,
denotes the transmit power,  denotes the noise power,
denotes the noise power,  and
and  are the transmitter and receiver antenna gains, respectively,
are the transmitter and receiver antenna gains, respectively,  denotes the wavelength of the transmitted signal,
denotes the wavelength of the transmitted signal,  denotes the frequency of the transmitted signal,
denotes the frequency of the transmitted signal,  is the velocity of radio-wave propagation in free space, which is equal to the speed of light.
is the velocity of radio-wave propagation in free space, which is equal to the speed of light.
Since MNs follow the macroscopic mobility model, we resort to developing the two-dimensional integral (9) to compute the throughput of the link between an MN and its assigned RN. In (9),  denotes the coordinates of the left downward vertex of the
denotes the coordinates of the left downward vertex of the  th busy square
th busy square  .
.  denotes the throughput of the link between one MN in
denotes the throughput of the link between one MN in  and one RN placed at
and one RN placed at  .
.  denotes the side length of each square
denotes the side length of each square

The CARP problem is formulated as follows. Given  MNs each with transmission range
MNs each with transmission range  that are distributed within a set of busy squares and
that are distributed within a set of busy squares and  RNs each with capability
RNs each with capability  , find the optimal positions for the RNs such that the aggregated throughput of all established links between MNs and RNs are maximized.
, find the optimal positions for the RNs such that the aggregated throughput of all established links between MNs and RNs are maximized.
7. Maximizing Aggregate Throughput: Technical Approaches
In this section, we investigate the CARP problem of deploying a set of RNs to maximize the total throughput of DAWN. We first consider the optimal relay assignment for fixed RN positions, which can be solved using the Hungarian method. On this basis, we propose the GICA approach to tackle the CARP problem. In addition, since the CARP problem falls into a binary integer programming formulation, the branch and bound algorithm [22] is adopted to produce the optimal solution as the benchmark for the GICA approach.
7.1. Relay Assignment for Fixed RN Positions (RA-CARP)
At any time, MNs are distributed within a set of busy squares. The feasible circles of these busy squares intersect and yield a set of shared regions  A fixed number of RNs
A fixed number of RNs  are deployed at the set of centroid points
are deployed at the set of centroid points 
 . Each RN can support at most
. Each RN can support at most  MNs to access the network in the squares that it covers. Now the RA-CARP problem is formulated as
MNs to access the network in the squares that it covers. Now the RA-CARP problem is formulated as

where  denotes that
denotes that  is connected with
is connected with  and 0 otherwise;
and 0 otherwise;  denotes the index of the busy square where
denotes the index of the busy square where  is.
is.  denotes the index of the shared region where
denotes the index of the shared region where  is placed. The second constraint denotes that each MN can at most connect to one RN. The third constraint shows that at most
is placed. The second constraint denotes that each MN can at most connect to one RN. The third constraint shows that at most  MNs can connect to one RN.
MNs can connect to one RN.
Given MNs placed within busy squares and RNs deployed in some shared regions, the bipartite graph can be generated as in Figure 5. It can be seen that for each MN-RN pair, there are  edges each with a weight equal to the capacity value of the corresponding link. Note that for those pairs that the RN does not cover the MN, the edges are assigned weights equal to 0. We now can generate a gain matrix
edges each with a weight equal to the capacity value of the corresponding link. Note that for those pairs that the RN does not cover the MN, the edges are assigned weights equal to 0. We now can generate a gain matrix  shown as
shown as

where  and
and  . We now present the Hungarian method [2] as follows.
. We now present the Hungarian method [2] as follows.
Step 1.
If  is not a square matrix, we have to augment
is not a square matrix, we have to augment  into a square matrix by padding rows or columns with all zeros.
into a square matrix by padding rows or columns with all zeros.
Step 2.
Multiply the matrix  by
by  .
.
Step 3.
Subtract the minimum value of each row from row entries.
Step 4.
Subtract the minimum value of each column from column entries.
Step 5.
Select rows and columns across which you draw lines, such that all zeros are covered and that no more lines have been drawn than necessary.
Step 6.
If the number of lines equals the number of rows, choose a combination of zero elements from the modified gain matrix such that the position of each chosen element is incident on a unique row and column. Then the optimal assignment result consists of the RN-MN pairs as represented by the chosen elements in the modified gain matrix. If the number of lines is less than the number of rows, go to Step 7.
Step 7.
Find the smallest element which is not covered by any of the lines. Then subtract it from each entry which is not covered by the lines and add it to each entry which is at the intersection of a vertical and horizontal line. Go back to Step 5.
7.2. Relay Placement for Maximal Aggregate Throughput (CARP)
We claim Theorem 4 about complexity of the CARP problem.
Theorem 4.
The CARP problem is NP-complete.
Proof.
See Appendix .
Since the CARP problem is NP-complete, we introduce a heuristic approach GICA to solve the problem. To measure the performance of GICA, we also present the optimal method for the CARP problem.
7.2.1. Greedy Incremental Capacity (GICA)
According to Algorithm 3, the algorithm works as follows.  denotes the set of centroid points that have been chosen to place RNs.
denotes the set of centroid points that have been chosen to place RNs.  denotes the set of centroid points of all shared regions.
denotes the set of centroid points of all shared regions.  denotes the set of centroid points that have been chosen.
denotes the set of centroid points that have been chosen.  denotes a current set of centroid points with each hosting one RN. At line 4, each centroid point in
denotes a current set of centroid points with each hosting one RN. At line 4, each centroid point in  is added to
is added to  and the set
and the set  is obtained. The procedure at line 5 calculates and stores the total throughput yielded by the Hungarian method based on
is obtained. The procedure at line 5 calculates and stores the total throughput yielded by the Hungarian method based on  .
.  denotes the calculated optimal association between MNs and RNs. After executing the procedure of lines 4 and 5 for
denotes the calculated optimal association between MNs and RNs. After executing the procedure of lines 4 and 5 for  times, the best next centroid point to place one RN is found (line 7) and added to
times, the best next centroid point to place one RN is found (line 7) and added to  (line 8). Therefore, after greedily choosing centroid points one by one for
(line 8). Therefore, after greedily choosing centroid points one by one for  times, we can finally obtain the set of centroid points
times, we can finally obtain the set of centroid points  to place RNs.
to place RNs.
Algorithm 3: GICA.
GICA( )
)
-
1
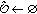 ;
; -
2
for i=1 to
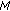
-
3
for j=1 to
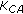
-
4
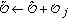
-
5
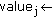 RA-CARP(
RA-CARP(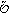 )
) -
6
end for;
-
7
[maximum, index]=Max(value);
-
8
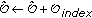 ;
; -
9
end for;
-
10
return
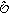 ;
;
7.2.2. Optimal Solution to CARP Problem
We show that the RA-CARP can be formulated as a binary integer programming problem when RNs are placed at fixed positions. Subsequently, the GICA method utilizes the Hungarian method to greedily place one RN at an iteration. Therefore, the solutions yielded by GICA cannot be guaranteed optimal because the RN assignment and placement are considered separately. It would be natural to believe that only when we search all solution space can the optimal solution be produced.
Hereby we introduce two binary variables  and
and 
 denotes that
denotes that  is connected with
is connected with  and 0 otherwise;
and 0 otherwise;  denotes that
denotes that  is placed at the centroid point of the
is placed at the centroid point of the  th shared region and 0 otherwise. Then we can jointly formulate the CARP problem as
th shared region and 0 otherwise. Then we can jointly formulate the CARP problem as

Since the objective term  contains the product of two variables
contains the product of two variables  and
and  , it is difficult to solve. According to [23], the product of multiple binary variables
, it is difficult to solve. According to [23], the product of multiple binary variables  can be substituted by a new variable
can be substituted by a new variable  with two constraints that ensure that
with two constraints that ensure that  if there exists
if there exists  , and
, and  if for all
if for all  . Therefore, we transform (12) into a binary integer programming problem shown as
. Therefore, we transform (12) into a binary integer programming problem shown as

Now the CARP problem is formulated as a binary integer programming problem. We then utilize the branch and bound algorithm to solve it. The algorithm searches for an optimal solution by solving a series of LP-relaxation problems, in which the binary integer requirement on the variables  is replaced by the weaker constraint
is replaced by the weaker constraint  . More details can be referred to [22].
. More details can be referred to [22].
7.3. Complexity Analysis
We first discuss the computation complexity of the Hungarian method to assign MNs when RNs are placed at fixed positions. According to [2], the complexity is  .
.
Then we analyze the complexity of the GICA algorithm. Let  denote the number of shared regions. Based on Algorithm 3, as the procedure on lines 4 to 5 is iterated
denote the number of shared regions. Based on Algorithm 3, as the procedure on lines 4 to 5 is iterated  times, the computation complexity of the GICA algorithm is
times, the computation complexity of the GICA algorithm is  .
.
The optimal method to the CARP problem uses the branch and bound algorithm to solve a binary integer programming problem. As the number of binary variables is  , the worst case complexity for the optimal method is
, the worst case complexity for the optimal method is  . It is apparent that the complexity of the GICA algorithm is much lower than the optimal algorithm.
. It is apparent that the complexity of the GICA algorithm is much lower than the optimal algorithm.
8. Simulation Results
In this section, we present the numerical results obtained from the simulation using high level programming language. For the CORP problem, we compare the performance of the GICO algorithm and the CES algorithm. For the CARP problem, we compare the performance of the GICA algorithm and the optimal algorithm. It is illustrated that the two greedy algorithms both merit close-to-optimal performance and low complexity.
8.1. Simulation Setup
We present the simulation results in a  square disaster area. The CI values of each square are initially set as 5 or randomly chosen in the interval
square disaster area. The CI values of each square are initially set as 5 or randomly chosen in the interval  in Table 1. We implement two initial distributions of MNs: 40 MNs assemble at
in Table 1. We implement two initial distributions of MNs: 40 MNs assemble at  or evenly divided at 4 corners
or evenly divided at 4 corners  ,
,  ,
,  ,
,  . Thus we can obtain four different scenarios with each of the two distributions of CI values when MNs follow each of the two initial deployments. The bandwidth for each channel is
. Thus we can obtain four different scenarios with each of the two distributions of CI values when MNs follow each of the two initial deployments. The bandwidth for each channel is  Mbps. The area of each square is
Mbps. The area of each square is  . Disaster relief efficiency coefficient is
. Disaster relief efficiency coefficient is  , which means each first responder can clear 1 unit of CI per unit time. The transmit power of MNs
, which means each first responder can clear 1 unit of CI per unit time. The transmit power of MNs  is set to 1 watt. The transmitter and receiver antenna gains
is set to 1 watt. The transmitter and receiver antenna gains  . The frequency is
. The frequency is  Hz. The noise power
Hz. The noise power  is
is  watt. The path loss exponent is set as
watt. The path loss exponent is set as  . The transmission range
. The transmission range  of MNs is set as
of MNs is set as  meters.
meters.
 .
.8.2. Simulation Results for Maximal Coverage
We introduce coverage percentage as the measurement of coverage performance, which is defined as the ratio of the number of covered MNs to the total number of MNs working in the disaster area.
Figure 7 shows the covering percentage of four scenarios for the entire disaster area relief process. It is clear that GICO performs very close to the optimal CES algorithm. In addition, results of all four scenarios share a similarity; the covering percentage is quite high during both initial and final periods (equal to 1), while lower during the middle of the disaster area relief process. The reason is that in the middle of the process, all the MNs are working in many widely distributed busy squares within the disaster area, thus the covering percentage is low due to limited covering range of RNs. On the other hand, in both initial and final periods, MNs are located in only a few spatially close squares, which renders covering the MNs an easy task as long as the channel resources are abundant. It is also worth pointing out that results from Figure 7(c) vibrate more dynamically than other 3 subfigures. This phenomenon shows that the number of busy squares is relatively small during the disaster area relief process if the first responder starts from one location and the CI values are random.
The covering percentage over the entire disaster area relief process in four scenarios. ,
,  ,
,  . (a) At initial stage, 40 MNs are in
. (a) At initial stage, 40 MNs are in  at time 0, and CI values of all squares are 5, (b) At initial stage, 40 MNs are evenly deployed in
at time 0, and CI values of all squares are 5, (b) At initial stage, 40 MNs are evenly deployed in  ,
,  ,
, ,
,  at time 0, and CI values of all squares are 5, (c) At initial stage, 40 MNs are in
at time 0, and CI values of all squares are 5, (c) At initial stage, 40 MNs are in  at time 0, and CI values of all squares are randomly chosen between 1 and 10, (d) At initial stage, 40 MNs are evenly deployed in
at time 0, and CI values of all squares are randomly chosen between 1 and 10, (d) At initial stage, 40 MNs are evenly deployed in  ,
,  ,
,  at time 0. CI values of all squares are randomly chosen between 1 and 10
at time 0. CI values of all squares are randomly chosen between 1 and 10
Next, in Figure 8, we look at the average covering percentage over the entire disaster area relief process for four scenarios when the capability of each RN changes. As can be observed, both algorithms yield better coverage performance if each RN can support more MNs. This is because more channel resources brought by RNs can accommodate more MNs. In addition, it is worth mentioning that as the capability of RNs is enlarged, less improvement is rendered for the covering percentage. The reason is that when one RN can cover more MNs, less uncovered MNs are left to boost the covering percentage in the future. In the end, it is clear that the GICO algorithm produces close-to-optimal solutions.
Average covering percentage over the entire relief process versus different capability of RNs in four scenarios. ,
,  . (a) At initial stage, 40 MNs are in
. (a) At initial stage, 40 MNs are in  at time 0, and CI values of all squares are 5, (b) At initial stage, 40 MNs are evenly deployed in
at time 0, and CI values of all squares are 5, (b) At initial stage, 40 MNs are evenly deployed in  ,
,  ,
, ,
,  at time 0, and CI values of all squares are 5, (c) At initial stage, 40 MNs are in
at time 0, and CI values of all squares are 5, (c) At initial stage, 40 MNs are in  at time 0, and CI values of all squares are randomly chosen between 1 and 10, (d) At initial stage, 40 MNs are evenly deployed in
at time 0, and CI values of all squares are randomly chosen between 1 and 10, (d) At initial stage, 40 MNs are evenly deployed in  ,
,  ,
,  at time 0. CI values of all squares are randomly chosen between 1 and 10
at time 0. CI values of all squares are randomly chosen between 1 and 10
In Figure 9, we compare the performance of GICO and CES in terms of the average covering percentage over the entire disaster area relief process when the number of RNs changes. It is clearly shown that the GICO algorithm produces close-to-optimal solutions. As expected, in all four scenarios, both GICO and CES yield better performance in terms of average covering percentage as the number of RNs increases. This can be explained by the fact that more channel resources brought by RNs can accommodate more MNs. The coverage percentage asymptotically approaches 1 when the number of RNs becomes more than 6 for one starting location and 10 for 4 starting locations. By comparing the 4 subfigures, we can point out that the two curves corresponding with the scenarios that MNs start from 1 corner rises more sharply than the curves demonstrating scenarios that MNs start from 4 corners. The rationale is that during early periods, when MNs start from 4 corners, MNs disperse quickly to more squares than the case starting from a single location. Then limited RNs would produce better performance with MNs more crowded. Therefore, when RNs are very limited, it is preferable to start the MNs from 1 corner for coverage-oriented DAWN.
Average covering percentage over the entire relief process versus different number of RNs in four scenarios. ,
,  . (a) At initial stage, 40 MNs are in
. (a) At initial stage, 40 MNs are in  at time 0, and CI values of all squares are 5, (b) At initial stage, 40 MNs are evenly deployed in
at time 0, and CI values of all squares are 5, (b) At initial stage, 40 MNs are evenly deployed in  ,
,  ,
, ,
,  at time 0, and CI values of all squares are 5, (c) At initial stage, 40 MNs are in
at time 0, and CI values of all squares are 5, (c) At initial stage, 40 MNs are in  at time 0, and CI values of all squares are randomly chosen between 1 and 10, (d) At initial stage, 40 MNs are evenly deployed in
at time 0, and CI values of all squares are randomly chosen between 1 and 10, (d) At initial stage, 40 MNs are evenly deployed in  ,
,  ,
,  at time 0. CI values of all squares are randomly chosen between 1 and 10
at time 0. CI values of all squares are randomly chosen between 1 and 10
8.3. Simulation Results for Maximal Throughput
In Figure 10, we look at the average total throughput over the entire disaster area relief process for four scenarios when the number of RNs changes. As expected, it can be noted that both algorithms yield better performance in terms of total link throughput when the number of RNs increases, which is due to the fact that more RNs can accommodate more MNs or produce more reliable links. In addition, it is worth mentioning that as the capability of RNs increases, less improvement is rendered for the total link throughput. This is because when the capacity of channels is larger, less chances are given for those uncovered MNs or MNs with unreliable links to improve the total throughput. By comparing the 4 subfigures, we can see that when the capability of RNs is small, GICA produces better results for the scenarios that MNs start from 1 corner than that of all MNs starting from 4 corners. This is because during early periods, when MNs start from one corner, MNs expand less quickly to more squares than the scenarios that MNs start from 4 corners. Therefore, when the capability of RNs is very limited, it is preferable to start MNs from 1 corner for capacity-oriented DAWN, too. In the end, it is easily seen that the GICA algorithm produces close-to-optimal solutions.
Average total link throughput over the entire relief process versus different number of RNs in four scenarios. ,
,  . (a) At initial stage, 40 MNs are in
. (a) At initial stage, 40 MNs are in  at time 0, and CI values of all squares are 5, (b) At initial stage, 40 MNs are evenly deployed in
at time 0, and CI values of all squares are 5, (b) At initial stage, 40 MNs are evenly deployed in 


 at time 0, and CI values of all squares are 5, (c) At initial stage, 40 MNs are in
at time 0, and CI values of all squares are 5, (c) At initial stage, 40 MNs are in  at time 0, and CI values of all squares are randomly chosen between 1 and 10, (d) At initial stage, 40 MNs are evenly deployed in
at time 0, and CI values of all squares are randomly chosen between 1 and 10, (d) At initial stage, 40 MNs are evenly deployed in  ,
,  ,
,  at time 0. CI values of all squares are randomly chosen between 1 and 10
at time 0. CI values of all squares are randomly chosen between 1 and 10
Next, in Figure 11, we look at the average total throughput over the entire disaster area relief process when the capability of RNs changes. It can be noted that for four scenarios, both algorithms yield better performance in terms of total link throughput when each RN can support more MNs. The rationale behind is that more channel resources brought by RNs can accommodate more MNs or produce more reliable links. In addition, it can be observed that as the capability of RNs is enlarged, less improvement is rendered for total link throughput. This is because when one RN can cover more MNs, less uncovered MNs are left. By comparing the 4 subfigures, it can be found that although the algorithms yield similar results for 4 different scenarios when the capability of RNs is small, the throughput performance converges at a higher value as the capability of RNs increases for scenarios that MNs start from 1 corner than scenarios that MNs start from 4 corners. This phenomenon stems from the fact that when MNs start from 1 corner, a smaller average number of busy squares are generated over the disaster relief process. Even when the capability for RNs is high, the network throughput performance still suffers from wide distribution of the MNs for scenarios that MNs start from 4 corners. Therefore, it is preferable to start MNs from 1 corner for capacity-oriented DAWN regardless of the capability of RNs. In the end, as can be observed, the GICA algorithm produces close-to-optimal solutions.
Average covering percentage over the entire relief process versus different capabilities of RNs in four scenarios. ,
,  . (a) At initial stage, 40 MNs are in
. (a) At initial stage, 40 MNs are in  at time 0, and CI values of all squares are 5, (b) At initial stage, 40 MNs are evenly deployed in
at time 0, and CI values of all squares are 5, (b) At initial stage, 40 MNs are evenly deployed in 


 at time 0, and CI values of all squares are 5, (c) At initial stage, 40 MNs are in
at time 0, and CI values of all squares are 5, (c) At initial stage, 40 MNs are in  at time 0, and CI values of all squares are randomly chosen between 1 and 10, (d) At initial stage, 40 MNs are evenly deployed in
at time 0, and CI values of all squares are randomly chosen between 1 and 10, (d) At initial stage, 40 MNs are evenly deployed in  ,
,  ,
,  at time 0. CI values of all squares are randomly chosen between 1 and 10
at time 0. CI values of all squares are randomly chosen between 1 and 10
9. Conclusion
In this paper, we study the dynamic deployment of mobile relays in DAWN to enable and improve the communications for the first responders during their operations. A mobility model is used to capture the movement pattern of the MNs and their communications to the RNs. Given a fixed number of relay nodes, the optimization problem is to determine the locations of the RNs as the MNs move in the disaster area nomadically. Two performance objectives, including maximal node coverage and maximal network capacity, are considered, respectively, in this study.
In the coverage problem (CORP), the performance objective is to place the RNs that can connect the maximum number of MNs in the network. As a preliminary step, we employ a maximal matching method to find the optimal relay node assignment for the static network scenario, that is, all RNs are fixed. Subsequently, we present the greedy incremental coverage algorithm (GICO) and the optimal constrained exhaustive search (CES) algorithms. The GICO algorithm is suboptimal but with significantly less computational complexity than the CES algorithm. The simulation results show that GICO algorithm can achieve close to optimal performance at different network setup and configurations.
In the capacity problem (CARP), the performance objective is to maximize the aggregated network throughput for all MNs in the DAWN. As an initial step, we first consider the relay node assignment for the static case that can be solved using the Hungarian method. Similarly, we also present both the greedy incremental capacity algorithm (GICA) and the optimal algorithm. The optimal solution for CARP can be obtained through the binary integer programming approach but at much higher computational complexity. The simulation results show that the GICA algorithm can produce near optimal results.
In addition, it is observed that network generally yields better coverage and throughput performance for scenarios in which all MNs start from 1 corner than from 4 corners of a disaster area. The tradeoff is that it would require longer time to clear the entire disaster area. As a conclusion, we advocate using the greedy algorithms to determine the dynamic relay placement in the deployment of disaster area wireless networks, in which real-time computation is practically more important.
Appendices
A. Proof of Theorem 2
NP-completeness applies directly not to optimization problems, however, but to decision problems, in which the answer is simply "yes" or "no" [24]. We first present the decision problem CORP-D associated with the CORP problem as follows. Given a set of busy squares, the number of MNs in each square, the transmission range  and
and  RNs each with capability
RNs each with capability  , is it possible to cover all MNs using exactly
, is it possible to cover all MNs using exactly  RNs? To prove the NP-completeness of the CORP problem, it suffices to prove that the decision problem CORP-D is NP-complete.
RNs? To prove the NP-completeness of the CORP problem, it suffices to prove that the decision problem CORP-D is NP-complete.
We start by arguing that CORP-D NP. Then we prove that the CORP-D problem is NP-hard by showing that MSC
NP. Then we prove that the CORP-D problem is NP-hard by showing that MSC CORP-D, (
CORP-D, ( denotes a transformation of polynomial time. MSC denotes the NP-complete minimum set cover problem). Because the CORP-D problem is both NP and NP-hard, it is NP-complete.
denotes a transformation of polynomial time. MSC denotes the NP-complete minimum set cover problem). Because the CORP-D problem is both NP and NP-hard, it is NP-complete.
To show CORP-D NP, we deploy
NP, we deploy  RNs in the shared regions. Then to find if such deployment of
RNs in the shared regions. Then to find if such deployment of  RNs can cover all MNs is tantamount to solving the RA-CORP problem. As the RA-CORP problem has been proved to be solved in polynomial time, CORP-D
RNs can cover all MNs is tantamount to solving the RA-CORP problem. As the RA-CORP problem has been proved to be solved in polynomial time, CORP-D  NP.
NP.
We next prove that MSC CORP-D, which shows that CORP-D is NP-hard. Let
CORP-D, which shows that CORP-D is NP-hard. Let  be an instance of the
be an instance of the  problem, where
problem, where  denotes the collection of subsets of a set
denotes the collection of subsets of a set  ,
,  denotes the minimum cardinality of the set
denotes the minimum cardinality of the set  such that
such that  and
and  . To obtain an instance of the CORP-D problem we only need to define the capacity bound
. To obtain an instance of the CORP-D problem we only need to define the capacity bound  for each RN. Let
for each RN. Let  be the number of all MNs. Then we build the relationship between instances of the CORP-D problem and the MSC problem as follows.
be the number of all MNs. Then we build the relationship between instances of the CORP-D problem and the MSC problem as follows.  Each element in the set
Each element in the set  corresponds to one MN;
corresponds to one MN;  each shared region corresponds with one subset
each shared region corresponds with one subset  .
. 
 is covered by the
is covered by the  th shared region if
th shared region if  . Then we must prove that
. Then we must prove that  RNs can cover all MNs if, and only if, there exists
RNs can cover all MNs if, and only if, there exists  , such that
, such that  and
and  .
.
First, suppose that  MNs in a set of busy squares can be covered by
MNs in a set of busy squares can be covered by  RNs, each with a capacity of
RNs, each with a capacity of  . Then for
. Then for  deployed at one shared region, the corresponding subset is chosen as one element in
deployed at one shared region, the corresponding subset is chosen as one element in  . Since
. Since  RNs can cover all
RNs can cover all  MNs, it is easy to see that
MNs, it is easy to see that  and
and  .
.
Now assume that there exists  such that
such that  and
and  . For
. For  we can place one RN
we can place one RN  at the
at the  th shared region. In the meantime,
th shared region. In the meantime,  covers
covers  if
if  . Since
. Since  all
all  MNs are covered by the RNs. Since
MNs are covered by the RNs. Since  , the number of RNs placed is no larger than
, the number of RNs placed is no larger than  .
.
Thus we have shown that the CORP-D problem is NP-complete, which completes the proof.
B. Proof of Theorem 4
We start by arguing that CARP-D NP (CARP-D is the decision problem associated with the CARP problem). Then we prove that CARP-D is NP-hard by showing that CORP-D
NP (CARP-D is the decision problem associated with the CARP problem). Then we prove that CARP-D is NP-hard by showing that CORP-D CARP-D. Because the problem CARP-D is both NP and NP-hard, the problem CARP is NP-complete.
CARP-D. Because the problem CARP-D is both NP and NP-hard, the problem CARP is NP-complete.
To show CARP-D NP, we deploy
NP, we deploy  RNs in the shared regions. Then to find if such deployment of
RNs in the shared regions. Then to find if such deployment of  RNs can produce the objective amount of throughput is tantamount to solving the RA-CARP problem. As the RA-CARP problem has been proved to be solved in polynomial time, the problem CARP-D
RNs can produce the objective amount of throughput is tantamount to solving the RA-CARP problem. As the RA-CARP problem has been proved to be solved in polynomial time, the problem CARP-D NP.
NP.
We next prove that CORP-D CARP-D, which shows that the problem CARP-D is NP-hard. Let
CARP-D, which shows that the problem CARP-D is NP-hard. Let  and a positive integer
and a positive integer  be an instance of the CORP-D problem. To obtain an instance of the CARP-D problem we only need define the capacity of each link between one MN and RN. Let the capacity for every link between each RN and MN be 1 unit. Then we recognize the instance of the CARP-D problem the same as the instance of the CORP-D problem. This transformation surely consumes polynomial time. Subsequently, we must prove that
be an instance of the CORP-D problem. To obtain an instance of the CARP-D problem we only need define the capacity of each link between one MN and RN. Let the capacity for every link between each RN and MN be 1 unit. Then we recognize the instance of the CARP-D problem the same as the instance of the CORP-D problem. This transformation surely consumes polynomial time. Subsequently, we must prove that  units of throughput can be produced if and only if
units of throughput can be produced if and only if  MNs can be covered by the same set of RNs.
MNs can be covered by the same set of RNs.
First, suppose that  MNs in a set of busy squares can be covered by
MNs in a set of busy squares can be covered by  RNs. Then for
RNs. Then for  covered by
covered by  , one link is established between
, one link is established between  and
and  to produce one unit of capacity. Since
to produce one unit of capacity. Since  MNs are covered, it is easy to see that
MNs are covered, it is easy to see that  units of throughput can be produced.
units of throughput can be produced.
Now we assume that the overall network capacity is  units. Then for each link between
units. Then for each link between  and
and  , we render
, we render  cover
cover  . As there are
. As there are  links available, each associated with one MN,
links available, each associated with one MN,  MNs can be covered by the same set of RNs.
MNs can be covered by the same set of RNs.
Thus we have shown that the problem CARP-D is NP-complete, which completes the proof.
References
Guo W, Huang X, Liu Y: Dynamic relay deployment for disaster area wireless networks. Wireless Communications and Mobile Computing 2008.
Kuhn HW: The hungarian method for the assignment problem. Naval Research Logistics Quarterly 1955., 2(1-2):
Hiroaki U, Jun T, Kazuki S, Takaaki U, Teruo H: A manet based system for gathering location and personal information from victims in disasters. IEIC Technical Report 2005, 105(260):13-18.
Kanchanasut K, Tunpan A, Awal MA, Das DK, Wongsaardsakul T, Tsuchimoto Y: A multimedia communication system for collaborative emergency response operation in disaster-affected areas. Internet Education and Research Laboratory, Asian Insitute of Technology, Bangkok, Thailand; January 2007.
Malan D, Fulford-Jones T, Welsh M, Moulton S: An ad hoc sensor network infrastructure for emergency medical care. Proceedings of the Workshop on Applications of Mobile Embedded Systems in Conjunction with the 2nd International Conference on Mobile Systems, Applications and Services (Mobisys '04), June 2004, Boston, Mass, USA
Zussman G, Segall A: Energy efficient routing in ad hoc disaster recovery networks. Ad Hoc Networks 2003, 1(4):405-421. 10.1016/S1570-8705(03)00041-6
Shibata Y, Sato Y, Ogasawara N, Chiba G: Ballooned wireless mesh network for emergency information system. Proceedings of the 22nd International Conference on Advanced Information Networking and Applications-Workshops (WAINA '08), March 2008, Quebec, Canada 1118-1122.
Frost V, Melamed B: Traffic modeling for telecommunications networks. IEEE Communications Magazine 1994, 32(3):70-81. 10.1109/35.267444
Leung KK, Massey WA, Whitt W: Traffic models for wireless communication networks. IEEE Journal on Selected Areas in Communications 1994, 12(8):1353-1364. 10.1109/49.329340
Lo C, Wolff R, Bernhardt R: An estimate of network database transaction volume to support universal personal communications service. Proceedings of the 1st International Conference on Universal Personal Communications (ICUPC '92), September-October 1992, Dallas, Tex, USA 1-6.
Bouchard RJ, Pyers CE: Use of gravity model for describing urban travel. Highway Research Record 1965, 88: 1-43.
Lam D, Cox DC, Widom J: Teletraffic modeling for personal communications services. IEEE Communications Magazine 1997, 35(2):79-87. 10.1109/35.565664
Markoulidakis JG, Lyberopoulos GL, Tsirkas DF, Sykas ED: Mobility modeling in third-generation mobile telecommunications systems. IEEE Personal Communications 1997, 4(4):41-56. 10.1109/98.612276
Slater PB: International migration and air travel: global smoothing and estimation. Applied Mathematics and Computation 1993, 53(2-3):225-234. 10.1016/0096-3003(93)90103-L
Aschenbruck N, Gerhards-Padilla E, Gerharz M, Frank M, Martini P: Modelling mobility in disaster area scenarios. Proceedings of the 10th ACM Symposium on Modeling, Analysis, and Simulation of Wireless and Mobile Systems (MSWiM '07), October 2007, Chania, Greece 4-12.
Nelson S, Harris A, Kravets R: Eventdriven, rolebased mobility in disaster recovery networks. Proceedings of the 2nd Workshop on Challenged Networks (CHANTS '07), September 2007, Montréal, Canada
Kim S, Ko J-G, Yoon J, Lee H: Multiple-objective metric for placing multiple base stations in wireless sensor networks. Proceedings of the 2nd International Symposium on Wireless Pervasive Computing (ISWPC '07), Feburary 2007 627-631.
Shi Y, Hou YT: Approximation algorithm for base station placement in wireless sensor networks. Proceedings of the 4th Annual IEEE Communications Society Conference on Sensor, Mesh and Ad Hoc Communications and Networks (SECON '07), June 2007, San Diego, Calif, USA 512-519.
Hou YT, Shi Y: Optimal base station selection for anycast routing in wireless sensor networks. IEEE Transactions on Vehicular Technology 2006, 55(3):813-821. 10.1109/TVT.2006.873822
Pan J, Hou YT, Cai L, Shi Y, Shen S: Topology control for wireless sensor networks. Proceedings of the 3rd International Workshop on Discrete Algorithms and Methods for Mobile Computing and Communications (ICDCS '99), August 1999, Seattle, Wash, USA
Pothen A, Fan C: Computing the block triangular form of a sparse matrix. ACM Transactions on Mathematical Software 1990, 16(4):303-324. 10.1145/98267.98287
Wolsey LA: Integer Programming. John Wiley & Sons, New York, NY, USA; 1998.
Belegundu AD, Chandrupatla TR: Optimization Concepts and Applications in Engineering. Prentice-Hall, Upper Saddle River, NJ, USA; 1999.
Cormen T, Leiserson C, Rivest R, Stein C: Introduction to Algorithms. MIT Press, Cambridge, MA, USA; 2002.
Acknowledgments
This work has been supported in part by the National Science Foundation (NSF) through Award ECS-0725522 and by the Faculty Advancement in Research Awards from WPI. This work was presented in part at 3rd Intl. Conf. Wireless Algorithms, Systems and Applications, 2008.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Guo, W., Huang, X. On Coverage and Capacity for Disaster Area Wireless Networks Using Mobile Relays. J Wireless Com Network 2009, 251314 (2009). https://doi.org/10.1155/2009/251314
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/251314






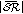
 belongs to
belongs to 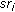
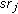 from
from  ;
; belongs to
belongs to 
 to
to 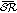 ;
;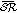 ;
; ;
;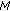

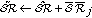
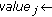 RA-CORP(
RA-CORP(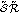 )
) ;
;
 are points
are points  ,
,  and
and  . Then the centroid point
. Then the centroid point  of the triangle
of the triangle  is regarded as the position of any RN that is placed within
is regarded as the position of any RN that is placed within  .
.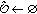 ;
;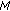
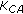
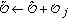
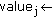 RA-CARP(
RA-CARP(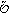 )
)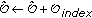 ;
;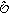 ;
;



