- Research Article
- Open access
- Published:
Residue Number System Arithmetic Assisted Coded Frequency-Hopped OFDMA
EURASIP Journal on Wireless Communications and Networking volume 2009, Article number: 263695 (2009)
Abstract
We propose an RNS arithmetic-based FH pattern design approach that is well suited and easy to implement for practical OFDMA systems. The proposed FH scheme guarantees orthogonality among intracell users while randomizing the intercell interferences and providing frequency diversity gains. We present detailed construction procedures and performance analysis for both independent and cluster hopping scenarios. Using simulation results, we demonstrate the gains due to frequency diversity and intercell interference diversity on the system bit error rate (BER) performance. Furthermore, the BER performance gain is consistent across all cells unlike other FH pattern design schemes such as the Latin squares (LSs-)-based FH pattern design where wide performance variations are observed across cells.
1. Introduction
Orthogonal frequency division multiplexing (OFDM) has been widely accepted as an enabling technology for next generation wireless communication systems. In OFDM, high-rate data streams can be broken down into a number of parallel lower-rate streams, thereby avoiding the need for complex equalization. OFDM also forms the foundation for a multiple access scheme termed as orthogonal frequency division multiple access (OFDMA). In OFDMA, each user is assigned a fraction of available subcarriers based upon his/her demand for bandwidth. The advantages of OFDMA include (1) the flexibility in subcarriers' allocation; (2) the absence of multiuser interference due to subcarriers' orthogonality; (3) the simplicity of the receiver design [1].
In order to enhance system throughput and spectral efficiency, frequency hopping (FH) is generally used in OFDMA cellular systems. It is desirable for FH patterns to satisfy the following conditions [2]: (i) minimize intracell interference; (ii) average intercell interference; (iii) avoid ambiguity while identifying users; (iv) exploit frequency diversity by forcing hops to span a large bandwidth. The first aspect is relatively easy to achieve by using orthogonal hopping patterns within a cell. To average intercell interferences, hopping patterns are constructed in a way that two users in different cells interfere with each other only during a small fraction of all hops. The third condition requires base stations to have the capability of distinguishing different users efficiently according to their unique FH signatures. Finally, the last requirement not only ensures the security of the transmission, but also mitigates the effect of fading by exploiting frequency diversity.
Frequency hopping pattern design has received considerable attention in both commercial and military communication systems. There has been extensive work on designing FH-OFDMA systems [3–10]. In [3], concepts of fast frequency hopping along with OFDM are illustrated. In [4], authors show that the expected number of collisions per symbol under both independent and cluster hopping does not depend on the hopping strategy. In their later work [5], it is shown that the number of collisions can be further reduced by using space-frequency coding in multiple-antenna systems. Orthogonal Latin squares (LSs) are presented as FH patterns in TCM/BICM coded OFDMA in [6]. In LS-aided FH-OFDMA systems, it is seen that there is a wide variability in the performance of users in different cells. Therefore, it is not an effective scheme if one considers fairness to be important. Welch-Costas array is introduced in [7] and evaluated in [8] for coded FH-OFDMA. Here, although users across cells experience significant performance improvements, users within a cell may not occupy all of the available bandwidth to exploit full frequency diversity. Other aspects focusing on preventing hostile jamming and pilot-assisted channel estimation in FH-OFDMA are explored in [9, 10], respectively.
In this paper, we propose a novel frequency hopping pattern design strategy based on RNS arithmetic for practical OFDMA cellular systems. We show that the resulting patterns are orthogonal within a cell and intersect only once across cells in a frequency hopping cycle. RNS arithmetic has found applications in many areas. However, its use in designing frequency hopping patterns is rarely considered [11, 12]. In [11], the design procedure can be visualized as a "top-down" approach where a given bandwidth is divided into multiple candidate subbands based on a predetermined moduli set. As a result, if the moduli set changes, the bandwidth of subcarriers varies. In this work, the division of bandwidth into candidate subcarriers is assumed to be given or determined in advance. Therefore, we can consider our proposed approach as a "bottom-up" method driven by grouping and indexing the subcarriers according to the RNS arithmetic. For practical OFDMA cellular systems, the proposed "bottom-up" approach is more feasible. For example, in downlink OFDMA cellular systems, a fixed number of subcarriers (e.g., 1024) with identical subcarrier bandwidth within each cell is usually assumed. Furthermore, for reducing intercell interference, [11] suggests the use of different moduli sets for adjacent cells. This approach results in adjacent cells employing different numbers of subcarriers with different bandwidths across cells. Once again, this is a stringent requirement that may not be feasible in practice. In this work, we invoke the use of the so-called two-stage and multistage selection algorithms to construct RNS-FH patterns such that (1) different users can use the spectral resources simultaneously within each cell and (2) the same number of subcarriers can be employed from cell to cell. Additionally, the proposed FH sequences force the intracell interferences to zero and average out the intercell interferences. The performance of the proposed FH pattern incorporating with both independent and cluster hopping schemes is characterized. Simulation results show that RNS-FH OFDMA has significantly better BER performance relative to traditional OFDMA scheme without FH. Another aspect that makes RNS-FH pattern design outperforms other existing FH techniques is that user hopping patterns span a larger bandwidth. Therefore, the channel fades associated with consecutive hops become independent. Moreover, with the use of FEC codes over multiple hops, the system can correct errors due to subcarriers that experience deep fades or subcarriers that are severely interfered by others.
The rest of the paper is organized as follows. In Section 2, system model along with signal transmission scheme, access strategies, and interference models is introduced. In Section 3, detailed RNS-FH pattern design procedures along with comparisons with the existing technique are presented. Simulation results with performance analysis are given in Section 4. Finally, we conclude this paper in Section 5.
2. System Model
In this section, we first describe the signal transmission scheme for each individual user in an OFDMA system. Then, we introduce the access model and interference model under both independent and cluster hopping schemes.
2.1. Signal Transmission Scheme
The block diagram of FEC coded FH-OFDMA system is shown in Figure 1. Here, data bits of every user are first channel coded and then mapped to complex constellation points. We assume that there are  users in the system, utilizing a total of
users in the system, utilizing a total of  OFDM subcarriers. Each user is assigned a specific set of subcarriers out of the total available subcarriers according to his/her data rates. Let
OFDM subcarriers. Each user is assigned a specific set of subcarriers out of the total available subcarriers according to his/her data rates. Let  be the number of subcarriers allocated to user
be the number of subcarriers allocated to user  . Then, user
. Then, user  transmits the information symbols
transmits the information symbols  (
( represents the transpose operation) on the assigned
represents the transpose operation) on the assigned  subcarriers. Therefore, the baseband transmitted signal of user
subcarriers. Therefore, the baseband transmitted signal of user  can be expressed as
can be expressed as

where  represents the time-domain signal, and
represents the time-domain signal, and  denotes one OFDM symbol duration. Since this is an OFDMA system, it is important to remember that every user is assigned a different set of subcarriers for transmission, and this allocation is dynamic in the case of frequency hopping OFDMA. That is, in the IFFT module, the frequency assignment follows a predetermined FH pattern. Moreover, each user transmits zeros on subcarriers which are not assigned to him/her.
denotes one OFDM symbol duration. Since this is an OFDMA system, it is important to remember that every user is assigned a different set of subcarriers for transmission, and this allocation is dynamic in the case of frequency hopping OFDMA. That is, in the IFFT module, the frequency assignment follows a predetermined FH pattern. Moreover, each user transmits zeros on subcarriers which are not assigned to him/her.
For convenience, we note  as the subcarrier that is assigned to user
as the subcarrier that is assigned to user  . Hence,
. Hence,  information symbols vector of user
information symbols vector of user  can be written as
can be written as

The discrete form of the transmitted signal  is then given as,
is then given as,

where  is the IFFT matrix defined as
is the IFFT matrix defined as

where  .
.
Let  denote the channel impulse response vector, then its Fourier transform is
denote the channel impulse response vector, then its Fourier transform is

where  represents the Hermitian transpose. In general, each channel impulse response is a function of time and access delay which can be modeled as a tapped delay line, that is,
represents the Hermitian transpose. In general, each channel impulse response is a function of time and access delay which can be modeled as a tapped delay line, that is,

where  is the number of multipaths and
is the number of multipaths and  is the time delay of the
is the time delay of the  th path. The tap coefficients are independent, zero mean, circularly symmetric complex Gaussian random processes at each instant
th path. The tap coefficients are independent, zero mean, circularly symmetric complex Gaussian random processes at each instant  , that is,
, that is,  with the total power normalized to unity, that is,
with the total power normalized to unity, that is,  . In this work, we use Jakes' model to describe the time/frequency variation of each channel coefficient. Therefore, the spaced frequency (
. In this work, we use Jakes' model to describe the time/frequency variation of each channel coefficient. Therefore, the spaced frequency ( ) spaced time (
) spaced time ( ) correlation function of the channel frequency response can be expressed as [13]
) correlation function of the channel frequency response can be expressed as [13]

where  is the Doppler frequency.
is the Doppler frequency.
At the receiver end, after FFT, the received signal corresponding to user  on subcarrier
on subcarrier  is
is

Then, the overall received signal which is a superposition of the signals transmitted from all  users is
users is

where  is the Fourier transform of the noise vector.
is the Fourier transform of the noise vector.
2.2. Access Model
In this part, clustered and independent FH-OFDMA are introduced, and closed form expressions of the expected number of collisions per symbol under both of these two hopping strategies are presented.
2.2.1. Clustered FH-OFDMA
In cluster hopping, each user selects a set of continuous subcarriers, termed cluster, to transmit the information symbols. Specifically, the hopping takes place among clusters of subcarriers based on predetermined FH patterns. Therefore, collisions occur among clusters first, and then across all OFDM subcarriers within that cluster. The expected number of symbol losses per cluster collision corresponds to [4]

where  is the number of subcarriers per cluster and
is the number of subcarriers per cluster and  represents the probability that at least one interfering user collides with the desired user. For cluster hopping, we have
represents the probability that at least one interfering user collides with the desired user. For cluster hopping, we have  hopping clusters. Therefore, the collision probability between the desired user and the interfering user in one cluster is
hopping clusters. Therefore, the collision probability between the desired user and the interfering user in one cluster is  . Hence, the probability that at least one of the
. Hence, the probability that at least one of the  users collides with the desired user can be expressed as
users collides with the desired user can be expressed as

For convenience, throughout the rest of this paper, we assume that each user employs the same number of subcarriers ( ) per cluster.
) per cluster.
2.2.2. Independent FH-OFDMA
In independent hopping, subcarriers occupied by a user are selected independently from all available subcarriers. In other words,  subcarriers in one cluster are not continuous anymore, and they are chosen in a pseudorandom fashion across the frequency spectrum. With independent hopping, the expected number of symbols lost per symbol collision is given by [4]
subcarriers in one cluster are not continuous anymore, and they are chosen in a pseudorandom fashion across the frequency spectrum. With independent hopping, the expected number of symbols lost per symbol collision is given by [4]

where  is the probability that
is the probability that  subcarriers out of
subcarriers out of  subcarriers occupied by each user experience collisions due to interfering users.
subcarriers occupied by each user experience collisions due to interfering users.
Theorem 1.
For independent FH-OFDMA scheme described above,  corresponds to
corresponds to

Proof.
 is the probability that
is the probability that  subcarriers of the desired user collide with the subcarriers of interfering user given that each user occupies a total of
subcarriers of the desired user collide with the subcarriers of interfering user given that each user occupies a total of  subcarriers. It is evident that the number of possible combinations of
subcarriers. It is evident that the number of possible combinations of  subcarriers that experience collisions is
subcarriers that experience collisions is  . Define
. Define  as the probability that
as the probability that  symbols are collision-free given that each user occupies
symbols are collision-free given that each user occupies  subcarriers. Furthermore, define
subcarriers. Furthermore, define  as the conditional probability that
as the conditional probability that  symbols collide given that
symbols collide given that  symbols are collision-free. Therefore, we can write
symbols are collision-free. Therefore, we can write  as
as

Here,  corresponds to
corresponds to

Equation (15) denotes the probability that the desired user's remaining  subcarriers are collision-free while none of the other
subcarriers are collision-free while none of the other  users within the same cell occupies these subcarriers.
users within the same cell occupies these subcarriers.  is expressed as [4]
is expressed as [4]

Equation (16) represents the conditional probability that each of the  subcarriers of the desired user collides given that the other
subcarriers of the desired user collides given that the other  subcarriers are collision-free. By substituting (15) and (16) into (14), we obtain the result in (13).
subcarriers are collision-free. By substituting (15) and (16) into (14), we obtain the result in (13).
2.3. Interference Model
In this paper, we model intercell interferences as additive complex Gaussian-distributed distortions. This model is accurate when interferences from adjacent cells are perfectly randomized with respect to the cell of interest. Models specific to clustered and independent FH-OFDMA are presented in the following.
2.3.1. Clustered FH-OFDMA
In clustered FH-OFDMA, if interference occurs on any symbol on one subcarrier in the cluster, all other symbols in the same cluster will also experience interferences from adjacent cells. Hence, the interference for the  th user can be modeled as [6]
th user can be modeled as [6]

where  is an
is an  vector, representing the received signal of user
vector, representing the received signal of user  ;
;  is the
is the  transmitted signal vector;
transmitted signal vector;  is an
is an  matrix that contains the frequency domain representations of channel impulse response;
matrix that contains the frequency domain representations of channel impulse response;  is an
is an  vector whose components are complex Gaussian random variables with zero mean and variance
vector whose components are complex Gaussian random variables with zero mean and variance  . Here, the
. Here, the  vector
vector  is the interference vector that captures the interference from all adjacent cells. The components of
is the interference vector that captures the interference from all adjacent cells. The components of  are i.i.d complex Gaussian random variables independent of
are i.i.d complex Gaussian random variables independent of  and
and  with mean zero, variances
with mean zero, variances  . The variances correspond to
. The variances correspond to

where  denotes the symbol signal-to-interference ratio and
denotes the symbol signal-to-interference ratio and  characterizes the presence/absence of a collision between users in different cells. That is, if there is a collision,
characterizes the presence/absence of a collision between users in different cells. That is, if there is a collision,  equals to one; if there is no collision,
equals to one; if there is no collision,  is set to zero. Furthermore,
is set to zero. Furthermore,  can be modeled as Bernoulli's random variable with probability of collision equals to
can be modeled as Bernoulli's random variable with probability of collision equals to  (i.e.,
(i.e.,  and
and  ), which can be expressed as
), which can be expressed as

where  is the number of active users. If the system is fully loaded, then
is the number of active users. If the system is fully loaded, then  . If there is a collision, that is,
. If there is a collision, that is,  , then all subcarriers in the cluster will be affected by the intercell interference.
, then all subcarriers in the cluster will be affected by the intercell interference.
2.3.2. Independent FH-OFDMA
In independent hopping, since subcarriers are selected independently of all other subcarriers according to predetermined FH patterns, collisions occur independently. Hence, for the  th subcarrier of the
th subcarrier of the  th user,
th user,

Here, the interference power  of the i.i.d complex Gaussian random variable
of the i.i.d complex Gaussian random variable  corresponds to
corresponds to

where  with probabilities
with probabilities  and
and  , respectively. The collision probability
, respectively. The collision probability  is given by
is given by

For a fully loaded system with independent hopping,  is identical to
is identical to  becomes to one.
becomes to one.
3. RNS-FH Pattern Design
RNS is defined by the choice of  number of positive integers
number of positive integers  (
( ), referred to as moduli [14]. If all the moduli are pairwise relative primes to each other, any integer
), referred to as moduli [14]. If all the moduli are pairwise relative primes to each other, any integer  which falls in the range of
which falls in the range of  can be uniquely and unambiguously represented by the residue sequence (
can be uniquely and unambiguously represented by the residue sequence ( ), where
), where  and
and  for
for  . Here,
. Here,  is used to describe the
is used to describe the  th user FH address. To recover
th user FH address. To recover  , or to distinguish users at the base station, Chinese remainder theorem (CRT) is generally used which is well known for its capability of solving a set of linear congruences, simultaneously. According to CRT, it can be shown that the numerical value of
, or to distinguish users at the base station, Chinese remainder theorem (CRT) is generally used which is well known for its capability of solving a set of linear congruences, simultaneously. According to CRT, it can be shown that the numerical value of  can be computed as [15]
can be computed as [15]

where  and
and  for
for  .
.
Theorem 2.
The residue sequences obtained using the RNS arithmetic as described above are orthogonal.
Proof.
In order to prove that the residue sequences are orthogonal, we need to show that every  in the range of
in the range of  has a unique residue set that is different from residue sets generated by other integers within the same range. We will prove this by contradiction as follows.
has a unique residue set that is different from residue sets generated by other integers within the same range. We will prove this by contradiction as follows.
Assuming that  and
and  are different integers which are in the same range of
are different integers which are in the same range of  with the same residue set. That is,
with the same residue set. That is,

Therefore, we have

Thus, we can conclude from (25) that  is actually the least common multiple (LCM) of
is actually the least common multiple (LCM) of  . Furthermore, if
. Furthermore, if  are pairwise relative primes to each other, their LCM is
are pairwise relative primes to each other, their LCM is  and it must be that
and it must be that  is a multiple of
is a multiple of  . However, this statement does not hold since
. However, this statement does not hold since  and
and  . Therefore, by contradiction,
. Therefore, by contradiction,  and
and  should not have the same residue set. In general, the residue set (
should not have the same residue set. In general, the residue set ( ) generated by
) generated by  is unique and can be used to represent the integer
is unique and can be used to represent the integer  if
if  .
.
Following the RNS arithmetic presented above, we propose to design FH patterns that satisfy all the requirements described in Section 1 while avoiding the limitations in [11]. Detailed procedures of constructing RNS-FH patterns are given in the following subsections. The first part describes the two-stage algorithm, while the second part introduces the multistage algorithm which can be considered as generalization of the two-stage algorithm. At the end of this section, we compare our proposed RNS-FH pattern design strategy with the method presented in [11].
3.1. Two-Stage Algorithm
In this part, the detailed procedures of constructing RNS-FH patterns via the so-called two-stage algorithm is introduced. We present the algorithm for a cluster hopping OFDMA system. It is straightforward to extend the algorithm to the independent hopping scenario. The steps involved in the two-stage selection algorithm are given as follows.
-
(1)
Divide the total available subcarriers
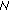 into
into 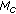 clusters with each cluster containing
clusters with each cluster containing 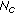 number of contiguous subcarriers.
number of contiguous subcarriers. -
(2)
If
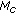 can be written as a product of two pairwise relative primes, for example,
can be written as a product of two pairwise relative primes, for example, 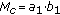 , we can first group
, we can first group  clusters into
clusters into 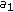 groups with
groups with 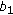 clusters in each group. Then, we index the groups from
clusters in each group. Then, we index the groups from  to
to 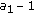 .
. -
(3)
Index the clusters in each group from 0 to
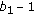 .
. -
(4)
At the 0th time slot, assign integer
 to user
to user 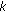 as its FH address according to its access order to the system, where
as its FH address according to its access order to the system, where 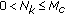 .
. -
(5)
If
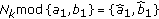 , then user
, then user 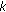 selects the
selects the 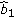 th cluster out of the
th cluster out of the 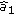 th group for transmission.
th group for transmission. -
(6)
At the
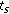 th time slot, assign integer
th time slot, assign integer 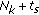 to user
to user 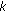 as its current FH address and repeat step 5.
as its current FH address and repeat step 5. -
(7)
Repeat steps 4–6 until one mutually orthogonal FH pattern is obtained.
-
(8)
If
 can be expressed as products of other combinations of two pairwise relative primes, for example,
can be expressed as products of other combinations of two pairwise relative primes, for example, 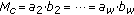 , then
, then  different orthogonal FH patterns can be obtained by repeating steps 2–7,
different orthogonal FH patterns can be obtained by repeating steps 2–7,  times.
times.
An example is given in Figure 2 to illustrate the two-stage RNS-assisted frequency hopping strategy. Here, 6 users access the system ( ); the total number of subcarriers is 30 (
); the total number of subcarriers is 30 ( ) and they are divided into 6 clusters (
) and they are divided into 6 clusters ( ) with each cluster containing 5 contiguous subcarriers (
) with each cluster containing 5 contiguous subcarriers ( ). At the 0th time slot, the FH address assigned to the 5th user is 5 according to his/her access order to the system. Therefore,
). At the 0th time slot, the FH address assigned to the 5th user is 5 according to his/her access order to the system. Therefore,  . User 5 will choose the 2nd cluster of subcarriers out of the 1st group of clusters to transmit. At the 1st time slot, the FH address assigned to this user becomes
. User 5 will choose the 2nd cluster of subcarriers out of the 1st group of clusters to transmit. At the 1st time slot, the FH address assigned to this user becomes  . Obviously,
. Obviously,  , then he/she will select the 0th cluster of subcarriers out of the 0th group of clusters for transmission at this time. This process continues until one FH sequence of length
, then he/she will select the 0th cluster of subcarriers out of the 0th group of clusters for transmission at this time. This process continues until one FH sequence of length  is constructed.
is constructed.
3.2. Multistage Algorithm
The multistage algorithm is an extension of the two-stage algorithm. Introducing the multistage algorithm cannot only enhance the flexibility of the pattern design, but also strengthen the robustness of the entire FH scheme. We describe the multistage algorithm assuming an independent hopping scheme with each user employing the same number of subcarriers, that is,  for
for  . The steps involved in the multistage algorithm correspond to the following.
. The steps involved in the multistage algorithm correspond to the following.
-
(1)
If
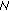 can be written as a product of
can be written as a product of 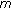 pairwise relative primes, for example,
pairwise relative primes, for example, 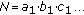 , we can first group
, we can first group 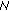 subcarriers into
subcarriers into  groups with
groups with 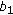 subgroups in each group. Then, we index the first-stage groups from 0 to
subgroups in each group. Then, we index the first-stage groups from 0 to 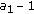 .
. -
(2)
Index the second-stage groups in each first-stage group from 0 to
 . Then group the subcarriers in each second-stage group into
. Then group the subcarriers in each second-stage group into 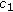 subgroups.
subgroups. -
(3)
Similar steps continue on until all of the subcarriers are grouped and indexed at the
 th-stage.
th-stage. -
(4)
At the 0th time slot, assign integer set
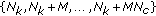 to user
to user 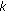 as its FH addresses, where
as its FH addresses, where 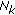 is its access order to the system,
is its access order to the system, 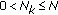 .
. -
(5)
If
 , then user
, then user 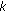 first selects the
first selects the 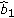 th second-stage group out of the
th second-stage group out of the 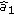 th first-stage group, then similar selecting procedures continue on until the subcarrier at the
th first-stage group, then similar selecting procedures continue on until the subcarrier at the 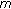 th-stage has been extracted out for transmission.
th-stage has been extracted out for transmission. -
(6)
The process in step 5 is repeated on the other elements in the integer set of user
 until
until 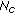 subcarriers have been extracted out for user
subcarriers have been extracted out for user 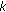 to transmit.
to transmit. -
(7)
At the
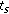 th time slot, assign integer set
th time slot, assign integer set 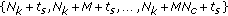 as the current FH addresses of user
as the current FH addresses of user  and repeat steps 5-6.
and repeat steps 5-6. -
(8)
Repeat steps 4–7 until one mutually orthogonal FH pattern is obtained.
-
(9)
If
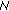 can be expressed as products of other combinations of
can be expressed as products of other combinations of 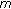 pairwise relative primes, for example,
pairwise relative primes, for example, 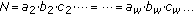 , then
, then  different orthogonal FH patterns can be obtained by repeating steps 1–8,
different orthogonal FH patterns can be obtained by repeating steps 1–8,  times.
times.
It is easy to visualize the multistage algorithm by using a tree diagram. An example is given in Figure 3. Here, 30 users access the system ( ); a total of 30 subcarriers are used, that is,
); a total of 30 subcarriers are used, that is,  . Two specific examples are illustrated as follows: (1) consider user 2. The subcarriers used by this user at the 0th time slot can be calculated as follows:
. Two specific examples are illustrated as follows: (1) consider user 2. The subcarriers used by this user at the 0th time slot can be calculated as follows:  ; that is, in the 0th first-stage group, the 2nd subcarrier out of the 2nd second-stage group is selected for transmission. This is indicated with a solid line in Figure 3; (2) consider user 27.
; that is, in the 0th first-stage group, the 2nd subcarrier out of the 2nd second-stage group is selected for transmission. This is indicated with a solid line in Figure 3; (2) consider user 27.  ; that is, in the 1st first-stage group, the 2nd subcarrier out of the 0th second-stage group is selected by the 27th user for transmission at the 0th time slot. This is indicated with a dashed line in the figure. This procedure continues until an FH sequence of length
; that is, in the 1st first-stage group, the 2nd subcarrier out of the 0th second-stage group is selected by the 27th user for transmission at the 0th time slot. This is indicated with a dashed line in the figure. This procedure continues until an FH sequence of length  is completed. We should note that in this example, the system is fully loaded (
is completed. We should note that in this example, the system is fully loaded ( ). For
). For  , each user is assigned a set of FH addresses rather than one unique FH signature. For example, consider user 2 in Figure 3, the 2nd subcarrier occupied by user 2 at the 0th time slot is determined starting from his/her current FH address
, each user is assigned a set of FH addresses rather than one unique FH signature. For example, consider user 2 in Figure 3, the 2nd subcarrier occupied by user 2 at the 0th time slot is determined starting from his/her current FH address  and following the steps as before. These steps are repeated until
and following the steps as before. These steps are repeated until  subcarriers for user 2 are identified. Extrapolating the procedure across the time axis, an entire FH sequence of length
subcarriers for user 2 are identified. Extrapolating the procedure across the time axis, an entire FH sequence of length  is designed.
is designed.
With respect to the design procedures, the major difference between independent hopping and cluster hopping is the following: in independent hopping, each FH address specifies a single subcarrier that can be used. Therefore, if users have very high bandwidth/rate or other QoS requirements, multiple FH addresses can be given to accommodate. In cluster hopping scenario, a user may demand only one unique FH address as a single address completely specifies all  subcarriers required for transmission. Fully loaded independent hopping system is a special case of cluster hopping with one subcarrier in each cluster.
subcarriers required for transmission. Fully loaded independent hopping system is a special case of cluster hopping with one subcarrier in each cluster.
From Figures 2 and 3, it is evident that the proposed RNS-FH patterns guarantee the orthogonality among different users within a cell. That is, users within the same cell will not interfere with each other when they simultaneously access the system. The next example, which is shown in Figure 4, demonstrates that if different RNS-FH patterns are assigned to adjacent cells, intercell interferences can be perfectly averaged. In this example,  is set to 10 while the moduli sets used to construct FH patterns in cells 1 and 2 are
is set to 10 while the moduli sets used to construct FH patterns in cells 1 and 2 are  and
and  , respectively. From Figure 4, it is evident that every user in cell 1 experiences interference from different users from cell 2 during each of his/her hops. For example, in the first OFDM symbol duration, user 1 in cell 1 is interfered by user 8 from cell 2; in the next OFDM symbol slot, user 1 is interfered by user 5 from cell 2 and so on. In general, users from different cells collide only once during a frequency hopping cycle under the proposed scheme. Therefore, full interference diversity is exploited in the case of RNS-FH patterns.
, respectively. From Figure 4, it is evident that every user in cell 1 experiences interference from different users from cell 2 during each of his/her hops. For example, in the first OFDM symbol duration, user 1 in cell 1 is interfered by user 8 from cell 2; in the next OFDM symbol slot, user 1 is interfered by user 5 from cell 2 and so on. In general, users from different cells collide only once during a frequency hopping cycle under the proposed scheme. Therefore, full interference diversity is exploited in the case of RNS-FH patterns.
The properties of the proposed RNS-FH patterns can be summarized as follows.
-
(1)
At most, a size of
 mutually orthogonal FH pattern can be obtained for the independent hopping scheme. The size becomes
mutually orthogonal FH pattern can be obtained for the independent hopping scheme. The size becomes  for the cluster hopping.
for the cluster hopping. -
(2)
If
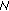 (
(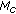 ) can be written as a product of
) can be written as a product of 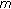 pairwise relative primes, then at least,
pairwise relative primes, then at least, 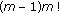 different RNS-FH patterns can be obtained.
different RNS-FH patterns can be obtained. -
(3)
With the use of the same moduli set, for independent hopping, RNS-FH patterns constructed after
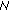 frames (
frames (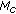 for cluster hopping) are actually periodical extensions of the RNS-FH pattern designed during the first
for cluster hopping) are actually periodical extensions of the RNS-FH pattern designed during the first  (
( ) frames.
) frames. -
(4)
With knowledge of moduli and residue, the base station can regenerate the entire RNS-FH pattern using the CRT.
3.3. Comparison with [11]
In this section, we compare our proposed RNS-FH pattern design method with the technique presented in [11] (which also considers RNS as the design metric).
First of all, although both strategies (one proposed here and the other presented in [11]) use the RNS arithmetic as a basis, the mechanisms of determining the hopping sequence are different. In [11], the FH scheme can be visualized as a "top-down" approach where a given bandwidth is divided into multiple candidate subcarriers in multistages according to the predetermined moduli set (see [11, Figure 2]). That is, the choice of the moduli set (top level decision) determines the number of subcarriers that can be used (bottom level decision) for hopping. This scheme is driven in conjunction with MFSK-modulated signals and a reference register  , which has the same length as the moduli set (
, which has the same length as the moduli set ( ), providing reference to each user in order to enable synchronous transmission. However, in our work, we assume that the division of the frequency bandwidth has already been done in advance. That is, the number of subcarriers that can be used for hopping is given (bottom level decision). Based on this number, we employ a proper moduli set to group and index each of the candidate subcarriers (top level decision). Therefore, we can interpret our proposed initialization process as a "bottom-up" approach (see Figure 3). It is important to note that in practical OFDMA cellular systems, the division of the bandwidth within a cell is usually fixed and predetermined (e.g., 1024 subcarriers). Therefore, our "bottom-up" approach is more suitable for such practical systems. Furthermore, unlike the length-
), providing reference to each user in order to enable synchronous transmission. However, in our work, we assume that the division of the frequency bandwidth has already been done in advance. That is, the number of subcarriers that can be used for hopping is given (bottom level decision). Based on this number, we employ a proper moduli set to group and index each of the candidate subcarriers (top level decision). Therefore, we can interpret our proposed initialization process as a "bottom-up" approach (see Figure 3). It is important to note that in practical OFDMA cellular systems, the division of the bandwidth within a cell is usually fixed and predetermined (e.g., 1024 subcarriers). Therefore, our "bottom-up" approach is more suitable for such practical systems. Furthermore, unlike the length- reference register
reference register  that is used in [11], the FH scheme proposed in this paper invokes the use of only a length-one register to store the time index which in turn can be used to calculate current FH address of each user at the base station.
that is used in [11], the FH scheme proposed in this paper invokes the use of only a length-one register to store the time index which in turn can be used to calculate current FH address of each user at the base station.
Secondly, for reducing intercell interference, [11] suggests the use of different moduli sets for adjacent cells. Since the choice of the moduli set determines the number of subcarriers used for hopping, a different moduli set in adjacent cells will result in different number of subcarriers in adjacent cells. If the total bandwidth is the same for all cells, this approach translates into subcarriers in adjacent cells having different bandwidths. This may be an unrealistic assumption for practical OFDMA systems. If the method in [11] is applied to a practical scenario using fixed number of subcarriers (each with the same bandwidth), high intercell interference will result (as shown in Figure 8). Our proposed "bottom-up" approach does not suffer from this drawback as it is built on the premise that the number of subcarriers and their bandwidths are fixed across cells.
In summary, the method proposed in this work is flexible and well suited for practical OFDMA cellular systems.
4. Simulation Results
Parameters of the simulated system are provided in Table 1. The cyclic prefix within one OFDM symbol duration is assumed long enough to eliminate ISI (intersymbol interference). Two 6-ray channel pulse responses are considered following the UTRA vehicular test environment [16]. In Figure 5, the correlation functions of these two channels are plotted versus the variation of  , while
, while  slot and
slot and  . From Figure 5, we can conclude that if small hopping intervals occur frequently in an FH pattern, Veh B can provide more frequency diversity than Veh A.
. From Figure 5, we can conclude that if small hopping intervals occur frequently in an FH pattern, Veh B can provide more frequency diversity than Veh A.
Theoretical (see (10) and (12) and simulated expected number of collisions per symbol in RNS-FH OFDMA are given in Figure 6. The high collision probability severely limits the number of active users that can be simultaneously supported by the FH system.
In Figure 7, bit error rate (BER) versus SNR of RNS-FH OFDMA under both cluster and independent hopping is plotted. The main objective of this example is to characterize the effects of frequency diversity exploited by RNS-FH patterns on system performance. Here, we assume that 10 users are in the system with 11 subcarriers assigned to each via the two-stage RNS hopping strategy. For cluster hopping, the moduli set used is  , while for independent hopping, it is
, while for independent hopping, it is  . It is observed that both independent and clustered RNS-FH OFDMA dramaticallyoutperforms the regular OFDMA scheme without hopping in both Veh A and Veh B environments. Another observation is that under both independent and cluster hopping, the system performs better in Veh A. That is, in the proposed RNS-FH patterns, large hopping intervals occur more frequently than small hopping distances. This characteristic is very important since it reveals that users occupy a wide bandwidth during a small fraction of all hops. Furthermore, since independent hopping scheme results in a much larger FH pattern than cluster hopping, more frequency diversity can be exploited in the independent hopping case. This is also clearly reflected by the simulation results shown in Figure 7. For example, at a BER level of
. It is observed that both independent and clustered RNS-FH OFDMA dramaticallyoutperforms the regular OFDMA scheme without hopping in both Veh A and Veh B environments. Another observation is that under both independent and cluster hopping, the system performs better in Veh A. That is, in the proposed RNS-FH patterns, large hopping intervals occur more frequently than small hopping distances. This characteristic is very important since it reveals that users occupy a wide bandwidth during a small fraction of all hops. Furthermore, since independent hopping scheme results in a much larger FH pattern than cluster hopping, more frequency diversity can be exploited in the independent hopping case. This is also clearly reflected by the simulation results shown in Figure 7. For example, at a BER level of  , nearly 8 dB gain is offered by independent hopping relative to cluster hopping in Veh A environment.
, nearly 8 dB gain is offered by independent hopping relative to cluster hopping in Veh A environment.
Figure 8 quantifies the intercell interferences experienced by different users in the cell of interest, averaged across time. The  -axis represents the indices of the users within the cell of interest while the
-axis represents the indices of the users within the cell of interest while the  -axis characterizes the time-averaged intercell interference-to-signal power ratio for a given user. Two situations are considered: (1) different RNS-FH patterns are allocated to the cell of interest and the interfering cell (denoted by the solid line); (2) the same RNS-FH pattern as the cell of interest is assigned to the interfering cell (denoted by the dashed line). Here, we model the intercell interference as additive Gaussian-distributed distortion. Therefore, in scenario (1), users in the cell of interest will experience different interferences from the interfering cell across all hops, which in turn induces interference diversity. Figure 8 clearly demonstrates that by employing the proposed method (i.e., allocating a different RNS-FH pattern to the interfering cell), the intercell interference floor can be significantly lowered relative to the scenario where all cells employ identical RNS-FH patterns.
-axis characterizes the time-averaged intercell interference-to-signal power ratio for a given user. Two situations are considered: (1) different RNS-FH patterns are allocated to the cell of interest and the interfering cell (denoted by the solid line); (2) the same RNS-FH pattern as the cell of interest is assigned to the interfering cell (denoted by the dashed line). Here, we model the intercell interference as additive Gaussian-distributed distortion. Therefore, in scenario (1), users in the cell of interest will experience different interferences from the interfering cell across all hops, which in turn induces interference diversity. Figure 8 clearly demonstrates that by employing the proposed method (i.e., allocating a different RNS-FH pattern to the interfering cell), the intercell interference floor can be significantly lowered relative to the scenario where all cells employ identical RNS-FH patterns.
Figures 9 and 10 show the effects of intercell interference diversity on system performance. BER versus signal-to-interference ratio (SIR) is plotted under cluster and independent hopping in Figures 9 and 10, respectively. For cluster hopping, the FH pattern assigned to the interfering cell is constructed by using  while it is
while it is  for the independent hopping scenario. We simulate the case where the same RNS-FH pattern used in the cell of interest is assigned to adjacent interfering cells. Thus, users in the cell of interest will be affected by the same interferences from adjacent cells during all hops. Therefore, no interference diversity is exploited. Simulation results also reflect this feature. When the same RNS-FH pattern is assigned, frequency diversity as a result of hopping reduces the interference floor. Therefore, the no hopping case still exhibits the worst BER performance. When different patterns are allocated to interfering cells, the interference diversity along with frequency diversity further improves system BER performance. For example, in cluster hopping (Figure 9), with different pattern assignments, nearly 3 dB gain at a BER level of
for the independent hopping scenario. We simulate the case where the same RNS-FH pattern used in the cell of interest is assigned to adjacent interfering cells. Thus, users in the cell of interest will be affected by the same interferences from adjacent cells during all hops. Therefore, no interference diversity is exploited. Simulation results also reflect this feature. When the same RNS-FH pattern is assigned, frequency diversity as a result of hopping reduces the interference floor. Therefore, the no hopping case still exhibits the worst BER performance. When different patterns are allocated to interfering cells, the interference diversity along with frequency diversity further improves system BER performance. For example, in cluster hopping (Figure 9), with different pattern assignments, nearly 3 dB gain at a BER level of  is achieved relative to the system employing identical hopping. This gain grows to 5 dB under independent hopping scenario (Veh B environment).
is achieved relative to the system employing identical hopping. This gain grows to 5 dB under independent hopping scenario (Veh B environment).
BER versus user loads is plotted in Figures 11 and 12 under cluster and independent hopping, respectively, in both Veh A and Veh B. Effects of frequency and interference diversities on system performance are explored at given SNR and SIR. It is evident that the system throughput can be significantly enhanced by assigning different RNS-FH patterns to different cells, while it is severely limited if no hopping occurs. Furthermore, the performance gap between the identical hopping and the different hopping decreases with the increase in user loads. That is, the benefit of intercell interference diversity is greater for lower user loads.
Figure 13 illustrates that by increasing the cluster size (the number of subcarriers in one cluster), or the number of active users, the number of collisions increases. This in turn induces degradation in BER performance as can be seen from Figure 13.
Finally, we compare our proposed RNS-FH pattern design strategy with state-of-the-art FH pattern designs. Specifically, our benchmark for comparison is the Latin squares (LSs-)-aided FH pattern design presented in [6]. In our proposed RNS-FH pattern, the spacing between hops in time and frequency is far enough that subcarriers employed in a single time slot are weakly correlated. This feature provides remarkable performance improvements that are consistent across all cells. However, in Latin squares (LSs-)-aided FH pattern design, performances in different cells may vary a lot. Relative comparisons are given in Figure 14, where two Latin squares-based FH patterns  and
and  [6] are employed. In LS
[6] are employed. In LS  , smaller hops happen more frequently, and for such smaller hops, Veh B exploits more frequency diversity than Veh A. The opposite is also true for LS
, smaller hops happen more frequently, and for such smaller hops, Veh B exploits more frequency diversity than Veh A. The opposite is also true for LS  . Using simulation results, we first observe that in RNS-aided FH-OFDMA, different RNS-FH patterns provide nearly the same BER performance, while it varies a lot in LS-aided FH-OFDMA; the second observation is that our proposed RNS-FH patterns have similar BER performances to LS
. Using simulation results, we first observe that in RNS-aided FH-OFDMA, different RNS-FH patterns provide nearly the same BER performance, while it varies a lot in LS-aided FH-OFDMA; the second observation is that our proposed RNS-FH patterns have similar BER performances to LS  while outperforming LS
while outperforming LS  . Although there may exist LS-aided FH pattern that has better performance than the proposed scheme, the performance variations in LS-aided FH pattern design really limit their applications.
. Although there may exist LS-aided FH pattern that has better performance than the proposed scheme, the performance variations in LS-aided FH pattern design really limit their applications.
5. Conclusions
In this paper, we propose an RNS arithmetic-based FH pattern design that is well suited and easy to implement for practical OFDMA cellular systems. RNS-FH patterns not only guarantee zero collision within a cell, but also average the intercell interferences by assigning different FH patterns to adjacent cells. Additionally, by having a large spacing between the hopping frequencies, the RNS-FH patterns exploit frequency diversity effectively and provide significant improvement in BER performance. The BER performance gain is consistent across all cells unlike other FH pattern design schemes such as the LS-based method where wide performance variations are observed across cells. Simulation experiments demonstrate the superior performance of the RNS-FH scheme in terms of frequency diversity and intercell interference diversity under both independent and cluster hopping strategies.
References
Gault S, Hachem W, Ciblat P: Performance analysis of an OFDMA transmission system in a multicell environment. IEEE Transactions on Communications 2007, 55(4):740-751.
Simon MK, Omura JK, Scoltz RA, Levitt BK: Spread Spectrum Communications. Computer Science Press, Rockville, Md, USA; 1985.
Scholand T, Faber T, Seebens A, et al.: Fast frequency hopping OFDM concept. Electronics Letters 2005, 41(13):748-749. 10.1049/el:20050644
Kurt T, Deliç H: On symbol collisions in FH-OFDMA. Proceedings of the 59th IEEE Vehicular Technology Conference (VTC '04), May 2004, Milan, Italy 4: 1859-1863.
Kurt T, Deliç H: Space-frequency coding reduces the collision rate in FH-OFDMA. IEEE Transactions on Wireless Communications 2005, 4(5):2045-2049.
Stamatiou K, Proakis JG: A performance analysis of coded frequency-hopped OFDMA. Proceedings of IEEE Wireless Communications and Networking Conference (WCNC '05), March 2005, New Orleans, La, USA 2: 1132-1137.
Maric SV, Moreno O: Using costas arrays to construct frequency hop patterns for OFDM wireless systems. Proceedings of the 40th IEEE Conference on Information Sciences and Systems (CISS '06), March 2007, Princeton, NJ, USA 505-507.
Wang C, Zhang X, Yang D: Evaluation of welch-costas frequency hopping pattern for OFDM cellular system. Proceedings of the 18th IEEE International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC '07), September 2007, Athens, Greece 1-5.
Li T, Ling Q, Ren J: A spectrally efficient frequency hopping system. Proceedings of the 50th IEEE Global Telecommunications Conference (GLOBECOM '07), November 2007, Washington, DC, USA 2997-3001.
Popovic BM, Li Y: Frequency-hopping pilot patterns for OFDM cellular systems. IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences 2006, E89-A(9):2322-2328. 10.1093/ietfec/e89-a.9.2322
Yang L-L, Hanzo L: Residue number system assisted fast frequency-hopped synchronous ultra-wideband spread-spectrum multiple-access: a design alternative to impulse radio. IEEE Journal on Selected Areas in Communications 2002, 20(9):1652-1663. 10.1109/JSAC.2002.805059
Chen J, Lv T, Zheng H: Joint cross-layer design for wireless QoS content delivery. Proceedings of IEEE International Conference on Communications (ICC '04), June 2004, Paris, France 7: 4243-4247.
Proakis JG: Digital Communications. 4th edition. McGraw Hill, New York, NY, USA; 2001.
Watson KW, Hastings CW: Self-checked computation using residue arithmetic. Poceeding of the IEEE 1966, 54(12):1920-1931.
Yang L-L, Hanzo L: Redundant residue number system based error correction codes. Proceedings of the 54th IEEE Vehicular Technology Conference (VTC '01), October 2001, Atlantic City, NJ, USA 3: 1472-1476.
ETSI TR 101 112, UMTS 30.03, V3.1.0, Annex B, Std.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zhu, D., Natarajan, B. Residue Number System Arithmetic Assisted Coded Frequency-Hopped OFDMA. J Wireless Com Network 2009, 263695 (2009). https://doi.org/10.1155/2009/263695
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/263695

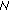 into
into 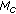 clusters with each cluster containing
clusters with each cluster containing 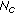 number of contiguous subcarriers.
number of contiguous subcarriers.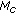 can be written as a product of two pairwise relative primes, for example,
can be written as a product of two pairwise relative primes, for example, 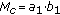 , we can first group
, we can first group  clusters into
clusters into 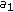 groups with
groups with 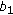 clusters in each group. Then, we index the groups from
clusters in each group. Then, we index the groups from  to
to 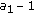 .
.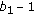 .
. to user
to user 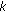 as its FH address according to its access order to the system, where
as its FH address according to its access order to the system, where 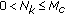 .
.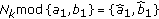 , then user
, then user 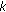 selects the
selects the 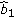 th cluster out of the
th cluster out of the 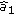 th group for transmission.
th group for transmission.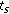 th time slot, assign integer
th time slot, assign integer 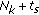 to user
to user 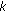 as its current FH address and repeat step 5.
as its current FH address and repeat step 5. can be expressed as products of other combinations of two pairwise relative primes, for example,
can be expressed as products of other combinations of two pairwise relative primes, for example, 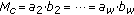 , then
, then  different orthogonal FH patterns can be obtained by repeating steps 2–7,
different orthogonal FH patterns can be obtained by repeating steps 2–7,  times.
times.
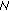 can be written as a product of
can be written as a product of 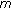 pairwise relative primes, for example,
pairwise relative primes, for example, 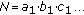 , we can first group
, we can first group 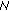 subcarriers into
subcarriers into  groups with
groups with 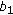 subgroups in each group. Then, we index the first-stage groups from 0 to
subgroups in each group. Then, we index the first-stage groups from 0 to 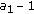 .
. . Then group the subcarriers in each second-stage group into
. Then group the subcarriers in each second-stage group into 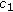 subgroups.
subgroups. th-stage.
th-stage.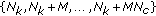 to user
to user 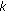 as its FH addresses, where
as its FH addresses, where 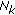 is its access order to the system,
is its access order to the system, 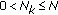 .
. , then user
, then user 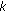 first selects the
first selects the 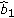 th second-stage group out of the
th second-stage group out of the 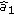 th first-stage group, then similar selecting procedures continue on until the subcarrier at the
th first-stage group, then similar selecting procedures continue on until the subcarrier at the 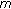 th-stage has been extracted out for transmission.
th-stage has been extracted out for transmission. until
until 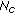 subcarriers have been extracted out for user
subcarriers have been extracted out for user 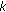 to transmit.
to transmit.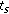 th time slot, assign integer set
th time slot, assign integer set 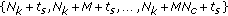 as the current FH addresses of user
as the current FH addresses of user  and repeat steps 5-6.
and repeat steps 5-6.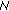 can be expressed as products of other combinations of
can be expressed as products of other combinations of 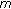 pairwise relative primes, for example,
pairwise relative primes, for example, 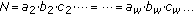 , then
, then  different orthogonal FH patterns can be obtained by repeating steps 1–8,
different orthogonal FH patterns can be obtained by repeating steps 1–8,  times.
times.

 mutually orthogonal FH pattern can be obtained for the independent hopping scheme. The size becomes
mutually orthogonal FH pattern can be obtained for the independent hopping scheme. The size becomes  for the cluster hopping.
for the cluster hopping.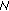 (
(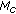 ) can be written as a product of
) can be written as a product of 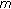 pairwise relative primes, then at least,
pairwise relative primes, then at least, 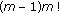 different RNS-FH patterns can be obtained.
different RNS-FH patterns can be obtained.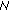 frames (
frames (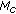 for cluster hopping) are actually periodical extensions of the RNS-FH pattern designed during the first
for cluster hopping) are actually periodical extensions of the RNS-FH pattern designed during the first  (
( ) frames.
) frames.


 .
.

 .
.
 .
.
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 .
.

 .
.

 .
.

 , LS
, LS
 and
and
 are used, different moduli sets
are used, different moduli sets
 and
and
 are applied to construct RNS-FH patterns,
are applied to construct RNS-FH patterns,
 .
.