- Research Article
- Open access
- Published:
A User Cooperation Stimulating Strategy Based on Cooperative Game Theory in Cooperative Relay Networks
EURASIP Journal on Wireless Communications and Networking volume 2009, Article number: 294942 (2009)
Abstract
This paper proposes a user cooperation stimulating strategy among rational users. The strategy is based on cooperative game theory and enacted in the context of cooperative relay networks. Using the pricing-based mechanism, the system is modeled initially with two nodes and a Base Station (BS). Within this framework, each node is treated as a rational decision maker. To this end, each node can decide whether to cooperate and how to cooperate. Cooperative game theory assists in providing an optimal system utility and provides fairness among users. Under different cooperative forwarding modes, certain questions are carefully investigated, including "what is each node's best reaction to maximize its utility?" and "what is the optimal reimbursement to encourage cooperation?" Simulation results show that the nodes benefit from the proposed cooperation stimulating strategy in terms of utility and thus justify the fairness between each user.
1. Introduction
Cooperative diversity [1, 2] has been widely proposed for applications in wireless networks. In a wireless network consists of a collection of nodes, each having a single antenna, cooperative diversity assists to enlarge system coverage and increase link reliability. Cooperative diversity works by having the network nodes assist in data transmission, thus achieving a virtual antenna array. This occurs through having a number of nodes to transmit redundant signals over different paths, which allows the destination terminal to receive average channel variations.
The benefits of cooperative diversity are highly desirable for those wireless applications in which the chief concerns are bandwidth and energy. However, while it is realistic to assume cooperation under some circumstances, in commercial applications, there is no reason for assuming that the network nodes will cooperate unselfishly. In fact, given that nodes are independent entities and that random cooperative acts will expend their resources, nodes are necessarily selfish. In other words, nodes consume their resources solely to maximize their benefits. There is no apparent benefit in a user forwarding data for other nodes. At the same time, however, the node would also prefer to have other nodes forward its own data.
In such a situation, a game theoretic approach can be used to model the network and to guide the interactions between rational decision-makers. In [3], a cooperation strategy based on the Nash Bargaining Solution (NBS) was proposed to solve two basic problems, specifically when to cooperate and how to cooperate. The authors first present a symmetric system model comprising of two users and an access point (AP). With reference to cooperative game theory, and based on the Nash bargaining solution, a cooperation bandwidth allocation strategy is then proposed. In [4], a pricing algorithm was presented for multihop wireless networks that encourage forwarding among autonomous nodes via reimbursement. In [5], a power-aware reputation system to stimulate cooperation on power-aware routing was formulated for ad hoc networks and to help each node determine its cooperation willingness from its own reputation. Based on the results given in [6], [7] presented a pricing game for stimulating cooperative diversity among selfish nodes in a commercial wireless ad hoc network. The work in [8] then reviewed this research and offered an evaluation of the various game theoretic approaches for stimulating cooperation. Essentially, this illustrated the sensitivity of the game theoretic approach to the choice of utility functions.
In the context of cooperative relay network, one user might individually select its best relay user and form a request for cooperation. Nevertheless, considering the random arrival position and the mobile nature of each user, the mobile terminal which initiates cooperative transmission in turn may not be the optimal forwarding candidate for the relay. To this end, the concept of using pricing to foster cooperation among users is arguably more appropriate than to having users cooperatively relaying data for each other as described in [3]. With gains obtained from cooperation, the relay can either select other appropriate nodes for cooperation or can choose to transmit directly. However, when it comes to pricing-based schemes, a noncooperative game theory is often used as a starting point. This is shown by researchers contributing to [4–8]. The main disadvantage of these works is that they concentrate on individual user utility, rather than utility of the entire system. By contrast, based on cooperative game theory, the scheme proposed in [3] can achieve general Pareto optimal performance for cooperative games. This will help in maximizing an entire system payoff, while also ensuring fairness.
Stimulated by the aforementioned research, this paper proposes a pricing and utility framework for stimulating cooperation among users. Different from previous pricing-based research results, the proposed framework consisting of an asymmetric model of two nodes and a Base Station (BS), as provided by cooperative game theory. In this framework, each node, namely, the source and the relay, is treated as rational and with its own choice of whether, and how to cooperate. Moreover, the "asymmetric" is characterized as the source having a chance to get the relay's help, and with the payoff being a remuneration; while the relay will cooperatively forward to the BS, the data which originated from the source then gains reimbursement from the source. To provide an optimal system utility while keeping fairness among users, the Nash Bargaining Solution is used to address the following questions: "What is each node's best reaction to maximize its utility?" and "What is the appropriate reimbursement the source should pay so as to encourage cooperation as well as maintain fairness?" Using two different cooperative forwarding modes, specifically, Amplify-and-Forward (AF) and Decode-and-Forward (DF) cooperation, the analysis for this study is then verified by extensive computer simulations.
The rest of this paper is organized as follows. Section 2 presents the system model, and Section 3 defines the utility functions used in this paper. Section 4 proposes a scheme based on cooperative game theory for helping the source to determine its optimal level of reimbursement. Based on the NBS, the model will also allow for the relay to judge its best reaction according to the reimbursement. Section 5 presents simulation results to demonstrate the effectiveness of the proposed scheme. Section 6 discusses some related implementation issues, and the conclusion is provided in Section 7.
2. System Model
In the considered framework, a set of users consist of the nodes in the network. Each node can perform a set of actions: for example, transmit its data to the BS directly, have another node cooperatively forward its data, not forward for other node at all, or forward only a fraction of other node's data. To represent a user's payoff over a set of action profiles precisely, the term "utility" is exploited here according to the game theory. Moreover, for the sake of stimulating cooperative behavior between nodes, pricing mechanism is introduced. As shown in Figure 1, a pricing-based asymmetric relay model is considered. This model includes two users (nodes) and one BS. Both nodes assume the BS as the final destination, while the BS charges each transmitting node the common unit price of  . We suppose an interference free model where user transmissions are considered as orthogonal to each other. Assume that the system is based on frequency division multiple access and each node is allocated a
. We suppose an interference free model where user transmissions are considered as orthogonal to each other. Assume that the system is based on frequency division multiple access and each node is allocated a  hertz bandwidth for transmitting its own packets. As illustrated in Figure 1, if a source wants its potential relay to cooperatively transmit
hertz bandwidth for transmitting its own packets. As illustrated in Figure 1, if a source wants its potential relay to cooperatively transmit  as a fraction of its own data to the BS, the relay must be compensated via a unit reimbursement price of μ for forwarding. As far as relay is concerned, to maximize its utility, it is only willing to use
as a fraction of its own data to the BS, the relay must be compensated via a unit reimbursement price of μ for forwarding. As far as relay is concerned, to maximize its utility, it is only willing to use  fraction
fraction  of its bandwidth to relay an
of its bandwidth to relay an  fraction of the data that has origins from the source. The remaining
fraction of the data that has origins from the source. The remaining  fraction of the source's data as well as the
fraction of the source's data as well as the  fraction of the relay's data will be transmitted directly to the BS.
fraction of the relay's data will be transmitted directly to the BS.
In this model, the relay might choose to use AF or DF cooperation methods for forwarding the source's data to the BS and consequently gains remuneration from the source. Thus, the diversity gain of the source heavily depends on how much fraction data is devoted by the relay to cooperative transmission. By contrast, the relay revenue actually depends on how much the source is willing to pay. Given there are no neutrals to monitor "cheating" behaviors between selfish nodes and the assumption of rational behavior for each node; then the pricing rule is readily be violated by the participants. For instance, the source may require the relay to forward its data first and then compensates no reimbursement for the relay. Alternately, the relay may require the source to prepay but not forward any of its data at all.
We address this problem with a dynamic cooperative game model. In this model, given certain constraints, each node will determine on its own strategy in a sequenced, yet nonsimultaneous manner. For instance, when wanting to benefit from cooperation, the source has to first select a best fraction of data  as well as an appropriate reimbursement price of
as well as an appropriate reimbursement price of  to reward the relay. On the other hand, in order to maximize its utility, the relay will independently decide how much fraction of the data to transmit that originates from the source. Note that through selecting an optimal value of
to reward the relay. On the other hand, in order to maximize its utility, the relay will independently decide how much fraction of the data to transmit that originates from the source. Note that through selecting an optimal value of  and
and  , the source also aims at maximizing its own utility. Furthermore, the payment
, the source also aims at maximizing its own utility. Furthermore, the payment  charged by the BS remains constant during the interaction between the source and the relay.
charged by the BS remains constant during the interaction between the source and the relay.
From the aforementioned description, it can be inferred that the variables  ,
,  , and
, and  reflect the rational decisions made by the each node, and that one participant's strategy will undoubtedly affect the choice of the other user. Intuitively, both nodes can expect optimal tradeoffs between their payout and payoff, and the choice of cooperation thus heavily depends on whether the cooperative behavior will bring maximum individual utility. In order to model the complicated interaction between each participant, we will first address this issue from the aspect of utility function. Followed by the well-designed utility functions, the remaining section presents a suitable solution for the framework described above and one which also invites a win-win situation. Besides, to clarify the analysis, some parameters are formally defined. These notations will be helpful to analytically obtain each user's payoff:
reflect the rational decisions made by the each node, and that one participant's strategy will undoubtedly affect the choice of the other user. Intuitively, both nodes can expect optimal tradeoffs between their payout and payoff, and the choice of cooperation thus heavily depends on whether the cooperative behavior will bring maximum individual utility. In order to model the complicated interaction between each participant, we will first address this issue from the aspect of utility function. Followed by the well-designed utility functions, the remaining section presents a suitable solution for the framework described above and one which also invites a win-win situation. Besides, to clarify the analysis, some parameters are formally defined. These notations will be helpful to analytically obtain each user's payoff:
-
(i)
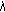 : per unit price the BS charges for data transmission;
: per unit price the BS charges for data transmission; -
(ii)
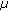 : the source reimbursement price per unit data;
: the source reimbursement price per unit data; -
(iii)
 : fraction of data requested by the source for cooperative transmission;
: fraction of data requested by the source for cooperative transmission; -
(iv)
 : fraction of data forwarded by the relay;
: fraction of data forwarded by the relay; -
(v)
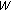 : bandwidth for transmission.
: bandwidth for transmission.
3. Utility Functions
To appropriately denote a user's preferences over a set of action profiles, a good representative approximation is indispensible. Here, the concept of utility function is adopted. The utility function, which maps a set of action alternatives into real numbers, is used to properly represent the payoff of each node. Thereupon, how to define a meaningful and delicate utility function for the proposed model is an essential problem. As stated in [9], cooperative diversity is a physical layer protocol that affects physical layer variables. In particular, the two variables of interest are throughput achieved and transmission power consumed. In the game theoretic model, the utility measures of the system need to incorporate these two parameters into a reasonable fashion. That is to say, for equal power, higher throughput should translate into higher utility. Similarly, for equal throughput, lower power should bring increased utility. According to the research results presented in [10], a user's utility is measured in the physical unit of bits-per-joule and is defined as

In this function, utility  is proportional to throughput
is proportional to throughput  and inversely proportional to power
and inversely proportional to power  . The utility is interpreted as the number of information bits received per joule of energy consumed. Specifically, suppose that the source and the relay both have a utility function denoted by formula (1) for transmission; the choice of cooperation thus depends on the utility achieved. If utility gained from cooperation is higher than utility achieved by noncooperation, then the node should choose to cooperate. However, the cooperating utility is only acquired when both nodes choose to cooperate. If only one of the two nodes is cooperating, then the cooperating node obviously does not achieve a cooperating utility.
. The utility is interpreted as the number of information bits received per joule of energy consumed. Specifically, suppose that the source and the relay both have a utility function denoted by formula (1) for transmission; the choice of cooperation thus depends on the utility achieved. If utility gained from cooperation is higher than utility achieved by noncooperation, then the node should choose to cooperate. However, the cooperating utility is only acquired when both nodes choose to cooperate. If only one of the two nodes is cooperating, then the cooperating node obviously does not achieve a cooperating utility.
In the proposed pricing-based game theoretic model, the BS always charges the users for service based on throughput. To maximize its utility, the source first selects an optimal fraction of data to be cooperatively transmitted by the relay and also provides a certain reimbursement price as an incentive for forwarding. Then, the source derives utility from this by the increased throughput it achieves with comparatively less power. Meanwhile, the relay gains utility from the payment made to it by the source. The interaction between the source and the relay includes the following.
The source optimizes  and
and  to maximize its utility using the following sequence.
to maximize its utility using the following sequence.
-
(i)
Source and relay interact in cooperative game to determine forwarding preferences.
-
(ii)
Source adaptively sets the value of
 as well as
as well as  .
. -
(iii)
Source calculates its utility.
The relay optimizes  to maximize its utility using the following sequence.
to maximize its utility using the following sequence.
-
(i)
Relay dynamically sets the value of
 .
. -
(ii)
Relay calculates its revenue.
Each node has a set of preferences, modeled by its utility, which should take into account the amount of data it transfers and the consequent price it pays. The best response function is how the node will behave, assuming that it acts in self-interest. Consequently, the utility functions adopted in the proposed framework should not only incorporate the parameters such as throughput and power but also embody each node's preferences, for instance, the choice of  ,
,  , and
, and  . Combined with the pricing-based algorithm described in [4–9, 11], the utility functions in this paper for the source
. Combined with the pricing-based algorithm described in [4–9, 11], the utility functions in this paper for the source  and the relay
and the relay  are constructed as
are constructed as


Equation (2) stands for the utility obtained by the source through cooperative transmission while the formula (3) actually represents the corresponding payoff of the relay. Depending on user's role (relay or source), the utility functions comprise of two parts. The direct transmission part accounts for the satisfaction received in transmitting data and the associated BS charges. The cooperative transmission part accommodates both actual and opportunity costs of forwarding data along with the respective pricing rewards. More specially, in the case of cooperation, the source utility is the satisfaction measure achieved where cooperation subtracts the total price paid to the BS and the relay. While the relay utility under cooperation is simply the total revenue it earns from the source subtracts the total price it pays to the BS. Here, variables  and
and  represent the transmission power of the source as well as the relay, respectively.
represent the transmission power of the source as well as the relay, respectively.  which is also called the efficiency function, denotes the probability of correct reception of a frame [3]. This is given by
which is also called the efficiency function, denotes the probability of correct reception of a frame [3]. This is given by

With frames of M bits, BER is the bit error rate and γ denotes the received signal-to-noise ratio (SNR). The BER, for noncoherent frequency shift keyed (FSK) transmission, can be expressed as

where  is the transmit power,
is the transmit power,  is the noise power, and
is the noise power, and  is the channel path gain. According to [10],
is the channel path gain. According to [10],  is calculated as
is calculated as  ,
,  being the distance between the transmitter and the receiver in meters. Back to (2) and (3),
being the distance between the transmitter and the receiver in meters. Back to (2) and (3),  and
and  stand respectively, for the SNR of the channel from the source to the BS as well as from the relay to the BS. Here
stand respectively, for the SNR of the channel from the source to the BS as well as from the relay to the BS. Here  represents the effective SNR which is achieved by the source through cooperative transmission. According to different cooperative forwarding methods, the expression of
represents the effective SNR which is achieved by the source through cooperative transmission. According to different cooperative forwarding methods, the expression of  differs for AF cooperation by the relay and is given as follows [12]:
differs for AF cooperation by the relay and is given as follows [12]:

 denotes the SNR of the wireless channels from the source to the relay, whereas a case of DF cooperation by the relay, is represented as [13, 14]
denotes the SNR of the wireless channels from the source to the relay, whereas a case of DF cooperation by the relay, is represented as [13, 14]

Based on the system model presented in Section 2, the proposed utility functions in (2) and (3) are executed by each node as follows: firstly, the BS periodically broadcasts current value of  , and each node constructs its utility function individually according to the role it plays. By obtaining the information of
, and each node constructs its utility function individually according to the role it plays. By obtaining the information of  and
and  , the source will decide whether to adopt cooperative transmission. If utility gained from cooperation is greater than utility achieved by noncooperation, the source adaptively chooses the optimal value of
, the source will decide whether to adopt cooperative transmission. If utility gained from cooperation is greater than utility achieved by noncooperation, the source adaptively chooses the optimal value of  and
and  to maximize its payoff. The source then sends
to maximize its payoff. The source then sends  fraction of its data to the relay along with the information of reimbursement price
fraction of its data to the relay along with the information of reimbursement price  and waits for reply. Once the relay receives this data request, by combining it with the value of
and waits for reply. Once the relay receives this data request, by combining it with the value of  , it will independently derive the optimal value of
, it will independently derive the optimal value of  from (3). By listening to the acknowledgment sent by the BS, the source finally calculates its utility according to formula (2) and further adjusts the value of
from (3). By listening to the acknowledgment sent by the BS, the source finally calculates its utility according to formula (2) and further adjusts the value of  and
and  if necessary. The interaction between the source and the relay continues and eventually converges at the equilibrium point.
if necessary. The interaction between the source and the relay continues and eventually converges at the equilibrium point.
It is worth noting that in the case of cooperation, the variables  and
and  which represent the respective cooperating preferences for the source and the relay are subjected to the following constraints:
which represent the respective cooperating preferences for the source and the relay are subjected to the following constraints:

The above condition can be interpreted as follows: firstly, for the source which requests the relay to cooperatively transmit  fraction of its data to the BS, then
fraction of its data to the BS, then  should be no larger than one. On the other hand, a relay can, at most, forward the same amount of data originating from the source. Finally, to create a meaningful cooperative scheme, both
should be no larger than one. On the other hand, a relay can, at most, forward the same amount of data originating from the source. Finally, to create a meaningful cooperative scheme, both  and
and  should be nonnegative.
should be nonnegative.
4. Cooperative Game Approaches
In this section, cooperative game theory is used to analyze the problem outlined in Section 3. First we will briefly introduce the concepts of bargaining problem and the related solution methods. Then, based on the NBS, a cooperative scheme is presented in detail which outlines the best policy for each node to maximize its utility.
4.1. Basic Concepts and Theorems
The bargaining problem of cooperative game theory can be described as follows [15, 16]: assume that there are  players, with
players, with  ,
,  , representing the minimum payoff that the
, representing the minimum payoff that the  player would expect or the disagreement point when
player would expect or the disagreement point when  players do not agree on a compromise. Let
players do not agree on a compromise. Let  be a nonempty convex and closed set representing the feasible set of payoff allocations for players if they work together. Assume that
be a nonempty convex and closed set representing the feasible set of payoff allocations for players if they work together. Assume that  is a nonempty, closed, and convex set. Let
is a nonempty, closed, and convex set. Let  , then the pair
, then the pair  is called a K-person bargaining problem [17]. Within the feasible set
is called a K-person bargaining problem [17]. Within the feasible set  , we now define the notion of Pareto optimal concept as representing selection criterion for bargaining solutions.
, we now define the notion of Pareto optimal concept as representing selection criterion for bargaining solutions.
Definition 1.
The point  is said to be Pareto optimal if and only if there is no other allocation
is said to be Pareto optimal if and only if there is no other allocation  such that
such that  for all
for all  .
.
Pareto optimality is also called Pareto efficient, which means that it is impossible to find another point which leads to superior performance for all players. In general, for a  -person bargaining game, there might be an infinite number of Pareto optimal points [15]. To select the optimal point, additional criteria are needed. Such criteria are the so-called fairness axioms, these characterizing the Nash Bargaining Solution. The NBS is briefly explained as follows.
-person bargaining game, there might be an infinite number of Pareto optimal points [15]. To select the optimal point, additional criteria are needed. Such criteria are the so-called fairness axioms, these characterizing the Nash Bargaining Solution. The NBS is briefly explained as follows.
Definition 2.
 is said to be a NBS in set
is said to be a NBS in set  (
( ), such that
), such that  if the following four axioms are satisfied:
if the following four axioms are satisfied:
 Pareto Optimality
Pareto Optimality
There does not exist  , such that
, such that  .
.
 Independence of Irrelevant Alternatives
Independence of Irrelevant Alternatives
If  ,
,  , then
, then  .
.
 Independence of Linear Transformations
Independence of Linear Transformations
For any linear scale transformation  ,
,  .
.
 Symmetry
Symmetry
If  is invariant under all exchanges of agents, then
is invariant under all exchanges of agents, then  .
.
Nash demonstrated a unique solution function for a  -player bargaining problem and one which satisfies all the above four axioms. The solution is explicated in the following theorem.
-player bargaining problem and one which satisfies all the above four axioms. The solution is explicated in the following theorem.
Theorem 1.
Existence and Uniqueness of NBS (Nash's Theorem). There is a unique solution function  that satisfies all four axioms, and this solution satisfies
that satisfies all four axioms, and this solution satisfies

The Nash solution selects the allocation that maximizes the product of the expected gains, this known as the Nash product.
4.2. A Cooperative Scheme
As discussed above, the cooperative game in the cooperative relay networks can be defined as follows. According to each user's role, each node has  (
( ,
,  , where
, where  indicates the source and
indicates the source and  denotes the relay) as its objective function. This is written in formulas (2) and (3), where
denotes the relay) as its objective function. This is written in formulas (2) and (3), where  is bounded above and has a nonempty, closed, and convex support. The goal is to maximize all
is bounded above and has a nonempty, closed, and convex support. The goal is to maximize all  simultaneously, and
simultaneously, and  , also called the initial agreement point, represents the minimal performance. The problem, then, is to find an optimal operating point that maximizes the utility for all users and ensure that the point is optimal and fair.
, also called the initial agreement point, represents the minimal performance. The problem, then, is to find an optimal operating point that maximizes the utility for all users and ensure that the point is optimal and fair.
With the help of NBS, for the problem mentioned above, the NBS function is expressed as

where  and
and  denote the utility of the source under the conditions of direct transmission as well as denote the relay. More specially, in the case of noncooperation, the source and relay utility are simply the satisfaction measure achieved by subtracting the total price paid to the BS. From the properties of NBS functions, it can be concluded that a node will choose to quit cooperate, if the utility obtained through the cooperative transmission is smaller than the utility obtained through a direct transmission. In other words, since each node is a rational decision-maker with independent choice, it will only choose to transmit cooperatively if the performance is better than that of direct transmission.
denote the utility of the source under the conditions of direct transmission as well as denote the relay. More specially, in the case of noncooperation, the source and relay utility are simply the satisfaction measure achieved by subtracting the total price paid to the BS. From the properties of NBS functions, it can be concluded that a node will choose to quit cooperate, if the utility obtained through the cooperative transmission is smaller than the utility obtained through a direct transmission. In other words, since each node is a rational decision-maker with independent choice, it will only choose to transmit cooperatively if the performance is better than that of direct transmission.
Given the above situation, we then have

For simplicity, we keep the variables  ,
,  , and W to be constant. Moreover, since
, and W to be constant. Moreover, since  ,
,  , represents the minimal utility the user can obtain through direct transmission, it should follow that
, represents the minimal utility the user can obtain through direct transmission, it should follow that  . Consequently, we can infer that
. Consequently, we can infer that  , this providing the constraint of the charge provided by the BS.
, this providing the constraint of the charge provided by the BS.
The next object is to determine the optimal value of  ,
,  and an appropriate reimbursement price for
and an appropriate reimbursement price for  .
.
Assuming  =
=  ,
,  =
=  ,
,  =
=  and
and  =
=  , then we have
, then we have

Again, let  =
=  and
and  =
=  , then the problem becomes
, then the problem becomes

From the above relations, it can be derived that

Since the parameter  represents the bandwidth allocated to each node for transmission which remains constant, recalling the NBS function given in (9), our main target then lies in to find the optimal value of
represents the bandwidth allocated to each node for transmission which remains constant, recalling the NBS function given in (9), our main target then lies in to find the optimal value of  ,
,  , and
, and  that maximize the product of
that maximize the product of  .
.
Assume  and that by substituting (14) into (8), we now have
and that by substituting (14) into (8), we now have

The relationships derived in (13) are also depicted in Figure 2, where the four dash-dot lines stand for the four constraints. The shaded region represents the set of points  that satisfy the restrictions of (15). After this, we need to find the exact maximization point for the product of
that satisfy the restrictions of (15). After this, we need to find the exact maximization point for the product of  .
.
To maintain the fairness among nodes, the condition for solving the equation derived in (13) is to assume that  . This essentially means that the expected payoff of each node is the same after cooperation. This assumption can be explained as follows.
. This essentially means that the expected payoff of each node is the same after cooperation. This assumption can be explained as follows.
Firstly, to maximize its payoff, the source will choose an optimal value of  as well as an appropriate value of
as well as an appropriate value of  . If cooperative transmission is more advantageous compared with direct transmission, then the source will undoubtedly perform the following actions: to have the relay transmit as much fraction of its data as possible, and at the same time to cut off its payout. This essentially means that the best policy for the source is to increase the value of
. If cooperative transmission is more advantageous compared with direct transmission, then the source will undoubtedly perform the following actions: to have the relay transmit as much fraction of its data as possible, and at the same time to cut off its payout. This essentially means that the best policy for the source is to increase the value of  and to decrease the value of
and to decrease the value of  .
.
On the other hand, with the knowledge of the values of  and
and  , the relay calculates the expected payoff. It then decides on its own strategy, which is a typical two person bargaining problem. Under the circumstances that the cooperation can bring more payoff than a noncooperation case, the best course of action for the relay in response to the source's choice is equally to maximize its own revenue and, at the same time, to cut down expense paid to the BS. This indicates that its best policy is to decrease the value of
, the relay calculates the expected payoff. It then decides on its own strategy, which is a typical two person bargaining problem. Under the circumstances that the cooperation can bring more payoff than a noncooperation case, the best course of action for the relay in response to the source's choice is equally to maximize its own revenue and, at the same time, to cut down expense paid to the BS. This indicates that its best policy is to decrease the value of  as less as possible.
as less as possible.
Unfortunately, without an impartial third party to avoid the selfish behavior of each node, it is hard to arrive at a balancing solution that insures maximum utilities of both nodes as well as fairness. Alternatively, with the restriction to have both nodes receive the same expected payoff, if one node chooses to adopt a different strategy, it will definitely harm another node's payoff. Under cooperative game theory, this is also explained as a necessary commitment from each participant [16]. In other words, this condition strikes a balance between the two participants, in that it is impossible to make any individual improvement unless at least some other participants are worse off, which gives the definition of Pareto optimal.
Under the above considerations, we now have  . From the definition of variables
. From the definition of variables  ,
,  ,
,  , and
, and  , it can be inferred that all of them are nonnegative. When
, it can be inferred that all of them are nonnegative. When  , it yields
, it yields  , which can be interpreted as follows: if cooperative transmission is adopted, both nodes can improve their payoff compared with direct transmission; otherwise both nodes will choose to cease the cooperation. According to the constraint inequality, if
, which can be interpreted as follows: if cooperative transmission is adopted, both nodes can improve their payoff compared with direct transmission; otherwise both nodes will choose to cease the cooperation. According to the constraint inequality, if  , it is easy to derive that the coordinate product XY is maximized. Consequently, the corresponding data allocation scheme is equivalent to
, it is easy to derive that the coordinate product XY is maximized. Consequently, the corresponding data allocation scheme is equivalent to

Equation (16) provides a solution to the bargain problem depicted in expression (9). It can be explained that: when adopting a cooperation strategy, in order for the source node to maximize utility, the best strategy is to set  . This allows the relay to cooperatively transmit all its data to the destination. Consequently, it is derived that
. This allows the relay to cooperatively transmit all its data to the destination. Consequently, it is derived that  .
.
The next challenge is to resolve the appropriate value of  that maximizes the payoff on both sides. Since the relay will only forward the data originated from the source, there are subsequently the following restrictions:
that maximizes the payoff on both sides. Since the relay will only forward the data originated from the source, there are subsequently the following restrictions:

By substituting the expression of  ,
, ,
, , and
, and  into (17), we have
into (17), we have

The inequalities can be transformed into

The possible value range of  is illustrated in inequalities (19). When adopting cooperation, the best strategy for the source is to inspire the relay transmitting for the same fraction of the data required by the source. This yieldsn=m=1, and hence, the optimal value of μ is given as
is illustrated in inequalities (19). When adopting cooperation, the best strategy for the source is to inspire the relay transmitting for the same fraction of the data required by the source. This yieldsn=m=1, and hence, the optimal value of μ is given as

Through the obtainable  in function (20), the relay will receive the greatest reward and the source will get maximum benefit from cooperative diversity; therefore the maximum payoff of both participants can be achieved. Consequently, when
in function (20), the relay will receive the greatest reward and the source will get maximum benefit from cooperative diversity; therefore the maximum payoff of both participants can be achieved. Consequently, when  , we now have (
, we now have ( ,
, ) = (
) = ( ,
, ). This corresponds to the point shown in Figure 2 in which the line depicted by
). This corresponds to the point shown in Figure 2 in which the line depicted by  =
= intersects with the line depicted by
intersects with the line depicted by  .
.
Alternatively, if  , then the maximization problem described in expression (9) appropriates all the utilities greater than those of the noncooperation case. Essentially, this means that both
, then the maximization problem described in expression (9) appropriates all the utilities greater than those of the noncooperation case. Essentially, this means that both  and
and  are greater than zero. Moreover, when substituting the expression in terms of
are greater than zero. Moreover, when substituting the expression in terms of  ,
,  into the restriction given in (8), it can be derived that the only possible results derived is
into the restriction given in (8), it can be derived that the only possible results derived is  . This results in (
. This results in ( ,
, ) =
) =  . This situation can be interpreted as follows: when cooperation does not provide greater payoff for the nodes involved, they will consequently cease the cooperation. Given the payment if other variables remain constant, the value of
. This situation can be interpreted as follows: when cooperation does not provide greater payoff for the nodes involved, they will consequently cease the cooperation. Given the payment if other variables remain constant, the value of  , which is closely related to the channel quality and the payment, is a critical requirement for cooperation. When
, which is closely related to the channel quality and the payment, is a critical requirement for cooperation. When  is below zero, both nodes will choose to transmit directly. However, as long as
is below zero, both nodes will choose to transmit directly. However, as long as  is above zero, to transmit cooperatively is obviously superior to other strategies. The shift in condition from noncooperation to cooperation will occur when
is above zero, to transmit cooperatively is obviously superior to other strategies. The shift in condition from noncooperation to cooperation will occur when  is equal to zero. Accordingly, there must be a sudden change in the amount of
is equal to zero. Accordingly, there must be a sudden change in the amount of  ,
,  , and
, and  , from zero to a certain positive value which is determined by the preceding equations:
, from zero to a certain positive value which is determined by the preceding equations:

It should be noted that the left-side expression in inequalities (21) is the direct result of  in the form of
in the form of  , which should be greater than zero. As a result, the above expressions (21) are derived to clarify the circumstances under which two nodes should cooperate.
, which should be greater than zero. As a result, the above expressions (21) are derived to clarify the circumstances under which two nodes should cooperate.
5. Simulation Results
The simulation scenario we adopted is similar to the model described in [3]. Consider a network composed of three nodes. A BS is located in the origin and the source is situated 800 meters far from the BS in the  -axis, the coordinates of the source being given as (800,0). When the relay moves along the
-axis, the coordinates of the source being given as (800,0). When the relay moves along the  -axis toward the source, then coordinates are (
-axis toward the source, then coordinates are ( ). The value of
). The value of  varies from 400 meters to 1400 meters. Other parameters used in the simulation include
varies from 400 meters to 1400 meters. Other parameters used in the simulation include  ,
,  ,
,  Hz, and
Hz, and  W. The transmitting power is assumed to be 0.1 W for both nodes, and the unit price of
W. The transmitting power is assumed to be 0.1 W for both nodes, and the unit price of  charged by BS is assumed to be 0.1.
charged by BS is assumed to be 0.1.
Using the source and the relay utility functions described in (2) and (3), we plot the source utility and the relay utility for varying relay to BS distances.
Figures 3 and 4 show each node's utility in the case of cooperation, respectively, for AF or DF forwarding as well as in the case of direct transmission. As can be observed, when the distance between the source and the relay is below 600, neither node cooperates, and the utility values therefore converge to the noncooperation ones. However, as the relay is approaching the source, or more specifically, when  m, then both nodes start to cooperate. Owing to the relay's good channel condition, both nodes, via cooperation, will improve their revenue. This occurs when the source receives diversity gain by cooperative transmission, whereas the relay receives a deserved reimbursement from the source. Notice that for all nodes, the cooperating utility outstrips the noncooperating utility by a wide margin. This is the original framework we set forth, and one which underlies how the proposed scheme can enhance system performance. This is achieved by adopting proper cooperation. It is also worth noting that the source utility under cooperation is close to that of the relay, this being due to the fact that our strategy is aimed at maintaining fairness among each user. In itself, and compared with traditional pricing-based schemes which only maximize the source's utility, this is a distinctive characteristic. Subsequently, we arrive at an optimal source reimbursement price, and one which maximizes a participant's utility without hindering another user's payoff. Furthermore, our results are obtained when the reimbursement price
m, then both nodes start to cooperate. Owing to the relay's good channel condition, both nodes, via cooperation, will improve their revenue. This occurs when the source receives diversity gain by cooperative transmission, whereas the relay receives a deserved reimbursement from the source. Notice that for all nodes, the cooperating utility outstrips the noncooperating utility by a wide margin. This is the original framework we set forth, and one which underlies how the proposed scheme can enhance system performance. This is achieved by adopting proper cooperation. It is also worth noting that the source utility under cooperation is close to that of the relay, this being due to the fact that our strategy is aimed at maintaining fairness among each user. In itself, and compared with traditional pricing-based schemes which only maximize the source's utility, this is a distinctive characteristic. Subsequently, we arrive at an optimal source reimbursement price, and one which maximizes a participant's utility without hindering another user's payoff. Furthermore, our results are obtained when the reimbursement price  is equal to
is equal to  . It is hard to tell from these two figures whether the value of
. It is hard to tell from these two figures whether the value of  is optimal, and we address this problem in Figures 5 and 6.
is optimal, and we address this problem in Figures 5 and 6.
Figures 5 and 6 display the product of  for the resulting different values of
for the resulting different values of  when the relay adopts AF or DF forwarding. To demonstrate the distinct advantage of the proposed strategy, we also plot the situation when
when the relay adopts AF or DF forwarding. To demonstrate the distinct advantage of the proposed strategy, we also plot the situation when  is equal to a constant value. These figures show that when cooperation happens,
is equal to a constant value. These figures show that when cooperation happens,  is maximized only when
is maximized only when  equals to the optimal value
equals to the optimal value  . This is because the reimbursement price that is paid by the source to the relay is determined variously, by the channel quality between the source and the relay. It is also determined variously between the relay and the BS. With these dynamic values for μ , the relay node will receive a deserved reward if it honestly participates in cooperation. Furthermore, the source also reaps cooperative diversity, thereby producing the revenue maximization for both nodes. However, if the source chooses a small constant value of
. This is because the reimbursement price that is paid by the source to the relay is determined variously, by the channel quality between the source and the relay. It is also determined variously between the relay and the BS. With these dynamic values for μ , the relay node will receive a deserved reward if it honestly participates in cooperation. Furthermore, the source also reaps cooperative diversity, thereby producing the revenue maximization for both nodes. However, if the source chooses a small constant value of  , as the channel condition between them becomes better, the source will gain more than the relay. As a consequence, in order to increase its revenue, the best reaction for the relay is to forward a smaller fraction of data required by the source. This will lead to diminishment in the product value. On the other hand, if the source adopts a large constant value of
, as the channel condition between them becomes better, the source will gain more than the relay. As a consequence, in order to increase its revenue, the best reaction for the relay is to forward a smaller fraction of data required by the source. This will lead to diminishment in the product value. On the other hand, if the source adopts a large constant value of  , it will lose more than it gains. When the relay is moving toward the source, in the region roughly between 600 m and 1200 m,
, it will lose more than it gains. When the relay is moving toward the source, in the region roughly between 600 m and 1200 m,  becomes positive. In other words, the cooperation brings advantages for each user. However, when
becomes positive. In other words, the cooperation brings advantages for each user. However, when  m,
m,  is almost zero. In this application, whether users cooperate or not will bring no further benefits. This suggests that the source should consider selecting another optimal relay. Moreover, when the relay adopts different forwarding scheme, that is, AF or DF, the results in terms of utilities also differ slightly as depicted in the figures.
is almost zero. In this application, whether users cooperate or not will bring no further benefits. This suggests that the source should consider selecting another optimal relay. Moreover, when the relay adopts different forwarding scheme, that is, AF or DF, the results in terms of utilities also differ slightly as depicted in the figures.
Figure 7 illustrates the changing values of  . When
. When  m, each node transmits directly, this being denoted by
m, each node transmits directly, this being denoted by  . Users start to cooperate when
. Users start to cooperate when  m, which can be interpreted as the point when the channel quality is good enough for cooperation, and the source is willing to pay (the relay) an appropriate reward for forwarding data to the BS. However, when the relay is gradually far from the BS, and as its channel condition becomes worse little by little, the source will decrease the reimbursement price accordingly. It is worth noting that when the relay is very far from the BS, that is,
m, which can be interpreted as the point when the channel quality is good enough for cooperation, and the source is willing to pay (the relay) an appropriate reward for forwarding data to the BS. However, when the relay is gradually far from the BS, and as its channel condition becomes worse little by little, the source will decrease the reimbursement price accordingly. It is worth noting that when the relay is very far from the BS, that is,  m, the result is equivalent to a noncooperation case even though the source can still choose cooperative transmission. Again, it can be observed that there is a slight difference between the AF forwarding and the DF forwarding schemes.
m, the result is equivalent to a noncooperation case even though the source can still choose cooperative transmission. Again, it can be observed that there is a slight difference between the AF forwarding and the DF forwarding schemes.
Figures 8 and 9 show the system's sum utility of the AF and DF cooperation. In the context of cooperation, it can be observed that when the relay moves across the cooperation starting point of  m, there is a sudden change in the value of the sum utility. This is in accordance with our previous analysis. Besides, it should also be noted that for all the candidate values of
m, there is a sudden change in the value of the sum utility. This is in accordance with our previous analysis. Besides, it should also be noted that for all the candidate values of  , the cooperating utility is greater than that of the noncooperation case. Moreover, the system's sum utility is maximized when the optimal reward value
, the cooperating utility is greater than that of the noncooperation case. Moreover, the system's sum utility is maximized when the optimal reward value  is adopted. As such, the advantage is gradually diminished when the relay moves far from the BS.
is adopted. As such, the advantage is gradually diminished when the relay moves far from the BS.
Figures 10 and 11 plot the fraction of data that each user has dedicated for the cooperation. Regardless of whether the relay adopts the AF or DF forwarding scheme, when the source chooses a small constant reimbursement price value, then, the relay forwards only a fraction of the data required by the source. On the other hand, and according to the Nash bargaining solution, when the optimal reward value  is employed, the best relay strategy involves forwarding the same fraction of data originated from the source. This leads to the maximized utilities of both nodes. By utilizing the dynamic value of
is employed, the best relay strategy involves forwarding the same fraction of data originated from the source. This leads to the maximized utilities of both nodes. By utilizing the dynamic value of  , both nodes win from cooperation, and at the same time the fairness among each participant is also guaranteed.
, both nodes win from cooperation, and at the same time the fairness among each participant is also guaranteed.
6. Implementation Issues
Concerning the implementation, it is obvious that the proposed strategy can be applied to current cellular networks. In current researched relay-based cellular networks, when referring to the typical two user cooperation scenarios, most academic papers assumed that once the selection pair is achieved, the selected relay will unconditionally forward data for the other user. Actually, when a mobile is helping a neighbor mobile by forwarding data, it is sacrificing its throughput for the sake of another one, and such behavior has to be taken into consideration when the average user throughput is calculated. In other words, the selected relay sacrifices its throughput without any incentives basis, which is not going to happen in the commercial cellular networks.
The strategy presented in this paper is aimed to address this problem by way of stimulating cooperative behavior. Through signaling channels, when a mobile wants to deploy cooperation with another mobile, it can independently construct its utility function and calculate the optimal fraction of data to be sent cooperatively by the relay as well as the appropriate reimbursement price. On the other hand, the relay can also adaptively decide how much fraction of the data to transmit that originates from the source so as to maximize its utility. This is achieved by utilizing the proposed algorithm to maximize both participants' revenue as well as to maintain fairness.
7. Conclusion
This paper presents a user cooperation stimulating strategy based on cooperative game theory in the context of a cooperative relay network. Using a pricing-based mechanism, an asymmetric model is comprehensively discussed, consisting of two nodes and a BS. In this framework, each node is treated as a rational decision-maker, determining its own choice of whether, to cooperate and how. In order to provide an optimal system utility while keeping fairness among users, we turn to cooperative game theory. Under different cooperative forwarding modes, the questions "what is each node's best reaction to maximize its utility?" and "what is the appropriate reimbursement the source should pay to encourage cooperation?" have been systematically addressed. Finally, simulation results demonstrate the benefit that the nodes derive from the proposed strategy in terms of utility, and the fairness among each user is guaranteed.
References
Politis C, Oda T, Dixit S, et al.: Cooperative networks for the future wireless world. IEEE Communications Magazine 2004, 42(9):70-79. 10.1109/MCOM.2004.1336723
Pabst R, Walke BH, Schultz DC, et al.: Relay-based deployment concepts for wireless and mobile broadband radio. IEEE Communications Magazine 2004, 42(9):80-89. 10.1109/MCOM.2004.1336724
Zhang Z, Shi J, Chen HH, et al.: A cooperation strategy based on nash bargaining solution in cooperative relay networks. IEEE Transactions on Vehicular Technology 2008, 57(4):2570-2577.
Ileri O, Mau SC, Mandayam NB: Pricing for enabling forwarding in self-configuring ad hoc networks. IEEE Journal on Selected Areas in Communications 2005, 23(1):151-161.
Lu D, Wu H, Zhang Q, et al.: PARS: stimulating cooperation for power-aware routing in ad-hoc networks. Proceedings of the IEEE International Conference on Communications (ICC '05), May 2005, Seoul, South Korea 5: 3187-3191.
Saraydar CU, Mandayam NB, Goodman DJ: Efficient power control via pricing in wireless data networks. IEEE Transactions on Communications 2002, 50(4):291-303.
Shastry N, Adve RS: Stimulating cooperative diversity in wireless ad hoc networks through pricing. Proceedings of the IEEE International Conference on Communications (WCNC '06), June 2006, Istanbul, Turkey 8: 3747-3752.
Ji J, Adve RS: Evaluation of game theoretic approaches to cooperative wireless network design. Proceedings of the 23rd Biennial Symposium on Communications, June 2006, Kingston, Canada 75-79.
Katoozian M, Navaie K, Yanikomeroglu H: Utility-based adaptive radio resource allocation in OFDM wireless networks with traffic prioritization. IEEE Transactions on Wireless Communications 2009, 8(1):66-71.
Han Z, Ji Z, Liu KJR: Fair multiuser channel allocation for OFDMA networks using Nash bargaining solutions and coalitions. IEEE Transactions on Communications 2005, 53(8):1366-1376. 10.1109/TCOMM.2005.852826
Chen Y, Kishore S: A game-theoretic analysis of decode-and-forward user cooperation. IEEE Transactions on Wireless Communications 2008, 7(5):1941-1951.
Host-Madsen A, Zhang J: Capacity bounds and power allocation for wireless relay channels. IEEE Transactions on Information Theory 2005, 51(6):2020-2040. 10.1109/TIT.2005.847703
Goodman D, Mandayam N: Power control for wireless data. IEEE Personal Communications 2000, 7(2):48-54. 10.1109/98.839331
Laneman JN, Tse DNC, Wornell GW: Cooperative diversity in wireless networks: efficient protocols and outage behavior. IEEE Transactions on Information Theory 2004, 50(12):3062-3080. 10.1109/TIT.2004.838089
Rosenmüller J: Game Theory: Stochastics, Information, Strategies and Cooperation. Kluwer Academic Publishers, Dordrecht, The Netherlands; 2000.
Osborne MJ: An Introduction to Game Theory. Oxford University, New York, NY, USA; 2004.
Grosu D, Chronopoulos AT, Leung MY: Load balancing in distributed systems: an approach using cooperative games. Proceedings of the 16th International Symposium on Parallel and Distributed Processing (IPDPS '02), April 2002, Fort Lauderdale, Fla, USA 52-61.
Acknowledgments
This work is supported by the National 863 High Tech R&D Program of China (Project no. 2009AA01Z262), Chinese 973 Project under the Grant no. 2009CB320400, Natural Science Foundation of China (key Project no. 60632030, 60832009).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Jiang, F., Tian, H. & Zhang, P. A User Cooperation Stimulating Strategy Based on Cooperative Game Theory in Cooperative Relay Networks. J Wireless Com Network 2009, 294942 (2009). https://doi.org/10.1155/2009/294942
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/294942

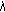 : per unit price the BS charges for data transmission;
: per unit price the BS charges for data transmission;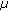 : the source reimbursement price per unit data;
: the source reimbursement price per unit data; : fraction of data requested by the source for cooperative transmission;
: fraction of data requested by the source for cooperative transmission; : fraction of data forwarded by the relay;
: fraction of data forwarded by the relay;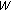 : bandwidth for transmission.
: bandwidth for transmission. as well as
as well as  .
. .
.
 that satisfy the restrictions when
that satisfy the restrictions when
 .
.



 versus different locations of the relay under AF forwarding.
versus different locations of the relay under AF forwarding.

 versus different locations of the relay under DF forwarding.
versus different locations of the relay under DF forwarding.

 versus different locations of the relay.
versus different locations of the relay.



