- Research Article
- Open access
- Published:
Monte Carlo Solutions for Blind Phase Noise Estimation
EURASIP Journal on Wireless Communications and Networking volume 2009, Article number: 296028 (2009)
Abstract
This paper investigates the use of Monte Carlo sampling methods for phase noise estimation on additive white Gaussian noise (AWGN) channels. The main contributions of the paper are (i) the development of a Monte Carlo framework for phase noise estimation, with special attention to sequential importance sampling and Rao-Blackwellization, (ii) the interpretation of existing Monte Carlo solutions within this generic framework, and (iii) the derivation of a novel phase noise estimator. Contrary to the ad hoc phase noise estimators that have been proposed in the past, the estimators considered in this paper are derived from solid probabilistic and performance-determining arguments. Computer simulations demonstrate that, on one hand, the Monte Carlo phase noise estimators outperform the existing estimators and, on the other hand, our newly proposed solution exhibits a lower complexity than the existing Monte Carlo solutions.
1. Introduction
Instabilities of local oscillators are an inherent impairment of coherent communication schemes [1, 2]. Such instabilities give rise to a time-varying phase difference between the oscillator at the transmitter and the receiver sides. As the phase of the transmitted symbols conveys (part of) the information of a coherent transmission, the carrier phase must be known to the receiver before the recovery of the transmitted information can take place. Estimation of the carrier phase is henceforth a crucial task of a coherent receiver.
As long as frugality with respect to the available resources is deemed important, this estimation process should occur without inserting too many training or pilot symbols into the transmitted data sequence. The presence of training symbols in the data sequence reduces the spectral efficiency and power efficiency of the transmission. Estimating the carrier phase based on the unknown information carrying data symbols is definitely more efficient in that respect.
Spurred by its great importance, the research on phase noise estimation evolved into a relatively mature state nowadays. There already exists a myriad of estimation strategies and most of them achieve a satisfactory performance—at least under the specific circumstances for which they were designed [1–5]. The existing estimators range from feed-forward techniques assuming a piecewise constant carrier phase over the duration of a predefined interval [1–3] to more advanced algorithms which track the movements of the carrier phase from symbol to symbol [4, 5]. Despite all these ad hoc efforts, no optimal solutions—from a classical estimation point of view—to the phase noise estimation problem have yet been presented. Optimal estimation of the phase noise, for example, in a maximum-likelihood or maximum a posteriori sense, without knowing the transmitted information turns out to be an extremely complicated task.
The purpose of the present paper is exactly to investigate the phase noise problem within a classical estimation context. We will define an optimal receiver strategy and explore the extent to which Monte Carlo methods can be used to obtain a practical implementation of this optimal receiver. In doing so, we will furnish a thorough overview of Monte Carlo methods and their application to phase noise estimation. It is only fair to point out that Monte Carlo methods have already been considered for phase noise estimation in the past [6, 7]. However, these solutions are limited to uncoded systems and explore only one of the possible Monte Carlo techniques. In this paper, we will lay out a more general Monte Carlo framework and integrate the existing estimators within this framework. We will also present a novel estimator and demonstrate that it bears a lower complexity than the existing techniques.
This paper is organized as follows. Section 2 describes the channel model. The objective of the paper and the connection with existing phase noise estimators is outlined in Section 3. Since it is unfair to assume that everyone working in the field of phase noise estimation is acquainted with Monte Carlo methods, we devote an entire and relatively large section of this paper to the introduction of Monte Carlo methods and sequential importance sampling in particular (Section 4). The framework presented in Section 4 is thereafter applied to the phase noise problem for uncoded and coded systems in Sections 5 and 6, respectively. Finally, Section 7 provides numerical results and Section 8 wraps up the paper.
2. Channel Model
2.1. Phase Noise Channel Model
We consider a digital communication scheme, where the information is conveyed by  complex-valued data symbols
complex-valued data symbols  . These symbols take on values from a predefined constellation set
. These symbols take on values from a predefined constellation set  . The average energy of the symbols is equal to
. The average energy of the symbols is equal to  . Concerning the channel model, we consider a discrete-time additive white Gaussian noise channel (AWGN), susceptible to Wiener phase noise. In order to not overcomplicate the analysis, other receiver impairments are ignored. The received signal samples can, therefore, be written as
. Concerning the channel model, we consider a discrete-time additive white Gaussian noise channel (AWGN), susceptible to Wiener phase noise. In order to not overcomplicate the analysis, other receiver impairments are ignored. The received signal samples can, therefore, be written as


for  and
and  uniformly distributed within
uniformly distributed within  . The additive (thermal) noise samples
. The additive (thermal) noise samples  are zero-mean i.i.d. complex-valued and circular symmetric Gaussian variables, with a variance of the real and imaginary part equal to
are zero-mean i.i.d. complex-valued and circular symmetric Gaussian variables, with a variance of the real and imaginary part equal to  . The zero-mean i.i.d. Gaussian random variables
. The zero-mean i.i.d. Gaussian random variables  are real-valued with a variance equals to
are real-valued with a variance equals to  . The channel model can equivalently be described by the following two probability functions:
. The channel model can equivalently be described by the following two probability functions:


We assume that the receiver knows these distributions and is able to evaluate them for different values of  ,
,  ,
,  and
and  .
.
2.2. Linearized Phase Noise Channel Model
The carrier phase affects the received signal in a nonlinear way. As will become apparent in the remainder of this paper, it can be useful to linearize this model. We convert the channel model (1) into a linear form as follows:

where  represents an initial estimate of the phase at instant
represents an initial estimate of the phase at instant  . This approximation is valid as long as
. This approximation is valid as long as  . Hence, the linearized channel model can only be invoked if
. Hence, the linearized channel model can only be invoked if  is small, and an accurate phase estimate
is small, and an accurate phase estimate  is available.
is available.
3. Problem Formulation and Prior Work
In a coherent communication scheme, the receiver needs to know the phase  at each time instant
at each time instant  before detection can take place. The traditional way to acquire this information is by estimating the carrier phase. If the carrier phase remains constant over a relatively long period, standard feed-forward estimation techniques can be applied. In the presence of severe phase noise, however, other more ingenious techniques are called upon. Before we describe our approach in that regard, let us review some of the existing solutions.
before detection can take place. The traditional way to acquire this information is by estimating the carrier phase. If the carrier phase remains constant over a relatively long period, standard feed-forward estimation techniques can be applied. In the presence of severe phase noise, however, other more ingenious techniques are called upon. Before we describe our approach in that regard, let us review some of the existing solutions.
3.1. Prior Work
Existing phase noise estimators or trackers have one thing in common. Their derivation does not stem from a probabilistic analysis, but is rather driven by pragmatic (and scenario dependent) arguments. Incidentally, the use of feedback loops or phase-locked loops is common practice [1].
A typical form to which these estimators can generally be reduced is

where  is a positive parameter,
is a positive parameter,  denotes the phase estimate at instant
denotes the phase estimate at instant  , and
, and  denotes an estimate (soft or hard decision) of
denotes an estimate (soft or hard decision) of  , using the phase estimate from a previous time instant and possible additional information from a decoder (see also Section 6). Obviously, there exist other estimators as well, for example, [8]. To our knowledge, however, their application is limited to pilot symbols only. Estimators of the form (6) are based on the linear model (5) and exploit the fact that
, using the phase estimate from a previous time instant and possible additional information from a decoder (see also Section 6). Obviously, there exist other estimators as well, for example, [8]. To our knowledge, however, their application is limited to pilot symbols only. Estimators of the form (6) are based on the linear model (5) and exploit the fact that  hazards an estimate of the difference between
hazards an estimate of the difference between  and the true value of
and the true value of  . The impact of the phase noise and the additive (thermal) noise can be balanced by tuning the parameter
. The impact of the phase noise and the additive (thermal) noise can be balanced by tuning the parameter  . Provided the linearized model (5) is a valid approximation, the optimal values, in a minimum mean squared error sense, of
. Provided the linearized model (5) is a valid approximation, the optimal values, in a minimum mean squared error sense, of  follow from the extended Kalman filter equations [9].
follow from the extended Kalman filter equations [9].
For a wide range of applications, these existing estimators render a satisfactory performance, but they nevertheless lack a rock-solid theoretical foundation. In the next section, we will outline our strategy to settle this issue.
3.2. Probabilistic Solution
In order to lay the foundation for the analysis in the next two sections, let us investigate what really determines the performance of the communication system. For now, we will assume that the transmitted symbols are a priori independent (and hence uncoded). The extension to coded systems is covered separately in Section 6. We can define the following on-the-fly detection rule:

where  is a shorthand notation for
is a shorthand notation for  . The on-the-fly label stems from the fact that a decision on
. The on-the-fly label stems from the fact that a decision on  can be made based on readily available information at time instant
can be made based on readily available information at time instant  , that is, the received samples
, that is, the received samples  . Detectors that exploit "future" received information are not considered here. It is easily shown that a detector defined by (7) minimizes the symbol error probability, again, for a receiver that only has access to received information up to instant
. Detectors that exploit "future" received information are not considered here. It is easily shown that a detector defined by (7) minimizes the symbol error probability, again, for a receiver that only has access to received information up to instant  . From this, it seems that all it takes to devise an optimal receiver is to compute and maximize
. From this, it seems that all it takes to devise an optimal receiver is to compute and maximize  . We can perform a marginalization with respect to the unknown phase
. We can perform a marginalization with respect to the unknown phase  and exploit the fact that the transmitted symbols are uncorrelated. With Bayes' rule, the probability function can thus be rewritten as
and exploit the fact that the transmitted symbols are uncorrelated. With Bayes' rule, the probability function can thus be rewritten as

A closed-form expression for  follows immediately from the combination of (3) and the prior distribution
follows immediately from the combination of (3) and the prior distribution  . Hence, the remainder of this paper will focus on the derivation of
. Hence, the remainder of this paper will focus on the derivation of  and the ensuing computation of the integral in (8). In particular, we will investigate the use of Monte Carlo methods for the computation of (8).
and the ensuing computation of the integral in (8). In particular, we will investigate the use of Monte Carlo methods for the computation of (8).
4. Monte Carlo Framework
The purpose of this section is to provide a succinct introduction to Monte Carlo techniques. Section 5 addresses the specific application to our phase noise problem.
4.1. Particle Representation
Representing a distribution by means of samples or particles drawn from it is an appealing alternative in case the actual distribution defies an analytical representation. The rationale behind the particle filtering approach is that as long as we generate enough samples from the distribution, further processing with this distribution can be performed using particles of the distribution rather than the actual distribution. An example will serve to illustrate this benefit.
Suppose that we can easily generate a number of samples  whose statistics are specified by a distribution
whose statistics are specified by a distribution  . Then, we are able to approximate expectations of the form
. Then, we are able to approximate expectations of the form

by means of a particle evaluation

It can be shown that  converges to
converges to  as the number of particles grows [10]. Hence, as long as we are able to draw samples from
as the number of particles grows [10]. Hence, as long as we are able to draw samples from  , it is not necessary to solve the integral from (9) analytically. The next section elaborates the case when sampling from
, it is not necessary to solve the integral from (9) analytically. The next section elaborates the case when sampling from  is not that straightforward.
is not that straightforward.
4.2. Importance Sampling
The technique outlined above only makes sense when it is easy to draw samples from  . If this is not the case, we can still proceed by using another well-chosen distribution
. If this is not the case, we can still proceed by using another well-chosen distribution  from which it is easy to draw samples, and draw samples from it. Denoting these samples again by
from which it is easy to draw samples, and draw samples from it. Denoting these samples again by  , the integral from (9) can be approximated by
, the integral from (9) can be approximated by

where the so-called importance weights are given by
are given by

These weights are normalized such that  . The idea is to assign different weights to the samples
. The idea is to assign different weights to the samples  to compensate for the difference between the target distribution
to compensate for the difference between the target distribution  and the importance sampling distribution
and the importance sampling distribution  . Again, it can be shown that
. Again, it can be shown that  converges to
converges to  for a large number of samples and under mild conditions with respect to the choice of
for a large number of samples and under mild conditions with respect to the choice of  [10].
[10].
In the remainder, we denote the particle representation of a distribution  by
by  .
.
4.3. Sequential Importance Sampling
The true power of the Monte Carlo framework gets unlocked when it is applied to hidden Markov (or state-space) models. An observation  is said to be the output of a hidden Markov process if it complies with
is said to be the output of a hidden Markov process if it complies with

where  denotes the (hidden) state variable of the Markov process and the symbol
denotes the (hidden) state variable of the Markov process and the symbol  means that the right-hand side is the probability function of the variable on the left-hand side. Note that we do not impose any restriction about the nature of
means that the right-hand side is the probability function of the variable on the left-hand side. Note that we do not impose any restriction about the nature of  or
or  , these can be discrete or continuous, scalar or vector variables.
, these can be discrete or continuous, scalar or vector variables.
A typical problem associated with a Markov process involves the derivation of the a posteriori state distribution  or inferences thereof. The purpose of this section is to explain how to draw samples from
or inferences thereof. The purpose of this section is to explain how to draw samples from  in a recursive manner, the process called sequential importance sampling (SIS).
in a recursive manner, the process called sequential importance sampling (SIS).
4.3.1. Derivation of the Algorithm
The first step entails the factorization of our target distribution and manipulating it into a recursive expression

The first transition follows from Bayes' rule and the omission of the normalizing constant  , whereas the second transition exploits the Markov nature of the problem. Now, suppose that we already have a particle representation
, whereas the second transition exploits the Markov nature of the problem. Now, suppose that we already have a particle representation  , where the samples
, where the samples  are drawn from a distribution
are drawn from a distribution  . From (12), we know that the corresponding importance weights are then given by
. From (12), we know that the corresponding importance weights are then given by  . The next step is to draw, for every sample
. The next step is to draw, for every sample  , a new sample
, a new sample  from a distribution
from a distribution  , such that
, such that  represents a sample from
represents a sample from

The associated importance weights follow from (14) and (15):

The choice of the importance sampling distribution plays an important role with respect to the performance and stability of the algorithm. The next section elaborates this issue furthermore. To conclude this section, we summarize the operation of the SIS algorithm in Algorithm 1.
plays an important role with respect to the performance and stability of the algorithm. The next section elaborates this issue furthermore. To conclude this section, we summarize the operation of the SIS algorithm in Algorithm 1.
Algorithm 1: Sequential importance sampling.
-
(1)
Start from a sample representation

(see Section 4.2).
-
(2)
for
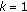 to
to  do
do -
(3)
for
 to
to  do
do -
(4)
Draw new sample
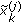 from
from 
-
(5)
Update the importance weights

-
(6)
Normalize the importance weights
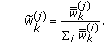
-
(7)
Set
 .
. -
(8)
 is a new sample of
is a new sample of  .
. -
(9)
end for
-
(10)
end for
4.3.2. Degeneracy of Sequential Importance Sampling
One particularly annoying problem with SIS is that the variance of the importance weights increases as  becomes larger [11]. This is an adverse property as it is intuitively clear that for a fixed number of samples, the best approximation, in terms of its ability to evaluate the expectation of a function (11), to a distribution is obtained using equal-weight samples. The increasing variance is so persevering that almost all samples bear a negligible weight after a few recursions. This implies that the distribution is represented by far less particles than the
becomes larger [11]. This is an adverse property as it is intuitively clear that for a fixed number of samples, the best approximation, in terms of its ability to evaluate the expectation of a function (11), to a distribution is obtained using equal-weight samples. The increasing variance is so persevering that almost all samples bear a negligible weight after a few recursions. This implies that the distribution is represented by far less particles than the  original particles. Obviously, this does not bode well for the accuracy of the approximation of the distribution and the performance of ensuing algorithms. A detriment that manifests itself especially when dealing with high-dimensional state spaces, that is, where the state variable
original particles. Obviously, this does not bode well for the accuracy of the approximation of the distribution and the performance of ensuing algorithms. A detriment that manifests itself especially when dealing with high-dimensional state spaces, that is, where the state variable  is actually a vector. Fortunately, this problem can be resolved by taking the following measures.
is actually a vector. Fortunately, this problem can be resolved by taking the following measures.
(1) Choice of the Sampling Distribution
It is important to carefully design the importance sampling distribution. The distribution should generate particles or samples in the regions of the state space corresponding to high values of the distribution that we wish to approximate (in this case, the posterior probability function). In this way, the correction administered by the weights can be kept to a bare minimum. It can be shown [11] that the variance of the weights is minimized for

The corresponding weight update equation then becomes

Note that the weight update (18) does not depend on the current sample  . This intuitively explains the optimality of (17) since the particular choice of the samples
. This intuitively explains the optimality of (17) since the particular choice of the samples  does not alter the weights, and hence, does not affect (read: increase) their variance. Unfortunately, this design measure will only slow down the process of degeneration; it will not bring it to a standstill. Furthermore, as will become apparent through the remainder of this paper, it is often very difficult to draw samples from (17). In this case, there is no alternative than to use a suboptimal distribution. The prior importance distribution
does not alter the weights, and hence, does not affect (read: increase) their variance. Unfortunately, this design measure will only slow down the process of degeneration; it will not bring it to a standstill. Furthermore, as will become apparent through the remainder of this paper, it is often very difficult to draw samples from (17). In this case, there is no alternative than to use a suboptimal distribution. The prior importance distribution  forms a good alternative as it is often easy to sample from it. The corresponding weight update function follows from (16) and is given by
forms a good alternative as it is often easy to sample from it. The corresponding weight update function follows from (16) and is given by  .
.
(2) Resampling
A more effective approach to avoid degeneracy is resampling. The idea is to remove samples with negligible weight from the set and to include better chosen samples (which actually contribute in a meaningful manner to the representation of the target distribution). There are several methods to implement this rule in practice. The prevailing method is simply to draw  new and equal-weight samples from the old distribution (defined by the weights of the old samples). Samples associated with low importance weights are most probably eliminated by this rule [11, 12].
new and equal-weight samples from the old distribution (defined by the weights of the old samples). Samples associated with low importance weights are most probably eliminated by this rule [11, 12].
(3) Rao-Blackwellization
Lesser known, but no less interesting is the Rao-Blackwellization method. The idea is that whenever it is possible to perform some part of the recursion analytically, it definitely pays to do so. More specifically, it is possible to show, as an instance of the Rao-Blackwell theorem [13, 14], that integrating out some of the state variables in (9) analytically improves the accuracy of the approximation (11). Moreover, it allows to sharply reduce the number of samples used in the SIS algorithm and to mitigate the degeneracy. In order to provide a formal outline of the procedure, let us assume that the state variable  consists of two parts
consists of two parts  . Rao-Blackwellization boils down to converting the approximation from (11) into
. Rao-Blackwellization boils down to converting the approximation from (11) into

where

and where  . Again, it can be shown that
. Again, it can be shown that  converges to
converges to  , defined in (9), for a large number of samples. Obviously, it only makes sense to rearrange (9) into (19) if
, defined in (9), for a large number of samples. Obviously, it only makes sense to rearrange (9) into (19) if  can be computed analytically, and the integration from (20) is tractable.
can be computed analytically, and the integration from (20) is tractable.
In a similar vein, we can also retrieve a Rao-Blackwellized version of the SIS algorithm [14]. It turns out that the weight update equation is now given by

and the optimal importance sampling distribution is given by

It is interesting to point out that, in general, the sequence  is no longer a Markov process, neither is the observation
is no longer a Markov process, neither is the observation  independent from
independent from  given
given  .
.
5. Phase Noise Estimation for Uncoded Systems
Geared with the Monte Carlo framework from the previous section, we are now ready to tackle our original phase noise problem.
5.1. Joint Phase and Symbol Sampling
In a first attempt, we cast the problem under investigation immediately into the SIS algorithm by defining  . The original state space model from (1), (2) is then a special case of the general model from (13). Application of the SIS algorithm immediately results in a sampled version of the a posteriori probability function
. The original state space model from (1), (2) is then a special case of the general model from (13). Application of the SIS algorithm immediately results in a sampled version of the a posteriori probability function  .
.
The optimal importance sampling function is defined in (17), and can be decomposed as follows:

The decomposition above allows to produce the symbol and phase samples in two steps. First, we draw the symbol sample, and then for each symbol sample, we generate a phase sample:


In order to produce these samples, we need the above functions in a closed-form expression. The first probability function can be written as follows:

The exact evaluation of the right-hand side of (26) requires a numerical integration which is not very practical. However, as shown in Appendix A.1, we can obtain the following closed-form approximation, valid for small  :
:

Note that  is equal to
is equal to  up to a scaling factor. It remains to normalize this function before samples can be drawn.
up to a scaling factor. It remains to normalize this function before samples can be drawn.
In Appendix A.2, we show that the distribution from (25) can be reduced to

where  and
and  are given by
are given by


From (28), it follows that the updated samples  are obtained by generating Gaussian samples with mean
are obtained by generating Gaussian samples with mean  and variance
and variance  . Finally, the associated weight update function (18) follows immediately from (27)
. Finally, the associated weight update function (18) follows immediately from (27)

Benefits and Drawbacks
The benefit of this algorithm is that it renders an asymptotically optimal solution, for a high number of particles, to the phase noise problem, provided that the linearized channel model approximation is accurate.
The major drawbacks are as follows.
-
(i)
The sample space is two-dimensional. In general, more samples are required to represent a distribution of more than one variable. Obviously, this weighs on the overall complexity.
-
(ii)
In order to generate a new sample pair
 , one has to evaluate (27), (29), and (31). These equations are relatively complicated and have to be executed for all
, one has to evaluate (27), (29), and (31). These equations are relatively complicated and have to be executed for all  .
. -
(iii)
Finally, the algorithm is based on the linearized channel model and tends to be less accurate for higher values of
 .
.
5.2. Rao-Blackwellization
To overcome the drawbacks encountered with the previous method, we explore the application of the Rao-Blackwellization method in this section. We distinguish two separate approaches. The first one is a symbol-based sampling method. This method is not new and has already been investigated in [6], albeit without establishing the link with the Rao-Blackwellization framework. For completeness, we provide a Rao-Blackwellized derivation of the algorithm in this paper.
In the second and new approach, we only draw samples of the carrier phase. As we will demonstrate, this offers significant computational advantages.
5.2.1. Symbol-Based Sampling
We apply the Rao-Blackwellization method from Section 4.3.2 by setting  and
and  . The optimal importance sampling distribution is given by (22), which, for the current scenario, breaks down to
. The optimal importance sampling distribution is given by (22), which, for the current scenario, breaks down to

The distribution  can be found in a recursive manner by applying a Kalman filter to the state space model of (5), (2), which is equivalent to an extended Kalman filter applied to (1), (2). In Kalman parlance, the requested distribution corresponds to the prediction step of the Kalman filter. For every symbol sequence
can be found in a recursive manner by applying a Kalman filter to the state space model of (5), (2), which is equivalent to an extended Kalman filter applied to (1), (2). In Kalman parlance, the requested distribution corresponds to the prediction step of the Kalman filter. For every symbol sequence  , we should run a Kalman filter to keep track of the carrier phase distribution. This means that we should run
, we should run a Kalman filter to keep track of the carrier phase distribution. This means that we should run  Kalman filters in parallel with the SIS algorithm. Denoting the mean and variance of the carrier phase distribution by
Kalman filters in parallel with the SIS algorithm. Denoting the mean and variance of the carrier phase distribution by  and
and  , respectively, the integral from (32) can be evaluated analytically as follows:
, respectively, the integral from (32) can be evaluated analytically as follows:

where  . The weight update function follows from (21) and is given by
. The weight update function follows from (21) and is given by

Denote the mean and variance of the carrier variable at instant  conditioned on the observations up to instant
conditioned on the observations up to instant  by
by  and
and  , as follows: This succinct derivation captures the main idea and furnishes the key equations of the symbol-based sampling approach.
, as follows: This succinct derivation captures the main idea and furnishes the key equations of the symbol-based sampling approach.
Benefits and Drawbacks
The main benefit of this approach is the reduction of the sample space to one dimension. By running a Kalman filter in parallel with the particle filter, the posterior distribution of the carrier phase can be tracked analytically.
However, the following two drawbacks remain.
-
(i)
The algorithm still relies on the linearized channel model and suffers from the disadvantages mentioned in Section 5.1.
-
(ii)
The computational complexity remains high due to the required evaluation of (33), (34), and the Kalman filter evaluation.
5.2.2. Phase-Based Sampling
In this second method, samples are drawn of the carrier phase rather than of the data symbols. We will distinguish two different approaches within this method. In the first approach, we use the optimal importance sampling distribution, whereas in the second approach, an alternative distribution is explored. We will show that the suboptimal sampling method results in a lower overall complexity.
(a) Optimal Distribution
The optimal importance sampling distribution for the present case follows again from (22) as follows:

The second transition follows from the fact that  is a Markov process, provided that the transmitted symbols are independent. The first distribution in the last line has already been derived in Section 5.1. We can simply reuse the result obtained there if we replace
is a Markov process, provided that the transmitted symbols are independent. The first distribution in the last line has already been derived in Section 5.1. We can simply reuse the result obtained there if we replace  by
by  in (28). The second factor in (35) is also known and given by (26). Hence, as it turns out,
in (28). The second factor in (35) is also known and given by (26). Hence, as it turns out,  is a mixture of Gaussian distributions. Sampling from this, a distribution is very simple. First, draw a sample
is a mixture of Gaussian distributions. Sampling from this, a distribution is very simple. First, draw a sample  from
from  . Then, draw a phase sample from
. Then, draw a phase sample from  . The weight update equation is again given by (31).
. The weight update equation is again given by (31).
This approach is almost identical to the approach from Section 5.1. The only difference is that the samples of the data symbols are not stored. Hence, this method will not mitigate the inconveniences of the earlier described methods. Note that this approach has also been investigated in [7].
(b) Prior Distribution
By carefully selecting the importance sampling distribution, however, we can obtain a significant saving in the overall complexity. In this paragraph, we explore the prior distribution of the phase (at instant  given phase samples up to
given phase samples up to  ) as a candidate sampling distribution:
) as a candidate sampling distribution:

Drawing samples from this distribution is very simple. All we need is to generate Gaussian noise samples and plug them into (2). The weight update function follows from inserting (36) into (21) and is given by

The functions in the right-hand side of (37) follow immediately from the channel model and are known.
Benefits and Drawbacks
The apparent simplicity of the latter method raises high hopes regarding the computational complexity. The only drawback of this method is that it does not use the optimal importance sampling distribution. However, as we will show in Section 7, the slightly more samples required to surmount degeneration are more than compensated by the reduced complexity of the method.
6. Phase Noise Estimation for Coded Systems
Let us now investigate how we can extend the algorithms described above to a coded system. For such a coded system, (8) is no longer valid. The a posteriori probability of a symbol typically depends on all the entire frame of received signals. Therefore, (8) should be replaced with

Straightforward application of the SIS algorithm is no longer possible for two reasons. First, the code constraint prohibits to draw samples from  in a recursive manner. In particular, the evaluation of the importance sampling and particle update equations is prohibitive in the presence of a code constraint on the symbols. Second, the integral in (38) cannot be evaluated using the importance sampling technique as we have no closed-form solution for
in a recursive manner. In particular, the evaluation of the importance sampling and particle update equations is prohibitive in the presence of a code constraint on the symbols. Second, the integral in (38) cannot be evaluated using the importance sampling technique as we have no closed-form solution for  . The evaluation of
. The evaluation of  requires a complicated decoding step, which has to be executed for every possible sample of
requires a complicated decoding step, which has to be executed for every possible sample of  . Obviously, this becomes impractical for a large number of samples.
. Obviously, this becomes impractical for a large number of samples.
Fortunately, we can extend the algorithms described above to a coded setup by means of iterative receiver processing. As shown in [15–19], there exists a solid framework based on factor graph theory that dictates how the estimation and the decoding can be decoupled in a coded setup. It can be shown that the factor graph solution converges to the optimal solution under mild conditions. The loops that arise in the factor graph representation of the receiver should not be too short. Extending the above algorithms to a coded system boils down to replacing the prior probabilities of the symbols  with the extrinsic probabilities provided by the decoder. These extrinsic probabilities are updated by the decoder and exchanged in an iterative fashion with the estimator which, on its turn, updates the phase estimates. This process repeats until convergence of the algorithm is achieved. More details on this approach can be found in [15, 16]. Section 7 illustrates the performance of the resulting iterative receiver.
with the extrinsic probabilities provided by the decoder. These extrinsic probabilities are updated by the decoder and exchanged in an iterative fashion with the estimator which, on its turn, updates the phase estimates. This process repeats until convergence of the algorithm is achieved. More details on this approach can be found in [15, 16]. Section 7 illustrates the performance of the resulting iterative receiver.
7. Numerical Results
We ran computer simulations to evaluate the performance of the algorithms described above. We have adopted the Wiener phase noise model from (1)-(2) and applied a QPSK signaling. Unless mentioned otherwise,  samples were used to represent the target distributions in the evaluation of the various Monte Carlo-based methods. The results form Figures 1 and 2 are for an uncoded setup, whereas Figures 3 and 4 pertain to a coded system. In this latter case, a rate-
samples were used to represent the target distributions in the evaluation of the various Monte Carlo-based methods. The results form Figures 1 and 2 are for an uncoded setup, whereas Figures 3 and 4 pertain to a coded system. In this latter case, a rate-  16-state recursive convolutional code was employed, and
16-state recursive convolutional code was employed, and  iterations between the decoder and the estimator were performed.
iterations between the decoder and the estimator were performed.
The following paragraphs tender a discussion of the obtained results.
Ambiguities
Let us begin with an uncoded configuration. If the transmitted symbols are unknown, it is impossible to assess the true value of the carrier phase based on the received signal. For QPSK, for instance, the carrier phase can only be known up to a four-fold ambiguity. Figure 1 demonstrates this fact. It portrays a histogram of the samples from the distribution  , which were obtained through the evaluation of the phase-based sampling algorithm from Section 5.2.2 (with the optimal sampling distribution). In Figure 1, only the symbols at instants
, which were obtained through the evaluation of the phase-based sampling algorithm from Section 5.2.2 (with the optimal sampling distribution). In Figure 1, only the symbols at instants  are known to the receiver. Hence, the distribution
are known to the receiver. Hence, the distribution  for
for  is based solely on unknown symbols. As expected, the distribution exhibits 4 local maxima (at
is based solely on unknown symbols. As expected, the distribution exhibits 4 local maxima (at  intervals). At
intervals). At  , however, these ambiguities have been resolved because of the known symbols inserted before
, however, these ambiguities have been resolved because of the known symbols inserted before  . This result indicates that it is necessary to insert pilot symbols in the data stream (at regular time instants).
. This result indicates that it is necessary to insert pilot symbols in the data stream (at regular time instants).
Performance
Figures 2 and 3 illustrate the BER performance of various algorithms for an uncoded and coded setups, respectively. We considered the transmission of blocks of  QPSK symbols, with the periodic insertion of one pilot symbol per
QPSK symbols, with the periodic insertion of one pilot symbol per  symbols (
symbols ( pilot overhead). The scenarios labeled phase-based A and B correspond to the phase-based sampling algorithm from Section 5.2.2, using the optimal and prior importance sampling distributions, respectively. The symbol-based algorithm corresponds to the algorithm which was proposed in [6] and has also been described in Section 5.2.1. These Monte Carlo approaches have also been compared to conventional phase noise estimators. Performance curves are included for an extended Kalman filter, using either hard-symbol decisions, soft-symbol decisions, or pilot symbols only (see also Section 3.1). In a coded setup, these soft or hard symbol decisions are based on the available posteriori probabilities of the symbols (available during the specific iteration).
pilot overhead). The scenarios labeled phase-based A and B correspond to the phase-based sampling algorithm from Section 5.2.2, using the optimal and prior importance sampling distributions, respectively. The symbol-based algorithm corresponds to the algorithm which was proposed in [6] and has also been described in Section 5.2.1. These Monte Carlo approaches have also been compared to conventional phase noise estimators. Performance curves are included for an extended Kalman filter, using either hard-symbol decisions, soft-symbol decisions, or pilot symbols only (see also Section 3.1). In a coded setup, these soft or hard symbol decisions are based on the available posteriori probabilities of the symbols (available during the specific iteration).
As we can observe from Figures 2 and 3, it definitely pays to exploit information from the unknown data symbols. The estimators that are only based on pilot symbols give rise to a significant performance degradation. On the other hand, there is no much difference between the performance of the various blind estimators in the uncoded setup. This confirms that in an uncoded setup, the conventional estimators exhibit a satisfactory performance. In the coded configuration, however, the Monte Carlo methods outperform the conventional methods. Apparently, these conventional ad hoc methods fail to operate at the lower SNR-values that can be achieved with the use of coding. We furthermore observe that the phase-based estimators exhibit the best performance. The reason that the symbol-based method performs not as good is due to the fact that at high SNRs, the importance sampling distribution is very peaky. Therefore, almost all samples drawn from the distribution  will be equal to each other. Hence, it takes a lot more samples to provide an accurate representation of this latter distribution, and the algorithm will suffer from cycle-slip-like phenomena [20].
will be equal to each other. Hence, it takes a lot more samples to provide an accurate representation of this latter distribution, and the algorithm will suffer from cycle-slip-like phenomena [20].
Complexity
Finally, we will examine the computational complexity of the different Monte Carlo-based methods. First, we note that the complexity of each of the presented algorithms scales linearly with the number of samples. Hence, it suffices to determine (i) the complexity per sample and (ii) the number of samples required to achieve a satisfactory performance.
It is hard to assess the complexity of the algorithms in an analytical manner. Therefore, we compared their relative complexity per sample based on the duration of an actual implementation on a Matlab simulation platform. Table 1 displays the results. Apparently, the phase-based sampling method with the prior importance sampling distribution bears the lowest complexity. Based on the simplicity of this estimator operation (see Section 5.2.2), this result does not come as a surprise.
It remains is to compare the performance of the algorithms with respect to the number of samples used in their evaluation. Figure 4 illustrates this behavior for the coded scenario. It turns out that the phase-based sampling methods converge much faster to the asymptotic performance, which is defined as the performance for  . Furthermore, the difference between the two phase-based sampling methods is negligible. Hence, based on the results from Table 1, the phase-based sampling method with the prior importance sampling distribution has the lowest overall complexity. These findings advocate the use of this last method to deal with phase noise on coded systems.
. Furthermore, the difference between the two phase-based sampling methods is negligible. Hence, based on the results from Table 1, the phase-based sampling method with the prior importance sampling distribution has the lowest overall complexity. These findings advocate the use of this last method to deal with phase noise on coded systems.
8. Conclusions
This paper explored the use of Monte Carlo methods for phase noise estimation. Starting with a short survey on Monte Carlo methods, several techniques were introduced, such as sequential importance sampling and Rao-Blackwellization, laying the foundation for the development of various phase noise estimators. It turned out that there are two feasible Monte Carlo approaches to tackle the phase noise problem. The first one boils down to drawing samples from the a posteriori distribution of the symbols and updating them in a recursive manner. The carrier phase trajectory is hereby tracked analytically. This approach has previously been examined in [6]. The other approach entails the sequential sampling of the a posteriori carrier phase distribution. Two different importance sampling distributions can be used for this method. The use of the optimal sampling distribution has been explored in [7], whereas this paper also considers the use of the prior sampling distribution. Computer simulations show that the performance complexity tradeoff is optimized for the phase-based sampling method with a prior importance sampling distribution.
References
Meyr H, Moeneclaey M, Fechtel SA: Digital Communication Receivers: Synchronization, Channel Estimation, and Signal Processing. Volume 2. John Wiley & Sons, New York, NY, USA; 1997.
Mengali U, D'Andrea AN: Synchronization Techniques for Digital Receivers. Plenum Press, New York, NY, USA; 1997.
Benvenuti L, Giugno L, Lottici V, Luise M: Codeaware carrier phase noise compensation on turbo-coded spectrally-efficient high-order modulations. Proceedings of the 8th International Workshop on Signal Processing for Space Communications (SPSC '03), September 2003, Catania, Italy 1: 177-184.
Noels N, Steendam H, Moeneclaey M: Carrier phase tracking from turbo and LDPC coded signals affected by a frequency offset. IEEE Communications Letters 2005, 9(10):915-917. 10.1109/LCOMM.2005.10020
Colavolpe G, Barbieri A, Caire G: Algorithms for iterative decoding in the presence of strong phase noise. IEEE Journal on Selected Areas in Communications 2005, 23(9):1748-1757.
Panayırcı E, Çırpan H, Moeneclaey M: A sequential Monte Carlo method for blind phase noise estimation and data detection. Proceedings of the 13th European Signal Processing Conference (EUSIPCO '05), September 2005, Antalya, Turkey
Amblard PO, Brossier JM, Moisan E: Phase tracking: what do we gain from optimality? Particle filtering versus phase-locked loops. Signal Processing 2003, 83(1):151-167. 10.1016/S0165-1684(02)00386-9
Bhatti J, Moeneclaey M: Pilot-aided carrier synchronization using an approximate DCT-based phase noise model. Proceedings of the 7th IEEE International Symposium on Signal Processing and Information Technology (ISSPIT '07), December 2007, Cairo, Egypt 1143-1148.
Anderson BDO, Moore JB: Optimal Filtering. Prentice-Hall, Englewood Cliffs, NJ, USA; 1979.
Doucet A, Godsill S, Andrieu C: On sequential Monte Carlo sampling methods for Bayesian filtering. Statistics and Computing 2000, 10(3):197-208. 10.1023/A:1008935410038
Doucet A: On sequential simulation-based methods for Bayesian filtering. Department of Engineering, Cambridge University, Cambridge, UK; 1998.
Cappé O, Godsill SJ, Moulines E: An overview of existing methods and recent advances in sequential Monte Carlo. Proceedings of the IEEE 2007, 95(5):899-924.
Gelfand AE, Smith AFM: Sampling-based approaches to calculating marginal densities. Journal of the American Statistical Association 1990, 85(410):398-409. 10.2307/2289776
Andrieu C, Doucet A: Particle filtering for partially observed Gaussian state space models. Journal of the Royal Statistical Society. Series B 2002, 64(4):827-836. 10.1111/1467-9868.00363
Simoens F: Iterative multiple-input multiple-output communication systems, Ph.D. thesis. Ghent University, Ghent, Belgium; 2008.
Wymeersch H: Iterative Receiver Design. Cambridge University Press, Cambridge, UK; 2007.
Dauwels J, Loeliger H-A: Phase estimation by message passing. Proceedings of the IEEE International Conference on Communications (ICC '04), June 2004, Paris, France 1: 523-527.
Wiberg N: Codes and decoding on general graphs, Ph.D. thesis. Linköping University, Linköping, Sweden; 1996.
Worthen AP, Stark WE: Unified design of iterative receivers using factor graphs. IEEE Transactions on Information Theory 2001, 47(2):843-849. 10.1109/18.910595
Meyr H, Ascheid G: Synchronization in Digital Communications. John Wiley & Sons, New York, NY, USA; 1990.
Acknowledgments
The first author gratefully acknowledges the support from the Research Foundation-Flanders (FWO Vlaanderen). This work is also supported by the European Commission in the framework of the FP7 Network of Excellence in Wireless Communications NEWCOM++ (Contract no. 216715), the Turkish Scientific and Technical Research Institute (TUBITAK) under Grant no. 108E054, and the Research Fund of Istanbul University under Projects UDP-2042/23012008, UDP-1679/10102007.
Author information
Authors and Affiliations
Corresponding author
Appendices
A.1. Derivation of (27)
First, we assume that the likelihood function (3) only takes on significant values in the neighborhood of  . Invoking the linearized channel model from (5), this allows to rewrite (3) as follows:
. Invoking the linearized channel model from (5), this allows to rewrite (3) as follows:


This approximation is valid for values of  situated in the neighborhood of
situated in the neighborhood of  . We can now combine (A.1) and (4) into
. We can now combine (A.1) and (4) into


The last approximation is valid for small  . Finally, multiplication with the prior symbol distribution
. Finally, multiplication with the prior symbol distribution  yields (27).
yields (27).
A.2. Derivation of (28)
The derivation of (28) draws on the linearized channel model distribution (A.1) and the following straightforward manipulations:


where  and
and  are defined in (29) and (30), respectively.
are defined in (29) and (30), respectively.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Simoens, F., Duyck, D., Çırpan, H. et al. Monte Carlo Solutions for Blind Phase Noise Estimation. J Wireless Com Network 2009, 296028 (2009). https://doi.org/10.1155/2009/296028
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/296028

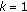 to
to  do
do to
to  do
do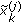 from
from 

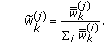
 .
. is a new sample of
is a new sample of  .
. , one has to evaluate (27), (29), and (31). These equations are relatively complicated and have to be executed for all
, one has to evaluate (27), (29), and (31). These equations are relatively complicated and have to be executed for all  .
. .
.
 obtained by the phase-based sampling algorithm (
obtained by the phase-based sampling algorithm ( ,
,  , uncoded QPSK). The dashed line indicates the true value of
, uncoded QPSK). The dashed line indicates the true value of  .
.

