- Research Article
- Open access
- Published:
Dynamic Subcarrier Allocation for Real-Time Traffic over Multiuser OFDM Systems
EURASIP Journal on Wireless Communications and Networking volume 2009, Article number: 298451 (2009)
Abstract
A dynamic resource allocation algorithm to satisfy the packet delay requirements for real-time services, while maximizing the system capacity in multiuser orthogonal frequency division multiplexing (OFDM) systems is introduced. Our proposed cross-layer algorithm, called Dynamic Subcarrier Allocation algorithm for Real-time Traffic (DSA-RT), consists of two interactive components. In the medium access control (MAC) layer, the users' expected transmission rates in terms of the number of subcarriers per symbol and their corresponding transmission priorities are evaluated. With the above MAC-layer information and the detected subcarriers' channel gains, in the physical (PHY) layer, a modified Kuhn-Munkres algorithm is developed to minimize the system power for a certain subcarrier allocation, then a PHY-layer resource allocation scheme is proposed to optimally allocate the subcarriers under the system signal-to-noise ratio (SNR) and power constraints. In a system where the number of mobile users changes dynamically, our developed MAC-layer access control and removal schemes can guarantee the quality of service (QoS) of the existing users in the system and fully utilize the bandwidth resource. The numerical results show that DSA-RT significantly improves the system performance in terms of the bandwidth efficiency and delay performance for real-time services.
1. Introduction
Demands for real-time multimedia applications are increasing rapidly for broadband wireless networks. Orthogonal frequency division multiplexing (OFDM) is considered a promising technique in such systems. In this paper, we consider multiuser systems [1] where multiple users are allowed to transmit simultaneously on different subcarriers per OFDM symbol. Mobile users on certain OFDM subchannels may experience deep frequency-selective fading in a multipath propagation environment. Since each user may have a different subchannel impulse response, a poor subchannel for one user may be a good subchannel for another user. Clearly, if a user who suffers from poor subchannel gain can be reassigned to a better subchannel, the total throughput can be increased. This is also known as multiuser diversity. Since the subcarrier gains vary from user to user, to achieve higher system capacity and spectral efficiency, it is better to allocate subcarriers and the corresponding power dynamically according to the instantaneous channel states of all users.
To support QoS for multiple services, packet scheduling has been identified as an important mechanism in wired networks. When considering the multipath fading, high error rate, and time-varying channel capacity in wireless links, some new packet scheduling algorithms are developed, such as channel state dependent round Robin (CSD-RR) [2], feasible earliest due date (FEDD) [3], modified largest weighted delay first (M-LWDF) [4], and link-adaptive LWDF [5] algorithms. CSD-RR schedules the packets whose channel is in the "Good'' state in a Round Robin fashion. FEDD focuses on scheduling the packet which has the smallest time to expiry and whose channel is in the "Good'' state. M-LWDF schedules the packet according to  , where
, where  is the head-of-the-line packet delay for queue
is the head-of-the-line packet delay for queue  ,
,  is the channel capacity with respect to flow
is the channel capacity with respect to flow  , and
, and  are arbitrary positive constants. M-LWDF is proven to be a throughput-optimal scheduling algorithm. Link-adaptive LWDF aims to satisfy the stringent packet delay constraints, but without any guarantees. The objectives of these algorithms are to maximize the system spectral efficiency by exploiting the random channel variations and to provide QoS guarantees to the users by deferring the transmissions on the deep fading links and compensating for them when the links recover. However, all these scheduling algorithms are based on packet scheduling, and multiple frequency subcarrier scheduling, which may be implemented in multiuser OFDM systems, is not considered. In the PHY layer, the total power resource is limited. Given the required number of subcarriers of different users, how to minimize the power allocation for the users on the subcarriers under users' SNR requirements is still a problem. To solve this problem, a suboptimal subcarrier allocation algorithm based on constructive assignment and iterative improvement is proposed in [6] and adopted in [7]. The algorithm exploits the similarity between the subcarrier allocation problem and the classical assignment problem. However, the algorithm can only provide a suboptimal allocation. An optimal solution to this power minimization problem is the Kuhn-Munkres algorithm proposed for the classical assignment problem [8]. Kuhn-Munkres is based on the Hungarian algorithm [9]. OFDM subarrier allocation using this method has been studied in [10]. However, an important assumption in that paper is that the number of assigned subcarriers for the users is known. Actually, without this information, the Kuhn-Munkres algorithm cannot perform the subcarrier allocation. In addition, in most of the proposed scheduling algorithms, the dynamic variation of the number of active users in the system is ignored.
are arbitrary positive constants. M-LWDF is proven to be a throughput-optimal scheduling algorithm. Link-adaptive LWDF aims to satisfy the stringent packet delay constraints, but without any guarantees. The objectives of these algorithms are to maximize the system spectral efficiency by exploiting the random channel variations and to provide QoS guarantees to the users by deferring the transmissions on the deep fading links and compensating for them when the links recover. However, all these scheduling algorithms are based on packet scheduling, and multiple frequency subcarrier scheduling, which may be implemented in multiuser OFDM systems, is not considered. In the PHY layer, the total power resource is limited. Given the required number of subcarriers of different users, how to minimize the power allocation for the users on the subcarriers under users' SNR requirements is still a problem. To solve this problem, a suboptimal subcarrier allocation algorithm based on constructive assignment and iterative improvement is proposed in [6] and adopted in [7]. The algorithm exploits the similarity between the subcarrier allocation problem and the classical assignment problem. However, the algorithm can only provide a suboptimal allocation. An optimal solution to this power minimization problem is the Kuhn-Munkres algorithm proposed for the classical assignment problem [8]. Kuhn-Munkres is based on the Hungarian algorithm [9]. OFDM subarrier allocation using this method has been studied in [10]. However, an important assumption in that paper is that the number of assigned subcarriers for the users is known. Actually, without this information, the Kuhn-Munkres algorithm cannot perform the subcarrier allocation. In addition, in most of the proposed scheduling algorithms, the dynamic variation of the number of active users in the system is ignored.
In this paper, we propose a cross-layer resource allocation scheduling algorithm, named DSA-RT, for real-time services under frequency-selective fading channel in multiuser OFDM systems. This algorithm has two cooperative components: the MAC-layer scheduling/control scheme and the PHY-layer resource allocation scheme. At the MAC layer, based on queuing theory, active users' expected resource requirements to satisfy delay constrains are calculated in terms of the number of subcarriers per OFDM symbol. With the support of our MAC-layer scheduling scheme, the number of required subcarriers and the users' transmission priorities are given. At the PHY layer, based on the modified Kuhn-Munkres algorithm, a PHY-layer resource allocation algorithm is proposed to satisfy all users' requirements under the system SNR and power constraints and to decide the real subcarrier allocation for each active user. (Users admitted to the system are termed active users. Once new users are admitted, they will be allocated resources (subcarriers) by the access control scheme.) When considering a system where the number of active users changes dynamically, if there are still subcarriers left in an OFDM symbol, the access of new mobile users will be considered. In addition, if the dropping rates of certain users violate their maximum tolerable limits, a removal scheme is triggered to remove the aggressive users so as to guarantee the QoS of the other existing users. With the cooperation of the MAC and PHY layer schemes, our proposed algorithm offers the following advantages: (1) based on queuing theory, real-time users' delay requirements can be evaluated in terms of the number of subcarriers required, leading to a more flexible scheduling algorithm which can effectively guarantee the QoS for real-time services in multiuser OFDM systems; (2) with the number of the expected subcarriers and transmission priority information from the MAC layer, the proposed PHY-layer resource allocation scheme aims to maximize the bandwidth usage under the current channel state, system SNR, and power constraints; (3) when the number of mobile users is dynamically changed, the access control and removal schemes can dynamically adjust system flows and provide delay-related guarantee for the active users in the system.
The rest of this paper is organized as follows. The system model is introduced in Section 2. The detailed description of DSA-RT is presented in Section 3. The simulation results are given in Section 4. Section 5 draws the conclusions.
2. System Model
Figure 1 shows our downlink OFDM system model at a base station (BS). As in previous work [2–5], channel state information (CSI) is assumed to be available at BSs. Assume that the frequency bandwidth is divided into  subcarriers, and there are
subcarriers, and there are  active users, where
active users, where  is changed dynamically and follows a Poisson distribution. BSs are in charge of subcarrier scheduling and resource allocation. We assume a fixed modulation for all subcarriers. The total transmission power is constrained at
is changed dynamically and follows a Poisson distribution. BSs are in charge of subcarrier scheduling and resource allocation. We assume a fixed modulation for all subcarriers. The total transmission power is constrained at  and will be optimally allocated to each subcarrier.
and will be optimally allocated to each subcarrier.
BS establishes a queue for each user. Packets are assumed to have equal length of  bits each. Head of line (HOL) packets of queues are scheduled on different subcarriers in different OFDM symbols based on transmission priorities obtained in Section 3. The transmission process for each user can be modelled as an M/G/1 queue. Define the average system time of user
bits each. Head of line (HOL) packets of queues are scheduled on different subcarriers in different OFDM symbols based on transmission priorities obtained in Section 3. The transmission process for each user can be modelled as an M/G/1 queue. Define the average system time of user  as
as  ; the delay requirement of real-time user
; the delay requirement of real-time user  can be formulated as
can be formulated as

where  is the delay bound of user
is the delay bound of user  .
.
Denote the channel gain obtained by user  on subcarrier
on subcarrier  by
by  and the number of bits supported in a subcarrier by
and the number of bits supported in a subcarrier by  . Define
. Define  to be an allocation indicator:
to be an allocation indicator:

Our objective is to maximize the total system throughput, subject to the constraints on the total transmission power, user SNR requirements, and delay constraints. The optimization problem can be expressed as follows:

subject to

where  represents the SNR requirement of user
represents the SNR requirement of user  . C1 states that the total subcarriers allocated to all users are less than or equal to
. C1 states that the total subcarriers allocated to all users are less than or equal to  ; C2 shows that the total transmission power should be less than or equal to the system power limit, while satisfying all users' SNR requirements; C3 means that no more than one user transmits in the same subcarrier; C4 is the average delay requirement of each user.
; C2 shows that the total transmission power should be less than or equal to the system power limit, while satisfying all users' SNR requirements; C3 means that no more than one user transmits in the same subcarrier; C4 is the average delay requirement of each user.
The solution of the above optimization problem (3) is not explicit due to the fact that C4 is not directly related to  . Thus in the following section, we will establish the relationship between them and give the suboptimal subcarrier allocation solution
. Thus in the following section, we will establish the relationship between them and give the suboptimal subcarrier allocation solution  for each symbol with lower computational complexity.
for each symbol with lower computational complexity.
3. Cross-Layer Algorithm Description
Based on queuing theory, the MAC-layer scheduling scheme is developed to calculate the users' transmission priorities and their corresponding specific bandwidth requirements in terms of the number of subcarriers. With the channel state information, users' SNR requirements and the system power constraints, the PHY-layer resource allocation scheme can deduce the maximum attainable throughput for each supported user. In addition, the MAC-layer access control and removal scheme will be triggered to adjust the number of users being served and provide the QoS guarantee for the active users in the system.
3.1. MAC-Layer Scheduling Scheme
In our system, we assume that each user has one type of real-time traffic. The packet arrivals of user  follow an independent Poisson process with rate
follow an independent Poisson process with rate  , and each user has a delay upper bound
, and each user has a delay upper bound  . Furthermore, we assume that users have infinite buffers, and the same class users have the same
. Furthermore, we assume that users have infinite buffers, and the same class users have the same  settings. Since the transmission process for each user can be modelled as an M/G/1 queue, the delay constraint on system time
settings. Since the transmission process for each user can be modelled as an M/G/1 queue, the delay constraint on system time  is given by [11]
is given by [11]

where  is the average service time and
is the average service time and  . Since
. Since  , a necessary condition for the delay requirement on system time in (13) is
, a necessary condition for the delay requirement on system time in (13) is

By solving the above inequality, we can easily obtain the lower bound of the average transmission rate for user  . Since
. Since  is known by the supported modulation, we further scale the average transmission rate in terms of subcarriers, represented by
is known by the supported modulation, we further scale the average transmission rate in terms of subcarriers, represented by  . Given the per-link
. Given the per-link  , the waiting time of the HOL packet
, the waiting time of the HOL packet  , and the delay constraint
, and the delay constraint  , an active user's transmission priority and exact bandwidth requirement in terms of the number of subcarriers per symbol are obtained by the following modified LWDF scheduling algorithm.
, an active user's transmission priority and exact bandwidth requirement in terms of the number of subcarriers per symbol are obtained by the following modified LWDF scheduling algorithm.
In our algorithm, the system time is scaled in terms of OFDM symbol time. The remaining time to the deadline of the HOL packet at queue  is
is

where  is the OFDM symbol time. The smaller the value of
is the OFDM symbol time. The smaller the value of  is, the more urgently user
is, the more urgently user  needs to transmit the corresponding packet. In addition, if
needs to transmit the corresponding packet. In addition, if  is the number of bits left in the HOL packet of user
is the number of bits left in the HOL packet of user  , then till the due time of the packet, the average required transmission rate in terms of the number of subcarriers in the following symbol time is given by
, then till the due time of the packet, the average required transmission rate in terms of the number of subcarriers in the following symbol time is given by

Compared with the deduced  , we define the rate proportional index as follows:
, we define the rate proportional index as follows:

 is defined to indicate the urgent state. Its value could be positive or negative. If its value is below zero, this means that the required number of subcarriers exceeds the average number, which indicates that congestion may happen. It is also easily observed that the smaller the value of
is defined to indicate the urgent state. Its value could be positive or negative. If its value is below zero, this means that the required number of subcarriers exceeds the average number, which indicates that congestion may happen. It is also easily observed that the smaller the value of  , the more urgent the transmission of the corresponding HOL packet. As in LWDF algorithm, we also consider the factors of the waiting time and transmission rate for each user. However, instead of considering the users' attainable bandwidths, we consider the users' required bandwidths under the delay bound constraints, which are more important for real-time services. Our scheduling is described as follows. Once the channel is idle, each user will calculate its transmission priority by
, the more urgent the transmission of the corresponding HOL packet. As in LWDF algorithm, we also consider the factors of the waiting time and transmission rate for each user. However, instead of considering the users' attainable bandwidths, we consider the users' required bandwidths under the delay bound constraints, which are more important for real-time services. Our scheduling is described as follows. Once the channel is idle, each user will calculate its transmission priority by

where  is a positive constant used to adjust the weight of
is a positive constant used to adjust the weight of  . The function
. The function  is defined as
is defined as

From the above analyses, the user with the smaller value given by (10) will enjoy a higher transmission priority. From the definition of  , if a user's required number of subcarriers exceeds the total number
, if a user's required number of subcarriers exceeds the total number  provided by a symbol, even if we allocate the whole symbol to this user, its delay requirement will not be met. Therefore, the HOL packet of this user will be dropped to save bandwidth for other users.
provided by a symbol, even if we allocate the whole symbol to this user, its delay requirement will not be met. Therefore, the HOL packet of this user will be dropped to save bandwidth for other users.
Up to now, our MAC-layer scheduling scheme gives the transmission priority list of the HOL packets according to (10) for the active users and their expected transmission rates in terms of the number of subcarriers in each symbol from (8). However these rates are only the users' expected rates. Considering the users' channel states, SNR requirements, and system power limit in the PHY layer, the real subcarrier allocation will be performed according to the following scheme.
3.2. PHY-Layer Resource Allocation Scheme
In the MAC layer, our algorithm has already considered the real-time traffic delay requirement and given the expected transmission rate in terms of the number of subcarriers and users' transmission priorities. In the PHY layer, with the different subcarriers' channel states, system SNR and power constraints, our PHY-layer scheme aims to optimize the initial allocation indicator  with the following constraint:
with the following constraint:

To solve this problem, a dynamic PHY-layer resource allocation scheme is proposed which is divided into the following steps.
-
(a)
Initial subcarrier allocation. With the total number of subcarrier limit
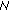 , we initially assign the users the required numbers of subcarriers according to their priorities till
, we initially assign the users the required numbers of subcarriers according to their priorities till 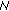 subcarriers are used up or all
subcarriers are used up or all 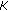 users are assigned.
users are assigned. -
(b)
Power minimization. Given a subcarrier allocation, the following modified Kuhn-Munkres algorithm is used to obtain an optimal allocation to minimize the system power under the users' SNR requirements. Denote the minimized power as
 .
. -
(c)
Power comparison. Compare
 with the system power limit
with the system power limit 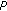 , and consider the following cases:
, and consider the following cases:-
(i)
if
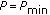 , then the power resource is fully utilized, and the current subcarrier allocation
, then the power resource is fully utilized, and the current subcarrier allocation 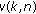 is the final solution;
is the final solution; -
(ii)
if
 , then the system power cannot support all currently assigned subcarriers. So our scheme will reduce the subcarrier allocation from the lowest priority user. Given
, then the system power cannot support all currently assigned subcarriers. So our scheme will reduce the subcarrier allocation from the lowest priority user. Given  requirement for user
requirement for user 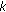 , among the assigned subcarriers for this user, the smaller the value of
, among the assigned subcarriers for this user, the smaller the value of  on subcarrier
on subcarrier  , the larger the power consumption on it. So the subcarrier reduction will be performed in ascending subcarrier gain order one by one. Then go to Step (b) in the next iteration, till the updated
, the larger the power consumption on it. So the subcarrier reduction will be performed in ascending subcarrier gain order one by one. Then go to Step (b) in the next iteration, till the updated  is less than
is less than  ;
; -
(iii)
if
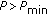 , more power resource can be utilized. Then our scheme considers the remaining subcarrier resource. We represent the total number of the assigned subcarriers as
, more power resource can be utilized. Then our scheme considers the remaining subcarrier resource. We represent the total number of the assigned subcarriers as  . If
. If 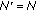 , the subcarriers are used up, and we maintain the current
, the subcarriers are used up, and we maintain the current  solution. If
solution. If  , the remaining subcarriers are assigned evenly to the current active users till the updated
, the remaining subcarriers are assigned evenly to the current active users till the updated  reaches
reaches 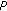 . If new users' access requirements are received, the access control scheme to be introduced in the next subsection will guide the assignment.
. If new users' access requirements are received, the access control scheme to be introduced in the next subsection will guide the assignment.
-
(i)
Modified Kuhn-Munkres Algorithm
In the following, we will firstly introduced the Kuhn-Munkres algorithm to find the perfect matching with the maximum sum of edge weights for a bipartite graph. Then a modified algorithm is described for OFDM power allocation. To minimize the system power, the modified algorithm is applied with negative weights.
A graph is denoted by  , where
, where  is the vertex set, and
is the vertex set, and  is the edge set of the graph. If
is the edge set of the graph. If  with
with  and each edge in
and each edge in  has one endpoint in
has one endpoint in  and the other in
and the other in  , the graph
, the graph  is a bipartite graph, which can also be denoted as
is a bipartite graph, which can also be denoted as  . The bipartite graph is very useful for some applications, such as an assignment problem which can be depicted as follows. Given a weighted complete bipartite graph
. The bipartite graph is very useful for some applications, such as an assignment problem which can be depicted as follows. Given a weighted complete bipartite graph  , where edge
, where edge  has weight
has weight  , find a matching
, find a matching  from
from  to
to  with maximum weight. In an application,
with maximum weight. In an application,  could be a set of workers,
could be a set of workers,  a set of jobs, and
a set of jobs, and  the earnings made by assigning worker
the earnings made by assigning worker  to job
to job  . The goal of the assignment problem is to find the optimal (best total earnings) matching.
. The goal of the assignment problem is to find the optimal (best total earnings) matching.
For a bipartite graph  , if the cardinalities of
, if the cardinalities of  and
and  , denoted as
, denoted as  and
and  , are equal, then this bipartite graph is symmetric. For single objective optimization, it has been proved that the Kuhn-Munkres algorithm can always find the maximum weight matching for a bipartite graph with
, are equal, then this bipartite graph is symmetric. For single objective optimization, it has been proved that the Kuhn-Munkres algorithm can always find the maximum weight matching for a bipartite graph with  computational complexity. The Kuhn-Munkres algorithm is based on the procedure of the Hungarian algorithm [9]. Matrix
computational complexity. The Kuhn-Munkres algorithm is based on the procedure of the Hungarian algorithm [9]. Matrix  has elements
has elements  , which represent the earnings of assigning worker
, which represent the earnings of assigning worker  to job
to job  as shown in Figure 2 (a).
as shown in Figure 2 (a).
Step 1.
Let  ,
,  be the bipartite sets. Initialize two labels
be the bipartite sets. Initialize two labels  and
and  by
by  ,
, 
 . In Figure 2 (b), the numbers written at the left and the top of the matrix express the values of
. In Figure 2 (b), the numbers written at the left and the top of the matrix express the values of  and
and  , respectively.
, respectively.
Step 2.
Obtain the excess matrix  by the following:
by the following:  . This is shown in Figure 2 (c).
. This is shown in Figure 2 (c).
Step 3.
Find the subgraph  that includes vertices
that includes vertices  and
and  satisfying
satisfying  and the corresponding edge
and the corresponding edge  . Then find the maximum matching
. Then find the maximum matching  of
of  by the Hungarian algorithm, and underline the entries in the weight matrix. (There are various ways to find the maximum matching. See, e.g, [12].) A maximum matching is a matching with the largest possible number of edges. In this example, the maximum matching is found to be
by the Hungarian algorithm, and underline the entries in the weight matrix. (There are various ways to find the maximum matching. See, e.g, [12].) A maximum matching is a matching with the largest possible number of edges. In this example, the maximum matching is found to be  ,
,  , and
, and  , as shown in Figure 2 (d). If
, as shown in Figure 2 (d). If  is a perfect matching, that is, the number of edges in a maximum matching is equal to the cardinality of worker set (
is a perfect matching, that is, the number of edges in a maximum matching is equal to the cardinality of worker set ( ), the optimal assignment is obtained. Otherwise, go to the next step.
), the optimal assignment is obtained. Otherwise, go to the next step.
Step 4.
Let  be a vertex cover of
be a vertex cover of  , and let
, and let  and
and  . The vertex cover
. The vertex cover  is a vertex set of
is a vertex set of  which contains at least one endpoint of each edge. In this example,
which contains at least one endpoint of each edge. In this example,  is chosen to be the nodes corresponding to Workers 1 and 3 and Job 4. So
is chosen to be the nodes corresponding to Workers 1 and 3 and Job 4. So  corresponds to Workers 1 and 3, and
corresponds to Workers 1 and 3, and  corresponds to Job 4. Now find
corresponds to Job 4. Now find  . For example, if
. For example, if  equals 1 in Figure 2, decrease
equals 1 in Figure 2, decrease  by
by  for the rows of
for the rows of  and increase
and increase  by
by  for the columns of
for the columns of  . Then go to Step 2.
. Then go to Step 2.
Steps 2 to 4 are repeated until the perfect matching  , that is, the optimal assignment, is obtained.
, that is, the optimal assignment, is obtained.
For a bipartite graph  , if the cardinalities of
, if the cardinalities of  and
and  , denoted as
, denoted as  and
and  , are not equal, then this bipartite graph is asymmetric. In our modified Kuhn-Munkres algorithm, we enhance an asymmetric graph to a symmetric one, and then solve the optimization problem as in the symmetric case. Firstly, suppose that the resource on both
, are not equal, then this bipartite graph is asymmetric. In our modified Kuhn-Munkres algorithm, we enhance an asymmetric graph to a symmetric one, and then solve the optimization problem as in the symmetric case. Firstly, suppose that the resource on both  and
and  cannot be reused, we append
cannot be reused, we append  all-zero rows or columns to the weight matrix to construct a square matrix, and then transform the problem to a symmetric bipartite matching, as shown in Figure 3.
all-zero rows or columns to the weight matrix to construct a square matrix, and then transform the problem to a symmetric bipartite matching, as shown in Figure 3.
Secondly, for some special cases in which the redundant resource may be reused, the modified Kuhn-Munkres algorithm reproduces the corresponding columns or rows till the matrix is transformed to a square matrix. If necessary, all-zero columns or rows will be added. If  and the elements in
and the elements in  is reusable, Figure 4 shows the case where the remaining elements in
is reusable, Figure 4 shows the case where the remaining elements in  may reuse the elements in
may reuse the elements in  with the same probability. If
with the same probability. If  , given the number of required elements in
, given the number of required elements in  by the elements in
by the elements in  , namely,
, namely,  , then the square matrix may be constructed by reproducing the rows in demand, as shown in Figure 5.
, then the square matrix may be constructed by reproducing the rows in demand, as shown in Figure 5.
In the downlink OFDM system model, as in previous work, channel state information (CSI) is assumed to be available at base stations (BSs). In a multiuser system with frequency-selective fading, each user may experience a different channel frequency response, which is related to its location. The total frequency bandwidth is divided into  orthogonal subchannels, and suppose there are currently
orthogonal subchannels, and suppose there are currently  active users in the system. Assume that
active users in the system. Assume that  is the subchannel set for user
is the subchannel set for user  ,
,  is the cardinality of set
is the cardinality of set  . The value of
. The value of  is initially obtained from the MAC layer scheduling scheme and dynamically changed by the PHY allocation scheme. Therefore, for user
is initially obtained from the MAC layer scheduling scheme and dynamically changed by the PHY allocation scheme. Therefore, for user  , the required transmission power in time slot
, the required transmission power in time slot  is given by
is given by

where  is the detected subchannel gain of user
is the detected subchannel gain of user  on subchannel
on subchannel  . Then the total system required power can be expressed as
. Then the total system required power can be expressed as

With the above problem formulation, the minimization of the system power  as required in the second step of the PHY-layer allocation scheme may be converted to a bipartite matching problem. The edge weight for user
as required in the second step of the PHY-layer allocation scheme may be converted to a bipartite matching problem. The edge weight for user  on subcarrier
on subcarrier  is
is  . Therefore, similar to the case illustrated in Figure 5, the modified Kuhn-Munkres algorithm may be applied to give an optimal solution to the minimization of the system power.
. Therefore, similar to the case illustrated in Figure 5, the modified Kuhn-Munkres algorithm may be applied to give an optimal solution to the minimization of the system power.
3.3. Access Control and Removal Scheme
In real networks, the number of active users changes dynamically. Without access control, the bandwidth may be inadequate. In addition, particularly for real-time traffic, without a removal scheme, not only may the QoS of the users newly granted access not be guaranteed but also the previously granted access users will suffer from QoS degradation. Therefore, the MAC-layer access control and removal schemes are introduced in our DSA-RT algorithm.
As analyzed in the previous subsection, a new user's QoS requirements should be considered when  and
and

As introduced in Section 3.1, the new user's QoS requirements can be evaluated by  . Access control will check if this requirement can be satisfied with the remaining power and subcarrier resources. If yes, the new user can be allocated subcarrier resources; otherwise, it continues to wait.
. Access control will check if this requirement can be satisfied with the remaining power and subcarrier resources. If yes, the new user can be allocated subcarrier resources; otherwise, it continues to wait.
Even with access control, real-time transmission systems may still encounter an overloaded situation due to the time-varying wireless channel and variable bit rates. As presented in [13], a useful removal scheme can effectively guarantee the QoS of the existing users and will not be adversely affected by the admission of new users. Our scheme assumes that the dropping rate of user  is sampled for each constant time interval
is sampled for each constant time interval  , and the last sample time is
, and the last sample time is  . So the dropping rate of user
. So the dropping rate of user  is defined by
is defined by

where  and
and  are the numbers of dropped packets and the total transmitted packets of user
are the numbers of dropped packets and the total transmitted packets of user  during time
during time  . Assume
. Assume  is the maximum dropping rate which user
is the maximum dropping rate which user  can tolerate. At each sample time or when the number of users in the system changes, our removal scheme will select the user to be removed by the following rule:
can tolerate. At each sample time or when the number of users in the system changes, our removal scheme will select the user to be removed by the following rule:

where the selected set consists of the users whose  values violate their corresponding dropping rate bound
values violate their corresponding dropping rate bound  . If the traffic is bursty, we may change
. If the traffic is bursty, we may change  to adjust the dropping rate more frequently.
to adjust the dropping rate more frequently.
3.4. Implementation of DSA-RT
Thanks to the cooperation of the above schemes, for each OFDM symbol, our algorithm DSA-RT can give the suboptimal solution  of the optimization problem addressed in Section 2. The computational delay is not expected to be a problem. The number of operations required by the algorithm is approximately
of the optimization problem addressed in Section 2. The computational delay is not expected to be a problem. The number of operations required by the algorithm is approximately  , which translates to a computational delay of a small fraction of a symbol time with the support of current chips. In addition, if we want to lower the computational delay, multiple symbols can be combined as one scheduling unit, but this will affect the scheduling efficiency. It is a tradeoff. The flow chart of the implementation of our algorithm is shown in Figure 6.
, which translates to a computational delay of a small fraction of a symbol time with the support of current chips. In addition, if we want to lower the computational delay, multiple symbols can be combined as one scheduling unit, but this will affect the scheduling efficiency. It is a tradeoff. The flow chart of the implementation of our algorithm is shown in Figure 6.
4. Simulation Results
In this section, the performance of the proposed DSA-RT scheduling algorithm is investigated and compared with CSD-RR, FEDD, and M-LWDF [2–4]. We consider QPSK modulation in multiuser OFDM downlink systems. However, other modulations are supported with different SNR constraints. The IFFT size is 128, and the OFDM symbol duration is equal to 200 microseconds [14]. We consider the quasistatic flat fading channel with multipath [15]. Assume that the users arrive as a Poisson process with parameter  , and their active times in the system follow the exponential distribution with mean 10 seconds. In this section, we assume that all users have the same type of real-time traffic. During each user's active time, the packet arrivals follow the Poisson distribution. The packets have a fixed length of 1000 bytes, and the mean traffic rate is 1 Mbps. The delay bound is set to be 50 milliseconds. In simulations, we consider one type of real-time traffic, so we fixed the packet length. However, if multiple types of real-time traffics are supported, a variable length is acceptable in our algorithm. In our simulations, we vary the user arrival rates
, and their active times in the system follow the exponential distribution with mean 10 seconds. In this section, we assume that all users have the same type of real-time traffic. During each user's active time, the packet arrivals follow the Poisson distribution. The packets have a fixed length of 1000 bytes, and the mean traffic rate is 1 Mbps. The delay bound is set to be 50 milliseconds. In simulations, we consider one type of real-time traffic, so we fixed the packet length. However, if multiple types of real-time traffics are supported, a variable length is acceptable in our algorithm. In our simulations, we vary the user arrival rates  from 0.01 to 0.1 and compare the delay and dropping rate performance of some packet scheduling algorithms and our proposed DSA-RT algorithm. All simulations are in Matlab 7.3. The simulation time of each experiment is 100 seconds and we repeat it 100 times.
from 0.01 to 0.1 and compare the delay and dropping rate performance of some packet scheduling algorithms and our proposed DSA-RT algorithm. All simulations are in Matlab 7.3. The simulation time of each experiment is 100 seconds and we repeat it 100 times.
The average delay is the mean of the delay of all packets not dropped. For each successfully delivered packet, the delay is calculated as the difference between the departure and arrival times. In DSA-RT, packets which have been dropped will not re-enter the system. Figure 7 shows the delay comparisons of DAS-RT and three other packet scheduling algorithms. It is obvious that our algorithm distinctly improves the delay performance, particularly when the traffic density is high. Accordingly, as shown in Figure 8, the dropping rates of our algorithm at any user arrival rate are also much lower than the other three algorithms. DSA-RT is developed to schedule at the subcarrier level and tries to provide delay guarantees for the real-time traffics. Therefore, it has the best delay and dropping rate performance. Based on the consideration of channel state, CSD-RR has better performance than M-LWDF and FEDD. By considering the system capacity and queuing, the throughput performance of M-LWDF is optimal, but the delay performance still needs to be improved. FEDD gives the packet with the earliest deadline of the highest transmission priority. However, with the bandwidth and channel state constraints, the transmission still has a high probability to fail within its deadline. Therefore, it has the poorest performance.
5. Conclusion
In this paper, DSA-RT aims to satisfy the packet delay requirements of real-time traffics in multiuser OFDM system, while maximizing the system bandwidth efficiency. This algorithm consists of two cooperative components. At the MAC layer, based on queuing theory and the modified LWDF algorithm, active users' expected transmission rates in terms of the number of subcarreirs per symbol and their corresponding transmission priorities are deduced. With different subcarrier states, based on our modified Kuhn-Munkres algorithm, a PHY-layer resource allocation scheme is developed to satisfy the users' requirements under the system SNR and power constraints. When considering a system where the number of active users changes dynamically, the access control and removal scheme can fully utilize the bandwidth resource and guarantee the QoS of the existing users in the system. Finally, compared with other widely used scheduling algorithms, simulation results show that our proposed algorithm significantly improves the system performance for real-time users in multiuser OFDM systems.
References
Lawrey E: Multiuser OFDM. Proceedings of the International Symposium on Signal Processing and Its Applications (ISSPA '99), August 1999, Brisbane, Australia 761-764.
Bhagwat P, Krishna A, Tripathi S: Enhancing throughput over wireless LAN's using channel state dependent packet scheduling. Proceedings of 17th Annual Joint Conference of the IEEE Computer and Communications Societie (INFOCOM '98), March 1998, San Francisco, Calif, USA 1103-1111.
Shakkottai S, Srikant R: Scheduling real-time traffic with deadlines over a wireless channel. Wireless Networks 2002, 8(1):13-26. 10.1023/A:1012763307361
Andrews M, Kumaran K, Ramanan K, Stolyar A, Whiting P, Vijayakumar R: Providing quality of service over a shared wireless link. IEEE Communications Magazine 2001, 39(2):150-153. 10.1109/35.900644
Zhang YJ, Liew SC: Link-adaptive largest-weighted-throughput packet scheduling for real-time traffics in wireless OFDM networks. Proceedings of IEEE Global Telecommunications Conference (GLOBECOM '05), November-December 2005, St. Louis, Mo, USA 5: 2490-2494.
Cheong YYW, Tsui CY, Cheng RS, Letaief KB: A realtime sub-carrier allocation scheme for multiple access downlink OFDM transmission. Proceedings of the 49th IEEE Vehicular Technology Conference (VTC '99), September 1999, Amsterdam, The Netherlands 2: 1124-1128.
Diao Z, Shen D, Li VOK: CPLD-PGPS scheduler in wireless OFDM systems. IEEE Transactions on Wireless Communications 2006, 5(10):2923-2931.
Munkres J: Algorithms for the assignment and transportation problems. Journal of the Society for Industrial and Applied Mathematics 1957, 5(1):32-38. 10.1137/0105003
Kuhn HW: The Hungarian method for the assignment problem. Naval Research Logistic Quarterly 1955, 2: 83-97. 10.1002/nav.3800020109
Zhu J, Bing B, Li Y, Xu J: An adaptive subchannel allocation algorithm for OFDM-based wireless home networks. Proceedings of the 1st IEEE Consumer Communications and Networking Conference, (CCNC '04), January 2004, Las Vegas, Nev, USA 352-356.
Bertsekas D, Gallager R: Data Networks. 2nd edition. Prentice-Hall, Englewood Cliffs, NJ, USA; 1992.
West DB: Introduction to Graph Theory. Prentice-Hall, Englewood Cliffs, NJ, USA; 2001.
Kwon E, Kim S-G, Lee J: Overload control with removal algorithm for real-time flows in wireless networks. Proceedings of the IEEE 63rd Vehicular Technology Conference (VTC '06), May 2006, Melbourne, Australia 3: 1127-1131.
Cai J, Shen X, Mark JW: Downlink resource management for packet transmission in OFDM wireless communication systems. Proceedings of IEEE Global Telecommunications Conference (GLOBECOM '03), December 2003, San Francisco, Calif, USA 6: 2999-3003.
Xiao C, Zheng YR, Beaulieu NC: Second-order statistical properties of the WSS Jakes' fading channel simulator. IEEE Transactions on Communications 2002, 50(6):888-891. 10.1109/TCOMM.2002.1010606
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Sun, F., You, M. & Li, V.O.K. Dynamic Subcarrier Allocation for Real-Time Traffic over Multiuser OFDM Systems. J Wireless Com Network 2009, 298451 (2009). https://doi.org/10.1155/2009/298451
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/298451

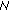 , we initially assign the users the required numbers of subcarriers according to their priorities till
, we initially assign the users the required numbers of subcarriers according to their priorities till 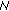 subcarriers are used up or all
subcarriers are used up or all 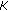 users are assigned.
users are assigned. .
. with the system power limit
with the system power limit 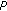 , and consider the following cases:
, and consider the following cases: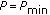 , then the power resource is fully utilized, and the current subcarrier allocation
, then the power resource is fully utilized, and the current subcarrier allocation 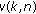 is the final solution;
is the final solution; , then the system power cannot support all currently assigned subcarriers. So our scheme will reduce the subcarrier allocation from the lowest priority user. Given
, then the system power cannot support all currently assigned subcarriers. So our scheme will reduce the subcarrier allocation from the lowest priority user. Given  requirement for user
requirement for user 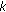 , among the assigned subcarriers for this user, the smaller the value of
, among the assigned subcarriers for this user, the smaller the value of  on subcarrier
on subcarrier  , the larger the power consumption on it. So the subcarrier reduction will be performed in ascending subcarrier gain order one by one. Then go to Step (b) in the next iteration, till the updated
, the larger the power consumption on it. So the subcarrier reduction will be performed in ascending subcarrier gain order one by one. Then go to Step (b) in the next iteration, till the updated  is less than
is less than  ;
;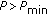 , more power resource can be utilized. Then our scheme considers the remaining subcarrier resource. We represent the total number of the assigned subcarriers as
, more power resource can be utilized. Then our scheme considers the remaining subcarrier resource. We represent the total number of the assigned subcarriers as  . If
. If 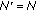 , the subcarriers are used up, and we maintain the current
, the subcarriers are used up, and we maintain the current  solution. If
solution. If  , the remaining subcarriers are assigned evenly to the current active users till the updated
, the remaining subcarriers are assigned evenly to the current active users till the updated  reaches
reaches 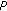 . If new users' access requirements are received, the access control scheme to be introduced in the next subsection will guide the assignment.
. If new users' access requirements are received, the access control scheme to be introduced in the next subsection will guide the assignment.


 .
.

 .
.


