- Research Article
- Open access
- Published:
Two-Hop Secure Communication Using an Untrusted Relay
EURASIP Journal on Wireless Communications and Networking volume 2009, Article number: 305146 (2009)
Abstract
We consider a source-destination pair that can only communicate through an untrusted intermediate relay node. The intermediate node is willing to employ a designated relaying scheme to facilitate reliable communication between the source and the destination. Yet, the information it relays needs to be kept secret from it. In this two-hop communication scenario, where the use of the untrusted relay node is essential, we find that a positive secrecy rate is achievable. The center piece of the achievability scheme is the help provided by either the destination node with transmission capability, or an external "good samaritan" node. In either case, the helper performs cooperative jamming that confuses the eavesdropping relay and disables it from being able to decipher what it is relaying. We next derive an upper bound on the secrecy rate for this system. We observe that the gap between the upper bound and the achievable rate vanishes as the power of the relay node goes to infinity. Overall, the paper presents a case for intentional interference, that is, cooperative jamming, as an enabler for secure communication.
1. Introduction
Information theoretic security was proposed by Shannon [1]. The idea of measuring secrecy using mutual information lends itself naturally to the investigation of how the channel can influence secrecy and further to the characterization of the fundamental limit of secure transmission rate. Wyner, in [2], defined the wiretap channel, and showed that secure communication from a transmitter to a "legitimate" receiver is possible when the signal received by the wiretapper (eavesdropper) is degraded with respect to that received by the legitimate receiver. Reference [3] identified the secrecy capacity of the general discrete memoryless wiretap channel. The secrecy capacity of the Gaussian wiretap channel is found in [4].
Recent progress in this area has extended classical information theory channel models to include secrecy constraints. Examples are the multiple access channel, the broadcast channel, the two-way channel, the three-node relay channel and the two-user interference channel [5–13]. These studies are beginning to lead to insights for designing secure wireless communication systems from the physical layer up. Prominent such examples include using multiple antennas to steer the transmitted signal away from an eavesdropper [14–16], transmitting with the intention of jamming the eavesdropper [8, 10, 17], and taking advantage of variations in channel state to provide secrecy [18–20].
The focus of this work is on a class of relay networks where the source and the destination have no direct link and thus can only communicate utilizing an intermediate relay node. This models the practical scenario where direct communication between the source and the destination is too "expensive" in terms of power consumption: direct communication may be used to send some very low rate control packages, for example to initialize the communication, but it is infeasible to sustain a nontrivial reliable communication rate due to the power constraint.
In such a scenario, the source-destination pair needs the relay to communicate. On the other hand, more often than not, this relay node may be "untrusted" [11]. This does not mean the relay node is malicious, in fact quite the opposite, it may be part of the network and we will assume that it is willing to faithfully carry out the designated relaying scheme. The relay simply has a lower security clearance in the network and hence is not trusted with the confidential message it is relaying. Equivalently, we can assume the confidential message is one used for identification of the source node for authentication, which should never be revealed to a relay node in order not to be vulnerable to an impersonation attack. In all these cases, we must assume there is an eavesdropper colocated at the relay node when designing the system.
The "untrusted" relay model, or the eavesdropper being colocated with the relay node, was first studied in [9] for the general relay channel, with a rather pessimistic outlook, finding that for the degraded or the reversely degraded relay channel the relay node should not be deployed. More optimistic results for the relay channel with a colocated eavesdropper have been identified recently in [11, 21, 22]. Specifically, it has been shown that the cooperation from the relay may, in fact, be essential to achieving nonzero secrecy rate [11, 21]. The model is later extended to the more symmetric case in [23, 24] where the relay also has a confidential message of its own, which must be kept secret from the destination.
All these models assume that a direct link between the source and the destination is present including our previous work [11]. In contrast, when there is no direct link, it is impossible for this network to convey a confidential message from the source to the destination while keeping it secret from the relay [9]. This is because the destination can only receive signals from the relay resulting in a physically degraded relay channel [25]. Therefore, the relay knows everything the destination knows regarding the confidential message, and the secrecy capacity is zero.
The differentiating feature of the model studied in this work from those described above including [11] is that the destination has transmission capability. This opens the possibility of the destination node to actively participate in ensuring the secrecy of the information it wants to obtain. In an effort to address a practical two-hop communication scenario, we shall consider each node to be half-duplex, which leads to a two-phase communication model. In addition, feedback to the source is not considered in the channel model. Interestingly, in this model, the transmission capability of the destination proves to be the enabler of secure communication. By recruiting the help of the destination to do "cooperative jamming", positive secrecy rate can be achieved that would not have been possible otherwise. We also remark that in case the transmission by the destination is not possible or desired, the help from an external cooperative jammer will do as well.
The idea of using a helpful jammer goes back to [17, 26, 27] and has since been used in many different models. Besides the multiple access, two-way [8] and relay wiretap channels [10], other recent results that use "cooperative jamming" as the part of the achievability scheme, include [28–30]. In [28], a separate jammer is added to the classical Gaussian wiretap channel model. The jamming signal is revealed to the legitimate receiver via a wired link so that an advantage over the eavesdropper is gained. Reference [30] does not assume the wired connection, and employs a scheme tantamount to the two user multiple access channel with an external eavesdropper where one of the users perform cooperative jamming. Reference [29] considers the case where both the eavesdropper and the legitimate receiver observes a modulus  channel and the destination carries out the jamming. We note that all these works deal with an external eavesdropper, in contrast to the focus of this work, which is an untrusted (but legitimate) node in the network.
channel and the destination carries out the jamming. We note that all these works deal with an external eavesdropper, in contrast to the focus of this work, which is an untrusted (but legitimate) node in the network.
In general, the optimality of recruiting a helpful jammer remains open as the converse results are limited. For the Gaussian case, the main difficulty is to find a upper bound for which the optimal input distribution can be found and evaluated. Doing so usually involves the introduction of genie information, as in the converse for the Gaussian wiretap channel [4], MIMO wiretap channel [14] and MAC wiretap channel [31]. The proofs then typically invoke the entropy power inequality, as in [4], or the generalized entropy power inequality, as in [32].
In this work, we derive a computable upper bound for the model in consideration by first introducing a second eavesdropper, an approach first used for a three-node relay channel in [11]. Next, after several steps of genie arguments, the channel is transformed into a wiretap channel with a helpful jammer, whose outer bound is then evaluated. The resulting bound is nontrivial in the sense that it is strictly tighter than the bound for the same channel without secrecy constraints. We also prove that it is tighter than an upper bound derived using the generalized entropy power inequality following a similar approach to [32], when the maximum sum received SNR at the relay is greater than  dB. We show that the gap between the bound and the achievable rates converges to zero when the power of the relay goes to infinity.
dB. We show that the gap between the bound and the achievable rates converges to zero when the power of the relay goes to infinity.
The paper is organized as follows. Section 2 presents the channel model and the two-phase protocol that utilizes cooperative jamming. In Section 3, we derive the achievable rates. Section 4 presents our upper bound and compares with other known upper bounds. Section 5 presents the numerical results. Finally, Section 6 presents the conclusion.
The following notation is used throughout this work: We use  to denote the entropy,
to denote the entropy,  to denote the differential entropy, and
to denote the differential entropy, and  to denote any variable that goes to 0 when
to denote any variable that goes to 0 when  goes to
goes to  . We define
. We define  .
.
2. Channel Model
The system model is shown in Figure 1. We assume all nodes are half-duplex and the communication alternates between two phases, called phase one and phase two respectively. During phase one, shown with solid lines in Figure 1, the source transmits signal  . At the same time, the destination node transmits jamming signal
. At the same time, the destination node transmits jamming signal  in order to confuse the relay node. The signal received by the relay in phase one,
in order to confuse the relay node. The signal received by the relay in phase one,  , is given by
, is given by

where  is a zero mean Gaussian random variable with unit variance. In an effort to reflect on the design of a practical system, we assume that the computation of
is a zero mean Gaussian random variable with unit variance. In an effort to reflect on the design of a practical system, we assume that the computation of  ,
,  does not rely on the signals received by node
does not rely on the signals received by node  in the past.
in the past.
In phase two, shown with dashed lines, the relay transmits signal  , which is computed from the local randomness at the relay, the signal transmitted and received by the relay in the past.
, which is computed from the local randomness at the relay, the signal transmitted and received by the relay in the past.
The signal received by the destination in phase two is denoted by  , which is given below:
, which is given below:

where  is a zero mean Gaussian random variable with unit variance.
is a zero mean Gaussian random variable with unit variance.
The channel alternates between these two phases according to a random or deterministic schedule, which is generated by a global controller independently from the signals associated with the channel model. Hence here the term "schedule" is simply a finite number of channel uses which are either marked as phase one or phase two. We use  to denote the number of channel uses marked as phase one, and
to denote the number of channel uses marked as phase one, and  to denote the number of channel uses marked as phase two. It should be noted that in general the
to denote the number of channel uses marked as phase two. It should be noted that in general the  channel uses of phase one are not consecutive. Neither are the
channel uses of phase one are not consecutive. Neither are the  channel uses of phase two. We assume the schedule is stable, in the sense that the following limit exists:
channel uses of phase two. We assume the schedule is stable, in the sense that the following limit exists:

For a given  , we use
, we use  to denote a sequence of schedules with increasing number of channel uses
to denote a sequence of schedules with increasing number of channel uses  such that (3) holds. According to this definition,
such that (3) holds. According to this definition,  becomes the limit of the time sharing factor of phase one in the schedule
becomes the limit of the time sharing factor of phase one in the schedule  as
as  .
.
When transmitting signals, the source, the destination, and the relay must satisfy certain power constraints. The average power constraints for the source, the jammer and the relay can be expressed as follows:


where

is the total number of channel uses.
For the purpose of completeness, we also introduce the notation  to denote the average power of node
to denote the average power of node  during phase one. Since node
during phase one. Since node  and
and  are only transmitting during phase one,
are only transmitting during phase one,  and
and  are related as
are related as

Similarly, we use  to denote the average power of the relay node during phase two. Since the relay node only transmits during the second phase,
to denote the average power of the relay node during phase two. Since the relay node only transmits during the second phase,  is related to
is related to  as follows:
as follows:

After a number of phases, the destination node (node  ) decodes a message
) decodes a message  from the signals it transmitted during the periods of phase one and the signals it received during the periods of phase two. For reliable communication,
from the signals it transmitted during the periods of phase one and the signals it received during the periods of phase two. For reliable communication,  should equal the message
should equal the message  from the source node with high probability. Hence we have the following requirement:
from the source node with high probability. Hence we have the following requirement:

The message  must also be kept secret from the eavesdropper at the relay node, who can infer the value of
must also be kept secret from the eavesdropper at the relay node, who can infer the value of  based on the following knowledges available to it.
based on the following knowledges available to it.
-
(1)
The local randomness at the relay, denoted by
 .
. -
(2)
The
 signals the relay transmitted during the periods of phase one, denoted by
signals the relay transmitted during the periods of phase one, denoted by  .
. -
(3)
The
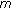 signals the relay transmitted during the periods of phase two, denoted by
signals the relay transmitted during the periods of phase two, denoted by  .
.
The information on  that the eavesdropper can extract from these knowledges should be limited. Hence we have the following secrecy constraint:
that the eavesdropper can extract from these knowledges should be limited. Hence we have the following secrecy constraint:

Since  is a Markov chain, we have
is a Markov chain, we have

Therefore, the secrecy constraint can be expressed as

For a given  , and sequences of schedule
, and sequences of schedule  , the secrecy rate
, the secrecy rate  is defined as
is defined as

such that (9) and (12) are fulfilled. When deriving achievable rate, we will focus on a specific sequence of schedules  , and maximize the secrecy rate over
, and maximize the secrecy rate over  . When deriving the upper bound, we will consider all possible sequences of
. When deriving the upper bound, we will consider all possible sequences of  .
.
Remark 1.
Since the signals transmitted by node  and
and  do not depend on the signals they received in the past,
do not depend on the signals they received in the past,  is a Markov chain. Therefore,
is a Markov chain. Therefore,

Hence, the following secrecy constraint can be used instead:

Remark 2.
We observe that in the system model shown in Figure 1, the destination, as the sender of the jamming signal during the periods of phase one, has perfect knowledge of this signal. This can be viewed as a special case of the model shown in Figure 2, where the destination only has a noisy copy of the jamming signal  . If the jamming signal is corrupted by a noise sequence
. If the jamming signal is corrupted by a noise sequence  that is independent of the noise sequences at the other receivers, then the secrecy capacity of the model in Figure 2 can not be larger than the secrecy capacity of the model in Figure 1. This is because giving this noise sequence to the destination as genie information would simply reveal the jamming signal
that is independent of the noise sequences at the other receivers, then the secrecy capacity of the model in Figure 2 can not be larger than the secrecy capacity of the model in Figure 1. This is because giving this noise sequence to the destination as genie information would simply reveal the jamming signal  to it. Therefore, any upper bound we derive for Figure 1 is also an upper bound for Figure 2.
to it. Therefore, any upper bound we derive for Figure 1 is also an upper bound for Figure 2.
Remark 3.
An apparent vulnerability of the described two phase protocol is that the destination may not be aware that the source has initiated its transmission. In this case, without the protection of the jamming signal from the destination, the message from the source would be revealed to the relay node and hence compromised. To prevent this from happening, proper initialization of the protocol is necessary.
3. Achievable Rate
In this section, we derive the achievable secrecy rate with the following sequence of deterministic periodic schedules.
The channel alternates between  channel uses for phase one and
channel uses for phase one and  channel uses for phase two, where
channel uses for phase two, where  and
and  are two positive integers. The alternation takes
are two positive integers. The alternation takes  times. Hence
times. Hence  and
and  . For a given
. For a given  , the sequence of schedules is obtained by letting
, the sequence of schedules is obtained by letting  and
and

With this sequence of schedules, we have the following theorem.
Theorem 1.
The following secrecy rate is achievable for the model in Figure 1:

where  is the variance of the Gaussian quantization noise determined by:
is the variance of the Gaussian quantization noise determined by:

where  is defined in (7),
is defined in (7),  is defined in (8).
is defined in (8).
Proof.
The proof is given in the appendix.
Remark 4.
It can be seen from (17) that, for any fixed time sharing factor  the relay should always transmit at maximum power
the relay should always transmit at maximum power  . However, the optimal transmission power of the source may be less than
. However, the optimal transmission power of the source may be less than  . This can be seen as follows: For a given jamming power
. This can be seen as follows: For a given jamming power  , the achievable rate is not a monotonically increasing function of
, the achievable rate is not a monotonically increasing function of  . This is because, if
. This is because, if  or
or  ,
,  , indicating that even if the source power budget is
, indicating that even if the source power budget is  , the optimal transmission power is actually finite. Let this value be
, the optimal transmission power is actually finite. Let this value be  .
.  may or may not fall into the interval
may or may not fall into the interval  , which is the range of power consumption allowed for phase one. If it does, then the source should transmit with power
, which is the range of power consumption allowed for phase one. If it does, then the source should transmit with power  rather than
rather than  . If not, then the corresponding optimal value needs to be determined.
. If not, then the corresponding optimal value needs to be determined.
Remark 5.
If the power constraint of the relay  , then
, then  ,
,  . The achievable rate converges to
. The achievable rate converges to

4. Upper Bound
In this section, we derive an upper bound for the secrecy rate.
We first need to determine the optimal schedule. It turns out that it is easy to find: We simply let the first  channel uses be phase one, and the remaining
channel uses be phase one, and the remaining  channel uses be phase two. The optimality of this schedule can be proved as follows.
channel uses be phase two. The optimality of this schedule can be proved as follows.
Suppose a different schedule is used. Since the signals received in the past are not used for encoding purposes at node  and
and  , we can always move the channel uses of phase one to the front without affecting the signals transmitted by these two nodes. On the other hand, we notice that the relay can only use signals received in the past to compute its transmission signals. However, during phase one, the relay only receives signals. Since moving phase one ahead only means the relay could receive signals sooner, doing so will not limit the capability of the relay to calculate its transmitted signals. Consequently, we observe that no matter what schedule is used to achieve a secrecy rate, we can always modify this schedule such that all channel uses of phase one are ahead of those of phase two and still achieve the same secrecy rate. Hence in the following we only consider the optimal schedule.
, we can always move the channel uses of phase one to the front without affecting the signals transmitted by these two nodes. On the other hand, we notice that the relay can only use signals received in the past to compute its transmission signals. However, during phase one, the relay only receives signals. Since moving phase one ahead only means the relay could receive signals sooner, doing so will not limit the capability of the relay to calculate its transmitted signals. Consequently, we observe that no matter what schedule is used to achieve a secrecy rate, we can always modify this schedule such that all channel uses of phase one are ahead of those of phase two and still achieve the same secrecy rate. Hence in the following we only consider the optimal schedule.
We also observe we can transform the channel into the one shown in Figure 3. The jammer and the receiver are now drawn separately, since the jammer does not use the signal received in the past to compute the jamming signal. Note that Figure 3 is similar to Figure 12 used in the achievability proof except that the dimension of the signals is changed from  to
to  .
.
We next leverage a technique first used in [11, 22] to derive the upper bound. Specifically, the upper bound is obtained via the following transformations.
( ) First, we add a second eavesdropper to the channel, as shown by Figure 4. Its received signal is denoted by
) First, we add a second eavesdropper to the channel, as shown by Figure 4. Its received signal is denoted by  and over
and over  channel uses
channel uses  is given by
is given by

Here  is a Gaussian noise with the same distribution as
is a Gaussian noise with the same distribution as  .
.  can be arbitrarily correlated with
can be arbitrarily correlated with  . Since
. Since

we have

Therefore,

From (15), this means

Hence the message  is kept secret from the second eavesdropper. This means, for a given coding scheme that achieves secrecy rate in Figure 3, the same secrecy rate is achievable with the introduction of this additional eavesdropper.
is kept secret from the second eavesdropper. This means, for a given coding scheme that achieves secrecy rate in Figure 3, the same secrecy rate is achievable with the introduction of this additional eavesdropper.
( ) Next, we remove the first eavesdropper at the relay. Doing so will not decrease secrecy rate either, since we have one less secrecy constraint.
) Next, we remove the first eavesdropper at the relay. Doing so will not decrease secrecy rate either, since we have one less secrecy constraint.
From (24), the secrecy rate can be upper bounded via  . To do that, we provide the signal
. To do that, we provide the signal  to the destination by a genie. Similarly, the signal
to the destination by a genie. Similarly, the signal  is revealed to both the relay and the destination.
is revealed to both the relay and the destination.  is then bounded by
is then bounded by






The genie information  causes the signal
causes the signal  to be useless to the relay, as shown by (25)-(26). Equation (28) is due to the fact that once the signal received by the relay
to be useless to the relay, as shown by (25)-(26). Equation (28) is due to the fact that once the signal received by the relay  is given, the signal transmitted by the relay
is given, the signal transmitted by the relay  , which is computed from
, which is computed from  , is independent from the jamming signal
, is independent from the jamming signal  and the confidential message
and the confidential message  . Finally, revealing the genie information
. Finally, revealing the genie information  to the relay and the destination essentially removes the influence of the jamming signal from the relay link, as shown by (28)–(30). These are essentially a consequence of the link noises being independent. The resulting channel is equivalent to the one shown in Figure 5, and can be viewed as a special case of the channel in [8, 33]. Similar techniques to those in [31, 33] can be used here to bound the secrecy rate. Let
to the relay and the destination essentially removes the influence of the jamming signal from the relay link, as shown by (28)–(30). These are essentially a consequence of the link noises being independent. The resulting channel is equivalent to the one shown in Figure 5, and can be viewed as a special case of the channel in [8, 33]. Similar techniques to those in [31, 33] can be used here to bound the secrecy rate. Let  . Then (30) becomes
. Then (30) becomes







Here (34) follows from the fact that  determines
determines  . The first term in (37) is maximized when
. The first term in (37) is maximized when  and
and  are i.i.d. Gaussian sequences [14]. Let the variance of each component of
are i.i.d. Gaussian sequences [14]. Let the variance of each component of  be
be  ,
,  . Let
. Let  be the correlation factor between
be the correlation factor between  and
and  . Then (37) is equal to
. Then (37) is equal to

It can be verified that, for any fixed  , equation (37) is an increasing function of
, equation (37) is an increasing function of  and
and  . Therefore, the upper bound is maximized with maximum average power. Equation (38) can then be tightened by minimizing it over
. Therefore, the upper bound is maximized with maximum average power. Equation (38) can then be tightened by minimizing it over  . The optimal
. The optimal  is given below:
is given below:

where

As a result, we have the following theorem.
Theorem 2.
The secrecy rate of the channel in Figure 12 is upper bounded by

where  is given by (39).
is given by (39).  ,
,  , and
, and  are the average power constraints of node
are the average power constraints of node  and the relay for the time sharing factor
and the relay for the time sharing factor  .
.
Remark 6.
If we further fix  and let
and let  , then
, then  .
.  converges to
converges to  given by
given by

The difference of the upper bound and the achievable rate converges to

We observe that the difference is only a function of  . By comparison, the gap between the achievable rate and the trivial upper bound
. By comparison, the gap between the achievable rate and the trivial upper bound  is
is  , which is unbounded.
, which is unbounded.
Remark 7.
If we instead fix  , and let
, and let  , then
, then  . The achievable rate converges to (19). In this case, if we further let
. The achievable rate converges to (19). In this case, if we further let  , the upper bound given by (41) converges to
, the upper bound given by (41) converges to

Comparing it with (19), we observe the difference of the upper bound and the achievable rate converges to  . Hence, in this case, our upper bound is asymptotically tight.
. Hence, in this case, our upper bound is asymptotically tight.
Remark 8.
The first term in the bound (41) is strictly smaller than the trivial bound  obtained by removing the secrecy constraints. To show that, simply let
obtained by removing the secrecy constraints. To show that, simply let  . Equation (41) becomes
. Equation (41) becomes

The second term in (45) is always negative.
4.1. Comparison with the Bound Derived with Generalized Entropy Power Inequality
Recently the generalized entropy power inequality [34] was used to derive a computable upper bound for the Gaussian multiple access channel with secrecy constraints [32]. Here the same technique is applicable and another computable upper bound for the model in Figure 1 can be derived. It is of interest to know which bound is tighter. Next, we prove that as long as  , this upper bound is always looser than the bound given by (38)-(39).
, this upper bound is always looser than the bound given by (38)-(39).
First, we briefly describe the derivation of the bound based on the approach in [32]:




Here step  follows from Fano's inequality. (49) can be written as:
follows from Fano's inequality. (49) can be written as:



Step  follows from
follows from  being independent.
being independent.
Next, like [32, equation ( 76)], we invoke the inequality from [34] and obtain

Hence (52) can be upper bounded with

This expression is maximized when  are chosen to be i.i.d. Gaussian sequences. Dividing by the total number of channel uses
are chosen to be i.i.d. Gaussian sequences. Dividing by the total number of channel uses  , the final expression of the upper bound is given by
, the final expression of the upper bound is given by

Remark 9.
Note that (55) is also tighter than the bound  when
when  . Hence it is a nontrivial bound when
. Hence it is a nontrivial bound when  .
.
Remark 10.
When  , then
, then  ,
,  . Comparing (19) with (55), the gap between the achievable rates and the bound given by (55) is
. Comparing (19) with (55), the gap between the achievable rates and the bound given by (55) is

which is smaller than  bit/channel use.
bit/channel use.
We next show that for any given  , if
, if  , (55) is always bigger than the first term in (41). We omit the time sharing factor
, (55) is always bigger than the first term in (41). We omit the time sharing factor  in the front since they are present in both expressions. Then we pick
in the front since they are present in both expressions. Then we pick  such that
such that

Note that this is a valid choice for  since the right hand side is within the interval
since the right hand side is within the interval  . Then (41), after canceling
. Then (41), after canceling  in the front, becomes
in the front, becomes

Hence we only need to verify that (55) is greater than (58) when  . This is equivalent to verifying
. This is equivalent to verifying

or  . A sufficient condition for this to hold is to require
. A sufficient condition for this to hold is to require  . Substitute (57) into this requirement we get
. Substitute (57) into this requirement we get  .
.
Remark 11.
Since the gap between the achievable rates and the bound given by (55) is bounded by  bit/channel use when
bit/channel use when  , the gap between the achievable rates and the bound given by (41) is also bounded by
, the gap between the achievable rates and the bound given by (41) is also bounded by  bit/channel use when
bit/channel use when  and
and  . Note that since when
. Note that since when  we have
we have  , the condition
, the condition  is equivalent to
is equivalent to  .
.
Remark 12.
For the case that  , it is not clear between (55) and (41) which bound is tighter. However, for these cases, the secrecy capacity is so small that the bounds are of no consequence.
, it is not clear between (55) and (41) which bound is tighter. However, for these cases, the secrecy capacity is so small that the bounds are of no consequence.
5. Numerical Results
Shown in Table 1 are the six cases of interest, corresponding to different power budgets of the relay and the jammer and whether time sharing factor  is fixed. We included the cases with fixed time sharing factor because in a real system, for simplicity the time sharing factor may not be dynamically adjusted according to power budgets. The numerical result of each case is shown in the figures listed in the table. We stress that, though not explicitly considered in the numerical results, for the more general case where the cooperative jammer is external, as shown in Figure 2, the upper bound still holds, but the gap between the upper bound and achievable rates would be wider.
is fixed. We included the cases with fixed time sharing factor because in a real system, for simplicity the time sharing factor may not be dynamically adjusted according to power budgets. The numerical result of each case is shown in the figures listed in the table. We stress that, though not explicitly considered in the numerical results, for the more general case where the cooperative jammer is external, as shown in Figure 2, the upper bound still holds, but the gap between the upper bound and achievable rates would be wider.
Figures 6 and 7 demonstrate the asymptotic behavior described in Remark 6 when the power of relay goes to  . Note that in this case the optimal time sharing factor
. Note that in this case the optimal time sharing factor  converges to 1. Figures 8 and 9 demonstrate the case where the power the relay is finite, and the time sharing factor
converges to 1. Figures 8 and 9 demonstrate the case where the power the relay is finite, and the time sharing factor  is fixed. In all four cases, we observe the upper bound is close to the achievable rate when relay's power is larger than the power of the source and the jammer. In this region, typically, the achievable rate increases linearly with the source SNR. In Figure 6, the gap between the upper bound and achievable rate goes to zero as
is fixed. In all four cases, we observe the upper bound is close to the achievable rate when relay's power is larger than the power of the source and the jammer. In this region, typically, the achievable rate increases linearly with the source SNR. In Figure 6, the gap between the upper bound and achievable rate goes to zero as  . In Figure 7, the upper bound almost coincides with the achievable rate. The gap, given by (43), equals
. In Figure 7, the upper bound almost coincides with the achievable rate. The gap, given by (43), equals  bits/channel use.
bits/channel use.
Also shown in each figure is the cut-set bound without secrecy constraints. The improvement provided by the new bounds depends on the power budget. In general, the improvement is small if the power of the jammer is large. Note that since we have normalized all channel gains and included them into the power constraint, the power budget difference can be considered a consequence of the difference in link gains.
Figure 9 also illustrates the power control problem described in Remark 4. Without power control at the source node, the achievable rate will eventually decrease to zero. Note that this behavior crystallizes only when the relay's power is limited.
Finally, in Figures 10 and 11, we compare the achievable rates and the upper bound when each are maximized over the time sharing factor  . The gap between the upper bound and the achievable rate is now wider because the second term in the upper bound (41) is the same as the upper bound without secrecy constraint. The role played by the second term (41) becomes significant when the bound is optimized over the time sharing factor, which as pointed out in [35], has a tendency to balance the two terms in the bound (41). However, as shown in these figures, compared to the upper bound without secrecy constraints, the new bound still offers significant improvement.
. The gap between the upper bound and the achievable rate is now wider because the second term in the upper bound (41) is the same as the upper bound without secrecy constraint. The role played by the second term (41) becomes significant when the bound is optimized over the time sharing factor, which as pointed out in [35], has a tendency to balance the two terms in the bound (41). However, as shown in these figures, compared to the upper bound without secrecy constraints, the new bound still offers significant improvement.
6. Conclusion
In this paper, we have considered a relay network without a direct link, where relaying is essential for the source and the destination to communicate despite the fact that the relay node is untrusted. Imposing secrecy constraints at the relay node, contrary to the previous work, we have shown that a nonzero secrecy rate is indeed achievable. This is accomplished by enlisting the help of the destination (or another dedicated node) who transmits to jam the relay, and uses the jamming signal as side information. We have derived an upper bound for the secrecy rate with the assumption that no feedback is used for encoding at the source or destination. The new upper bound is strictly tighter than the upper bound without secrecy constraints. We have also proved that it is tighter than an upper bound derived from generalized entropy power inequality when the maximum sum received SNR at the relay is greater than  dB. The gap between the bound and the achievable rates converges to
dB. The gap between the bound and the achievable rates converges to  when the power of the transmitter, the relay and the jammer goes to
when the power of the transmitter, the relay and the jammer goes to  . Numerical results show that our upper bound is in general close to the achievable rate, and is indistinguishable from it for a fixed time sharing factor with a relay whose power is in abundance.
. Numerical results show that our upper bound is in general close to the achievable rate, and is indistinguishable from it for a fixed time sharing factor with a relay whose power is in abundance.
In this work, we considered the case where the source or the jammer does not make use of the relay transmission for encoding purposes. An upper bound for the secrecy rate when feedback is used is recently found in [36]. A gap exists between the upper bound and the achievable rate in [36], which is bounded by  bit per channel use but does not vanish when the power of the transmitter, the relay and the jammer goes to infinity. By comparison, the bound presented in this work is asymptotically tighter in this case.
bit per channel use but does not vanish when the power of the transmitter, the relay and the jammer goes to infinity. By comparison, the bound presented in this work is asymptotically tighter in this case.
We conclude by reiterating that our findings in this paper presents cooperative jamming as an enabler for secrecy from an internal eavesdropper, and motivates further investigation of such cooperation ideas in more general settings including those in larger networks. We also comment whether and when cooperative jamming actually yields the secrecy capacity (region) for various multiuser channels remain open problems in information theory.
References
Shannon CE: Communication theory of secrecy systems. Bell System Technical Journal 1949, 28(4):656-715.
Wyner AD: The wire-tap channel. Bell System Technical Journal 1975, 54(8):1355-1387.
Csiszár I, Körner J: Broadcast channels with confidential messages. IEEE Transactions on Information Theory 1978, 24(3):339-348. 10.1109/TIT.1978.1055892
Leung-Yan-Cheong SK, Hellman ME: The Gaussian wire-tap channel. IEEE Transactions on Information Theory 1978, 24(4):451-456. 10.1109/TIT.1978.1055917
Liang Y, Poor HV: Multiple-access channels with confidential messages. IEEE Transactions on Information Theory 2008, 54(3):976-1002.
Tekin E, Serbetli S, Yener A: On secure signaling for the Gaussian multiple access wire-tap channel. Proceedings of the 39th Asilomar Conference on Signals, Systems and Computers (ACSSC '05), October-November 2005, Pacific Grove, Calif, USA 1747-1751.
Tekin E, Yener A: The Gaussian multiple access wire-tap channel. IEEE Transactions on Information Theory 2008, 54(12):5747-5755.
Tekin E, Yener A: The general Gaussian multiple-access and two-way wiretap channels: achievable rates and cooperative jamming. IEEE Transactions on Information Theory 2008, 54(6):2735-2751.
Oohama Y: Relay channels with confidential messages. submitted to IEEE Transactions on Information Theory http://arxiv.org/abs/cs/0611125 submitted to IEEE Transactions on Information Theory
Lai L, El Gamal H: The relay-eavesdropper channel: cooperation for secrecy. IEEE Transactions on Information Theory 2008, 54(9):4005-4019.
He X, Yener A: Cooperation with an untrusted relay: a secrecy perspective. 2008.http://arxiv.org/abs/0910.1511 submitted to IEEE Transactions on Information Theory
Liu R, Maric I, Spasojevic P, Yates RD: Discrete memoryless interference and broadcast channels with confidential messages: secrecy rate regions. IEEE Transactions on Information Theory 2008, 54(6):2493-2507.
Liu R, Poor HV: Multi-antenna Gaussian broadcast channels with confidential messages. Proceedings of IEEE International Symposium on Information Theory (ISIT '08), July 2008, Toronto, Canada 2202-2206.
Khisti A, Wornell G: Secure transmission with multiple antennas: the MISOME wiretap channel. to appear in IEEE Transactions on Information Theory http://allegro.mit.edu/pubs/posted/journal/2007-khisti-wornell-it.pdf to appear in IEEE Transactions on Information Theory
Oggier F, Hassibi B: The secrecy capacity of the MIMO wiretap channel. Proceedings IEEE International Symposium on Information Theory (ISIT '08), July 2008, Toronto, Canada 524-528.
Shafiee S, Liu N, Ulukus S: Towards the secrecy capacity of the gaussian MIMO wire-tap channel: the 2-2-1 channel. IEEE Transactions on Information Theory 2009, 55(9):4033-4039.
Tekin E, Yener A: Achievable rates for the general Gaussian multiple access wire-tap channel with collective secrecy. Proceedings of the 44th Annual Allerton Conference on Communication, Control, and Computing, September 2006, Urbana-Champaign, Ill, USA
Liang Y, Poor HV, Shamai S: Secure communication over fading channels. IEEE Transactions on Information Theory 2008, 54(6):2470-2492.
Gopala PK, Lai L, El Gamal H: On the secrecy capacity of fading channels. IEEE Transactions on Information Theory 2008, 54(10):4687-4698.
Koyluoglu O, El-Gamal H, Lai L, Poor HV: Interference alignment for secrecy. 2008.http://arxiv.org/abs/0810.1187 submitted to IEEE Transactions on Information Theory
He X, Yener A: On the equivocation region of relay channels with orthogonal components. Proceedings of the 41st Asilomar Conference on Signals, Systems and Computers (ACSSC '07), November 2007, Pacific Grove, Calif, USA 883-887.
He X, Yener A: The role of an untrusted relay in secret communication. Proceedings of IEEE International Symposium on Information Theory (ISIT '08), July 2008, Toronto, Canada 2212-2216.
Ekrem E, Ulukus S: Secrecy in cooperative relay broadcast channels. Proceedings of IEEE International Symposium on Information Theory (ISIT '08), July 2008, Toronto, Canada 2217-2221.
Ekrem E, Ulukus S: Secrecy in cooperative relay broadcast channels. 2008.http://www.ece.umd.edu/ulukus/papers/journal/crbc-secrecy.pdf submitted to IEEE Transactions on Information Theory
Cover TM, El Gamal AA: Capacity theorems for the relay channel. IEEE Transactions on Information Theory 1979, 25(5):572-584. 10.1109/TIT.1979.1056084
Goel S, Negi R: Secret communication in presence of colluding eavesdroppers. Proceedings of IEEE Military Communications Conference (MILCOM '05), October 2005, Atlatnic City, NJ, USA
Negi R, Goel S: Secret communication using artificial noise. Proceedings of the 62nd IEEE Vehicular Technology Conference (VTC '05), September 2005, Stockholm, Sweden 3: 1906-1910.
Jørgensen ML, Yanakiev BR, Kirkelund GE, Popovski P, Yomo H, Larsen T: Shout to secure: physical-layer wireless security with known interference. Proceedings of the 50th Annual IEEE Global Telecommunications Conference (GLOBECOM '07), November 2007, Washington, DC, USA 33-38.
Lai L, El Gamal H, Poor HV: The wiretap channel with feedback: encryption over the channel. IEEE Transactions on Information Theory 2008, 54(11):5059-5067.
Tang X, Liu R, Spasojevic P, Poor HV: Interference-assisted secret communication. Proceedings of IEEE Information Theory Workshop (ITW '08), May 2008, Porto, Portugal 164-168.
Tekin E, Yener A: Secrecy sum-rates for the multiple-access wire-tap channel with ergodic block fading. Proceedings of the 45th Annual Allerton Conference on Communication, Control, and Computing, September 2007, Urbana-Champaign, Ill, USA
Ekrem E, Ulukus S: On the secrecy of multiple access wiretap channel. Proceedings of the 46th Annual Allerton Conference on Communication, Control, and Computing, September 2008, Urbana-Champaign, Ill, USA 1014-1021.
Tang X, Liu R, Spasojevic P, Poor HV: The Gaussian wiretap channel with a helping interferer. Proceedings of IEEE International Symposium on Information Theory (ISIT '08), July 2008, Toronto, Canada 389-393.
Madiman M, Barron A: Generalized entropy power inequalities and monotonicity properties of information. IEEE Transactions on Information Theory 2007, 53(7):2317-2329.
Liang Y, Veeravalli VV, Poor HV: Resource allocation for wireless fading relay channels: max-min solution. IEEE Transactions on Information Theory 2007, 53(10):3432-3453.
He X, Yener A: On the role of feedback in two-way secure communication. Proceedings of the 42nd Asilomar Conference on Signals, Systems and Computers (ACSSC '08), October 2008, Pacific Grove, Calif, USA 1093-1097.
Acknowledgments
This work was presented in part at the IEEE Globecom Conference, December 2008. This work is supported in part by the National Science Foundation with Grants CCR-0237727, CCF-051483, CNS-0716325, CNS-0721445, and the DARPA ITMANET Program with Grant W911NF-07-1-0028.
Author information
Authors and Affiliations
Corresponding author
Appendix
Proof of Theorem 1
We first introduce several supporting results used in proving Theorem 1.
In [11, 21], we presented the following achievable secrecy rate for a general relay channel.
Theorem 3.
Consider a relay network with conditional distribution  , with
, with  ,
,  being the input from the source and the relay respectively, and
being the input from the source and the relay respectively, and  ,
, being the signals received by the relay and the destination, respectively. For the distribution
being the signals received by the relay and the destination, respectively. For the distribution


the following range of rates  is achievable:
is achievable:


with


Theorem 3 follows from the achievable equivocation region given in [11, Theorem  ] by simply considering rates
] by simply considering rates  that equal the equivocation rate
that equal the equivocation rate  . The proof of Theorem 3 is given in [11]. The outline of the achievable scheme is as follows: The relay does compress-and-forward as described in [25]. Therefore, as in [25],
. The proof of Theorem 3 is given in [11]. The outline of the achievable scheme is as follows: The relay does compress-and-forward as described in [25]. Therefore, as in [25],  is independent from
is independent from  in the input distribution expression (A.1). The same decoder in [25] is used at the destination. The same codebook as [25] is used at the source node. However, instead of mapping the message to the codeword deterministically as in [25], a stochastic encoder is used at the source node. In this encoder, the codewords are randomly binned into several bins. The size of each bin is
in the input distribution expression (A.1). The same decoder in [25] is used at the destination. The same codebook as [25] is used at the source node. However, instead of mapping the message to the codeword deterministically as in [25], a stochastic encoder is used at the source node. In this encoder, the codewords are randomly binned into several bins. The size of each bin is  where
where  is the total number of channel uses. The message
is the total number of channel uses. The message  determines which bin to use by the encoder. The actual transmitted codeword is then randomly chosen from the bin according to a uniform distribution. This randomness serves to confuse the eavesdropper at the relay node at the cost of the rate as shown by the term
determines which bin to use by the encoder. The actual transmitted codeword is then randomly chosen from the bin according to a uniform distribution. This randomness serves to confuse the eavesdropper at the relay node at the cost of the rate as shown by the term  in (A.2).
in (A.2).
We next extend this result by considering a relay channel with a jammer defined by


where  is the signal transmitted by the jammer and the notation
is the signal transmitted by the jammer and the notation  follows the definition above. Then, if the jammer transmits an i.i.d. signal according to distribution
follows the definition above. Then, if the jammer transmits an i.i.d. signal according to distribution  and
and  , the induced channel
, the induced channel  is given below:
is given below:


and it is also a memoryless relay channel. Hence, we can use Theorem 3 and obtain the following corollary.
Corollary 1.
The following secrecy rate is achievable:


with


We next reformulate our channel in Figure 1 in a way such that Corollary 1 can be applied. This is shown in Figure 12. Here we can draw the jammer and the receiver separately, since the jammer does not use the signal received in the past to compute the jamming signal. The  and
and  are the parameters of the schedule described in Section 3. We then observe Figure 12 can be viewed as a three node relay network with a jammer, defined as follows:
are the parameters of the schedule described in Section 3. We then observe Figure 12 can be viewed as a three node relay network with a jammer, defined as follows:


where


The input distributions to this vector input channel are chosen as


where  ,
,  and
and  are given below.
are given below.
(1)Let  , where
, where  is the average power consumption of node
is the average power consumption of node  during the periods of phase one. Hence
during the periods of phase one. Hence  .
.
(2)Let the auxiliary random variable in compress-and-forward  be
be  . Let
. Let  , where
, where  ,
,
(3)Let  and
and  ,
,
where  denotes an
denotes an  identity matrix. With (
identity matrix. With ( )–(
)–( ), we have
), we have






From (A.10),  . Therefore (A.13) equals
. Therefore (A.13) equals








(A.17) equals:










































In (A.14), (A.20), (A.26), (A.30), (A.36), and (A.37), we use (A.10) repeatedly, which says that with compress-and-forward, the input distribution are chosen such that  are independent.
are independent.
Substituting the values of  ,
,  ,
,  and
and  into Corollary 1, dividing both sides by
into Corollary 1, dividing both sides by  , and taking the limit
, and taking the limit  , we proved the theorem.
, we proved the theorem.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
He, X., Yener, A. Two-Hop Secure Communication Using an Untrusted Relay. J Wireless Com Network 2009, 305146 (2009). https://doi.org/10.1155/2009/305146
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/305146

 .
. signals the relay transmitted during the periods of phase one, denoted by
signals the relay transmitted during the periods of phase one, denoted by  .
.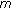 signals the relay transmitted during the periods of phase two, denoted by
signals the relay transmitted during the periods of phase two, denoted by  .
.




 ,
,
 , optimal
, optimal


 ,
,
 dB, optimal
dB, optimal


 dB,
dB,
 ,
,


 dB,
dB,
 dB,
dB,


 dB,
dB,
 , optimized over
, optimized over


 dB,
dB,
 dB, optimized over
dB, optimized over
 , power control at the source node enabled.
, power control at the source node enabled.
