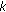- Research Article
- Open access
- Published:
Secured Communication over Frequency-Selective Fading Channels: A Practical Vandermonde Precoding
EURASIP Journal on Wireless Communications and Networking volume 2009, Article number: 386547 (2009)
Abstract
We study the frequency-selective broadcast channel with confidential messages (BCC) where the transmitter sends a confidential message to receiver 1 and a common message to receivers 1 and 2. In the case of a block transmission of  symbols followed by a guard interval of
symbols followed by a guard interval of  symbols, the frequency-selective channel can be modeled as a
symbols, the frequency-selective channel can be modeled as a  Toeplitz matrix. For this special type of multiple-input multiple-output channels, we propose a practical Vandermonde precoding that projects the confidential messages in the null space of the channel seen by receiver 2 while superposing the common message. For this scheme, we provide the achievable rate region and characterize the optimal covariance for some special cases of interest. Interestingly, the proposed scheme can be applied to other multiuser scenarios such as the
Toeplitz matrix. For this special type of multiple-input multiple-output channels, we propose a practical Vandermonde precoding that projects the confidential messages in the null space of the channel seen by receiver 2 while superposing the common message. For this scheme, we provide the achievable rate region and characterize the optimal covariance for some special cases of interest. Interestingly, the proposed scheme can be applied to other multiuser scenarios such as the  -user frequency-selective BCC with
-user frequency-selective BCC with  confidential messages and the two-user frequency-selective BCC with two confidential messages. For each scenario, we provide the secrecy degree of freedom (s.d.o.f.) region of the corresponding channel and prove the optimality of the Vandermonde precoding. One of the appealing features of the proposed scheme is that it does not require any specific secrecy encoding technique but can be applied on top of any existing powerful encoding schemes.
confidential messages and the two-user frequency-selective BCC with two confidential messages. For each scenario, we provide the secrecy degree of freedom (s.d.o.f.) region of the corresponding channel and prove the optimality of the Vandermonde precoding. One of the appealing features of the proposed scheme is that it does not require any specific secrecy encoding technique but can be applied on top of any existing powerful encoding schemes.
1. Introduction
We consider a secured medium such that the transmitter wishes to send a confidential message to its receiver while keeping the eavesdropper, tapping the channel, ignorant of the message. Wyner [1] introduced this model named the wiretap channel to model the degraded broadcast channel where the eavesdropper observes a degraded version of the receiver's signal. In this model, the confidentiality is measured by the equivocation rate, that is, the mutual information between the confidential message and the eavesdropper's observation. For the discrete memoryless degraded wiretap channel, Wyner characterized the capacity-equivocation region and showed that a nonzero secrecy rate can be achieved [1]. The most important operating point on the capacity-equivocation region is the secrecy capacity, that is, the largest reliable communication rate such that the eavesdropper obtains no information about the confidential message (the equivocation rate is as large as the message rate). The secrecy capacity of the Gaussian wiretap channel was given in [2]. Csiszár and Körner considered a more general wiretap channel in which a common message for both receivers is sent in addition to the confidential message [3]. For this model known as the broadcast channel with confidential (BCC) messages, the rate-tuple of the common and confidential messages was characterized.
Recently, a significant effort has been made to opportunistically exploit the space/time/user dimensions for secrecy communications (see, e.g., [4–14] and references therein). In [4], the secrecy capacity of the ergodic slow fading channels was characterized and the optimal power/rate allocation was derived. The secrecy capacity of the parallel fading channels was given [6, 7] where [7] considered the BCC with a common message. Moreover, the secrecy capacity of the wiretap channel with multiple antennas has been studied in [8–13, 15] and references therein. In particular, the secrecy capacity of the multiple-input multiple-output (MIMO) wiretap channel has been fully characterized in [5, 11, 12, 14] and more recently its closed-form expressions under a matrix covariance constraint have been derived in [15]. Furthermore, a large number of recent works have considered the secrecy capacity region for more general broadcast channels. In [16], the authors studied the two-user MIMO Gaussian BCC where the capacity region for the case of one common and one confidential message was characterized. The two-user BCC with two confidential messages, each of which must be kept secret to the unintended receiver, has been studied in [17–20]. In [18], Liu and Poor characterized the secrecy capacity region for the multiple-input single-output (MISO) Gaussian BCC where the optimality of the secret dirty paper coding (S-DPC) scheme was proved. A recent contribution [19] extended the result to the MIMO Gaussian BCC. The multireceiver wiretap channels have been also studied in [21–26] (and reference therein) where the confidential messages to each receiver must be kept secret to an external eavesdropper. It has been proved that the secrecy capacity region of the MIMO Gaussian multireceiver wiretap channels is achieved by S-DPC [24, 26].
However, very few work have exploited the frequency selectivity nature of the channel for secrecy purposes [27] where the zeros of the channel provide an opportunity to "hide" information. This paper shows the opportunities provided by the broad-band channel and studies the frequency-selective BCC where the transmitter sends one confidential message to receiver 1 and one common message to both receivers 1 and 2. The channel state information (CSI) is assumed to be known to both the transmitter and the receivers. We consider the quasistatic frequency-selective fading channel with  paths such that the channel remains fixed during an entire transmission of
paths such that the channel remains fixed during an entire transmission of  blocks for an arbitrary large
blocks for an arbitrary large  . It should be remarked that in general the secrecy rate cannot scale with signal-to-noise ratio (SNR) over the channel at hand, unless the channel of receiver 2 has a null frequency band of positive Lebesgue measure (on which the transmitter can "hide'' the confidential message). In this contribution, we focus on the realistic case where receiver 2 has a full frequency band (without null subbands) but operates in a reduced dimension due to practical complexity issues. This is typical of current orthogonal frequency division multiplexing (OFDM) standards (such as IEEE802.11a/WiMax or LTE [28–30]) where a guard interval of
. It should be remarked that in general the secrecy rate cannot scale with signal-to-noise ratio (SNR) over the channel at hand, unless the channel of receiver 2 has a null frequency band of positive Lebesgue measure (on which the transmitter can "hide'' the confidential message). In this contribution, we focus on the realistic case where receiver 2 has a full frequency band (without null subbands) but operates in a reduced dimension due to practical complexity issues. This is typical of current orthogonal frequency division multiplexing (OFDM) standards (such as IEEE802.11a/WiMax or LTE [28–30]) where a guard interval of  symbols is inserted at the beginning of each block to avoid the interblock interference and both receivers discard these
symbols is inserted at the beginning of each block to avoid the interblock interference and both receivers discard these  symbols. We assume that both users have the same standard receiver, in particular receiver 2 cannot change its hardware structure. Studying secure communications under this assumption is of interest in general and can be justified since receiver 2 is actually a legitimate receiver which can receive a confidential message in other communication periods. Of course, if receiver 2 is able to access the guard interval symbols, it can extract the confidential message and the secrecy rate falls down to zero. Although we restrict ourselves to the reduced dimension constraint in this paper, other constraints on the limited capability at the unintended receiver such as energy consumption or hardware complexity might provide a new paradigm to design physical layer secrecy systems.
symbols. We assume that both users have the same standard receiver, in particular receiver 2 cannot change its hardware structure. Studying secure communications under this assumption is of interest in general and can be justified since receiver 2 is actually a legitimate receiver which can receive a confidential message in other communication periods. Of course, if receiver 2 is able to access the guard interval symbols, it can extract the confidential message and the secrecy rate falls down to zero. Although we restrict ourselves to the reduced dimension constraint in this paper, other constraints on the limited capability at the unintended receiver such as energy consumption or hardware complexity might provide a new paradigm to design physical layer secrecy systems.
In the case of a block transmission of  symbols followed by a guard interval of
symbols followed by a guard interval of  symbols discarded at both receivers, the frequency-selective channel can be modeled as an
symbols discarded at both receivers, the frequency-selective channel can be modeled as an  MIMO Toeplitz matrix. In this contribution, we aim at designing a practical linear precoding scheme that fully exploits the degrees of freedom (d.o.f.) offered by this special type of MIMO channels to transmit both the common message and the confidential message. To this end, let us start with the following remarks. On one hand, the idea of using OFDM modulation to convert the frequency-selective channel represented by the Toeplitz matrix into a set of parallel fading channel turns out to be useless from a secrecy perspective. Indeed, it is known that the secrecy capacity of the parallel wiretap fading channels does not scale with SNR [7]. On the other hand, recent contributions [5, 11, 12, 14, 15] showed that the secrecy capacity of the MIMO wiretap channel grows linearly with SNR, that is,
MIMO Toeplitz matrix. In this contribution, we aim at designing a practical linear precoding scheme that fully exploits the degrees of freedom (d.o.f.) offered by this special type of MIMO channels to transmit both the common message and the confidential message. To this end, let us start with the following remarks. On one hand, the idea of using OFDM modulation to convert the frequency-selective channel represented by the Toeplitz matrix into a set of parallel fading channel turns out to be useless from a secrecy perspective. Indeed, it is known that the secrecy capacity of the parallel wiretap fading channels does not scale with SNR [7]. On the other hand, recent contributions [5, 11, 12, 14, 15] showed that the secrecy capacity of the MIMO wiretap channel grows linearly with SNR, that is,  where
where  denotes the secrecy degree of freedom (s.d.o.f.) (to be specified). In the high SNR regime, the secrecy capacity of the MISO/MIMO wiretap channel is achieved by sending the confidential message in the null space of the eavesdropper's channel [10, 11, 14, 15, 18, 19]. Therefore, OFDM modulation is highly suboptimal in terms of the s.d.o.f.
denotes the secrecy degree of freedom (s.d.o.f.) (to be specified). In the high SNR regime, the secrecy capacity of the MISO/MIMO wiretap channel is achieved by sending the confidential message in the null space of the eavesdropper's channel [10, 11, 14, 15, 18, 19]. Therefore, OFDM modulation is highly suboptimal in terms of the s.d.o.f.
Inspired by these remarks, we propose a linear Vandermonde precoder that projects the confidential message in the null space of the channel seen by receiver 2 while superposing the common message. Thanks to the orthogonality between the precoder of the confidential message and the channel of receiver 2; receiver 2 obtains no information on the confidential message. This precoder is regarded as a single-antenna frequency beamformer that nulls the signal in certain directions seen by receiver 2. The Vandermonde structure comes from the fact that the frequency beamformer is of the type  where
where  is one of the roots of the channel seen by receiver 2. Note that Vandermonde matrices [31] have already been considered for cognitive radios [32] and CDMA systems [33] to reduce/null interference but not for secrecy applications. One of the appealing aspects of Vandermonde precoding is that it does not require a specific secrecy encoding technique but can be applied on top of any classical capacity achieving encoding scheme.
is one of the roots of the channel seen by receiver 2. Note that Vandermonde matrices [31] have already been considered for cognitive radios [32] and CDMA systems [33] to reduce/null interference but not for secrecy applications. One of the appealing aspects of Vandermonde precoding is that it does not require a specific secrecy encoding technique but can be applied on top of any classical capacity achieving encoding scheme.
For the proposed scheme, we characterize its achievable rate region, the rate-tuple of the common message, the confidential message, respectively. Unfortunately, the optimal input covariances achieving their boundary are generally difficult to compute due to the nonconvexity of the weighted sum rate maximization problem. Nevertheless, we show that there are some special cases of interest such as the secrecy rate and the maximum sum rate point which enable an explicit characterization of the optimal input covariances. In addition, we provide the achievable d.o.f. region of the frequency-selective BCC, reflecting the behavior of the achievable rate region in the high SNR regime, and prove that the Vandermonde precoding achieves this region. More specifically, it enables to simultaneously transmit  streams of the confidential message and
streams of the confidential message and  streams of the common message for
streams of the common message for  simultaneously over a block of
simultaneously over a block of  dimensions. Interestingly, the proposed Vandermonde precoding can be applied to multiuser secure communication scenarios: (a) a
dimensions. Interestingly, the proposed Vandermonde precoding can be applied to multiuser secure communication scenarios: (a) a  -user frequency-selective BCC with
-user frequency-selective BCC with  confidential messages and one common message, (b) a two-user frequency-selective BCC with two confidential messages and one common message. For each scenario, we characterize the achievable s.d.o.f. region of the corresponding frequency-selective BCC and show the optimality of the Vandermonde precoding.
confidential messages and one common message, (b) a two-user frequency-selective BCC with two confidential messages and one common message. For each scenario, we characterize the achievable s.d.o.f. region of the corresponding frequency-selective BCC and show the optimality of the Vandermonde precoding.
The paper is organized as follows. Section 2 presents the frequency-selective fading BCC. Section 3 introduces the Vandermonde precoding and characterizes its achievable rate region as well as the optimal input covariances for some special cases. Section 4 provides the application of the Vandermonde precoding to the multiuser secure communications scenarios. Section 5 shows some numerical examples of the proposed scheme in the various settings, and finally Section 6 concludes the paper.
Notation. In the following, upper (lower boldface) symbols will be used for matrices (column vectors) whereas lower symbols will represent scalar values,  will denote transpose operator,
will denote transpose operator,  conjugation, and
conjugation, and  hermitian transpose.
hermitian transpose.  ,
,  represent the
represent the  identity matrix,
identity matrix,  zero matrix.
zero matrix.  denote a determinant, rank, trace of a matrix
denote a determinant, rank, trace of a matrix  , respectively.
, respectively.  denotes the sequence
denotes the sequence  .
.  ,
,  ,
,  ,
,  ,
,  ,
,  denote the realization of the random variables
denote the realization of the random variables  ,
,  ,
,  ,
,  ,
,  ,
,  . Finally, "
. Finally, " '' denotes less or equal to in the positive semidefinite ordering between positive semidefinite matrices, that is, we have
'' denotes less or equal to in the positive semidefinite ordering between positive semidefinite matrices, that is, we have  if
if  is positive semidefinite.
is positive semidefinite.
2. System Model
We consider the quasistatic frequency-selective fading BCC illustrated in Figure 1. The received signal  of receivers 1, 2 at block
of receivers 1, 2 at block  is given by
is given by

where  denote an
denote an  Toeplitz matrix with the
Toeplitz matrix with the  -path channel vector
-path channel vector  of user 1,
of user 1,  of user 2, respectively,
of user 2, respectively,  denotes the transmit vector, and finally
denotes the transmit vector, and finally  are mutually independent additive white Gaussian noise (AWGN). The input vector is subject to the power constraint given by
are mutually independent additive white Gaussian noise (AWGN). The input vector is subject to the power constraint given by

where we let  . The structure of
. The structure of  is given by
is given by

We assume that the channel matrices  ,
,  remain constant for the whole duration of the transmission of
remain constant for the whole duration of the transmission of  blocks and are known to all terminals. At each block
blocks and are known to all terminals. At each block  , we transmit
, we transmit  symbols by appending a guard interval of size
symbols by appending a guard interval of size  larger than the delay spread, which enables to avoid the interference between neighbor blocks.
larger than the delay spread, which enables to avoid the interference between neighbor blocks.
The transmitter wishes to send a common message  to two receivers and a confidential message
to two receivers and a confidential message  to receiver 1. A
to receiver 1. A  code consists of the following: (1) two message sets
code consists of the following: (1) two message sets  and
and  with the messages
with the messages  uniformly distributed over the sets
uniformly distributed over the sets  ,
,  , respectively; (2) a stochastic encoder that maps each message pair
, respectively; (2) a stochastic encoder that maps each message pair  to a codeword
to a codeword  ; (3) one decoder at receiver 1 that maps a received sequence
; (3) one decoder at receiver 1 that maps a received sequence  to a message pair
to a message pair  and another at receiver 2 that maps a received sequence
and another at receiver 2 that maps a received sequence  to a message
to a message  . The average error probability of a
. The average error probability of a  code is defined as
code is defined as

where  denotes the error probability when the message pair
denotes the error probability when the message pair  is sent defined by
is sent defined by

The secrecy level of the confidential message  at receiver 2 is measured by the equivocation rate
at receiver 2 is measured by the equivocation rate  defined as
defined as

which is the normalized entropy of the confidential message conditioned on the received signal at receiver 2 and available CSI.
A rate-equivocation tuple  is said to be achievable if for any
is said to be achievable if for any  there exists a sequence of codes
there exists a sequence of codes  such that we have
such that we have

In this paper, we focus on the perfect secrecy case where receiver 2 obtains no information about the confidential message  , which is equivalent to
, which is equivalent to  . In this setting, an achievable rate region
. In this setting, an achievable rate region  of the general BCC (expressed in bit per channel use per dimension) is given by [3]
of the general BCC (expressed in bit per channel use per dimension) is given by [3]

where the union is over all possible distribution  ,
,  ,
,  satisfying [20, Lemma 1]
satisfying [20, Lemma 1]

where  might be a deterministic function of
might be a deterministic function of  . Recently, the secrecy capacity region
. Recently, the secrecy capacity region  of the two-user MIMO-BCC (1) was characterized in [16] and is given by all possible rate tuples
of the two-user MIMO-BCC (1) was characterized in [16] and is given by all possible rate tuples  satisfying
satisfying

for some  with
with  denotes the input covariance satisfying
denotes the input covariance satisfying  and
and  ,
,  denotes the channel matrix of receiver 1, 2, respectively. Obviously, when only the confidential message is transmitted to receiver 1, the frequency-selective BCC (1) reduces to the MIMO flat-fading wiretap channel whose secrecy capacity has been characterized in [10–12, 14, 15]. In particular, Bustin et al. derived its closed-form expression under a power-covariance constraint [15]. Under a total power (trace) constraint, the secrecy capacity of the MIMO Gaussian wiretap channel is expressed as [19, Theorem 3]
denotes the channel matrix of receiver 1, 2, respectively. Obviously, when only the confidential message is transmitted to receiver 1, the frequency-selective BCC (1) reduces to the MIMO flat-fading wiretap channel whose secrecy capacity has been characterized in [10–12, 14, 15]. In particular, Bustin et al. derived its closed-form expression under a power-covariance constraint [15]. Under a total power (trace) constraint, the secrecy capacity of the MIMO Gaussian wiretap channel is expressed as [19, Theorem 3]

where  are the generalized eigen-values greater than one of the following pencil:
are the generalized eigen-values greater than one of the following pencil:

(In [15, 19] the authors consider the real matrices  ,
,  . Nevertheless, it is conjectured that for complex matrices the following expression without
. Nevertheless, it is conjectured that for complex matrices the following expression without  in the prelog holds.) As explicitly characterized in [15, Theorem 2], the optimal input covariance achieving the above region is chosen such that the confidential message is sent over
in the prelog holds.) As explicitly characterized in [15, Theorem 2], the optimal input covariance achieving the above region is chosen such that the confidential message is sent over  subchannels where receiver 1 observes stronger signals than receiver 2. Moreover, in the high SNR regime the optimal strategy converges to beamforming into the null subspace of
subchannels where receiver 1 observes stronger signals than receiver 2. Moreover, in the high SNR regime the optimal strategy converges to beamforming into the null subspace of  [5, 11, 12, 14] as for the MISO case [14, 18]. In order to characterize the behavior of the secrecy capacity region in the high SNR regime, we define the d.o.f. region as
[5, 11, 12, 14] as for the MISO case [14, 18]. In order to characterize the behavior of the secrecy capacity region in the high SNR regime, we define the d.o.f. region as

where  denotes s.d.o.f. which corresponds precisely to the number
denotes s.d.o.f. which corresponds precisely to the number  of the generalized eigenvalues greater than one in the high SNR.
of the generalized eigenvalues greater than one in the high SNR.
3. Vandermonde Precoding
For the frequency-selective BCC specified in Section 2, we wish to design a practical linear precoding scheme which fully exploits the d.o.f. offered by the frequency-selective channel. We remarked previously that for a special case when only the confidential message is sent to receiver 1 (without a common message), the optimal strategy consists of beamforming the confidential signal into the null subspace of receiver 2. By applying this intuitive result to the special Toeplitz MIMO channels  ,
,  while including a common message, we propose a linear precoding strategy named Vandermonde precoding. Prior to the definition of the Vandermonde precoding, we provide some properties of a Vandermonde matrix [31].
while including a common message, we propose a linear precoding strategy named Vandermonde precoding. Prior to the definition of the Vandermonde precoding, we provide some properties of a Vandermonde matrix [31].
Property 1.
Given a full-rank Toeplitz matrix  , there exists a Vandermonde matrix
, there exists a Vandermonde matrix  for
for  whose structure is given by
whose structure is given by

where  are the
are the  roots of the polynomial
roots of the polynomial  with
with  coefficients of the channel
coefficients of the channel  . Clearly
. Clearly  satisfies the following orthogonal condition:
satisfies the following orthogonal condition:

and  if
if  are all different.
are all different.
It is well known that as the dimension of  and
and  increases, the Vandermonde matrix
increases, the Vandermonde matrix  becomes ill-conditioned unless the roots are on the unit circle. In other words, the elements of each column either grow in energy or tend to zero [31]. Hence, instead of the brut Vandermonde matrix (14), we consider a unitary Vandermonde matrix obtained either by applying the Gram-Schmidt orthogonalization or singular value decomposition (SVD) on
becomes ill-conditioned unless the roots are on the unit circle. In other words, the elements of each column either grow in energy or tend to zero [31]. Hence, instead of the brut Vandermonde matrix (14), we consider a unitary Vandermonde matrix obtained either by applying the Gram-Schmidt orthogonalization or singular value decomposition (SVD) on  .
.
Definition 1.
We let  be a unitary Vandermonde matrix obtained by orthogonalizing the columns of
be a unitary Vandermonde matrix obtained by orthogonalizing the columns of  . We let
. We let  be a unitary matrix in the null space of
be a unitary matrix in the null space of  such that
such that  . The common message
. The common message  , the confidential message
, the confidential message  , is sent along
, is sent along  ,
,  , respectively. We call
, respectively. We call  Vandermonde precoder.
Vandermonde precoder.
Further, the precoding matrix  for the confidential message satisfies the following property.
for the confidential message satisfies the following property.
Lemma 2.
Given two Toeplitz matrices  ,
,  where
where  ,
,  are linearly independent, there exists a unitary Vandermonde matrix
are linearly independent, there exists a unitary Vandermonde matrix  for
for  satisfying
satisfying

Proof.
Appendix A.
In order to send the confidential message intended to receiver 1 as well as the common message to both receivers over the frequency-selective channel (1), we consider the Gaussian superposition coding based on the Vandermonde precoder of Definition 1. Namely, at block  , we form the transmit vector as
, we form the transmit vector as

where the common message vector  and the confidential message vector
and the confidential message vector  are mutually independent Gaussian vectors with zero mean and covariance
are mutually independent Gaussian vectors with zero mean and covariance  ,
,  , respectively. Under this condition, the input covariances subject to
, respectively. Under this condition, the input covariances subject to

satisfy the power constraint (2). We let  denote the feasible set
denote the feasible set  satisfying (18).
satisfying (18).
Theorem 3.
The Vandermonde precoding achieves the following secrecy rate region:

where  denotes the convex hull and we let
denotes the convex hull and we let  ,
,  ,
,  .
.
Proof.
Due to the orthogonal property (16) of the unitary Vandermonde matrix, receiver 2 only observes the common message, which yields the received signals given by

where we drop the block index. We examine the achievable rate region  of the Vandermonde precoding. By letting the auxiliary variables
of the Vandermonde precoding. By letting the auxiliary variables  and
and  , we have
, we have

Plugging these expressions to (8), we obtain (19).
The boundary of the achievable rate region of the Vandermonde precoding can be characterized by solving the weighted sum rate maximization. Any point  on the boundary of the convex region
on the boundary of the convex region  is obtained by solving
is obtained by solving

for nonnegative weights  satisfying
satisfying  . When the region
. When the region  , obtained without convex hull, is nonconvex, the set of the optimal covariances
, obtained without convex hull, is nonconvex, the set of the optimal covariances  achieving the boundary point might not be unique. Figure 2 depicts an example in which the achievable rate region
achieving the boundary point might not be unique. Figure 2 depicts an example in which the achievable rate region  is obtained by the convex hull operation on the region
is obtained by the convex hull operation on the region  , that is, replacing the non-convex subregion by the line segment
, that is, replacing the non-convex subregion by the line segment  ,
,  . For the weight ratio
. For the weight ratio  corresponding to the slope of the line segment
corresponding to the slope of the line segment  ,
,  , there exist two optimal sets of the covariances yielding the points
, there exist two optimal sets of the covariances yielding the points  and
and  (which clearly dominate the point
(which clearly dominate the point  ). These points are the solution to the weighted sum rate maximization (22). In summary, an optimal covariance set achieving (22) (might not be unique) is the solution of
). These points are the solution to the weighted sum rate maximization (22). In summary, an optimal covariance set achieving (22) (might not be unique) is the solution of

where we let

Following [34, Section II-C] (and also [7, Lemma 2]), we remark that the solution to the max-min problem (23) can be found by hypothesis testing of three cases,  ,
,  , and
, and  . Formally, we have the following lemma.
. Formally, we have the following lemma.
Lemma 4.
The optimal  , solution of (23), is given by one of the three solutions.
, solution of (23), is given by one of the three solutions.
Case 1.
 maximizes
maximizes

and satisfies  .
.
Case 2.
 maximizes
maximizes

and satisfies  .
.
Case 3.
 maximizes
maximizes

and satisfies  for some
for some  .
.
Before considering the weighted sum rate maximization (23), one applies SVD to  ,
, 

where  ,
,  , and
, and  are unitary,
are unitary,  contain positive singular values
contain positive singular values  ,
,  , respectively. Following [7, Theorem 3], one applies Lemma 4 to solve the weighted sum rate maximization.
, respectively. Following [7, Theorem 3], one applies Lemma 4 to solve the weighted sum rate maximization.
Theorem 5.
The set of the optimal covariances  , achieving the boundary of the achievable rate region
, achieving the boundary of the achievable rate region  of the Vandermonde precoding, corresponds to one of the following three solutions.
of the Vandermonde precoding, corresponds to one of the following three solutions.
Case 1.
 , if
, if  , solution of the following KKT conditions, satisfies
, solution of the following KKT conditions, satisfies 

where  with a positive semidefinite
with a positive semidefinite  for
for  ,
,  is determined such that
is determined such that  , and we let
, and we let  .
.
Case 2.
 if the following
if the following  fulfills
fulfills  .
.
We let  and
and  where
where  ,
,  are diagonal with the
are diagonal with the  th element given by
th element given by

where  is determined such that
is determined such that  .
.
Case 3.
 , if
, if  , solution of the following KKT conditions, satisfies
, solution of the following KKT conditions, satisfies  for some
for some 

where  with a positive semidefinite
with a positive semidefinite  for
for  ,
,  is determined such that
is determined such that  .
.
Proof.
Appendix B.
Remark 6.
Due to the non-concavity of the underlying weighted sum rate functions, it is generally difficult to characterize the boundary of the achievable rate region  except for some special cases. The special cases include the corner points, in particular, the secrecy rate for the case of sending only the confidential message (
except for some special cases. The special cases include the corner points, in particular, the secrecy rate for the case of sending only the confidential message ( ), as well as the maximum sum rate point for the equal weight case (
), as well as the maximum sum rate point for the equal weight case ( ). It is worth noticing that under equal weight the objective functions in three cases are all concave in
). It is worth noticing that under equal weight the objective functions in three cases are all concave in  ,
,  since
since  is concave if
is concave if  and
and  is concave if
is concave if  and
and  .
.
The maximum sum rate point  can be found by applying the following greedy search [7].
can be found by applying the following greedy search [7].
Greedy Search to Find the Maximum Sum Rate Point
( ) Find
) Find  ,
,  maximizing
maximizing  and check
and check  . If yes stop. Otherwise go to (2).
. If yes stop. Otherwise go to (2).
( ) Find
) Find  ,
,  maximizing
maximizing  and check
and check  . If yes stop. Otherwise go to (3).
. If yes stop. Otherwise go to (3).
( ) Find
) Find  ,
,  maximizing
maximizing  and check
and check  for some
for some  .
.
For the special case of  , Theorem 5 yields the achievable secrecy rate with the Vandermonde precoding.
, Theorem 5 yields the achievable secrecy rate with the Vandermonde precoding.
Corollary 7.
The Vandermonde precoding achieves the secrecy rate

where the last equality is obtained by applying SVD to  and plugging the power allocation of (30) with
and plugging the power allocation of (30) with  ,
,  ,
,  is determined such that
is determined such that  .
.
Finally, by focusing the behavior of the achievable rate region in the high SNR regime, we characterize the achievable d.o.f. region of the frequency-selective BCC (1).
Theorem 8.
The d.o.f. region of the frequency-selective BCC (1) with  Toeplitz matrices
Toeplitz matrices  is given as a union of
is given as a union of  satisfying
satisfying


where  ,
,  denote non-negative integers. The Vandermonde precoding achieves the above d.o.f. region.
denote non-negative integers. The Vandermonde precoding achieves the above d.o.f. region.
Proof.
The achievability follows rather trivially by applying Theorem 3. By considering equal power allocation over all  streams such that
streams such that  ,
,  , we obtain the rate tuple
, we obtain the rate tuple  where
where 

We first notice that the prelog factor of  as
as  depends only on the rank of
depends only on the rank of  . From Lemma 2, we obtain
. From Lemma 2, we obtain



where (a) follows from orthogonality between  and
and  , (b) follows from the fact that
, (b) follows from the fact that  is unitary satisfying
is unitary satisfying  . Notice that (36) yields
. Notice that (36) yields  . For the d.o.f.
. For the d.o.f.  of the common message, (36) and (38) yield
of the common message, (36) and (38) yield

which is dominated by the pre-log of  in (37). This establishes the achievability.
in (37). This establishes the achievability.
The converse follows by noticing that the inequalities (33) and (34) correspond to trivial upper bounds. The first inequality (33) corresponds to the s.d.o.f. of the MIMO wiretap channel with the legitimate channel  and the eavesdropper channel
and the eavesdropper channel  , which is bounded by
, which is bounded by  . The second inequality (34) follows because the total number of streams for receiver 1 cannot be larger than the d.o.f. of
. The second inequality (34) follows because the total number of streams for receiver 1 cannot be larger than the d.o.f. of  , that is,
, that is,  .
.
Figure 3 illustrates the region  of the frequency-selective BCC over
of the frequency-selective BCC over  dimensions. We notice that the s.d.o.f. constraint (33) yields the line segment
dimensions. We notice that the s.d.o.f. constraint (33) yields the line segment  ,
,  while the constraint (34) in terms of the total number of streams for receiver 1 yields the line segment
while the constraint (34) in terms of the total number of streams for receiver 1 yields the line segment  ,
,  .
.
4. Multiuser Secure Communications
In this section, we provide some applications of the Vandermonde precoding in the multi-user secure communication scenarios where the transmitter wishes to send confidential messages to more than one intended receivers. The scenarios that we address are: (a) a  -user frequency-selective BCC with
-user frequency-selective BCC with  confidential messages and one common message, (b) a two-user frequency-selective BCC with two confidential messages and one common message. For each scenario, by focusing on the behavior in the high SNR regime, we characterize the achievable s.d.o.f. region and show the optimality of the Vandermonde precoding.
confidential messages and one common message, (b) a two-user frequency-selective BCC with two confidential messages and one common message. For each scenario, by focusing on the behavior in the high SNR regime, we characterize the achievable s.d.o.f. region and show the optimality of the Vandermonde precoding.
4.1. K + 1-User BCC with K Confidential Messages
As an extension of Section 3, we consider the  -user frequency-selective BCC where the transmitter sends
-user frequency-selective BCC where the transmitter sends  confidential messages
confidential messages  to the first
to the first  receivers as well as one common message
receivers as well as one common message  to all receivers. Each of the confidential messages must be kept secret to receiver
to all receivers. Each of the confidential messages must be kept secret to receiver  . Notice that this model, called multireceiver wiretap channel, has been studied in the literature ([20, 22–26] and reference therein). In particular, the secrecy capacity region of the Gaussian MIMO multireceiver wiretap channel has been characterized in [24, 26] for
. Notice that this model, called multireceiver wiretap channel, has been studied in the literature ([20, 22–26] and reference therein). In particular, the secrecy capacity region of the Gaussian MIMO multireceiver wiretap channel has been characterized in [24, 26] for  , an arbitrary
, an arbitrary  , respectively, where the optimality of the S-DPC is proved.
, respectively, where the optimality of the S-DPC is proved.
The received signal  of receiver
of receiver  and the received signal
and the received signal  of receiver
of receiver  at any block are given by
at any block are given by


where  is the transmit vector satisfying the total power constraint and
is the transmit vector satisfying the total power constraint and  ,
,  are mutually independent AWGN with covariance
are mutually independent AWGN with covariance  . We assume that the
. We assume that the  vectors
vectors  ,
,  of length
of length  are linearly independent and perfectly known to all the terminals. As an extension of the frequency-selective BCC in Section 2, we say that the rate tuple
are linearly independent and perfectly known to all the terminals. As an extension of the frequency-selective BCC in Section 2, we say that the rate tuple  is achievable if for any
is achievable if for any  there exists a sequence of codes
there exists a sequence of codes  such that
such that

where we denote  and define
and define

An achievable secrecy rate region  for the case of
for the case of  , when the transmitter sends two confidential messages in the presence of an external eavesdropper, is provided in [25, Theorem 1]. This theorem can be extended to an arbitrary
, when the transmitter sends two confidential messages in the presence of an external eavesdropper, is provided in [25, Theorem 1]. This theorem can be extended to an arbitrary  while including the common message. Formally we state the following lemma.
while including the common message. Formally we state the following lemma.
Lemma 9.
An achievable rate region of the  +1-user BCC, where the transmitter sends
+1-user BCC, where the transmitter sends  confidential messages intended to the first
confidential messages intended to the first  receivers as well as a common message to all users, is given as a union of all non-negative rate-tuple satisfying
receivers as well as a common message to all users, is given as a union of all non-negative rate-tuple satisfying

where  denotes a permutation over the subset
denotes a permutation over the subset  ,
,  denotes the cardinality of
denotes the cardinality of  , we let
, we let  , and the random variables
, and the random variables  ,
,  ,
,  ,
,  ,
,  satisfy the Markov chain
satisfy the Markov chain

Proof.
Appendix C.
Notice that the second term of the last equation in (44) can be also expressed by

It can be easily seen that without the secrecy constraint the above region reduces to the Marton's achievable region for the general  -user broadcast channel [35].
-user broadcast channel [35].
In order to focus on the behavior of the region in the high SNR regime, we define the s.d.o.f. region as

where  denotes the d.o.f. of the common message and
denotes the d.o.f. of the common message and  denotes the s.d.o.f. of confidential message
denotes the s.d.o.f. of confidential message  . As an extension of Theorem 8, we have the following s.d.o.f. region result.
. As an extension of Theorem 8, we have the following s.d.o.f. region result.
Theorem 10.
The s.d.o.f. region of the  -user frequency-selective BCC (40) is a union of
-user frequency-selective BCC (40) is a union of  satisfying
satisfying


where  are non-negative integers. The Vandermonde precoding achieves this region.
are non-negative integers. The Vandermonde precoding achieves this region.
Proof.
Appendix D.
Figure 4 illustrates the region  for the case of
for the case of  confidential messages. It can be easily seen that the constraint (49) in terms of the total number of streams for the virtual receiver yields the subspace
confidential messages. It can be easily seen that the constraint (49) in terms of the total number of streams for the virtual receiver yields the subspace  ,
,  ,
,  while the s.d.o.f. constraint (48) for the virtual receiver yields the subspace
while the s.d.o.f. constraint (48) for the virtual receiver yields the subspace  ,
,  ,
,  ,
,  . We remark that for the special case of one confidential message and one common message (
. We remark that for the special case of one confidential message and one common message ( ), the region reduces to Figure 3.
), the region reduces to Figure 3.
Remark 11.
When only the  confidential messages are transmitted to the
confidential messages are transmitted to the  intended receivers in the presence of the eavesdropper, the s.d.o.f. region has the equivalent MIMO interpretation [36]. More specifically, the frequency-selective BCC (40) is equivalent to the MIMO-BCC where the transmitter with
intended receivers in the presence of the eavesdropper, the s.d.o.f. region has the equivalent MIMO interpretation [36]. More specifically, the frequency-selective BCC (40) is equivalent to the MIMO-BCC where the transmitter with  dimensions (antennas) sends messages to
dimensions (antennas) sends messages to  receivers with
receivers with  antennas each in the presence of the eavesdropper with
antennas each in the presence of the eavesdropper with  antennas. The secrecy constraint (orthogonal constraint) consumes
antennas. The secrecy constraint (orthogonal constraint) consumes  dimensions of the channel seen by the virtual receiver and lets the number of effective transmit antennas be
dimensions of the channel seen by the virtual receiver and lets the number of effective transmit antennas be  . The resulting channel is the MIMO-BC without secrecy constraint with
. The resulting channel is the MIMO-BC without secrecy constraint with  transmit antennas and
transmit antennas and  receivers with
receivers with  antennas each, whose multiplexing gain is
antennas each, whose multiplexing gain is  (we assume
(we assume  ). Figure 5 illustrates the example with
). Figure 5 illustrates the example with  ,
,  ,
,  .
.
4.2. Two-User BCC with Two Confidential Messages
We consider the two-user BCC where the transmitter sends two confidential messages  ,
,  as well as one common message
as well as one common message  . Each of the confidential messages must be kept secret to the unintended receiver. This model has been studied in [17–19] for the case of two confidential messages and in [20] for the case of two confidential messages and a common message. In [19], the secrecy capacity region of the MIMO Gaussian BCC was characterized. The received signal at receivers 1, 2 at any block is given, respectively, by
. Each of the confidential messages must be kept secret to the unintended receiver. This model has been studied in [17–19] for the case of two confidential messages and in [20] for the case of two confidential messages and a common message. In [19], the secrecy capacity region of the MIMO Gaussian BCC was characterized. The received signal at receivers 1, 2 at any block is given, respectively, by

where  is the input vector satisfying the total power constraint and
is the input vector satisfying the total power constraint and  ,
,  are mutually independent AWGN with covariance
are mutually independent AWGN with covariance  . We assume the channel vectors
. We assume the channel vectors  ,
,  are linearly independent.
are linearly independent.
We say that the rate tuple  is achievable if for any
is achievable if for any  there exists a sequence of codes
there exists a sequence of codes  such that
such that

where we define the average error probability as

where  is the output of decoders 1, 2, respectively. A secrecy achievable rate region of the two-user BCC with two confidential messages and a common message is given by [20, Theorem 1]
is the output of decoders 1, 2, respectively. A secrecy achievable rate region of the two-user BCC with two confidential messages and a common message is given by [20, Theorem 1]

where the random variables satisfy the Markov chain

We extend Theorem 8 to the two-user frequency-selective BCC (50) and obtain the following s.d.o.f. result.
Theorem 12.
The s.d.o.f. region of the two-user frequency-selective BCC (50) is a union of  satisfying
satisfying


where  are non-negative integers. The Vandermonde precoding achieves the region.
are non-negative integers. The Vandermonde precoding achieves the region.
Proof.
Appendix F.
Figure 6 represents the s.d.o.f. region  over
over  dimensions of the two-user frequency-selective BCC. The per-receiver s.d.o.f. constraints (55) yield the subspace
dimensions of the two-user frequency-selective BCC. The per-receiver s.d.o.f. constraints (55) yield the subspace  ,
,  ,
,  ,
,  for user 1 and the subspace
for user 1 and the subspace  ,
,  ,
,  ,
,  for user 2. The constraints (56) in terms of the total number of streams per receiver yield the subregion
for user 2. The constraints (56) in terms of the total number of streams per receiver yield the subregion  ,
,  ,
,  for user 1 and the subregion
for user 1 and the subregion  ,
,  ,
,  for user 2. For the special case of one confidential message and one common message, the region reduces to Figure 3.
for user 2. For the special case of one confidential message and one common message, the region reduces to Figure 3.
Remark 13.
Comparing Theorems 10, 12 as well as Figures 4, 6 for  , it clearly appears that the s.d.o.f. of
, it clearly appears that the s.d.o.f. of  -user BCC with
-user BCC with  confidential messages is dominated by the s.d.o.f. of
confidential messages is dominated by the s.d.o.f. of  -user BCC with
-user BCC with  confidential messages. In other words, the s.d.o.f. region critically depends on the assumption on the eavesdropper(s) to whom each confidential message must be kept secret.
confidential messages. In other words, the s.d.o.f. region critically depends on the assumption on the eavesdropper(s) to whom each confidential message must be kept secret.
Remark 14.
When only two confidential messages are transmitted in the two-user frequency-selective BCC, the set of the s.d.o.f. has the equivalent MIMO interpretation [36]. More specifically, the frequency-selective BCC (40) is equivalent to the MIMO-BCC where the transmitter with  dimensions (antennas) sends two confidential messages to two receivers with
dimensions (antennas) sends two confidential messages to two receivers with  antennas. The secrecy constraint consumes
antennas. The secrecy constraint consumes  dimensions for each MIMO link and lets the number of effective transmit antennas be
dimensions for each MIMO link and lets the number of effective transmit antennas be  for each user. The resulting channel is a two parallel
for each user. The resulting channel is a two parallel  point-to-point MIMO channel without eavesdropper. Notice that the same parallel MIMO links can be obtained by applying the block diagonalization on the MIMO-BC without secrecy constraint [36]. In other words, the secrecy constraint in the BCC with inner eavesdroppers is equivalent to the orthogonal constraint in the classical MIMO-BC. Figure 7 shows the example with
point-to-point MIMO channel without eavesdropper. Notice that the same parallel MIMO links can be obtained by applying the block diagonalization on the MIMO-BC without secrecy constraint [36]. In other words, the secrecy constraint in the BCC with inner eavesdroppers is equivalent to the orthogonal constraint in the classical MIMO-BC. Figure 7 shows the example with  ,
,  and
and  confidential messages.
confidential messages.
5. Numerical Examples
In order to examine the performance of the proposed Vandermonde precoding, this section provides some numerical results in different settings.
5.1. Secrecy Rate versus SNR
We evaluate the achievable secrecy rate  in (32) when the transmitter sends only a confidential message to receiver 1 (without a common message) in the presence of receiver 2 (eavesdropper) over the frequency-selective BCC studied in Section 3.
in (32) when the transmitter sends only a confidential message to receiver 1 (without a common message) in the presence of receiver 2 (eavesdropper) over the frequency-selective BCC studied in Section 3.
5.1.1. MISO Wiretap Channel
For the sake of comparison (albeit unrealistic), we consider the special case of the frequency-selective wiretap channel when receiver 1 has a scalar observation and the eavesdropper has  observations. This is equivalent to the MISO wiretap channel with the receiver 1 channel
observations. This is equivalent to the MISO wiretap channel with the receiver 1 channel  and the eavesdropper channel
and the eavesdropper channel  . Without loss of generality, we assume that the observation at receiver 1 is the first row of
. Without loss of generality, we assume that the observation at receiver 1 is the first row of  . We consider that all entries of
. We consider that all entries of  ,
,  are i.i.d.
are i.i.d.  and average the secrecy rate over a large number of randomly generated channels with
and average the secrecy rate over a large number of randomly generated channels with  ,
,  . In Figure 8, we compare the optimal beamforming strategy [10, 13, 14] and the Vandermonde precoding as a function of SNR
. In Figure 8, we compare the optimal beamforming strategy [10, 13, 14] and the Vandermonde precoding as a function of SNR  . Since only one stream is sent to receiver 1, the s.d.o.f. is
. Since only one stream is sent to receiver 1, the s.d.o.f. is  . In fact, the MISO secrecy capacity in the high SNR regime is given by
. In fact, the MISO secrecy capacity in the high SNR regime is given by

where  is the beamforming vector. The Vandermonde precoding achieves
is the beamforming vector. The Vandermonde precoding achieves

where  denotes the
denotes the  th column of
th column of  orthogonal to
orthogonal to  . Clearly, there exists a constant gap between (57) and (58) due to the suboptimal choice of the beamforming vector.
. Clearly, there exists a constant gap between (57) and (58) due to the suboptimal choice of the beamforming vector.
5.1.2. MIMO Wiretap Channel
We consider the frequency-selective wiretap channel with  ,
,  . Although there exists a closed-form expression under a power-covariance constraint [15], the secrecy capacity under a total power constraint in (11) is still difficult to compute (especially for a large dimension of
. Although there exists a closed-form expression under a power-covariance constraint [15], the secrecy capacity under a total power constraint in (11) is still difficult to compute (especially for a large dimension of  and
and  ) because it requires a search over all possible power covariances constraints. Therefore, in Figure 9, we compare the averaged secrecy rate achieved by the generalized SVD scheme [5] and the Vandermonde precoding. We assume that all entries of
) because it requires a search over all possible power covariances constraints. Therefore, in Figure 9, we compare the averaged secrecy rate achieved by the generalized SVD scheme [5] and the Vandermonde precoding. We assume that all entries of  are i.i.d.
are i.i.d.  . For the Vandermonde precoding, we show the achievable rate with waterfilling power allocation (32) and equal power allocation (36) by allocating
. For the Vandermonde precoding, we show the achievable rate with waterfilling power allocation (32) and equal power allocation (36) by allocating  to
to  streams. As observed, these two suboptimal schemes achieve the same s.d.o.f. of
streams. As observed, these two suboptimal schemes achieve the same s.d.o.f. of  although the generalized SVD incurs a substantial power loss. The result agrees well with Theorem 8. We remark also that the optimal waterfilling power allocation yields a negligible gain.
although the generalized SVD incurs a substantial power loss. The result agrees well with Theorem 8. We remark also that the optimal waterfilling power allocation yields a negligible gain.
5.2. The Maximum Sum Rate Point (R0, R1) versus SNR
We consider the frequency-selective BCC with one confidential message to receiver 1 and one common message to two receivers. In particular, we characterize the maximum sum rate-tuple corresponding to  on the boundary of the achievable rate region
on the boundary of the achievable rate region  . Figure 10 shows the averaged maximum sum rate-tuple
. Figure 10 shows the averaged maximum sum rate-tuple  of the Vandermonde precoding both with optimal input covariance computed by the greedy algorithm and with equal power allocation. We remark that there is essentially no loss with the equal power allocation.
of the Vandermonde precoding both with optimal input covariance computed by the greedy algorithm and with equal power allocation. We remark that there is essentially no loss with the equal power allocation.
5.3. Two-User Secrecy Rate Region in the Frequency-Selective BCC
We consider the two-user frequency-selective BCC where the transmitter sends two confidential messages (no common message) of Section 4.2. For the sake of comparison (albeit unrealistic), we consider the special case of one observation  at each receiver. Notice that the two-user frequency-selective BCC is equivalent to the two-user MISO BCC with
at each receiver. Notice that the two-user frequency-selective BCC is equivalent to the two-user MISO BCC with  whose secrecy capacity region is achieved by the S-DPC scheme [18]. The proposed Vandermonde precoding achieves the secrecy rate region given by all possible rate-tuples
whose secrecy capacity region is achieved by the S-DPC scheme [18]. The proposed Vandermonde precoding achieves the secrecy rate region given by all possible rate-tuples 

satisfying  where
where  denotes the
denotes the  th column of
th column of  orthogonal to
orthogonal to  ,
,  orthogonal to
orthogonal to  , respectively. Figure 11 compares the averaged secrecy rate region of the Vandermonde precoding, zero-forcing beamforming, and the optimal S-DPC scheme for
, respectively. Figure 11 compares the averaged secrecy rate region of the Vandermonde precoding, zero-forcing beamforming, and the optimal S-DPC scheme for  where all entries of
where all entries of  are i.i.d.
are i.i.d.  . As observed, the Vandermonde precoding achieves the near-optimal rate region. As the number of paths
. As observed, the Vandermonde precoding achieves the near-optimal rate region. As the number of paths  increases, the gap with respect to the S-DPC becomes smaller since the Vandermonde precoding tends to choose the optimal beamformer matched to the channels.
increases, the gap with respect to the S-DPC becomes smaller since the Vandermonde precoding tends to choose the optimal beamformer matched to the channels.
6. Conclusions
We considered the secured communication over the frequency-selective channel by focusing on the frequency-selective BCC. In the case of a block transmission of  symbols followed by a guard interval of
symbols followed by a guard interval of  symbols discarded at both receivers, the frequency-selective channel can be modeled as an
symbols discarded at both receivers, the frequency-selective channel can be modeled as an  Toeplitz matrix. For this special type of MIMO channels, we proposed a practical yet order-optimal Vandermonde precoding which enables to send
Toeplitz matrix. For this special type of MIMO channels, we proposed a practical yet order-optimal Vandermonde precoding which enables to send  streams of the confidential messages and
streams of the confidential messages and  streams of the common messages simultaneously over a block of
streams of the common messages simultaneously over a block of  dimensions. The key idea here consists of exploiting the frequency dimension to "hide" confidential information in the zeros of the channel seen by the unintended receiver similarly to the spatial beamforming. We also provided some application of the Vandermonde precoding in the multiuser secured communication scenarios and proved the optimality of the proposed scheme in terms of the achievable s.d.o.f. region.
dimensions. The key idea here consists of exploiting the frequency dimension to "hide" confidential information in the zeros of the channel seen by the unintended receiver similarly to the spatial beamforming. We also provided some application of the Vandermonde precoding in the multiuser secured communication scenarios and proved the optimality of the proposed scheme in terms of the achievable s.d.o.f. region.
We conclude this paper by noticing that there exists a simple approach to establish secured communications. More specifically, perfect secrecy can be built in two separated blocks: (1) a precoding that cancels the channel seen by the eavesdropper to fulfill the equivocation requirement, (2) the powerful off-the-shelf encoding techniques to achieve the secrecy rate. Since the practical implementation of secrecy encoding techniques (double binning) remains a formidable challenge, such design is of great interest for the future secrecy systems.
References
Wyner AD: The wiretap channel. Bell System Technical Journal 1975., 54:
Leung-Yan-Cheong SK, Hellman ME: The Gaussian wire-tap channel. IEEE Transactions on Information Theory 1978, 24(4):451-456. 10.1109/TIT.1978.1055917
Csiszár I, Körner J: Broadcast channels with confidential messages. IEEE Transactions on Information Theory 1978, 24(3):339-348. 10.1109/TIT.1978.1055892
Gopala PK, Lai L, El Gamal H: On the secrecy capacity of fading channels. IEEE Transactions on Information Theory 2008, 54(10):4687-4698.
Khisti A, Wornell G: The MIMOME channel. Proceedings of the 45th Annual Allerton Conference on Communication, Control, and Computing, 2007
Liu T, Prabhakaran V, Vishwanath S: The secrecy capacity of a class of parallel Gaussian compound wiretap channels. Proceedings of the IEEE International Symposium on Information Theory (ISIT '08), 2008, Toronto, Canada 116-120.
Liang Y, Poor HV, Shamai S: Secure communication over fading channels. IEEE Transactions on Information Theory 2008, 54(6):2470-2492.
Goel S, Negi R: Secret communication in presence of colluding eavesdroppers. Proceedings of the 62nd IEEE Vehicular Technology Conference (VTC '05), 2005, Atlantic City, NJ, USA 3:
Parada P, Blahut R: Secrecy capacity of SIMO and slow fading channels. Proceedings of the IEEE International Symposium on Information Theory (ISIT '05), 2005 2152-2155.
Khisti A, Wornell G: Secure transmission with multiple antennas: the MISOME wiretap channel. submitted to IEEE Transactions on Information Theory, 2007
Liu T, Shamai S: A note on the secrecy capacity of the multi-antenna wiretap channel. submitted to IEEE Transactions on Information Theory, 2007
Oggier F, Hassibi B: The secrecy capacity of the MIMO wiretap channel. Proceedings of the IEEE International Symposium on Information Theory (ISIT '08), 2008, Toronto, Canada 524-528.
Shafiee S, Ulukus S: Achievable rates in Gaussian MISO channels with secrecy constraints. Proceedings of the IEEE International Symposium on Information Theory, 2007 2466-2470.
Khisti A, Wornell G, Wiesel A, Eldar Y: On the Gaussian MIMO wiretap channel. Proceedings of the IEEE International Symposium on Information Theory (ISIT '07), 2007, Nice, France 2471-2475.
Bustin R, Liu R, Poor HV, Shamai (Shitz) S: An MMSE approach to the secrecy capacity of the MIMO Gaussian wiretap channel. EURASIP Journal on Wireless Communications and Networking. In press
Ly HD, Liu T, Liang Y: MIMO broadcasting with common, private, and confidential messages. Proceedings of the International symposium on Information Theory and Its Applications (ISITA '08), December 2008, Auckland, New Zealand
Liu R, Maric I, Spasojevic P, Yates RD: Discrete memoryless interference and broadcast channels with confidential messages: secrecy rate regions. IEEE Transactions on Information Theory 2008, 54(6):2493-2507.
Liu R, Poor HV: Secrecy capacity region of a multi-antenna Gaussian broadcast channel with confidential messages. IEEE Transactions on Information Theory 2009, 55(3):1235-1249.
Liu R, Liu T, Poor HV, Shamai (Shitz) S: MIMO Gaussian broadcast channels with confidential messages. Proceedings of the IEEE Symposium on Information Theory (ISIT '09), June-July 2009, Seoul, Korea
Choo LC, Wong KK: The K-receiver broadcast channel with confidential messages. Proceedings of the IEEE International Symposium on Information Theory (ISIT '09), 2009, Seoul, Korea
Khisti A, Tchamkerten A, Wornell GW: Secure broadcasting over fading channels. IEEE Transactions on Information Theory 2008, 54(6):2453-2469.
Choo LC, Wong KK: The three-receiver broadcast channel with degraded message sets and confidential messages. submitted to IEEE Transactions on Information Theory
Ekrem E, Ulukus S: Secrecy capacity of a class of broadcast channels with an eavesdropper. submitted to EURASIP Journal on Wireless Communications and Networking
Ekrem E, Ulukus S: The secrecy capacity region of the Gaussian MIMO multi-receiver wiretap channel. submitted to IEEE Transactions on Information Theory
Bagherikaram G, Motahari AS, Khandani AK: The secrecy rate region of the broadcast channel. preprint, 2008, http://arxiv.org/abs/0806.4200
Bagherikaram G, Motahari AS, Khandani AK: The secrecy capacity region of the Gaussian MIMO broadcast channel. preprint, 2009, http://arxiv.org/abs/0903.3261
Koyluoglu OO, El Gamal H, Lai L, Poor HV: Interference alignment for secrecy. preprint, 2008, http://arxiv.org/abs/0810.1187
ANSI/IEEE Std 802.11, Edition (R2003), 1999, http://standards.ieee.org/getieee802/download/802.11-1999.pdf
Air Interface for Fixed and Mobile Broadband Wireless Access Systems, 2005, http://standards.ieee.org/getieee802/download/802.16e-2005.pdf
Ryan Ø, Debbah M: Asymptotic behaviour of random vandermonde matrices with entries on the unit circle. IEEE Transactions on Information Theory 2009., 55(7):
Cardoso LS, Kobayashi M, Ryan Ø, Debbah M: Vandermonde frequency division multiplexing for cognitive radio. Proceedings of the 9th IEEE Workshop on Signal Processing Advances in Wireless Communications (SPAWC '08), 2008, Recife, Brazil 421-425.
Scaglione A, Giannakis GB, Barbarossa S: Lagrange/Vandermonde MUI eliminating user codes forquasi-synchronous CDMA in unknown multipath. IEEE Transactions on Signal Processing 2000, 48(7):2057-2073. 10.1109/78.847790
Poor HV: An Introduction to Signal Detection and Estimation. Springer, New York, NY, USA; 1994.
Viswanath P, Tse DNC: Sum capacity of the vector Gaussian broadcast channel and uplink-downlink duality. IEEE Transactions on Information Theory 2003, 49(8):1912-1921. 10.1109/TIT.2003.814483
Lee J, Jindal N: High SNR analysis for MIMO broadcast channels: dirty paper coding versus linear precoding. IEEE Transactions on Information Theory 2007, 53(12):4787-4792.
Viswanathan H, Venkatesan S, Huang H: Downlink capacity evaluation of cellular networks with known-interference cancellation. IEEE Journal on Selected Areas in Communications 2003, 21(5):802-811. 10.1109/JSAC.2003.810346
Zhang X, Chen J, Wicker SB, Berger T: Successive coding in multiuser information theory. IEEE Transactions on Information Theory 2007, 53(6):2246-2254.
Cover T, Thomas J: Elements of Information Theory. John Wiley & Sons, New York, NY, USA; 1991.
Acknowledgments
The work is supported by the European Commission in the framework of the FP7 Network of Excellence in Wireless COMmunications NEWCOM++. The work of M. Debbah is supported by Alcatel-Lucent within the Alcatel-Lucent Chair on Flexible Radio at Supelec. The authors wish to thank Yingbin Liang for helpful discussions, and the anonymous reviewers for constructive comments. The material in this paper was partially presented at IEEE 19th International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC), Cannes, France, September 2008.
Author information
Authors and Affiliations
Corresponding author
Appendices
A. Proof of Lemma 2
In this appendix, we consider the rank of  where
where  satisfies the orthogonality
satisfies the orthogonality  . By letting
. By letting  denote the
denote the  th column of
th column of  we have
we have  for the case of
for the case of  . We define the matrix
. We define the matrix  orthogonal to
orthogonal to  by appending
by appending  rows
rows  to
to 


Notice that all  rows are linearly independent. By definition of
rows are linearly independent. By definition of  , it is not difficult to see that
, it is not difficult to see that  and
and  form a complete set of basis for an
form a complete set of basis for an  -dimensional linear space. Indeed for
-dimensional linear space. Indeed for  the matrix
the matrix  reduces to
reduces to  , while
, while  , a subset of a projection matrix onto the null space of
, a subset of a projection matrix onto the null space of  is appended to
is appended to  . Hence
. Hence  can be expressed as
can be expressed as


where  is the projection of
is the projection of  onto the row vectors of
onto the row vectors of  with an
with an  coefficient matrix
coefficient matrix  ,
,  is the projection of
is the projection of  onto the row vectors of
onto the row vectors of  with an
with an  coefficient matrix
coefficient matrix 


where (a) follows from the orthogonality  and
and  , (b) follows from
, (b) follows from  . The equality (c) is obtained as follows. We notice
. The equality (c) is obtained as follows. We notice


where in (d) adding  does not change the rank, (e) follows because any set of
does not change the rank, (e) follows because any set of  rows taken from
rows taken from  is linearly independent (from the assumption that
is linearly independent (from the assumption that  ,
,  are linearly independent). Since
are linearly independent). Since  is orthogonal to
is orthogonal to  , (A.4) yields
, (A.4) yields


which establishes (c).
B. Proof of Theorem 5
We consider the following three cases given in Lemma 4.
Case 1.
Supposing  , we consider the objective function
, we consider the objective function  in (25). The objective is concave only when
in (25). The objective is concave only when  . Nevertheless, we consider the KKT conditions which are necessary for the optimality. It can be easily shown that the KKT conditions are given by (29) where
. Nevertheless, we consider the KKT conditions which are necessary for the optimality. It can be easily shown that the KKT conditions are given by (29) where  is the Lagrangian dual matrix associated to the positive semidefiniteness constraint of
is the Lagrangian dual matrix associated to the positive semidefiniteness constraint of  for
for  and
and  is the Lagrangian dual variable associated to the total power constraint. It clearly appears that for
is the Lagrangian dual variable associated to the total power constraint. It clearly appears that for  the objective is concave in
the objective is concave in  ,
,  and the problem at hand is convex. In this case, any convex optimization algorithm, the gradient-based algorithm [37] for example, can be applied to find the optimal solution while the algorithm converges to a local optimal solution for
and the problem at hand is convex. In this case, any convex optimization algorithm, the gradient-based algorithm [37] for example, can be applied to find the optimal solution while the algorithm converges to a local optimal solution for  .
.
Case 2.
Supposing  , we consider the objective function
, we consider the objective function  in (26). Since the problem is convex (
in (26). Since the problem is convex ( is concave and the constraint is linear in
is concave and the constraint is linear in  ), the KKT conditions are necessary and sufficient for optimality. We form the Lagrangian and obtain the following KKT conditions:
), the KKT conditions are necessary and sufficient for optimality. We form the Lagrangian and obtain the following KKT conditions:


where  is the Lagrangian dual matrix associated to the positive semidefiniteness constraint of
is the Lagrangian dual matrix associated to the positive semidefiniteness constraint of  for
for  and
and  is the Lagrangian dual variable associated to the total power constraint. By creating
is the Lagrangian dual variable associated to the total power constraint. By creating  parallel channels via SVD on
parallel channels via SVD on  ,
,  in (28), we readily obtain the solution (30).
in (28), we readily obtain the solution (30).
Case 3.
For  , we consider the objective function
, we consider the objective function  in (27). In the following we focus on
in (27). In the following we focus on  . Notice that if
. Notice that if  we have
we have  which yields the corner point
which yields the corner point  where
where  denotes the secrecy rate characterized in (32). The KKT conditions, necessary for the optimality, are given by (31) where
denotes the secrecy rate characterized in (32). The KKT conditions, necessary for the optimality, are given by (31) where  is the Lagrangian dual matrix associated to the positive semidefiniteness constraints for
is the Lagrangian dual matrix associated to the positive semidefiniteness constraints for  and
and  is the Lagrangian dual variable associated to the total power constraint. The gradient-based algorithm [37] can be applied to find the solution satisfying these KKT conditions. Although this algorithm yields the optimal and unique solution for
is the Lagrangian dual variable associated to the total power constraint. The gradient-based algorithm [37] can be applied to find the solution satisfying these KKT conditions. Although this algorithm yields the optimal and unique solution for  , the algorithm converges to a local optimal solution for
, the algorithm converges to a local optimal solution for  .
.
C. Proof of Lemma 9
In the following, we provide the encoding/decoding scheme to achieve a vertex point within  corresponding to a specific encoding order
corresponding to a specific encoding order  . Our proof builds on the successive Gel'fand-Pinsker coding [38] and random binning for ensuring the perfect secrecy. The overall region
. Our proof builds on the successive Gel'fand-Pinsker coding [38] and random binning for ensuring the perfect secrecy. The overall region  is obtained by taking the union over all possible
is obtained by taking the union over all possible  encoding orders followed by the convex hull operation. We extensively use the notation
encoding orders followed by the convex hull operation. We extensively use the notation  to denote a set of jointly typical sequences
to denote a set of jointly typical sequences  of length
of length  with respect to the distribution
with respect to the distribution  . We let
. We let  arbitrary small for a large
arbitrary small for a large  .
.
(a) Codebook Generation
Fix  and
and  . We define for
. We define for 


and we let  . the joint distribution factors as The stochastic encoder randomly generates
. the joint distribution factors as The stochastic encoder randomly generates
-
(i)
i.i.d. codewords
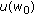 according
according  where
where 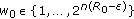 .
. -
(ii)
For user
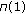 ,
,  i.i.d. codewords
i.i.d. codewords 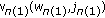 with
with 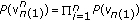 , where the indices are given by
, where the indices are given by (C2)
(C2) -
(iii)
For user
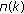 ,
,  i.i.d. codewords
i.i.d. codewords 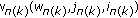 with
with 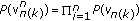 , where the indices are given by
, where the indices are given by (C3)
(C3)
(b) Encoding
To send the messages  , we first choose randomly the index
, we first choose randomly the index  and the corresponding codeword
and the corresponding codeword  . Given the common message
. Given the common message  , we choose randomly the codeword
, we choose randomly the codeword  within the bin
within the bin  , that is, the index
, that is, the index  , such that
, such that  . Then successively choose the codeword
. Then successively choose the codeword  , that is, the indices
, that is, the indices  , such that
, such that


If there are more than one such sequence, it randomly selects one. Finally the encoder selects according to  .
.
(c) Decoding
The received signals at the  legitimate receivers are
legitimate receivers are  , the outputs of the channels
, the outputs of the channels  for any
for any  . Receiver
. Receiver  chooses
chooses  so that
so that


if such pair  exists and unique. Otherwise it declares an error.
exists and unique. Otherwise it declares an error.
(d) Error Probability Analysis
Without loss of generality, we assume that the message set is  . We remark that an error is declared if one or more of the following events occur.
. We remark that an error is declared if one or more of the following events occur.
-
(i)
Encoding fails


From the construction of the codebook above, we have  .
.
-
(ii)
Decoding step 1 fails; there does not exist a jointly typical sequence for some
 , that is,
, that is,


From joint typicality [39] we have  for any
for any  .
.
-
(iii)
Decoding step 2 fails; there exits other sequences satisfying the joint typicality for some


It can be shown that we have  if
if


for any  . Hence, the error probability
. Hence, the error probability  if the rate-tuple satisfies (44).
if the rate-tuple satisfies (44).
(e) Equivocation Calculation
To prove the equivocation requirement


where we denote  , we remark that it is sufficient to verify the above inequality for
, we remark that it is sufficient to verify the above inequality for  due to [24, Lemma 1]. Hence, we check whether the the sum rate secrecy constraint is satisfied by the proposed encoding strategy.
due to [24, Lemma 1]. Hence, we check whether the the sum rate secrecy constraint is satisfied by the proposed encoding strategy.


where (a) follows because the conditioning decrease the entropy, (b) follows from Fano's inequality [39] stating that for a sufficiently large  we have
we have


where  denotes the eavesdropper's error probability when decoding
denotes the eavesdropper's error probability when decoding  with the knowledge on the message indices
with the knowledge on the message indices  . We have that
. We have that  as
as  if
if  . (c) follows from the Markov chain
. (c) follows from the Markov chain  , (d) follows by ignoring a nonnegative term
, (d) follows by ignoring a nonnegative term  , (e) follows because
, (e) follows because  for any permutation
for any permutation  over the set
over the set  , (f) follows because
, (f) follows because  for any
for any  , finally (g) follows because the successive encoder yields the sum rate given by
, finally (g) follows because the successive encoder yields the sum rate given by


This establishes the achievability.
D. Proof of Theorem 10
The achievability follows by extending Theorem 8 to the case of  confidential messages. First we remark that as a straightforward extension of Lemma 2 the following lemma holds.
confidential messages. First we remark that as a straightforward extension of Lemma 2 the following lemma holds.
Lemma D.15.
For  , there exists a matrix
, there exists a matrix  with
with  orthonormal columns with size
orthonormal columns with size  satisfying
satisfying




where  denotes the number of columns of
denotes the number of columns of 
A sketch of proof is given in Appendix E.
We let  be unitary matrix with
be unitary matrix with  orthonormal columns in the null space of
orthonormal columns in the null space of  such that
such that  . In other words, the Vandermonde precoder
. In other words, the Vandermonde precoder  is a squared unitary matrix satisfying
is a squared unitary matrix satisfying  . Based on the Vandermonde precoder
. Based on the Vandermonde precoder  , we construct the transmit vector
, we construct the transmit vector  as
as


where  are mutually independent Gaussian vectors with zero mean and covariance
are mutually independent Gaussian vectors with zero mean and covariance  satisfying
satisfying  . From the orthogonality properties (D.1), the received signals become
. From the orthogonality properties (D.1), the received signals become


where receiver  observes the common message, the intended confidential message, and the interference from other users, while receiver
observes the common message, the intended confidential message, and the interference from other users, while receiver  observes only the common message. By letting
observes only the common message. By letting  ,
,  for
for  ,
,  and considering the equal power allocation to all
and considering the equal power allocation to all  streams, we readily obtain
streams, we readily obtain








and we also have  from the independency between
from the independency between  conditioned on
conditioned on  . Plugging this together with (D.7) and (D.8) into (44), we have
. Plugging this together with (D.7) and (D.8) into (44), we have


In order to find the d.o.f. region, we notice








where (a) follows from orthogonality between  and
and  for
for  , (b) follows from the fact that
, (b) follows from the fact that  is unitary satisfying
is unitary satisfying  , and (c) follows from Lemma D.15. From (D.11) and (D.12), we readily obtain
, and (c) follows from Lemma D.15. From (D.11) and (D.12), we readily obtain  , which is dominated by (D.10). Combining (D.12) and (D.13), we obtain
, which is dominated by (D.10). Combining (D.12) and (D.13), we obtain  for
for  . This completes the achievability.
. This completes the achievability.
The converse follows by a natural extension of Theorem 8 to the  -user BCC. To obtain the constraint (48), we consider that the first
-user BCC. To obtain the constraint (48), we consider that the first  receivers perfectly cooperate to decode the
receivers perfectly cooperate to decode the  confidential messages and one common message. By treating these
confidential messages and one common message. By treating these  receivers as a virtual receiver with
receivers as a virtual receiver with  antennas, we immediately obtain the bound (48) corresponding to the s.d.o.f. of the MIMO wiretap channel with the virtual receiver channel
antennas, we immediately obtain the bound (48) corresponding to the s.d.o.f. of the MIMO wiretap channel with the virtual receiver channel  and the eavesdropper channel
and the eavesdropper channel  . The bound (49) is obtained by noticing that the total number of streams that receiver
. The bound (49) is obtained by noticing that the total number of streams that receiver  can decode is limited by the d.o.f. of
can decode is limited by the d.o.f. of  , that is,
, that is,  . Namely, we have the following
. Namely, we have the following  inequalities:
inequalities:


which yields  . Further by letting
. Further by letting  for any
for any  and and
and and  for any
for any  , we obtain
, we obtain  . Adding the last inequality and (48), we obtain (49). This establishes the converse.
. Adding the last inequality and (48), we obtain (49). This establishes the converse.
E. Proof of Lemma D.15
We consider  for a subset
for a subset  . First we let
. First we let  denote
denote  orthonormal columns that form a unitary Vandermonde matrix orthogonal to
orthonormal columns that form a unitary Vandermonde matrix orthogonal to  . For any subset
. For any subset  , we let
, we let  be the unitary matrix formed by
be the unitary matrix formed by  columns corresponding to the subset
columns corresponding to the subset  taken from
taken from  . Since a unitary matrix formed by
. Since a unitary matrix formed by  for any
for any  can be expressed equivalently as
can be expressed equivalently as  , we consider
, we consider  . For a given
. For a given  , we let
, we let  denote a unitary matrix composed by
denote a unitary matrix composed by  columns corresponding to the complementary set
columns corresponding to the complementary set  such that
such that  . In order to derive the rank, we follow the same approach as Appendix A. We define the matrix
. In order to derive the rank, we follow the same approach as Appendix A. We define the matrix  orthogonal to
orthogonal to  by appending
by appending  to
to 


where the  rows are linearly independent. Since
rows are linearly independent. Since  and
and  form a complete set of an
form a complete set of an  -dimensional linear space,
-dimensional linear space,  can be expressed as
can be expressed as


where  is a coefficient matrix with dimension
is a coefficient matrix with dimension  ,
,  respectively. By recalling that any set of
respectively. By recalling that any set of  rows taken from
rows taken from  is linearly independent for
is linearly independent for  (from the assumption that
(from the assumption that  are linearly independent), we can repeat the same argument as Appendix A and obtain
are linearly independent), we can repeat the same argument as Appendix A and obtain


which yields the result.
F. Proof of Theorem 12
The achievability follows by generalizing Theorem 8 for the case of two confidential messages. We remark that by symmetry Lemma 2 for one beamforming matrix  can be trivially extended to two beamforming matrices
can be trivially extended to two beamforming matrices  and
and  . Namely, we have
. Namely, we have
Lemma F.16.
For  and
and  , there exists
, there exists  with
with  orthnormal columns for
orthnormal columns for  satisfying
satisfying




Further, we let  be a unitary matrix with
be a unitary matrix with  orthonormal columns in the null space of
orthonormal columns in the null space of  such that
such that  . We construct
. We construct  by Gaussian superposition coding based on the Vandermonde precoder
by Gaussian superposition coding based on the Vandermonde precoder  ,
,  , and
, and  . From (F.1), each user observes the vector of its confidential message and that of the common message, that is,
. From (F.1), each user observes the vector of its confidential message and that of the common message, that is,


By letting  ,
,  for
for  ,
,  and considering equal power allocation to all streams with
and considering equal power allocation to all streams with  , we readily obtain
, we readily obtain


We remark


where (a) follows from orthogonality between  and
and  for
for  , (b) follows because
, (b) follows because  or
or  spans a complete
spans a complete  -dimensional space. These equations yield
-dimensional space. These equations yield  for
for  . This establishes the achievability.
. This establishes the achievability.
The converse follows by noticing that the constraints (55) and (56) correspond to trivial upper bounds. To obtain (55), we consider the special case when the transmitter sends only one confidential message to one of two receivers in the presence of the eavesdropper. When sending one confidential message to receiver 1, the two-user frequency-selective BCC reduces to the MIMO wiretap channel with the legitimate channel  and the eavesdropper channel
and the eavesdropper channel  , whose s.d.o.f. is upper bounded by
, whose s.d.o.f. is upper bounded by  . The same bound holds for receiver 2 when transmitting one confidential message to receiver 2 in the presence the eavesdropper (receiver 1). The upper bounds (56) follow because the total number of streams per receiver is limited by the individual
. The same bound holds for receiver 2 when transmitting one confidential message to receiver 2 in the presence the eavesdropper (receiver 1). The upper bounds (56) follow because the total number of streams per receiver is limited by the individual  MIMO link. This establishes the converse.
MIMO link. This establishes the converse.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Kobayashi, M., Debbah, M. & Shamai (Shitz), S. Secured Communication over Frequency-Selective Fading Channels: A Practical Vandermonde Precoding. J Wireless Com Network 2009, 386547 (2009). https://doi.org/10.1155/2009/386547
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/386547


 obtained by the convex hull on
obtained by the convex hull on
 .
.

 of frequency-selective BCC.
of frequency-selective BCC.
 over
over  dimensions of three-user frequency-selective BCC.
dimensions of three-user frequency-selective BCC.

 over
over  dimensions of
dimensions of  -user frequency-selective BCC.
-user frequency-selective BCC.

 ,
,
 (MISO wiretap channel).
(MISO wiretap channel).

 ,
,
 (MIMO wiretap channel).
(MIMO wiretap channel).

 in the frequency-selective BCC.
in the frequency-selective BCC.

 (MISO-BCC).
(MISO-BCC).
 according
according  where
where 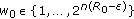 .
.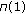 ,
,  i.i.d. codewords
i.i.d. codewords 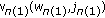 with
with 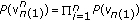 , where the indices are given by
, where the indices are given by
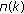 ,
,  i.i.d. codewords
i.i.d. codewords 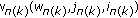 with
with 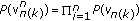 , where the indices are given by
, where the indices are given by
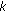 , that is,
, that is,