- Research Article
- Open access
- Published:
Synchronization Algorithms and Receiver Structures for Multiuser Filter Bank Uplink Systems
EURASIP Journal on Wireless Communications and Networking volume 2009, Article number: 387520 (2009)
Abstract
We address the synchronization problem in an uplink multiuser filter bank system. The system differs from orthogonal frequency division multiple access (OFDMA) since it deploys subchannel frequency confined pulses. User multiplexing is still accomplished by partitioning the tones among the active users. Users are asynchronous such that the received signals experience independent time offsets, carrier frequency offsets, and multipath fading. We first consider the synchronization problem in conventional receivers that implement an analysis filter bank with precompensation of the subchannel time and frequency offsets followed by recursive least square linear subchannel equalization. Several correlation metrics that use data training are described. Then, we consider the synchronization problem in a novel multiuser receiver that comprises two efficiently implemented fractionally spaced analysis filter banks. In this receiver, time/frequency compensation can be jointly done for all the users. Despite its lower complexity, we show that it approaches the performance of single-user transmission.
1. Introduction
In this paper, we consider the synchronization problem for filter bank (FB) modulation in a multiple access uplink wireless channel. In particular, we consider an FB system that uses frequency confined subchannel pulses. The users are multiplexed by partitioning the tones in a frequency division multiple access (FDMA) mode. This system is also referred to as multiuser filtered multitone (FMT) [1, 2]. Orthogonal frequency division multiple access (OFDMA) differs from multiuser FMT since it deploys rectangular time-domain pulses that exhibit a sinc frequency response [3]. The multiuser FMT transmitter can be efficiently implemented using an inverse fast Fourier transform (IFFT) followed by low-rate subchannel filtering [1, 4, 5]. The subchannel frequency confinement makes multiuser FMT more robust than OFDMA in an asynchronous uplink channel, where the signals of distinct users experience independent time offsets from propagation delays, carrier frequency offsets from misadjusted oscillators, or Doppler effects from movement, and propagation through multipath fading channels [6–8].
Although the synchronization problem in OFDM/OFDMA has received great attention and several results have been obtained, as, for instance, the algorithms in [9, 10], synchronization in FMT systems, and more in general in multiuser FMT, has not been extensively investigated. Synchronization involves the estimation of the users' time and frequency offsets as well as the estimation of the channel impulse response. In [11], a blind scheme has been considered for synchronization in single-user FMT that exploits the redundancy of the oversampled FB. In [12], both time domain and frequency domain algorithms with data training have been investigated. In [13], a nondata-aided timing recovery scheme has been proposed for single-user FB modulation.
The synchronization problem depends on the particular receiver structure adopted. In this paper, we first describe two conventional receiver structures. The first receiver uses an analysis FB that is matched to the individual subchannels after time and frequency compensation. The second receiver deploys an FB, where compensation is done at user level, that is, a single value for the time phase, and the carrier frequency offset is deployed for all the subchannels of a given user. Then, symbol-spaced subchannel recursive least square (RLS) equalization is performed [14]. In both cases, we address the problem of estimating the time and frequency offsets. We consider a training approach and devise several metrics that exploit the subchannel separability of FMT deriving from the use of frequency confined subchannel pulses. We also propose an iterative approach where the analysis FB is iteratively matched to the received signals by estimating the time and frequency offsets at the FB output followed by feedback to the input [15].
A drawback of the above receivers is that they have high complexity. In particular, the subchannel-synchronized receiver does not allow for an efficient implementation. On the other hand, the user-synchronized receiver can be implemented via polyphase low-rate filtering followed by a fast Fourier transform. However, one analysis FB per user is required. Further, the synchronization stage is implemented at sampling time which yields extremely high complexity. Therefore, to simplify the complexity, we propose the use of a novel fractionally spaced analysis FB that allows jointly detecting all the subchannels of the asynchronous users with lower complexity compared to the traditional single-user receiver that requires one synchronous FB per user. In this receiver, the compensation of the time offsets and carrier frequency offsets is jointly performed for all users. The fractionally spaced outputs are processed by subchannel fractionally spaced RLS equalizers. The practical implementation of this multiuser receiver is studied, and a metric for the estimation of the parameters is proposed. Numerical results show that it nearly achieves the performance of single-user FMT. Further, its complexity is significantly lower than that of the conventional receivers both during the synchronization stage and the detection stage.
The paper is organized as follows: we describe the multiuser FMT system model in Section 2. In Section 3, we describe the three receiver structures considered in this paper. In Section 4, we address the synchronization problem and propose metrics for all three receivers. In Section 5, we study the complexity of these receivers. In Section 6, we report several performance results. Finally, the conclusions follow.
2. Multiuser FMT System Model
We consider a multiuser FB modulation architecture, where multiplexing is performed via partitioning the subchannels among the users (Figure 1). We denote by  the prototype subchannel pulse, where
the prototype subchannel pulse, where  is the sampling period. (The sampling period
is the sampling period. (The sampling period  is assumed to be the time unit and
is assumed to be the time unit and  denotes the set of integer numbers.) The subchannel carrier frequency is denoted by
denotes the set of integer numbers.) The subchannel carrier frequency is denoted by 
 where
where  is the total number of tones. It follows that the complex baseband transmitted signal of user
is the total number of tones. It follows that the complex baseband transmitted signal of user  can be written as
can be written as

where  is the
is the  subchannel data stream of user
subchannel data stream of user  that we assume to belong to the M-QAM constellation set and that has rate
that we assume to belong to the M-QAM constellation set and that has rate  with
with  In FMT, the prototype pulse has frequency confined response with Nyquist bandwidth
In FMT, the prototype pulse has frequency confined response with Nyquist bandwidth  The interpolation factor
The interpolation factor  is chosen to increase the frequency separation between subchannels and to ease the construction of finite impulse response (FIR) pulses that minimize the amount of intercarrier interference (ICI) and multiple access interference (MAI) at the receiver side. Distinct FMT subchannels are assigned to distinct users. Thus, the symbols in (1) are set to zero for the unassigned FMT subchannels:
is chosen to increase the frequency separation between subchannels and to ease the construction of finite impulse response (FIR) pulses that minimize the amount of intercarrier interference (ICI) and multiple access interference (MAI) at the receiver side. Distinct FMT subchannels are assigned to distinct users. Thus, the symbols in (1) are set to zero for the unassigned FMT subchannels:

where  denotes the set of
denotes the set of  subchannel indices that are assigned to user
subchannel indices that are assigned to user 
At the receiver, the complex discrete time received signal can be written as

where  and
and  is a sampling phase.
is a sampling phase.  is the number of users,
is the number of users,  is the time offset of user u that is due to asynchronous transmission and/or propagation delays,
is the time offset of user u that is due to asynchronous transmission and/or propagation delays,  and
and  are the carrier frequency and phase offset,
are the carrier frequency and phase offset,  is the fading channel impulse response, and
is the fading channel impulse response, and  is the additive white Gaussian noise with zero-mean contribution. We assume the time/frequency offset to be identical for all the subchannels that are assigned to a given user.
is the additive white Gaussian noise with zero-mean contribution. We assume the time/frequency offset to be identical for all the subchannels that are assigned to a given user.
3. Receiver Structures
The base station has to detect all users' signals that are affected, according to the model in (3), by carrier frequency offsets, and propagation delays, as well as by different dispersive channel impulse responses. In this section, we first describe two conventional receiver structures. Then, we propose a novel multiuser receiver that allows lowering the complexity.
3.1. Conventional Receivers
In the subchannel-synchronized receiver (SCS-RX), synchronization is done at subchannel level. That is, we deploy an analysis FB where each subchannel filter is matched to the transmit pulse, compensates the frequency offset by an amount  and adjusts the time phase by an amount
and adjusts the time phase by an amount  The outputs are then sampled at rate
The outputs are then sampled at rate  and processed by linear subchannel equalization before detection. The synchronization parameters,
and processed by linear subchannel equalization before detection. The synchronization parameters,  and
and  , have to be estimated. We use a training approach as it is explained in the next section. It should be noted that the optimal subchannel sampling phase can vary across the subchannels. This is because the propagation channel frequency selectivity translates into different subchannel equivalent impulse responses.
, have to be estimated. We use a training approach as it is explained in the next section. It should be noted that the optimal subchannel sampling phase can vary across the subchannels. This is because the propagation channel frequency selectivity translates into different subchannel equivalent impulse responses.
The subchannel output of user  can then be written as
can then be written as

where the superscript * denotes the complex conjugate operation and  is the sequence of filtered noise samples. The relation (4) has been obtained following the derivation in Appendix . We have separated the term that carries the useful data symbol from the term that represents the subchannel intersymbol (ISI) contribution, the ICI term that is generated by the subchannels of index
is the sequence of filtered noise samples. The relation (4) has been obtained following the derivation in Appendix . We have separated the term that carries the useful data symbol from the term that represents the subchannel intersymbol (ISI) contribution, the ICI term that is generated by the subchannels of index  of user
of user  , and the MAI term that is generated by the subchannels that belong to the other users. These interference terms are the consequence of using a nonperfectly orthogonal FB, the presence of time/frequency offset, and channel frequency selectivity. An interesting characteristic of FMT is that the ICI/MAI contribution is negligible when frequency-confined pulses are used. Ideally, it is null with perfectly confined pulses if the frequency offsets are smaller than half the guard band among subchannels, that is,
, and the MAI term that is generated by the subchannels that belong to the other users. These interference terms are the consequence of using a nonperfectly orthogonal FB, the presence of time/frequency offset, and channel frequency selectivity. An interesting characteristic of FMT is that the ICI/MAI contribution is negligible when frequency-confined pulses are used. Ideally, it is null with perfectly confined pulses if the frequency offsets are smaller than half the guard band among subchannels, that is,

where  is the excess band of the prototype pulse. Clearly, some intersymbol interference in each subchannel may be present and can be counteracted with subchannel equalization. In this paper, we consider linear equalizers. In fact the subchannel equivalent response is not an ideal pulse, and it can be written as
is the excess band of the prototype pulse. Clearly, some intersymbol interference in each subchannel may be present and can be counteracted with subchannel equalization. In this paper, we consider linear equalizers. In fact the subchannel equivalent response is not an ideal pulse, and it can be written as

where 
The inner sum in (6) represents the correlation between the prototype pulse and the pulse itself modulated by  If
If  , the analysis FB has a frequency mismatch with the synthesis FB. Further, the factor
, the analysis FB has a frequency mismatch with the synthesis FB. Further, the factor  that weights the useful data symbol in (4) introduces a time-variant rotation of the constellation.
that weights the useful data symbol in (4) introduces a time-variant rotation of the constellation.
On the other hand, if the estimation of the frequency offset is perfect, the equivalent impulse response reads

where  is the autocorrelation of the prototype pulse.
is the autocorrelation of the prototype pulse.
The SCS-RX not only compensates the time offset of a given user, but it also uses an optimal time phase for each subchannel. In fact  comprises both the propagation delay and the effect of the multipath channel that moves the position of the peak of the subchannel impulse responses as (7) shows. Such a peak is the amplitude of the useful data symbol in (4).
comprises both the propagation delay and the effect of the multipath channel that moves the position of the peak of the subchannel impulse responses as (7) shows. Such a peak is the amplitude of the useful data symbol in (4).
The SCS-RX has good performance as it will be shown in Section 6, but it has a significant drawback since it cannot be implemented using an efficient discrete Fourier transform (DFT) polyphase FB. The efficient FMT analysis FB comprises serial-to-parallel conversion of the received sample stream, low-rate subchannel filtering with pulses that are obtained by the polyphase decomposition of the prototype pulse, and finally a DFT [1, 4]. A unique time phase for all the subchannels must be used, which does not allow adjusting timing at the subchannel level.
To simplify the complexity of the SCS-RX, we can compensate the time offset with a common value  and the frequency offset with a common value
and the frequency offset with a common value  for all the subchannels of a given user. We refer to this receiver as user-synchronized receiver (US-RX). Now, one efficient analysis FB per user can be deployed whose realization can be done as described in [4] or in [5] when the tones are regularly interleaved among the users. Subchannel equalization with symbol-spaced equalizers is performed. Although the US-RX can be implemented in an efficient way, it still requires one FB per user. Further, it suffers from a performance penalty compared to the SCS-RX (Section 5).
for all the subchannels of a given user. We refer to this receiver as user-synchronized receiver (US-RX). Now, one efficient analysis FB per user can be deployed whose realization can be done as described in [4] or in [5] when the tones are regularly interleaved among the users. Subchannel equalization with symbol-spaced equalizers is performed. Although the US-RX can be implemented in an efficient way, it still requires one FB per user. Further, it suffers from a performance penalty compared to the SCS-RX (Section 5).
3.2. Fractionally Spaced Multiuser Receiver
To reduce further the complexity and increase the performance, we propose a novel architecture that uses only two fractionally spaced analysis FBs to detect all  signals that are partitioned among the
signals that are partitioned among the  users. The block diagram is depicted in Figure 2. We refer to this receiver as fractionally spaced multiuser receiver (FS-RX). The FB outputs are processed with fractionally spaced linear subchannel equalizers, whose coefficients are obtained according to the minimum mean square error (MMSE) criterion [16]. The use of a fractionally spaced equalizer allows having a common time phase for all the users. Fine synchronization is not required. Only synchronization at symbol level is required, and this can be done at the output of the bank of filters.
users. The block diagram is depicted in Figure 2. We refer to this receiver as fractionally spaced multiuser receiver (FS-RX). The FB outputs are processed with fractionally spaced linear subchannel equalizers, whose coefficients are obtained according to the minimum mean square error (MMSE) criterion [16]. The use of a fractionally spaced equalizer allows having a common time phase for all the users. Fine synchronization is not required. Only synchronization at symbol level is required, and this can be done at the output of the bank of filters.
It should be noted that with ideal band-limited pulses, neither ICI nor MAI is present also with this receiver. However, the use of an inexact sampling phase (as a result of imperfect synchronization) may yield increased subchannel ISI which has to be handled with equalization. Further, a problem to be solved is the joint compensation of the carrier frequency offsets that differ among the users. This is accomplished, in our proposal, by the correction of part of the frequency offset before the FB (precompensation), and part after it (postcompensation).
We define  where
where  is a positive integer, and
is a positive integer, and  is the least common multiple between
is the least common multiple between  and
and  Then, we define the frequency offset as the sum of an integer multiple of
Then, we define the frequency offset as the sum of an integer multiple of  and a fractional part
and a fractional part  that is,
that is,

where we choose the integer  according to the following rule:
according to the following rule:

that corresponds to minimize the fractional frequency offset at the output of the receiver FB as it will be explained in the following. In (9), we have assumed  such that adjacent FMT subchannels do not completely overlap as a result of the frequency offset.
such that adjacent FMT subchannels do not completely overlap as a result of the frequency offset.
Now, the FS-RX precompensates the integer part of the frequency offset by the estimated value  before subchannel filtering and it samples the outputs at rate
before subchannel filtering and it samples the outputs at rate  that is, we collect two samples per transmitted subchannel symbol. Therefore, the two subchannel outputs of index
that is, we collect two samples per transmitted subchannel symbol. Therefore, the two subchannel outputs of index  belonging to user u are
belonging to user u are

where  . The sampling phase
. The sampling phase  is set to zero and to
is set to zero and to  Further,
Further,  is the residual error in the correction of the integer part of the frequency offset. ICI and MAI terms are negligible due to the subchannel spectral containment. Their detailed expression is derived in Appendix . The subchannel equivalent response reads
is the residual error in the correction of the integer part of the frequency offset. ICI and MAI terms are negligible due to the subchannel spectral containment. Their detailed expression is derived in Appendix . The subchannel equivalent response reads

The factor  that weights the useful data symbol in (10) introduces a time-variant rotation of the constellation. However, it can be estimated and compensated at the subchannel filter output, that is, postcompensation. The factor
that weights the useful data symbol in (10) introduces a time-variant rotation of the constellation. However, it can be estimated and compensated at the subchannel filter output, that is, postcompensation. The factor  in the inner sum in (11) cannot be compensated, and it yields a frequency mismatch between the transmitted subchannel and the analysis subchannel filter which is minimized for
in the inner sum in (11) cannot be compensated, and it yields a frequency mismatch between the transmitted subchannel and the analysis subchannel filter which is minimized for  when the estimation of the integer part of the frequency offset is perfect. Therefore, the precompensation of only the integer part of the frequency offset translates in both a subchannel SNR loss and an increased ISI. However, as it is shown in Section 6, the penalty in performance can be negligible for practical frequency offset values, that is, when
when the estimation of the integer part of the frequency offset is perfect. Therefore, the precompensation of only the integer part of the frequency offset translates in both a subchannel SNR loss and an increased ISI. However, as it is shown in Section 6, the penalty in performance can be negligible for practical frequency offset values, that is, when  is small over the duration of the prototype pulse.
is small over the duration of the prototype pulse.
The joint correction of the integer part of the frequency offset for all the users can be realized in an efficient receiver implementation. Following the derivation in [4] for the single-user case, if we apply the polyphase decomposition with period  to the filtering operation in the first line of (10), under the hypothesis of precompensating the frequency offset by
to the filtering operation in the first line of (10), under the hypothesis of precompensating the frequency offset by  we obtain
we obtain

with


being the polyphase decomposition of the received sample stream.
Equations (12) and (13) suggest the scheme in Figure 2, where each of the two analysis FBs comprises the following steps:
-
(i)
serial-to-parallel conversion of the input sample stream, interpolation by a factor
 filtering with the polyphase pulses
filtering with the polyphase pulses 
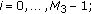
-
(ii)
computation of an
 DFT, and sampling the DFT outputs with index
DFT, and sampling the DFT outputs with index 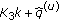 for
for 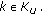 This is to obtain the subchannel signals of user
This is to obtain the subchannel signals of user  and to partly compensate the frequency shift introduced by the integer part of the carrier frequency offset;
and to partly compensate the frequency shift introduced by the integer part of the carrier frequency offset; -
(iii)
combining the signals in (12) for
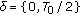 to obtain a set of
to obtain a set of 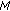 sample streams at rate
sample streams at rate 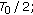
-
(iv)
compensation of the fractional frequency offset (after estimation) with multiplication by
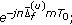
-
(v)
finally, a fractionally spaced subchannel equalizer processes the signals.
It should be noted that the correction of the integer part of the frequency offset is done by choosing the appropriate output tone of the  DFT (shifted tone). If we increase
DFT (shifted tone). If we increase  we reduce the amount of the residual frequency offset
we reduce the amount of the residual frequency offset  at the expense of complexity since the size of the DFT increases.
at the expense of complexity since the size of the DFT increases.
In the FS-RX, the parameters to be estimated are  and the integer part of the frequency offset. This is addressed in the next section.
and the integer part of the frequency offset. This is addressed in the next section.
4. Synchronization
We deploy a training approach to estimate the time/frequency offsets in the three receiver structures. Each user transmits a frame of data that comprises a known training data portion  ,
, 
 , that is, a training sequence per subchannel. The training sequence is also used to train the MMSE subchannel equalizer using a recursive least square algorithm (RLS) [14].
, that is, a training sequence per subchannel. The training sequence is also used to train the MMSE subchannel equalizer using a recursive least square algorithm (RLS) [14].
The estimation of the parameters can be done either at the input of the analysis FB or at the output of it, or jointly at the input and at the output of it. We refer to the first two approaches, respectively, as preestimation and as postestimation of the parameters. The third approach can be performed using an iterative procedure where we first filter the received signal with a bank of filters that is matched to the transmit FB. Second, the time offset and the frequency offset of the user are postestimated at its outputs. Third, we rerun the FB by now precompensating the received signal with the estimated time/frequency offset. The procedure is iteratively repeated. This iterative approach makes particularly sense for application to the SCS-RX and the US-RX. At each iteration, we essentially decrease the frequency mismatch between the synthesis and analysis FBs.
Therefore, at the first iteration (when we do not have any a priori knowledge of the time/frequency offset of the desired user) we run the following FB for the channels of user 

The outputs are used to compute a correlation metric with known training symbols. In particular, we consider three approaches for the correlation metric that are described in the next section. The metric allows determining an estimate of the time offset and the frequency offset, that are denoted as  and
and  respectively.
respectively.
Once the estimates above are computed, we rerun the receiver FB. However, now the FB can exploit the knowledge of the estimated time/frequency offset. Thus, for this new iteration we compute

Now, using the outputs in (16), we can recompute the synchronization metrics in an iterative fashion and estimate the time and frequency offsets for this new iteration.
In the following, we propose several synchronization metrics for the receivers structures herein described. They implement at the FB output an appropriately defined correlation with the training data. The correlation is done either in time (along the time dimension for a given subchannel) and/or in frequency (across the subchannels).
4.1. Metrics for the Conventional Receivers
Let us assume that the carrier frequency offsets fulfil the relation 
 such that they are small compared to the subchannel bandwidth which is a realistic assumption in a practical system. Then, (15) can be written as
such that they are small compared to the subchannel bandwidth which is a realistic assumption in a practical system. Then, (15) can be written as

for  and
and  , that is, in correspondence to the training sequence. In (17),
, that is, in correspondence to the training sequence. In (17),  denotes the equivalent subchannel impulse response that corresponds to (6) with the assumption
denotes the equivalent subchannel impulse response that corresponds to (6) with the assumption  and
and  . The expressions for the
. The expressions for the  and
and  are given in (A.3) and (A.4) of Appendix . Observing (17), if we assume the training sequence to have good autocorrelation properties, the following synchronization metric can be devised:
are given in (A.3) and (A.4) of Appendix . Observing (17), if we assume the training sequence to have good autocorrelation properties, the following synchronization metric can be devised:


It essentially performs a correlation with lag  of the subchannel outputs divided by the training data. An example of it is shown in Figure 3 for several subchannels of a user in an FMT system that deploys 32 tones and multiplexes 4 users by regularly interleaving the tones across them. The channel has an exponential power delay profile. More details on the system parameters are reported in Section 6. The peak of (18) is in correspondence to the training sequence. In fact, for
of the subchannel outputs divided by the training data. An example of it is shown in Figure 3 for several subchannels of a user in an FMT system that deploys 32 tones and multiplexes 4 users by regularly interleaving the tones across them. The channel has an exponential power delay profile. More details on the system parameters are reported in Section 6. The peak of (18) is in correspondence to the training sequence. In fact, for  we obtain
we obtain

where  denotes the function that returns the argument that maximizes the expression. It should be noted that the contribution of ICI and MAI in
denotes the function that returns the argument that maximizes the expression. It should be noted that the contribution of ICI and MAI in  is small due to the good spectral subchannel containment. The lag
is small due to the good spectral subchannel containment. The lag  is chosen to take into account the presence of subchannel ISI, and it has to be such that
is chosen to take into account the presence of subchannel ISI, and it has to be such that  is larger than the subchannel time dispersion. This is shown in Appendix . Figure 3 also shows that the peak of the correlation metric differs among subchannels.
is larger than the subchannel time dispersion. This is shown in Appendix . Figure 3 also shows that the peak of the correlation metric differs among subchannels.
Metric (18) is used to locate the training sequence and to estimate the time offset of subchannel  of user
of user  as follows:
as follows:

while it is used to estimate the frequency offset as follows:

where  returns the phase of the complex number
returns the phase of the complex number  . The frequency offset estimation holds for
. The frequency offset estimation holds for  The frequency offsets can then be averaged across the subchannels since, in our assumptions, they do not differ for a given user.
The frequency offsets can then be averaged across the subchannels since, in our assumptions, they do not differ for a given user.
Finally, we point out that if we use the iterative approach described above, at each iteration, the refinement of the frequency offset estimation is such that the residual frequency offset at the bank output decreases.
The metric described above can be applied also to the US-RX. In this case starting from the estimates given by (21) and (22), we compute the average values

From (23), we obtain a common value for the time phase and carrier frequency offset that are used for all subchannels assigned to user 
In a different method the outputs  defined in (19) are used to compute the following correlation:
defined in (19) are used to compute the following correlation:

where  . The metric (24) corresponds to the computation of a correlation over each subchannel of a given user, followed by averaging over the subchannels. If we choose
. The metric (24) corresponds to the computation of a correlation over each subchannel of a given user, followed by averaging over the subchannels. If we choose  , we just need two training symbols per subchannel which minimizes the amount of redundancy required for synchronization.
, we just need two training symbols per subchannel which minimizes the amount of redundancy required for synchronization.
Metric (24) is used for time synchronization of user  as follows:
as follows:

while it is used to estimate the frequency offset as follows:

The frequency offset estimation holds for  This metric is not suitable for the SCS-RX since it gives a common estimate for the offsets of the subchannels of user
This metric is not suitable for the SCS-RX since it gives a common estimate for the offsets of the subchannels of user  .
.
The metric (24) in correspondence to the training sequence reads

Therefore, while in (20) the maximum is in correspondence to the peak of the squared magnitude of the subchannel equivalent response, in (27) the maximum is in correspondence to the sum of the subchannel equivalent responses assigned to a given user. It should be noted that this metric turns out to be effective when the user is allocated to a sufficient number of subchannels.
4.2. Metric for the Fractionally Spaced Multiuser Receiver
Since the FS-RX processes  -spaced samples, we can derive a synchronization metric starting from (24) provided that we sample it by a factor
-spaced samples, we can derive a synchronization metric starting from (24) provided that we sample it by a factor  Further, this receiver requires an estimate of the integer part
Further, this receiver requires an estimate of the integer part  and the fractional part
and the fractional part  of the frequency offset. We emphasize that in the efficient implementation of Figure 2, the compensation of the integer part of the frequency offset is accomplished by selecting for each user of index u the
of the frequency offset. We emphasize that in the efficient implementation of Figure 2, the compensation of the integer part of the frequency offset is accomplished by selecting for each user of index u the  -point DFT outputs of index
-point DFT outputs of index  for
for  , where
, where  is equal to the estimated value of the integer frequency offset.
is equal to the estimated value of the integer frequency offset.
From these considerations, we modify (24) as follows:


where  ,
,  is efficiently obtained as in (12).
is efficiently obtained as in (12).
The metric (28) is used to jointly estimate the integer part of the frequency offset and the symbol timing for user u as follows:

According to (30), we search the peak of the correlation (28) for each of the  possible values of the integer frequency offset. The position of the highest peak yields both the estimate
possible values of the integer frequency offset. The position of the highest peak yields both the estimate  and the user timing
and the user timing 
It should be noted that (28) can be written in a way similar to (27) provided that  is expressed as in (11). Therefore, the parameter estimates are chosen to maximize the sum of the squared amplitudes of the useful signals.
is expressed as in (11). Therefore, the parameter estimates are chosen to maximize the sum of the squared amplitudes of the useful signals.
Finally, the fractional frequency offset is estimated as follows:

The fractional frequency offset estimation holds for  Since frequency precompensation can be done for a value up to
Since frequency precompensation can be done for a value up to  the practical FS-RX works for a larger range of carrier frequency offset than the SCS-RX and the US-RX that use the synchronization metrics described before. It should be noted that the constraint
the practical FS-RX works for a larger range of carrier frequency offset than the SCS-RX and the US-RX that use the synchronization metrics described before. It should be noted that the constraint  can be satisfied by increasing
can be satisfied by increasing  , since
, since  decreases according to (8).
decreases according to (8).
5. Complexity Comparison
To evaluate the complexity of the proposed receiver structures, we consider separately the stage where the synchronization parameters are estimated and the detection stage. They are characterized by a different amount of complexity. This is because while detection may use an efficient implementation for the FB, synchronization for the conventional receivers requires inefficient processing at sampling time  In our analysis, we do not consider the complexity introduced by the subchannel equalizer since it is identical for all structures. Further, we assume that
In our analysis, we do not consider the complexity introduced by the subchannel equalizer since it is identical for all structures. Further, we assume that  subchannels are assigned in a regularly interleaved fashion to each user
subchannels are assigned in a regularly interleaved fashion to each user  The pulse has length
The pulse has length  coefficients.
coefficients.
5.1. Estimation of the Synchronization Parameters
We now consider the synchronization stage. We have first subchannel filtering and then a subchannel metric. The SCS-RX and the US-RX require processing at sampling time  , while the FS-RX processes data streams at rate
, while the FS-RX processes data streams at rate  The complexity of the inefficient FB realization for the SCS-RX and the US-RX is equal to the following number of complex operations (sums and multiplications) per second (NOPS):
The complexity of the inefficient FB realization for the SCS-RX and the US-RX is equal to the following number of complex operations (sums and multiplications) per second (NOPS):

The FS-RX deploys the efficient realization also for the estimation of the parameters. Thus, its complexity is equal to

Now, we focus on the metrics described in Section 4. The SCS-RX uses the metric (18) that works at sampling time  and requires
and requires

The metric (24) for the US-RX requires

For the FS-RX, the metric (28) works at sampling rate  and requires
and requires

Finally, we point out that each synchronization metric requires a different number of calls to the functions  and
and  . In the SCS-RX, there are M calls to these functions; in the US-RX, there are
. In the SCS-RX, there are M calls to these functions; in the US-RX, there are  calls; in the FS-RX, there are
calls; in the FS-RX, there are  calls to function
calls to function  and
and  calls to the function
calls to the function  .
.
5.2. Detection
At the detection stage, the SCS-RX not only compensates the time/frequency offset of a given user (already estimated), but it also uses an optimal time phase and frequency offset for each subchannel. For this reason, it can be implemented only using an inefficient high-complexity FB with no polyphase implementation. It corrects the frequency offset at its input, and it has  subchannels (per user) realized by a mixer and a decimation filter with
subchannels (per user) realized by a mixer and a decimation filter with  coefficients. It requires
coefficients. It requires

The US-RX compensates the time/frequency offset for each user, but it deploys a common sampling phase for all the subchannels of a given user. In this case, the efficient implementation with an FB per user can be deployed and realized with the method in [4, 5]. Since the tones are interleaved, we can exploit the discrete Fourier transform (DFT) properties and use a  -point DFT, yielding
-point DFT, yielding

In (38), we take into account the fact that only  coefficients at the FB outputs differ from zero. Their position cyclically shifts in an a priori known fashion, which allows simplifying the computation of the periodic transform.
coefficients at the FB outputs differ from zero. Their position cyclically shifts in an a priori known fashion, which allows simplifying the computation of the periodic transform.
The FS-RX has a complexity that is essentially equal to (33) plus  NOPS due to the correction of the fractional frequency offset.
NOPS due to the correction of the fractional frequency offset.
5.3. Numerical Example
In Table 1, we report a numerical example in terms of complex operations per second per user. We consider the following set of parameters: 


 ,
, 
 and
and  . Further, we consider 4 or 8 users. These parameters are also used in the next section about system performance. Looking at the synchronization stage the FS-RX shows a significant advantage in terms of complexity with respect to the SCS-RX and the US-RX. This is due to the possibility of deploying an efficient implementation also during the synchronization stage. Looking at the detection stage, the US-RX and the FS-RX have similar complexity but are both less complex than the SCS-RX.
. Further, we consider 4 or 8 users. These parameters are also used in the next section about system performance. Looking at the synchronization stage the FS-RX shows a significant advantage in terms of complexity with respect to the SCS-RX and the US-RX. This is due to the possibility of deploying an efficient implementation also during the synchronization stage. Looking at the detection stage, the US-RX and the FS-RX have similar complexity but are both less complex than the SCS-RX.
6. Performance Results
To evaluate the performance of the proposed synchronization algorithms, we consider an FMT system with  tones. A single user or four asynchronous users with interleaved tone allocation are present. The interpolation factor is
tones. A single user or four asynchronous users with interleaved tone allocation are present. The interpolation factor is  The prototype pulse has duration
The prototype pulse has duration  and it is designed according to the method in [4] which yields a good frequency confinement with a theoretical bandwidth equal to
and it is designed according to the method in [4] which yields a good frequency confinement with a theoretical bandwidth equal to  To simulate the asynchronous uplink, we assume the carrier frequency offsets independent and uniformly distributed in
To simulate the asynchronous uplink, we assume the carrier frequency offsets independent and uniformly distributed in  while the time offsets are uniformly distributed in
while the time offsets are uniformly distributed in  The user channels are assumed Rayleigh faded with an exponential power delay profile with independent T-spaced taps that have average power
The user channels are assumed Rayleigh faded with an exponential power delay profile with independent T-spaced taps that have average power  with
with  and truncation at
and truncation at  20 dB. The data symbols and the training sequences belong to the 4 PSK signal set. The training sequences are randomly generated. If, for example, we assume a 20 MHz bandwidth the channel has overall duration equal to 500 nanoseconds, and the transmission rate is 32 Mbit/s. The subchannel equalizers have length equal to 3 taps. Clearly, if we increase the number of subcarriers, the subchannel equalizer length may be shortened.
20 dB. The data symbols and the training sequences belong to the 4 PSK signal set. The training sequences are randomly generated. If, for example, we assume a 20 MHz bandwidth the channel has overall duration equal to 500 nanoseconds, and the transmission rate is 32 Mbit/s. The subchannel equalizers have length equal to 3 taps. Clearly, if we increase the number of subcarriers, the subchannel equalizer length may be shortened.
First, we consider the convergence of the synchronization metrics as a function of the training sequence length. In Figures 4 and 5 we plot the standard deviation of the frequency offset estimation error as a function of the training sequence length, respectively, for the metric that is used in the US-RX and the FS-RX. The estimation error has zero mean. The factor  in the estimator is set equal to 3. The SNR is set to 20 dB, and the curves are reported for two values of maximum-normalized frequency offset
in the estimator is set equal to 3. The SNR is set to 20 dB, and the curves are reported for two values of maximum-normalized frequency offset  . Both single-user and four-user transmissions are considered. In the latter case the error standard deviation is averaged over the users.
. Both single-user and four-user transmissions are considered. In the latter case the error standard deviation is averaged over the users.
The curves show that the estimation error standard deviation rapidly decreases with the increase of the training sequence length (herein we consider a length equal to  symbols). Looking at Figure 4, where the US-RX is considered, we see that in the 4-user case a degradation with respect to the single-user case is obtained. This is justified by the fact that in the multiuser case each user deploys a fraction equal to
symbols). Looking at Figure 4, where the US-RX is considered, we see that in the 4-user case a degradation with respect to the single-user case is obtained. This is justified by the fact that in the multiuser case each user deploys a fraction equal to  of the total number subchannels. Therefore, less redundancy in the frequency domain is exploited with respect to the single-user case. For instance, a standard deviation equal to
of the total number subchannels. Therefore, less redundancy in the frequency domain is exploited with respect to the single-user case. For instance, a standard deviation equal to  is achieved with training sequences of length 10 for the single-user case and
is achieved with training sequences of length 10 for the single-user case and  , while the same value is obtained with training sequences of length 23 for the four users case (Figure 4(a)).
, while the same value is obtained with training sequences of length 23 for the four users case (Figure 4(a)).
The curves also show that the estimator is robust to a wide range of frequency offsets. In fact, they remain nearly unchanged for the two values of carrier frequency offset herein shown. In Figure 4, we also show the standard deviation of the estimation error using 1 and 2 iterations according to the method described in Section 4. The second iteration provides some small benefit only for large carrier frequency offsets.
In Figure 5, we consider the FS-RX, and we report the standard deviation of the estimation error  , where
, where  is obtained from the estimation of the integer and fractional part. Then, the standard deviation is averaged over the users. For both the single-user case and the multiuser case, the estimation error standard deviation is larger than that obtained in the US-RX. Some small improvement is obtained by increasing the frequency resolution of the receiver, that is, increasing Q from 1 to 4. The effect of increasing Q is beneficial in the bit error rate (BER) performance, as we discuss in the following, for high values of carrier frequency offset.
is obtained from the estimation of the integer and fractional part. Then, the standard deviation is averaged over the users. For both the single-user case and the multiuser case, the estimation error standard deviation is larger than that obtained in the US-RX. Some small improvement is obtained by increasing the frequency resolution of the receiver, that is, increasing Q from 1 to 4. The effect of increasing Q is beneficial in the bit error rate (BER) performance, as we discuss in the following, for high values of carrier frequency offset.
In Figures 6 and 7, we report average BER as a function of the SNR for a maximum carrier frequency offset normalized to the subcarrier spacing  The ideal curves assume perfect synchronization and channel estimation, while the other curves assume practical synchronization and channel estimation with a single iteration for the SCS-RX and the US-RX. For the ideal case, we use a 3-tap subchannel MMSE equalizer. For the practical case, we use RLS training of the equalizer over the known synchronization sequences. The training sequences have length 30 unless otherwise stated.
The ideal curves assume perfect synchronization and channel estimation, while the other curves assume practical synchronization and channel estimation with a single iteration for the SCS-RX and the US-RX. For the ideal case, we use a 3-tap subchannel MMSE equalizer. For the practical case, we use RLS training of the equalizer over the known synchronization sequences. The training sequences have length 30 unless otherwise stated.
First, we consider the ideal curves. The US-RX exhibits an error floor both for 1 user (Figure 6(a)) and 4 users (Figure 7(a)). The best performance is achieved by the SCS-RX which remains practically unchanged with 1 or 4 asynchronous users. This shows the robustness of the FMT scheme to the multiple access interference due to the good subchannel spectral containment. The proposed FS-RX with ideal synchronization nearly achieves the performance of the SCS-RX both with 1 and 4 users.
Now, we consider the practical curves which allow benchmarking the performance of the synchronization parameter estimators (Figures 6(b) and 7(b)). Figure 6(b) shows that with a single user the practical curves are close to the ideal ones for all the receivers. The proposed FS-RX with practical synchronization performs better than the practical SCS-RX in the single-user case. Herein, we consider  , since for
, since for  we have not found improvements. Further, a single iteration is used by the estimator in the SCS-RX and the US-RX. With four users (Figure 7(b)) the practical FS-RX performs close to the SCS-RX with a penalty of about 1 dB at
we have not found improvements. Further, a single iteration is used by the estimator in the SCS-RX and the US-RX. With four users (Figure 7(b)) the practical FS-RX performs close to the SCS-RX with a penalty of about 1 dB at  and 2 dB at
and 2 dB at  . However, it has lower complexity. We also report in Figure 7(b) the BER curve that has been obtained with the FS-RX that uses synchronization sequences of length 20 instead of 30. The BER penalty is significant only at high SNRs.
. However, it has lower complexity. We also report in Figure 7(b) the BER curve that has been obtained with the FS-RX that uses synchronization sequences of length 20 instead of 30. The BER penalty is significant only at high SNRs.
Comparing the practical curves with the ideal ones, we see that a higher loss is found for the 4-user case. This is because we have fewer subchannels per user, so when we compute the synchronization metrics we have less redundancy in the frequency dimension.
To understand the dependency from the frequency offset value, we report in Figures 8 and 9 the BER as a function of the maximum carrier frequency offset. The SNR is set to 20 dB. Again, we first analyze the ideal curves. For  both the SCS-RX and the US-RX have performance independent of
both the SCS-RX and the US-RX have performance independent of  since the frequency offset is fully compensated (Figure 8(a)). The US-RX has lower performance than the SCS-RX. For
since the frequency offset is fully compensated (Figure 8(a)). The US-RX has lower performance than the SCS-RX. For  , the SCS-RX and the US-RX exhibit a rapid performance degradation only for
, the SCS-RX and the US-RX exhibit a rapid performance degradation only for  This is due to the multiple access interference that degrades performance when the carrier frequency offsets are such that the subchannels may overlap by more than
This is due to the multiple access interference that degrades performance when the carrier frequency offsets are such that the subchannels may overlap by more than  the excess band of the pulse.
the excess band of the pulse.
The FS-RX (Figure 8(b) and 9(b)) with ideal synchronization has performance close to the SCS-RX. Increasing the factor Q from 1 to 4 improves performance for  .
.
Now looking at the practical curves, for all receivers the performance is close to the ideal curves. Larger, although nonsignificantly high, penalties are seen for the 4-user case. The estimators for the SCS-RX and the US-RX (Figures 8(a) and 9(a)) provide estimates for normalized carrier frequency offsets up to 0.13 using  , while for the FS-RX up to 0.63.
, while for the FS-RX up to 0.63.
It should be noted that in Figure 9(a) the practical curves for  are better than the ideal ones. This can be justified by the fact that for large frequency offsets the MAI interference from subchannel overlapping can become significant. In particular a frequency offset equal to
are better than the ideal ones. This can be justified by the fact that for large frequency offsets the MAI interference from subchannel overlapping can become significant. In particular a frequency offset equal to  among adjacent subchannels translates into a significant superposition that equals
among adjacent subchannels translates into a significant superposition that equals  the excess band of the pulse. Therefore, the full compensation of the frequency offsets provided by the SCS-RX and US-RX may not be the optimal choice. That is, for large frequency offsets an analysis FB that is not perfectly frequency matched can exhibit a higher signal-to-interference ratio at its outputs. This is what happens with the practical receiver that uses frequency offsets that differ from the ideal ones.
the excess band of the pulse. Therefore, the full compensation of the frequency offsets provided by the SCS-RX and US-RX may not be the optimal choice. That is, for large frequency offsets an analysis FB that is not perfectly frequency matched can exhibit a higher signal-to-interference ratio at its outputs. This is what happens with the practical receiver that uses frequency offsets that differ from the ideal ones.
The overall conclusion is that the FS-RX both with ideal and practical synchronization provides performance close to the SCS-RX yet allowing for an efficient DFT-based implementation.
7. Conclusions
In this paper, we have discussed a training-based synchronization approach for multiuser FB systems. Both two conventional receiver structures and a novel multiuser analysis FB with an efficient implementation have been described. The proposed synchronization metrics are based on a correlation approach that exploits the separability of subchannel signals that belong to different uplink users. An iterative analysis FB synchronization approach has also been considered for the conventional receivers. Simple RLS adaptive subchannel equalization has been used. The practical synchronization algorithms yield performance close to the ideal. The proposed novel multiuser receiver is an attractive solution both for its DFT-based implementation and for its performance with practical estimation of the parameters. With ideal synchronization, it achieves single-user transmission performance. Further, it shows a high robustness of the practical estimator to a wide range of time/frequency offset.
References
Cherubini G, Eleftheriou E, Ölçer S: Filtered multitone modulation for very high-speed digital subscriber lines. IEEE Journal on Selected Areas in Communications 2002, 20(5):1016-1028. 10.1109/JSAC.2002.1007382
Tonello AM: Asynchronous multicarrier multiple access: optimal and sub-optimal detection and decoding. Bell Labs Technical Journal 2002, 7(3):191-217.
Wong CY, Cheng RS, Letaief KB, Murch RD: Multiuser OFDM with adaptive subcarrier, bit, and power allocation. IEEE Journal on Selected Areas in Communications 1999, 17(10):1747-1758. 10.1109/49.793310
Tonello AM: Time domain and frequency domain implementations of FMT modulation architectures. Proceedings of IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP '06), May 2006, Toulouse, France 4: 625-628.
Tonello AM, Pecile F: Efficient Architectures for Multiuser FMT Systems and Application to Power Line Communications. IEEE Transactions on Communications May 2009., 57(5):
Kaiser S, Krzymien WA: Performance effects of the uplink asynchronism in a spread spectrum multi-carrier multiple access system. European Transactions on Telecommunications 1999, 10(4):399-406. 10.1002/ett.4460100409
van de Beek J, Börjesson P, Boucheret M, et al.: A time and frequency synchronization scheme for multiuser OFDM. IEEE Journal on Selected Areas in Communications 1999, 17(11):1900. 10.1109/49.806820
Tonello AM, Laurenti N, Pupolin S: Analysis of the uplink of an asynchronous multi-user DMT OFDMA system impaired by time offsets, frequency offsets, and multi-path fading. Proceedings of the 52nd IEEE Vehicular Technology Conference (VTC '00), September 2000, Boston, Mass, USA 3: 1094-1099.
Schmidl TM, Cox DC: Robust frequency and timing synchronization for OFDM. IEEE Transactions on Communications 1997, 45(12):1613-1621. 10.1109/26.650240
Cao Z, Tureli U, Yao Y-D: Deterministic multiuser carrier-frequency offset estimation for interleaved OFDMA uplink. IEEE Transactions on Communications 2004, 52(9):1585-1594. 10.1109/TCOMM.2004.833183
Assalini A, Tonello AM: Time-frequency synchronization in filtered multitone modulation based systems. Proceedings of the 6th International Symposium on Wireless Personal Multimedia Communications (WPMC '03), October 2003, Yokosuka, Japan 221-225.
Tonello AM, Rossi F: Synchronization and channel estimation for filtered multitone modulation. Proceedings of 7th International Symposium on Wireless Personal Multimedia Communications (WPMC '04), September 2004, Abano Terme, Italy 590-594.
Lottici V, Luise M, Saccomando C, Spalla F: Non-data-aided timing recovery for filter-bank multicarrier wireless communications. IEEE Transactions on Signal Processing 2006, 54(11):4365-4375.
Proakis JG: Digital Communications. 3rd edition. McGraw-Hill, Boston, Mass, USA; 1995.
Tonello AM, Pecile F: Iterative synchronization for multiuser filtered multitone systems. Proceedings of the 2nd International Symposium on Wireless Communications Systems Conference (ISWCS '05), September 2005, Siena, Italy 543-546.
Ungerboeck G: Fractional tap-spacing equalizer and consequences for clock recovery in data modems. IEEE Transactions on Communications 1976, 24(8):856-864. 10.1109/TCOM.1976.1093381
Acknowledgment
The work of this paper has been partially supported by the European Community's Seventh Framework Programme FP7/2007-2013 under Grant agreement no. 213311, Project OMEGA–Home Gigabit Networks.
Author information
Authors and Affiliations
Corresponding author
Appendices
A. Subchannel Output ICI and MAI Terms
In this appendix, we report the derivation of the ICI and MAI terms at the subchannel outputs in the SCS-RX and the FS-RX, that appear in (4) and (10), respectively.
First, we consider the SCS-RX. Substituting (1) and (3) in the first line of (4), we can write


where


Setting  and
and  in (A.2), that is, assuming negligible ICI and MAI, we obtain the subchannel equivalent response in (6) that we denote with
in (A.2), that is, assuming negligible ICI and MAI, we obtain the subchannel equivalent response in (6) that we denote with  From (A.1), setting
From (A.1), setting  and considering
and considering  with
with  we can write the ICI term as follows:
we can write the ICI term as follows:


while setting  and
and  , we obtain the MAI term as
, we obtain the MAI term as


We proceed in an analogous way for the FS-RX of Section 3.2 Substituting (1) and (3) in the first line of (10), we can write


where


Again, we can obtain the subchannel equivalent response, under the hypothesis of negligible ICI and MAI (11), setting  and
and  in (A.6). From (A.5), we can write the ICI term as follows:
in (A.6). From (A.5), we can write the ICI term as follows:


while the MAI term as follows:


B. Synchronization Metric Interference Terms
In this appendix, we compute the interference terms of the synchronization metrics in (20) and in (27). We can evaluate the expression of  in (20) if we substitute (17) in (18). Assuming that the ICI and MAI contributions are negligible, we can highlight the following interference terms that are generated by the propagation channel time dispersion:
in (20) if we substitute (17) in (18). Assuming that the ICI and MAI contributions are negligible, we can highlight the following interference terms that are generated by the propagation channel time dispersion:


where






The interferers in (B.2) and (B.3) are obtained from the product of the useful term and the ISI term in (17). Since the ISI coefficients have small weight compared to useful data amplitude, both (B.2) and (B.3) have power that is small compared to the useful signal power.
The term (B.4) is completely due to intersymbol interference. For this term, the above considerations are still applicable. Further, the use of a lag  larger than the subchannel duration allows reducing the contribution of this term since the two signals that are correlated in (B.4) have disjoint extensions.
larger than the subchannel duration allows reducing the contribution of this term since the two signals that are correlated in (B.4) have disjoint extensions.
An analogous analysis can be applied to the interference term  in (27), that is, the metric used for the US-RX. Assuming that the ICI and MAI contributions are negligible, we can highlight the following interference terms:
in (27), that is, the metric used for the US-RX. Assuming that the ICI and MAI contributions are negligible, we can highlight the following interference terms:


where






These terms have a structure similar to those in (B.2), (B.4), and the same considerations can be done for their evaluation.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Tonello, A.M., Pecile, F. Synchronization Algorithms and Receiver Structures for Multiuser Filter Bank Uplink Systems. J Wireless Com Network 2009, 387520 (2009). https://doi.org/10.1155/2009/387520
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/387520

 .
.

 filtering with the polyphase pulses
filtering with the polyphase pulses 
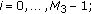
 DFT, and sampling the DFT outputs with index
DFT, and sampling the DFT outputs with index 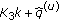 for
for 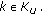 This is to obtain the subchannel signals of user
This is to obtain the subchannel signals of user  and to partly compensate the frequency shift introduced by the integer part of the carrier frequency offset;
and to partly compensate the frequency shift introduced by the integer part of the carrier frequency offset;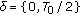 to obtain a set of
to obtain a set of 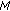 sample streams at rate
sample streams at rate 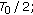
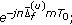


 SNR is equal to 20 dB.
SNR is equal to 20 dB.


 SNR is equal to 20 dB.
SNR is equal to 20 dB.


 PRACTICAL,
PRACTICAL, 

 PRACTICAL,
PRACTICAL, 

 Fractional Multiuser RX,
Fractional Multiuser RX, 

 Fractional Multiuser RX,
Fractional Multiuser RX, 