- Research Article
- Open access
- Published:
Outage Probability versus Fairness Trade-off in Opportunistic Relay Selection with Outdated CSI
EURASIP Journal on Wireless Communications and Networking volume 2009, Article number: 412837 (2009)
Abstract
We analyze the existing trade-offs in terms of system performance versus fairness of a cooperative system based on opportunistic relay selection (ORS) and with outdated channel state information (CSI). In particular, system performance is analytically evaluated in terms of outage probability, and the fairness behavior is assessed based on the power consumption at the different relays. In order to improve the fairness behavior of ORS while keeping the selection diversity gain, we propose a relay selection mechanism where the relay with the highest normalized signal-to-noise ratio (SNR) is selected for relaying the source's information. The proposed strategy is compared with existing relay selection strategies by adopting a novel graphical representation inspired by expected profit versus risk plots used in modern portfolio theory. As shown in the paper, this strategy allows operating the system in more favorable points of the outage versus fairness region.
1. Introduction
Cooperative diversity has been shown to be an efficient way to combat wireless impairments using low-complexity terminals [1–4]. Basically, these schemes allow for the exploitation of spatial diversity gains without the need of multiantenna technology. Different spatial paths are provided by sending/receiving the information to/from a set of cooperating terminals working as relays. By doing so, most of the advantages of multiple-input multiple-output (MIMO) techniques [5] can be extracted while keeping the complexity of the individual terminals reduced. Indeed, the benefits captured by cooperative communications are well extended in the research community, and standardization groups are considering the inclusion of cooperative techniques in practical systems. For instance, the IEEE 802.16j Relay Task Group [6] is involved in the incorporation of relaying mechanisms in the standard adopted by the new wireless system WiMAX [7].
Among the set of cooperative techniques, opportunistic relay selection (ORS) is a useful strategy for practical implementation [8]. This is because ORS is a low-complexity strategy consisting only in activating the best relay (in accordance to a given performance metric). Apart from the inherent simplicity of the proposed technique, this strategy avoids the need of synchronization (needed by most distributed space-time coding schemes) and reduces the power consumption of the terminals.
When ORS is implemented in a real system, however, there may exist a delay between the instants when the selection process is encompassed and the actual transmission of data from the selected relay takes place. In other words, the channel state of the selected relay considered at the selection decision can substantially differ from the actual one and, as a result, system performance is affected.
Besides, in an ORS scheme only the best relay is allowed to cooperate with the source. If channel conditions are not statistically equal for all relays, ORS may be unfair among relays. That is, relays with the worst channel conditions are never selected, and all the cooperation is performed by a reduced set of relays. This can induce a negative effect in the network behavior as one (or more) relay(s) can waste all the battery energy for the sake of cooperation.
Contributions
In this paper, we concentrate our efforts on the analytical study of the behavior of ORS based on decode and forward protocol in a realistic situation where the channel state information (CSI) available at the selection procedure is outdated. More specifically, we derive the exact expression for the outage probability, which is defined as the probability where the instantaneous capacity is below a target value. In order to improve the fairness of ORS, we adopt a fair relay selection strategy where the relay with the largest normalized SNR is selected for relaying the source's information. Furthermore, we explore the existing trade-offs in terms of system performance versus fairness among relays when different relay selection strategies are adopted. To do so, we propose an analysis tool inspired by mean versus standard deviation plots adopted in modern portfolio theory [9, 10]. In particular, we adapt such representation to the proposed ORS scenario by illustrating the gain in terms of system performance versus the difference among relays in terms of power consumption. As shown in the paper, this kind of representation is quite useful to quantify what the performance versus fairness trade-off of the proposed relaying strategy is.
Relation to Prior Work
The study of the impact of outdated CSI on ORS has been addressed by few works. For instance, it was shown in [11] that a selection relaying mechanism based on localization knowledge can outperform an opportunistic scheme with instantaneous information. Although it was not explicitly discussed, the reason for that is that available CSI was subject to delays. As a consequence, the selection scheme proposed in [11] may work better when decisions are made based on location information instead of instantaneous but outdated CSI (localization variations are considerably slower than those induced by the wireless channel). In this work, we shed some light into this issue by providing an analytical study of the behavior of ORS when CSI is outdated.
Concerning the fairness analysis of cooperative strategies, some studies deal with this topic in literature. In [12, 13] cooperation protocols based on power rewards were proposed for energy-constrained ad hoc networks in order to attain a fair situation where all the nodes run out of energy simultaneously. With the same objective in mind, a relay set selection protocol was proposed in [14]. In particular, the authors of that work proposed a multistate energy allocation method, where in each state a different set of relays are selected until these relays run out of energy. The fairness nature of the proposed strategy comes from the fact that the same energy is allocated to all the nodes of the active set, being this energy optimized with the aim of minimizing outage probability. In [15–17], cooperative schemes based on ORS with amplify and forward were adopted. The authors in [15] focused the study on the comparison of round robin with centralized and distributed ORS-based selection strategies. Clearly, better performance was achieved with the ORS strategies while preserving fairness in the temporal domain. In that case, nonetheless, fairness was assured due to the i.i.d channel modeling of the proposed scenario. In [16], a power saving technique was proposed, where transmit power at the relays was minimized according to SNR constraints. By doing so, a good balance between the diversity gain and fairness of battery usage was obtained but complexity and signaling requirements of the system were increased with the proposed power allocation method. On the other hand, the authors in [17] proposed a selection scheme based on the selection of the relay with the best weighted SNR aimed at improving the fair behavior of ORS (measured by the percentage of power consumption). In our work, we also consider a selection scheme based on weighted SNR but, as discussed later, different considerations must be adopted in the proposed scenario based on decode and forward protocol, and different conclusions are drawn. Besides, we propose a fairness analysis tool inspired in portfolio theory to facilitate the study of the existing trade-offs in terms of system performance versus fairness among relays in a realistic scenario where available CSI is subject to delays.
Organization
The corresponding system model is presented in Section 2. In Section 3, a closed-form expression for the outage probability of the proposed relay selection mechanism is derived, and some numerical results are provided to evaluate the performance of different relay selection schemes. After that, the fairness of the different relaying strategies is illustrated in Section 4 by using outage probability versus standard deviation of the power consumption plots. Finally, in Section 5, the summary and conclusions of this paper are presented.
2. System Model
Consider a wireless network where one mobile unit (source) sends information to the base station (destination). In order to improve system performance, a cooperative mechanism is considered. In particular, an ORS strategy is adopted in a scenario with  mobile units of the network working as relays. In Figure 1, we present an example of the proposed scenario. Notice that we have considered a parallel relay topology [18] where relays are linearly placed halfway between the source and the destination, in a segment of length
mobile units of the network working as relays. In Figure 1, we present an example of the proposed scenario. Notice that we have considered a parallel relay topology [18] where relays are linearly placed halfway between the source and the destination, in a segment of length  , where
, where  is also the distance of the source-destination link. It is worth noting, however, that the main results obtained in this paper depend on the relay selection mechanisms but not on the specific relay arrangement.
is also the distance of the source-destination link. It is worth noting, however, that the main results obtained in this paper depend on the relay selection mechanisms but not on the specific relay arrangement.
2.1. Signal Model
For the sake of notation simplicity, we define an arbitrary link  -
- between two nodes
between two nodes  and
and  . Node
. Node  can be the source (
can be the source ( =
=  ) or the
) or the  th relay (
th relay ( =
=  ), while node
), while node  can correspond to the
can correspond to the  th relay (
th relay ( =
=  ) or to the destination (
) or to the destination ( =
=  ). With this model in mind, the received signal in the link
). With this model in mind, the received signal in the link  -
- can be written as follows:
can be written as follows:

where  is the transmitted symbol from node
is the transmitted symbol from node  with power
with power  ,
,  is AWGN noise with zero mean and variance
is AWGN noise with zero mean and variance  (independent of the value of
(independent of the value of  ),
),  is the channel response between nodes
is the channel response between nodes  and
and  modeled as
modeled as  (Rayleigh fading), being
(Rayleigh fading), being  the channel strength depending on the simplified path-loss model [19],
the channel strength depending on the simplified path-loss model [19],  , with
, with  standing for the carrier wave-length,
standing for the carrier wave-length,  is a reference distance,
is a reference distance,  is the distance of the link A-B, and
is the distance of the link A-B, and  is the path-loss coefficient (being
is the path-loss coefficient (being  = 3 in this work). We assume a block-fading channel where the channel response remains constant during one time-slot and that the different channels (for changing A or B) are independently distributed. Concerning power allocation, we consider that total transmit power of the system,
= 3 in this work). We assume a block-fading channel where the channel response remains constant during one time-slot and that the different channels (for changing A or B) are independently distributed. Concerning power allocation, we consider that total transmit power of the system,  , is evenly distributed among the source and the selected relay,
, is evenly distributed among the source and the selected relay,  , that is,
, that is,  =
=  =
=  . We denote by
. We denote by  the instantaneous signal-to-noise ratio (SNR) experienced in the link
the instantaneous signal-to-noise ratio (SNR) experienced in the link  -
- in a given time-slot and by
in a given time-slot and by  its long-term average. Also, we define
its long-term average. Also, we define  as the SNR employed by the relay selection mechanism, which can differ from the actual SNR SNR
as the SNR employed by the relay selection mechanism, which can differ from the actual SNR SNR  but both of them have the same long-term average
but both of them have the same long-term average  (further details can be found in Section 2.3).
(further details can be found in Section 2.3).
Finally, it is worth pointing out that one of the main scopes of this work is to show the impact of outdated CSI on relay selection decisions, and, for the sake of mathematical tractability, we will be considering the capacity of a single carrier system. The study can be easily extended to OFDM by applying the same analysis to each subcarrier simultaneously, and, hence, it is applicable to WiMAX on a subcarrier per subcarrier basis.
2.2. Relaying Mechanism
In this work, we consider a half-duplex two-hop decode and forward (DF) protocol as relaying strategy. When using half-duplex DF, the transmission is divided in two time-slots. In the first time-slot, the source transmits the information to the relays, which attempt to demodulate and decode this information. In the second time-slot, the relays encode again the information and retransmit it to the destination [4]. In an ORS scheme, only the best relay is allowed to cooperate with the source. More specifically, the subset of relays able to decode the information is named as the decoding subset  , and, from that subset, the relay with the best relay-destination channel quality retransmits the information (see Figure 2).
, and, from that subset, the relay with the best relay-destination channel quality retransmits the information (see Figure 2).
Unlike other approaches, the scheme proposed in this work selects the relay with the largest normalized SNR instead of the largest absolute SNR because of practical considerations. In other words, the selected relay  is such that:
is such that:

The reason why we propose this selection strategy is due to the fairness introduced in the selection procedure as all relays will be chosen with the same probability. Thus, the power consumption of the different terminals is uniformly distributed, while diversity gains can still be efficiently extracted. This can help to improve the acceptance by the different users of cooperation mechanism since all of them contribute to common welfare with the same amount of battery. Notice that this strategy was also presented in [17]. In that paper, however, it was shown that the benefits provided by the largest normalized SNR in terms of fairness were not significant. It is then worth recalling that a different scenario based on amplify and forward was presented, and, for that reason, different conclusions were drawn (further details in Section 4.1). If the selection were based on the absolute SNR, some users may be reluctant to participate since they may experience battery consumption faster than the average.
Notice that the relay selection approach makes its decision based on the estimated version of the SNR,  . Concerning the accuracy of this estimate, it will depend on the way that CSI is provided. Here, we discuss two methodologies according to the adopted duplexing mode, that is, frequency (FDD) or time (TDD) division duplexing.
. Concerning the accuracy of this estimate, it will depend on the way that CSI is provided. Here, we discuss two methodologies according to the adopted duplexing mode, that is, frequency (FDD) or time (TDD) division duplexing.
-
(i)
FDD: since uplink and downlink channels operate at different frequency bands, feedback mechanisms are required. First of all, relays belonging to the decoding subset send a signalling message to the destination (i.e., BS) indicating that they are able to relay the message. This signalling message can be, for instance, a pilot sequence used by the BS to estimate the instantaneous SNRs of the different relays. Once the different SNRs are estimated, the BS selects the relay with the best quality and broadcasts this decision via a selection command (only
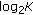 bits required).
bits required). -
(ii)
TDD: in the case that channel reciprocity between the uplink and downlink holds, each of the relays is able to know its own CSI. TDD: in the case that channel reciprocity between the uplink and downlink holds, each of the relays is able to know its own CSI. With this information, a possible selection strategy is that proposed in [20]. Those relays belonging to the decoding subset start a timer. The timer of each relay adopts as initial value a parameter inversely proportional to its instantaneous SNR. Then, the timer that first expires is that belonging to the best relay. In order to avoid collision, this relay signals its presence to the rest of relays via a flag packet before the relaying procedure is started (further details about strategies to avoid collision can be found in [20]). Clearly, channel reciprocity holds in TDD when the time coherence of the channel is higher than the time difference between uplink and downlink time slots. In the opposite case, the methodology adopted for the FDD case should be considered as well. With this information, a possible selection strategy is that proposed in [20]. Those relays belonging to the decoding subset start a timer. The timer of each relay adopts as initial value a parameter inversely proportional to its instantaneous SNR. Then, the timer that first expires is that belonging to the best relay. In order to avoid collision, this relay signals its presence to the rest of relays via a flag packet before the relaying procedure is started (further details about strategies to avoid collision can be found in [20]).
As can be observed in both strategies, there exists a time delay,  , between decision and relay transmission instants that may affect system performance.
, between decision and relay transmission instants that may affect system performance.
2.3. Modeling of CSI Delay
We consider that the SNR estimates available at the selection procedure were obtained from a channel state,  , which differs from the actual channel response at the relay retransmission instant,
, which differs from the actual channel response at the relay retransmission instant,  , due to the effect commented above. Indeed
, due to the effect commented above. Indeed  is an outdated version of
is an outdated version of  , that is, these two random variables are samples of the same Gaussian process. Then,
, that is, these two random variables are samples of the same Gaussian process. Then,  conditioned on
conditioned on  follows a Gaussian distribution [21]:
follows a Gaussian distribution [21]:

where parameter  (with
(with  ) is the correlation coefficient between
) is the correlation coefficient between  and
and  (degree of CSI accuracy), having different expressions according to the channel model. Under the assumption of Jakes' model, for instance, the correlation coefficient takes the value
(degree of CSI accuracy), having different expressions according to the channel model. Under the assumption of Jakes' model, for instance, the correlation coefficient takes the value  , where
, where  stands for the Doppler frequency,
stands for the Doppler frequency,  is the delay mentioned in the previous subsection, and
is the delay mentioned in the previous subsection, and  denotes the zero-order Bessel function of the first kind.
denotes the zero-order Bessel function of the first kind.
From the above discussion, it is straightforward to show that the actual SNR,  , conditioned on its estimate,
, conditioned on its estimate,  , follows a noncentral chi-square distribution with 2 degrees of freedom, whose probability density function (pdf) takes the following expression [21]:
, follows a noncentral chi-square distribution with 2 degrees of freedom, whose probability density function (pdf) takes the following expression [21]:

where  stands for the zero-order-modified Bessel function of the first kind, and one should take into consideration that the long-term average of
stands for the zero-order-modified Bessel function of the first kind, and one should take into consideration that the long-term average of  is equal to
is equal to  .
.
3. Outage Probability Analysis
In this section, we analyze the behavior of the proposed relay selection strategy in terms of outage probability. To do so, we first obtain an analytical expression for the outage probability. After that, we show some numerical examples where the proposed fair strategy is compared to other existing relay selection strategies.
3.1. Analytical Expression of the Outage Probability
The outage probability is defined as the probability where the instantaneous capacity of the system is below a predefined value  . Since we consider a two-hop DF scenario, we should start the analysis by studying the decoding subset
. Since we consider a two-hop DF scenario, we should start the analysis by studying the decoding subset  , that is, the subset of relays that are not in outage in the source-to-relay link:
, that is, the subset of relays that are not in outage in the source-to-relay link:

Note that we have considered that outage in the first hop occurs when instantaneous capacity is lower than 2 (as it will do in the relay-to-destination link). By doing so, the resulting end-to-end spectral efficiency is
(as it will do in the relay-to-destination link). By doing so, the resulting end-to-end spectral efficiency is  as the proposed two-hop scheme requires two time-slots to transmit the information from the source to the destination.
as the proposed two-hop scheme requires two time-slots to transmit the information from the source to the destination.
By defining now  as an arbitrary decoding subset with
as an arbitrary decoding subset with  relays, we can easily compute its probability as [8] follows:
relays, we can easily compute its probability as [8] follows:

where the second equality comes from the Rayleigh fading assumption, and  has been defined as
has been defined as  for the sake of notation simplicity. With this last expression, the outage probability of ORS can be written as follows [8]:
for the sake of notation simplicity. With this last expression, the outage probability of ORS can be written as follows [8]:

where the second summation is over all the possible decoding subsets  (i.e., the
(i.e., the  possible subsets of
possible subsets of  relays taken from the
relays taken from the  relays). As for
relays). As for  , this is the probability where the selected relay is in outage conditioned on the fact that the decoding subset is
, this is the probability where the selected relay is in outage conditioned on the fact that the decoding subset is  . In [8], this probability was solved by assuming an ideal scenario with an absolute SNR selection. Our contribution here is to adapt the outage expression to a (realistic) scenario with outdated CSI and a max-normalized SNR strategy. Indeed, the only term in (7) affected by these two particularities is
. In [8], this probability was solved by assuming an ideal scenario with an absolute SNR selection. Our contribution here is to adapt the outage expression to a (realistic) scenario with outdated CSI and a max-normalized SNR strategy. Indeed, the only term in (7) affected by these two particularities is  . This is because a node belongs to the decoding subset if it has perfectly decoded the information, which is independent of CSI delays and relay selection decisions. Conversely,
. This is because a node belongs to the decoding subset if it has perfectly decoded the information, which is independent of CSI delays and relay selection decisions. Conversely,  depends on the relay selection accuracy, and this clearly depends on both
depends on the relay selection accuracy, and this clearly depends on both  and how the relay has been selected. When
and how the relay has been selected. When  = 0, that probability is clearly equal to 1 as there are no active nodes to relay the transmission. For
= 0, that probability is clearly equal to 1 as there are no active nodes to relay the transmission. For  , we should first define
, we should first define  as the event where relay
as the event where relay  is selected (i.e.,
is selected (i.e.,  =
=  ) under the assumption that the decoding subset is
) under the assumption that the decoding subset is  . By doing so, we can re-rewrite
. By doing so, we can re-rewrite  as follows:
as follows:

where  stands for the cumulative density function (CDF),
stands for the cumulative density function (CDF),  is equal to 1/
is equal to 1/ due to the fairness property of the proposed relay selection strategy (i.e., all the normalized estimated SNRs have the same statistics), and
due to the fairness property of the proposed relay selection strategy (i.e., all the normalized estimated SNRs have the same statistics), and  is given by (4). Note that
is given by (4). Note that  can be easily computed since this relay selection problem is statistically equivalent to the scheduling problem observed in a multiuser broadcast channel with independently distributed Rayleigh fading channels and a max-normalized SNR scheduler. More specifically, the following equation can be obtained [22]:
can be easily computed since this relay selection problem is statistically equivalent to the scheduling problem observed in a multiuser broadcast channel with independently distributed Rayleigh fading channels and a max-normalized SNR scheduler. More specifically, the following equation can be obtained [22]:

By plugging (9) and (4) into (8), we obtain an integral equation already solved in a previous work by the authors related with multiuser diversity and delayed CSI [21] (details are omitted for brevity):

Finally, by introducing (10) along with (6) in (7), the outage probability can be written as follows:

where the first term is related to the case that the decoding subset is an empty set (i.e.,  = 0).
= 0).
Finally, it is worth noting that although the analysis has been carried out from an information theoretic point of view, it can be readily extended to a practical scheme with adaptive coding and modulation (e.g., a WiMAX system). Notice that the expression derived in this section evaluates the probability of having instantaneous SNR lower than a specified value given by the Shannon capacity,  , and this value can be set equal to the different SNR thresholds of the adaptive coding and modulation modes.
, and this value can be set equal to the different SNR thresholds of the adaptive coding and modulation modes.
3.2. Numerical Evaluation
As far as numerical evaluation is concerned, special attention has been paid to carry out a fair comparison in a realistic scenario. It has been considered the wireless scenario presented in Section 2 with a parallel relay topology as shown in Figure 1, where the distance of the source-to-destination link is  = 100 meters, the carrier frequency is set to
= 100 meters, the carrier frequency is set to  = 3.5 GHz (in close alignment with the commercial WiMAX equipments deployed in the European Community), the target rate is
= 3.5 GHz (in close alignment with the commercial WiMAX equipments deployed in the European Community), the target rate is  = 1 bits/seg/Hz, and the number of relays is
= 1 bits/seg/Hz, and the number of relays is  = 5. In order to obtain the outage probability of the proposed system, we adopt Monte Carlo simulation, where in each realization the different channels (
= 5. In order to obtain the outage probability of the proposed system, we adopt Monte Carlo simulation, where in each realization the different channels ( ,
,  , and
, and  ) are modeled as described in Sections 2.1 and 2.3. Finally, we define system SNR as the average received SNR of the single-hop scheme. For each value of system SNR, the cooperative schemes use the same total power
) are modeled as described in Sections 2.1 and 2.3. Finally, we define system SNR as the average received SNR of the single-hop scheme. For each value of system SNR, the cooperative schemes use the same total power  as that needed by the single-hop scenario to achieve this SNR value. By doing so, we are fairly evaluating the advantage of using cooperation as the total transmit power of the system is kept constant. Besides, for the sake of benchmarking, we compare the outage probability of the proposed cooperative scheme with that obtained without cooperation and the following relay selection strategies.
as that needed by the single-hop scenario to achieve this SNR value. By doing so, we are fairly evaluating the advantage of using cooperation as the total transmit power of the system is kept constant. Besides, for the sake of benchmarking, we compare the outage probability of the proposed cooperative scheme with that obtained without cooperation and the following relay selection strategies.
-
(i)
Round robin. This strategy is theoretically the fairest strategy as it is based on iteratively selecting the different relays of the decoding subset.
-
(ii)
Conventional ORS (max SNR). Clearly this technique does not care about fairness among relays as it selects the relay with the maximum absolute SNR.
As observed in Figure 3, the outage probability expression derived in the previous subsection completely agrees with the simulation results. It is also observed that the proposed max-normalized SNR strategy is able to extract the diversity gains of the cooperative system as results corresponding with  = 1 are quite overlapped with those obtained with the (outage optimal) max SNR scheme. However, performance of both strategies is quite sensitive to the value of
= 1 are quite overlapped with those obtained with the (outage optimal) max SNR scheme. However, performance of both strategies is quite sensitive to the value of  . Outage performance is significantly affected when
. Outage performance is significantly affected when  moves away from 1. In particular, one can observe that only a slight improvement can be obtained by using ORS-based cooperation with respect to a direct transmission strategy when
moves away from 1. In particular, one can observe that only a slight improvement can be obtained by using ORS-based cooperation with respect to a direct transmission strategy when  = 0.5. Apart from that, it is also observed that the gap between the max-normalized and max SNR strategies becomes wider for decreasing values of
= 0.5. Apart from that, it is also observed that the gap between the max-normalized and max SNR strategies becomes wider for decreasing values of  . This is because the higher SNR peaks generation capability of the conventional ORS strategy compensates more efficiently the CSI uncertainties.
. This is because the higher SNR peaks generation capability of the conventional ORS strategy compensates more efficiently the CSI uncertainties.
As for the round-robin strategy, it is clearly observed that this is not a useful technique in terms of outage probability as better performance can be obtained without cooperation. This is mainly due to the fact that better results can be obtained by concentrating total power and transmission time in a single-hop communication instead of dividing them between the source and a relay terminal that has been selected (data link layer) without CSI (physical layer) considerations. It is then emphasized the need of adopting cross-layer strategies in the design of cooperative communication systems.
4. Fairness Analysis
In the previous section, we have explored the performance of the different transmission techniques in terms of outage probability. Nonetheless, this analysis has been performed without considering the fairness among selected relays; this last issue is important to improve the acceptance by the different users of cooperation mechanisms. In this section, we concentrate our efforts on the study of the fairness behavior of the different relay selection mechanisms, and we show that there exists a trade-off in terms of system performance versus fairness among relays. To do so, we use a graphical representation based on modern portfolio theory that helps to easily quantify such trade-off.
4.1. Fairness Criterion
In this work, we measure the fairness among relays in terms of the percentage of power consumption used for relaying purposes. This metric was also adopted in [17] but, here, some differences are observed as we consider a scenario based on decode and forward where the power used by the selected relays remains constant. In the proposed scenario, in particular, the power consumption destined to cooperation purposes is originated by the following mechanisms.
-
(1)
Receiving procedure. In the first time-slot of the decode and forward procedure, the receiver circuitry of each relay consumes power to receive the signal and to measure the SNR in order to estimate if the relay is able to decode signal.
-
(2)
Relay selection mechanisms. According to the relay selection strategies presented in Section 2.2, relays belonging to the decoding subset dedicate battery power to the following actions:
-
(i)
FDD: battery power is mainly used to transmit the signaling message to the destination indicating that the relay is able to retransmit the information.
-
(ii)
TDD: power consumption is mainly caused by the internal timing procedure and, in the case of the best relay, by the transmission of the flag packet to the rest of relays.
-
(i)
-
(3)
Decoding and retransmission procedure. Once the relay selection procedure is finished, the selected relay decodes/encodes the source's information and retransmits it to the destination. Clearly, this is the most power demanding mechanism where the fair behavior of the relay selection strategy plays a crucial role.
As will be commented in the next subsection, we study the fairness by analyzing the standard deviation of power consumption among relays (adopting a similar approach than that presented in [17]). Therefore, mechanism (1) described above does not affect the standard deviation measure as all the relays perform that procedure. Basically, differences among relays will be observed in mechanisms (2) and (3). However, because mechanism (2) is carried out by all the relays in the decoding subset and the involved power consumption can be neglected in comparison with that destined to (3), we focus our study in the analysis of the decoding and retransmission procedure. In such a procedure, a fix amount of power is consumed when it is executed. On one hand, decoding and encoding the source's message always need the same power budget. On the other hand, the proposed scenario considers that selected relays transmit with the assigned constant power  . As a result, computing the amount of percentage of power allocated to each relay is equivalent to obtaining the percentage of time where each relay is active. In such circumstances, the standard deviation of the percentage of power consumption of the different relays is obtained in this work by computing the standard deviation of the fraction of time periods where relays are activated for relaying the source's information. For that reason, we propose the use of the max-normalized SNR strategy as all the relays in the decoding subset will be chosen with the same probability. As commented previously, the behavior of the proposed strategy could be quite different when a different relaying protocol is adopted (see, e.g., [17]).
. As a result, computing the amount of percentage of power allocated to each relay is equivalent to obtaining the percentage of time where each relay is active. In such circumstances, the standard deviation of the percentage of power consumption of the different relays is obtained in this work by computing the standard deviation of the fraction of time periods where relays are activated for relaying the source's information. For that reason, we propose the use of the max-normalized SNR strategy as all the relays in the decoding subset will be chosen with the same probability. As commented previously, the behavior of the proposed strategy could be quite different when a different relaying protocol is adopted (see, e.g., [17]).
4.2. System Performance versus Fairness Trade-Offs Representation
As observed in Section 3.2, the fair behavior provided by the max-normalized SNR and round-robin strategies penalizes system performance (specially for decreasing values of  in the former case). Therefore, it seems that there exists a trade-off in terms of the degree of fairness among the different relays and its impact in terms of system performance. In this section, we are devoted to show the existence of such a trade-off with the help of an analysis tool inspired by means versus standard deviation plots adopted in modern portfolio theory [9, 10]. This kind of representation is used in financial market theory with the aim of assessing the existing trade-offs in terms of the expected profit (mean) versus the possible risk (standard deviation) when a possible investment is considered. In this work, we adapt such representation to the proposed wireless scenario based on cooperative communications by illustrating the gain in terms of system performance (outage probability) versus the difference among relays in terms of power consumption (standard deviation of the percentage of power consumption). By doing so, we can easily quantify what the performance versus fairness trade-off of the different relaying strategies is.
in the former case). Therefore, it seems that there exists a trade-off in terms of the degree of fairness among the different relays and its impact in terms of system performance. In this section, we are devoted to show the existence of such a trade-off with the help of an analysis tool inspired by means versus standard deviation plots adopted in modern portfolio theory [9, 10]. This kind of representation is used in financial market theory with the aim of assessing the existing trade-offs in terms of the expected profit (mean) versus the possible risk (standard deviation) when a possible investment is considered. In this work, we adapt such representation to the proposed wireless scenario based on cooperative communications by illustrating the gain in terms of system performance (outage probability) versus the difference among relays in terms of power consumption (standard deviation of the percentage of power consumption). By doing so, we can easily quantify what the performance versus fairness trade-off of the different relaying strategies is.
Before analyzing the behavior of the different relaying schemes, it is worth mentioning that this portfolio-based representation is also adopted in several works related with the design of resource allocation mechanisms in wireless networks. More specifically, Bartolome introduced this methodology in the wireless communications community to study the degree of fairness of the MIMO Broadcast Channel with zero-forcing transmit beamforming when different bit allocation techniques are adopted [23]. By using the mean versus standard deviation plots, trade-offs in terms of global rate versus fairness among users were easily showed. Then, it was proved that this approach facilitates the design and comparison of different resource allocation algorithms according to the desired degree of fairness. This technique can also be found in studies about the comparison of optimum versus zero-forcing beamforming [24], design of fair algorithms in a context where an orthogonal linear precoding is adopted [25, 26], and the study of the robustness of multiuser systems against CSI imperfections [27].
In Figure 4, the outage probability versus the standard deviation of the power consumption of the different relays is represented for the relay selection mechanisms discussed in the previous section, where each point in the plot of the ORS-based cooperation mechanisms (max-norm SNR and max SNR) is related with a different  (with
(with  ). We start the analysis by considering a scenario with system SNR equal to 10 dB. Although the consideration of the direct transmission could not make sense here, we have included the outage probability of this case in order to assess if system performance gain obtained with a cooperative strategy justifies the battery consumption of the terminals for relaying purposes. Notice that the standard deviation of the direct transmission case is set equal to 0. Besides, it is also worth noting that the standard deviation of the ORS-based mechanisms does not depend on parameter
). We start the analysis by considering a scenario with system SNR equal to 10 dB. Although the consideration of the direct transmission could not make sense here, we have included the outage probability of this case in order to assess if system performance gain obtained with a cooperative strategy justifies the battery consumption of the terminals for relaying purposes. Notice that the standard deviation of the direct transmission case is set equal to 0. Besides, it is also worth noting that the standard deviation of the ORS-based mechanisms does not depend on parameter  as relay selection decisions are independent of the level of CSI inaccuracy. In other words, the standard deviation of the power consumption depends on the degree of fairness applied by the ORS-based schemes on the relay selection procedure, but for a given degree of fairness, it is only the outage probability that depends on the quality of the channel estimate but not the power consumption distribution.
as relay selection decisions are independent of the level of CSI inaccuracy. In other words, the standard deviation of the power consumption depends on the degree of fairness applied by the ORS-based schemes on the relay selection procedure, but for a given degree of fairness, it is only the outage probability that depends on the quality of the channel estimate but not the power consumption distribution.
As observed in the figure, the highest standard deviation is obtained with the max SNR strategy. Clearly, it is observed how the good performance results of the conventional ORS strategy are attained at the expense of a considerable reduction in terms of fairness. Indeed, the standard deviation observed in that case amounts to approximately 13%, resulting in a faster battery consumption of those relays with better channel conditions. Concerning the max-normalized SNR and round robin strategies, the fairer behavior of these strategies is reflected by the lower standard deviation obtained in these cases (1.6% and 2%, resp.).
Surprisingly, the fairest cooperative strategy is the max-normalized SNR strategy instead of the round robin one. The round robin scheme iteratively selects the different relays of the decoding subset. In the case of low and medium system SNRs, the probability that the decoding subset has all the relays of the system is reduced. In these circumstances, relays closer to the source have a higher probability to be able to retransmit the signal and, thus, to belong to the decoding subset. Then, the power consumption of these relays in relaying procedures is higher than that used by the rest of relays. When the rest of relays are in the decoding subset, the relay selection mechanism selects them iteratively without taking into account that these relays have not been activated for too long, and some actions should be adopted in order to compensate this situation. In the max-normalized SNR strategy, however, relays are selected when their SNRs are in their own peaks, and, then, some compensation actions are implicitly carried out by the selection strategy.
The origin of this last effect is clarified by analyzing in Figure 4 results corresponding to a scenario with system SNR equal to 20 dB. As observed, the standard deviation of both the round robin and max-normalized SNR strategies is quite similar. In that case, the decoding subset has the  relays of the system with a high probability, and, then, the problems reducing the fair behavior of these strategies are alleviated. In the figure, one can also observe that the conventional ORS strategy is less fair when the system SNR is increased. This is because in the low- and mid-SNR regimes situations where the decoding subset is only formed by the worst relays can happen. In those cases, the relay selection mechanism will activate a subset of relays that never will be chosen when all the relays of the system are in the decoding subset. In order to extend such analysis, we also present a graphical representation where the SNR dependance of the system is clearly reflected (see Figure 5). As observed in the figure, when the SNR of the system is increased, the fairness of the round robin and max-normalized SNR strategies is improved, whereas the system becomes less fair in the max SNR case due to the reasoning discussed above.
relays of the system with a high probability, and, then, the problems reducing the fair behavior of these strategies are alleviated. In the figure, one can also observe that the conventional ORS strategy is less fair when the system SNR is increased. This is because in the low- and mid-SNR regimes situations where the decoding subset is only formed by the worst relays can happen. In those cases, the relay selection mechanism will activate a subset of relays that never will be chosen when all the relays of the system are in the decoding subset. In order to extend such analysis, we also present a graphical representation where the SNR dependance of the system is clearly reflected (see Figure 5). As observed in the figure, when the SNR of the system is increased, the fairness of the round robin and max-normalized SNR strategies is improved, whereas the system becomes less fair in the max SNR case due to the reasoning discussed above.
As for the existing trade-offs in terms of system performance versus fairness, one can easily assess the behavior of the different strategies thanks to the proposed representation. More specifically the following conclusions can be drawn.
-
(i)
The best performance results are obtained with the conventional ORS strategy. However, the fairness of the system is considerably penalized.
-
(ii)
An appropriate strategy to exploit cooperative diversity while keeping a good performance versus fairness trade-off is the max-normalized SNR strategy. Indeed, it is shown that this strategy can present a better fairness behavior than that provided by round robin.
-
(iii)
For low
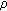 values and high system restrictions in terms of outage probability, conventional ORS strategy could be the most appropriate strategy. For high
values and high system restrictions in terms of outage probability, conventional ORS strategy could be the most appropriate strategy. For high  values, however, it is clear that more benefits are obtained with max-normalized SNR as similar results are obtained in terms of outage probability but the fairness among relays is substantially improved.
values, however, it is clear that more benefits are obtained with max-normalized SNR as similar results are obtained in terms of outage probability but the fairness among relays is substantially improved. -
(iv)
The round robin strategy is not useful for exploiting cooperation benefits.
Finally, one can also notice that the proposed representation helps to assess the viability of using a cooperative technique as direct transmission results have also been included in the figures. In particular, one can observe in Figures 4 and 5 that it could be better to use a direct transmission when the SNR is high and/or CSI is not accurate enough (low  values). This is because, similar outage probability results can be obtained without destining battery power to cooperation purposes.
values). This is because, similar outage probability results can be obtained without destining battery power to cooperation purposes.
5. Conclusions
In this work, we have studied the impact of outdated CSI in cooperative systems. The analysis has been carried out in terms of the trade-off of outage probability versus fairness of the system. To do so, an analytical expression has been obtained for the outage probability of an ORS scenario, whereas the difference among relays in terms of power consumption has been considered as a fairness measure and obtained by means of simulations. In order to assure a good balance in terms of performance versus fairness, we have proposed a relay selection strategy based on the max-normalized SNR criterion. The proposed strategy has been compared with existing relay selection strategies with the help of an analysis plot inspired in modern portfolio theory. In particular, we have represented the existing trade-offs of the different relaying mechanisms by plotting the outage probability versus the standard deviation of the power consumption. It has been shown that the max-normalized SNR guarantees a good performance versus fairness trade-off when available CSI is sufficiently accurate. When CSI is not accurate enough, however, direct transmission could be a better strategy.
References
Sendonaris A, Erkip E, Aazhang B: User cooperation diversity—part I: system description. IEEE Transactions on Communications 2003, 51(11):1927-1938. 10.1109/TCOMM.2003.818096
Sendonaris A, Erkip E, Aazhang B: User cooperation diversity—part II: implementation aspects and performance analysis. IEEE Transactions on Communications 2003, 51(11):1939-1948. 10.1109/TCOMM.2003.819238
Laneman JN, Tse DNC, Wornell GW: Cooperative diversity in wireless networks: efficient protocols and outage behavior. IEEE Transactions on Information Theory 2004, 50(12):3062-3080. 10.1109/TIT.2004.838089
Nabar RU, Bölcskei H, Kneubühler FW: Fading relay channels: performance limits and space-time signal design. IEEE Journal on Selected Areas in Communications 2004, 22(6):1099-1109. 10.1109/JSAC.2004.830922
Gesbert D, Shafi M, Shiu D-S, Smith PJ, Naguib A: From theory to practice: an overview of MIMO space-time coded wireless systems. IEEE Journal on Selected Areas in Communications 2003, 21(3):281-302. 10.1109/JSAC.2003.809458
IEEE 802.16's Relay Task Group http://wirelessman.org/relay
Ghosh A, Wolter DR, Andrews JG, Chen R: Broadband wireless access with WiMax/802.16: current performance benchmarks, and future potential. IEEE Communications Magazine 2005, 43(2):129-136.
Bletsas A, Shin H, Win MZ: Cooperative communications with outage-optimal opportunistic relaying. IEEE Transactions on Wireless Communications 2007, 6(9):3450-3460.
Markowitz H: Portfolio selection. The Journal of Finance 1952, 7(1):77-91. 10.2307/2975974
Markowitz H: Foundations of portfolio theory. The Journal of Finance 1991, 46(2):469-477. 10.2307/2328831
Zhao B, Valenti MC: Practical relay networks: a generalization of hybrid-ARQ. IEEE Journal on Selected Areas in Communications 2005, 23(1):7-18.
Dai L, Cimini LJ Jr.: Improved fairness in energy-constrained cooperative ad-hoc networks. Proceedings of the 40th Annual Conference on Information Sciences and Systems (CISS '06), March 2006, Princeton, NJ, USA 734-738.
Dai L, Chen W, Letaief KB, Cao Z: A fair multiuser cooperation protocol for increasing the throughput in energy-constrained ad-hoc networks. Proceedings of IEEE International Conference on Communications (ICC '06), June 2006, Istanbul, Turkey 8: 3633-3638.
Chen W, Dai L, Letaief KB, Cao Z: Fair and efficient resource allocation for cooperative diversity in ad-hoc wireless networks. Proceedings of IEEE Wireless Communications and Networking Conference (WCNC '07), March 2007, Hong Kong 4099-4104.
Krikidis I, Belfiore JC: Three scheduling schemes for amplify-and-forward relay environments. IEEE Communications Letters 2007, 11(5):414-416.
Huang W-J, Chiu F-H, Kuo C-CJ, Hong Y-W: Comparison of power control schemes for relay sensor networks. Proceedings of IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP '07), April 2007, Honolulu, Hawaii, USA 3: 477-480.
Michalopoulos DS, Karagiannidis GK: PHY-layer fairness in amplify and forward cooperative diversity systems. IEEE Transactions on Wireless Communications 2008, 7(3):1073-1083.
Laneman JN: Cooperative diversity in wireless networks: algorithms and architectures, Ph.D. dissertation. Massachusetts Institute of Technology, Cambridge, Mass, USA; August 2002.
Goldsmith A: Wireless Communications. Cambridge University Press, Cambridge, UK; 2005.
Bletsas A, Khisti A, Reed DP, Lippman A: A simple cooperative diversity method based on network path selection. IEEE Journal on Selected Areas in Communications 2006, 24(3):659-672.
Vicario JL, Antón-Haro C: Analytical assessment of multi-user vs. spatial diversity trade-offs with delayed channel state information. IEEE Communications Letters 2006, 10(8):588-590. 10.1109/LCOMM.2006.1665119
Yang L, Alouini M-S: Performance analysis of multiuser selection diversity. Proceedings of IEEE International Conference on Communications (ICC '04), June 2004, Paris, France 5: 3066-3070.
Bartolomé D: Fairness analysis of wireless beamforming schedulers, Ph.D. dissertation. Universitat Politecnica de Catalunya, Barcelona, Spain; January 2005.
Bengtsson M, Bartolomé D, Vicario JL, Antón-Haro C: Beamforming and bit-loading strategies for multi-user SDMA with admission control. Proceedings of the 16th IEEE International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC '05), September 2005, Berlin, Germany 2: 842-846.
Bosisio R, Primolevo G, Simeone O, Spagnolini U: Fair scheduling and orthogonal linear precoding/decoding in broadcast MIMO systems. Proceedings of the 16th IEEE International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC '05), September 2005, Berlin, Germany 2: 832-836.
Zagami A: Beamforming and bit-loading strategies for multi-user MIMO systems, M.S. thesis. Universitat Politecnica de Catalunya and Politecnico di Torino, Barcelona, Spain; June 2006.
Vicario JL, Antón-Haro C: A unified approach to the analytical assessment of multi-user diversity with imperfect channel state information: ergodic capacity and robustness analysis. European Transactions on Telecommunications 2007, 18(6):573-582. 10.1002/ett.1234
Acknowledgement
This work was supported by the Spanish Government Project TEC2008-06305/TEC.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Vicario, J.L., Bel, A., Morell, A. et al. Outage Probability versus Fairness Trade-off in Opportunistic Relay Selection with Outdated CSI. J Wireless Com Network 2009, 412837 (2009). https://doi.org/10.1155/2009/412837
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/412837


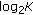 bits required).
bits required).
 . For the max-normalized SNR strategy, symbols are associated with the simulated results whereas lines correspond to the theoretical expression. (
. For the max-normalized SNR strategy, symbols are associated with the simulated results whereas lines correspond to the theoretical expression. ( = 5 relays,
= 5 relays,  = 1 bit/s/Hz,
= 1 bit/s/Hz,  = 100 m).
= 100 m).
 and System SNR (
and System SNR ( ,
,  = 5 relays,
= 5 relays,  = 1 bit/s/Hz,
= 1 bit/s/Hz,  = 100 m. Solid line: System SNR = 10 dB, dashed line: System SNR = 20 dB).
= 100 m. Solid line: System SNR = 10 dB, dashed line: System SNR = 20 dB).
 and System SNR (System
and System SNR (System  dB,
dB,  = 5 relays,
= 5 relays,  = 1 bit/s/Hz,
= 1 bit/s/Hz,  = 100 m. Solid line:
= 100 m. Solid line:  = 0.8, dashed line:
= 0.8, dashed line:  = 0.5).
= 0.5).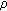 values and high system restrictions in terms of outage probability, conventional ORS strategy could be the most appropriate strategy. For high
values and high system restrictions in terms of outage probability, conventional ORS strategy could be the most appropriate strategy. For high  values, however, it is clear that more benefits are obtained with max-normalized SNR as similar results are obtained in terms of outage probability but the fairness among relays is substantially improved.
values, however, it is clear that more benefits are obtained with max-normalized SNR as similar results are obtained in terms of outage probability but the fairness among relays is substantially improved.