- Research Article
- Open access
- Published:
Securing OFDM over Wireless Time-Varying Channels Using Subcarrier Overloading with Joint Signal Constellations
EURASIP Journal on Wireless Communications and Networking volume 2009, Article number: 437824 (2009)
Abstract
A method of overloading subcarriers by multiple transmitters to secure OFDM in wireless time-varying channels is proposed and analyzed. The method is based on reverse piloting, superposition modulation, and joint decoding. It makes use of channel randomness, reciprocity, and fast decorrelation in space to secure OFDM with low overheads on encryption, decryption, and key distribution. These properties make it a good alternative to traditional software-based information security algorithms in systems where the costs associated with such algorithms are an implementation obstacle. A necessary and sufficient condition for achieving information theoretic security in accordance with channel and system parameters is derived. Security by complexity is assessed for cases where the condition for information theoretic security is not satisfied. In addition, practical means for implementing the method are derived including generating robust joint constellations, decoding data with low complexity, and mitigating the effects of imperfections due to mobility, power control errors, and synchronization errors.
1. Introduction
Orthogonal Frequency Division Multiplexing (OFDM) is a leading choice for many current and future air interfaces. When using OFDM over a wireless channel the broadcast nature of the channel exposes transmission to eavesdropping. Securing communication links from eavesdropping is commonly done by implementing enciphering and deciphering algorithms in software, and is usually detached from the physical layer of communication. Prominent methods rely on public keys cryptography such as RSA [1], or symmetric cryptography with a common secret, such as the US National Data Encryption Standard (DES) [2]. There are some encryption methods which rely on the physical layer of communication for their implementation, such as spread spectrum Frequency Hopping (FH) and Direct Sequence (DS) [3]. In FH and DS a key has to be generated and distributed securely between the communicating parties. The key is used to set the FH hopping pattern or DS spreading sequence. Prominent key distribution methods rely on the Diffie-Hellman algorithm [4]. Encryption, decryption, and key distribution impose overheads on data throughput, energy consumption, memory space, and computation power. These overheads are a crucial implementation issue for low complexity systems with strict constraints on system resources [5], such as sensor and mobile networks [6–8].
Secrecy capacity analysis of random, noisy, and fading channels showed that in theory, a communication link can be perfectly secured from eavesdropping for certain limited information rates [9–11]. Recent work provided specific analysis of the secrecy capacity of wireless fading channels [12–17]. Past work suggested practical methods for using randomness in the wireless channel to alleviate the need for key distribution. In [18–20], reciprocal channel estimation of a slow fading wireless time varying channel was used as a common secret to generate and distribute encryption keys to be used by traditional encryption algorithms. In [21] a differential frequency modulation technique coupled with reverse piloting was used in a multitone channel to achieve secure transmission for point-to-point systems. In [22] a practical approach is depicted for key agreement in wireless channels based on multilevel and Low Density Parity Check (LDPC) codes. In [18–22] the wireless channel was assumed to be a reciprocal slow flat fading channel, which decorrelates rapidly in space. The assumptions of reciprocity and space decorrelation were well established in previous work [21] and are adopted in this work as well.
It is common practice in wireless communications to have the transmitter use asynchronous bursts of transmission to access the channel. The burst starts with a prior known pilot signal followed by modulated data symbols. The pilot is used by the receiver to estimate the channel. The receiver then uses the channel estimate to compensate for channel attenuation and phase prior to decoding. Decoding of the received data symbols is done based on the a prior known signal constellation of the transmitter. Since the wireless channel changes with time, a pilot signal has to be sent every channel coherence time. An eavesdropper can use the pilot signal to estimate the channel from the transmitter to itself and decode the information in exactly the same manner as the intended receiver. This means that sending a pilot signal from the transmitter to the receiver compromises security.
In [23] the asynchronous burst transmission approach was replaced with synchronous transmission to achieve security. A reverse piloting protocol was proposed to secure transmission bursts in a narrow-band single carrier point-to-point system over slow flat fading channels. Synchronous transmission allows for the pilot signal to be sent from the receiver instead of the transmitter. The transmitter can estimate the channel from the receiver to itself using the receiver's pilot signal and deduce the channel from itself to the receiver based on channel reciprocity. The transmitter can then send a burst of channel-compensated data symbols over the same frequency as the pilot, and the receiver would receive a readily decodable channel-compensated signal. The receiver can use decision feedback to compensate for small changes in the channel, so that its channel estimate remains accurate until the original channel is fully decorrelated in time. After the channel decorrelates in time the receiver can send a new pilot signal. Since no pilot signal is sent from the transmitter, the eavesdropper would be deprived of estimating the channel from the transmitter to itself prior to receiving the data symbols, and would be forced to estimate the channel using blind estimation. Even for a noiseless channel, no decoding of the data would be possible until blind estimation is completed because the eavesdropper will not be able to map the received symbols to decoded bits. In this work, the reverse piloting protocol presented in [23] is elaborated to support a plurality of transmitters in a superposition modulation setting with joint decoding at the receiver. It is shown that the elaborated protocol can be practically used to obtain information theoretic security and security by complexity with low implementation complexity, no memory requirements and no overhead on throughput and energy.
In contradistinction to previous work in literature, the focus of this work is on facilitating channel overloading of multiple transmitters over subcarriers in an OFDM system. The purpose is to increase security strength and decoding gain for transmitters in an OFDM system with limited emission power, memory space, and online computation power. Although we focus our attention on OFDM, our analysis and results hold for securing narrowband single carrier transmission as well. The novelty of this work is in suggesting the use of reverse piloting for implementing superposition modulation with joint decoding to achieve information security. The main contributions are in two categories: analysis of security strength of the proposed method and practical implementation of the proposed method. The analysis of security strength results in a quantitative condition for achieving information theoretic security, given a prior known channel and system parameters and assessment of security by complexity when the condition is not satisfied. Practical implementation considerations include generating robust signal constellations, low complexity Maximum Likelihood(ML) decoding, network-optimization, evaluation of the effects of mobility, power control errors and synchronization errors, and formulating simple piloting rules for mitigating their effect.
The rest of the paper is organized as follows. In Section 2 the method is presented using a multiple access protocol. In Section 3 the mathematical model used for analysis is defined. In Section 4 security strength is analyzed. In Section 5 practical implementation is considered. Section 6 depicts an illustrative scenario of Rayleigh fading and three transmitters, and Section 7 concludes the work.
2. Proposed Method
In the proposed method the frequency and phase of subcarriers from multiple transmitters are matched and synchronized at the receiver. All transmitters transmit together and their start of transmission is coordinated by the receiver to have their signals reach the receiver simultaneously. All transmitters use the same subcarrier frequencies. The receiver is equipped with a single Matched Filter (MF) matched to each subcarrier. Each transmitter is assigned (offline) a set of arbitrary Base Band (BB) symbols to represent its information bits. Since the transmit-channel-receive path is linear, the receiver's MF output is a sum of the BB symbols of all the transmitters, and represents the transmitted bits of all the transmitters at once. This is in fact superposition modulation of multiple transmitters on a single subcarrier which is repeated individually for multiple subcarriers. The BB symbol sets are computed offline to have all their possible summations create a signal constellation with highest resistance to noise. The receiver decodes the information bits of all the transmitters at once from a single received symbol as if originating from a single transmitter. Since the received signal constellation is jointly formed by all the transmitters BB symbols, the proposed method is herein termed Joint Constellation Multiple Access(JCMA). A multiple access reverse piloting protocol over a single subcarrier is given in what follows to implement the method.
-
(1)
The receiver obtains knowledge on signal propagation time from each transmitter to itself through some standard association procedure.
-
(2)
The receiver assigns index anddelay parameter to each transmitter.
-
(3)
Each transmitter uses its index to access a preloaded table for retrieving a BB symbol set.
-
(4)
The receiver sends a pilot signal and starts sensing for an incoming signal.
-
(5)
Each transmitter individually estimates the reciprocal channel's phase and amplitude using the pilot signal from the receiver.
-
(6)
Each transmitter awaits its delay and sends a burst of information symbols compensated for channel phase and amplitude.
-
(7)
The receiver receives a burst of joint information symbols, which belong to its predefined joint signal set.
-
(8)
The receiver decodes all transmitters at once.
-
(9)
The receiver uses decision feedback to compensate for slow channel decorrelation in time.
-
(10)
Steps 4–9 are repeated after a channel decorrelation period has passed.
A preliminary simpler version of the proposed protocol in this work was disclosed in [24], with the purpose of enhancing decoding but no information security considerations.
JCMA is superposition modulation with joint decoding. It should be distinguished from the well-known Superposition Modulation with Successive Decoding (SM-SD) [25]. In SM-SD the transmitters transmit at the same time and frequency and a joint signal is formed at the receiver. Each transmitter's symbol is treated as noise to the other transmitters. The receiver decodes the information of each transmitter individually in a successive manner. First, the transmitter with the highest received signal energy is decoded. The decoded bits are used as feedback to remove the transmitter's signal from the received joint signal. The next transmitter with the highest received signal energy is decoded and so on. In SM-SD the transmitters send pilot signals to facilitate channel estimation at the receiver. As explained before, this compromises security. In JCMA pilots are sent only by the receiver. It follows that knowledge of the channel is obtained only by the transmitters.
JCMA should also be distinguished from multiuser detection [26] and rather recent advances in cooperative transmit diversity [27]. In multiuser detection the structure of the interfering signals from multiple transmitters is used to reduce their effect. The achievable coding gains are considerable, but the use of multiple MFs is required and the computational complexity grows exponentially with the number of transmitters. In addition, no security is gained. In cooperative transmit diversity, the transmitter sends its own information while relaying the information of another transmitter to the receiver. The method offers some performance gains, but the limited power of the relaying transmitter has to be distributed between the data streams of the participating nodes and no security is gained.
Beside SM-SD and multiuser detection, literature presents other approaches to channel overloading of transmitters over the same frequency band. For example, the work in [28–30] uses symbol-synchronous superposition modulation to create a joint rectangular lattice at the receiver to support multiple transmitters using trellis codes. There are also numerous works dealing with the adder-channel for performing joint coding from multiple transmitters through superimposed signals. In general, codebooks of individual transmitters are optimized under some criterion over the joint signal at the receiver—usually the focus is on coding gain. More relevant to the focus of this work is the work in [31, 32], where the joint minimal Euclidean distance was used as the optimizing criterion of a symbol-synchronous superimposed signal. A comprehensive review of other channel overloading techniques is provided in [39].
The work in [25, 27–32] addresses the issue of designing joint signal constellations to satisfy various optimization criteria according to the problem explored. We are unaware of previous work (including [25, 27–32]) using secure, low complexity, joint symbol by symbol decoding as the optimization criteria.
As would be apparent in the following sections, the suggested method offers a low complexity solution for securing OFDM over the time-varying wireless channel. The receiver uses a single MF and performs decoding of multiple transmitters with the same complexity as decoding a single transmitter. The transmitters' complexity is the same as that of a point-to-point scenario without security features. No memory space, computation power, or transmitted energy is required in order to secure transmission. For comparison, consider the analysis of energy consumption due to implementing security algorithms performed in [5]. In [5], it was shown that a typical sensor-node using asymmetric key establishment coupled with symmetric encryption per transmission session losses 20%–80% of its battery life due to encryption, depending on the session length. See [5] for energy consumption of RSA, DES, and DH in specific systems. Other analysis provided in [8] considered the Central Processing Unit(CPU), memory and transmission overheads required for implementing standard security algorithms implemented in specific off-the-shelf nodes. The analysis in [8] concluded that DES is too resource demanding to be used in a sensor network and that a minimum of 128 KB RAM and ability to tolerate a considerable delay in data delivery are required to implement security algorithms of lesser strength. See [8] for CPU processing and memory and transmission overheads of encryption algorithms DES, TEA, RC6, RC5, and SkipJack in specific systems.
3. Mathematical Model
In JCMA a joint constellation is constructed over each subcarrier separately. It follows that most of the analysis can be done using a model for a single subcarrier. In what follows, a single subcarrier is considered. The expansion of the analysis to an entire OFDM symbol is done when evaluating security of the entire OFDM transmission.
The BB model of the multiple access scheme for a single subcarrier is depicted in Figure 1,  represent the transmitted complex BB symbols. Subcarriers in OFDM experience flat fading. It follows that the channel over a single subcarrier is flat and is described by a single complex number
represent the transmitted complex BB symbols. Subcarriers in OFDM experience flat fading. It follows that the channel over a single subcarrier is flat and is described by a single complex number  . The transmitted symbols are summed via channel superposition and the MF output, without noise, is given by
. The transmitted symbols are summed via channel superposition and the MF output, without noise, is given by  Also,
Also,  is the BB additive white complex Gaussian noise. The received signal
is the BB additive white complex Gaussian noise. The received signal  is fed to an ML decision device, which decodes all the transmitted bits at once, as if originating from a single transmitter (the so-called "super-user" in [25]).
is fed to an ML decision device, which decodes all the transmitted bits at once, as if originating from a single transmitter (the so-called "super-user" in [25]).
Let us define

where  is an information-carrying symbol with unit energy which belongs to a predefined set
is an information-carrying symbol with unit energy which belongs to a predefined set  . It is assumed that
. It is assumed that  is small enough to allow the transmitter to adjust its power within its power constraint. If this is not the case, communication would be severed, as would also happen in a standard point to point scenario.
is small enough to allow the transmitter to adjust its power within its power constraint. If this is not the case, communication would be severed, as would also happen in a standard point to point scenario.
For now, it is assumed that  are known without error at the
are known without error at the  th transmitter-perfect Channel State Information (CSI), and that
th transmitter-perfect Channel State Information (CSI), and that  remains constant during the decorrelation time. In later sections, derivations to the model are defined to analyze the effects of imperfect CSI and mobility on system performance.
remains constant during the decorrelation time. In later sections, derivations to the model are defined to analyze the effects of imperfect CSI and mobility on system performance.
From (1) and Figure 1 it follows that

The joint signal constellation at the receiver is made up of all the permutations in  which generate
which generate  .
.
Note that  are sets of complex numbers, where
are sets of complex numbers, where  In addition,
In addition,  is the number of bits per symbol per transmitter, and
is the number of bits per symbol per transmitter, and  is a set of complex numbers made of all possible summations of
is a set of complex numbers made of all possible summations of  numbers, where each number belongs to a different set
numbers, where each number belongs to a different set  . Moreover,
. Moreover, 

 where
where  for all
for all  .
.
The symbol sets are determined offline. For additive Gaussian noise, the minimum Euclidian distance in the joint constellation represented by  should be maximal while constraining the average instantaneous energy over the transmitter symbols to be less than
should be maximal while constraining the average instantaneous energy over the transmitter symbols to be less than  (peak power constraint on transmitted power). Finding the best BB symbol sets is explicitly formulated as follows.
(peak power constraint on transmitted power). Finding the best BB symbol sets is explicitly formulated as follows.
Given the definition:

find  which yield
which yield  , while satisfying the constraint:
, while satisfying the constraint:

For additive Gaussian noise, ML detection translates to finding the joint constellation symbol  in
in  which has the smallest Euclidean distance from the received symbol
which has the smallest Euclidean distance from the received symbol  , so
, so

4. Security Analysis
To facilitate analysis, we assume that the eavesdropper uses a single MF for decoding the data. At first glance, this seems to be an unreasonable limitation on the eavesdropper resources. The justification for this constraint would be given as part of the discussion in this section.
In JCMA, the joint constellation at the receiver's MF output is the result of a coherent sum of the transmitter BB symbols and is unique to the location of the transmitters and receiver in space. This is achieved due to the individual compensation of delay, phase, and attenuation of each transmitter. The receiver's joint constellation would always be the same and the bit mapping from the transmitters to the joint symbols would be known a prior to the receiver. Since an eavesdropper would naturally occupy a different location in space, the transmitters BB symbols would create a different joint constellation than that of the receiver. This is practically always true even when the eavesdropper is close to the receiver because the wireless channel decorrelates fast in space. A distance of a few carrier wavelengths apart (a few centimeters for frequencies of the order of GHz) decorrelates the channel almost completely [33]. It follows that the eavesdropper would have no a prior knowledge of the bit mapping from transmitters to joint symbols. This is the basis for achieving information theoretic security.
The joint constellation is constructed optimally at the receiver's location in space. It follows that the joint constellation at the eavesdropper location would have suboptimal structure and would change after every reverse pilot sent due to different channel compensation performed at the transmitters. In addition, the signals from the transmitters would not reach the eavesdropper simultaneously. It follows that even after discovering the bit mapping from transmitters to joint symbols, the eavesdropper would have to decode the information based on a deteriorated joint signal constellation and the decoding complexity would be higher than that of the receiver. This is the basis for security by complexity.
For decoding data successfully the eavesdropper must first perform blind channel estimation to map its received joint constellation symbols to information bits. Finding the bit mapping is an act of deciphering, where the received joint symbols are the cipher-text, the channel coefficients are the encryption key and the information bits are the encrypted message. After deciphering, the eavesdropper must decode the data from a deteriorated signal.
4.1. Information Theoretic Security
We start by describing the JCMA BB model as a Shannon secrecy model. Figure 2 depicts the secrecy model for an eavesdropper. The pilot from the receiver invokes key generation and distribution from the wireless medium to the transmitters. This key is the channel estimates at the transmitters. Each part of the key is known exclusively at each transmitter. In accordance with the Shannon secrecy model and its notation in [34], the message  as defined in [34] corresponds to the vector of transmitted symbols across the transmitters. This joint message is encrypted by the transmitters—each transmitter transforms its symbol by scaling and rotating it with the key. So
as defined in [34] corresponds to the vector of transmitted symbols across the transmitters. This joint message is encrypted by the transmitters—each transmitter transforms its symbol by scaling and rotating it with the key. So  in [34] corresponds to the vector of channel estimates at the transmitters. For the receiver's location in space, the channel itself performs a deciphering operation by rotating and scaling the encrypted message back to the original
in [34] corresponds to the vector of channel estimates at the transmitters. For the receiver's location in space, the channel itself performs a deciphering operation by rotating and scaling the encrypted message back to the original  . For the eavesdropper location in space the channel performs another enciphering operation with another key
. For the eavesdropper location in space the channel performs another enciphering operation with another key  , being the channels from the transmitters to the eavesdropper location. The eavesdropper constellation point
, being the channels from the transmitters to the eavesdropper location. The eavesdropper constellation point  corresponds to the cryptogram
corresponds to the cryptogram  in [34]. The eavesdropper has to decipher
in [34]. The eavesdropper has to decipher  from
from  using all possible prior knowledge, such as the offline-determined transmitters BB symbol sets, the channel statistics, and the prior probabilities of the messages
using all possible prior knowledge, such as the offline-determined transmitters BB symbol sets, the channel statistics, and the prior probabilities of the messages  .
.
A new key is generated every time a reverse pilot signal is sent by the receiver. Due to the time varying nature of the fading channel, a key uncorrelated with previous keys is invoked after the channel decorrelates in time. This is why the receiver is required to track the channel during the decorrelation period. Note that encryption and decryption are done automatically by the channel, so no overheads are required for these operations.
The unicity distance was defined in [34] as the amount of intercepted cryptograms by the eavesdropper beyond which the eavesdropper can deduce the key. Equivalently, the cryptogram is undecipherable when the message length is less than the unicity distance [34]. So, to achieve information theoretic security the message should be enciphered by a new key before the eavesdropper gathers enough cryptograms for deciphering. To secure an entire OFDM transmission burst, the number of joint symbols within the channel decorrelation period must be less than the unicity distance.
In the point-to-point narrow-band scenario ( ) described in [23] a single channel took part in encrypting a single message. It was shown that the channel acts as a shift cipher for cases where the phase of the complex Random Variable (RV) representing the channel is uniformly distributed. Uniform distribution of phase is a common assumption for describing wireless time-varying channels. For the multipoint to point scenario we assume that the phase of each channel is uniformly distributed over the range
) described in [23] a single channel took part in encrypting a single message. It was shown that the channel acts as a shift cipher for cases where the phase of the complex Random Variable (RV) representing the channel is uniformly distributed. Uniform distribution of phase is a common assumption for describing wireless time-varying channels. For the multipoint to point scenario we assume that the phase of each channel is uniformly distributed over the range  . We derive the unicity distance for JCMA based on this single assumption. For clarity of presentation we consider the case where a single bit is transmitted by each transmitter (
. We derive the unicity distance for JCMA based on this single assumption. For clarity of presentation we consider the case where a single bit is transmitted by each transmitter ( ). The derivation scales easily for general
). The derivation scales easily for general  .
.
The received joint constellation at the eavesdropper is given by (see Figure 2)

Using amplitude-phase representation a single transmitter symbol set is given by

The structure of any signal constellation must be constrained to achieve an output signal with zero mean, so that no power is wasted. This means that the two signals in the constellation are antipodal:

Using  ,
,  ,
,  (7) and (8) in (6) give
(7) and (8) in (6) give

where  and
and 
We find that  originating from a single transmitter arrives at the eavesdropper with the same amplitude
originating from a single transmitter arrives at the eavesdropper with the same amplitude  for either of the two possible bit values. The phase of
for either of the two possible bit values. The phase of  is the sum of three RVs. Two of the RVs (
is the sum of three RVs. Two of the RVs ( ,
, ) are uniformly and independently distributed over the range
) are uniformly and independently distributed over the range  and the third (
and the third ( ) assumes one of two possible values
) assumes one of two possible values  corresponding to the two possible bit values.
corresponding to the two possible bit values.
Since the phase is uniformly distributed and cyclic over  , taking its colinear values (multiplying the RV with
, taking its colinear values (multiplying the RV with  ) results in the same distribution. It follows that the Probability Density Function (PDF) of
) results in the same distribution. It follows that the Probability Density Function (PDF) of  is equal to the PDF of
is equal to the PDF of  which is the result of convolution of two uniform PDFs:
which is the result of convolution of two uniform PDFs:

Due to the cyclic property of the phase (modulo  ), (10) is equivalent to
), (10) is equivalent to

It follows that  is uniformly distributed over the range
is uniformly distributed over the range  . Adding
. Adding  to
to  results in a cyclic shift of phase values over the range
results in a cyclic shift of phase values over the range  but does not change the PDF regardless the value of
but does not change the PDF regardless the value of  . It follows that
. It follows that  is always uniformly distributed over the range
is always uniformly distributed over the range  . This means that the mappings from the two possible transmitter bit values to a received symbol
. This means that the mappings from the two possible transmitter bit values to a received symbol  at the eavesdropper are equally probable.
at the eavesdropper are equally probable.
Since the channel decorrelates fast across space, the received individual symbols from the different transmitters at the eavesdropper  are uncorrelated, each received symbol from a transmitter has two equally probable bit mappings. The result is
are uncorrelated, each received symbol from a transmitter has two equally probable bit mappings. The result is  equally probable bit mappings for the joint signal constellation at the eavesdropper. It follows that JCMA is analogous to a substitution cipher with
equally probable bit mappings for the joint signal constellation at the eavesdropper. It follows that JCMA is analogous to a substitution cipher with  equally probable keys.
equally probable keys.
The unicity distance of a substitution cipher is given by [34]

where  is the entropy of the key. Also,
is the entropy of the key. Also,  is the efficiency of the information source defined as
is the efficiency of the information source defined as  , where
, where  is the redundancy of the information source [34]. In our case,
is the redundancy of the information source [34]. In our case,  and the JCMA unicity distance is given by
and the JCMA unicity distance is given by

The model in Figure 2 depicts a single subcarrier. Neighboring subcarriers in OFDM experience similar channel response due to channel correlation across bandwidth. This means that neighboring subcarriers can be used by the eavesdropper to discover their similar channel response (encryption key). It is common to assume that the channel decorrelates in frequency every coherence bandwidth ( ). To be on the safe side, it is assumed that all subcarriers within
). To be on the safe side, it is assumed that all subcarriers within  experience exactly the same channel. This is a strict assumption, since subcarriers which are less than
experience exactly the same channel. This is a strict assumption, since subcarriers which are less than  apart are not fully correlated.
apart are not fully correlated.
Secrecy is required for the entire data transmission burst. This means that the unicity distance must be larger than the number of received joint symbols during the channel decorrelation period ( ) times the number of subcarriers within the channel coherence bandwidth (
) times the number of subcarriers within the channel coherence bandwidth ( ). It follows from (13) that for
). It follows from (13) that for

information theoretic security is achieved for the entire data burst.
Note that  and
and  are given by
are given by

where  is the transmitted symbol time.
is the transmitted symbol time.
The channel temporal decorrelation time ( ), is governed by the Doppler spread (
), is governed by the Doppler spread ( ) and is defined as
) and is defined as

where  is set to achieve sufficient channel decorrelation in time. However,
is set to achieve sufficient channel decorrelation in time. However,  is determined by the relative movement of the transmitter with respect to the receiver described by the Doppler shift, and by the movement of reflectors in their path. Moreover,
is determined by the relative movement of the transmitter with respect to the receiver described by the Doppler shift, and by the movement of reflectors in their path. Moreover,  increases with mobility and carrier frequency. In the context of encryption strength a short channel decorrelation time (higher mobility) is preferred. This results in a higher key generating rate. In this sense, the worse-case scenario is a stationary transmitter and receiver, for which
increases with mobility and carrier frequency. In the context of encryption strength a short channel decorrelation time (higher mobility) is preferred. This results in a higher key generating rate. In this sense, the worse-case scenario is a stationary transmitter and receiver, for which  has the smallest possible value.
has the smallest possible value.
Using (15), (16) in (14) results in

If the system and channel parameters satisfy (17) the data transmission burst is secured from eavesdropping.
If (17) is difficult to satisfy due to small  , security can be obtained by shortening the number of data symbols in the transmission burst so that it equals the unicity distance. This results in an equality in (14) regardless of the channel decorrelation period. This approach would result in throughput reduction as the transmitters must wait in idle mode for the channel to decorrelate. Throughput loss can be avoided by having multiple JCMA groups accessing the channel in a TDMA fashion, so that one group uses the channel while the others wait for it to decorrelate. Alternatively, the protocol can be applied to only some of the subcarriers preferably spaced apart as much as possible across the bandwidth.
, security can be obtained by shortening the number of data symbols in the transmission burst so that it equals the unicity distance. This results in an equality in (14) regardless of the channel decorrelation period. This approach would result in throughput reduction as the transmitters must wait in idle mode for the channel to decorrelate. Throughput loss can be avoided by having multiple JCMA groups accessing the channel in a TDMA fashion, so that one group uses the channel while the others wait for it to decorrelate. Alternatively, the protocol can be applied to only some of the subcarriers preferably spaced apart as much as possible across the bandwidth.
We now justify constraining the use of a single MF at the eavesdropper. An MF is the optimal demodulator for achieving a maximal SNR from the received signal [35]. Using multiple MFs connected to a signal antenna makes no sense because the joint constellation is constructed over a single complex dimension for any number of transmitters. It follows that the optimal choice for the eavesdropper is to use a single MF with soft decoding. If the eavesdropper would try to use multiple antennas for finding the bit mapping faster (for decreasing the unicity distance), the result would be multiple equivalent deciphering problems and the eavesdropper would gain nothing as far as deciphering time is concerned.
4.2. Security by Complexity
In the previous section, information theoretic security of the entire data transmission burst was found. Deciphering amounted to discovering the bit mapping from the transmitters to each joint symbol. Knowledge of the mapping is obtained by the eavesdropper after the unicity distance has passed only if the eavesdropper uses the best possible algorithm to decipher the data. After deciphering is accomplished, the eavesdropper still has to decode the data. When information theoretic security is not achievable, security boils down to making decoding much more difficult for the eavesdropper compared to the intended receiver. We identify four such security-by-complexity features of JCMA.
-
(1)
The eavesdropper would have difficulty to know the expected joint symbol constellation at its MF output, since it has no knowledge of the channel compensation done at each transmitter, no immediate knowledge of the CSI from the nodes to itself, and it receives noisy samples.
-
(2)
The signals from the group nodes would not reach the eavesdropper simultaneously, resulting in an overlap of past and present symbols.
-
(3)
The eavesdropper joint constellation would change every decorrelation period. This is due to the changing of channel compensation at the transmitters. This makes it impossible to design a constant and computationally efficient decoding algorithm, meaning that the eavesdropper would have to perform an exhaustive search for ML detection of every received symbol. At the same time, the receiver decoding algorithm would be constant because each channel instance is compensated for.
-
(4)
The joint constellation formed at the eavesdropper MF output is not optimal for decoding, since it was made to be optimal at a different and unique location in space—that of the receiver.
Due to Factor 1, the eavesdropper must first decide on its joint signal constellation. This precedes deciphering (mapping bits to joint symbols) and could prove to be a difficult task, since the joint samples are noisy and the joint constellation changes with every new pilot from the receiver.
The deterioration of the signal at the eavesdropper due to Factor 2 is substantial when the eavesdropper is far from the receiver and is difficult to evaluate as it depends greatly on the multipath propagation of the transmitted signal. Factor 2 could be compromised when the eavesdropper is close enough to the receiver.
Due to Factor 3, the asymptotic decoding complexity of the eavesdropper is  , corresponding to an exhaustive search over all possible constellation points. It would be shown in Section 5that the asymptotic decoding complexity of the receiver is
, corresponding to an exhaustive search over all possible constellation points. It would be shown in Section 5that the asymptotic decoding complexity of the receiver is  . The difference in complexity can become substantial for small
. The difference in complexity can become substantial for small  as well. For example, for
as well. For example, for  the receiver would be required to perform five simple calculations per symbol, while the eavesdropper would have to calculate and compare 32 Euclidean distances. Although the decoding complexity of the eavesdropper is expected to be high, it is prudent to assume that the eavesdropper might have unlimited computational power, which would allow it to perform ML detection using exhaustive search, so Factor 3 could be compromised.
the receiver would be required to perform five simple calculations per symbol, while the eavesdropper would have to calculate and compare 32 Euclidean distances. Although the decoding complexity of the eavesdropper is expected to be high, it is prudent to assume that the eavesdropper might have unlimited computational power, which would allow it to perform ML detection using exhaustive search, so Factor 3 could be compromised.
Due to Factor 4, the eavesdropper has to perform decoding using a suboptimal joint symbol constellation and is expected to suffer a considerable penalty on Bit Error Rate(BER) compared to the receiver. The exact decoding loss depends on the number of transmitters, and the characteristics of the channel which prevents a general analysis. Evaluation of decoding loss for three transmitters over a Rayleigh channel is given in Section 6.
The eavesdropper could use soft decoding and reception using multiple antennas to achieve decoding gains. However, at least some of the gains can be matched by the receiver. The illustrative scenario provided in Section 6 demonstrates that the required gain to match the receiver's hard-decoding BER is 20 dB for three transmitters in Rayleigh fading.
5. Practical Implementation
JCMA is based on superposition modulation with joint decoding. Superposition modulation schemes require accurate symbol synchronization and power control, and are adversely affected by mobility. These limitations are commonly deemed prohibitive in practical applications. Although superposition modulation is assumed in many theoretical works, practical means of implementation are usually not addressed, see [28–32], for examples.
To implement JCMA, robust joint signal constellations and the transmitters' symbols sets that construct them must be found offline. The joint constellations must not result in performance loss. Efficient low complexity joint decoding must be formulated as well. The expected increased sensitivity to synchronization and power control errors must be mitigated without increasing implementation complexity. These issues are addressed in what follows.
5.1. Joint Signal Constellations
5.1.1. Decoding Gain for Power Limited Transmitters
The overall signal energy collected by the receiver's MF in JCMA grows with the number of transmitters. However, this does not necessarily mean that performance would be enhanced. The BER of ML detection in Gaussian noise is governed by the Euclidean distance between points in the constellation [35]. A key requirement for enhancing performance with JCMA is that the increased energy per joint symbol translates to an increase in the minimal Euclidean distance. In what follows, a probabilistic approach is taken to prove that this is indeed the case.
From (2),

where the index  is introduced to denote that
is introduced to denote that  was created by
was created by  transmitters.
transmitters.
Assuming equal probability for each transmitted symbol per transmitter,

Let  and
and  denote the mean value and the variance of the RV
denote the mean value and the variance of the RV  respectively. It is assumed that the transmitters transmit independent data and, therefore,
respectively. It is assumed that the transmitters transmit independent data and, therefore,  are mutually independent. For
are mutually independent. For  sufficiently large,
sufficiently large,  is a complex normal RV with mean
is a complex normal RV with mean  and variance
and variance

The following RV is defined

where  and
and  are two received constellation points. Since the probability for receiving one joint constellation point is independent of the probability for receiving any other constellation point,
are two received constellation points. Since the probability for receiving one joint constellation point is independent of the probability for receiving any other constellation point,  and
and  are independent RVs. Also,
are independent RVs. Also,  and
and  are characterized by complex normal distributions with mean
are characterized by complex normal distributions with mean  and variance
and variance  . Another RV is defined as
. Another RV is defined as

where  has a chi-squared distribution with two degrees of freedom and its PDF is given by [36]
has a chi-squared distribution with two degrees of freedom and its PDF is given by [36]

where  is the squared Euclidean distance between two randomly chosen points from the joint constellation. It follows that for Gaussian noise,
is the squared Euclidean distance between two randomly chosen points from the joint constellation. It follows that for Gaussian noise,  governs system performance as it is directly related to BER.
governs system performance as it is directly related to BER.
To proceed, let us define a  such that
such that

where  is a small positive number. However, (24) means that the probability that the Euclidian distance between two arbitrarily chosen points from the joint constellation would be greater than
is a small positive number. However, (24) means that the probability that the Euclidian distance between two arbitrarily chosen points from the joint constellation would be greater than  is very close to 1.
is very close to 1.
Let us find  that satisfies (24). From (23),
that satisfies (24). From (23),

Introducing (24) to (25) yields

From (20), it follows that  therefore, from (26),
therefore, from (26),

The minimum distance increases (in a probability sense) as  increases. In other words, the increased energy reaching the receiver is translated to increased distance between joint constellation points at the receiver.
increases. In other words, the increased energy reaching the receiver is translated to increased distance between joint constellation points at the receiver.
Now consider a Time Division Multiple Access(TDMA) system with power limited transmitters and the same data rate as a JCMA system. To maintain the same data rate as that of the JCMA system, the constellation of each transmitter would have to become more crowded as  increases. Because the overall constellation power remains constant, the minimal distance of the received constellation would decrease and performance would deteriorate.
increases. Because the overall constellation power remains constant, the minimal distance of the received constellation would decrease and performance would deteriorate.
5.1.2. Suboptimal Symbol Search
To find the optimal joint constellation, one must solve (3), (4) analytically. The goal is to find BB symbol sets which maximize the minimal Euclidean distance in the resulting joint symbol constellation. This is an optimization problem with quadratic constraint. While a closed form solution may be found under limiting assumptions, this approach is avoided and suboptimal search methods are used instead. This alternative approach is justified because optimization is done only once for a set of transmitters and is performed offline, so there is no need for a fast real-time solution.
For simplicity of presentation it is assumed that each transmitter has two symbols in its symbol set, which means that each transmitter has a single information bit represented in the joint constellation (or chip when forward error correction is employed). To make sure no transmission power is wasted, each BB symbol set is made to be a rotated and scaled version of Binary Phase Shift Keying(BPSK). This insures that the mean value of each BB symbol set and the mean value of the joint constellation are zero. The derivations that follow are easily applicable to more than one bit (chip) per symbol.
A random search approach can be used, for which symbol sets are found using a Monte Carlo simulation. A random set of BB symbols for each transmitter is randomly generated and is normalized to meet the power constraint in (4). The resulting joint constellation is derived and its minimal Euclidean distance as defined in (3) is evaluated. This process is repeated in numerous trials and the collection of BB sets which result in the best joint constellation is chosen. It is possible to add constraints on the BB symbol sets sizes to comply with Quality of Service (QoS) demands. In addition, the peak power constraints may vary across transmitters to address unequal channel fading attenuations which could represent near-far scenarios common in multiple access scenarios. Preliminary results for such optimization scenarios were presented in [37]. The solutions found with the random symbol search are asymptotically optimal as the number of search trials approaches infinity.
A parametric symbol search approach can be used as well. The phase and amplitude of each BB constellation point is quantized with some resolution. The resulting joint constellation is tested for each sample of phase and amplitude. The granularity of the parametric search increases with the quantization resolution, and the result is asymptotically optimal for infinitely small granularity.
To explore the proposed approach the joint constellation for  transmitters was optimized using a random symbol search. For comparison, a TDMA system using a
transmitters was optimized using a random symbol search. For comparison, a TDMA system using a  -QAM constellation is used, which results in the same overall bit rate. Figure 3 displays the gain in
-QAM constellation is used, which results in the same overall bit rate. Figure 3 displays the gain in  for the received constellations. It is clearly seen that JCMA results in better constellations for all tested
for the received constellations. It is clearly seen that JCMA results in better constellations for all tested  . This result shows that the performance gain buildup proven before is achievable using the random symbol search approach and that JCMA is energy efficient. An example of a joint constellation obtained via random symbol search is given in Section 6.
. This result shows that the performance gain buildup proven before is achievable using the random symbol search approach and that JCMA is energy efficient. An example of a joint constellation obtained via random symbol search is given in Section 6.
5.2. Maximum Likelihood Detection
The received joint signal sample at the MF output is to be decoded based on the expected joint constellation using ML detection. ML detection in the presence of Gaussian noise boils down to finding the constellation point which is closest to the received sample (minimal Euclidean distance). Performing ML detection using exhaustive search over all possible constellation points has algorithmic complexity of  . This complexity grows exponentially with the number of transmitters. For systems with constrained resources, exhaustive search might be impractical to implement even for small values of
. This complexity grows exponentially with the number of transmitters. For systems with constrained resources, exhaustive search might be impractical to implement even for small values of  . For example,
. For example,  requires calculating and comparing eight Euclidean distances for every received symbol. This complexity problem exists for any single transmitter user constellation with
requires calculating and comparing eight Euclidean distances for every received symbol. This complexity problem exists for any single transmitter user constellation with  constellation points. Traditionally, in point-to-point systems the decoding complexity is reduced by using suboptimal constellations such as rectangular QAM. Suboptimal constellations are designed to exhibit structural symmetries which are used for efficient decoding of the received samples [38].
constellation points. Traditionally, in point-to-point systems the decoding complexity is reduced by using suboptimal constellations such as rectangular QAM. Suboptimal constellations are designed to exhibit structural symmetries which are used for efficient decoding of the received samples [38].
The JCMA constellation exhibits structural symmetries as well. Using a simple manipulation on the expression for the received joint symbol gives

Symmetry lines can be drawn between the BB symbols of  shifted to
shifted to  . If the symmetry lines are drawn for all
. If the symmetry lines are drawn for all  symbol sets, the receiver's observation space is divided to decision regions with a constellation point at the center of each region. The ML decoding problem in Gaussian noise reduces to finding the decision region in which the received sample is located.
symbol sets, the receiver's observation space is divided to decision regions with a constellation point at the center of each region. The ML decoding problem in Gaussian noise reduces to finding the decision region in which the received sample is located.
Assuming the angles of the symmetry lines with the real axis value in the complex plane are given by  , the following guidelines for finding a computationally efficient ML decoding algorithm are defined.
, the following guidelines for finding a computationally efficient ML decoding algorithm are defined.
-
(1)
Rotate the received joint symbol sample
 by an angle of
by an angle of  :
: 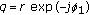 .
. -
(2)
If
 is to the right of the symmetry line intersection with the real axis, set
is to the right of the symmetry line intersection with the real axis, set  , else set
, else set  .
. -
(3)
Repeat steps 1,2 for all
 .
. -
(4)
Use
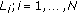 to access a predefined Look Up Table (LUT) containing the bit loading of the constellation point in the decision region of the received sample.
to access a predefined Look Up Table (LUT) containing the bit loading of the constellation point in the decision region of the received sample.
The algorithmic complexity of the suggested efficient ML decoding is  . This is also the complexity of traditional
. This is also the complexity of traditional  -QAM ML decoding of a single transmitter with equal rate to a JCMA system with
-QAM ML decoding of a single transmitter with equal rate to a JCMA system with  transmitters and 1 bit per symbol per transmitter.
transmitters and 1 bit per symbol per transmitter.
5.3. Effects of Imperfect Power Control, Synchronization Errors and Mobility
JCMA requires synchronization between the transmitters at the symbol level. This is a higher synchronization demand than that of TDMA, for example. Methods with equivalent synchronization demands as those of JCMA are symbol-synchronous Code Division Multiple Access (CDMA) [26, 41], SM-SD [25], and the methods defined in [28–32]. In addition, JCMA demands a higher accuracy in power control. In this section, the effects of synchronization errors, power control errors, and mobility on JCMA are discussed. For coherency of presentation, the rigorous analysis leading to this discussion is given in Appendix .
Lack of perfect synchronization is manifested by errors in the channel phase estimates, and inaccurate power control is manifested by errors in the channel amplitude estimate. It follows that both are accurately modeled by an additive complex RV representing an error in the channel estimate (CSI errors). The effects of CSI errors (phase and amplitude) on system performance are analyzed in a comparative manner to TDMA. Since the transmitters are required to be simple in design, we assume that each transmitter obtains its CSI by estimating the channel coefficient using some linear estimator, such as a linear Minimum Mean Square Error(MMSE) estimator.
In Appendix the required energy of the JCMA receiver sent pilot signal is found with respect to that of a TDMA system, so that the JCMA system performance loss would be the same as the TDMA system performance loss. This analysis results in a quantitative estimate of the effects of synchronization and power control errors, and the required pilot energy to support the synchronization demands of JCMA. In Appendix it is shown that in order to achieve the same synchronization/power control error in JCMA as that of TDMA while maintaining the decoding gain, the pilot energy used for channel estimation must have  times more energy. This increase in energy can be achieved by using longer pilots resulting in decreased throughput or by increasing pilot signal power. Alternatively, the performance gain can be waived by reducing the transmitters' power emission resulting in no need for increasing pilot energy.
times more energy. This increase in energy can be achieved by using longer pilots resulting in decreased throughput or by increasing pilot signal power. Alternatively, the performance gain can be waived by reducing the transmitters' power emission resulting in no need for increasing pilot energy.
In JCMA a pilot is sent every channel decorrelation time. In Appendix the rate of pilot transmission for JCMA is calculated to achieve the same channel decorrelation as for TDMA. This analysis results in a quantitative estimate of the effects of mobility of transmitters and the required system resources to support such mobility (throughput loss due to pilot signal transmission). It is also shown that the JCMA system effectively shortens the channel decorrelation time. This results in a need for more frequent pilot transmission which causes throughput reduction. As far as security is concerned, the shortening of decorrelation time is a benefit. This is because faster variation in the channel allows for a higher cryptographic key generating rate. If the coding gain is waived by reducing power emission, the decorrelation time is the same for JCMA and TDMA and no overhead on throughout is incurred.
Following the analysis in Appendix we define the following piloting rule: if the transmitters in a JCMA setting use all their available power, decoding gain and faster key generating rate are obtained at the expense of higher energy consumption. To support these benefits without degrading decoding the receiver's pilot energy must be increased times the number of transmitters. Alternatively, the decoding gain and fast channel decorrelation can be waived by reducing the transmitters' power emission. This would result in same energy consumption as that of a single transmitter and there would be no need to increase pilot energy.
5.4. Network Management
JCMA is expected to operate in a multiple access scenario. Multiple access scenarios require network management protocols to resolve near-far problems, facilitate QoS requirements, and optimize the overall data throughput.
In the classical CDMA near-far scenario, a dominant transmitter deprives other transmitters from service by masking their transmitted signal at the receiver. The solution is to use power-control by the receiver to reduce the power of the dominant transmitter so that other transmitters can be detected as well. In JCMA each transmitter adjusts its power emission according to channel fading and the symbol set it is assigned by the receiver. The receiver can solve near-far scenarios by assigning symbol sets which should be received with low power to transmitters with higher attenuating channels. Transmitters with lower attenuating channels can be assigned a symbol set with higher power in the joint constellation.
Another possible solution is to match transmitters into JCMA groups according to the channel they experience over different subcarriers. This is an extension of OFDM-Access (OFDMA). In OFDMA subcarriers are allocated to different transmitters according to the quality of their channel over the frequency selective bandwidth. The basic idea is to allocate parts of the bandwidth to each transmitter in an efficient way so that the overall network throughput is increased. In JCMA transmitters should be grouped to facilitate the construction of the joint signal constellation at the receiver with minimal power-loss due to power reduction at the dominant transmitters.
In addition, it is possible to perform offline optimization of symbol sets to resolve specific near-far scenarios. The resulting symbol sets would be kept at the transmitters' symbol sets tables and used when the receiver dims it appropriate. This possibility does not exist in a classical CDMA system.
Offline optimization of symbol sets can be defined with different sizes of the transmitters' symbols sets. A transmitter with a larger symbol set size would be represented at the joint constellation with more bits and so its throughout would be higher than that of the other transmitters.
6. Illustrative Scenario—Rayleigh Fading
Performance in Rayleigh fading channels is evaluated in what follows. First, the channel conditions for achieving information theoretic security are depicted for various  in accordance with the condition in (17). Following analysis of information theoretic security, a JCMA setting of three transmitters is depicted, including generating the joint constellation and an algorithm for efficient ML decoding. The effects of security factors 1, 3, and 4 described before are evaluated and demonstrated as well. A scenario with three transmitters was also used in the preliminary analysis given in [40].
in accordance with the condition in (17). Following analysis of information theoretic security, a JCMA setting of three transmitters is depicted, including generating the joint constellation and an algorithm for efficient ML decoding. The effects of security factors 1, 3, and 4 described before are evaluated and demonstrated as well. A scenario with three transmitters was also used in the preliminary analysis given in [40].
6.1. Information Theoretic Security
Recall that  in (17) has to be set according to the temporal decorrelation behavior of the channel. The normalized temporal autocorrelation function for a Rayleigh fading channel is given by [33]
in (17) has to be set according to the temporal decorrelation behavior of the channel. The normalized temporal autocorrelation function for a Rayleigh fading channel is given by [33]

where  is the zero-order Bessel function of the first kind and
is the zero-order Bessel function of the first kind and  is the time difference.
is the time difference.  for the shortest elapsed time. This is equivalent to setting
for the shortest elapsed time. This is equivalent to setting  in (29), so it makes sense to set
in (29), so it makes sense to set  .
.
Using  in (17) results in
in (17) results in

Figure 4 depicts the minimum  required for achieving information theoretic security for the entire channel decorrelation period as a function of
required for achieving information theoretic security for the entire channel decorrelation period as a function of  for
for  and
and  . The arrows directions indicate increasing values of
. The arrows directions indicate increasing values of  . It is evident that increasing
. It is evident that increasing  lowers the required
lowers the required  dramatically for a given
dramatically for a given  . The decrease is moderated as
. The decrease is moderated as  increases. For
increases. For  the required
the required  is very high, making it difficult to use the method for securing the entire decorrelation period. However, for
is very high, making it difficult to use the method for securing the entire decorrelation period. However, for  the required
the required  is reasonably low for practical channels. For example, consider the IEEE
is reasonably low for practical channels. For example, consider the IEEE  standard (a.k.a. mobile WiMax) [42]. In [42] the delay spread is assumed to be
standard (a.k.a. mobile WiMax) [42]. In [42] the delay spread is assumed to be  , which means that
, which means that  . For this value of
. For this value of  , the Rayleigh fading channel achieves security for
, the Rayleigh fading channel achieves security for  when
when  respectively. Assuming a carrier frequency of
respectively. Assuming a carrier frequency of  , these values of
, these values of  correspond to relative velocities between transmitter and receiver of
correspond to relative velocities between transmitter and receiver of 
 respectively. These velocities are expected for many mobile scenarios.
respectively. These velocities are expected for many mobile scenarios.
6.2. Security by Complexity—Three Transmitters
In this illustrative Rayleigh fading scenario, subcarriers are overloaded by 3 transmitters in a JCMA setting. The symbol sets  were found using a random symbol search with
were found using a random symbol search with  defined in (3) being the optimizing criterion and (4) being the optimization constraint. The following symbol sets were found offline and assigned arbitrarily to the transmitters:
defined in (3) being the optimizing criterion and (4) being the optimization constraint. The following symbol sets were found offline and assigned arbitrarily to the transmitters:

The received joint constellation at the intended receiver along with the corresponding bit mapping is depicted in Figure 5. Each set of 3 bits represents the bits of TX1, TX2, and TX3 from left to right, respectively. Notice that the average energy of the received constellation is larger than 1. Interestingly, this joint constellation has the exact structure of a type of 8QAM constellation used in some industry standards for a single transmitter signal [43, page 53]. Note that the joint constellation is not Gray coded. Although this increases BER, it would be shown below that performance is satisfactory.
Next an efficient ML decoding algorithm is designed, based on constellation symmetries. The algorithm comprises three steps for decoding a received joint sample  .
.
(1)Rotate the received sample:  .
.
(2)Calculate

(3)Use Table 1 for decoding.
For hard decoding, each table entry denotes the decoded bits of TX1, TX2, and TX3 from left to right, respectively. For soft decoding, the distance between  and the closest joint constellation point has to be evaluated. This efficient decoding algorithm consists of three easy steps and its complexity is much lower than that of exhaustive ML decoding. The JCMA setting is compared to a TDMA transmitter using a power efficient circular 8-QAM constellation with the same power constraint. The 8-QAM constellation is depicted in Figure 6.
and the closest joint constellation point has to be evaluated. This efficient decoding algorithm consists of three easy steps and its complexity is much lower than that of exhaustive ML decoding. The JCMA setting is compared to a TDMA transmitter using a power efficient circular 8-QAM constellation with the same power constraint. The 8-QAM constellation is depicted in Figure 6.
In Figure 7, hard decoding BER versus SNR (defined here as the ratio between the average energy per transmitter symbol and the noise variance at the receiver) is depicted for the JCMA setting and compared to TDMA. Results were obtained using computer simulation. A gain of 4.4 dB is achieved with JCMA while adhering to the transmitters' power constraint. This means that the increased overall energy invested in JCMA (3 times more than TDMA, equivalent to 4.7 dB) was successfully translated to performance gain. The marginal loss of 0.3 dB is attributed to the lack of Gray coding. Note that the efficient ML decoding algorithm performs as well as the exhaustive ML decoding algorithm.
To analyze the impact of security Factor 4 described in Section 4.2, BER of the receiver is also compared to that of an eavesdropper using a single MF and exhaustive ML hard decoding. Both receiver and eavesdropper experience a Rayleigh fading on all channels. It is clear that for the eavesdropper ML decoding BER is unsatisfactory for decoding the data. For example, if the receiver operates at  of 9 dB, it would experience a BER of
of 9 dB, it would experience a BER of  , and the eavesdropper would experience a BER of
, and the eavesdropper would experience a BER of  . It follows that for the given scenario the eavesdropper cannot effectively decode the messages from the nodes, even when the unicity distance has passed and security factors 1–3 described in Section 4.2 are compromised.
. It follows that for the given scenario the eavesdropper cannot effectively decode the messages from the nodes, even when the unicity distance has passed and security factors 1–3 described in Section 4.2 are compromised.
The eavesdropper can reduce BER by applying soft decoding instead of hard decoding and also apply multiple antennas reception. However, to match the receivers hard decoding BER of  the eavesdropper would need to achieve an SNR gain of 20 dB, and at least some of the gain achieved by the eavesdropper would be matched by implementing low complexity soft decoding at the receiver. It follows that the decoding complexity of the eavesdropper must be high enough to obtain an SNR gain of at least 20 dB. The SNR gain required at the eavesdropper for decoding is a clear indication of security by complexity.
the eavesdropper would need to achieve an SNR gain of 20 dB, and at least some of the gain achieved by the eavesdropper would be matched by implementing low complexity soft decoding at the receiver. It follows that the decoding complexity of the eavesdropper must be high enough to obtain an SNR gain of at least 20 dB. The SNR gain required at the eavesdropper for decoding is a clear indication of security by complexity.
To gain insight on the impact of security factors 1 and 3 described in Section 4.2 on decoding, representative joint constellations of the eavesdropper are depicted in Figure 8. Note how the joint constellation varies from pilot to pilot, implying the high decoding complexity. In addition, note how close the constellation points are to one another, implying the high probability for decoding errors.
7. Conclusion
A multiple access method for securing OFDM over wireless time-varying channels was proposed and analyzed. The method uses reverse piloting for implementing superposition modulation with joint decoding at the receiver. It makes use of channel randomness, reciprocity, and fast decorrelation in space to secure transmission with low overheads. Security strengths of the method were evaluated and practical means of implementation were suggested based on analytical analysis. Channel and system parameters were explicitly derived for achieving information theoretic security of entire transmission bursts, and features of security by complexity were assessed and demonstrated. Means for generating and efficiently decoding joint constellations were presented. It was proven that in addition to security, the method also offers decoding gain for power-limited transmitters. The effects of imperfections due to mobility, power control errors, and synchronization errors were analyzed and practical means for addressing them were given. It was proven and demonstrated that both security strength and decoding gain increase with the number of transmitters and that information theoretic security with low overheads is achievable for mobile scenarios in practical communication systems. Implementing the method requires the same computational complexity as a standard point-to-point communication system, and mitigating the effects of mobility, power control errors, and synchronization errors reduces to a simple piloting rule. The low computational complexity and feasibility of implementation make the method a good solution for securing OFDM transmission in wireless systems where the complexity associated with implementing traditional security algorithms is prohibitive.
References
Rivest RL, Shamir A, Adleman L: A method for obtaining digital signatures and public-key cryptosystems. Communications of the ACM 1978, 21(2):120-126. 10.1145/359340.359342
U.S. National Bureau of Standards (NBS) : Data Encryption Standard. Federal Information Processing Standards Publication 46 (FIPS-46), 1977
Simon MK, Omura JK, Scholtz RA, Levitt BK: Spread Spectrum Communications Handbook. McGraw-Hill, New York, NY, USA; 2002.
Diffie W, Hellman ME: New directions in cryptography. IEEE Transactions on Information Theory 1976, 22(6):644-654. 10.1109/TIT.1976.1055638
Potlapally NR, Ravi S, Raghunathan A, Jha NK: A study of the energy consumption characteristics of cryptographic algorithms and security protocols. IEEE Transactions on Mobile Computing 2006, 5(2):128-143.
Yang H, Luo H, Ye F, Lu S, Zhang L: Security in mobile ad hoc networks: challenges and solutions. IEEE Wireless Communications 2004, 11(1):38-47. 10.1109/MWC.2004.1269716
Eltoweissy M, Moharrum M, Mukkamala R: Dynamic key management in sensor networks. IEEE Communications Magazine 2006, 44(4):122-130.
Guimarães G, Souto E, Sadok D, Kelner J: Evaluation of security mechanisms in wireless sensor networks. Proceedings of the IEEE Systems Communications (ISWCS '05), August 2005 428-433.
Wyner AD: The wire-tap channel. Bell System Technical Journal 1975, 54(8):1355-1387.
Ozarow LH, Wyner AD: Wire-tap channel II. Bell System Technical Journal 1984, 63: 2135-2157.
Maurer UM: Secret key agreement by public discussion from common information. IEEE Transactions on Information Theory 1993, 39(3):733-742.
Hero AO III: Secure space-time communication. IEEE Transactions on Information Theory 2003, 49(12):3235-3249. 10.1109/TIT.2003.820010
Gopala PK, Lai L, El Gamal H: On the secrecy capacity of fading channels. IEEE Transactions on Information Theory 2008, 54(10):4687-4698.
Liang Y, Poor HV: Secure communication over fading channels. Proceedings of the 44th Annual Allerton Conference on Communication Control, and Computing, September 2006, Monticello, Ill, USA
Liang Y, Poor HV, Shamai S: Secrecy capacity region of fading broadcast channels. Proceedings of the IEEE International Symposium on Information Theory (ISIT '07), June 2007, Nice, France 1291-1295.
Liang Y, Poor HV, Shamai S: Secrecy capacity region of parallel broadcast channels. Proceedings of the IEEE Information Theory and Applications Workshop (ITA '07), February 2007, San Diego, Calif, USA 245-250.
Debbah M, Kobayashi M: On the secrecy capacity of frequency-selective fading channels: a practical vandermonde approach. Proceedings of IEEE Annual International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC '08), September 2008, Cannes, France 1-5.
Hershey JE, Hassan AA, Yarlagadda R: Unconventional cryptographic keying variable management. IEEE Transactions on Communications 1995, 43(1):3-6. 10.1109/26.385951
Azimi-Sadjadi B, Kiayias A, Mercado A, Yener B: Robust key generation from signal envelopes in wireless networks. Proceedings of the 14th ACM Conference on Computer and Communications Security (CCS '07), October 2007, Alexandria, Va, USA
Aono T, Higuchi K, Ohira T, Komiyama B, Sasaoka H: Wireless secret key generation exploiting reactance-domain scalar response of multipath fading channels. IEEE Transactions on Antennas and Propagation 2005, 53(11):3776-3784.
Koorapaty H, Hassan AA, Chennakeshu S: Secure information transmission for mobile radio. IEEE Communications Letters 2000, 4(2):52-55. 10.1109/4234.824754
Bloch M, Barros J, Rodrigues MRD, McLaughlin SW: Wireless information-theoretic security. IEEE Transactions on Information Theory 2008, 54(6):2515-2534.
Tsouri GR, Wulich D: Reverse piloting protocol for securing time varying wireless channels. Proceedings of the 7th Annual Wireless Telecommunications Symposium (WTS '08), April 2008, Pomona, Calif, USA 125-131.
Tsouri GR, Wulich D: Joint Constellation Multiple Access—PCT patent pending. SigNexT Comm., (WO/2007/039908), http://www.wipo.int/pctdb/en/wo.jsp?IA=WO2007039908
Goldsmith A: Wireless Communications. Cambridge University Press, Cambridge, UK; 2006.
Verdu S: Multiuser Detection. Cambridge University Press, Cambridge, UK; 1998.
Larsson EG, Vojcic BR: Cooperative transmit diversity based on superposition modulation. IEEE Communications Letters 2005, 9(9):778-780. 10.1109/LCOMM.2005.1506700
Brännström FN, Aulin TM, Rasmussen LK: Constellation-constrained capacity for trellis code multiple access systems. Proceedings of the IEEE Global Telecommunications Conference (GLOBECOM '01), December 2001, San Antonio, Tex, USA 2: 791-795.
Brännström FN, Aulin TM, Rasmussen LK: Capacity considerations for trellis code multiple access systems. Proceedings of the IEEE Information Theory Workshop, September 2001, Cairns, Australia 153-155.
Brännström FN, Aulin TM, Rasmussen LK: Iterative detectors for trellis-code multiple-access. IEEE Transactions on Communications 2002, 50(9):1478-1485. 10.1109/TCOMM.2002.802563
Ross JAF, Taylor DP: Vector assignment scheme for M+N users in N-Dimensional global additive channel. IEEE Electronic Letters 1992, 28(17):1634-1636. 10.1049/el:19921040
Ross JAF, Taylor DP: Multiuser signaling in the symbol-synchronous AWGN channel. IEEE Transactions on Information Theory 1995, 41(4):1174-1178. 10.1109/18.391265
Lee WC: Mobile Communication Engineering. McGraw-Hill, New York, NY, USA; 1982.
Shannon CE: Communication theory of secrecy systems. Bell Systems Technical Journal 1949, 28: 656-715.
Proakis JG: Digital Communication. McGraw Hill, New York, NY, USA; 2000.
Papoulis A: Probability, Random Variables, and Stochastic Processes. 3rd edition. McGraw-Hill, New York, NY, USA; 1991.
Tsouri GR, Wulich D: Wireless channel access through jointly formed signal constellations. Proceedings of the IEEE Annual International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC '06), September 2006, San Diego, Calif, USA 1-5.
Lee EA, Messerschmitt DG: Digital Communication. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1988.
Vanhaverbeke F: Digital communications through oversaturated channels, Ph.D. thesis. Ghent University, Ghent, Belgium; 2005. http://telin.ugent.be/~fv/eigen_publicaties.html
Tsouri GR, Wulich D: A Physical transmission security layer for wireless multiple access communication systems. Proceedings of the European Signal Processing Conference (EUSIPCO '07), September 2007, Poznan, Poland
Verdú S: Capacity region of gaussian CDMA channels: the symbol- synchronous case. Proceedings of 24th Allerton Conference on Communication, Control and Computing, October 1986, Urbana, Ill, USA 1025-1034.
IEEE : Part 11: wireless LAN medium access control (MAC) and physical layer (PHY) specifications. IEEE Standard 802.16e, November 2005
ANSI/SCTE 79-1 : Data Over Cable Systems 2.0, Part 1: Radio Frequency Interface. 2003.
Li Y: Pilot-symbol-aided channel estimation for OFDM in wireless systems. IEEE Transactions on Vehicular Technology 2000, 49(4):1207-1215. 10.1109/25.875230
Edfors O, Sandell M, Beek JJD, Wilson SK, Borjesson PO: OFDM channel estimation by singular value decomposition. IEEE Transactions on Communications 1998, 46(7):931-939. 10.1109/26.701321
Berriche L, Abed-Meraim K, Belfiore JC: Cramer-rao bounds for MIMO channel estimation. Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP '04), May 2004, Montreal, Canada 4: 397-400.
Hassibi B, Hochwald BM: How much training is needed in multiple-antenna wireless links? IEEE Transactions on Information Theory 2003, 49(4):951-963. 10.1109/TIT.2003.809594
Dong M, Tong L: Optimal design and placement of pilot symbols for channel estimation. IEEE Transactions on Signal Processing 2002, 50(12):3055-3069. 10.1109/TSP.2002.805504
Tang X, Alouini MS, Goldsmith AJ: Effect of channel estimation error on MQAM BER performance in rayleigh fading. IEEE Transactions on Communications 1999, 47(12):1856-1864. 10.1109/26.809706
Van Trees HL: Detection, Estimation, and Modulation Theory—Part I. John Wiley & Sons, New York, NY, USA; 2001.
Georgiadis A: Gain, phase imbalance, and phase noise effects on error vector magnitude. IEEE Transactions on Vehicular Technology 2004, 53(2):443-449. 10.1109/TVT.2004.823477
Shafik RA, Rahman MS, Islam AHMR, Ashraf NS: On the error vector magnitude as a performance metric and comparative analysis. Proceedings of the 2nd International Conference on Emerging Technologies (ICET '06), November 2006, Islamabad, Pakistan 27-31.
Pinto JL, Darwazeh I: Error vector magnitude relation to magnitude and phase distortion in 8-PSK systems. Electronics Letters 2001, 37(7):437-438. 10.1049/el:20010291
Author information
Authors and Affiliations
Corresponding author
Appendix
A. Effects of Imperfections on Performance
TDMA reference system
The TDMA BB model for a single transmitter (indexed  ) with CSI errors and power control is depicted in Figure 9, where
) with CSI errors and power control is depicted in Figure 9, where  is the energy per symbol needed at the receiver to achieve a certain performance level,
is the energy per symbol needed at the receiver to achieve a certain performance level,  is the complex valued channel fading coefficient,
is the complex valued channel fading coefficient,  is the TDMA symbol, and
is the TDMA symbol, and  is the channel estimation error.
is the channel estimation error.
Since the transmitters are required to be simple in design, we assume that a linear estimator is used at each transmitter for estimating the channel coefficient, such as a linear MMSE estimator. For MMSE estimators,  is modeled as a complex normal random variable with zero mean and arbitrary variance [44–49], and
is modeled as a complex normal random variable with zero mean and arbitrary variance [44–49], and  is uncorrelated with
is uncorrelated with  .
.
At RX, the channel is estimated and compensated for phase by an erroneous estimate of the channel  . The channel estimated at RX is fed back to the transmitter for allowing the transmitter to compensate for channel fading before performing power control. It is assumed this is done without error. It follows that,
. The channel estimated at RX is fed back to the transmitter for allowing the transmitter to compensate for channel fading before performing power control. It is assumed this is done without error. It follows that,  represents the TX compensation for fading.
represents the TX compensation for fading.
Power control is achieved by setting  and compensating for the fading
and compensating for the fading  . It follows that
. It follows that


Since channel estimation has to be fairly accurate, the pilot energy is such that high SNR is achieved for channel estimation. It follows that  is expected to be much smaller in magnitude than
is expected to be much smaller in magnitude than  and so
and so  Using this assumption (A.1) reduces to
Using this assumption (A.1) reduces to


The term  represents the synchronization error and its variance is with relation to
represents the synchronization error and its variance is with relation to  .
.
Figure 9
Single transmitter in TDMA.
JCMA System
The JCMA BB model for a single transmitter with CSI errors and power control is depicted in Figure 10, where  and
and  are the JCMA transmitted symbol and channel estimation error of transmitter
are the JCMA transmitted symbol and channel estimation error of transmitter  respectively.
respectively.
Here the channel is estimated at TX alone and is compensated prior to transmission. In the same manner as in (A.2) it follows that for a single transmitter,


The last estimation in (A.3) is given using a Taylor expansion with  . The synchronization error of a single transmitter in JCMA
. The synchronization error of a single transmitter in JCMA  has the same statistics as that of TDMA.
has the same statistics as that of TDMA.
Now consider the entire JCMA system:


The JCMA synchronization error is  .
.
The estimation errors  are uncorrelated and identically distributed. The same is true for the channels
are uncorrelated and identically distributed. The same is true for the channels  and information symbols
and information symbols  . It follows that
. It follows that


The channel is estimated at TX using a pilot signal from RX. Channel estimation using pilot signaling is well established in theory and practice [44–49], and an "efficient estimate" as defined in [50] is obtained. This means that the Cramer Rao Bound (CRB) for the channel estimation error is achievable.
It is assumed that all transmitters are able to compensate for the channel fading  with their limited peak power. This means that
with their limited peak power. This means that  is higher than some threshold value. If
is higher than some threshold value. If  falls beneath this threshold the transmitter fails to compensate for it and the connection between this transmitter and the receiver cannot be maintained. This phenomenon occurs in all multiple access methods in fading channels and is usually solved at a high level protocol. In cellular telephony, for example, a failing transmitter roams to a different Base Station (BS) for service.
falls beneath this threshold the transmitter fails to compensate for it and the connection between this transmitter and the receiver cannot be maintained. This phenomenon occurs in all multiple access methods in fading channels and is usually solved at a high level protocol. In cellular telephony, for example, a failing transmitter roams to a different Base Station (BS) for service.
The CRB for efficient ML estimation of a random variable in AWGN is given by [50]


where  is the energy of the pilot symbol, and
is the energy of the pilot symbol, and  is the AWGN noise variance.
is the AWGN noise variance.
Using (A.6), it is possible to calculate the needed increase in pilot energy for JCMA in order to achieve the same synchronization/power control error as that of TDMA. For this the error variances must be equated:


Since the variance of a sum is the sum of variance, (A.7) is also


Equivalently, in accordance with (A.2), (A.4):


where  are all uncorrelated and have zero mean, so (A.9) is also
are all uncorrelated and have zero mean, so (A.9) is also


Note that  because it is assumed that the transmitter can compensate for fading, so
because it is assumed that the transmitter can compensate for fading, so  is higher than some threshold. According to the peak power constraint,
is higher than some threshold. According to the peak power constraint,  and (A.10) reduces to
and (A.10) reduces to


Now using (A.6),


Equation (A.12) reduces to the compact expression:


Equation (A.13) gives the required energy of the JCMA pilot signal sent by the receiver to achieve the same degradation in decoding as for an equivalent TDMA system.
Figure 10
Single transmitter in JCMA.
Channel decorrelation manifests itself in a shift of the joint constellation points from their original position. The probability for a more significant shift increases as time passes from the last channel estimation time (pilot transmission time). It follows that channel decorrelation directly influences the shift in constellation points over time. We evaluate this influence by deriving the expected shift of a constellation point over time. A closely related approach is used when evaluating transmitter performance in the presence of linear and nonlinear distortions using Error Vector Magnitude (EVM) [51–53]. EVM is a well-founded parameter used to characterize the quality of communication and is closely related to BER [51–53].
An EVM-like approach is used here for JCMA. Disregarding the additive noise and errors in the channel estimate at the receiver, the received constellation points of any communication system are supposed to remain constant over time. However, as the channel decorrelates the points shift randomly, due to a discrepancy between the last channel estimate and the true value of the time-varying channel.
The shift of a specific constellation point over time is a stochastic process defined as


where  is the last time the channel was estimated (a pilot signal was sent) and
is the last time the channel was estimated (a pilot signal was sent) and  where
where  denotes the constellation set. For ease of notation the
denotes the constellation set. For ease of notation the  index is dropped from the following derivation. There is a one to one mapping between
index is dropped from the following derivation. There is a one to one mapping between  and
and  given by
given by


It follows that


In a classical EVM approach, the variance of  should be averaged over all points in the constellation. Because the focus of analysis is performance degradation of a communication link due to channel decorrelation, it would be biased in favor of JCMA to normalize
should be averaged over all points in the constellation. Because the focus of analysis is performance degradation of a communication link due to channel decorrelation, it would be biased in favor of JCMA to normalize  , since higher overall energy is invested in the JCMA constellation. In the following analysis the conditional variance of
, since higher overall energy is invested in the JCMA constellation. In the following analysis the conditional variance of  is evaluated without normalization and then averaged over all points in the constellation:
is evaluated without normalization and then averaged over all points in the constellation:






The channels are i.i.d, therefore,


where  for all (
for all ( .),
.),


where  is the channel autocorrelation function and depends on the channel fading statistics. Notice that since the in-phase and quadrature components of all channels are uncorrelated,
is the channel autocorrelation function and depends on the channel fading statistics. Notice that since the in-phase and quadrature components of all channels are uncorrelated,  is a real function and, therefore,
is a real function and, therefore,  . It follows that
. It follows that


Using (A.20), (A.21), (A.22) in (A.18) yields


where the superscript  was reintroduced.
was reintroduced.
For TDMA this variance is given by


where  . Obviously,
. Obviously,  and
and  increases with
increases with  . It is easy to show that if normalization of
. It is easy to show that if normalization of  was initially introduced to (A.18), the result would have been the same for TDMA and JCMA.
was initially introduced to (A.18), the result would have been the same for TDMA and JCMA.
To compare decorrelation times (A.23) and (A.24) should be equated. Let  and
and  be the time passed between consecutive pilots in JCMA and TDMA respectfully. Equating (A.23) and (A.24) yields
be the time passed between consecutive pilots in JCMA and TDMA respectfully. Equating (A.23) and (A.24) yields


Now, using (A.23) and (A.24) in (A.25),


The solution to (A.26) depends on the channel fading instance and the symbols being transmitted. Averaging over all channel instances and symbol types on both sides of (A.26) gives




However,  for all
for all  , so (A.28) reduces to
, so (A.28) reduces to


The functions  and
and  are monotonic decreasing functions until full decorrelation is reached for the first time, so if the inverse of (A.29) is taken and noting that
are monotonic decreasing functions until full decorrelation is reached for the first time, so if the inverse of (A.29) is taken and noting that  , we get
, we get


Rearranging  gives
gives


Since  ,
,  which means that
which means that  . It follows that JCMA effectively shortens the decorrelation time of the channel.
. It follows that JCMA effectively shortens the decorrelation time of the channel.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Tsouri, G.R., Wulich, D. Securing OFDM over Wireless Time-Varying Channels Using Subcarrier Overloading with Joint Signal Constellations. J Wireless Com Network 2009, 437824 (2009). https://doi.org/10.1155/2009/437824
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/437824



 by an angle of
by an angle of  :
: 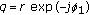 .
. is to the right of the symmetry line intersection with the real axis, set
is to the right of the symmetry line intersection with the real axis, set  , else set
, else set  .
. .
.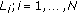 to access a predefined Look Up Table (LUT) containing the bit loading of the constellation point in the decision region of the received sample.
to access a predefined Look Up Table (LUT) containing the bit loading of the constellation point in the decision region of the received sample.
 .
.



