- Research Article
- Open access
- Published:
Physical Layer Security Game: Interaction between Source, Eavesdropper, and Friendly Jammer
EURASIP Journal on Wireless Communications and Networking volume 2009, Article number: 452907 (2010)
Abstract
Physical layer security is an emerging security area that achieves perfect secrecy data transmission between intended network nodes, while malicious nodes that eavesdrop the communication obtain zero information. The so-called secrecy capacity can be improved using friendly jammers that introduce extra interference to the eavesdroppers. We investigate the interaction between the source that transmits the useful data and friendly jammers who assist the source by "masking" the eavesdropper. To obtain distributed solution, we introduce a game theoretic approach. The game is defined such that the source pays the jammers to interfere the eavesdropper, therefore, increasing the secrecy capacity. The friendly jammers charge the source with a certain price for the jamming, and there is a tradeoff for the price. If too low, the profit of the jammers is low; and if too high, the source would not buy the "service" (jamming power) or would buy it from other jammers. To analyze the game outcome, we investigate a Stackelburg type of game and construct a distributed algorithm. Our analysis and simulation results show the effectiveness of friendly jamming and the tradeoff for setting the price. The distributed game solution is shown to have similar performances to those of the centralized one.
1. Introduction
The future communication systems will be decentralized and adhoc, therefore allowing various types of network mobile terminals to join and leave. This aspect makes the whole system vulnerable and susceptible to attacks. Anyone within communication range can listen and possibly extract information. While these days we have numerous cryptographic methods with high level security, there is no system with perfect security on physical layer. Therefore, the physical layer security is regaining a new attention. The main goal of this paper is to design a decentralized system that will protect the broadcasted data and make it impossible for the eavesdropper to receive the packets even if it knows the encoding/decoding schemes used by the transmitter/receiver. In approaches where physical layer security is applied, the main objective is to maximize the rate of reliable information from the source to the intended destination, while all malicious nodes are kept as ignorant of that information as possible. This maximum reliable rate is known as secrecy capacity.
This line of work was pioneered by Wyner, who defined the wiretap channel and established the possibility to create almost perfect secure communication links without relying on private (secret) keys [1]. Wyner showed that when the eavesdropper channel is a degraded version of the main channel, the source and the destination can exchange perfectly secure messages at a nonzero rate. The main idea proposed by him is to exploit the additive noise impairing the eavesdropper by using a stochastic encoder that maps each message to many codewords according to an appropriate probability distribution. With this scheme, a maximal equivocation (i.e., uncertainty) is induced at the eavesdropper. In other words, a maximal level of secrecy is obtained. By ensuring that the equivocation rate is arbitrarily close to the message rate, one can achieve perfect secrecy in the sense that the eavesdropper is now limited to learn almost nothing about the source-destination messages from its observations. Follow-up work by Leung-Yan-Cheong and Hellman characterized the secrecy capacity of the additive white Gaussian noise (AWGN) wiretap channel [2]. In their landmark paper, Csiszar and Korner generalized Wyner's approach by considering the transmission of confidential messages over broadcast channels [3]. Recently, there have been considerable efforts on generalizing these studies to the wireless channel and multiuser scenarios (see [2, 4–11] and references therein). Jamming [12–14] has been studied for a long time to analyze the hostile behaviors of malicious nodes. Recently, jamming has been employed to physical layer security to reduce the eavesdropper's ability to decode the source's information [15]. In other words, the jamming is friendly in this context. Moreover, the friendly helper can assist the secrecy by sending codewords, and bring further gains relative to unstructured Gaussian noise [15–17].
Game theory [18] is a formal framework with a set of mathematical tools to study some complex interactions among interdependent rational players. During the past decade, there has been a surge in research activities that employ game theory to model and analyze modern distributed communication systems. Most of these works [19–22] concentrate on the distributed resource allocation for wireless networks. As far as the authors' knowledge, the game theory has not yet been used in the physical layer security.
In this paper, we investigate the interaction between the source and its friendly jammers using game theory. Although the friendly jammers help the source by reducing the data rate that is "leaking" from the source to the malicious node, at the same time they also reduce the useful data rate from the source to the destination. Using well chosen amounts of power from the friendly jammers, the secrecy capacity can be maximized. In the game that we define here, the source pays the jammers to interfere the malicious eavesdropper, and therefore, to increase the secrecy capacity. The friendly jammers charge the source with a certain price for their service of jamming the eavesdropper. One could notice that there is a tradeoff for the proposed price. If the price of a certain jammer is too low, its profit is also low; if its price is too high, the source will buy from the other jammers. In modeling the outcome of the above games our analysis uses the Stackelberg type of game. Initially, the existence of equilibrium will be studied. Then, a distributed algorithm will be proposed and its convergence will be investigated. The outcome of the distributed algorithm will be compared to the centralized genie aided solution. Some implementation concerns are also discussed. From the simulation results, we can see the efficiency of friendly jamming and tradeoff for setting the price, the source prefers buying service from only one jammer, and the centralized scheme and the proposed game scheme have similar performance.
The rest of the paper is organized as follows. In Section 2, the system model of physical layer security with friendly jamming users is described. In Section 3, the game models are formulated, and the outcomes as well as properties of the game are analyzed. Simulation results are shown in Section 4, and conclusions are drawn in Section 5.
2. System Model
We consider a network with a source, a destination, a malicious eavesdropper node, and  friendly jammer nodes as shown in Figure 1. The malicious node tries to eavesdrop the transmitted data coming from the source node. When the eavesdropper channel from the source to the malicious node is a degraded version of the main source-destination channel, the source and destination can exchange perfectly secure messages at a nonzero rate. By transmitting a message at a rate higher than the rate of the malicious node, the malicious node can learn almost nothing about the messages from its observations. The maximum rate of secrecy information from the source to its intended destination is defined by the term secrecy capacity.
friendly jammer nodes as shown in Figure 1. The malicious node tries to eavesdrop the transmitted data coming from the source node. When the eavesdropper channel from the source to the malicious node is a degraded version of the main source-destination channel, the source and destination can exchange perfectly secure messages at a nonzero rate. By transmitting a message at a rate higher than the rate of the malicious node, the malicious node can learn almost nothing about the messages from its observations. The maximum rate of secrecy information from the source to its intended destination is defined by the term secrecy capacity.
Suppose the source transmits with power  . The channel gains from the source to the destination and from the source to the malicious node are
. The channel gains from the source to the destination and from the source to the malicious node are  and
and  , respectively. Each friendly jammer
, respectively. Each friendly jammer  ,
,  , transmits with power
, transmits with power  and the channel gains from it to the destination and the malicious node are
and the channel gains from it to the destination and the malicious node are  and
and  , respectively. We denote by
, respectively. We denote by  the set of indices
the set of indices  . If the path loss model is used, the channel gain is given by the distance to the negative power of the path loss coefficient. The thermal noise for each channel is
. If the path loss model is used, the channel gain is given by the distance to the negative power of the path loss coefficient. The thermal noise for each channel is  and the bandwidth is
and the bandwidth is  . The channel capacity for the source to the destination is
. The channel capacity for the source to the destination is

The channel capacity from the source to the malicious node is

The secrecy capacity is

where  . Both
. Both  and
and  are decreasing and convex functions of jamming power
are decreasing and convex functions of jamming power  . However,
. However,  might not be a monotonous and convex function.(Minus of two convex functions is not a convex function anymore.) This is because the jamming power might decrease
might not be a monotonous and convex function.(Minus of two convex functions is not a convex function anymore.) This is because the jamming power might decrease  faster than
faster than  . As a result,
. As a result,  might increase in some region of value
might increase in some region of value  . When
. When  further increases, both
further increases, both  and
and  approach zero.As a result,
approach zero.As a result,  approaches zero. So, the questions are whether or not
approaches zero. So, the questions are whether or not  can be increased, and how to control the jamming power in a distributed manner so as to achieve the maximal
can be increased, and how to control the jamming power in a distributed manner so as to achieve the maximal  . We will try to solve the problems in the following section using a game theoretical approach.
. We will try to solve the problems in the following section using a game theoretical approach.
3. Game for Physical Layer Security
In this section, we study how to use game theory to analyze the physical layer security. First, we define the game between the source and friendly jammers. Next, we optimize the source and jammer sides, respectively. Then, we prove some properties of the proposed game. Furthermore, a comparison with the centralized scheme is constructed. Finally, we discuss some implementation concerns.
3.1. Game Definition
The source can be modeled as a buyer who wants to optimize its secrecy capacity minus cost by modifying the "service" (jamming power  ) from the friendly jammers, that is,
) from the friendly jammers, that is,


where  is the gain per unit capacity,
is the gain per unit capacity,  is the maximal power that a jammer can provide, and
is the maximal power that a jammer can provide, and  is the cost to pay for the other friendly jamming nodes. Here
is the cost to pay for the other friendly jamming nodes. Here

where  is the price per unit power for the friendly jammer,
is the price per unit power for the friendly jammer,  is the friendly jammer's power, and
is the friendly jammer's power, and  is the set of friendly jammers. From (4) we note that the source will not participate in the game if
is the set of friendly jammers. From (4) we note that the source will not participate in the game if  , or in other words, the secrecy capacity is zero. For each jammer,
, or in other words, the secrecy capacity is zero. For each jammer,  is the utility function of the price and power bought by the source. For the jammer's (seller's) utility, in this paper we define the following utility:
is the utility function of the price and power bought by the source. For the jammer's (seller's) utility, in this paper we define the following utility:

where  is a constant to balance from the payment
is a constant to balance from the payment  from the source and the transmission cost
from the source and the transmission cost  . With different values of
. With different values of  , jammers have different strategies for asking the price
, jammers have different strategies for asking the price  . Notice that
. Notice that  is also a function of the vector of prices
is also a function of the vector of prices  , since the power that the source will buy also depends on the price that the friendly jammers ask. Hence, for each friendly jammer, the optimization problem is
, since the power that the source will buy also depends on the price that the friendly jammers ask. Hence, for each friendly jammer, the optimization problem is

In the next two subsections, we analyze the optimal strategies for the source and friendly jammers to maximize their own utilities.
3.2. Source (Buyer) Side Analysis
Introducing  , and
, and  , we have
, we have

For the source (buyer) size, we analyze the case  . By differentiating (4), we have
. By differentiating (4), we have

Rearranging the above equation, we have

where

The solutions of the quartic equation (11) can be expressed in closed form but this is not the primary goal here. It is important that the solution we are interested in is given by the following function:

Note that  . Since
. Since  satisfies the polynomial function, we can have the optimal strategy as
satisfies the polynomial function, we can have the optimal strategy as

Because of the complexity of the closed form solution of the quartic equation in (14), we also consider two special cases: low interference case and high interference case.
3.2.1. Interference at the Destination Is Much Smaller than the Noise
Remember the definitions:  , and
, and  . Imagine a situation in which all jammers are close to the malicious node and far from the destination node. In that case the interference from the jammers to the destination is very small in comparison to the additive noise and therefore we have
. Imagine a situation in which all jammers are close to the malicious node and far from the destination node. In that case the interference from the jammers to the destination is very small in comparison to the additive noise and therefore we have

Then

Rearranging we get

Solving the above equation we obtain a closed-form solution

where

Finally, by comparing  with the power under the boundary conditions (
with the power under the boundary conditions ( ,
,  , and
, and  ), the optimal
), the optimal  in the low SNR region can be obtained.
in the low SNR region can be obtained.
3.2.2. One Jammer with Interference That Is Much Higher than the Noise but Much Smaller than the Received Power at the Destination and the Malicious Node
In this case the interference from the jammer is much higher than the additive noise but much smaller than the power of the received signal at the destination and the malicious node. In other words, that means  and
and  . Therefore the utility function of the source is given by
. Therefore the utility function of the source is given by

If  ,
,  is a decreasing function of
is a decreasing function of  . As a result,
. As a result,  is optimized when
is optimized when  , that is, the jammer would not participate the game. On the other hand, if
, that is, the jammer would not participate the game. On the other hand, if  , in order to find the maximizing powers we have to calculate
, in order to find the maximizing powers we have to calculate

Hence

From this equation we get the optimal closed-form solution  , and similarly by comparing
, and similarly by comparing  with the power under the boundary conditions (
with the power under the boundary conditions ( ,
,  , and
, and  ), we can obtain the optimal solution for the this special case.
), we can obtain the optimal solution for the this special case.
3.3. Friendly Jammer (Seller) Side Analysis
In this subsection, we study how the friendly jammers can set the optimal price to maximize its utility. By differentiating the utility in (7) and setting it to zero, we have

This is equivalent to

This happens either if  or if
or if

From the closed form solution of  the solution of
the solution of  will be a function given as
will be a function given as

Notice that  should be positive. Otherwise, the friendly jammer would not play.
should be positive. Otherwise, the friendly jammer would not play.
3.4. Properties
In this subsection, we prove some properties of the proposed game. First, we prove that the power is monotonous function of the price under the two extreme cases. The properties can help for the proof of equilibrium existence in the later part of this subsection.
Property 1.
Under the two special cases, the optimal power consumption  for friendly jammer
for friendly jammer  is monotonous with its price
is monotonous with its price  , when the other friendly jammers prices are fixed. The proof is straightforward from (18) and (22).
, when the other friendly jammers prices are fixed. The proof is straightforward from (18) and (22).
We investigate the following analysis of the relation between the price and the power. We find out that the friendly jammer power  bought from the source is convex in its own price
bought from the source is convex in its own price  under some conditions. To prove this we need to check whether the second derivative
under some conditions. To prove this we need to check whether the second derivative 
In the first special case in which the interference is small

The above equation is greater than zero when  is small. This means when the interference is small and the price is small, the power is convex as a function of the price.
is small. This means when the interference is small and the price is small, the power is convex as a function of the price.
In the second special case in which the interference is severe

This means when the interference is severe, the power is a convex function of the price.
Next, we investigate the equilibrium of the proposed game. At the equilibrium, no user can improve its utility by changing its own strategy only. We first define the Stackelberg equilibrium as follows.
Definition 1.
 and
and  are the Stackelberg equilibrium of the proposed game, if when
are the Stackelberg equilibrium of the proposed game, if when  is fixed,
is fixed,

and when  is fixed,
is fixed,

Finally, from the analysis in the previous two subsections, we can show the following property for the proposed game.
Property 2.
The pair of  in (14) and
in (14) and  in (26) is the Stackelberg equilibrium for the proposed game.
in (26) is the Stackelberg equilibrium for the proposed game.
Notice that there might be multiple roots in (11), as a result, there might be multiple Stackelberg equilibria. In the simulation results shown in later section, we will show that the proposed scheme can still achieve the equilibria with better performances than those of the no-jammer case.
3.5. Distributed Algorithm and Convergence
In this subsection, we study how the distributed game can converge to the Stackelberg equilibrium defined in the above subsection. After rearranging (23), we have

where  and
and  is the price update function. Notice that
is the price update function. Notice that  is a function of
is a function of  . The information for the update can be obtained from the source node. This is similar to the distributed power control [25]. The update of the friendly jammers' prices can be written in a vector form as
. The information for the update can be obtained from the source node. This is similar to the distributed power control [25]. The update of the friendly jammers' prices can be written in a vector form as

where  , and the iteration is from time
, and the iteration is from time  to time
to time  . Next we show that the convergence of the proposed scheme by proving that the price update function in (32) is a standard function [23] defined as follows.
. Next we show that the convergence of the proposed scheme by proving that the price update function in (32) is a standard function [23] defined as follows.
Definition 2.
A function  is standard, if for all
is standard, if for all  , the following properties are satisfied
, the following properties are satisfied
-
(1)
Positivity:
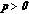 .
. -
(2)
Monotonicity: if
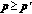 , then
, then  , or
, or 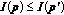 .
. -
(3)
Scalability: for all
 ,??
,??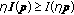 .
.
In [23], it has been proved that the price will converge to the fixed point (i.e., the Stackelberg equilibrium in our case) from any feasible initial price vector. The positivity is very easy to prove. If the price  goes up, the source would buy less from the
goes up, the source would buy less from the  friendly jammer. As a result,
friendly jammer. As a result,  in (23) is negative, and we prove positivity
in (23) is negative, and we prove positivity  .
.
The monotonicity and scalability can only be shown in the two special cases. For the low interference case, from (18) it is obvious that

which is monotonically increasing in  . For scalability, we have
. For scalability, we have

since  .
.
For the large interference case, from (22) we have

which is monotonically increasing in  and scalable.
and scalable.
For more general cases, the analysis is tractable. In the simulation section later, we employ the general simulation setups. The simulation results show that the proposed scheme can converge and outperform the no-jammer case.
3.6. Centralized Scheme
Traditionally, the centralized scheme is employed assuming that all channel information is known. The objective is to optimize the secrecy capacity under the constraints of maximal jamming power.

The centralized solution is found by maximizing the secrecy capacity only. If we do not consider the constraint, we have

Rearranging we get

Using the KKT condition theorem [24], the final solution would be obtained by comparing the boundary conditions (i.e.,  ,
,  , and
, and  ).
).
Notice that our proposed algorithm is distributive, in the sense that only the pricing information needs to be exchanged. In the simulation results, we compare the proposed game theoretical approach with this centralized scheme.
Finally, from the simulation results in the next section, we see that the distributed solution and the centralized solution are asymptotically the same if  is sufficiently large (the source cares more about the secrecy capacity than for the payment, i.e., the source is sufficiently rich).
is sufficiently large (the source cares more about the secrecy capacity than for the payment, i.e., the source is sufficiently rich).
3.7. Implementation Discussion
There are several implementation concerns for the proposed scheme. First, the channel information from the source to the malicious eavesdropper might not be known or accurately known. Under this condition, the secrecy capacity formula should be rewritten considering the uncertainty. If the direction of arrival is known, multiple antenna techniques can be employed such as in [11]. Second, the proposed scheme needs to iteratively update the price and power information. A natural question arises if the distributed scheme has less signalling than the centralized scheme. The comparison is similar to distributed and centralized power control in the literature [23, 25]. Since the channel condition is continuously changing, the distributed solution only needs to update the difference of the parameters such as power and price to be adaptive, while the centralized scheme requires all channel information in each time period. As a result, the distributed solution has a clear advantage and dominates the current and future wireless network designs. For example, the power control for cellular networks, the open loop power control is done only once during the link initialization, while the close loop power control (distributed power allocation such as [23]) is performed 1500 times for UMTS and 800 times for CDMA2000. Finally, for the multisource multidestination case, there are two possible choices to solve the problem. First, we can use clustering method to divide the network into sub-networks, and then employ the single-source-destination pair and multiple-friendly-jammer solution proposed in this paper. If we believe that the jamming power can be useful for multiple eavesdroppers, some techniques such as double auction could be investigated. The detailed discussion is beyond the scope of this paper and would be considered in our future research.
4. Simulation Results
The simulation is set up as follows. The source and friendly jammer have power of 0.02, the bandwidth is 1, the noise level is  , the propagation loss factor is
, the propagation loss factor is  , and AWGN channel is assumed. The source, destination, and eavesdropper are located at the coordinates (0,0), (100,0), and (50,50), respectively. Here we select
, and AWGN channel is assumed. The source, destination, and eavesdropper are located at the coordinates (0,0), (100,0), and (50,50), respectively. Here we select  for the friendly jammer utility in (7).
for the friendly jammer utility in (7).
For single friendly jammer case, we show the simulation with the friendly jammer at the location of (50,75) and (10,75). In Figure 2, we show the secrecy capacity as a function of the jamming power. We can see that with the increase of the jamming power, the secrecy capacity first increases and then decreases. This is because the jamming power has different effects on  and
and  . So there is an optimal point for the jamming power. Also the optimal point depends on the location of the friendly jammer, and the friendly jammer close to the eavesdropper is more effective to improve the secrecy capacity. Moreover, notice that the curve is neither convex nor concave. Figure 3 shows how the amount of the power bought by the source from the jammer depends on the requested price. We can see that the power is reduced if the price goes high. At some point, the source would stop buying the power. So there is a tradeoff for setting the price, that is, if the price too high, the source would buy less power or even stop buying.
. So there is an optimal point for the jamming power. Also the optimal point depends on the location of the friendly jammer, and the friendly jammer close to the eavesdropper is more effective to improve the secrecy capacity. Moreover, notice that the curve is neither convex nor concave. Figure 3 shows how the amount of the power bought by the source from the jammer depends on the requested price. We can see that the power is reduced if the price goes high. At some point, the source would stop buying the power. So there is a tradeoff for setting the price, that is, if the price too high, the source would buy less power or even stop buying.
For the two-jammer case, we set up the following simulations. Malicious node is located at (50,90), the first friendly jammer is located at (50,50), and the second friendly jammer is located at (50,75). In Figures 4, 5 and 6, the source's utility  , the first jammer's utility
, the first jammer's utility  , and the second jammer's utility
, and the second jammer's utility  as function of both users' price, are shown respectively. We can see that the source would buy service from only one of the friendly jammers. If the friendly jammer asks too low price, the jammer's utility is very low. On the other hand, if the jammer asks too high price, it risks the situation in which the source would buy the service from the other friendly jammer. There is an optimal price for each friendly jammer to ask, and the source would always select the one that can provide the best performance improvement.
as function of both users' price, are shown respectively. We can see that the source would buy service from only one of the friendly jammers. If the friendly jammer asks too low price, the jammer's utility is very low. On the other hand, if the jammer asks too high price, it risks the situation in which the source would buy the service from the other friendly jammer. There is an optimal price for each friendly jammer to ask, and the source would always select the one that can provide the best performance improvement.
Next, we set up a simulation of mobility. The first friendly jammer is fixed at (50,50), while the second friendly jammer moves from (−50,75) to (100,75). In Figure 7, we show the source utilities of the centralized scheme and the proposed game. We can see that the centralized scheme serves as a performance upper bound. The game result is not far away from the upper bound, while the game solution can be implemented in a distributed manner. The performance game is trivial when the friendly jammer 2 is close to the malicious eavesdropper from (20,75) to (70,75). In Figure 8, we show the jammers' power as a function of jammer 2's location. We can see that depending on the jammers' location, the source switches between two jammers for the best performance. Moreover, the source also buys the optimal amount of jamming power: when the jammer is close to the malicious eavesdropper, the source would buy less power since the jammer is more effective to improve the secrecy capacity. In Figure 9, we show the corresponding friendly jammers' utilities of the proposed game.
Finally, we show the effect of parameter  for the friendly jammer utility in (7). When
for the friendly jammer utility in (7). When  is large, the friendly jammer's utility reduces quick if the source does not buy the service. As a result, the friendly jammer would not ask arbitrary price, and performance gap to the optima solution is small. In Figure 10, we show the secrecy capacity as a function of
is large, the friendly jammer's utility reduces quick if the source does not buy the service. As a result, the friendly jammer would not ask arbitrary price, and performance gap to the optima solution is small. In Figure 10, we show the secrecy capacity as a function of  when the second jammer is located at (0,75). We can see that the performance gap is shrinking when
when the second jammer is located at (0,75). We can see that the performance gap is shrinking when  is increasing. Notice that for the condition in which the game almost converges to the optimal solution, most value of
is increasing. Notice that for the condition in which the game almost converges to the optimal solution, most value of  will achieve good solution, for example, the second friendly jammer located at (50,75).
will achieve good solution, for example, the second friendly jammer located at (50,75).
5. Conclusions
Physical layer security is an emerging security technique that is an alternative for traditional cryptographic-based protocols to achieve perfect secrecy capacity as eavesdroppers obtain zero information. Jamming has been shown in the literature to effectively improve secrecy capacity. In this paper, we investigate the interaction between the source and friendly jammers using the game theory in order to have a distributed solution. The source pays the friendly jammers to interfere the malicious eavesdropper such that the secrecy capacity is increased, and therefore the security of the network. The friendly jammers charge the source with a price for the jamming. To analyze the game outcome, we investigate the Stackelburg game and construct a distributed algorithm. Some properties such as equilibrium and convergence are analyzed. From the simulation results, we conclude the following. First, there is a tradeoff for the price: If the price is too low, the profit is low; and if the price is too high, the source would not buy or buy from other jammers. Second, for the multiple jammer case, the source would buy service from only one jammer. Third, the centralized scheme and distributed scheme have similar performance, especially when  is sufficiently large. Overall, the proposed game theoretical scheme can achieve a comparable performance with distributed implementation.
is sufficiently large. Overall, the proposed game theoretical scheme can achieve a comparable performance with distributed implementation.
References
Wyner AD: The wire-tap channel. Bell System Technical Journal 1975, 54(8):1355-1387.
Leung-Yan-Cheong SK, Hellman ME: The Gaussian wiretap channel. IEEE Transactions on Information Theory 1978, 24: 451-456. 10.1109/TIT.1978.1055917
Csiszar I, Korner J: Broadcast channels with confidential messages. IEEE Transactions on Information Theory 1978, 24(3):339-348. 10.1109/TIT.1978.1055892
Hero AO III: Secure space-time communication. IEEE Transactions on Information Theory 2003, 49(12):3235-3249+3351. 10.1109/TIT.2003.820010
Li Z, Trappe W, Yates R: Secret communication via multi-antenna transmission. Proceedings of the 41st Annual Conference on Information Sciences and Systems (CISS '07), March 2007, Baltimore, Md, USA 905-910.
Negi R, Goelm S: Secret communication using artificial noise. Proceedings of IEEE Vehicular Technology Conference, September 2005 3: 1906-1910.
Parada P, Blahut R: Secrecy capacity of SIMO and slow fading channels. Proceedings of IEEE International Symposium on Information Theory (ISIT '05), September 2005, Adelaide, South Australia 2152-2155.
Shafiee S, Ulukus S: Achievable rates in Gaussian MISO channels with secrecy constraints. Proceedings of IEEE International Symposium on Information Theory, June 2007, Nice, France 2466-2470.
Liang Y, Poor HV, Shamai S: Secure communication over fading channels. IEEE Transactions on Information Theory 2008, 54(6):2470-2492.
Gopala PK, Lai L, El Gamal H: On the secrecy capacity of fading channels. IEEE Transactions on Information Theory 2008, 54(10):4687-4698.
Dong L, Han Z, Petropulu AP, Poor HV: Secure collaborative beamforming. Proceedings of Allerton Conference on Communication, Control, and Computing, October 2008, Allerton, Ill, USA
Kashyap A, Başar T, Srikant R: Correlated jamming on MIMO Gaussian fading channels. IEEE Transactions on Information Theory 2004, 50(9):2119-2123. 10.1109/TIT.2004.833358
Shafiee S, Ulukus S: Mutual Information Games in Multi-user Channels with Correlated Jamming. IEEE Trans. on Information Theory 2009, 55(10):4598-4607.
Brady MH, Mohseni M, Cioffi JM: Spatially-correlated jamming in Gaussian multiple access and broadcast channels. Proceedings of the 40th IEEE Conference on Information Sciences and Systems (CISS '06), March 2006, Princeton, NJ, USA 1635-1639.
Lai L, El Gamal H: The relay-eavesdropper channel: cooperation for secrecy. IEEE Transactions on Information Theory 2008, 54(9):4005-4019.
Tang X, Liu R, Spasojević P, Poor HV: The Gaussian wiretap channel with a helping interferer. Proceedings of IEEE International Symposium on Information Theory (ISIT '08), July 2008, Toronto, Canada 389-393.
Tang X, Liu R, Spasojević P, Poor HV: Interference-assisted secret communication. Proceedings of the IEEE Information Theory Workshop (ITW '08), May 2008, Porto, Portugal 164-168.
Fudenberg D, Tirole J: Game Theory. MIT Press, Cambridge, Mass, USA; 1991.
Saraydar CU, Mandayam NB, Goodman DJ: Efficient power control via pricing in wireless data networks. IEEE Transactions on Communications 2002, 50(2):291-303. 10.1109/26.983324
Scutari G, Barbarossa S, Palomar DP: Potential games: a framework for vector power control problems with coupled constraints. Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '06), May 2006, Toulouse, France 4: 241-244.
Wang B, Han Z, Liu KJR: Distributed relay selection and power control for multiuser cooperative communication networks using buyer/seller game. Proceedings of Annual IEEE Conference on Computer Communications (INFOCOM '07), May 2007, Anchorage, Alaska, USA 544-552.
Bonneau N, Debbah M, Altman E, Hjørungnes A: Non-atomic games for multi-user systems. IEEE Journal on Selected Areas in Communications 2008, 26(7):1047-1058.
Yates RD: A framework for uplink power control in cellular radio systems. IEEE Journal on Selected Areas in Communications 1995, 13(7):1341-1347. 10.1109/49.414651
Boyd S, Vandenberghe L: Convex Optimization. Cambridge University Press, Cambridge, UK; 2006.
Han Z, Liu KJR: Resource Allocation for Wireless Networks: Basics, Techniques, and Applications. Cambridge University Press, Cambridge, UK; 2008.
Acknowledgments
This work was supported by NSF CNS-0910461 and NSF CNS-0905556 and was supported by the Research Council of Norway through the project entitled "Mobile-to-Mobile Communication Systems (M2M)."
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Han, Z., Marina, N., Debbah, M. et al. Physical Layer Security Game: Interaction between Source, Eavesdropper, and Friendly Jammer. J Wireless Com Network 2009, 452907 (2010). https://doi.org/10.1155/2009/452907
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/452907

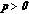 .
.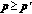 , then
, then  , or
, or 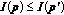 .
. ,??
,??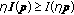 .
.


 versus the prices of both users.
versus the prices of both users.

 versus the prices of both users.
versus the prices of both users.

 versus the prices of both users.
versus the prices of both users.

 versus the location of the second jammer.
versus the location of the second jammer.



 on the game.
on the game.