- Research Article
- Open access
- Published:
On the Performance Gain of Hybrid Decode-Amplify-Forward Cooperative Communications
EURASIP Journal on Wireless Communications and Networking volume 2009, Article number: 479463 (2009)
Abstract
We investigate the performance of adaptive decode-forward (ADF), amplify-forward (AF), and hybrid decode-amplify-forward (HDAF) relaying protocol. Specifically, we derive the closed-form expression of symbol error probability (SEP) for these three relaying protocols. For the AF protocol, we derive a simpler and more tractable final result than previously published work. Furthermore, analyzing the high signal-to-noise ratio (SNR) regime, we derive an asymptotically tight approximation for SEP. The approximation is used to assess an important aspect between the three different relaying protocols, i.e., the SEP performance gain of HADF over the two conventional relaying schemes ADF and AF. It is shown that the performance gain of HDAF over ADF and AF significantly depends on the relative value of channel conditions between source-to-relay and relay-to-destination links. Interestingly, it is shown that HDAF has no benefit compare to the two others if the relay is located close to the source. In contrast, the performance gains of HDAF over the ADF and AF scheme are remarkably large as the relay moves nearby the destination. Specifically, the numerical results given as well as our analysis indicate that for QPSK modulation, HDAF outperforms ADF and AF with a performance improvement by 5 dB and 6 dB, respectively.
1. Introduction
The research in the area of cooperative communications dates back to the work of [1], where the capacity of relaying channels with three terminals was studied. The basic idea of this cooperative system is that a source broadcasts information to both the relay and the destination; the relay retransmits the information about the same message to the destination; then, the destination combines the information received from both the source and the relay to enhance the reliability, thereby achieving spatial diversity albeit each terminal has only a single antenna. More recently, it has been shown that cooperative diversity can be modeled with multiple terminals and therefore attain a spatial diversity gain in a distributed fashion [2–6]. Cooperative relaying protocols can be subcategorized according to their forwarding scheme as amplify-forward (AF) and decode-forward (DF). An AF scheme simplifies relaying operation in order to minimize cooperation overhead. In AF relaying mode, relay terminals simply amplify the signal received from the source and forward it to the destination without performing any sort of signal regeneration. In DF relaying mode, the relay fully decodes and then transmits the received message to the destination. The DF mode can be further classified as ( ) fixed decode-forward (FDF): the relay always forwards its received message, where potential propagating errors could lead to wrong decision at the destination, and (
) fixed decode-forward (FDF): the relay always forwards its received message, where potential propagating errors could lead to wrong decision at the destination, and ( ) adaptive decode-forward (ADF): the relay will not be active if the signal from the source is corrupted. In [7], focusing on the worst case scenarios, it has been shown from simulation results that the performance of FDF and AF modes is not much different, and is pretty bad in both cases. A hybrid scheme of ADF and AF for orthogonal frequency division multiplexing (OFDM) systems has been proposed in [8]. Depending on the channel condition of the source-to-relay link on each subcarrier, the better protocol between ADF and AF is selected. Simulation results have verified the advantage of the proposed hybrid scheme. Recently, a hybrid scheme combining AF and FDF with soft-decision, namely decode-amplify-forward protocol, has been reported in [9]. By having the relay perform soft decoding and forward the reliability information at the output of its decoder to the destination, this hybrid scheme cleverly combines the merit of both AF and DF mode.
) adaptive decode-forward (ADF): the relay will not be active if the signal from the source is corrupted. In [7], focusing on the worst case scenarios, it has been shown from simulation results that the performance of FDF and AF modes is not much different, and is pretty bad in both cases. A hybrid scheme of ADF and AF for orthogonal frequency division multiplexing (OFDM) systems has been proposed in [8]. Depending on the channel condition of the source-to-relay link on each subcarrier, the better protocol between ADF and AF is selected. Simulation results have verified the advantage of the proposed hybrid scheme. Recently, a hybrid scheme combining AF and FDF with soft-decision, namely decode-amplify-forward protocol, has been reported in [9]. By having the relay perform soft decoding and forward the reliability information at the output of its decoder to the destination, this hybrid scheme cleverly combines the merit of both AF and DF mode.
In this paper, we focus on a cooperative communication scheme with hybrid decode-amplify-forward (HDAF) protocol combining the AF mode and ADF mode with hard decision and study its symbol error probability (SEP) performance over Rayleigh fading channels. Instead of remaining silent during the second-hop transmission if the signal is corrupted as in the ADF protocol, the HDAF scheme can increase the performance by having the relay perform in the AF mode. When the relay has full knowledge about the instantaneous fading channel of the source-to-relay link, it can operate in channel state information (CSI)-assisted AF relay mode. Besides, when only the channel mean power of the first hop is available at the relay, semiblind AF relay is considered. In this paper, we focus on CSI-assisted AF relays and Rayleigh fading channels for all links.
Our contribution is summarized as follows. In [10], the SEP performance of CSI-assisted AF relay was obtained from the moment-generating function (MGF) of the harmonic mean of two independent exponential variables. As a result, the MGF expression is given in integral form, containing the hypergeometric function. In contrast, in this paper, we derive the simple MGF formulas including only elementary functions, without introducing any hypergeometric functions. We further show that our result is numerically identical but provide a simpler mathematical expression compared to the works in [10]. This finding enables us to calculate asymptotically tight approximations for SEP of the AF protocol. Recently, the SEP approximation for AF relays has been investigated in [11]. It has been shown that although both formulas, that is, our approximation and [11,  ], are derived independently they can be expressed in a similar form, only with the difference at the scale value. Interestingly, we demonstrate that our SEP approximation for the AF protocol is tighter than the work given in [11].
], are derived independently they can be expressed in a similar form, only with the difference at the scale value. Interestingly, we demonstrate that our SEP approximation for the AF protocol is tighter than the work given in [11].
These findings lead to deriving the performance gain of HDAF over ADF and AF systems. We show that the gain of HDAF over ADF and AF depends on the relative values of channel quality of source-to-relay and relay-to-destination link. When the relay is placed halfway between the source and destination, we observe an improvement of 1 dB and 1.5 dB in SEP performance of HDAF scheme over ADF and AF, respectively. Specifically, it is shown that for QPSK modulation HDAF can increase SEP performance by 5 dB and 6 dB, respectively, compared to ADF and AF as the channel quality of relay-to-destination link is much better than that of source-to-relay link.
The remaining parts of this paper are organized as follows. In Section 2, we briefly review the system and channel model for cooperative communications. In Section 3, we then derive the associated SEP performance gain in the high  regime. Numerical results are provided in Section 4 to verify our analysis. Some discussion and future work have been addressed in Section 5. Finally, Section 6 concludes the paper.
regime. Numerical results are provided in Section 4 to verify our analysis. Some discussion and future work have been addressed in Section 5. Finally, Section 6 concludes the paper.
2. System and Channel Model
Let us consider the specific half-duplex cooperative relay-based wireless system with three terminals as shown in Figure 1, where the direct communication between the source S and destination D is assisted by the relay R. The communication occurs in two hops. During the first-hop transmission (broadcasting phase) spanning one symbol-interval, the source S sends the symbol to the relay R and destination D. In the second-hop transmission (relaying phase) lasting one symbol-interval, for the DF mode, the relay terminal decodes the message and forwards it to the destination. For the AF mode, the received signal from the source-to-relay link is retransmitted with an amplifying parameter  to satisfy the power constraint at the relay (i.e., equal power allocation between S and R). In this paper, to simplify the analysis we only consider the orthogonal AF (OAF) protocol, that is, the source S remains silent in the relaying phase. In contrast, a nonorthogonal AF protocol (the source S continues to transmit in the relaying phase) which improves the performance compared to the OAF scheme has been investigated in [12–14]. Finally, the destination combines the signals from two hops transmission using a maximum-ratio-combining (MRC) scheme to enhance the reliability. We assume that the channels of all links induce quasistatic fading, that is, the channel remains constant for the duration of a frame and changes independently to a new value for each subsequent frame. Furthermore, we restrict our attention to the ADF protocol as the relay does not propagate the error message to the destination as in the FDF scheme.
to satisfy the power constraint at the relay (i.e., equal power allocation between S and R). In this paper, to simplify the analysis we only consider the orthogonal AF (OAF) protocol, that is, the source S remains silent in the relaying phase. In contrast, a nonorthogonal AF protocol (the source S continues to transmit in the relaying phase) which improves the performance compared to the OAF scheme has been investigated in [12–14]. Finally, the destination combines the signals from two hops transmission using a maximum-ratio-combining (MRC) scheme to enhance the reliability. We assume that the channels of all links induce quasistatic fading, that is, the channel remains constant for the duration of a frame and changes independently to a new value for each subsequent frame. Furthermore, we restrict our attention to the ADF protocol as the relay does not propagate the error message to the destination as in the FDF scheme.
The received signals at the destination and relay, respectively, during the broadcasting phase are given as

where  is the transmitted signal at the source with the average transmit power per symbol
is the transmitted signal at the source with the average transmit power per symbol  . Depending on the relaying operation during the second-hop transmission, the received signals at the destination for ADF and AF mode, respectively, are given as follows:
. Depending on the relaying operation during the second-hop transmission, the received signals at the destination for ADF and AF mode, respectively, are given as follows:

In (1) and (2), the notations  ,
,  , and
, and  ,
,  , represent the fading channel magnitude with the channel mean power
, represent the fading channel magnitude with the channel mean power  , received signals, and additive white Gaussian noise (AWGN) with variance
, received signals, and additive white Gaussian noise (AWGN) with variance  , respectively. It is noted that all random variables
, respectively. It is noted that all random variables  , where
, where  denotes the complex Gaussian random variable with zero mean and variance
denotes the complex Gaussian random variable with zero mean and variance  , and
, and  are statistically independent. At the destination, the received signals from the source and relay are combined together using the MRC technique.
are statistically independent. At the destination, the received signals from the source and relay are combined together using the MRC technique.
In case of the ADF protocol, if the relay correctly decodes the message, it will be forwarded to the destination during the relaying phase. Then, the instantaneous  of the MRC output is given by
of the MRC output is given by

where  and
and  are the instantaneous
are the instantaneous  of source-to-destination link and relay-to-destination link, respectively. Otherwise, the relay remains silent, hence, in this case we have
of source-to-destination link and relay-to-destination link, respectively. Otherwise, the relay remains silent, hence, in this case we have

For the AF protocol, as stated earlier, the amplifying parameter  is chosen based on the power constraint between the two phases. In this paper, without considering the power optimization problem, we assume the relay consumes the same amount of power as the source does in the first hop. In case of available instantaneous CSI at R (CSI-assisted relay), an amplifying parameter
is chosen based on the power constraint between the two phases. In this paper, without considering the power optimization problem, we assume the relay consumes the same amount of power as the source does in the first hop. In case of available instantaneous CSI at R (CSI-assisted relay), an amplifying parameter  can be formulated as [10]
can be formulated as [10]

where  is the common
is the common  of each link without fading [5]. Hence, the instantaneous
of each link without fading [5]. Hence, the instantaneous  after MRC for CSI-assisted AF protocol is expressed as [10]
after MRC for CSI-assisted AF protocol is expressed as [10]

For the second term in (6), it is somewhat difficult to find the CDF and MGF. Fortunately, it can be tightly bounded in the form of harmonic mean of two independent exponent random variables as [10]

where

3. Symbol Error Probability and Performance Gain
In this section, we derive closed-form expressions for SEP of  -PSK modulation with three relaying protocols, that is, ADF, AF, and HDAF, by applying the well-known MGF approach [15, 16]. We further show very tight approximations for SEP, induced from the numerical results given in Section 4, which help to assess asymptotic behavior of SEP in the high
-PSK modulation with three relaying protocols, that is, ADF, AF, and HDAF, by applying the well-known MGF approach [15, 16]. We further show very tight approximations for SEP, induced from the numerical results given in Section 4, which help to assess asymptotic behavior of SEP in the high  regime. In practice, the decoding decision at the relay is determined by checking the cyclic redundancy check (CRC) of a frame. However, in this paper, it is assumed that this decision is made symbol by symbol for mathematical tractability of SEP derivation. Denoting
regime. In practice, the decoding decision at the relay is determined by checking the cyclic redundancy check (CRC) of a frame. However, in this paper, it is assumed that this decision is made symbol by symbol for mathematical tractability of SEP derivation. Denoting  as the probability that the relay correctly decodes the symbol, we have [15, 16]
as the probability that the relay correctly decodes the symbol, we have [15, 16]

where  and
and  is the MGF of
is the MGF of  defined as
defined as

where  is the expectation operator over the random variable
is the expectation operator over the random variable  .
.
3.1. Adaptive Decode-Forward Relay Protocol
By defining  and
and  as the average SEP associated with the events that the relay correctly and incorrectly decodes the symbol transmitted from the source, respectively, the average SEP of the ADF protocol can be written as
as the average SEP associated with the events that the relay correctly and incorrectly decodes the symbol transmitted from the source, respectively, the average SEP of the ADF protocol can be written as

From the expressions of  and
and  given in (3) and (4), respectively, along with the fact that
given in (3) and (4), respectively, along with the fact that  and
and  are statistically independent, we have
are statistically independent, we have

Moreover, by substituting (9) in (12), we obtain the SEP of ADF as follows

By assessing the SEP expression of ADF given in (13) at large SNR, we observe that the negative term is much smaller compared to two positive terms as there are three MGF values included in the last term. Therefore, eliminating the last term (negative term) of (13) leads to the SEP approximation

Since  ,
,  , it is obvious that
, it is obvious that  obeys an exponential distribution with parameter
obeys an exponential distribution with parameter  and as a consequence the MGF of
and as a consequence the MGF of  can be written as
can be written as

Also, at the high  regime, that is,
regime, that is,  , the MGF of
, the MGF of  , by omitting the unit value in (15), can be approximated by
, by omitting the unit value in (15), can be approximated by

Eventually, from (14) and (16) the approximation of  is obtained as
is obtained as

where

3.2. Amplify-Forward Relay Protocol
From (7) and using the fact that  and
and  are assumed to be statistically independent, the average SEP of the AF protocol is given by
are assumed to be statistically independent, the average SEP of the AF protocol is given by

where  and
and  is derived in the appendix. In [10], the closed-form expression of SEP for AF relay is given in the form of hypergeometric function. We will show in the next section that both formulas, that is, our final expression of
is derived in the appendix. In [10], the closed-form expression of SEP for AF relay is given in the form of hypergeometric function. We will show in the next section that both formulas, that is, our final expression of  given in (A.8) and [10,
given in (A.8) and [10,  ], provide the identical numerical result. It is worth mentioning that our final expression, contains only elementary functions and therefore is much simpler than [10,
], provide the identical numerical result. It is worth mentioning that our final expression, contains only elementary functions and therefore is much simpler than [10,  ]. This finding helps us to derive the asymptotically tight approximation of SEP for both AF and HDAF relay protocols. Moreover, using the asymptotic approximation of
]. This finding helps us to derive the asymptotically tight approximation of SEP for both AF and HDAF relay protocols. Moreover, using the asymptotic approximation of  in (A.10), a tight approximation of
in (A.10), a tight approximation of  in the high
in the high  can be obtained as follows:
can be obtained as follows:

Remark 1.
In [11], the SEP of the AF protocol has been approximated in the high SNR regime using the McLaurin series expansion of the probability distribution function (PDF) of  given in (7). Specifically, for
given in (7). Specifically, for  -PSK modulation and Rayleigh fading channels for all links, the SEP approximation for the AF protocol derived in [11] is rewritten in terms of our notations as follows [11,
-PSK modulation and Rayleigh fading channels for all links, the SEP approximation for the AF protocol derived in [11] is rewritten in terms of our notations as follows [11,  ]:
]:

Examining the two expressions of approximated SEP given in (20) and (21), we can see that although both formulas are derived independently they produce a similar form, only with the difference at the scale value. In the next section, we numerically show that our approximation (20) is tighter than (21) deduced in [11].
3.3. Hybrid Decode-Amplify-Forward Relay Protocol
With the HDAF relaying scheme, the relay operates in DF mode if it can correctly decode the message from the source, otherwise the relay acts in AF mode. Let us denote  as the average SEP associated with the event that the relay incorrectly decode the source's symbol, hence, the SEP in this protocol can be expressed as
as the average SEP associated with the event that the relay incorrectly decode the source's symbol, hence, the SEP in this protocol can be expressed as

where the first term in (22) corresponds to the ADF mode and the second term indicates the AF mode. Since  are statistically independent with
are statistically independent with  and
and  , from (3) and (7), we obtain
, from (3) and (7), we obtain

We next substitute (9) in (23) and the above formula can be rewritten as

Similarly as in the ADF protocol, by eliminating the last term in (24), the SEP approximation of HDAF can be determined by

Using the fact that  and the approximation of
and the approximation of  given in (A.10) of the appendix, we can tightly asymptotically approximate
given in (A.10) of the appendix, we can tightly asymptotically approximate  as
as

3.4. Performance Gain of HDAF over ADF and AF
We now assess the behavior of SEP performance for the considered three relay protocols in the high  regime by analyzing their approximations. As can clearly be seen from (17), (20), and (26), the three protocols result in a diversity order of two since the SEP expressions are inversely proportional to
regime by analyzing their approximations. As can clearly be seen from (17), (20), and (26), the three protocols result in a diversity order of two since the SEP expressions are inversely proportional to  . In other words, the related three SEP curves plotted in log-log scales are parallel with the slope of order two in the high
. In other words, the related three SEP curves plotted in log-log scales are parallel with the slope of order two in the high  regime as illustrated in Figure 2. Intuitively, the HDAF scheme outperforms both ADF and AF. These observations inspired us to deduce the performance gain that can be achieved with HDAF compared to the two conventional protocols ADF and AF. To answer this question, we adapt the concept of relaying gain
regime as illustrated in Figure 2. Intuitively, the HDAF scheme outperforms both ADF and AF. These observations inspired us to deduce the performance gain that can be achieved with HDAF compared to the two conventional protocols ADF and AF. To answer this question, we adapt the concept of relaying gain  . Here,
. Here,  with
with  is the SEP performance gain of HDAF compared to the
is the SEP performance gain of HDAF compared to the  protocol. As shown in Figure 2, we have
protocol. As shown in Figure 2, we have

The limit operation in (27) implies that the gain  is obtained in the high
is obtained in the high  regime. In this context, we now calculate
regime. In this context, we now calculate  and
and  . Substituting (17) and (26) in (27) and performing some elementary manipulations,
. Substituting (17) and (26) in (27) and performing some elementary manipulations,  can be expressed as
can be expressed as

Substituting (20) and (26) in (27), the gain  to be considered here is given by
to be considered here is given by

Regarding the channel mean power of each link, we also assume that the relay is placed in between the source and destination. The path loss of each link is assumed to follow an exponential-decay model. As such, if the distance between the source S and destination D is given as  , then
, then  . For example, a path-loss exponent of
. For example, a path-loss exponent of  corresponds to a typical nonline-of-sight propagation scenario. This geometrical model has been widely used in the context of relay networks (see, e.g., [11, 17]). According to this physical model, when the relay is located close to the source or the destination we have
corresponds to a typical nonline-of-sight propagation scenario. This geometrical model has been widely used in the context of relay networks (see, e.g., [11, 17]). According to this physical model, when the relay is located close to the source or the destination we have  or
or  , respectively. As the relay is located half-way between the source and destination, we have
, respectively. As the relay is located half-way between the source and destination, we have  .
.
In view of (28) and (29), the following general observations can be made for the respective gains.
-
(i)
With a fixed modulation scheme, that is,
 is constant,
is constant,  depends only on the ratio between channel mean power of the relay-to-destination link and that of source-to-relay link.
depends only on the ratio between channel mean power of the relay-to-destination link and that of source-to-relay link. -
(ii)
As the relay moves closely to the source, we have
 leading to
leading to  . We can intuitively explain this result as follows. As the channel of source-to-relay link is very good, the probability that the relay correctly decodes the source's signal is high. As a result, the HDAF scheme mostly acts in the DF mode. However, there may be some rare situations in which the relay cannot decode the source's message and HDAF will act in the AF mode to assist the direct communication. That is the reason HDAF still achieves some very small gain, which also can be neglected, in this particular case. Furthermore, for the AF scheme, the compound source-relay-destination path can be approximated by the inferior channel between source-to-relay and relay-to-destination links. Hence, the AF mode now provides a similar performance as ADF. In other words, the three protocols almost result in identical performance.
. We can intuitively explain this result as follows. As the channel of source-to-relay link is very good, the probability that the relay correctly decodes the source's signal is high. As a result, the HDAF scheme mostly acts in the DF mode. However, there may be some rare situations in which the relay cannot decode the source's message and HDAF will act in the AF mode to assist the direct communication. That is the reason HDAF still achieves some very small gain, which also can be neglected, in this particular case. Furthermore, for the AF scheme, the compound source-relay-destination path can be approximated by the inferior channel between source-to-relay and relay-to-destination links. Hence, the AF mode now provides a similar performance as ADF. In other words, the three protocols almost result in identical performance. -
(iii)
In contrast, the gain is significant when the relay is located nearby the destination, that is,
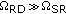 . We can similarly explain this result as in the case the relay is close to the source.
. We can similarly explain this result as in the case the relay is close to the source. -
(iv)
Examining the function
 (deduced from (18), with
(deduced from (18), with  (equality occurs for BPSK modulation), we can easily see that the global maximum value of
(equality occurs for BPSK modulation), we can easily see that the global maximum value of 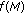 is 2/3. Consequently, we have
is 2/3. Consequently, we have 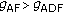 . In other words, the HDAF scheme always provides more gain over AF than over ADF. This again confirms a well-known result that ADF always outperforms AF scheme.
. In other words, the HDAF scheme always provides more gain over AF than over ADF. This again confirms a well-known result that ADF always outperforms AF scheme.
Next, regarding the relaying gain  , we introduce several specific examples for QPSK modulation (substituting
, we introduce several specific examples for QPSK modulation (substituting  in (18) yields
in (18) yields  and
and  ).
).
-
(i)
For a symmetric cooperative system, that is,
 , we have
, we have 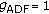 dB and
dB and  dB.
dB. -
(ii)
For an asymmetric cooperative system, where the relay is close to the source, that is,
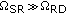 ,
, 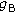 goes to zero. In this special case, the HDAF scheme has no benefit compared to ADF and AF.
goes to zero. In this special case, the HDAF scheme has no benefit compared to ADF and AF. -
(iii)
For an asymmetric cooperative system, where the relay is located nearby the destination, that is,
 ,
, 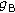 becomes remarkably large. Specifically, in case of
becomes remarkably large. Specifically, in case of  , HDAF achieves an increase in SEP performance of 5.03 dB and 6.15 dB compared to ADF and AF scheme, respectively.
, HDAF achieves an increase in SEP performance of 5.03 dB and 6.15 dB compared to ADF and AF scheme, respectively.
4. Numerical Results
In order to validate our analysis given in the previous section, numerical results are provided in the sequel. Figures 3, 4, and 5 plot the SEP of QPSK modulation versus transmit 
 for the considered three relay protocols taking into account the relay's location as the relay is placed halfway between the source and destination, the relay is close to the source, and the relay is close to the destination, respectively.
for the considered three relay protocols taking into account the relay's location as the relay is placed halfway between the source and destination, the relay is close to the source, and the relay is close to the destination, respectively.
4.1. Verification of Our Analysis
We display the exact SEP curves given by (12), (19), and (23) and the approximations given by (17), (20), and (26). As a reference point, for the AF and HDAF protocol we also show the results calculated with the expression given in [10,  ]. As can clearly be seen from these figures, our numerical results exactly match with those calculated from [10,
]. As can clearly be seen from these figures, our numerical results exactly match with those calculated from [10,  ]. However, with the complex expression of the MGF of the harmonic mean of two exponential random variables given in [10,
]. However, with the complex expression of the MGF of the harmonic mean of two exponential random variables given in [10,  ], one may not be able to perform the tight approximation of SEP leading to relaying gain
], one may not be able to perform the tight approximation of SEP leading to relaying gain  as our result in (A.6) does. The results shown also reveal that the approximation of SEP becomes very tight in the high
as our result in (A.6) does. The results shown also reveal that the approximation of SEP becomes very tight in the high  regime.
regime.
In order to avoid dense graphical figures, we display the comparison of two approximations, that is, our approach and the approximation reported in [11,  ], in separated examples. We compare the tightness of two SEP approximations, that is, our expression given in (20) and one derived in [11,
], in separated examples. We compare the tightness of two SEP approximations, that is, our expression given in (20) and one derived in [11,  ] which is again shown in (21). For this purpose, we compute the relative error of two SEP approximations and exact SEP as follows:
] which is again shown in (21). For this purpose, we compute the relative error of two SEP approximations and exact SEP as follows:

We consider the SEP of AF protocol for QPSK modulation versus average SNR ranging from 10 to 30 dB (medium to high SNR regime) as the relay is located half-way between the source and destination, close to the source, and nearby the destination in Figures 6, 7, and 8, respectively. In these three figures, we plot the relative errors deduced from our approach and the approximation reported in [11] in the log-log scale. As can clearly be observed, our approach results in much smaller error than that of [11] for the whole considered range of SNR in the three examples. Also we see that the relative error curves of [11] yield an error floor in the high SNR regime.
4.2. Assessment of the Performance Gain
In case of the symmetric system, examining the results in the high  regime of Figure 3, we can see that the performance of HDAF increases about 1 dB and 1.5 dB over those of ADF and AF scheme, respectively. As the relay moves close to the source, the results presented in Figure 4 show that the three protocols result in nearly the same SEP performance. No gain is achieved in this particular case. In contrast, as the relay is located close to the destination, it is obvious from the Figure 5 that HDAF remarkably outperforms ADF and AF with a performance improvement by 5 dB and 6 dB, respectively. All of these observations confirm our examples given in Section 3.4.
regime of Figure 3, we can see that the performance of HDAF increases about 1 dB and 1.5 dB over those of ADF and AF scheme, respectively. As the relay moves close to the source, the results presented in Figure 4 show that the three protocols result in nearly the same SEP performance. No gain is achieved in this particular case. In contrast, as the relay is located close to the destination, it is obvious from the Figure 5 that HDAF remarkably outperforms ADF and AF with a performance improvement by 5 dB and 6 dB, respectively. All of these observations confirm our examples given in Section 3.4.
5. Discussion and Future Work
The conventional ADF protocol, also the one considered in this paper, is limited by the fact that the decision time is fixed a priori. When the channel quality of the source-to-relay link is very good, for example, in case of the relay being close to the source, the relay will be able to decode very quickly. Hence, being forced to wait until half-time before the relay can transmit leads to some waste of resources. Recently, the dynamic decode and forward (DDF) protocol has been proposed in [12] where the decision time is a random variable. The drawback faced by ADF can be overcome using the DDF scheme. More recently, a novel variant of the DDF protocol with low encoding/decoding complexity making the DDF protocol more realistic has been proposed in [13]. Interestingly, the Alamouti-DDF presented in [13] results in the same instantaneous SNR as in (3). Both DDF schemes in [12, 13] achieve the optimal diversity-multiplexing tradeoff (DMT) for all the classes of DF protocols. Clearly, employing DDF in the HDAF scheme is an interesting topic for our future research.
In this paper, we use CRC to perform error detection at the relay. This type of error detection codes is widely used in research on cooperative communications. However, as the channel of source-to-relay link is poor, to avoid a high undetected error probability at the relay, we need to increase the CRC's bits which results in an extra amount of redundancy. An alternative practical approach based on Forney's rule has been presented in [18]. It has been shown in [18] that CRC can be replaced by the bounded distance decoder for error detection. The replacement of CRC by DDF with bounded distance decoder is another direction for future work on the performance gain of HDAF.
Together with conventional performance metrics such as SEP, DMT is also widely applied to effectively assess and compare existing communication systems. Recently, the DMT of several relay protocols has been extensively studied in [12–14, 18]. It would be interesting to derive the DMT of HDAF to investigate its improvement over ADF and AF protocols.
6. Conclusions
In this paper, we have investigated the hybrid scheme between fixed decode-forward and amplify-forward relay protocol, namely HDAF. For the AF relay protocol, we have derived a simpler and more tractable final result than previously published work. This finding enabled us to calculate the asymptotically tight approximation for SEP, leading to deriving the performance gain of HDAF over ADF and AF systems. We also compared the SEP performance among these three schemes. It has been shown that HDAF outperforms ADF and AF in terms of SEP performance. The performance gain depends on the relay's location. The gain is significant as the relay gets close to the destination and vice versa.
Appendix
Derivation of MGF of Random Variable  Given in (8)
Given in (8)
Based on (8), the CDF of  can be given by
can be given by

The lower limit of the integral in (A.1) comes to the fact that  is always greater than or equal to
is always greater than or equal to  (since
(since  , it is easy to see that
, it is easy to see that  ). Taking the differentiation in (A.1) with respect to
). Taking the differentiation in (A.1) with respect to  , the PDF of
, the PDF of  is given by
is given by

Let  and for the sake of simplicity denote
and for the sake of simplicity denote  with
with  . Then, (A.2) can be rewritten as follows:
. Then, (A.2) can be rewritten as follows:

Hence, the MGF of  can be expressed as
can be expressed as

Substituting (A.3) in (A.4) and exchanging the order of the integrals of  and
and  , we have
, we have


where

The integral in (A.6) can be hand-calculated with the help of [19, ( )] and [20] as follows:
)] and [20] as follows:

where  . Our final expression in (A.8) is simpler and more tractable than [10,
. Our final expression in (A.8) is simpler and more tractable than [10,  ], which contains the Gauss hypergeometric function. Both formulas, that is, (A.8) and [10,
], which contains the Gauss hypergeometric function. Both formulas, that is, (A.8) and [10,  ], lead to the same numerical result but (A.8) is more helpful to analyze the SEP performance in the high
], lead to the same numerical result but (A.8) is more helpful to analyze the SEP performance in the high  regime by providing the asymptotically tight approximation of
regime by providing the asymptotically tight approximation of  .
.
Moreover, as the  is high, that is,
is high, that is,  goes to infinity, we have
goes to infinity, we have

Hence,  can be tightly approximated as follows:
can be tightly approximated as follows:

References
Cover TM, El Gamal AA: Capacity theorems for the relay channel. IEEE Transactions on Information Theory 1979, 25(5):572-584. 10.1109/TIT.1979.1056084
Sendonaris A, Erkip E, Aazhang B: User cooperation diversity—part I: system description. IEEE Transactions on Communications 2003, 51(11):1927-1938. 10.1109/TCOMM.2003.818096
Sendonaris A, Erkip E, Aazhang B: User cooperation diversity—part II: implementation aspects and performance analysis. IEEE Transactions on Communications 2003, 51(11):1939-1948. 10.1109/TCOMM.2003.819238
Laneman JN, Wornell GW: Distributed space-time-coded protocols for exploiting cooperative diversity in wireless networks. IEEE Transactions on Information Theory 2003, 49(10):2415-2425. 10.1109/TIT.2003.817829
Laneman JN, Tse DNC, Wornell GW: Cooperative diversity in wireless networks: efficient protocols and outage behavior. IEEE Transactions on Information Theory 2004, 50(12):3062-3080. 10.1109/TIT.2004.838089
Nabar RU, Bölcskei H, Kneubühler FW: Fading relay channels: performance limits and space-time signal design. IEEE Journal on Selected Areas in Communications 2004, 22(6):1099-1109. 10.1109/JSAC.2004.830922
Yu M, Li J: Is amplify-and-forward practically better than decode-and-forward or vice versa? Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP '05), March 2005, Philadenphia, Pa, USA 3: 365-368.
Can B, Yomo H, De Carvalho E: Hybrid forwarding scheme for cooperative relaying in OFDM based networks. Proceedings of the IEEE International Conference on Communications, June 2006, Istanbul, Turkey 10: 4520-4525.
Bao X, Li J: Efficient message relaying for wireless user cooperation: decode-amplify-forward (DAF) and hybrid DAF and coded-cooperation. IEEE Transactions on Wireless Communications 2007, 6(11):3975-3984.
Hasna MO, Alouini M-S: End-to-end performance of transmission systems with relays over Rayleigh-fading channels. IEEE Transactions on Wireless Communications 2003, 2(6):1126-1131. 10.1109/TWC.2003.819030
Ribeiro A, Cai X, Giannakis GB: Symbol error probabilities for general cooperative links. IEEE Transactions on Wireless Communications 2005, 4(3):1264-1273.
Azarian K, El Gamal H, Schniter P: On the achievable diversity-multiplexing tradeoff in half-duplex cooperative channels. IEEE Transactions on Information Theory 2005, 51(12):4152-4172. 10.1109/TIT.2005.858920
Murugan A, Azarian K, Gamal HE: Cooperative lattice coding and decoding in half-duplex channels. IEEE Journal on Selected Areas in Communications 2007, 25(2):268-278.
Kumar PV, Vinodh K, Anand M, Elia P: Diversity-multiplexing gain tradeoff and DMT-optimal distributed space-time codes for certain cooperative communication protocols: overview and recent results. Proceedings of the Information Theory and Applications Workshop, January 2007, San Diego, Calif, USA
Simon MK, Alouini M-S: A unified approach to the performance analysis of digital communication over generalized fading channels. Proceedings of the IEEE 1998, 86(9):1860-1877. 10.1109/5.705532
Simon MK, Alouini M-S: Digital Communication over Fading Channels: A Unified Approach to Performance Analysis. John Wiley & Sons, New York, NY, USA; 2000.
Kramer G, Gastpar M, Gupta P: Cooperative strategies and capacity theorems for relay networks. IEEE Transactions on Information Theory 2005, 51(9):3037-3063. 10.1109/TIT.2005.853304
Kumar KR, Caire G: Coding and decoding for the dynamic decode and forward relay protocol. Proceedings of the IEEE International Symposium on Information Theory, 2008 2380-2384.
Gradshteyn IS, Ryzhik IM: Table of Integrals, Series, and Products. 6th edition. Academic Press, San Diego, Calif, USA; 2000.
Gradshteyn IS, Ryzhik IM: Errata for Table of Integrals, Series, and Products. 6th edition. Academic Press, Orlando, Fla, USA; 2005.
Acknowledgments
The authors would like to thank the reviewers and the Editor for their careful reviews and constructive comments.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Duong, T.Q., Zepernick, HJ. On the Performance Gain of Hybrid Decode-Amplify-Forward Cooperative Communications. J Wireless Com Network 2009, 479463 (2009). https://doi.org/10.1155/2009/479463
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/479463


 is constant,
is constant,  depends only on the ratio between channel mean power of the relay-to-destination link and that of source-to-relay link.
depends only on the ratio between channel mean power of the relay-to-destination link and that of source-to-relay link. leading to
leading to  . We can intuitively explain this result as follows. As the channel of source-to-relay link is very good, the probability that the relay correctly decodes the source's signal is high. As a result, the HDAF scheme mostly acts in the DF mode. However, there may be some rare situations in which the relay cannot decode the source's message and HDAF will act in the AF mode to assist the direct communication. That is the reason HDAF still achieves some very small gain, which also can be neglected, in this particular case. Furthermore, for the AF scheme, the compound source-relay-destination path can be approximated by the inferior channel between source-to-relay and relay-to-destination links. Hence, the AF mode now provides a similar performance as ADF. In other words, the three protocols almost result in identical performance.
. We can intuitively explain this result as follows. As the channel of source-to-relay link is very good, the probability that the relay correctly decodes the source's signal is high. As a result, the HDAF scheme mostly acts in the DF mode. However, there may be some rare situations in which the relay cannot decode the source's message and HDAF will act in the AF mode to assist the direct communication. That is the reason HDAF still achieves some very small gain, which also can be neglected, in this particular case. Furthermore, for the AF scheme, the compound source-relay-destination path can be approximated by the inferior channel between source-to-relay and relay-to-destination links. Hence, the AF mode now provides a similar performance as ADF. In other words, the three protocols almost result in identical performance.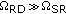 . We can similarly explain this result as in the case the relay is close to the source.
. We can similarly explain this result as in the case the relay is close to the source. (deduced from (18), with
(deduced from (18), with  (equality occurs for BPSK modulation), we can easily see that the global maximum value of
(equality occurs for BPSK modulation), we can easily see that the global maximum value of 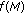 is 2/3. Consequently, we have
is 2/3. Consequently, we have 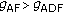 . In other words, the HDAF scheme always provides more gain over AF than over ADF. This again confirms a well-known result that ADF always outperforms AF scheme.
. In other words, the HDAF scheme always provides more gain over AF than over ADF. This again confirms a well-known result that ADF always outperforms AF scheme. , we have
, we have 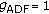 dB and
dB and  dB.
dB.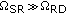 ,
, 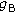 goes to zero. In this special case, the HDAF scheme has no benefit compared to ADF and AF.
goes to zero. In this special case, the HDAF scheme has no benefit compared to ADF and AF. ,
, 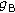 becomes remarkably large. Specifically, in case of
becomes remarkably large. Specifically, in case of  , HDAF achieves an increase in SEP performance of 5.03 dB and 6.15 dB compared to ADF and AF scheme, respectively.
, HDAF achieves an increase in SEP performance of 5.03 dB and 6.15 dB compared to ADF and AF scheme, respectively.
 .
.
 .
.
 .
.


 Given in (8)
Given in (8)