- Research Article
- Open access
- Published:
Secrecy Capacity of a Class of Orthogonal Relay Eavesdropper Channels
EURASIP Journal on Wireless Communications and Networking volume 2009, Article number: 494696 (2009)
Abstract
The secrecy capacity of relay channels with orthogonal components is studied in the presence of an additional passive eavesdropper node. The relay and destination receive signals from the source on two orthogonal channels such that the destination also receives transmissions from the relay on its channel. The eavesdropper can overhear either one or both of the orthogonal channels. Inner and outer bounds on the secrecy capacity are developed for both the discrete memoryless and the Gaussian channel models. For the discrete memoryless case, the secrecy capacity is shown to be achieved by a partial decode-and-forward (PDF) scheme when the eavesdropper can overhear only one of the two orthogonal channels. Two new outer bounds are presented for the Gaussian model using recent capacity results for a Gaussian multiantenna point-to-point channel with a multiantenna eavesdropper. The outer bounds are shown to be tight for two subclasses of channels. The first subclass is one in which the source and relay are clustered, and the eavesdropper receives signals only on the channel from the source and the relay to the destination, for which the PDF strategy is optimal. The second is a subclass in which the source does not transmit to the relay, for which a noise-forwarding strategy is optimal.
1. Introduction
In wireless networks for which nodes can benefit from cooperation and packet-forwarding, there is also a need to preserve the confidentiality of transmitted information from untrusted nodes. Information privacy in wireless networks has traditionally been the domain of the higher layers of the protocol stack via the use of cryptographically secure schemes. In his seminal paper on the three-node wiretap channel, Wyner showed that perfect secrecy of transmitted data from the source node can be achieved when the physical channel to the eavesdropper is noisier than the channel to the intended destination, that is, when the channel is a degraded broadcast channel [1]. This work was later extended by Csiszár and Körner to all broadcast channels with confidential messages, in which the source node sends common information to both the destination and the wiretapper and confidential information only to the destination [2].
Recently, the problem of secure communications has also been studied for a variety of multiterminal networks; see, for example, [3–10], and the references therein. In [11], Lai and El Gamal show that a relay node can facilitate the transmission of confidential messages from the source to the destination in the presence of a wiretapper, often referred to as an eavesdropper in the wireless setting. Lai and El Gamal develop the rate-equivocation region for this four node relay-eavesdropper channel and introduce a noise forwarding scheme in which the relay, even if it is unable to aid the source in its transmissions, transmits codewords independent of the source to confuse the eavesdropper. A special case where the eavesdropper receives a degraded version of the destination's signal is studied in [12]. In contrast, the relay channel with confidential messages in which the relay node acts as both a helper and eavesdropper is studied in [13]. Note that in all the three papers, the relay is assumed to be full-duplex; that is, it can transmit and receive simultaneously over the entire bandwidth.
In this paper, we study the secrecy capacity of a relay channel with orthogonal components in the presence of a passive eavesdropper node. The orthogonality comes from the fact that the relay and destination receive signals from the source on orthogonal channels; furthermore, the destination also receives transmissions from the relay on its (the destination's) channel. The orthogonal model implicitly imposes a half-duplex transmission and reception constraint on the relay. For this channel, in the absence of an eavesdropper, El Gamal and Zahedi showed that a partial decode-and-forward (PDF) strategy, in which the source transmits two messages on the two orthogonal channels and the relay decodes its received signal, achieves the capacity [14].
We study the secrecy capacity of this channel for both the discrete memoryless and Gaussian channel models. As a first step toward this, we develop a PDF strategy for the full-duplex relay eavesdropper channel and extend it to the orthogonal model. Further, since the eavesdropper can receive signals from either orthogonal channel or both, three cases arise in the development of the secrecy capacity. We specialize the outer bounds developed in [11] for the orthogonal case and show that, for the discrete memoryless channel, PDF achieves the secrecy capacity for the two cases where the eavesdropper receives signals in only one of the two orthogonal channels.
For the Gaussian model, we develop two new outer bounds using recent results on the secrecy capacity of the Gaussian multiple-input multiple-output channels in the presence of a multiantenna eavesdropper (MIMOME) in [4–6]. The first outer bound is a genie-aided bound that allows the source and relay to cooperate perfectly resulting in a Gaussian MIMOME channel for which jointly Gaussian inputs maximize the capacity. We show that these bounds are tight for a subclass of channels in which the multiaccess channel from the source and relay to the destination is the bottleneck link, and the eavesdropper is limited to receiving signals on the channel from the source and the relay to the destination. For a complementary subclass of channels in which the source-relay link is unusable due to noise resulting in a deaf relay, we develop a genie-aided bound where the relay and destination act like a two-antenna receiver. We also show that noise forwarding achieves this bound for this subclass of channels.
In [15], He and Yener study the secrecy rate of the channel studied here under the assumption that the relay is colocated with the eavesdropper, and the eavesdropper is completely cognizant of the transmit and receive signals at the relay. The authors found that using the relay does not increase the secrecy capacity, and hence there is no security advantage to using the relay. In this paper, we consider the eavesdropper as a separate entity and show that using the relay increases the secrecy capacity in some cases. In the model of [15], the eavesdropper can overhear only on the channel to the relay, while we consider three cases in which the eavesdropper can overhear on either or both the channels.
The paper is organized as follows. In Section 2, we present the channel models. In Section 3, we develop the inner and outer bounds on the secrecy capacity of the discrete memoryless model. We illustrate these results with examples in Section 4. In Section 5, we present inner and outer bounds for the Gaussian channel model and illustrate our results with examples. We conclude in Section 6.
2. Channel Models and Preliminaries
2.1. Discrete Memoryless Model
A discrete-memoryless relay eavesdropper channel is denoted by  such that the inputs to the channel in a given channel use are
such that the inputs to the channel in a given channel use are  and
and  at the source and relay, respectively, the outputs of the channel are
at the source and relay, respectively, the outputs of the channel are  ,
,  , and
, and  , at the relay, destination, and eavesdropper, respectively, and the channel transition probability is given by
, at the relay, destination, and eavesdropper, respectively, and the channel transition probability is given by  [11]. The channel is assumed to be memoryless; that is, the channel outputs at time
[11]. The channel is assumed to be memoryless; that is, the channel outputs at time  depend only on channel inputs at time
depend only on channel inputs at time  . The source transmits a message
. The source transmits a message  to the destination using the
to the destination using the  code consisting of
code consisting of
-
(1)
a stochastic encoder
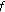 at the source such that
at the source such that 
-
(2)
a set of relay encoding functions
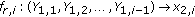 at every time instant
at every time instant  , and
, and -
(3)
a decoding function at the destination
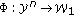 .
.
The average error probability of the code is defined as

The equivocation rate at the eavesdropper is defined as  . A perfect secrecy rate of
. A perfect secrecy rate of  is achieved if, for any
is achieved if, for any  , there exists a sequence of codes
, there exists a sequence of codes  and an integer
and an integer  such that, for all
such that, for all  , we have
, we have

The secrecy capacity is the maximum rate satisfying (2). The model described above considers a relay that transmits and receives simultaneously in the same orthogonal channel. Inner and outer bounds for this model are developed in [11, Theorem 1].
In this paper, we consider a relay eavesdropper channel with orthogonal components in which the relay receives and transmits on two orthogonal channels. The source transmits on both channels, one of which is received at the relay and the other at the destination. The relay transmits along with the source on the channel received at the destination. Thus, the source signal  consists of two parts
consists of two parts  and
and  , transmitted to the relay and the destination, respectively, such that
, transmitted to the relay and the destination, respectively, such that  . The eavesdropper can receive transmissions in one or both orthogonal channels such that
. The eavesdropper can receive transmissions in one or both orthogonal channels such that  denotes the received signal at the eavesdropper in orthogonal channel
denotes the received signal at the eavesdropper in orthogonal channel  ,
,  and
and  . More formally, the relay eavesdropper channel with orthogonal components is defined as follows.
. More formally, the relay eavesdropper channel with orthogonal components is defined as follows.
Definition 1.
A discrete-memoryless relay eavesdropper channel is said to have orthogonal components if the sender alphabet  and the channel can be expressed as
and the channel can be expressed as

Definition 1 assumes that the eavesdropper can receive signals in both channels. In general, the secrecy capacity bounds for this channel depend on the receiver capabilities of the eavesdropper. To this end, we explicitly include the following two definitions for the cases in which the eavesdropper can receive signals in only one of the channels.
Definition 2.
The eavesdropper is limited to receiving signals on the channel from the source to the relay, if

Definition 3.
The eavesdropper is limited to receiving signals on the channel from the source and the relay to the destination, if

Remark 4.
In the absence of an eavesdropper, that is, for  , the channels in (3)–(5) simplify to that of a relay channel with orthogonal components.
, the channels in (3)–(5) simplify to that of a relay channel with orthogonal components.
Thus, depending on the receiver capabilities at the eavesdropper, there are three cases that arise in developing the secrecy capacity bounds. For brevity, we henceforth identify the three cases as Cases 1, 2, and 3, where Cases 1 and 2 correspond to Definitions 2 and 3, respectively, and Case 3 is the general case where the eavesdropper receives signals from both the channels.
2.2. Gaussian Model
For a Gaussian relay eavesdropper channel with orthogonal components, the signals  and
and  received at the relay and the destination, respectively, in each time symbol
received at the relay and the destination, respectively, in each time symbol  , are
, are


where  is the channel gain from transmitter
is the channel gain from transmitter  to receiver
to receiver  , and where
, and where  and
and  are zero mean unit variance Gaussian random variables. The transmitted signals
are zero mean unit variance Gaussian random variables. The transmitted signals 
 , and
, and  are subject to average power constraints given by
are subject to average power constraints given by

where  denotes expectation of its argument. The signals at the eavesdropper are
denotes expectation of its argument. The signals at the eavesdropper are

where  and
and  are the channel gains from the source to the eavesdropper in the two orthogonal channels,
are the channel gains from the source to the eavesdropper in the two orthogonal channels,  is the channel gain from the relay to the eavesdropper,
is the channel gain from the relay to the eavesdropper,  and
and  are zero-mean unit variance Gaussian random variables assumed to be independent of the source and relay signals, and
are zero-mean unit variance Gaussian random variables assumed to be independent of the source and relay signals, and

Throughout the sequel, we assume that the channel gains are fixed and known at all nodes.
For a relay channel with orthogonal components, El Gamal and Zahedi of show that a strategy where the source uses each channel to send an independent message and the relay decodes the message transmitted in its channel achieves capacity [14]. Due to the fact that the relay has partial access to the source transmissions, this strategy is sometimes also referred to as partial decode and forward (see [16]). The achievable scheme involves block Markov superposition encoding while the converse is developed using the max-flow, min-cut bounds. The following proposition summarizes this result.
Proposition 5 ([14]).
The capacity of a relay channel with orthogonal component is given by

where the maximum is over all input distributions of the form

For the Gaussian model, the bounds in (11) are maximized by jointly Gaussian inputs transmitting at the maximum power and subject to (12).
Remark 6.
While the converse allows for all possible joint distributions of  ,
,  , and
, and  , from the form of the mutual information expressions in (11), it suffices to consider distributions only of the form given by (12).
, from the form of the mutual information expressions in (11), it suffices to consider distributions only of the form given by (12).
We use the standard notation for entropy and mutual information [17] and take all logarithms to the base 2 so that our rate units are bits. For ease of exposition, we write  to denote
to denote  and write
and write  to denote
to denote  . We also write random variables with uppercase letters (e.g.,
. We also write random variables with uppercase letters (e.g.,  ) and their realizations with the corresponding lowercase letters (e.g.,
) and their realizations with the corresponding lowercase letters (e.g.,  ). We drop subscripts on probability distributions if the arguments are lowercase versions of the corresponding random variables. Finally, for brevity, we henceforth refer to the channel studied here as the orthogonal relay eavesdropper channel.
). We drop subscripts on probability distributions if the arguments are lowercase versions of the corresponding random variables. Finally, for brevity, we henceforth refer to the channel studied here as the orthogonal relay eavesdropper channel.
3. Discrete Memoryless Channel: Outer and Inner Bounds
In this section, we develop outer and inner bounds for the secrecy capacity of the discrete-memoryless orthogonal relay eavesdropper channel. The proof of the outer bounds follows along the same lines as that in [11, Theorem 1] for the full-duplex relay-eavesdropper channel and is specialized for the orthogonal model considered here. The following theorem summarizes the bounds for the three cases in which the eavesdropper can receive in either one or both orthogonal channels.
Theorem 7.
An outer bound on the secrecy capacity of the relay eavesdropper channel with orthogonal components is given by the following.
Case 1.

Case 2.

Case 3.

where  ,
,  ,
,  , and
, and  are auxiliary random variables, and the maximum is over all joint distributions satisfying
are auxiliary random variables, and the maximum is over all joint distributions satisfying  .
.
Proof.
The proof is extended from the outer bound in [11, Theorem 1] to include auxiliary random variables corresponding to each of the transmitted signals and is developed in Appendix A.
Following Proposition 5, a natural question for the relay-eavesdropper channel with orthogonal components is whether the PDF strategy can achieve the secrecy capacity. To this end, we first develop the achievable PDF secrecy rates for the class of full-duplex relay-eavesdropper channels and then specialize the result for the orthogonal model. The following theorem summarizes the inner bounds on the secrecy capacity achieved by PDF for the full-duplex (nonorthogonal) relay-eavesdropper channels.
Theorem 8.
An inner bound on the secrecy capacity of a full-duplex relay eavesdropper channel, achieved using partial decode and forward, is given by

for all joint distributions of the form

Proof.
The proof is developed in Appendix B and uses block Markov superposition encoding at the source such that, in each block, the relay decodes a part of the source message while the eavesdropper has access to both source messages.
The following theorem specializes Theorem 8 for the orthogonal relay-eavesdropper channel.
Theorem 9.
An inner bound on the secrecy capacity of the orthogonal relay eavesdropper channel, achieved using partial decode and forward over all joint distributions of the form  , is given by the following.
, is given by the following.
Case 1.

Case 2.


Case 3.

Proof.
The proof is developed in Appendix C and involves specializing the bounds in Theorem 8 for the orthogonal model. It is further shown that the input distribution can be generalized to all joint probability distributions  .
.
The bounds in (20) can be generalized by randomizing the channel inputs. We now prove that PDF with randomization achieves the secrecy capacity.
Theorem 10.
The secrecy capacity of the relay channel with orthogonal complements is the following.
Case 1.

Case 2.

Case 3.

where  , and
, and  are auxiliary random variables, and the maximum is over all joint distributions satisfying
are auxiliary random variables, and the maximum is over all joint distributions satisfying  . Furthermore, for Case 3,
. Furthermore, for Case 3,

for all joint distributions satisfying  .
.
Proof.
The upper bounds follow from Theorem 7. For the lower bound, we prefix a memoryless channel with inputs 
 and
and  and transition probability
and transition probability  (this prefix can potentially increase the achievable secrecy rates as in [2, 11]). The time-sharing random variable
(this prefix can potentially increase the achievable secrecy rates as in [2, 11]). The time-sharing random variable  ensures that the set of achievable rates is convex.
ensures that the set of achievable rates is convex.
Remark 11.
In contrast to the nonsecrecy case, where the orthogonal channel model simplifies the cut-set bounds to match the inner PDF bounds, for the orthogonal relay-eavesdropper model in which the eavesdropper receives in both channels, that is, when the orthogonal receiver restrictions at the relay and intended destination do not apply to the eavesdropper, in general, the outer bound can be strictly larger than the inner PDF bound.
In the following section, we illustrate these results with three examples.
4. Examples
Example 12.
Consider an orthogonal relay eavesdropper channel with  . The outputs at the relay and destination are given by
. The outputs at the relay and destination are given by

while the output at the eavesdropper is

Since the destination can receive at most 1 bit in every use of the channel, the secrecy capacity of this channel is at most  bit per channel use. We now show that this secrecy capacity can be achieved. In each channel use, let the source send bit
bit per channel use. We now show that this secrecy capacity can be achieved. In each channel use, let the source send bit  such that
such that  ,
,  , and
, and  . Since
. Since  , the receiver obtains
, the receiver obtains  while the eavesdropper receives
while the eavesdropper receives  and
and  irrespective of the value of bit
irrespective of the value of bit  . Hence, a perfect secrecy capacity of
. Hence, a perfect secrecy capacity of  can be achieved.
can be achieved.
The code design in Example 12 did not require randomization. We now present an example where randomization is necessary.
Example 13.
Consider an orthogonal relay eavesdropper channel where all the input and output alphabets are the same and given by  . We write
. We write  ,
,  , and
, and  to denote the vector binary signals at the source and the relay. The outputs of this channel, shown in Figure 2(a), at the relay, destination, and the eavesdropper are given by
to denote the vector binary signals at the source and the relay. The outputs of this channel, shown in Figure 2(a), at the relay, destination, and the eavesdropper are given by

where  denotes the binary XOR operation. The capacity of this channel is at most 2 bits per channel use as the destination, via
denotes the binary XOR operation. The capacity of this channel is at most 2 bits per channel use as the destination, via  , can receive at most
, can receive at most  bits per channel use. We will now show that a secrecy capacity of 2 bits per channel use can be achieved. Consider the following coding scheme. In every channel use, the relay flips an unbiased coin to generate a bit
bits per channel use. We will now show that a secrecy capacity of 2 bits per channel use can be achieved. Consider the following coding scheme. In every channel use, the relay flips an unbiased coin to generate a bit  such that its transmitted signal is
such that its transmitted signal is

In every use of the channel, the source transmits  bits, denoted as
bits, denoted as  and
and  , using
, using

For these transmitted signals, the receiver and eavesdropper receive

Thus, the receiver receives both bits while the eavesdropper is unable to decode any information due to the randomness of  . This is an example where transmitting a random code from the relay is required to achieve the secrecy capacity.
. This is an example where transmitting a random code from the relay is required to achieve the secrecy capacity.
In the above two examples, the source to relay link was completely available to the eavesdropper, and hence the relay could at best be just used to send random bits. In the next example, we show that the secrecy capacity is achieved by the relay transmitting a part of the message as well as a random signal.
Example 14.
Consider an orthogonal relay eavesdropper channel where the input and output signals at the source, relay, and destination are binary two-tuples while  and
and  at the eavesdropper are binary alphabets. We write
at the eavesdropper are binary alphabets. We write  ,
,  , and
, and  to denote the vector binary signals at the source and the relay. The outputs at the relay, destination, and the eavesdropper are also vector binary signals given by
to denote the vector binary signals at the source and the relay. The outputs at the relay, destination, and the eavesdropper are also vector binary signals given by

as shown in Figure 2(b). As in the previous example, the capacity of this channel is also at most 2 bits per channel use. We now show that a secrecy capacity of 2 bits per channel use can be achieved for this example channel. Consider the following coding scheme: in the  th use of the channel, the source encodes 2 bits, denoted as
th use of the channel, the source encodes 2 bits, denoted as  and
and  as
as

The relay receives  in the previous use of the channel. Furthermore, in each channel use, it also generates a uniformly random bit
in the previous use of the channel. Furthermore, in each channel use, it also generates a uniformly random bit  , and transmits
, and transmits

With these transmitted signals, the received signals at the receiver and the eavesdropper are

Thus, over  uses of the channel the destination receives all
uses of the channel the destination receives all  bits transmitted by the source. On the other hand, in every use of the channel, the eavesdropper cannot decode either source bit.
bits transmitted by the source. On the other hand, in every use of the channel, the eavesdropper cannot decode either source bit.
5. Gaussian Model
5.1. Inner and Outer Bounds
We now develop inner and outer bounds for the Gaussian orthogonal relay eavesdropper channel. Determining the optimal input distribution for all the auxiliary random variables in the outer bounds in Theorem 10 is not straightforward. To this end, we develop new outer bounds using a recent result on the secrecy capacity of the class of Gaussian multiple input, multiple output, and multiantenna eavesdropper channels (see [4–6]). The class of MIMOME channels is characterized by a single source with an  vector input
vector input  and
and  and
and  vector outputs
vector outputs  and
and  at the intended destination and eavesdropper, respectively, given by
at the intended destination and eavesdropper, respectively, given by


where in every channel use  ,
,  and
and  are zero-mean Gaussian vectors with identity covariance matrices that are independent across time symbols. The channel input satisfies an average transmit power constraint:
are zero-mean Gaussian vectors with identity covariance matrices that are independent across time symbols. The channel input satisfies an average transmit power constraint:

In applying the multiantenna secrecy capacity results, we develop an outer bound in which the source and relay are modeled jointly as a multiantenna transmitter. However, unlike the average power constraint for the MIMOME channels in (37), our outer bound requires a per antenna power constraint. To this end, we apply the results developed in [5] in which a more general transmitter covariance constraint is considered such that

where  is a positive semidefinite matrix, and
is a positive semidefinite matrix, and  denotes that
denotes that  is a positive semidefinite matrix. The secrecy capacity of this channel is summarized in the following theorem.
is a positive semidefinite matrix. The secrecy capacity of this channel is summarized in the following theorem.
Lemma 15 ([5]).
The secrecy capacity of the MIMOME channel of (36) subject to (38) is given by

Remark 16.
The expression in (39) can also be written as

where he maximum is over all 
We now present an outer bound on the Gaussian orthogonal relay eavesdropper channel using Lemma 15.
Theorem 17.
An outer bound on the secrecy capacity of the Gaussian orthogonal relay eavesdropper channel is given by the following.
Case 1.

Case 2.

Case 3.

where the maximum is over all  where
where  has diagonal entries that satisfy (8).
has diagonal entries that satisfy (8).
Remark 18.
In (41a) and (41c), the  maximizing the outer bound on the secrecy capacity is
maximizing the outer bound on the secrecy capacity is  . On the other hand,
. On the other hand,  can be chosen to be arbitrary for (41b).
can be chosen to be arbitrary for (41b).
Proof.
An outer bound on the secrecy capacity of the relay eavesdropper channel results from assuming that the source and relay can cooperate over a noiseless link without causality constraints. Under this assumption, the problem reduces to that of a MIMOME channel. Thus, applying Lemma 15 and using the form in (40), for  , the secrecy capacity can be upper bounded as
, the secrecy capacity can be upper bounded as



where (44) follows from the orthogonal model in (3). Finally, applying the conditions on the eavesdropper receiver for the three cases simplifies the bounds in (44) to (41a), (41b), and (41c).
The PDF inner bounds developed in Section 3 for the discrete memoryless case can be applied to the Gaussian model with Gaussian inputs at the source and relay. In fact, for all three cases, the inner bounds require taking a minimum of two rates, one achieved jointly by the source and relay at the destination and the other achieved by the source at the relay and destination. Comparing the inner bounds in (19) with the outer bounds in for those channels in which the source and relay are clustered close enough that the bottle-neck link is the combined source-relay link to the destination and the eavesdropper overhears only the channel from the source and the relay to the destination, the secrecy capacity can be achieved. This is summarized in the following theorem.
Theorem 19.
For a class of clustered orthogonal Gaussian relay channels with

the secrecy capacity for Case 2 is achieved by PDF and is given by the following.
Case 2.

where the maximum is over  .
.
For a relay channel without secrecy constraints, the cut-set outer bounds are equivalent to two multiple-input multiple-output (MIMO) bounds, one that results from assuming a noiseless source-relay link and the other that results from assuming a noiseless relay-destination link. Under a secrecy constraint, the outer bound in Theorem 17 is based on the assumption of a noiseless source-relay link. The corresponding bound with a noiseless relay-destination link remains unknown.
We now consider a subclass of Gaussian orthogonal relay eavesdropper channels for which  For this subclass, the source does not send any messages on channel
For this subclass, the source does not send any messages on channel  , that is,
, that is,  . Such a subclass is a subset of a larger subclass of channels with very noisy unreliable links from the source to the relay. We present an upper bound on the secrecy capacity for this subclass and show that the noise-forwarding strategy introduced in [11] achieves this outer bound. Central to our proof is an additional constraint introduced in developing the outer bounds on the eavesdropper that does not decode the relay transmissions. Clearly, limiting the eavesdropper capabilities can only improve the secrecy rates, and thus, an outer bound for this channel with a constrained eavesdropper is also an outer bound for the original channel (with
. Such a subclass is a subset of a larger subclass of channels with very noisy unreliable links from the source to the relay. We present an upper bound on the secrecy capacity for this subclass and show that the noise-forwarding strategy introduced in [11] achieves this outer bound. Central to our proof is an additional constraint introduced in developing the outer bounds on the eavesdropper that does not decode the relay transmissions. Clearly, limiting the eavesdropper capabilities can only improve the secrecy rates, and thus, an outer bound for this channel with a constrained eavesdropper is also an outer bound for the original channel (with  in both cases) with an unconstrained eavesdropper. We show that the outer bound for the constrained channel can be achieved by the strategy of noise-forwarding developed for the unconstrained channel.
in both cases) with an unconstrained eavesdropper. We show that the outer bound for the constrained channel can be achieved by the strategy of noise-forwarding developed for the unconstrained channel.
Theorem 20.
The secrecy capacity of a subclass of Gaussian orthogonal relay eavesdropper channels with  for Cases 2 and 3 is given by
for Cases 2 and 3 is given by

Proof.
Outer Bound. Since  , it is sufficient to set
, it is sufficient to set  . This follows from the fact that due to a lack of a communication link between the source and the relay, that is,
. This follows from the fact that due to a lack of a communication link between the source and the relay, that is,  , the relay is oblivious to the source transmissions. Since the relay and the source do not share common randomness, one can set
, the relay is oblivious to the source transmissions. Since the relay and the source do not share common randomness, one can set  . Finally, since
. Finally, since  depends on
depends on  only via
only via  and
and  ,
,  is independent of
is independent of  .
.
We now provide two outer bounds for fixed  and
and  . Thus, the minimum of the two is also an outer bound. Maximizing over
. Thus, the minimum of the two is also an outer bound. Maximizing over  and
and  will then yield the outer bound as in the statement of Theorem 20.
will then yield the outer bound as in the statement of Theorem 20.
An outer bound on the secrecy capacity is obtained by applying Theorem 17 for Cases 2 and 3 as

where (48) holds because  and
and  are independent, and the Gaussian signaling is optimal, which follows from Theorem 17.
are independent, and the Gaussian signaling is optimal, which follows from Theorem 17.
We develop a second outer bound under the assumption that the relay and the destination have a noiseless channel such that they act like a two-antenna receiver. One can alternately view this as an improved channel that results from having a genie that shares perfectly the transmitted and received signals at the relay with the destination. Since  is independent of
is independent of  , the destination can perfectly cancel
, the destination can perfectly cancel  from its received signal, and thus, from (7), the effective received signal at the destination can be written as
from its received signal, and thus, from (7), the effective received signal at the destination can be written as

On the other hand for the constrained eavesdropper, since the relay's signal  acts as interference and is independent of
acts as interference and is independent of  , the information received at the eavesdropper is minimized when
, the information received at the eavesdropper is minimized when  is the worst case noise, that is, when it is Gaussian distributed [18, Theorem II.1]. The equivalent signal received at the eavesdropper is then
is the worst case noise, that is, when it is Gaussian distributed [18, Theorem II.1]. The equivalent signal received at the eavesdropper is then

where  is Gaussian with zero mean and unit variance. Thus, the constrained eavesdropper channel simplifies to a MIMOME channel with a single-antenna source transmitting
is Gaussian with zero mean and unit variance. Thus, the constrained eavesdropper channel simplifies to a MIMOME channel with a single-antenna source transmitting  and single-antenna receiver and eavesdropper receiving
and single-antenna receiver and eavesdropper receiving  and
and  , respectively. For this channel, from Lemma 15, the secrecy capacity of this constrained eavesdropper channel is upper bounded as
, respectively. For this channel, from Lemma 15, the secrecy capacity of this constrained eavesdropper channel is upper bounded as

Finally, since (51) is an upper bound for the channel with an eavesdropper constrained to ignore  , it is also an upper bound for the channel in which the eavesdropper is not constrained.
, it is also an upper bound for the channel in which the eavesdropper is not constrained.
Inner Bound. The lower bound follows from the noise forwarding strategy introduced in [11, Theorem 3]. In this strategy, the relay sends codewords independent of the source message, which helps in confusing the eavesdropper. The noise forwarding strategy transforms the relay-eavesdropper channel into a compound multiple access channel, where the source/relay to the receiver is the first multiple access channel, and the source/relay to the eavesdropper is the second one.
5.2. Illustration of Results
We illustrate our results for the Gaussian model for a class of linear networks in which the source is placed at the origin, and the destination is unit distance from the source at  . The eavesdropper is at
. The eavesdropper is at  . The channel gain
. The channel gain  , between transmitter
, between transmitter  and receiver
and receiver  , for each
, for each  and
and  , is modeled as a distance dependent path-loss gain given by
, is modeled as a distance dependent path-loss gain given by

where  is the path-loss exponent. The maximum achievable PDF secrecy rate is plotted as a function of the relay position along the line connecting the source and the eavesdropper as shown in Figure 3. Furthermore, as a baseline assuming that the relay does not transmit, that is,
is the path-loss exponent. The maximum achievable PDF secrecy rate is plotted as a function of the relay position along the line connecting the source and the eavesdropper as shown in Figure 3. Furthermore, as a baseline assuming that the relay does not transmit, that is,  , the secrecy capacity of the resulting direct link and the wire-tap channel for Cases 2 and 3, respectively, are included in all three plots in Figure 3. The rates are plotted in separate subfigures for the three cases in which the eavesdropper receives signals in only one or both channels. In all cases, the path loss exponent
, the secrecy capacity of the resulting direct link and the wire-tap channel for Cases 2 and 3, respectively, are included in all three plots in Figure 3. The rates are plotted in separate subfigures for the three cases in which the eavesdropper receives signals in only one or both channels. In all cases, the path loss exponent  is set to
is set to  , and the average power constraint on
, and the average power constraint on 
 , and
, and  is set to unity. In addition to PDF, the secrecy rate achieved by noise forwarding (NF) is also plotted.
is set to unity. In addition to PDF, the secrecy rate achieved by noise forwarding (NF) is also plotted.
In Figure 3, for all three cases, the PDF secrecy rates are obtained by choosing the input signal  to be Gaussian distributed and numerically optimizing the rates over the covariance matrix
to be Gaussian distributed and numerically optimizing the rates over the covariance matrix  (more precisely the three variances of
(more precisely the three variances of  ,
,  ,
,  and the pairwise correlation among these three variables). We observe that the numerical results match the theoretical capacity result for Case 2 that PDF is optimal when the relay is close to the source. Further, the upper bounds for Cases 2 and 3 are the same as seen also in (41b)-(41c). On the other hand, when the relay is farther away than the eavesdropper and destination are from the source, there are no gains achieved by using the relay relative to the nonrelay wiretap secrecy capacity. Finally, for Cases 2 and 3, NF performs better than PDF when the relay is closer to the destination.
and the pairwise correlation among these three variables). We observe that the numerical results match the theoretical capacity result for Case 2 that PDF is optimal when the relay is close to the source. Further, the upper bounds for Cases 2 and 3 are the same as seen also in (41b)-(41c). On the other hand, when the relay is farther away than the eavesdropper and destination are from the source, there are no gains achieved by using the relay relative to the nonrelay wiretap secrecy capacity. Finally, for Cases 2 and 3, NF performs better than PDF when the relay is closer to the destination.
6. Conclusions
We have developed bounds on the secrecy capacity of relay eavesdropper channels with orthogonal components in the presence of an additional passive eavesdropper for both the discrete memoryless and Gaussian channel models. Our results depend on the capability of the eavesdropper to overhear either or both of the two orthogonal channels that the source uses for its transmissions. For the discrete memoryless model, when the eavesdropper is restricted to receiving in only one of the two channels, we have shown that the secrecy capacity is achieved by a partial decode-and-forward strategy.
For the Gaussian model, we have developed a new outer bound using recent results on the secrecy capacity of Gaussian MIMOME channels. When the eavesdropper is restricted to overhearing on the channel from the source and the relay to the destination, our bound is tight for a subclass of channels where the source and the relay are clustered such that the combined link from the source and the relay to the destination is the bottleneck. Furthermore, for a subclass where the source-relay link is not used, we have developed a new MIMOME-based outer bound that matches the secrecy rate achieved by the noise forwarding strategy.
A natural extension to this model is to study the secrecy capacity of orthogonal relay channels with multiple relays and multiple eavesdroppers (see, e.g., [19]). Also, the problem of developing an additional outer bound that considers a noiseless relay destination link remains open for the channel studied here.
Appendices
A. Proof of Theorem 7
In this section, we will prove the upper bounds on the secrecy capacity for all the three cases. Following a proof similar to that in [11, Theorem 1], we bound the equivocation as

Now, let  be a random variable uniformly distributed over
be a random variable uniformly distributed over  and set
and set  ,
,  ,
,  ,
,  ,
,  ,
,  , and
, and  . We specialize the bounds in (A.1) separately for each case.
. We specialize the bounds in (A.1) separately for each case.
Case 1.
From (A.1), we have

Furthermore,

This proves the upper bound for Case 1.
Case 2.
From (A.1), we have

Furthermore,

This proves the upper bound for Case 2.
Case 3.
From (A.1), we have

Furthermore,

This proves the upper bound for Case 3. For perfect secrecy, setting  yields the upper bound on the secrecy capacity.
yields the upper bound on the secrecy capacity.
B. Proof of Theorem 8: PDF for Relay Eavesdropper Channel
Random Coding.
(1)Generate  independent and identically distributed (i.i.d.)
independent and identically distributed (i.i.d.)  's, each with probability
's, each with probability  . Label them
. Label them  ,
,  .
.
(2)For each  , generate
, generate  i.i.d.
i.i.d.  's, each with probability
's, each with probability  . Label these
. Label these  ,
,  .
.
(3)For every  , generate
, generate  i.i.d.
i.i.d.  's, each with probability
's, each with probability  . Label these
. Label these  ,
,  .
.
Random Partition
Randomly partition the set  into
into  cells
cells  .
.
Encoding
Let  be the message to be sent in block
be the message to be sent in block  where the total number of messages is
where the total number of messages is  . Further, let
. Further, let  where
where  . We can further partition
. We can further partition  into two parts
into two parts  of rates
of rates  and
and  , respectively. Assume that
, respectively. Assume that  are jointly
are jointly  -typical and
-typical and  . Then the codeword
. Then the codeword  will be transmitted in block
will be transmitted in block  .
.
Decoding
At the end of block  , we have the following.
, we have the following.
(1)The receiver estimates  by looking at jointly
by looking at jointly  -typical
-typical  with
with  . For sufficiently large
. For sufficiently large  , this decoding step can be done with arbitrarily small probability of error. Let the estimate of
, this decoding step can be done with arbitrarily small probability of error. Let the estimate of  be
be  .
.
(2)The receiver calculates a set  of
of  such that
such that  if
if  are jointly
are jointly  -typical. The receiver then declares that
-typical. The receiver then declares that  was sent in block
was sent in block  if
if  . The probability that
. The probability that  with arbitrarily high probability provided that
with arbitrarily high probability provided that  is sufficiently large and
is sufficiently large and  .
.
(3)The receiver declares that  was sent in block
was sent in block  if
if  are jointly
are jointly  -typical.
-typical.  with high probability if
with high probability if  and
and  is sufficiently large.
is sufficiently large.
(4)The relay upon receiving  declares that
declares that  was received if
was received if  are jointly
are jointly  -typical.
-typical.  with high probability if
with high probability if  and
and  is sufficiently large. Thus, the relay knows that
is sufficiently large. Thus, the relay knows that  .
.
Thus, we obtain

Therefore, the rate of transmission from  to
to  is bounded by
is bounded by

Equivocation Computation
From [11, Theorem 2, equation (41)], we have

Consider  . Since we know
. Since we know  , the only uncertainty is the knowledge of
, the only uncertainty is the knowledge of  which can be decoded from
which can be decoded from  with arbitrarily small probability of error since
with arbitrarily small probability of error since  . Hence,
. Hence,

thus giving  , and hence we get perfect secrecy.
, and hence we get perfect secrecy.
Thus, the secrecy rate is given by

C. Proof of Theorem 9: PDF for Relay Eavesdropper Channel with Orthogonal Components
From Theorem 8, a secrecy rate of

can be achieved by partial decode and forward. Let  and
and  such that the input distribution is of the form
such that the input distribution is of the form  . The achievable secrecy rate is then given by
. The achievable secrecy rate is then given by



The equality in (C.16) follows from the fact that  is a Markov chain. We further specialize the bounds for the three cases based on the receiving capability of the eavesdropper.
is a Markov chain. We further specialize the bounds for the three cases based on the receiving capability of the eavesdropper.
Case 1.

The maximization of the expression to the right of the equality in (C.17) over  is equivalent to maximizing over the more general distribution
is equivalent to maximizing over the more general distribution  , and henceforth, without loss of generality we consider the general probability distribution
, and henceforth, without loss of generality we consider the general probability distribution  .
.
We now prove that  which completes the proof of this part of the theorem. We have
which completes the proof of this part of the theorem. We have

Case 2.

Note that maximization of above term over  is equivalent to maximizing over general
is equivalent to maximizing over general  , and henceforth, without loss of generality we consider the general probability distribution
, and henceforth, without loss of generality we consider the general probability distribution  .
.
We now prove that  which completes the proof of this part of the theorem. We have
which completes the proof of this part of the theorem. We have

where the last step follows as was shown earlier in (C.18).
Case 3.

Note that maximization of above term over  is equivalent to maximizing over general
is equivalent to maximizing over general  .
.
We now prove that  which completes the proof of this part of the theorem. We have
which completes the proof of this part of the theorem. We have

where the last step follows as was shown earlier in (C.18).
References
Wyner A: The wire-tap channel. Bell System Technical Journal 1975, 54(8):1355-1387.
Csiszár I, Körner J: Broadcast channels with confidential messages. IEEE Transactions on Information Theory 1978, 24(3):339-348. 10.1109/TIT.1978.1055892
Tekin E, Yener A: The general Gaussian multiple-access and two-way wiretap channels: achievable rates and cooperative jamming. IEEE Transactions on Information Theory 2008, 54(6):2735-2751.
Khisti A, Wornell GW: The MIMOME channel. Proceedings of the 45th Annual Allerton Conference on Communication, Control, and Computing, September 2007, Monticello, Ill, USA
Liu T, Shamai S: A note on the secrecy capacity of the multi-antenna wiretap channel. IEEE Transactions on Information Theory 2009, 55(6):2547-2553.
Oggier F, Hassibi B: The secrecy capacity of the MIMO wiretap channel. Proceedings of the IEEE International Symposium on Information Theory, July 2008, Toronto, Canada 524-528.
Bloch M, Thangaraj A: Confidential messages to a cooperative relay. Proceedings of the IEEE Information Theory Workshop (ITW '08), May 2008, Porto, Portugal 154-158.
Liang Y, Poor HV: Multiple-access channels with confidential messages. IEEE Transactions on Information Theory 2008, 54(3):976-1002.
Liang Y, Poor HV, Shamai S: Secure communication over fading channels. IEEE Transactions on Information Theory 2008, 54(6):2470-2492.
Liang Y, Somekh-Baruch A, Poor HV, Shamai S, Verdú S: Capacity of cognitive interference channels with and without secrecy. IEEE Transactions on Information Theory 2009, 55(2):604-619.
Lai L, El Gamal H: The relay-eavesdropper channel: cooperation for secrecy. IEEE Transactions on Information Theory 2008, 54(9):4005-4019.
Yuksel M, Erkip E: The relay channel with a wire-tapper. Proceedings of the 41st Annual Conference on Information Sciences and Systems (CISS '07), March 2007 13-18.
Oohama Y: Capacity theorems for relay channels with confidential messages. Proceedings of the IEEE International Symposium on Information Theory, June 2007, Nice, France
El Gamal A, Zahedi S: Capacity of a class of relay channels with orthogonal components. IEEE Transactions on Information Theory 2005, 51(5):1815-1817. 10.1109/TIT.2005.846438
He X, Yener A: On the equivocation region of relay channels with orthogonal components. Proceedings of the 41st Annual Asilomar Conference on Signals, Systems and Computers, November 2007, Pacific Grove, Calif, USA 883-887.
Kramer G: Models and theory for relay channels with receive constraints. Proceedings of the 42nd Annual Allerton Conference on Communication, Control, and Computing, September 2004, Monticello, Ill, USA
Cover TM, Thomas JA: Elements of Information Theory. John Wiley & Sons, New York, NY, USA; 1991.
Diggavi SN, Cover TM: The worst additive noise under a covariance constraint. IEEE Transactions on Information Theory 2001, 47(7):3072-3081. 10.1109/18.959289
Aggarwal V, Sankar L, Calderbank AR, Poor HV: Information secrecy from multiple eavesdroppers in orthogonal relay channels. Proceedings of the IEEE International Symposium on Information Theory, June-July 2009, Seoul, Korea
Acknowledgments
The authors wish to thank Elza Erkip of Polytechnic Institute of NYU and Lifeng Lai and Ruoheng Liu of Princeton University for useful discussions related to this paper. The work of V. Aggarwal and A. R. Calderbank was supported in part by NSF under Grant 0701226, by ONR under Grant N00173-06-1-G006, and by AFOSR under Grant FA9550-05-1-0443. The work of L. Sankar and H. V. Poor was supported in part by the National Science Foundation under Grant CNS-06-25637. The material in this paper was presented in part at the Information Theory and Applications Workshop, San Diego, CA, 2009 and at the IEEE International Symposium on Information Theory, Seoul, Korea, 2009.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Aggarwal, V., Sankar, L., Calderbank, A.R. et al. Secrecy Capacity of a Class of Orthogonal Relay Eavesdropper Channels. J Wireless Com Network 2009, 494696 (2009). https://doi.org/10.1155/2009/494696
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/494696
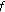 at the source such that
at the source such that 
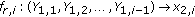 at every time instant
at every time instant  , and
, and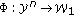 .
.


 , destination is at
, destination is at  , and eavesdropper is at
, and eavesdropper is at  . A distance fading model with
. A distance fading model with  is taken, and power constraints for
is taken, and power constraints for  ,
,  , and
, and  are all unity.Case 1Case 2Case 3
are all unity.Case 1Case 2Case 3