- Research Article
- Open access
- Published:
Secret Sharing over Fast-Fading MIMO Wiretap Channels
EURASIP Journal on Wireless Communications and Networking volume 2009, Article number: 506973 (2009)
Abstract
Secret sharing over the fast-fading MIMO wiretap channel is considered. A source and a destination try to share secret information over a fast-fading MIMO channel in the presence of an eavesdropper who also makes channel observations that are different from but correlated to those made by the destination. An interactive, authenticated public channel with unlimited capacity is available to the source and destination for the secret sharing process. This situation is a special case of the "channel model with wiretapper" considered by Ahlswede and Csiszár. An extension of their result to continuous channel alphabets is employed to evaluate the key capacity of the fast-fading MIMO wiretap channel. The effects of spatial dimensionality provided by the use of multiple antennas at the source, destination, and eavesdropper are then investigated.
1. Introduction
The wiretap channel considered in the seminal paper [1] is the first example that demonstrates the possibility of secure communications at the physical layer. It is shown in [1] that a source can transmit a message at a positive (secrecy) rate to a destination in such a way that an eavesdropper only gathers information at a negligible rate, when the source-to-eavesdropper channel is a degraded version of the source-to-destination channel, the source-to-eavesdropper and source-to-destination channels will hereafter be referred to as eavesdropper and destination channels, respectively. A similar result for the Gaussian wiretap channel is provided in [2]. The work in [3] further removes the degraded wiretap channel restriction showing that positive secrecy capacity is possible if the destination channel is "more capable" ("less noisy" for a full extension of the rate region in [1]) than the eavesdropper's channel. Recently, there has been a flurry of interest in extending these early results to more sophisticated channel models, including fading wiretap channels, multiinput multi-output (MIMO) wiretap channels, multiple-access wiretap channels, broadcast wiretap channels, and relay wiretap channels. We do not attempt to provide a comprehensive summary of all recent developments but highlight only those results that are most relevant to the present work. We refer interested readers to the introduction and reference list of [4] for a concise and extensive overview of recent works.
When the destination and eavesdropper channels experience independent fading, the strict requirement of having a more capable destination channel for positive secrecy capacity can be loosened. This is due to the simple observation that the destination channel may be more capable than the eavesdropper's channel under some fading realizations, even if the destination is not more capable than the eavesdropper on average. Hence, if the channel state information (CSI) of both the destination and eavesdropper channels is available at the source, it is shown in [4, 5] that a positive secrecy capacity can be achieved by means of appropriate power control at the source. The key idea is to opportunistically transmit only during those fading realizations for which the destination channel is more capable [6]. For block-ergodic fading, it is also shown in [5] (see also [7]) that a positive secrecy capacity can be achieved with a variable-rate transmission scheme without any eavesdropper CSI available at the source.
When the source, destination, and eavesdropper have multiple antennas, the resulting channel is known as a MIMO wiretap channel (see [8–12]), which may also have positive secrecy capacity. Since the MIMO wiretap channel is not degraded, the characterization of its secrecy capacity is not straightforward. For instance, the secrecy capacity of the MIMO wiretap channel is characterized in [9] as the saddle point of a minimax problem, while an alternative characterization based on a recent result for multiantenna broadcast channels is provided in [11]. Interestingly all characterizations point to the fact that the capacity achieving scheme is one that transmits only in the directions in which the destination channel is more capable than the eavesdropper's channel. Obviously, this is only possible when the destination and eavesdropper CSI is available at the source. It is shown in [9] that if the individual channels from antennas to antennas suffer from independent Rayleigh fading, and the respective ratios of the numbers of source and destination antennas to that of eavesdropper antennas are larger than certain fixed values, then the secrecy capacity is positive with probability one when the numbers of source, destination, and eavesdropper antennas become very large.
As discussed above, the availability of destination (and eavesdropper) CSI at the source is an implicit requirement for positive secrecy capacity in the fading and MIMO wiretap channels. Thus, an authenticated feedback channel is needed to send the CSI from the destination back to the source. In [5, 7], this feedback channel is assumed to be public, and hence the destination CSI is also available to the eavesdropper. In addition, it is assumed that the eavesdropper knows its own CSI. With the availability of a feedback channel, if the objective of having the source send secret information to the destination is relaxed to distilling a secret key shared between the source and destination, it is shown in [13] that a positive key rate is achievable when the destination and eavesdropper channels are two conditionally independent (given the source input symbols) memoryless binary channels, even if the destination channel is not more capable than the eavesdropper's channel. This notion of secret sharing is formalized in [14] based on the concept of common randomness between the source and destination. Assuming the availability of an interactive, authenticated public channel with unlimited capacity between the source and destination [14] suggests two different system models, called the "source model with wiretapper" (SW) and the "channel model with wiretapper" (CW). The CW model is similar to the (discrete memoryless) wiretap channel model that we have discussed before. The SW model differs in that the random symbols observed at the source, destination, and eavesdropper are realizations of a discrete memoryless source with multiple components. Both SW and CW models have been extended to the case of secret sharing among multiple terminals, with the possibility of some terminals acting as helpers [15–17]. Key capacities have been obtained for the two special cases in which the eavesdropper's channel is a degraded version of the destination channel and in which the destination and eavesdropper channels are conditionally independent [13, 14]. Similar results have been derived for multiterminal secret sharing [16, 17], with the two special cases above subsumed by the more general condition that the terminal symbols form a Markov chain on a tree. Authentication of the public channel can be achieved by the use of an initial short key and then a small portion of the subsequent shared secret message [18]. A detailed study of secret sharing over an unauthenticated public channel is given in [19–21].
Other approaches to employ feedback have also been recently considered [22–24]. In particular, it is shown in [22] that positive secrecy capacity can be achieved for the modulo-additive discrete memoryless wiretap channel and the modulo- channel if the destination is allowed to send signals back to the source over the same wiretap channel and both terminals can operate in full-duplex manner. In fact, for the former channel, the secrecy capacity is the same as the capacity of such a channel in the absence of the eavesdropper.
channel if the destination is allowed to send signals back to the source over the same wiretap channel and both terminals can operate in full-duplex manner. In fact, for the former channel, the secrecy capacity is the same as the capacity of such a channel in the absence of the eavesdropper.
In this paper, we consider secret sharing over a fast-fading MIMO wiretap channel. Thus, we are interested in the CW model of [14] with memoryless conditionally independent destination and eavesdropper channels and continuous channel alphabets. We provide an extension of the key capacity result in [14] for this case to include continuous channel alphabets (Theorem 1). Using this result, we obtain the key capacity of the fast-fading MIMO wiretap channel (Section 3). Our result indicates that the key capacity is always positive, no matter how large the channel gain of the eavesdropper's channel is; in addition this holds even if the destination and eavesdropper CSI is available only at the destination and eavesdropper, respectively. Of course, the availability of the public channel implies that the destination CSI could be fed back to the source. However, due to the restrictions imposed on the secret-sharing strategies (see Section 2), only causal feedback is allowed, and thus any destination CSI available at source is "outdated." This does not turn out to be a problem since, unlike the approaches mentioned above, the source does not use the CSI to avoid sending secret information when the destination is not more capable than the eavesdropper's channel. As a matter of fact, the fading process of the destination channel provides a significant part of the common randomness from which the source and the destination distill a secret key. This fact is readily obtained from the alternative achievability proof given in Section 4. We note that [25, 26] consider the problem key generation from common randomness over wiretap channels and exploit a Wyner-Ziv coding scheme to limit the amount of information conveyed from the source to the destination via the wiretap channel. Unlike these previous works, we only employ Wyner-Ziv coding to quantize the destination channel outputs. Our code construction still relies on a public channel with unlimited capacity to achieve the key capacity.
Finally, we also investigate the limiting value of the key capacity under three asymptotic scenarios. In the first scenario, the transmission power of the source becomes asymptotically high (Corollary 1). In the second scenario, the destination and eavesdropper have a large number of antennas (Corollary 2). In the third scenario, the gain advantage of the eavesdropper's channel becomes asymptotically large (Corollary 3). These three scenarios reveal two different effects of spatial dimensionality upon key capacity. In the first scenario, we show that the key capacity levels off as the power increases if the eavesdropper has no fewer antennas than the source. On the other hand, when the source has more antennas, the key capacity can increase without bound with the source power. In the second scenario, we show that the spatial dimensionality advantage that the eavesdropper has over the destination has exactly the same effect as the channel gain advantage of the eavesdropper. In the third scenario, we show that the limiting key capacity is positive only if the eavesdropper has fewer antennas than the source. The results in these scenarios confirm that spatial dimensionality can be used to combat the eavesdropper's gain advantage, which was already observed for the MIMO wiretap channel. Perhaps more surprisingly, this is achieved with neither the source nor destination needing any eavesdropper CSI.
2. Secret Sharing and Key Capacity
We consider the CW model of [14], and we recall its characteristics for completeness. We consider three terminals, namely, a source, a destination, and an eavesdropper. The source sends symbols from an alphabet  . The destination and eavesdropper observe symbols belonging to alphabets
. The destination and eavesdropper observe symbols belonging to alphabets  and
and  , respectively. Unlike in [14],
, respectively. Unlike in [14],  ,
,  , and
, and  need not to be discrete. In fact, in Section 3 we will assume that they are multi-dimensional vector spaces over the complex field. The channel from the source to the destination and eavesdropper is assumed memoryless. A generic symbol sent by the source is denoted by
need not to be discrete. In fact, in Section 3 we will assume that they are multi-dimensional vector spaces over the complex field. The channel from the source to the destination and eavesdropper is assumed memoryless. A generic symbol sent by the source is denoted by  and the corresponding symbols observed by the destination and eavesdropper are denoted by
and the corresponding symbols observed by the destination and eavesdropper are denoted by  and
and  , respectively. For notational convenience (and without loss of generality), we assume that
, respectively. For notational convenience (and without loss of generality), we assume that  are jointly continuous, and the channel is specified by the conditional probability density function (pdf)
are jointly continuous, and the channel is specified by the conditional probability density function (pdf)  . In addition, we restrict ourselves to cases in which
. In addition, we restrict ourselves to cases in which  and
and  are conditionally independent given
are conditionally independent given  , that is,
, that is,  , which is a reasonable model for symbols broadcast in a wireless medium. Hereafter, we drop the subscripts in pdfs whenever the concerned symbols are well specified by the arguments of the pdfs. We assume that an interactive, authenticated public channel with unlimited capacity is also available for communication between the source and destination. Here, interactive means that the channel is two-way and can be used multiple times, unlimited capacity means that it is noiseless and has infinite capacity, and public and authenticated mean that the eavesdropper can perfectly observe all communications over this channel but cannot tamper with the messages transmitted.
, which is a reasonable model for symbols broadcast in a wireless medium. Hereafter, we drop the subscripts in pdfs whenever the concerned symbols are well specified by the arguments of the pdfs. We assume that an interactive, authenticated public channel with unlimited capacity is also available for communication between the source and destination. Here, interactive means that the channel is two-way and can be used multiple times, unlimited capacity means that it is noiseless and has infinite capacity, and public and authenticated mean that the eavesdropper can perfectly observe all communications over this channel but cannot tamper with the messages transmitted.
We consider the class of permissible secret-sharing strategies suggested in [14]. Consider  time instants labeled by
time instants labeled by  , respectively. The
, respectively. The  channel is used
channel is used  times during these
times during these  time instants at
time instants at  . Set
. Set  . The public channel is used for the other (
. The public channel is used for the other ( ) time instants. Before the secret-sharing process starts, the source and destination generate, respectively, independent random variable
) time instants. Before the secret-sharing process starts, the source and destination generate, respectively, independent random variable  and
and  . To simplify the notation, let
. To simplify the notation, let  represent a sequence of messages/symbols
represent a sequence of messages/symbols  . Then a permissible strategy proceeds as follows.
. Then a permissible strategy proceeds as follows.
-
(i)
At time instant
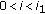 , the source sends message
, the source sends message  to the destination, and the destination sends message
to the destination, and the destination sends message 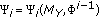 to the source. Both transmissions are carried over the public channel.
to the source. Both transmissions are carried over the public channel. -
(ii)
At time instant
 for
for  , the source sends the symbol
, the source sends the symbol 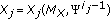 to the
to the  channel. The destination and eavesdropper observe the corresponding symbols
channel. The destination and eavesdropper observe the corresponding symbols 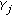 and
and 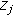 . There is no message exchange via the public channel, that is,
. There is no message exchange via the public channel, that is,  and
and  are both null.
are both null. -
(iii)
At time instant
 for
for  , the source sends message
, the source sends message  to the destination, and the destination sends message
to the destination, and the destination sends message 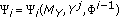 to the source. Both transmissions are carried over the public channel.
to the source. Both transmissions are carried over the public channel.
At the end of the  time instants, the source generates its secret key
time instants, the source generates its secret key  , and the destination generates its secret key
, and the destination generates its secret key  , where
, where  and
and  takes values from the same finite set
takes values from the same finite set  .
.
According to [14],  is an achievable key rate through the channel
is an achievable key rate through the channel  if for every
if for every  , there exists a permissible secret-sharing strategy of the form described above such that
, there exists a permissible secret-sharing strategy of the form described above such that
-
(1)
 ,
, -
(2)
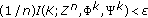 ,
, -
(3)
 ,
, -
(4)
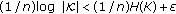 ,
,
for sufficiently large  . The key capacity of the channel
. The key capacity of the channel  is the largest achievable key rate through the channel. We are interested in finding the key capacity. For the case of continuous channel alphabets considered here, we also add the following power constraint to the symbol sequence
is the largest achievable key rate through the channel. We are interested in finding the key capacity. For the case of continuous channel alphabets considered here, we also add the following power constraint to the symbol sequence  sent out by the source:
sent out by the source:

with probability one (w.p.1) for sufficiently large  .
.
Theorem 1.
The key capacity of a CW model  with conditional pdf
with conditional pdf  is given by
is given by  .
.
Proof.
The case with discrete channel alphabets is established in [14, Corollary 2 of Theorem 2], whose achievability proof (also the ones in [16, 17]) does not readily extend to continuous channel alphabets. Nevertheless the same single backward message strategy suggested in [14] is still applicable for continuous alphabets. That strategy uses  time instants with
time instants with  for
for  . That is, the source first sends
. That is, the source first sends  symbols through the
symbols through the  channel; after receiving these
channel; after receiving these  symbols, the destination feeds back a single message at the last time instant to the source over the public channel. A carefully structured Wyner-Ziv code can be employed to support this secret-sharing strategy. The detailed arguments are provided in the alternative achievability proof in Section 4.
symbols, the destination feeds back a single message at the last time instant to the source over the public channel. A carefully structured Wyner-Ziv code can be employed to support this secret-sharing strategy. The detailed arguments are provided in the alternative achievability proof in Section 4.
Here we outline an achievability argument based on the consideration of a conceptual wiretap channel from the destination back to the source and eavesdropper suggested in [13, Theorem 3]. First, assume the source sends a sequence of i.i.d. symbols  , each distributed according to
, each distributed according to  , over the wiretap channel. Suppose that
, over the wiretap channel. Suppose that  . Because of the law of large numbers, we can assume that
. Because of the law of large numbers, we can assume that  satisfies the power constraint (1) without loss of generality. Let
satisfies the power constraint (1) without loss of generality. Let  and
and  be the observations of the the destinations and eavesdropper, respectively. To transmit a sequence
be the observations of the the destinations and eavesdropper, respectively. To transmit a sequence  of symbols independent of
of symbols independent of  , the destination sends
, the destination sends  back to the source via the public channel. This creates a conceptual memoryless wiretap channel from the destination with input symbol
back to the source via the public channel. This creates a conceptual memoryless wiretap channel from the destination with input symbol  to the source in the presence of the eavesdropper, where the source observes
to the source in the presence of the eavesdropper, where the source observes  while the eavesdropper observes
while the eavesdropper observes  .
.
Employing the continuous alphabet extension of the well known result in [3], the secrecy capacity of the conceptual wiretap channel (and hence the key capacity of the original channel) is lower bounded by

Note that the input symbol  has no power constraint since the public channel has infinite capacity. But
has no power constraint since the public channel has infinite capacity. But

where the third equality results from  due to the independence of
due to the independence of  and
and  , the first inequality follows from the fact
, the first inequality follows from the fact

which is again due to independence between  and
and  , and the inequality on the last line follows from
, and the inequality on the last line follows from  .
.
Without loss of generality and for notational simplicity, assume that  and
and  are both one-dimensional real random variables. Now, choose
are both one-dimensional real random variables. Now, choose  to be Gaussian distributed with mean
to be Gaussian distributed with mean  and variance
and variance  . Then
. Then

where the first inequality follows from [27, Theorem 8.6.5], and the last equality is due to the independence between  and
and  . Combining (3) and (5), for every
. Combining (3) and (5), for every  , we can choose
, we can choose  large enough such that
large enough such that

Since  is arbitrary, the key capacity is lower bounded by
is arbitrary, the key capacity is lower bounded by  .
.
The converse proof in [14] is directly applicable to continuous channel alphabets, provided that the average power constraint (1) can be incorporated into the arguments in [14, pp. 1129-1130]. This latter requirement is simplified by the additive and symmetric nature of the average power constraint [28, Section 3.6]. To avoid too much repetition, we outline below only the steps of the proof that are not directly available in [14, pp. 1129-1130].
For every permissible strategy with achievable key rate  , we have
, we have

where the second line follows from Fano's inequality, the third line results from conditions (1) and (7) in the definition of achievable key rate, and the last line is due to condition (5). Thus it suffices to upper bound  . From condition (3) in the definition of achievable key rate and the chain rule, we have
. From condition (3) in the definition of achievable key rate and the chain rule, we have

where the second inequality is due to the fact that  and
and  . By repeated uses of the chain rule, the construction of permissible strategies, and the memoryless nature of the
. By repeated uses of the chain rule, the construction of permissible strategies, and the memoryless nature of the  channel, it is shown in [14, pp. 1129-1130] that
channel, it is shown in [14, pp. 1129-1130] that

Now let  be a uniform random variable that takes value from
be a uniform random variable that takes value from  and is independent of all other random quantities. Define
and is independent of all other random quantities. Define  if
if  . Then it is obvious that
. Then it is obvious that  , and (9) can be rewritten as
, and (9) can be rewritten as

where the second inequality is due to the fact that  forms a Markov chain. On the other hand, the power constraint (1) implies that
forms a Markov chain. On the other hand, the power constraint (1) implies that

Combining (7), (8), and (10), we obtain

Since  can be arbitrarily small when
can be arbitrarily small when  is sufficiently large, (12), together with (11), gives
is sufficiently large, (12), together with (11), gives

where the last line is due to the fact that  .
.
3. Key Capacity of Fast-Fading MIMO Wiretap Channel
Consider that the source, destination, and eavesdropper have  ,
,  , and
, and  antennas, respectively. The antennas in each node are separated by at least a few wavelengths, and hence the fading processes of the channels across the transmit and receive antennas are independent. Using the complex baseband representation of the bandpass channel model:
antennas, respectively. The antennas in each node are separated by at least a few wavelengths, and hence the fading processes of the channels across the transmit and receive antennas are independent. Using the complex baseband representation of the bandpass channel model:

where
-
(i)
 is the
is the  complex-valued transmit symbol vector by the source,
complex-valued transmit symbol vector by the source, -
(ii)
 is the
is the  complex-valued receive symbol vector at the destination,
complex-valued receive symbol vector at the destination, -
(iii)
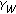 is the
is the 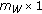 complex-valued receive symbol vector at the eavesdropper,
complex-valued receive symbol vector at the eavesdropper, -
(iv)
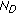 is the
is the  noise vector with independent identically distributed (i.i.d.) zero-mean, circular-symmetric complex Gaussian-distributed elements of variance
noise vector with independent identically distributed (i.i.d.) zero-mean, circular-symmetric complex Gaussian-distributed elements of variance 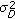 (i.e., the real and imaginary parts of each elements are independent zero-mean Gaussian random variables with the same variance),
(i.e., the real and imaginary parts of each elements are independent zero-mean Gaussian random variables with the same variance), -
(v)
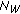 is the
is the  noise vector with i.i.d. zero-mean, circular-symmetric complex Gaussian-distributed elements of variance
noise vector with i.i.d. zero-mean, circular-symmetric complex Gaussian-distributed elements of variance  ,
, -
(vi)
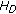 is the
is the 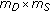 channel matrix from the source to destination with i.i.d. zero-mean, circular-symmetric complex Gaussian-distributed elements of unit variance,
channel matrix from the source to destination with i.i.d. zero-mean, circular-symmetric complex Gaussian-distributed elements of unit variance, -
(vii)
 is the
is the  channel matrix from the source to eavesdropper with i.i.d. zero-mean, circular-symmetric complex Gaussian-distributed elements of unit variance,
channel matrix from the source to eavesdropper with i.i.d. zero-mean, circular-symmetric complex Gaussian-distributed elements of unit variance, -
(viii)
 models the gain advantage of the eavesdropper over the destination.
models the gain advantage of the eavesdropper over the destination.
Note that  ,
,  ,
,  , and
, and  are independent. The wireless channel modeled by (14) is used
are independent. The wireless channel modeled by (14) is used  times as the
times as the  channel described in Section 2 with
channel described in Section 2 with  and
and  . We assume that the
. We assume that the  uses of the wireless channel in (14) are i.i.d. so that the memoryless requirement of the
uses of the wireless channel in (14) are i.i.d. so that the memoryless requirement of the  channel is satisfied. Since
channel is satisfied. Since  and
and  are included in the respective channel symbols observable by the destination and eavesdropper (i.e.,
are included in the respective channel symbols observable by the destination and eavesdropper (i.e.,  and
and  , resp.), this model also implicitly assumes that the destination and eavesdropper have perfect CSI of their respective channels from the source. In practice, we can separate adjacent uses of the wireless channel by more than the coherence time of the channel to approximately ensure the i.i.d. channel use assumption. Training (known) symbols can be sent right before or after (within the channel coherence period) by the source so that the destination can acquire the required CSI. The eavesdropper may also use these training symbols to acquire the CSI of its own channel. If the CSI required at the destination is obtained in the way just described, then a unit of channel use includes the symbol
, resp.), this model also implicitly assumes that the destination and eavesdropper have perfect CSI of their respective channels from the source. In practice, we can separate adjacent uses of the wireless channel by more than the coherence time of the channel to approximately ensure the i.i.d. channel use assumption. Training (known) symbols can be sent right before or after (within the channel coherence period) by the source so that the destination can acquire the required CSI. The eavesdropper may also use these training symbols to acquire the CSI of its own channel. If the CSI required at the destination is obtained in the way just described, then a unit of channel use includes the symbol  together with the associated training symbols. However, as in [29], we do not count the power required to send the training symbols (cf. (1)). Moreover we note that the source (and also the eavesdropper) may get some information about the outdated CSI of the destination channel, because information about the destination channel CSI, up to the previous use, may be fed back to the source from the destination via the public channel. More specifically, at time instant
together with the associated training symbols. However, as in [29], we do not count the power required to send the training symbols (cf. (1)). Moreover we note that the source (and also the eavesdropper) may get some information about the outdated CSI of the destination channel, because information about the destination channel CSI, up to the previous use, may be fed back to the source from the destination via the public channel. More specifically, at time instant  , the source symbol
, the source symbol  is a function of the feedback message
is a function of the feedback message  , which is in turn some function of the realizations of
, which is in turn some function of the realizations of  at time
at time  . We also note that neither the source nor destination has any eavesdropper CSI. Referring back to (14), these two facts imply that
. We also note that neither the source nor destination has any eavesdropper CSI. Referring back to (14), these two facts imply that  is independent of
is independent of  ,
,  ,
,  , and
, and  ; that is, the current source symbol
; that is, the current source symbol  is independent of the current channel state.
is independent of the current channel state.
Since the fading MIMO wiretap channel model in (14) is a special case of the CW model considered in Section 2, the key capacity  is given by Theorem 1 as
is given by Theorem 1 as

Note that

Substituting this back into (15), we get

As a result, the key capacity of the fast-fading wiretap channel described by (14) can be obtained by maximizing the conditional entropy  . This maximization problem is solved below.
. This maximization problem is solved below.
Theorem 2.
One has

where  denotes conjugate transpose.
denotes conjugate transpose.
Proof.
To determine the key capacity, we need the following upper bound on the conditional entropy  .
.
Lemma 1.
Let  and
and  be two jointly distributed complex random vectors of dimensions
be two jointly distributed complex random vectors of dimensions  and
and  , respectively. Let
, respectively. Let  ,
,  , and
, and  be the covariance of
be the covariance of  , covariance of
, covariance of  , and cross-covariance of
, and cross-covariance of  and
and  , respectively. If
, respectively. If  is invertible, then
is invertible, then

The upper bound is achieved when  is a circular-symmetric complex Gaussian random vector.
is a circular-symmetric complex Gaussian random vector.
Proof.
We can assume that both  and
and  have zero means without loss of generality. Also assume the existence of all unconditional and conditional covariances stated below. For each
have zero means without loss of generality. Also assume the existence of all unconditional and conditional covariances stated below. For each  ,
,

where  is the covariance of
is the covariance of  with respect to the conditional density
with respect to the conditional density  [29, Lemma 2]. This implies
[29, Lemma 2]. This implies

The second inequality above is due to the concavity of the function  over the set of positive definite symmetric matrices [30, 7.6.7], and the Jensen's inequality. To get the third inequality, observe that
over the set of positive definite symmetric matrices [30, 7.6.7], and the Jensen's inequality. To get the third inequality, observe that  can be interpreted as the covariance of the estimation error of estimating
can be interpreted as the covariance of the estimation error of estimating  by the conditional mean estimator
by the conditional mean estimator  . On the other hand,
. On the other hand,  is the covariance of the estimation error of using the linear minimum mean squared error estimator
is the covariance of the estimation error of using the linear minimum mean squared error estimator  instead. The inequality results from the fact that
instead. The inequality results from the fact that  (i.e.,
(i.e.,  is positive semidefinite) [31] and the inequality of
is positive semidefinite) [31] and the inequality of  if
if  and
and  are positive definite, and
are positive definite, and  [30, , 7.7.4].
[30, , 7.7.4].
Suppose that  is a circular-symmetric complex Gaussian random vector. For each
is a circular-symmetric complex Gaussian random vector. For each  , the conditional covariance of
, the conditional covariance of  , conditioned on
, conditioned on  , is the same as the (unconditional) covariance of
, is the same as the (unconditional) covariance of  . Since
. Since  is a circular-symmetric complex Gaussian random vector [29, Lemma 3] , so is
is a circular-symmetric complex Gaussian random vector [29, Lemma 3] , so is  conditioned on
conditioned on  . Hence by [29, Lemma 2], the upper bound in (20) is achieved with
. Hence by [29, Lemma 2], the upper bound in (20) is achieved with  , which also gives the upper bound in (21).
, which also gives the upper bound in (21).
To prove the theorem, we first obtain an upper bound on  and then show that the upper bound is achievable. Using Lemma 1, we have
and then show that the upper bound is achievable. Using Lemma 1, we have

where  and
and  are, respectively, the conditional covariances of
are, respectively, the conditional covariances of  and
and  , given
, given  and
and  , and
, and  and
and  are the corresponding conditional cross-covariances. Substituting (22) into (17), an upper bound on
are the corresponding conditional cross-covariances. Substituting (22) into (17), an upper bound on  is
is

Thus we need to solve the maximization problem (23). To do so, let  be the (nonnegative) eigenvalues of
be the (nonnegative) eigenvalues of  . Since both the distributions of
. Since both the distributions of  and
and  are invariant to any unitary transformation [29, Lemma 5], we can without any ambiguity define
are invariant to any unitary transformation [29, Lemma 5], we can without any ambiguity define

That is, we can assume  with no loss of generality. Then we have the following lemma, which suggests that the objective function in (23) is a concave function depending only on the eigenvalues of the covariance of
with no loss of generality. Then we have the following lemma, which suggests that the objective function in (23) is a concave function depending only on the eigenvalues of the covariance of  .
.
Lemma 2.
Suppose that  has an arbitrary covariance
has an arbitrary covariance  , whose (nonnegative) eigenvalues are
, whose (nonnegative) eigenvalues are  , then
, then

is concave in  .
.
Proof.
First write  and
and  . It is easy to see from (14) that
. It is easy to see from (14) that  , and
, and  . Then
. Then

where the last equality is due to the matrix inversion formula. Substituting this result into the left-hand side of (25), we obtain the right-hand side of (24), and hence (25).
To show concavity of  , it suffices to consider only diagonal
, it suffices to consider only diagonal  in
in  . Note that the mapping
. Note that the mapping  is linear in
is linear in  . Also the mapping
. Also the mapping  is matrix-concave in
is matrix-concave in  [32, Ex. 3.58]. Thus the composition theorem [32] gives that the mapping
[32, Ex. 3.58]. Thus the composition theorem [32] gives that the mapping  is matrix-concave in
is matrix-concave in  , since
, since  . Another use of the composite theorem together with the concavity of the function
. Another use of the composite theorem together with the concavity of the function  as mentioned in the proof of Lemma 1 shows that
as mentioned in the proof of Lemma 1 shows that  is concave in
is concave in  . Thus (25) implies that
. Thus (25) implies that  is also concave in
is also concave in  .
.
Hence it suffices to consider only those  with zero mean in (23).
with zero mean in (23).
Now define the constraint set  . Lemma 2 implies that we can find the upper bound on
. Lemma 2 implies that we can find the upper bound on  by calculating
by calculating  , whose value is given by the next lemma.
, whose value is given by the next lemma.
Lemma 3.
One has

Proof.
Since the elements of both  and
and  are i.i.d.,
are i.i.d.,  is invariant to any permutation of its arguments. This means that
is invariant to any permutation of its arguments. This means that  is a symmetric function. By Lemma 2,
is a symmetric function. By Lemma 2,  is also concave in
is also concave in  . Thus it is Schur-concave [33]. Hence a Schur-minimal element (an element majorized by any another element) in
. Thus it is Schur-concave [33]. Hence a Schur-minimal element (an element majorized by any another element) in  maximizes
maximizes  . It is easy to check that
. It is easy to check that  is Schur-minimal in
is Schur-minimal in  . Hence
. Hence  .
.
Combining the results in (23), (24), Lemmas 2 and 3, we obtain the upper bound on the key capacity as

where the identity  for invertible
for invertible  [34, Theorem 18.1.1] has been used.
[34, Theorem 18.1.1] has been used.
On the other hand, consider choosing  to have i.i.d. zero-mean, circular-symmetric complex Gaussian-distributed elements of variance
to have i.i.d. zero-mean, circular-symmetric complex Gaussian-distributed elements of variance  . Then conditioned on
. Then conditioned on  and
and  ,
,  are a circular-symmetric complex Gaussian random vector, by applying [29, Lemmas 3 and 4] to the linear model of (14). Hence Lemma 1 gives
are a circular-symmetric complex Gaussian random vector, by applying [29, Lemmas 3 and 4] to the linear model of (14). Hence Lemma 1 gives

where  , and
, and  . Substituting this back into (16) and using the matrix inversion formula to simplify the resulting expression, we obtain the same expression on the first line of (28) for
. Substituting this back into (16) and using the matrix inversion formula to simplify the resulting expression, we obtain the same expression on the first line of (28) for  . Thus the upper bound in (28) is achievable with this choice of
. Thus the upper bound in (28) is achievable with this choice of  ; hence it is in fact the key capacity.
; hence it is in fact the key capacity.
In Figure 1, the key capacities of several fast-fading MIMO channels with different numbers of source, destination, and eavesdropper antennas are plotted against the source signal-to-noise ratio (SNR)  , where
, where  . The channel gain advantage of the eavesdropper is set to
. The channel gain advantage of the eavesdropper is set to  . We observe that the key capacity levels off as
. We observe that the key capacity levels off as  increases in three of the four channels, except the case of
increases in three of the four channels, except the case of  , considered in Figure 1. It appears that the relative antenna dimensions determine the asymptotic behavior of the key capacity when the SNR is large. To more precisely study this behavior, we evaluate the limiting value of
, considered in Figure 1. It appears that the relative antenna dimensions determine the asymptotic behavior of the key capacity when the SNR is large. To more precisely study this behavior, we evaluate the limiting value of  as the input power
as the input power  of the source becomes very large. To highlight the dependence of
of the source becomes very large. To highlight the dependence of  on
on  , we use the notation
, we use the notation  .
.
Corollary 1.
 If
If  , then
, then

 Suppose that
Suppose that  . Define
. Define

Then  .
.
Proof.
First fix  or equivalently
or equivalently  , and consider the mapping
, and consider the mapping  defined in the proof of Lemma 2 as a function of
defined in the proof of Lemma 2 as a function of  . Also define
. Also define

Thus  . It is not hard to check that for any
. It is not hard to check that for any  , which implies that
, which implies that  . Hence
. Hence  is increasing in
is increasing in  . Since the elements of
. Since the elements of  are continuously i.i.d.,
are continuously i.i.d.,  w.p.1. Thus the matrix
w.p.1. Thus the matrix  (resp.,
(resp.,  ) is invertible w.p.1 when
) is invertible w.p.1 when  (resp.,
(resp.,  ).
).
Now, consider the case of  . As in (28), we have
. As in (28), we have

Since  is invertible w.p.1,
is invertible w.p.1,

Hence Part  of the lemma results from monotone convergence.
of the lemma results from monotone convergence.
For the case of  , the matrix inversion formula allows us to instead write
, the matrix inversion formula allows us to instead write

Since  is invertible w.p.1, we can also define
is invertible w.p.1, we can also define

Note that  . Since
. Since  is of rank
is of rank  w.p.1, it has the singular value decomposition
w.p.1, it has the singular value decomposition  , where
, where  is a diagonal matrix whose diagonal elements are the positive singular values of
is a diagonal matrix whose diagonal elements are the positive singular values of  . Also let
. Also let  ; that is,
; that is,  and
and  consist , respectively, of the first
consist , respectively, of the first  and the last
and the last  columns of
columns of  . Employing the unitary property of
. Employing the unitary property of  and
and  , it is not hard to verify that
, it is not hard to verify that


where  . From (37) and (38), it is clear that
. From (37) and (38), it is clear that  .
.
Further let  . Since
. Since  ,
,

Let  be the positive eigenvalues of
be the positive eigenvalues of  . Note that
. Note that  , because of the fact that the elements of
, because of the fact that the elements of  are continuously i.i.d. and are independent of the elements of
are continuously i.i.d. and are independent of the elements of  . Hence, from (38), (39), and the fact that
. Hence, from (38), (39), and the fact that  , we have
, we have

Now note that

where  denotes the Penrose-Moore pseudoinverse of
denotes the Penrose-Moore pseudoinverse of  . Then (40) implies that
. Then (40) implies that

Hence by Fatou's lemma, we get

From (38), it is clear that  increases without bound in
increases without bound in  w.p.1; hence
w.p.1; hence  also increases without bound. Combining this fact with (43), we arrive at the conclusion of Part
also increases without bound. Combining this fact with (43), we arrive at the conclusion of Part  of the lemma.
of the lemma.
Part  of the lemma verifies the observations shown in Figure 1 that the key capacity levels off as the SNR increases if the number of source antennas is no larger than that of eavesdropper antennas. When the source has more antennas, Part
of the lemma verifies the observations shown in Figure 1 that the key capacity levels off as the SNR increases if the number of source antennas is no larger than that of eavesdropper antennas. When the source has more antennas, Part  of the lemma suggests that the key capacity can grow without bound as
of the lemma suggests that the key capacity can grow without bound as  increases similarly to a MIMO fading channel with capacity
increases similarly to a MIMO fading channel with capacity  . Note that the matrix
. Note that the matrix  in the expression that defines
in the expression that defines  is a projection matrix to the orthogonal complement of the column space of
is a projection matrix to the orthogonal complement of the column space of  . Thus
. Thus  has the physical interpretation that the secret information is passed across the dimensions not observable by the eavesdropper. The most interesting aspect is that this mode of operation can be achieved even if neither the source nor the destination knows the channel matrix
has the physical interpretation that the secret information is passed across the dimensions not observable by the eavesdropper. The most interesting aspect is that this mode of operation can be achieved even if neither the source nor the destination knows the channel matrix  .
.
We note that the asymptotic behavior of the key capacity in the high SNR regime summarized in Corollary 1 is similar to the idea of secrecy degree of freedom introduced in [35]. The subtle difference here is that no up-to-date CSI of the destination channel is needed at the source.
Another interesting observation from Figure 1 is that for the case of  , the source power
, the source power  seems to have little effect on the key capacity. A small amount of source power is enough to get close to the leveling key capacity of about
seems to have little effect on the key capacity. A small amount of source power is enough to get close to the leveling key capacity of about  bit per channel use. This observation is generalized below by Corollary 2, which characterizes the effect of spatial dimensionality of the destination and eavesdropper on the key capacity when the destination and eavesdropper both have a large number of antennas.
bit per channel use. This observation is generalized below by Corollary 2, which characterizes the effect of spatial dimensionality of the destination and eavesdropper on the key capacity when the destination and eavesdropper both have a large number of antennas.
Corollary 2.
When  and
and  approach infinity in such a way that
approach infinity in such a way that  ,
,

Proof.
This corollary is a direct consequence of the fact that  and
and  w.p.1, which is in turn due to the strong law of large numbers.
w.p.1, which is in turn due to the strong law of large numbers.
Note that we can interpret the ratio  as the spatial dimensionality advantage of the eavesdropper over the destination. The expression for the limiting
as the spatial dimensionality advantage of the eavesdropper over the destination. The expression for the limiting  in the corollary clearly indicates that this spatial dimensionality advantage affects the key capacity in the same way as the channel gain advantage
in the corollary clearly indicates that this spatial dimensionality advantage affects the key capacity in the same way as the channel gain advantage  .
.
In Figure 2, the key capacities of several fast-fading MIMO channels with different numbers of source, destination, and eavesdropper antennas are plotted against the eavesdropper's channel gain advantage  , with
, with  dB. The results in Figure 2 show the other effect of spatial dimensionality. We observe that the key capacity decreases almost reciprocally with
dB. The results in Figure 2 show the other effect of spatial dimensionality. We observe that the key capacity decreases almost reciprocally with  in the channels with
in the channels with  and
and  , but stays almost constant for the channel with
, but stays almost constant for the channel with  . It seems that the relative numbers of source and eavesdropper antennas again play the main role in differentiating these two different behaviors of the key capacity. To verify that, we evaluate the limiting value of
. It seems that the relative numbers of source and eavesdropper antennas again play the main role in differentiating these two different behaviors of the key capacity. To verify that, we evaluate the limiting value of  as the gain advantage
as the gain advantage  of the eavesdropper becomes very large. To highlight the dependence of
of the eavesdropper becomes very large. To highlight the dependence of  on
on  , we use the notation
, we use the notation  .
.
Corollary 3.
One has

Proof.
Similar to the proof of Corollary 1.
Similar to the case of large SNR, when the number of source antennas is larger than that of the eavesdropper's antennas, secret information can be passed across the dimensions not observable by the eavesdropper. This can be achieved with neither the source nor the destination knowing the channel matrix  .
.
4. Alternative Achievability of Key Capacity
In this section, we provide an alternative proof of achievability for key capacity, which does not require the transmission of continuous symbols over the public channel. We derive the result from "first principles," which provides more insight on the desirable structure of a practical key agreement scheme. The main steps of the key agreement procedure are the following:
-
(1)
the source sends a sequence of i.i.d. symbols
 ;
; -
(2)
the destination "quantizes" its received sequence
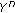 into
into  with a Wyner-Ziv compression scheme;
with a Wyner-Ziv compression scheme; -
(3)
the destination uses a binning scheme with the quantized symbol sequences to determine the secret key and the information to feedback to the source over the public channel;
-
(4)
the source exploits the information sent by the destination to reconstruct the destination's quantized sequence
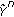 and uses the same binning scheme to generate its secret key.
and uses the same binning scheme to generate its secret key.
The secrecy of the resulting key is established by carefully structuring the binning scheme.
For the memoryless wiretap channel  specified by the joint pdf
specified by the joint pdf  , consider the quadruple
, consider the quadruple  defined by the joint pdf
defined by the joint pdf  with
with  to be specified later. We assume that
to be specified later. We assume that  takes values in the alphabet
takes values in the alphabet  . Given a sequence of
. Given a sequence of  elements
elements  unless otherwise specified. Similar notation and convention apply to all other sequences as well as their corresponding pdfs and conditional pdfs considered hereafter.
unless otherwise specified. Similar notation and convention apply to all other sequences as well as their corresponding pdfs and conditional pdfs considered hereafter.
4.1. Random Code Generation
Choose  such that
such that  and
and  , and let
, and let  denote the corresponding marginal. Note that the existence of such
denote the corresponding marginal. Note that the existence of such  can be assumed without loss of generality if
can be assumed without loss of generality if  and
and  . If
. If  , there is nothing to prove. Similarly, if
, there is nothing to prove. Similarly, if  , the construction below can be trivially modified to show that
, the construction below can be trivially modified to show that  is an achievable key rate.
is an achievable key rate.
Fix a small (small enough so that the various rate definitions and bounds on probabilities below make sense and are nontrivial)  . Let us define
. Let us define

For each  and
and  , generate
, generate  codewords
codewords  according to
according to  . The set of codewords
. The set of codewords  with
with  forms a subcode denoted by
forms a subcode denoted by  . The union of all subcodes
. The union of all subcodes  for
for  and
and  forms the code
forms the code  . For convenience, we denote the
. For convenience, we denote the  codewords in
codewords in  as
as  , where
, where  for
for  ,
,  , and
, and  . The code
. The code  and its subcodes
and its subcodes  is revealed to the source, destination, and eavesdropper. In the following, we refer to a codeword or its index in
is revealed to the source, destination, and eavesdropper. In the following, we refer to a codeword or its index in  interchangeably. Under this convention, the subcode
interchangeably. Under this convention, the subcode  are also the set that contains all the indices of its codewords. Denote
are also the set that contains all the indices of its codewords. Denote  and
and  .
.
4.2. Secret Sharing Procedure
For convenience, we define the joint typicality indicator function  that takes in a number of sequences as its arguments. The value of
that takes in a number of sequences as its arguments. The value of  is
is  if the sequences are
if the sequences are  -jointly typical, and the value is
-jointly typical, and the value is  otherwise. Further define the indicator function for the sequence pair
otherwise. Further define the indicator function for the sequence pair  :
:

where  is distributed according to
is distributed according to  in the definition above.
in the definition above.
The source generates a random sequence  distributed according to
distributed according to  . If
. If  satisfies the average power constraint (1), the source sends
satisfies the average power constraint (1), the source sends  through the
through the  channel. Otherwise, it ends the secret-sharing process. Since
channel. Otherwise, it ends the secret-sharing process. Since  satisfies
satisfies  , the law of large numbers implies that the probability of the latter event can be made arbitrarily small by increasing
, the law of large numbers implies that the probability of the latter event can be made arbitrarily small by increasing  . Hence we can assume below, with no loss of generality, that
. Hence we can assume below, with no loss of generality, that  satisfies (1) and is sent by the source. This assumption helps to make the probability calculations in Section 4.3 less tedious.
satisfies (1) and is sent by the source. This assumption helps to make the probability calculations in Section 4.3 less tedious.
Upon reception of the sequence  , the destination tries to quantize the received sequence. Let
, the destination tries to quantize the received sequence. Let  be the output of its quantizer. Specifically, if there is a unique sequence
be the output of its quantizer. Specifically, if there is a unique sequence  for some
for some  such that
such that  , then it sets the output of the quantizer to
, then it sets the output of the quantizer to  . If there is more than one such sequence,
. If there is more than one such sequence,  is set to be the smallest sequence index
is set to be the smallest sequence index  . If there is no such sequence, it sets
. If there is no such sequence, it sets  . Let
. Let  and
and  be the unique indices such that
be the unique indices such that  . The index
. The index  will be used as the key while the index
will be used as the key while the index  is fed back to the source over the public channel, that is,
is fed back to the source over the public channel, that is,  . If
. If  , set
, set  and choose
and choose  randomly over
randomly over  with uniform probabilities.
with uniform probabilities.
After receiving the feedback information  via the public channel, the source attempts to find a unique
via the public channel, the source attempts to find a unique  such that
such that  and
and  . If there is such a unique
. If there is such a unique  , the source decodes
, the source decodes  . If there is no such sequence or more than one such sequence, the source sets
. If there is no such sequence or more than one such sequence, the source sets  . If
. If  , it sets
, it sets  . Finally, if
. Finally, if  , the source generates its key
, the source generates its key  , such that
, such that  . If
. If  , it sets
, it sets  .
.
We also consider a fictitious receiver who observes the sequence  and obtains both indices
and obtains both indices  and
and  via the public channel. This receiver sets
via the public channel. This receiver sets  if
if  . Otherwise, it attempts to find a unique
. Otherwise, it attempts to find a unique  such that
such that  and
and  . If there is such a unique
. If there is such a unique  , the source decodes
, the source decodes  . If there is no such sequence or more than one such sequence, the source sets
. If there is no such sequence or more than one such sequence, the source sets  .
.
4.3. Analysis of Probability of Error
We use a random coding argument to establish the existence of a code with rates given by (46) such that  and
and  vanish in the limit of large block length
vanish in the limit of large block length  . Without further clarification, we note that the probabilities of the events below, except otherwise stated, are over the joint distribution of the codebook
. Without further clarification, we note that the probabilities of the events below, except otherwise stated, are over the joint distribution of the codebook  , codewords, and all other random quantities involved.
, codewords, and all other random quantities involved.
Before we proceed, we introduce the following lemma regarding the indicator function  .
.
Lemma 4.
 If
If  distributes according to
distributes according to  , then
, then  for sufficiently large
for sufficiently large  .
.
 If
If  distributes according to
distributes according to  , then
, then  for all
for all  .
.
 If
If  distributes according to
distributes according to  , then
, then  for all
for all  .
.
 If
If  distributes according to
distributes according to  , then
, then  for sufficiently large
for sufficiently large  .
.
Proof.
 This claim is actually shown in [36]. We briefly sketch the proof here using our notation for completeness and easy reference. By the reverse Markov inequality [36],
This claim is actually shown in [36]. We briefly sketch the proof here using our notation for completeness and easy reference. By the reverse Markov inequality [36],

where the second inequality is due to that fact that  for sufficiently large
for sufficiently large  .
.
 First, we only need to consider typical
First, we only need to consider typical  since the bound is trivial when
since the bound is trivial when  is not typical. Notice that for any such
is not typical. Notice that for any such  ,
,

Hence

Now

where the last inequality is due to (50).
 Same as Part
Same as Part  , interchanging the roles of
, interchanging the roles of  and
and  .
.
 From Part
From Part  , we get
, we get

Moreover we need to bound the probabilities of the following events pertaining to  .
.
Lemma 5.
 for sufficiently large
for sufficiently large  .
.
 For
For  ,
,  .
.
 When
When  is sufficiently large,
is sufficiently large,  uniformly for all
uniformly for all  .
.
 When
When  is sufficiently large,
is sufficiently large,  uniformly for all
uniformly for all  and
and  .
.
Proof.
 We will use an argument similar to the one in the achievability proof of rate distortion function in [27, Section 10.5] to bound
We will use an argument similar to the one in the achievability proof of rate distortion function in [27, Section 10.5] to bound  . First note that
. First note that  is the event that
is the event that  for all
for all  , and hence
, and hence

where the second equality is due to the fact that  are i.i.d. given each fixed
are i.i.d. given each fixed  . But
. But

where the inequality on the fourth line is due to the fact that  implies
implies  , and the last line results from the inequality
, and the last line results from the inequality  for all
for all  and positive integer
and positive integer  [27, Lemma 10.5.3]. Substituting (54) back into (53) and using Lemma 4 Part
[27, Lemma 10.5.3]. Substituting (54) back into (53) and using Lemma 4 Part  , we get
, we get

for sufficiently large  .
.
 Notice that for
Notice that for  ,
,

where the second equality results from the i.i.d. nature of  . Thus we have
. Thus we have

where the last inequality is due to Part  of Lemma 4 since
of Lemma 4 since  and
and  are independent.
are independent.
 From (56), we have the lower bound
From (56), we have the lower bound

where the first inequality is due to Part  of Lemma 4, and the second inequality is from Part
of Lemma 4, and the second inequality is from Part  of Lemma 4 when
of Lemma 4 when  is sufficiently large. Note that the same sufficiently large
is sufficiently large. Note that the same sufficiently large  is enough to guarantee the validity of the lower bound above for all
is enough to guarantee the validity of the lower bound above for all  .
.
 First note that, for
First note that, for  and
and  ,
,

Thus applying Part ( ) of the lemma, we get
) of the lemma, we get

uniformly for all  and
and  , when
, when  is sufficiently large. The third lower bound of (60) above is obtained from the inequality
is sufficiently large. The third lower bound of (60) above is obtained from the inequality  for any
for any  and positive integer
and positive integer  . The fourth lower bound is in turn based on the inequality
. The fourth lower bound is in turn based on the inequality  for
for  and positive integer
and positive integer  .
.
We first consider the error event  . Note that
. Note that

where  is the event
is the event  , and
, and  is the event that there is an
is the event that there is an  such that
such that  ,
,  , and
, and  . From (56), we have
. From (56), we have

where the equality on the fourth line is due to the i.i.d. nature of  , the equality on the fifth line results from the fact that
, the equality on the fifth line results from the fact that  (since
(since  ), and the inequality on the second last line is from the definition of the indicator function
), and the inequality on the second last line is from the definition of the indicator function  .
.
Similarly assuming  , we have from(56)
, we have from(56)

where the equality on the third line is due to the independence between  and
and  , and the last inequality results from Part
, and the last inequality results from Part  of Lemma 4 and the bound
of Lemma 4 and the bound  , which is a direct result of [27, Theorem 15.2.2]. Hence, substituting the bounds in (62) and (63) back into (61) and using Part
, which is a direct result of [27, Theorem 15.2.2]. Hence, substituting the bounds in (62) and (63) back into (61) and using Part  of Lemma 5, we obtain
of Lemma 5, we obtain

for  is sufficiently large.
is sufficiently large.
Next we consider the event  . Define
. Define  as the event
as the event  and
and  as the event that there is an
as the event that there is an  such that
such that  ,
,  , and
, and  . Then we have, when
. Then we have, when  is sufficiently large, uniformly for all
is sufficiently large, uniformly for all  and
and  ,
,

Note that the inequality on the third line of (65) results from upper bounds of  and
and  , which can be obtained in ways almost identical to the derivations in (62) and (63), respectively. The inequality on the fourth line is, on the other hand, due to Part
, which can be obtained in ways almost identical to the derivations in (62) and (63), respectively. The inequality on the fourth line is, on the other hand, due to Part  of Lemma 5.
of Lemma 5.
By expurgating the random code ensemble, we obtain the following lemma.
Lemma 6.
For any  and
and  sufficiently large, there exists a code
sufficiently large, there exists a code  with the rates
with the rates  ,
,  ,
,  , and
, and  given by (46) such that
given by (46) such that
-
(1)
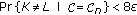 ,
, -
(2)
 ,
, -
(3)
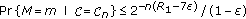 for all
for all 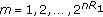 ,
, -
(4)
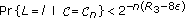 for all
for all  .
.
Proof.
Combining Part  of Lemma 5, (64), and (65), we have
of Lemma 5, (64), and (65), we have

for sufficiently large  . This implies that there must exist a
. This implies that there must exist a  satisfying
satisfying  ,
,  , and
, and  . Thus, Parts
. Thus, Parts  and
and  are proved.
are proved.
Now, fix this  . For
. For  , let
, let  be the
be the  th codeword of
th codeword of  . Then, by Part
. Then, by Part  of Lemma 4,
of Lemma 4,

hence, Part  results.
results.
Note that, for  ,
,

We know from the discussion above that  . Also from Part
. Also from Part  of the lemma,
of the lemma,

Putting these back into (68), we get

for sufficiently large  . Thus, Part
. Thus, Part  is proved.
is proved.
In the remainder of the paper, we use a fixed code  identified by Lemma 6. For convenience, we drop the conditioning on
identified by Lemma 6. For convenience, we drop the conditioning on  .
.
4.4. Secrecy Analysis
First we proceed to bound  . Note that
. Note that

Using Part  of Lemma 6 together with Fano's inequality gives
of Lemma 6 together with Fano's inequality gives  . Moreover Part
. Moreover Part  of Lemma 6 implies that
of Lemma 6 implies that  . Putting these bounds back into (71), we have
. Putting these bounds back into (71), we have

Next we bound  . Note that
. Note that

where the last inequality is obtained from Part  of Lemma 6 and Fano's inequality like before. In addition, it holds that
of Lemma 6 and Fano's inequality like before. In addition, it holds that

where the second last inequality follows from  , and the last inequality follows from
, and the last inequality follows from  (by definition of
(by definition of  and
and  ) and
) and  (by Fano's inequality applied to the fictitious receiver). By construction of the code
(by Fano's inequality applied to the fictitious receiver). By construction of the code  , it holds that
, it holds that  and
and  . In addition, Part
. In addition, Part  of Lemma 6 implies
of Lemma 6 implies  . Finally, note that
. Finally, note that  by the data-processing inequality since
by the data-processing inequality since  is a deterministic function of
is a deterministic function of  and the memoryless property of the channel between
and the memoryless property of the channel between  and
and  . Combining these observations and substituting the values of
. Combining these observations and substituting the values of  ,
,  , and
, and  given by (46) back into (73), we obtain
given by (46) back into (73), we obtain

when  is sufficiently large. Without any rate limitation on the public channel, we can choose the transition probability
is sufficiently large. Without any rate limitation on the public channel, we can choose the transition probability  such that
such that  ; therefore,
; therefore,

Since  can be chosen arbitrarily, Part
can be chosen arbitrarily, Part  of Lemma 6, (72), and (76), establish the achievability of the secret key rate
of Lemma 6, (72), and (76), establish the achievability of the secret key rate  .
.
5. Conclusion
We evaluated the key capacity of the fast-fading MIMO wiretap channel. We found that spatial dimensionality provided by the use of multiple antennas at the source and destination can be employed to combat a channel-gain advantage of the eavesdropper over the destination. In particular if the source has more antennas than the eavesdropper, then the channel gain advantage of the eavesdropper can be completely overcome in the sense that the key capacity does not vanish when the eavesdropper channel gain advantage becomes asymptotically large. This is the most interesting observation of this paper, as no eavesdropper CSI is needed at the source or destination to achieve the non-vanishing key capacity.
References
Wyner A: The wire-tap channel. Bell System Technical Journal 1975, 54: 1355-1387.
Leung-Yan-Cheong SK, Hellman M: The Gaussian wire-tap channel. IEEE Transactions on Information Theory 1978, 24(4):451-456. 10.1109/TIT.1978.1055917
Csiszár I, Korner J: Broadcast channels with confidential messages. IEEE Transactions on Information Theory 1978, 24(3):339-348. 10.1109/TIT.1978.1055892
Liang Y, Poor H, Shamai S: Secure communication over fading channels. IEEE Transactions on Information Theory 2008, 54(6):2470-2492.
Gopala P, Lai L, El Gamal H: On the secrecy capacity of fading channels. IEEE Transactions on Information Theory 2008, 54(10):4687-4698.
Bloch M, Barros J, Rodrigues M, McLaughlin SW: Wireless information-theoretic security. IEEE Transactions on Information Theory 2008, 54(6):2515-2534.
Khisti A, Tchamkerten A, Wornell G: Secure broadcasting over fading channels. IEEE Transactions on Information Theory 2008, 54(6):2453-2469.
Shafiee S, Liu N, Ulukus S: Towards the secrecy capacity of the Gaussian MIMO wire-tap channel: the 2-2-1 channel. IEEE Transactions on Information Theory 2009, 55(9):4033-4039.
Khisti A, Wornell G: The MIMOME channel. Proceedings of the 45th Annual Allerton Conference on Communication, Control, and Computing, October 2007, Monticello, IL, USA 8. http://arxiv.org/abs/0710.1325
Oggier F, Hassibi B: The secrecy capacity of the MIMO wiretap channel. Proceedings of the 45th Allerton Conference on Communication, Control and Computing, September 2007, Monticello, Ill, USA 848-855.
Liu T, Shamai S: A note on the secrecy capacity of the multi-antenna wiretap channel. IEEE Transactions on Information Theory 2009, 55(6):2547-2553.
Bustin R, Liu R, Poor HV, Shamai S: An MMSE approach to the secrecy capacity of the MIMO Gaussian wiretap channel. Proceedings of the IEEE International Symposium on Information Theory (ISIT '09), July 2009, Seoul, Korea 2602-2606.
Maurer UM: Secret key agreement by public discussion from common information. IEEE Transactions on Information Theory 1993, 39(3):733-742.
Ahlswede R, Csiszár I: Common randomness in information theory and cryptography—part I: secret sharing. IEEE Transactions on Information Theory 1993, 39(4):1121-1132. 10.1109/18.243431
Csiszár I, Narayan P: Common randomness and secret key generation with a helper. IEEE Transactions on Information Theory 2000, 46(2):344-366. 10.1109/18.825796
Csiszár I, Narayan P: Secrecy capacities for multiple terminals. IEEE Transactions on Information Theory 2004, 50(12):3047-3061. 10.1109/TIT.2004.838380
Csiszár I, Narayan P: Secrecy capacities for multiterminal channel models. IEEE Transactions on Information Theory 2008, 54(6):2437-2452.
Bennett CH, Brassard G, Crepeau C, Maurer UM: Generalized privacy amplification. IEEE Transactions on Information Theory 1995, 41(6):1915-1923. 10.1109/18.476316
Maurer U, Wolf S: Secret-key agreement over unauthenticated public channels—part I: definitions and a completeness result. IEEE Transactions on Information Theory 2003, 49(4):822-831. 10.1109/TIT.2003.809563
Maurer U, Wolf S: Secret-key agreement over unauthenticated public channels—part II: the simulatability condition. IEEE Transactions on Information Theory 2003, 49(4):832-838. 10.1109/TIT.2003.809560
Maurer U, Wolf S: Secret-key agreement over unauthenticated public channels—part III: privacy amplification. IEEE Transactions on Information Theory 2003, 49(4):839-851. 10.1109/TIT.2003.809559
Lai L, El Gamal H, Poor H: The wiretap channel with feedback: encryption over the channel. IEEE Transactions on Information Theory 2008, 54(11):5059-5067.
Tekin E, Yener A: Effects of cooperation on the secrecy of multiple access channels with generalized feedback. Proceedings of the 40th Annual Conference on Information Sciences and Systems (CISS '08), March 2008, Princeton, NJ, USA
Tekin E, Yener A: The general Gaussian multiple-access and two-way wiretap channels: achievable rates and cooperative jamming. IEEE Transactions on Information Theory 2008, 54(6):2735-2751.
Khisti A, Diggavi S, Wornell G: Secret-key generation with correlated sources and noisy channels. Proceedings of IEEE International Symposium on Information Theory (ISIT '08), July 2008, Toronto, Canada 1005-1009.
Prabhakaran V, Eswaran K, Ramchandran K: Secrecy via sources and channels—a secret key—secret message rate tradeoff region. Proceedings of the IEEE International Symposium on Information Theory (ISIT '08), July 2008, Toronto, Canada 1010-1014.
Cover T, Thomas J: Elements of Information Theory. 2nd edition. Wiley-Interscience, New York, NY, USA; 2006.
Han T: Information-Spectrum Methods in Information Theory. Springer, Berlin, Germany; 2003.
Telatar E: Capacity of multi-antenna Gaussian channels. European Transactions on Telecommunications 1999, 10(6):585-595. 10.1002/ett.4460100604
Horn R, Johnson C: Matrix Analysis. Cambridge University Press, Cambridge, UK; 1985.
Scharf LL: Statistical Signal Processing: Detection, Estimation, and Time Series Analysis. Addison-Wesley, New York, NY, USA; 1990.
Boyd S, Vandenberghe L: Convex Optimization. Cambridge University Press, Cambridge, UK; 2004.
Marshall A, Olkin I: Inequalities: Theory of Majorization and Its Applications. Academic Press, Boston, Mass, USA; 1979.
Harville D: Matrix Algebra from a Statistician's Perspective. Springer, New York, NY, USA; 1997.
Khisti A, Wornell G, Wiesel A, Eldar Y: On the Gaussian MIMO wiretap channel. Proceedings of the IEEE International Symposium on Information Theory (ISIT '07), June 2007, Nice, France 2471-2475.
Oohama Y: Gaussian multiterminal source coding. IEEE Transactions on Information Theory 1997, 43(6):1912-1923. 10.1109/18.641555
Acknowledgments
The work of T. F. Wong and J. M. Shea was supported in part by the National Science Foundation under Grant CNS-0626863 and by the Air Force Office of Scientific Research under Grant FA9550-07-10456. The authors would also like to thank Dr. Shlomo Shamai and the anonymous reviewers for their detailed comments and thoughtful suggestions. They are grateful to the reviewer who pointed out a significant oversight in the proof of Theorem 1 in the original version of the paper. They are also indebted to another reviewer who suggested the concavity argument in the proof of Lemma 2, which is much more elegant than the authors' original one.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Wong, T.F., Bloch, M. & Shea, J.M. Secret Sharing over Fast-Fading MIMO Wiretap Channels. J Wireless Com Network 2009, 506973 (2009). https://doi.org/10.1155/2009/506973
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/506973
 , the source sends message
, the source sends message  to the destination, and the destination sends message
to the destination, and the destination sends message  to the source. Both transmissions are carried over the public channel.
to the source. Both transmissions are carried over the public channel. for
for  , the source sends the symbol
, the source sends the symbol  to the
to the  channel. The destination and eavesdropper observe the corresponding symbols
channel. The destination and eavesdropper observe the corresponding symbols 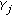 and
and 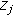 . There is no message exchange via the public channel, that is,
. There is no message exchange via the public channel, that is,  and
and  are both null.
are both null. for
for  , the source sends message
, the source sends message  to the destination, and the destination sends message
to the destination, and the destination sends message 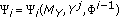 to the source. Both transmissions are carried over the public channel.
to the source. Both transmissions are carried over the public channel. ,
,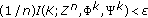 ,
, ,
,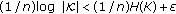 ,
, is the
is the  complex-valued transmit symbol vector by the source,
complex-valued transmit symbol vector by the source, is the
is the  complex-valued receive symbol vector at the destination,
complex-valued receive symbol vector at the destination,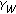 is the
is the 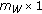 complex-valued receive symbol vector at the eavesdropper,
complex-valued receive symbol vector at the eavesdropper,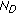 is the
is the  noise vector with independent identically distributed (i.i.d.) zero-mean, circular-symmetric complex Gaussian-distributed elements of variance
noise vector with independent identically distributed (i.i.d.) zero-mean, circular-symmetric complex Gaussian-distributed elements of variance 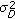 (i.e., the real and imaginary parts of each elements are independent zero-mean Gaussian random variables with the same variance),
(i.e., the real and imaginary parts of each elements are independent zero-mean Gaussian random variables with the same variance),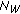 is the
is the  noise vector with i.i.d. zero-mean, circular-symmetric complex Gaussian-distributed elements of variance
noise vector with i.i.d. zero-mean, circular-symmetric complex Gaussian-distributed elements of variance  ,
,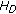 is the
is the 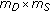 channel matrix from the source to destination with i.i.d. zero-mean, circular-symmetric complex Gaussian-distributed elements of unit variance,
channel matrix from the source to destination with i.i.d. zero-mean, circular-symmetric complex Gaussian-distributed elements of unit variance, is the
is the  channel matrix from the source to eavesdropper with i.i.d. zero-mean, circular-symmetric complex Gaussian-distributed elements of unit variance,
channel matrix from the source to eavesdropper with i.i.d. zero-mean, circular-symmetric complex Gaussian-distributed elements of unit variance, models the gain advantage of the eavesdropper over the destination.
models the gain advantage of the eavesdropper over the destination.
 dB, and
dB, and  .
.
 dB, where
dB, where  .
. ;
;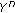 into
into  with a Wyner-Ziv compression scheme;
with a Wyner-Ziv compression scheme;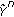 and uses the same binning scheme to generate its secret key.
and uses the same binning scheme to generate its secret key.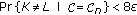 ,
, ,
,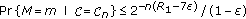 for all
for all 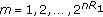 ,
,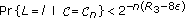 for all
for all  .
.