- Research Article
- Open access
- Published:
Downlink Scheduling for Multiclass Traffic in LTE
EURASIP Journal on Wireless Communications and Networking volume 2009, Article number: 510617 (2009)
Abstract
We present a design of a complete and practical scheduler for the 3GPP Long Term Evolution (LTE) downlink by integrating recent results on resource allocation, fast computational algorithms, and scheduling. Our scheduler has low computational complexity. We define the computational architecture and describe the exact computations that need to be done at each time step (1 milliseconds). Our computational framework is very general, and can be used to implement a wide variety of scheduling rules. For LTE, we provide quantitative performance results for our scheduler for full buffer, streaming video (with loose delay constraints), and live video (with tight delay constraints). Simulations are performed by selectively abstracting the PHY layer, accurately modeling the MAC layer, and following established network evaluation methods. The numerical results demonstrate that queue- and channel-aware QoS schedulers can and should be used in an LTE downlink to offer QoS to a diverse mix of traffic, including delay-sensitive flows. Through these results and via theoretical analysis, we illustrate the various design tradeoffs that need to be made in the selection of a specific queue-and-channel-aware scheduling policy. Moreover, the numerical results show that in many scenarios strict prioritization across traffic classes is suboptimal.
1. Introduction
The 3GPP standards' body has completed definition of the first release of the Long Term Evolution (LTE) system. LTE is an Orthogonal Frequency Division Multiple Access (OFDMA) system, which specifies data rates as high as 300 Mbps in 20 MHz of bandwidth. LTE can be operated as a purely scheduled system (on the shared data channel) in that all traffic including delay-sensitive services (e.g., VoIP or SIP signaling, see, e.g., [1, 2]) needs to be scheduled. Therefore, scheduler should be considered as a key element of the larger system design.
The fine granularity (180 KHz Resource Block times 1 millisecond Transmission Time Interval) afforded by LTE allows for packing efficiency and exploitation of time/frequency channel selectivity through opportunistic scheduling, thus enabling higher user throughputs. However, unlike what is typically the case in wired systems, more capacity does not easily translate to better user-perceived QoS for delay sensitive flows (VoIP, video-conferencing, stream video, etc.) in an opportunistic system. This is because a QoS scheduler has to carefully tradeoff maximization of total transmission rate versus balancing of various QoS metrics (e.g., packet delays) across users. In other words, one may need to sometimes schedule users whose delays/queues are becoming large but whose current channel is not the most favorable; see Section 2.1 for a review and discussion of results on best effort and QoS scheduling. Therefore, in this paper, we investigate the case for using queue- and channel-aware schedulers (see [3–5]) in an LTE downlink to deliver QoS requirements for a mix of traffic types.
We consider a very general scheduling framework, where each flow through its QoS class identifier (see Section 3.2) is mapped to a set of QoS parameters as required by the scheduler—the mapping can be changed to yield a different prioritization of flows; this requires no change in the computational framework. We make the following main contributions in this paper.
-
(i)
We extend much existing work on single-user queue- and channel-aware schedulers (i.e., schedulers which pick a single user to transmit to in each scheduling interval) to multiuser ones for wideband systems. We also develop a computational architecture which allows for efficient computation of the scheduling policies in such a setting. The computational complexity of our scheduler is essentially
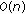 for
for  users—this complexity is amortized over multiple time steps.
users—this complexity is amortized over multiple time steps. -
(ii)
Through analysis and numerical results for different traffic models, we illustrate the various design choices (e.g., the specifics of the tradeoff mentioned earlier in this section) that need to be made while selecting a scheduling policy. We demonstrate that queue- and channel-aware schedulers lead to significant performance improvements for LTE. Such schedulers not only increase the system capacity in terms of the number of QoS flows that can be supported but also reduce resource utilization. Our simulation methodology is based on established network evaluation methodologies. We accurately model the LTE MAC layer, and selectively abstract the PHY layer.
While we focus on LTE in this paper, we note that the computational framework and the insights gained via the numerical studies can be extended to other orthogonal division frequency multiple access (OFDMA) technologies such as Worldwide Interoperability for Microwave Access (WiMax) and Ultra Mobile Broadband (UMB).
The rest of the paper is organized as follows. In Section 2, we provide a representative (but by no means complete) sample of results in literature and relate some of our contributions to the existing work. We also discuss in greater detail the key analytical results on wireless scheduling, and in doing so, make a case for considering queue- and channel-aware schedulers for both delay sensitive and best effort flows. The system model—LTE scheduling framework and how various functionalities can and have been used—is presented in Section 3. Having done that, the detailed scheduler design and implementation using fast computational algorithms is presented in Section 4. Details of simulation setup—the PHY layer abstraction, network deployment models, and traffic models—are presented in Section 5. Simulations demonstrating the performance of the scheduler for various traffic types, namely, best effort, video-conferencing, and streaming video, are presented in Section 6. Finally, Section 7 concludes the paper.
2. Scheduling in Wireless Systems: Prior Work and Discussion
Resource allocation in wireless networks is fundamentally different than that in wired networks due to the time-varying nature of the wireless channel [6]. There has been much prior work on scheduling policies in wireless networks to allocate resources among different flows based on the channels they see and the flow state; see, for example, the excellent overview articles [6, 7], and the references therein.
Much prior work in this area can be divided into two categories: scheduling for Elastic (non-real-time) flows, and that for real-time flows.
Scheduling for Elastic (Non-Real-Time) Flows
The end-user experience for an elastic flow is modeled by a concave increasing utility function of the average rate experienced by the flow [8]. The proportional fair algorithm (see, e.g., [9]), where all the resources are allocated to the flow with the maximum ratio of instantaneous spectral efficiency (which depends on the channel gain) to the average rate, has been analyzed in [10–14]. Roughly speaking, this algorithm maximizes the sum (over flows) of the log of long-run average rates allocated to the flows. For OFDMA-based systems, resource allocation algorithms which focus on maximizing sum rate (without fairness or minimum rate guarantees) include [15–19]. Efficient computational algorithms for maximizing the sum of general concave utility functions of the current and/or average rate were obtained recently in [20].
Scheduling for Real-Time Flows
Real-time flows are typically modeled by independent (of service) random packet arrival processes into their respective queues, and where packets have a delay target, for example, a maximum-delay deadline. A stabilizing scheduling policy in this setting is one which ensures that the queue lengths do not grow without bound. Stabilizing policies for different wireless network models have been characterized in, for example, [3–5, 21–23]. Under all stabilizing policies, even though the average rate seen by a flow is equal to its mean arrival rate, still the (distribution of) packet delay can be very different under different policies [6]; it is for the same reason that in order to meet the packet delay/QoS requirement of a real-time flow, it is not sufficient to only guarantee the allocation of at least a minimum average rate to the flow. Analytical results regarding the queue (or packet delay) distribution under the schedulers proposed in [3–5] were recently obtained in [24–26], and are discussed in the following subsection. For the case where packets are dropped if their delay exceeds the deadline, the scheduling policy in [27] minimizes the percentage of packets lost. Work on providing throughput guarantees for real-time flows includes [28, 29], and references therein.
The policies to schedule a mixture of elastic and real-time flows (with delay deadlines of the order of a second) have been considered in [30] for narrowband systems, and in [31] for wideband OFDMA systems where the latter assumes that the statistics of the packet arrival process of the real-time flows along with the channel statistics are known. The scheduling policy in [31] is persistent and only provides an average rate guarantee to the real-time flows, which, as pointed out earlier, is generally not sufficient to guarantee the packet delay targets. By contrast with the above two, in this paper we investigate whether, given the faster MAC turn-around times and larger bandwidths of LTE systems, the queue- and channel-aware scheduler can and should be used for real-time flows with delay deadlines of few tens of milliseconds. (The answer is yes.)
There is an extensive body of work that uses some of the above results in the design of scheduling policies for LTE specifically. The papers that investigate issues similar to those dealt with in this paper include [32–35]. In [32], it is shown that adaptive reuse can be beneficial when there is mix of VoIP and data flows, and VoIP is given strictly higher priority. A scheduling policy with strict priority across classes was also studied by [34]. Within a class, the proposed scheduling policy computes the resource allocation "chunk-by-chunk'' leading to a high computational complexity; the computational complexity of such schedulers can in fact be reduced significantly by using the fast computational algorithms presented in this paper. The work in [33] showed that strict prioritization for session initiation protocol (SIP) packets over other packets can lead to better performance. While strict prioritization for low rate flows such as SIP may be feasible, we show that in general it can lead to greatly sub-optimal resource utilization. Specifically, we design scheduling policies where the priority of a class of flows in not strict but rather opportunistic. The work in [35] studies a scheduling policy that gives equal priority to all QoS packets until their delay gets close to the deadline; when the packet delays get close to the deadline, the scheduling priority of such packets is increased. In fact, this policy can be seen as belonging to a wider class of queue- and channel-aware schedulers which smoothly partition the queue or delay state space in regions where channel conditions are given a higher weight and regions where the delay deadlines are given a higher weight. This is made precise in the following subsection.
Scheduling policies specifically for voice over internet protocol (VoIP) have been studied in, for example, [36–38]. Policies for full buffer traffic have been studied in, for example, [2, 39–44]; many of these papers focus on modifications to the proportional fair algorithm. A packing algorithm to deal with the constraints on resource assignment due to single-carrier FDMA on the uplink was studied in [45]. Fractional power control and admission control for the uplink have been studied in [46, 47], respectively.
2.1. Discussion
To motivate and put into context the simulations presented in this paper, here we summarize some of the key analytical results in the area of opportunistic scheduling. Through this section, it will suffice to picture a fixed number,  , of users sharing a wireless channel. Each user's data arrives to a queue as a random stream where it awaits transmission/service. The wireless channel is time-varying in that the transmission rates supported for each user vary randomly over time. A scheduling rule in this context selects a single user/queue to receive service in every scheduling instant. However, most of the single-user schedulers can be extended to multiuser versions (for wideband systems) with some effort; in Section 4.2 we present the extensions for the ones used in this paper.
, of users sharing a wireless channel. Each user's data arrives to a queue as a random stream where it awaits transmission/service. The wireless channel is time-varying in that the transmission rates supported for each user vary randomly over time. A scheduling rule in this context selects a single user/queue to receive service in every scheduling instant. However, most of the single-user schedulers can be extended to multiuser versions (for wideband systems) with some effort; in Section 4.2 we present the extensions for the ones used in this paper.
Among many others mentioned in the previous section, the work in [48] considers opportunistic scheduling in a setting where users' queues are infinitely backlogged (this full buffer setting is typically used to model elastic or best effort flows). They identify channel-aware opportunistic scheduling policies, which maximize the sum throughput (or, more generally, sum of any concave utility function of user throughput) under various types of fairness constraints. For example, let  denote the average rate offered to user
denote the average rate offered to user  over a long run (assuming the average exists, which does under stationary channels and scheduling rules) and any weights
over a long run (assuming the average exists, which does under stationary channels and scheduling rules) and any weights  be given, then a scheduler which maximizes
be given, then a scheduler which maximizes  is given like this: in any scheduling instant, if the users' time-varying channel spectral efficiencies take value
is given like this: in any scheduling instant, if the users' time-varying channel spectral efficiencies take value  (where
(where  is the spectral efficiency of
is the spectral efficiency of  th user's channel and is computed from its CQI), schedule a user
th user's channel and is computed from its CQI), schedule a user  satisfying
satisfying

Setting  equal to either the exponentially filtered average of allocated rate (see
equal to either the exponentially filtered average of allocated rate (see  in (6)) or the long-run average of spectral efficiency, denoted by
in (6)) or the long-run average of spectral efficiency, denoted by  , yields two versions of proportional fair (PF) scheduling. With
, yields two versions of proportional fair (PF) scheduling. With  in the above scheduler, define for later use
in the above scheduler, define for later use  , where expectation is with respect to random
, where expectation is with respect to random having the same distribution as the time-varying channel spectral efficiencies. The missing element in these works is the impact of queueing dynamics, which certainly cannot be ignored for QoS flows like voice, live and streaming video, and so forth.
having the same distribution as the time-varying channel spectral efficiencies. The missing element in these works is the impact of queueing dynamics, which certainly cannot be ignored for QoS flows like voice, live and streaming video, and so forth.
Once queueing dynamics are introduced, the opportunistic schedulers that are both queue- and channel-aware can and should be considered. Queue-awareness can be incorporated in a scheduler by, for example, replacing the fixed vector  in (1) with a vector field
in (1) with a vector field  on the state space of queue (or delay). That is, at any time when users' queues are in state
on the state space of queue (or delay). That is, at any time when users' queues are in state  and their channel spectral efficiencies are
and their channel spectral efficiencies are  , schedule a user
, schedule a user  satisfying
satisfying

Queue length  can be replaced/combined with head-of-line delay,
can be replaced/combined with head-of-line delay,  . We enumerate a few reasons why queue- and channel-aware schedulers should be considered.
. We enumerate a few reasons why queue- and channel-aware schedulers should be considered.
-
(a)
Opportunistic schedulers which are solely channel-aware may not even be stable (i.e., keep the users' queues bounded), unless chosen carefully, for example, using prior knowledge of mean arrival rates into the users' queues. See, for example, [49] which shows the instability of PF scheduling.
-
(b)
There are queue- and channel-aware schedulers that are throughput-optimal, that is, they ensure the queues' stability without any knowledge of arrival and channel statistics if indeed stability can be achieved under any other scheduler. Examples are MaxWeight [3], Exponential (Exp) rule [4], and Log rule [5], which have the same form as (2). Moreover, necessary and sufficient conditions on
 for the scheduler in (1) to be throughput optimal have also been shown [50, 51].
for the scheduler in (1) to be throughput optimal have also been shown [50, 51]. -
(c)
Throughput optimal schedulers, along with virtual token queues, can be used to offer minimum rate guarantees or maximize utility functions of user throughput under rate constraints [30, 52].
-
(d)
Even if stability of the queues were not a concern, still it is imperative for a QoS scheduler to be both channel- and queue-aware: in order to meet QoS requirements, one may need to sometimes schedule users whose delays/queues are becoming large but whose current channel is not the most favorable.
-
(e)
The work in [53] shows that under a constant load, scheduling algorithms that are oblivious to queue state will incur an average delay that grows at least linearly in number of users, whereas, channel- and queue-aware schedulers can achieve an average delay that is independent of the number of users.
Throughput optimal schedulers MaxWeight, Exp rule, and Log rule are defined as follows: when users' queues are in state  and their channel spectral efficiencies are
and their channel spectral efficiencies are  , schedulers MaxWeight, Exp, and Log rule serve a user
, schedulers MaxWeight, Exp, and Log rule serve a user  ,
,  , and
, and  , respectively, that is given by
, respectively, that is given by

for any fixed positive  's,
's,  's,
's,  ,
,  , and
, and  , and augmented with any fixed tie-breaking rule. Queue length
, and augmented with any fixed tie-breaking rule. Queue length  can be replaced with head-of-line delay,
can be replaced with head-of-line delay,  , to obtain the delay-driven version of each scheduler.
, to obtain the delay-driven version of each scheduler.
As hinted at by the aforementioned (d), a key challenge in designing a queue- and channel-aware scheduler, that is, choosing the vector field  , is determining an optimal tradeoff between maximizing current transmission rate (being opportunistic now) versus balancing unequal queues/delays (enhancing subsequent user diversity to enable future high rate opportunities, ensuring fairness amongst users, and delivering QoS requirements.) Key optimality properties (beyond and more interesting than stability) can be understood from the way a scheduler makes this tradeoff. Next, we examine how the three throughput optimal schedulers mentioned earlier make this tradeoff, and relate it to the known asymptotics of queues/delays under these schedulers.
, is determining an optimal tradeoff between maximizing current transmission rate (being opportunistic now) versus balancing unequal queues/delays (enhancing subsequent user diversity to enable future high rate opportunities, ensuring fairness amongst users, and delivering QoS requirements.) Key optimality properties (beyond and more interesting than stability) can be understood from the way a scheduler makes this tradeoff. Next, we examine how the three throughput optimal schedulers mentioned earlier make this tradeoff, and relate it to the known asymptotics of queues/delays under these schedulers.
It can be seen that by setting  for each
for each  in (3), all three schedulers reduce to PF when queue lengths of all users are equal or fairly close. However, "fairly close'' is interpreted differently by each scheduler. To define this more formally, assume that users' channels are stationary random processes and let
in (3), all three schedulers reduce to PF when queue lengths of all users are equal or fairly close. However, "fairly close'' is interpreted differently by each scheduler. To define this more formally, assume that users' channels are stationary random processes and let

(with  defined similarly) where the expectation is with respect to random
defined similarly) where the expectation is with respect to random having the same distribution as the time-varying channel spectral efficiencies. Then, in a stable queueing system under EXP rule,
having the same distribution as the time-varying channel spectral efficiencies. Then, in a stable queueing system under EXP rule,  is the average rate seen by the
is the average rate seen by the  th user, conditional on queues being in state
th user, conditional on queues being in state  . For an
. For an  user system and parameters
user system and parameters  in (3), Figure 1 illustrates the shape of the set
in (3), Figure 1 illustrates the shape of the set

that is, the partition of the queue state space where average rate of all users under Exp rule is the same as the average rate under PF; (sets  ,
,  defined similarly). With line
defined similarly). With line  as an axis, the partition
as an axis, the partition  is a cone, the partition
is a cone, the partition  is cylinder (with gradually increasing radius), and partition
is cylinder (with gradually increasing radius), and partition  is shaped like a French horn [5].
is shaped like a French horn [5].
As the queues move out of the partitions  due to an increase in
due to an increase in  and/or decrease in
and/or decrease in  , the rate allocation changes in favor of
, the rate allocation changes in favor of  , that is, each scheduler moves away from being proportional fair in order to balance unequal queues (or delays). If
, that is, each scheduler moves away from being proportional fair in order to balance unequal queues (or delays). If  continues to increase and/or
continues to increase and/or  decrease, each scheduler will eventually schedule only user 1 (whenever
decrease, each scheduler will eventually schedule only user 1 (whenever  ): the partition where MaxWeight, Exp rule, and Log rule schedule only the
): the partition where MaxWeight, Exp rule, and Log rule schedule only the  th queue (whenever
th queue (whenever  ) is, respectively, illustrated by
) is, respectively, illustrated by  ,
,  , and
, and  on Figure 1.
on Figure 1.
The exact shape of each partition in terms of width, curvature of boundaries, and so forth, depends on the parameters in (3) and on the finite set that  takes values in (defined by all the available MCSs). However, the shapes of partitions do not depend on the distribution of random
takes values in (defined by all the available MCSs). However, the shapes of partitions do not depend on the distribution of random  [26]. So these shapes are what an engineer will implicitly or explicitly design (by choosing a vector field
[26]. So these shapes are what an engineer will implicitly or explicitly design (by choosing a vector field  or changing parameters in (3)) in view of the QoS and rate requirements of users.
or changing parameters in (3)) in view of the QoS and rate requirements of users.
Beyond a visual description of partitions as a cone, cylinder, French horn, and so forth, the following mathematical description with useful insights can be given [5]: for any  and scalar
and scalar  and with
and with  's as in (3):
's as in (3):
-
(i)
 is constant in
is constant in  ,
, -
(ii)
 is decreasing in
is decreasing in  , and in the limit
, and in the limit  , only the longest queue(s) are scheduled (as long as their channels are nonzero),
, only the longest queue(s) are scheduled (as long as their channels are nonzero), -
(iii)
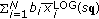 is increasing in
is increasing in  , and in the limit
, and in the limit  , the sum is the maximum possible. For example, with each
, the sum is the maximum possible. For example, with each  set to
set to 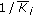 in (3),
in (3), 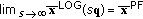 . This property is called radial sum-rate monotonicity (RSM).
. This property is called radial sum-rate monotonicity (RSM).
Therefore, as the queues grow linearly, (i.e., scaled up by a constant), Log rule (or any scheduler satisfying RSM) schedules in a manner that de-emphasizes queue-balancing in favor of increasing the total weighted service rate (with respect to weight vector  ); whereas, the Exp rule schedules in a manner that emphasizes queue-balancing at the cost of total weighted service rate. Then, it is shown in [25] that Exp rule minimizes the asymptotic probability of max-queue,
); whereas, the Exp rule schedules in a manner that emphasizes queue-balancing at the cost of total weighted service rate. Then, it is shown in [25] that Exp rule minimizes the asymptotic probability of max-queue,  , overflow (or, more precisely, the asymptotic exponential decay rate of max-queue distribution). Similarly, Log rule has been shown [26] to minimize the asymptotic probability of sum-queue,
, overflow (or, more precisely, the asymptotic exponential decay rate of max-queue distribution). Similarly, Log rule has been shown [26] to minimize the asymptotic probability of sum-queue,  , overflow.
, overflow.
2.1.1. Use of Queue- and Channel-Aware Schedulers for Elastic Traffic
Throughput optimal schedulers, like Exp and Log rules, can also be used for scheduling elastic flows which are often modeled as full/infinitely backlogged buffers instead of dynamic queues with random arrivals that are independent of service rate. This is done by using virtual token queues that are fed by deterministic arrivals at a constant rate  , and making scheduling decisions based on the virtual queues [30, 52]. If token rates
, and making scheduling decisions based on the virtual queues [30, 52]. If token rates  are feasible (i.e., lie within the opportunistic capacity region associated with the channel), then each user
are feasible (i.e., lie within the opportunistic capacity region associated with the channel), then each user  will be offered an average rate
will be offered an average rate  . Moreover, if token rates
. Moreover, if token rates  are not feasible, then recent asymptotic analysis of Exp [25] and Log [26] rules show that the average rates
are not feasible, then recent asymptotic analysis of Exp [25] and Log [26] rules show that the average rates  have the following interesting and desirable properties.
have the following interesting and desirable properties.
(i)Under Log rule,  is maximized subject to
is maximized subject to  . That is, Log rule splits users in two sets, for one set of users
. That is, Log rule splits users in two sets, for one set of users  , whereas for the other
, whereas for the other  , and the sets are chosen such that the total weighted rate
, and the sets are chosen such that the total weighted rate  is maximized.
is maximized.
(ii)Under Exp rule, variable  is minimized subject to
is minimized subject to  . That is, either each user's average rate
. That is, either each user's average rate  is decremented by
is decremented by  (compared to its required rate
(compared to its required rate  ), or decremented to 0 (i.e.,
), or decremented to 0 (i.e.,  ) if the required rate
) if the required rate  is already less than
is already less than  .
.
LTE is a purely scheduled system in that all traffic with diverse QoS requirements needs to be scheduled. LTE supports sufficiently short turn-around latency allowing for some opportunistic scheduling even for delay sensitive traffic (with delay tolerance of few tens of milliseconds). In this lies the motivation for simulations presented in Section 6 where we make the case that indeed queue- and channel-aware schedulers can be successfully used for delay sensitive traffic to increase the number of users that can be supported, as well as reduce the resource utilization under a given load.
3. System Model
3.1. Terminology
We introduce the following standard 3GPP terminology to be used in the rest of the document:
-
(i)
slot: basic unit of time, 0.5 millisecond,
-
(ii)
subframe: unit of time, 1?millisecond; resources are assigned at subframe granularity,
-
(iii)
eNB: evolved Node B, refers the base station,
-
(iv)
UE, user equipment, refers to the mobile,
-
(v)
PDCCH: physical downlink control channel, physical resources in time and frequency used to transmit control information from eNB to UE,
-
(vi)
PDSCH: physical downlink shared channel, physical resources in time and frequency used to transmit data from eNB to UE,
-
(vii)
CQI: channel quality indicator, measure of the signal to noise ratio (SINR) at the UE when eNB transmits at a reference power, fed back repeatedly from the UE to the eNB.
3.2. LTE Downlink Scheduling Framework
LTE is an OFDM system where spectral resources are divided in both time and frequency. A resource block (RB) consists of 180 kHz of bandwidth for a time duration of 1 millisecond. (Strict definition of a physical resource block in LTE is 180 KHz for 0.5 millisecond (slot), but for the purpose of the simulation this definition is adequate.) Thus, spectral resource allocation to different users on the downlink can be changed every 1 millisecond (subframe) at a granularity of 180 kHz. If hopping for frequency diversity is enabled, then hopping takes place at 0.5 millisecond point of the subframe (called slot). We use  to denote the total number of resource blocks in a single subframe.
to denote the total number of resource blocks in a single subframe.
LTE features a Hybrid-ARQ mechanism based on incremental redundancy. A transport block (consisting of data bytes to be transmitted in a subframe) is encoded using a rate 1/3 Turbo encoder and, depending on the CQI feedback, assigned RBs, and modulation, the encoded transport block is rate-matched appropriately to match the code rate supported by the indicated CQI. With each subsequent retransmission, additional coded bits can be sent reducing the effective code rate and/or improving the SINR. Though LTE allows the retransmission to be made at a different modulation scheme compared to the first transmission, this flexibility is not exploited in this paper.
Thus, in each subframe  , the scheduler grants spectral resources to users (UEs) for either fresh transmissions, or to continue past transmissions (retransmissions). We assume that each re-transmission of a packet occurs 8 ms (i.e., 8 subframes) after the previous transmission—packets are rescheduled for retransmission until they are successfully decoded at the UE, or the maximum (six) retransmissions have occurred. (LTE allows asynchronous HARQ retransmissions which means that retransmissions can occur any time after the ACK/NACK is received from the UE. In this paper, we do not exploit this flexibility and operate HARQ synchronously. Retransmissions occur with a delay in multiples of 8 ms.) For a new transmission, a modulation and coding scheme (MCS) is determined by a rate prediction algorithm which takes into account the most recent CQI report for the UE, and the past history of success/failure of transmissions to this UE—the rate prediction algorithm is explained in Section 4.1.
, the scheduler grants spectral resources to users (UEs) for either fresh transmissions, or to continue past transmissions (retransmissions). We assume that each re-transmission of a packet occurs 8 ms (i.e., 8 subframes) after the previous transmission—packets are rescheduled for retransmission until they are successfully decoded at the UE, or the maximum (six) retransmissions have occurred. (LTE allows asynchronous HARQ retransmissions which means that retransmissions can occur any time after the ACK/NACK is received from the UE. In this paper, we do not exploit this flexibility and operate HARQ synchronously. Retransmissions occur with a delay in multiples of 8 ms.) For a new transmission, a modulation and coding scheme (MCS) is determined by a rate prediction algorithm which takes into account the most recent CQI report for the UE, and the past history of success/failure of transmissions to this UE—the rate prediction algorithm is explained in Section 4.1.
The control resources (PDCCH) to convey scheduling grants to the users are time-multiplexed with the resources to transmit data (PDSCH) over the downlink. In particular, each subframe is divided into 14 symbols, of which up to three symbols at the start of the subframe can be used for control signalling. We do not model the details of the control channel signalling, but we do model the overhead associated with this signalling. Specifically, we assume that out of  symbols every subframe,
symbols every subframe,  symbols are used for control signalling. We also model the computational delays as illustrated in Figure 2.
symbols are used for control signalling. We also model the computational delays as illustrated in Figure 2.
Downlink scheduling time-line and computational delays. At time  the eNB assigns resources for a first transmission to UE
the eNB assigns resources for a first transmission to UE  ; the assignment is carried over PDCCH while the actual data is sent over PDSCH, both in subframe 0. ACK/NACK information to convey whether the first transmission was decoded successfully is fed back to the eNB by the UE in subframe 5. Subframe 8 is the earliest possible time when a retransmission (if needed) for this packet can occur.
; the assignment is carried over PDCCH while the actual data is sent over PDSCH, both in subframe 0. ACK/NACK information to convey whether the first transmission was decoded successfully is fed back to the eNB by the UE in subframe 5. Subframe 8 is the earliest possible time when a retransmission (if needed) for this packet can occur.
Downlink scheduling decisions can be made on the basis of the following information for each user.
-
(i)
QoS Class Identifier (QCI). In the LTE architecture downlink data flows from a Packet Gateway (called PDN GW) to eNB and then to the UE (user). The PDN GW to eNB is an IP link and the eNB to UE is over the wireless link. When the logical link from the bearer to the UE is set up (called a bearer), a QoS Class Identifier (QCI) is specified. This defines whether the bearer is guaranteed bit-rate or not, target delay and loss requirements, and so forth. The eNB translates the QCI attributes into logical channel attributes for the air-interface and the scheduler acts in accordance with those attributes. (We use the term user and logical channel interchangeably in this paper as we only state the results with one logical channel per user.)
-
(ii)
CQI. The channel quality indicator (CQI) reports are generated by the UE and fed back to the eNB in quantized form periodically, but with a certain delay. These reports contain the value of the signal-to-noise and -interference ratio (SINR) measured by the user. We denote by
 the most recent wideband CQI value received by the eNB at or before time
the most recent wideband CQI value received by the eNB at or before time 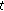 for user
for user  . The LTE system allows several reporting options for both wideband (over the system bandwidth) and subband (narrower than the system bandwidth) CQI, with the latter allowing exploitation of frequency selective fading.
. The LTE system allows several reporting options for both wideband (over the system bandwidth) and subband (narrower than the system bandwidth) CQI, with the latter allowing exploitation of frequency selective fading. -
(iii)
Buffer State. The buffer state refers to the state of the users' buffers, representing the data available for scheduling. We assume that for each user
 , the queue length in (the beginning of) subframe
, the queue length in (the beginning of) subframe 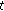 , denoted by
, denoted by  bits, and the delay of each packet in the queue, with
bits, and the delay of each packet in the queue, with  ms denoting the delay of head-of-line packet, is available at the scheduler.
ms denoting the delay of head-of-line packet, is available at the scheduler. -
(iv)
Phy ACK/NACK. At time
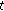 , ACK/NACK for all transmissions scheduled in subframe
, ACK/NACK for all transmissions scheduled in subframe  are known to the scheduler.
are known to the scheduler. -
(v)
Resource Allocation History: Scheduling decisions can also be based on scheduling decisions in the past. For example, if a user was allocated multiple RBs over the past few subframes, then its priority at the current subframe may be reduced (even though ACKs/NACKs are still pending). A commonly used approach is to maintain the average rate,
 at which a user is served. The average rate is updated at every time
at which a user is served. The average rate is updated at every time  using an exponential filter as follows:
using an exponential filter as follows: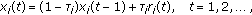 (6)
(6)where
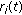 is the rate allocated to the
is the rate allocated to the  th user at time
th user at time  , and
, and 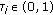 is a user specific constant; we refer to
is a user specific constant; we refer to 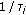 as time-constant for (rate averaging for) user
as time-constant for (rate averaging for) user  .
.
4. Scheduler Design for LTE
For each subframe  , the scheduler first assigns power and resource blocks to retransmissions for packets which were not decoded successfully at time
, the scheduler first assigns power and resource blocks to retransmissions for packets which were not decoded successfully at time  ; the modulation and coding scheme for a retransmission is kept the same as for the previous transmission. The remaining power and spectral resources are distributed among the remaining users for transmissions of new packets. Specifically, each assignment consists of the following:
; the modulation and coding scheme for a retransmission is kept the same as for the previous transmission. The remaining power and spectral resources are distributed among the remaining users for transmissions of new packets. Specifically, each assignment consists of the following:
-
(i)
the identity of the user for which the assignment is made,
-
(ii)
the number of RBs assigned,
-
(iii)
the transmission power for each RB,
-
(iv)
the modulation and coding scheme for packet transmission.
In this paper, we present the schedulers and fast computational algorithms for the case where power is distributed uniformly across RBs and only the wideband CQI is being reported. However, the schedulers can be extended to case where one or both of the above restrictions are removed. More specifically, each scheduler is described as a solution to an optimization problem, where the optimization problem can be readily extended to the case where one or both of the above restrictions are removed. Moreover, fast computational algorithms to solve these more complex optimization problems are presented in [20]. Finally, we note that while we model the overhead for the control channel PDCCH, we do not study algorithms for control channel format selection.
We break the scheduling algorithm into two parts.
-
(a)
Rate Prediction. The rate prediction algorithm maps (based on past history of transmissions for a UE) the CQI reports to a modulation and coding scheme that targets successful decoding in a specified number of transmissions of a packet. Even though a UE repeatedly sends CQI reports to the eNB, still rate prediction is essential in order to account for the uncertainty in the channel gain to the UE. This uncertainty arises due the following reasons:
-
(i)
wireless channels are time-varying,
-
(ii)
CQI is quantized to 4 bits and the quantized value may be too pessimistic (or optimistic),
-
(iii)
CQI reports received by the eNB from a UE may be based on the channel state a few subframes earlier,
-
(iv)
multiple retransmissions of a packet through H-ARQ may be desired to take advantage of the time diversity, where the channel can vary across the retransmissions.
-
(i)
-
(b)
Resource Assignment. Given an achievable spectral efficiency as determined by the rate prediction algorithm, the resource allocation for new transmissions is determined as a solution of a constrained optimization problem. The optimization problem depends on the scheduling policy (proportional fair, Exponential rule, etc.).
4.1. Rate Prediction
Rate prediction is the task of determining and adapting to channel conditions, the mapping of reported CQI to the selected transport format. We start with a baseline mapping (subsequently denoted by  ) that is optimal under AWGN channel. That is to say, assuming the channel gain is known and static, we optimize transport format for a fixed number of resources, such that the data packet is transmitted successfully to the UE in any targeted number of transmissions. The baseline mapping that is optimal for a static channel may no longer be so for a fading channel because the channel gain from an eNB to a UE can vary from one H-ARQ transmission to the next. Hence, the selection of the transport format has to take into account this uncertainty or variation in channel gains. One method of doing this is to use a link margin or backoff factor, that is adapted in a closed loop for each link individually, to adjust the transport format from that of the baseline.
) that is optimal under AWGN channel. That is to say, assuming the channel gain is known and static, we optimize transport format for a fixed number of resources, such that the data packet is transmitted successfully to the UE in any targeted number of transmissions. The baseline mapping that is optimal for a static channel may no longer be so for a fading channel because the channel gain from an eNB to a UE can vary from one H-ARQ transmission to the next. Hence, the selection of the transport format has to take into account this uncertainty or variation in channel gains. One method of doing this is to use a link margin or backoff factor, that is adapted in a closed loop for each link individually, to adjust the transport format from that of the baseline.
Specifically, if  th user's CQI is
th user's CQI is  , the user is allocated
, the user is allocated  RBs at time
RBs at time  , and has a termination target (for successful decoding of the packet at the UE) of
, and has a termination target (for successful decoding of the packet at the UE) of  H-ARQ transmissions, then let
H-ARQ transmissions, then let  denote the maximum number of bits that can be transmitted over a static AWGN channel with SINR
denote the maximum number of bits that can be transmitted over a static AWGN channel with SINR  . Then for a fading channel, we select the number of bits as
. Then for a fading channel, we select the number of bits as

where  is the backoff factor. The spectral efficiency (in bps/RB) for user
is the backoff factor. The spectral efficiency (in bps/RB) for user  is then given by
is then given by

The backoff value is adapted in a closed loop manner as described in what follows. If the
is adapted in a closed loop manner as described in what follows. If the  th user's transmission is indeed decoded correctly in (or under) the targeted number of transmissions,
th user's transmission is indeed decoded correctly in (or under) the targeted number of transmissions,  , then
, then  is decremented (to at most
is decremented (to at most  dB) by some fixed small
dB) by some fixed small  (dB), that is,
(dB), that is,

If, however, the transmission is decoded in more than  number of transmissions (or not decoded at all), then
number of transmissions (or not decoded at all), then  is incremented (to at most
is incremented (to at most  dB) by
dB) by  for some fixed
for some fixed  , that is,
, that is,

We note that the above rate prediction algorithm is fairly standard and has been studied in detail in [54].
For best effort flows,  is not fixed over time: it is set to 3 unless (i)
is not fixed over time: it is set to 3 unless (i)  is so high that setting
is so high that setting  to a lower value results in more than 20% increase in spectral efficiency
to a lower value results in more than 20% increase in spectral efficiency  (in which case
(in which case  is chosen to maximize
is chosen to maximize  ), (ii)
), (ii)  is too low for
is too low for  to be feasible (in which case
to be feasible (in which case  is set to the smallest feasible value). This allows for a high granularity in picking a spectral efficiency as well as for taking advantage of time diversity. For delay sensitive flows,
is set to the smallest feasible value). This allows for a high granularity in picking a spectral efficiency as well as for taking advantage of time diversity. For delay sensitive flows,  is always set to the smallest feasible value in order to minimize the latency incurred due to retransmissions of a packet.
is always set to the smallest feasible value in order to minimize the latency incurred due to retransmissions of a packet.
4.2. Scheduling Policies
In this subsection, we describe the schedulers used for simulation results presented in Section 6, whereas, the fast computational algorithms for these schedulers are presented in the following subsection. Best effort flows are scheduled using a utility maximizing scheduler, whereas, QoS flows are scheduled using Exp rule, Log rule, or Earliest-Deadline-First (EDF). An efficient computational architecture to compute the resource allocation corresponding to a subset of these policies is presented in the following subsection.
4.2.1. Utility Maximizing Scheduler for Best Effort
Recall that  denotes the exponentially filtered average rate of user
denotes the exponentially filtered average rate of user  , that is,
, that is,

where  is defined in (8),
is defined in (8),  is a parameter,
is a parameter,  is the number of RBs allocated to user
is the number of RBs allocated to user  in subframe
in subframe  , and
, and  . We set
. We set  for all users (i.e., the time constant of the exponential filter for rate averaging is
for all users (i.e., the time constant of the exponential filter for rate averaging is  subframe). Moreover, let
subframe). Moreover, let  be a concave continuously differentiable utility function (of average rate
be a concave continuously differentiable utility function (of average rate  ) associated with user
) associated with user  . We consider functions
. We consider functions  such that, for
such that, for  , we have
, we have

for some fixed  ; for example,
; for example,  for
for  . Then in any subframe
. Then in any subframe  , the utility maximizing scheduler allocates RBs
, the utility maximizing scheduler allocates RBs  where
where  is the number of users) in order to maximize
is the number of users) in order to maximize

We note the following points.
-
(a)
As
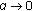 , the scheduler reduces to a proportional fair scheduler. Specifically, this scheduler will allocate the next fraction of available bandwidth resource to a user with maximum
, the scheduler reduces to a proportional fair scheduler. Specifically, this scheduler will allocate the next fraction of available bandwidth resource to a user with maximum  .
. -
(b)
As
 , this scheduler reduces to max sum-rate scheduler.
, this scheduler reduces to max sum-rate scheduler. -
(c)
As
 , it reduces to the max-min fair scheduler, that is, it maximizes the minimum average rate.
, it reduces to the max-min fair scheduler, that is, it maximizes the minimum average rate.
4.2.2. Delay-Driven Log and Exp Rules
Log and Exp rules used in simulations are similar to the ones introduced in Section 2.1 (see (3)), however, instead of scheduling, one user in every scheduling instant, we can now schedule one user in every RB in the current subframe. So the scheduler makes scheduling decisions one RB at a time, and updates queues and the buffer state (e.g., head-of-line delay) after each assignment.
We use the delay-driven version of these rules. Let  denote the wait time of the head-of-line packet in
denote the wait time of the head-of-line packet in  th user's queue at eNB in subframe
th user's queue at eNB in subframe  . Then under Log rule, in any subframe
. Then under Log rule, in any subframe  ,:
,:
-
(i)
the next available RB is allocated to a user
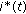 satisfying
satisfying (14)
(14)with ties broken in favor of the user with smallest index,
-
(ii)
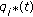 is decremented and
is decremented and 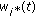 is updated based on the new buffer state. This is done before the scheduler computes the optimal user for the next RB.
is updated based on the new buffer state. This is done before the scheduler computes the optimal user for the next RB.
Parameters  are set to
are set to  ,
,  , and
, and  where
where  is the 99th percentile delay target of the
is the 99th percentile delay target of the  th user's flow. Recall the set
th user's flow. Recall the set  from Section 2.1, that is, the partition of state space of delay (or queue) where Log rule and PF take the same scheduling decision. Then the magnitude of vector
from Section 2.1, that is, the partition of state space of delay (or queue) where Log rule and PF take the same scheduling decision. Then the magnitude of vector  sets the width of this partition about the axis
sets the width of this partition about the axis  .
.
Exp rule is defined similarly, with (14) appropriately modified to,

Parameters  are set to
are set to  and
and  to either
to either  (in Section 6.2) or
(in Section 6.2) or  , (see [30] for setting Exp rule parameters; typically
, (see [30] for setting Exp rule parameters; typically  gives good performance). Just as in the case of Log rule, magnitude of vector
gives good performance). Just as in the case of Log rule, magnitude of vector  sets the width of partition
sets the width of partition  about the axis
about the axis  .
.
4.2.3. Earliest-Deadline-First Scheduler
This is a queue-aware nonopportunistic scheduler which, in each subframe  , allocates the next available RB to a user
, allocates the next available RB to a user  , and then updates
, and then updates  just as in the case of Log and Exp rule.
just as in the case of Log and Exp rule.
4.3. Efficient Computation of RB Allocation under Various Schedulers
We now describe an efficient computational framework to compute the bandwidth allocations for each subframe under utility maximization, queue-driven Log, and queue-driven MaxWeight scheduling policies. We also show how this framework can be used to compute an approximate version of the delay-driven versions.
We first consider a generic optimization problem over the number of resource blocks,  , allocated to each user
, allocated to each user  .:
.:

where  are concave increasing functions. We ignore the constraints that
are concave increasing functions. We ignore the constraints that  's are integers—LTE offers high enough resource granularity, that is, with appropriate rounding techniques the loss in optimality is negligible. The maximum bandwidth that can be allocated to user
's are integers—LTE offers high enough resource granularity, that is, with appropriate rounding techniques the loss in optimality is negligible. The maximum bandwidth that can be allocated to user  at time
at time  is given by
is given by

Using an appropriate definition of  , the computation of different scheduling policies can be formulated as the aforementioned optimization problem as follows.
, the computation of different scheduling policies can be formulated as the aforementioned optimization problem as follows.
-
(i)
Utility Maximization. Here, we define
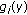 as
as (18)
(18)where we recall that
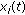 is the average rate allocated to user
is the average rate allocated to user  as computed by an exponential filter at time
as computed by an exponential filter at time  (see (11)).
(see (11)). -
(ii)
Queue-Driven Log Rule. For all
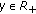 ,
,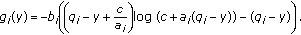 (19)
(19) -
(iii)
Queue-Driven MaxWeight Rule. In this case,
 is defined as
is defined as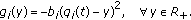 (20)
(20)
The delay-based versions of Log rule and MaxWeight can also be computed by first approximating those as queue-based rules like this: let  , that is, the average arrival rate over the wait time of the head of line packet. Then
, that is, the average arrival rate over the wait time of the head of line packet. Then  in delay-based rules can be substituted with
in delay-based rules can be substituted with  .
.
Define the projection operator over  as
as

This operator projects a real variable over the interval  .
.
Necessary and sufficient conditions for  to be optimal are given by [20]
to be optimal are given by [20]

The following bisection search on  can be used to solve the aforementioned problem [20]:
can be used to solve the aforementioned problem [20]:
Given ,
,  , tolerance
, tolerance  .
.
Repeat
-
(a)
Bisect.
 .
. -
(b)
Bandwidth Allocation. Compute
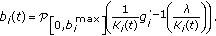 (23)
(23) -
(c)
Stopping Criterion. quit if
 .
. -
(d)
Update. If
 ,
,  , else
, else 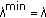 .
.
In practice, about 10 iterations are sufficient to obtain a solution for an accuracy required for scheduling in LTE. An exact complexity analysis, and the choice of the tolerance  to compute a solution within a certain bound of the optimal objective function are possible [20].
to compute a solution within a certain bound of the optimal objective function are possible [20].
4.4. Further Reduction of Computation by Optimizing over a Horizon
The computational burden of above algorithms (especially for large  and
and  ) can be reduced further by solving the convex optimization for a horizon of a few subframes rather than for each subframe. Specifically, we run the convex optimization and compute the optimal RB allocation to each user—called a user's RB target—over a horizon of a few subframes (say, 8). Then in each subsequent subframe till the next time the optimization is run, we allocate RBs by only doing the following computations (to fully exploit any CQI variation over the horizon).
) can be reduced further by solving the convex optimization for a horizon of a few subframes rather than for each subframe. Specifically, we run the convex optimization and compute the optimal RB allocation to each user—called a user's RB target—over a horizon of a few subframes (say, 8). Then in each subsequent subframe till the next time the optimization is run, we allocate RBs by only doing the following computations (to fully exploit any CQI variation over the horizon).
-
(i)
Update of QoS metric of users, that is,
 ,
, 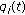 , and/or
, and/or 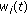 , based on RB assignments in each subframe (as they are made).
, based on RB assignments in each subframe (as they are made). -
(ii)
Update of spectral efficiency
 (for users for which a CQI report was received in the previous subframe).
(for users for which a CQI report was received in the previous subframe). -
(iii)
Update of users' priority, that is,
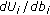 at
at 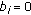 , once the above two updates have been made.
, once the above two updates have been made. -
(iv)
RBs are first allocated to the highest priority user till its target is met. If some RBs remain available, they are assigned to next highest priority user, and so on. Any degenerate cases, like data buffers or control resources running out are handled such that as many as possible number of RBs are assigned in each subframe.
Remark 1.
Beside reducing computational burden, solving the optimization for a horizon has an added advantage of reducing the required control signalling. This is because the a user's RB-target-over-a-horizon can now be allocated all at once in one subframe (or in a fewer number of subframes) rather than allocating only a few RBs per subframe over the duration of a horizon. For example, Figure 3 shows two schedules for a hypothetical 4-RBs-by-4-subframes scheduling problem; the two schedules are equivalent in terms of number of RBs assigned to each user. The schedule on the left is computed one subframe at a time, whereas the schedule on the right is computed using the method described earlier. That is, first, users' RB targets are computed once over the 4-RB-by-4-subframe horizon (by solving the convex program), then in each subsequent subframe, RBs (according to the computed targets) are allocated to the highest priority UE(s). Resultantly, the latter schedule has an advantage of requiring only 5 downlink grants on PDCCH versus 9 required by the former.
5. Simulation Framework
5.1. Network and Deployment Model
The deployment and channel models are mostly taken from the work in [55–58] and the relevant parameters are repeated here in Table 1. For the full-buffer simulation results, two-tiers (19 eNBs, 57 cells) with wrap-around was simulated with users in each eNB modeled explicitly. To save on simulation time, for the results with QoS traffic (e.g., streaming video or video conferencing) a two-step process was followed. First, the two-tier (19 eNBs, 57 cell) scenario was simulated under the assumption that all eNBs were transmitting at full power on the downlink (full loading). This was used to generate the distribution of SINRs (geometries) seen by UEs on the downlink, resulting from pathloss and shadowing. Wrap-around of cells as outlined in [58] was followed to avoid edge effects. Second, the center-cell alone was simulated with data traffic and schedulers, with each UE's SINR being drawn from the distribution calculated in the first step. Fast fading (time and frequency selective) was then generated for each UE to determine the instantaneous (per subframe) SINR.
For short-term fading, delay spread, and power-delay profile models from [57] are used. The Doppler spectrum is the classic U-shaped power spectrum that results from Jakes/Clarke's model. The UE speed simulated was 3 km/h. The effect of channel estimation error was accounted for by applying a channel specific backoff factor (such as  term in the PHY abstraction modeling section), determined through link-level simulations.
term in the PHY abstraction modeling section), determined through link-level simulations.
5.2. Physical Layer Modeling
System simulations are conducted over a large number of cells/sectors and large number of users. As such, characterizing the channel, the physical layer waveform and/or exact decoding process at short timescales becomes prohibitive in terms of computation and simulation time. Yet, a reasonably accurate behavioral model of the physical layer performance is critically important in obtaining the correct system level performance representation and in tuning MAC/RLC algorithms (such as the scheduler). Link level performance is typically characterized by packet-error-rate (PER) versus long-term average SINR curves, where the latter is computed over all channel realizations. Such a curve is not very useful to use in system level simulations as several critical aspects such as user and channel sensitive rate scheduling, hybrid-ARQ and link adaptation are dependent on the short-term average channel. In some instances, the benefits of MIMO and spatial beamforming would also not be captured (e.g., those schemes often involve dynamic feedback of the spatial channel and subsequent adaptation of antenna weights in accordance), as those too are dependent on the short-term channel realization. Furthermore, one aspect of the system simulation is to allow the tuning of algorithms such as rate prediction, power control, and so forth, and therefore, the dynamic nature of physical layer performance is important to capture in the system simulation.
A number of different approaches have been proposed and evaluated in the past (see [60] and references therein for a good summary). In most instances, an effective SINR that captures the channel and interference occurrences over all resource elements used in transmission of the encoded packet, is defined. [60, Equation (1)] generically defines effective SINR as follows:

where  represents the number of resource elements (time-frequency resources) used over the packet transmission thus far,
represents the number of resource elements (time-frequency resources) used over the packet transmission thus far,  is the index over the resource elements,
is the index over the resource elements,  represents the signal-to-interference and noise ratio on
represents the signal-to-interference and noise ratio on  th resource element, and
th resource element, and  is function that is specific to the model. Note that if hybrid-ARQ is used, then the summation term should include all the H-ARQ transmissions and associated resources. The factors
is function that is specific to the model. Note that if hybrid-ARQ is used, then the summation term should include all the H-ARQ transmissions and associated resources. The factors  and
and  allow adaptation of the model to the characteristics of modulation and coding used as well as any adjustments for coded packet length relative to a baseline curve. In this paper, we use
allow adaptation of the model to the characteristics of modulation and coding used as well as any adjustments for coded packet length relative to a baseline curve. In this paper, we use  for all
for all  . However, after calculating the effective SINR as described earlier, adjustments for packet size and channel estimation error are applied. These adjustments are computed using extensive link-level simulations for various fading channels and packet sizes. For the most part, the sensitivity to packet size is very minor and vanishes for packet sizes larger than around 500 bits. The work in [60] lists a few examples for the choice of
. However, after calculating the effective SINR as described earlier, adjustments for packet size and channel estimation error are applied. These adjustments are computed using extensive link-level simulations for various fading channels and packet sizes. For the most part, the sensitivity to packet size is very minor and vanishes for packet sizes larger than around 500 bits. The work in [60] lists a few examples for the choice of  as follows:
as follows:

The first expression represents the unconstrained Gaussian channel capacity, the second is an exponential approximation called (Effective Exponential SINR metric) and the last expression uses  the mutual information at an SINR
the mutual information at an SINR  , when modulation alphabet size of
, when modulation alphabet size of  is used. The last method, called Mutual Information Effective SINR Metric (MIESM), is widely used and is the method we will use in this paper. Once we compute the effective SINR per the above expression, then we look up the AWGN PER versus SINR curve corresponding to that modulation, code rate, and packet size to determine the probability of error. A binary random variable with that probability is then drawn and a corresponding error event is generated.
is used. The last method, called Mutual Information Effective SINR Metric (MIESM), is widely used and is the method we will use in this paper. Once we compute the effective SINR per the above expression, then we look up the AWGN PER versus SINR curve corresponding to that modulation, code rate, and packet size to determine the probability of error. A binary random variable with that probability is then drawn and a corresponding error event is generated.
Few additional points are noteworthy, described as follows.
-
(i)
Even though the aforementioned expressions are indexed by a resource element, in LTE, a resource element represents 1 sub-carrier (15 KHz) over 1 OFDM symbol (approximately 70 microseconds). This represents too fine a granularity and would slow down the simulation. Therefore, we use 1 resource block (180 KHz) over 1 subframe (1 millisecond) as the basic unit for generating the SINR in the simulation. Note that these values would lead to negligible, if any, loss in representation accuracy for practical delay spreads and Dopplers.
-
(ii)
Look-up table is used to calculate the mutual information indexed by SINR and modulation type. The LTE downlink uses 3 modulation types: QPSK, 16-QAM, and 64-QAM.
-
(iii)
We do not currently model modulation order adaptation on retransmissions.
-
(iv)
As suggested in [60], a single parameter
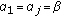 for all
for all 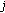 is used. In particular, a value of unity is used as mentioned earlier, with adjustments for channel estimation error and transport block size.
is used. In particular, a value of unity is used as mentioned earlier, with adjustments for channel estimation error and transport block size.
For CQI reporting, the effective SINR is calculated in a manner similar to the above, using LTE reference signals and the constrained capacity. The effective SINR is quantized to a 4-bit CQI value and fed back to the eNB. The table is generated from link curves in accordance with the block-error rate requirements of the LTE specification.
5.3. Traffic Models
The traffic models used for various simulations in Section 6 are, namely, full-buffer, streaming video, and live video. In full-buffer model, as the name suggests, each user's queue at eNB is assumed to always have infinite number of bits.
5.3.1. Streaming Video Model
Streaming video model is borrowed from [61], we summarize it here. Exactly 8 video packets arrive in a frame length of 100 milliseconds. Then the first arrival time from the beginning of a frame, as well as the seven subsequent interarrival times are independently drawn from a Pareto distribution with exponent 1.2 and truncated to [2.5 milliseconds, 12.5 milliseconds]. Moreover, packet sizes are independently drawn from a truncated Pareto distribution with exponent 0.8. The truncation depends on the desired mean rate, for example,  bytes for a mean rate of 90 kbps.
bytes for a mean rate of 90 kbps.
5.3.2. Live Video Model
Live video is modeled as an ON-OFF Markov process. When in ON state, a packet of fixed size is generated every 20 ms. The transition probabilities are such that half the time the process is in ON state. Moreover, mean dwelling time in either state is 2 seconds. Then the parameter which controls the mean rate of a live video flow is the packet size, for example, 1 kilobyte for a mean rate of 200 kbps. This model is similar to the VoIP model in [61] but with higher rate due to bigger packet sizes.
6. Simulation Results
In this section, we present the results of a simulation-based evaluation of opportunistic schedulers described in Section 4.2, and discuss the key insights into scheduler design. Three sets of results are presented, each considering a different model for the arrival traffic into the users' queues at eNBs. The three traffic models are, namely, saturated queues at the eNB, multirate streaming video, and a mix of streaming and live video; the three sets of results are discussed in what follows.
6.1. Queues at eNB Are Saturated
We start by presenting the results for the case where users' queues at the eNBs are saturated (or infinitely backlogged); these results provide a good comparison and calibration against other published studies.
6.1.1. Model
The network deployment model is as described in Section 5.1, with 57 cells (3 per eNB) and 20 users per cell. Figure 4 shows the empirical CDF of users' geometry, that is, users' SINR induced by the path-loss/shadowing model when all eNBs are transmitting at full power. Each user's queue at eNB is assumed to be infinitely backlogged, and the transmissions are scheduled according to a utility maximizing best effort scheduler described earlier in Section 4.2. Moreover, to limit the computational burden, the scheduler solves the underlying convex optimization problem once in every 8 subframes over a horizon of 8 milliseconds. Then in each subsequent subframe, the scheduler combines this solution with the current CQI and average rate to compute a schedule, as described in Section 4.4.
6.1.2. Results and Discussion
The performance measures of interest are the average cell throughput (i.e., cell throughput averaged across all 57 cells) and the distribution of individual users' throughput (i.e., time average of each user's rate) under various best effort schedulers, that is, as  associated with the utility function varies (see Section 4.2). Recall that
associated with the utility function varies (see Section 4.2). Recall that  reduces to max-min fair scheduling,
reduces to max-min fair scheduling,  to PF scheduling, and
to PF scheduling, and  to max-rate scheduling. Figure 5 shows the empirical CDFs of users' throughput (rate CDF for short) for the two cases,
to max-rate scheduling. Figure 5 shows the empirical CDFs of users' throughput (rate CDF for short) for the two cases,  and
and  , and Table 2 gives the respective cell throughput as well as the 5 and the 95 percentile read from the two rate CDFs. Clearly, users' throughput under the scheduler with
, and Table 2 gives the respective cell throughput as well as the 5 and the 95 percentile read from the two rate CDFs. Clearly, users' throughput under the scheduler with  is more fair than users' throughput under the scheduler with
is more fair than users' throughput under the scheduler with  , however, this fairness comes at the cost of 44% drop in the average cell throughput (see Table 2). Moreover, from the cross-over point of the two CDFs in Figure 5 and the percentiles in Table 2, as
, however, this fairness comes at the cost of 44% drop in the average cell throughput (see Table 2). Moreover, from the cross-over point of the two CDFs in Figure 5 and the percentiles in Table 2, as  is increased from 0 to 0.5, about half the users see a higher throughput (e.g., 3 times higher around the 95 percentile) at the cost of the other half seeing a lower throughput (e.g., 3 times lower around the 5 percentile). Similarly other tradeoffs between fairness and cell throughput can be obtained by varying
is increased from 0 to 0.5, about half the users see a higher throughput (e.g., 3 times higher around the 95 percentile) at the cost of the other half seeing a lower throughput (e.g., 3 times lower around the 5 percentile). Similarly other tradeoffs between fairness and cell throughput can be obtained by varying  , or by engineering other utility functions with desired slopes.
, or by engineering other utility functions with desired slopes.
6.1.3. Future Work
It is clear that rate CDFs in Figure 5 are optimal in that these cannot be dominated by the rate CDFs under any other scheduler (i.e., throughput of a user can only be improved at the cost of that of another). While the above simulation shows that the rate CDF can be controlled to a good degree by varying the utility function, still other more interesting scheduling objectives are, for example,
(i)deliver at least a minimum average rate  to each user
to each user  , or
, or
(ii)maximize a Utility function under minimum and maximum rate constraints.
Both these objectives can be met by devising appropriate utility functions that sharply increase at the minimum rate constraint and saturate at the maximum rate constraint. However, as briefly discussed in Subsection 2.1, these objectives can also be met using queue- and channel-aware schedulers augmented with virtual token queues. Such schedulers have been shown to offer greater control over the rate CDF [30, 52]. It would be interesting to obtain throughput numbers under these latter scheduling frameworks too.
6.2. Multirate Streaming Video
6.2.1. Model
The deployment model is as described in Section 5.1, with only 1 cell having 20 users. Therefore, the SNRs (induced by the path-loss and shadowing models) of the 20 users have the same empirical CDF as the SINR CDF of users in a multicell system (see Figure 4). Let  denote the SNR (induced by the path-loss and shadowing models) of user
denote the SNR (induced by the path-loss and shadowing models) of user  . We index the users in increasing order of
. We index the users in increasing order of  , that is, we have
, that is, we have  .
.
The  th user's queue at eNB is fed by a video stream (see Section 5.3) with mean rate
th user's queue at eNB is fed by a video stream (see Section 5.3) with mean rate  , and the transmissions are scheduled according to EDF, Log, or Exp rules described in Section 4.2. The parameters for each scheduler are fixed for a (soft) 99 percentile packet delay target of 250 milliseconds. We present results for two different operational scenarios.
, and the transmissions are scheduled according to EDF, Log, or Exp rules described in Section 4.2. The parameters for each scheduler are fixed for a (soft) 99 percentile packet delay target of 250 milliseconds. We present results for two different operational scenarios.
-
(a)
Load is 0.50 bps/Hz:
 kbps for
kbps for  and
and 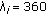 kbps for
kbps for  . That is, the mean rate of the video stream for the six lowest SNR users is 90 kbps, whereas, the mean rate of the video stream for the remaining fourteen users is 360 kbps.
. That is, the mean rate of the video stream for the six lowest SNR users is 90 kbps, whereas, the mean rate of the video stream for the remaining fourteen users is 360 kbps. -
(b)
Load is 0.64 bps/Hz:
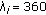 kbps for all users
kbps for all users  .
.
Figure 6 gives the plot of  for system load given in (a) and
for system load given in (a) and  for system load given in (b) versus
for system load given in (b) versus  for each user
for each user  . In order to better picture the system load, let us define the theoretical throughput
. In order to better picture the system load, let us define the theoretical throughput  that each user
that each user  will see over an AWGN channel under equal resource splitting and saturated queues, that is,
will see over an AWGN channel under equal resource splitting and saturated queues, that is,  ; (we note that this is roughly equal to the throughput users see under PF scheduling assuming infinitely back logged queues as in Section 6.1, that is, the gain due to opportunistic PF scheduling evens out the loss due to the errors and delays in CQI reports as well as errors in rate prediction). Figure 6 also gives a plot of
; (we note that this is roughly equal to the throughput users see under PF scheduling assuming infinitely back logged queues as in Section 6.1, that is, the gain due to opportunistic PF scheduling evens out the loss due to the errors and delays in CQI reports as well as errors in rate prediction). Figure 6 also gives a plot of  versus
versus  for
for  . For example, for the 6th user, rate
. For example, for the 6th user, rate  -
- , rate
, rate  -
- and rate
and rate  mbps are plotted against SNR
mbps are plotted against SNR  dB.
dB.
6.2.2. Results and Discussion
Recall that the EDF scheduler is not throughput optimal nor opportunistic. However, in the case (a) above, each  is chosen small enough for EDF scheduler to be stable; this, of course, does not guarantee that EDF will meet the QoS target of having the 99 percentile packet delay of less than 250 milliseconds. (The vector
is chosen small enough for EDF scheduler to be stable; this, of course, does not guarantee that EDF will meet the QoS target of having the 99 percentile packet delay of less than 250 milliseconds. (The vector  can be shown to lie in the capacity region achievable under non-opportunistic schedulers.) In fact, the mean and the 99 percentile packet delays of all users under EDF scheduler turn out to be around 670 milliseconds and 1325 milliseconds, respectively. However, under the opportunistic Log and Exp schedulers, all users comfortably meet their delay targets: Figure 7 shows the mean and 99 percentile packet delays of each user and overall system under Log and Exp schedulers. The delay target of 250 milliseconds is about ten times the channel coherence time and we see that for a reasonable system load, opportunistic scheduling greatly increases the number of QoS flows that can be admitted; (flows with tighter delay constraints are considered in the following subsection).
can be shown to lie in the capacity region achievable under non-opportunistic schedulers.) In fact, the mean and the 99 percentile packet delays of all users under EDF scheduler turn out to be around 670 milliseconds and 1325 milliseconds, respectively. However, under the opportunistic Log and Exp schedulers, all users comfortably meet their delay targets: Figure 7 shows the mean and 99 percentile packet delays of each user and overall system under Log and Exp schedulers. The delay target of 250 milliseconds is about ten times the channel coherence time and we see that for a reasonable system load, opportunistic scheduling greatly increases the number of QoS flows that can be admitted; (flows with tighter delay constraints are considered in the following subsection).
The results get more favorable to the Log rule as the system load increases to that mentioned in case (b) above (see Figure 7). QoS degrades more gracefully under the Log rule, in that 1 user under the LOG rule versus 19 under the Exp rule miss the soft delay target of 250 milliseconds. However, Exp rule still maintains a lower delay spread across users than the Log rule. Clearly, the Exp rule's strong bias toward balancing delays is excessively compromising the realized throughput, and eventually the mean delays and tails for almost all users. Although Exp rule asymptotically minimizes the exponential decay rate of the max-queue distribution irrespective of the values of parameters  , the pre-exponent must also be playing a role in determining the systems performance. The actual performance over the region of interest (not the theoretical asymptotic tail) achieved by the Exp rule is more sensitive to the values
, the pre-exponent must also be playing a role in determining the systems performance. The actual performance over the region of interest (not the theoretical asymptotic tail) achieved by the Exp rule is more sensitive to the values  . The RSM property of the Log rule naturally calibrates the scheduler to increased load. So unless parameters can be carefully tuned to possibly changing loads and unpredictable channel capacities, the Log rule appears to be more robust a scheduling policy. Intuitively, this is what one would expect from optimizing for the average/overall versus worst case asymptotic tail (see Section 2.1).
. The RSM property of the Log rule naturally calibrates the scheduler to increased load. So unless parameters can be carefully tuned to possibly changing loads and unpredictable channel capacities, the Log rule appears to be more robust a scheduling policy. Intuitively, this is what one would expect from optimizing for the average/overall versus worst case asymptotic tail (see Section 2.1).
Suppose the aforementioned simulations also had best effort flows which were scheduled only using the resources spared by the streaming video flows. In that case, it is desirable for a QoS scheduler to meet the delay targets of streaming flows by utilizing fewer resources. Table 3 gives the resource utilization, that is, average number of RBs allocated to streaming flows per subframe, under each scheduler considered earlier. So, for example, borrowing the cell throughput figure of 1.02 bps/Hz for PF scheduling from Table 2, the total throughput seen by the best effort flows in case (a) can be expected to be about 2 mbps under the LOG rule which is about 7% higher than that expected under the Exp rule.
6.3. Mix of Live and Streaming Video
6.3.1. Model
Except for the traffic model, the system is identical to the one described earlier, that is, the streaming video simulation. The traffic model is as follows. As before, the users are indexed in increasing order of SNR  . Then the queue at the eNB of each (odd) user
. Then the queue at the eNB of each (odd) user  is fed by a streaming video source (see Section 5.3), whereas the queue for each (even) user
is fed by a streaming video source (see Section 5.3), whereas the queue for each (even) user  is fed by a live video source. Video rates of each user are described later with the results. The 99 percentile delay target for live video flows is 80 milliseconds, whereas the target for streaming is 250 milliseconds as before. Transmissions are scheduled according to Log and Exp rules in two different manners.
is fed by a live video source. Video rates of each user are described later with the results. The 99 percentile delay target for live video flows is 80 milliseconds, whereas the target for streaming is 250 milliseconds as before. Transmissions are scheduled according to Log and Exp rules in two different manners.
-
(i)
Strict Priority Given to Live Video Flows. Live video flows are scheduled first (according to Log and Exp rules with parameters set according to the delay target of 80 ms), if any RBs are left over after scheduling the live video flows, those are allocated to the streaming flows (again using Log and Exp rules with parameters set according to the delay target of 250 milliseconds). This scheduling method will be referred to as priority-Exp and priority-Log rules.
-
(ii)
All Flows Compete for Resources. Live video flows are not prioritized in order of scheduling. Setting of scheduler parameters is described later with the results. Since resources are completely shared by the two classes of flows, this scheduling method will be referred to as complete-sharing, and written as cs-Exp and cs-Log rule for short.
6.3.2. Results and Discussion
We first determine by trail the highest arrival rate that all live video flows can be set to while still meeting the delay targets under both the priority-Exp and priority-Log rules. This turns out be around 200 kbps. The detailed results from this trial are not shown, however, we present the following interesting observation: even though the channel is loaded to its capacity under the priority-Exp and priority Log rules when all live video flows are set to 200 kbps, we find that the system can still admit up to 10 streaming video users (5 higher SNR users at rate 360 kbps and 5 lower SNR users at 90 kbps) under priority-Exp and priority-Log rules while meeting their delay targets of 250 milliseconds. This is because the capacity (in terms of number of users that can be supported) of a time-varying channel is constrained by the delay targets: the longer the delay targets, the greater the opportunity to wait for a good channel thus exploiting opportunistic gain.
Since we want to mix live and streaming flows (the former with a much tighter delay deadline than the latter) and investigate the pros and cons of priority versus complete-sharing scheduling, we set the arrival rate of each live video flow to  kbps (instead of a maximum possible of 200 kbps) to make the problem interesting. That is, for each user
kbps (instead of a maximum possible of 200 kbps) to make the problem interesting. That is, for each user  we have
we have  kbps. Next, we set the arrival rate for all streaming video flows to
kbps. Next, we set the arrival rate for all streaming video flows to  kbps, that is, for each user
kbps, that is, for each user  we have
we have  kbps. Figure 8 illustrates
kbps. Figure 8 illustrates  and
and  versus
versus  for each user
for each user  .
.
Figure 9 shows the 99 percentile delays seen by both live and streaming video flows under priority-Log and priority-Exp rule (right two curves). Under these priority schedulers, while all live video users clearly meet their delay targets, 1 streaming video user under priority-Log while 3 under priority-Exp rule miss their soft delay targets of 250 milliseconds: the resources left over after scheduling live video users prove too scarce to meet the delay targets of all streaming video users. The question naturally arises: will delay performance improve if, instead of strictly prioritizing live video users, the users are opportunistically prioritized by using the parameters in each scheduler and letting all users compete for resources?
We find that when scheduler parameters for each user are set according to their delay targets, both cs-Log and cs-Exp rules comfortably meet the delay targets for streaming video users but fail for three or four live video users by up to 30 milliseconds (these results are not plotted). This is not desirable since streaming video delay targets are soft and if a scheduler must degrade performance a little, it should pick a streaming video user for that. While the priority schedulers were giving insufficient resources to the streaming flows, the complete-sharing schedulers are giving insufficient resources to the live flows.
Both cs-Log and cs-Exp rules can be made to give higher priority to the live video users by, for example, setting the parameters of live video users for a delay target of lower than 80 ms. Indeed, when the scheduler parameters of live video users are set according to the delay target of 50 milliseconds for Exp rule and 10 milliseconds for Log rule, all users meet their delay targets under cs-Exp rule, whereas, all but 1 live video users do under cs-Log rule (see Figure 9, left two curves). Table 4 gives resource utilization under each scheduler and shows that cs-Log rule makes available the most resources for any best effort users in the system, although by a small margin.
We conclude that although complete-sharing scheduling involves more complexity (due to the need for correctly setting relative priority of different classes), it not only reduces system utilization but it also improves system capacity in terms of number of users that can be supported. Infact, in a slightly different setting, [62] quantifies the capacity gains due to a candidate complete-sharing scheduler presented therein, with the caveat that indeed as QoS requirements on real-time traffic become tighter, the opportunistic gain due to complete-sharing diminishes as, eventually, one would need to simply give strict priority to real-time traffic. While call setup/SIP traffic cannot be treated as having the same priority as, say, streaming video (see [1]), our simulations show that perhaps cs-Exp or cs-Log scheduler can used to appropriately prioritize the SIP traffic.
7. Conclusions
LTE is a purely scheduled system that allows dynamic scheduling for diverse traffic types including delay-sensitive flows. By leveraging recent results on resource allocation and scheduling, we design a practical LTE downlink scheduler and characterized its performance for three traffic scenarios, namely, full-buffer, streaming video (loose delay constraint), and mixed streaming and live video (tight delay constraint). We show that the proposed utility maximizing scheduler offers good control over the rate CDF for the full buffer case. Similarly, we show that Exp and Log rules can support a mix of QoS traffic while increasing system capacity in terms of number of users that can be supported and, at the same time, reducing resource utilization.
Having evaluated various scheduling policies with a simpler (although complete) design, future work includes the implementation of other interesting features offered by LTE specifications, for example, asynchronous and adaptive HARQ for downlink, power shaping, and frequency-selective scheduling. Moreover, new scheduling policies will be considered, for example, one that resembles Exp rule when sum-delay is small but resembles Log rule when sum-delay is large (see Figure 1) can perhaps keep the delay spread small across users while still offering graceful degradation of service when system load increases (due to changes in traffic or wireless channel.)
References
Wernersson M, Wanstedt S, Synnergren P: Effects of QOS scheduling strategies on performance of mixed services over LTE. Proceedings of the 18th IEEE International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC '07), September 2007 1-5.
Pokhariyal A, Monghal G, Pedersen KI, et al.: Frequency domain packet scheduling under fractional load for the UTRAN LTE downlink. Proceedings of the 65th IEEE Vehicular Technology Conference (VTC '07), April 2007 699-703.
Andrews M, Kumaran K, Ramanan K, Stolyar A, Vijayakumar R, Whiting P: Scheduling in a queuing system with asynchronously varying service rates. Probability in the Engineering and Informational Sciences 2004, 18(2):191-217.
Shakkottai S, Stolyar A: Scheduling for multiple flows sharing a time-varying channel: the exponential rule. In Analytic Methods in Applied Probability, American Mathematical Society Translations, Series 2, A Volume in Memory of F. Karpelevich. Volume 207. American Mathematical Society, Providence, RI, USA; 2002:185-202.
Sadiq B, Baek SJ, de Veciana G: Delay-optimal opportunistic scheduling and approximations: the Log rule. Proceedings of the 27th Annual Joint Conference on the IEEE Computer and Communications Societies (INFOCOM '09), April 2009 1-9.
Shakkottai S, Rappaport T: Research challenges in wireless networks: a technical overview. Proceedings of the 5th International Symposium on Wireless Personal Multimedia Communications (WPMC '02), October 2002 1: 12-18.
Georgiadis L, Neely MJ, Tassiulas L: Resource allocation and cross-layer control in wireless networks. Foundations and Trends in Networking 2006, 1(1):1-144. 10.1561/1700000002
Kelly FP, Maulloo AK, Tan D: Rate control for communication networks: shadow prices, proportional fairness and stability. Journal of the Operational Research Society 1998, 49(3):237-252.
Tse D, Viswanath P: Fundamentals of Wireless Communcation. Cambridge University Press, Cambridge, UK; 2005.
Holtzman JM: Asymptotic analysis of proportional fair algorithm. Proceedings of the 12th IEEE International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC '01), September-October 2001, San Diego, Calif, USA 2: F33-F37.
Borst S: User-level performance of channel-aware scheduling algorithms in wireless data networks. Proceedings of the 22nd Annual Joint Conference on the IEEE Computer and Communications Societies (INFOCOM '03), March-April 2003, San Francisco, Calif, USA 1: 321-331.
Kushner HJ, Whiting PA: Convergence of proportional-fair sharing algorithms under general conditions. IEEE Transactions on Wireless Communications 2004, 3(4):1250-1259. 10.1109/TWC.2004.830826
Huang J, Subramanian VG, Agrawal R, Berry R: Downlink scheduling and resource allocation for OFDM systems. Proceedings of the Conference on Information Sciences and Systems (CISS '06), 2006
Stolyar AL: On the asymptotic optimality of the gradient scheduling algorithm for multiuser throughput allocation. Operations Research 2005, 53(1):12-25. 10.1287/opre.1040.0156
Jang J, Lee KB: Transmit power adaptation for multiuser OFDM systems. IEEE Journal on Selected Areas in Communications 2003, 21(2):171-178. 10.1109/JSAC.2002.807348
Hoo LMC, Halder B, Tellado J, Cioffi JM: Multiuser transmit optimization for multicarrier broadcast channels: asymptotic FDMA capacity region and algorithms. IEEE Transactions on Communications 2004, 52(6):922-930. 10.1109/TCOMM.2004.829570
Zhang YJ, Letaief KB: Multiuser adaptive subcarrier-and-bit allocation with adaptive cell selection for ofdm systems. IEEE Transactions on Wireless Communications 2004, 3(5):1566-1575. 10.1109/TWC.2004.833501
Yin H, Liu H: An efficient multiuser loading algorithm for OFDM-based broadband wireless systems. Proceedings of the IEEE Global Communications Conference (GLOBECOM '00), 2000
Seong K, Mohseni M, Cioffi JM: Optimal resource allocation for OFDMA downlink systems. Proceedings of the IEEE International Symposium on Information Theory (ISIT '06), July 2006 1394-1398.
Madan R, Boyd SP, Lall S: Fast algorithms for resource allocation in cellular networks. to appear in IEEE/ACM Transactions on Networking
Tassiulas L, Ephremides A: Stability properties of constrained queueing systems and scheduling policies for maximum throughput in multihop radio networks. Proceedings of the 29th IEEE Conference on Decision and Control (CDC '90), December 1990 4: 2130-2132.
Neely MJ, Modiano E, Rohrs CE: Power and server allocation in a multi-beam satellite with time varying channels. Proceedings of the 21st Annual Joint Conference of the IEEE Computer and Communications Societies (INFOCOM '02), 2002 3: 1451-1460.
Neely MJ, Modiano E, Rohrs CE: Dynamic power allocation and routing for time-varying wireless networks. Proceedings of the 22nd Annual Joint Conference of the IEEE Computer and Communications Societies (INFOCOM '03), March-April 2003 1: 745-755.
Venkataramanan VJ, Lin X: On wireless scheduling algorithms for minimizing the queue-overflow probability. submitted to IEEE/ACM Transactions on Networking
Stolyar AL: Large deviations of queues sharing a randomly time-varying server. Queueing Systems 2008, 59(1):1-35. 10.1007/s11134-008-9072-y
Sadiq B, de Veciana G: Large deviation sum-queue optimality of a radial sum-rate monotone opportunistic scheduler. submitted to IEEE Transactions on Information Theory
Shakkottai S, Srikant R: Scheduling real-time traffic with deadlines over a wireless channel. Wireless Networks 2002, 8(1):13-26. 10.1023/A:1012763307361
Chen N, Jordan S: Throughput in processor-sharing queues. IEEE Transactions on Automatic Control 2007, 52(2):299-305.
Chen N, Jordan S: Downlink scheduling with probabilistic guarantees on short-term average throughputs. Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC '08), March-April 2008, Las Vegas, Nev, USA 1865-1870.
Shakkottai S, Stolyar A: Scheduling algorithms for a mixture of real-time and non-real-time data in HDR. Proceedings of the 17th International Teletraffic Congress (ITC '01), 2001
Agarwal R, Majjigi V, Vannithamby R, Cioffi JM: Efficient scheduling for heterogeneous services in OFDMA downlink. Proceedings of the IEEE Global Telecommunications Conference (GLOBECOM '07), November 2007 3235-3239.
Lerida M: Adaptive radio resource management for VoIP and data traffic in 3GPP LTE networks, M.S. thesis. KTH Royal Institute of Technology, Stockholm, Sweden; 2008.
Wernersson M, Wänstedt S, Synnergren P: Effects of QOS scheduling strategies on performance of mixed services over LTE. Proceedings of the 18th IEEE International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC '07), September 2007, Athens, Greece 1-5.
Gidlund M, Laneri J-C: Scheduling algorithms for 3GPP longterm evolution systems: from a quality of service perspective. Proceedings of the 10th IEEE International Symposium on Spread Spectrum Techniques and Applications (ISSSTA '08), August 2008 114-117.
Lei H, Yu M, Zhao A, Chang Y, Yang D: Adaptive connection admission control algorithm for LTE systems. Proceedings of the IEEE Vehicular Technology Conference (VTC '08), May 2008 2336-2340.
Jiang D, Wang H, Malkamaki E, Tuomaala E: Principle and performance of semi-persistent scheduling for VoIP in LTE system. Proceedings of the International Conference on Wireless Communications, Networking and Mobile Computing (WiCOM '07), September 2007 2861-2864.
Choi S, Jun K, Shin Y, Kang S, Choi B: MAC scheduling scheme for VoIP traffic service in 3G LTE. Proceedings of the 66th IEEE Vehicular Technology Conference (VTC '07), September-October 2007, Baltimore, Md, USA 1441-1445.
Wang H, Jiang D: Performance comparison of control-less scheduling policies for VoIP in LTE UL. Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC '08), March-April 2008, Las Vegas, Nev, USA 2497-2501.
Pokhariyal A, Monghal G, Pedersen KI, et al.: Frequency domain packet scheduling under fractional load for the UTRAN LTE downlink. Proceedings of the 65th IEEE Vehicular Technology Conference (VTC '07), April 2007, Dublin, Ireland 699-703.
Ning X, Ting Z, Ying W, Ping Z: A MC-GMR scheduler for shared data channel in 3GPP LTE system. Proceedings of the 64th IEEE Vehicular Technology Conference (VTC '06), September 2006, Montreal, Canada 1-5.
Kela P, Puttonen J, Kolehmainen N, Ristaniemi T, Henttonen T, Moisio M: Dynamic packet scheduling performance in UTRA long term evolution downlink. Proceedings of the 3rd International Symposium on Wireless Pervasive Computing (ISWPC '08), May 2008 308-313.
Assaad M, Mourad A: New frequency-time scheduling algorithms for 3GPP/LTE-like OFDMA air interface in the downlink. Proceedings of the IEEE Vehicular Technology Conference (VTC '08), May 2008 1964-1969.
Beh KC, Armour S, Doufexi A: Joint time-frequency domain proportional fair scheduler with HARQ for 3GPP LTE systems. Proceedings of the 68th IEEE Vehicular Technology Conference (VTC '08), September 2008 1-5.
Al-Rawi M, Jantti R, Torsner J, Sagfors M: Opportunistic uplink scheduling for 3G LTE systems. Proceedings of the 4th International Conference on Innovations in Information Technology (IIT '07), November 2007 705-709.
Calabrese FD, Michaelsen PH, Rosa C, et al.: Search-tree based uplink channel aware packet scheduling for UTRAN LTE. Proceedings of the IEEE Vehicular Technology Conference (VTC '08), May 2008 1949-1953.
Castellanos CU, Villa DL, Rosa C, et al.: Performance of uplink fractional power control in UTRAN LTE. Proceedings of the IEEE Vehicular Technology Conference (VTC '08), May 2008 2517-2521.
Anas M, Rosa C, Calabrese FD, Michaelsen PH, Pedersen KI, Mogensen PE: QoS-aware single cell admission control for UTRAN LTE uplink. Proceedings of the IEEE Vehicular Technology Conference (VTC '08), May 2008 2487-2491.
Liu X, Chong EKP, Shroff NB: A framework for opportunistic scheduling in wireless networks. Computer Networks 2003, 41(4):451-474. 10.1016/S1389-1286(02)00401-2
Andrews M: Instability of the proportional fair scheduling algorithm for HDR. IEEE Transactions on Wireless Communications 2004, 3(5):1422-1426. 10.1109/TWC.2004.833419
Eryilmaz A, Srikant R, Perkins JR: Stable scheduling policies for fading wireless channels. IEEE/ACM Transactions on Networking 2005, 13(2):411-424.
Zhou C, Wunder G: General stability conditions in wireless broadcast channels. Proceedings of the 46th Annual Allerton Conference on Communication, Control, and Computing, September 2008 675-682.
Andrews M, Qian L, Stolyar A: Optimal utility based multi-user throughput allocation subject to throughput constraints. Proceedings of the 24th IEEE Annual Joint Conference of the Computer and Communications Societies (INFOCOM '05), March 2005 4: 2415-2424.
Neely MJ: Order optimal delay for opportunistic scheduling in multiuser wireless uplinks and downlinks. IEEE/ACM Transactions on Networking 2008, 16(5):1188-1199.
Yavuz M, Paranchych D: Adaptive rate control in high data rate wireless networks. Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC '03), March 2003 2: 866-871.
3GPP TR 25.814 : Physical layer aspects for evolved universal terrestrial radio access (UTRA). http://www.3gpp.org/
3GPP TR 25.848 : Physical layer aspects of utra high speed downlink packet access. http://www.3gpp.org/
3GPP 25.896 : Feasibility study for enhanced uplink for UTRA FDD. http://www.3gpp.org/
3GPP2 C.R1002-0 Version 1.0 : CDMA2000 evaluation methodology. http://www.3gpp2.org/
Rappaport TS: Wireless Communications: Principles and Practice. Prentice-Hall, Upper Saddle River, NJ, USA; 2002.
Brueninghaus K, Astélyt D, Salzer T, et al.: Link performance models for system level simulations of broadband radio access systems. Proceedings of the IEEE International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC '05), 2005 4: 2306-2311.
NGMN radio access performance evaluation methodology 2008.
Patil S, de Veciana G: Managing resources and quality of service in heterogeneous wireless systems exploiting opportunism. IEEE/ACM Transactions on Networking 2007, 15(5):1046-1058.
Acknowledgments
This work was performed while B. Sadiq was at Qualcomm Flarion Technologies. This research was supported in part by NSF grant CNS-0721532. The authors thank Shelley Gu, Shailesh Patil, Sundeep Rangan, Niranjan Ratnakar, and Siddharth Ray for their help in developing the LTE system simulation infrastructure for studying scheduling algorithms. The authors also thank Raja Bachu for many discussions on the LTE specification.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Sadiq, B., Madan, R. & Sampath, A. Downlink Scheduling for Multiclass Traffic in LTE. J Wireless Com Network 2009, 510617 (2009). https://doi.org/10.1155/2009/510617
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/510617
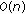 for
for  users—this complexity is amortized over multiple time steps.
users—this complexity is amortized over multiple time steps. for the scheduler in (1) to be throughput optimal have also been shown [
for the scheduler in (1) to be throughput optimal have also been shown [
 is constant in
is constant in  ,
, is decreasing in
is decreasing in  , and in the limit
, and in the limit  , only the longest queue(s) are scheduled (as long as their channels are nonzero),
, only the longest queue(s) are scheduled (as long as their channels are nonzero),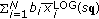 is increasing in
is increasing in  , and in the limit
, and in the limit  , the sum is the maximum possible. For example, with each
, the sum is the maximum possible. For example, with each  set to
set to 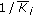 in (3),
in (3), 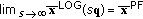 . This property is called radial sum-rate monotonicity (RSM).
. This property is called radial sum-rate monotonicity (RSM).
 the most recent wideband CQI value received by the eNB at or before time
the most recent wideband CQI value received by the eNB at or before time  for user
for user  . The LTE system allows several reporting options for both wideband (over the system bandwidth) and subband (narrower than the system bandwidth) CQI, with the latter allowing exploitation of frequency selective fading.
. The LTE system allows several reporting options for both wideband (over the system bandwidth) and subband (narrower than the system bandwidth) CQI, with the latter allowing exploitation of frequency selective fading. , the queue length in (the beginning of) subframe
, the queue length in (the beginning of) subframe  , denoted by
, denoted by  bits, and the delay of each packet in the queue, with
bits, and the delay of each packet in the queue, with  ms denoting the delay of head-of-line packet, is available at the scheduler.
ms denoting the delay of head-of-line packet, is available at the scheduler.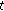 , ACK/NACK for all transmissions scheduled in subframe
, ACK/NACK for all transmissions scheduled in subframe  are known to the scheduler.
are known to the scheduler. at which a user is served. The average rate is updated at every time
at which a user is served. The average rate is updated at every time  using an exponential filter as follows:
using an exponential filter as follows: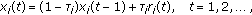
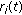 is the rate allocated to the
is the rate allocated to the  th user at time
th user at time  , and
, and 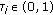 is a user specific constant; we refer to
is a user specific constant; we refer to 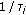 as time-constant for (rate averaging for) user
as time-constant for (rate averaging for) user  .
.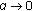 , the scheduler reduces to a proportional fair scheduler. Specifically, this scheduler will allocate the next fraction of available bandwidth resource to a user with maximum
, the scheduler reduces to a proportional fair scheduler. Specifically, this scheduler will allocate the next fraction of available bandwidth resource to a user with maximum  .
. , this scheduler reduces to max sum-rate scheduler.
, this scheduler reduces to max sum-rate scheduler. , it reduces to the max-min fair scheduler, that is, it maximizes the minimum average rate.
, it reduces to the max-min fair scheduler, that is, it maximizes the minimum average rate.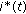 satisfying
satisfying
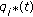 is decremented and
is decremented and 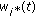 is updated based on the new buffer state. This is done before the scheduler computes the optimal user for the next RB.
is updated based on the new buffer state. This is done before the scheduler computes the optimal user for the next RB.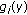 as
as
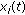 is the average rate allocated to user
is the average rate allocated to user  as computed by an exponential filter at time
as computed by an exponential filter at time  (see (11)).
(see (11)).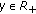 ,
,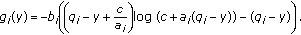
 is defined as
is defined as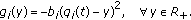
 .
.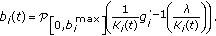
 .
. ,
,  , else
, else 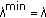 .
. ,
, 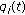 , and/or
, and/or 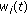 , based on RB assignments in each subframe (as they are made).
, based on RB assignments in each subframe (as they are made). (for users for which a CQI report was received in the previous subframe).
(for users for which a CQI report was received in the previous subframe).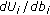 at
at  , once the above two updates have been made.
, once the above two updates have been made.
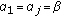 for all
for all 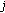 is used. In particular, a value of unity is used as mentioned earlier, with adjustments for channel estimation error and transport block size.
is used. In particular, a value of unity is used as mentioned earlier, with adjustments for channel estimation error and transport block size.

 (PF) and
(PF) and
 .
.
 kbps for
kbps for  and
and 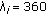 kbps for
kbps for  . That is, the mean rate of the video stream for the six lowest SNR users is 90 kbps, whereas, the mean rate of the video stream for the remaining fourteen users is 360 kbps.
. That is, the mean rate of the video stream for the six lowest SNR users is 90 kbps, whereas, the mean rate of the video stream for the remaining fourteen users is 360 kbps.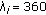 kbps for all users
kbps for all users  .
.



 )-tick represents streaming video user's delay.
)-tick represents streaming video user's delay.