- Research Article
- Open access
- Published:
Propagation in Tunnels: Experimental Investigations and Channel Modeling in a Wide Frequency Band for MIMO Applications
EURASIP Journal on Wireless Communications and Networking volume 2009, Article number: 560571 (2009)
Abstract
The analysis of the electromagnetic field statistics in an arched tunnel is presented. The investigation is based on experimental data obtained during extensive measurement campaigns in a frequency band extending from 2.8 GHz up to 5 GHz and for a range varying between 50 m and 500 m. Simple channel models that can be used for simulating MIMO links are also proposed.
1. Introduction
Narrowband wireless communications in confined environments, such as tunnels, have been widely studied for years, and a lot of experimental results have been presented in the literature in environmental categories ranging from mine galleries and underground old quarries to road and railway tunnels [1–4].
However, in most cases, measurements dealt with channel characterization for few discrete frequencies, often around 900 MHz and 1800 MHz. For example, in [5, 6] Zhang et al. report statistical narrowband and wideband measurement results. In [7], results on planning of the Global System for Mobile Communication for Railway (GMS-R) are presented. In [8], simulations and measurements are also described in the same GSM frequency band. In [9], the prediction of received power in the out-of-zone of a dedicated short range communications (DSRC) system operating inside a typical arched highway tunnel is discussed, and in this case the channel impulse response was measured with a sounder at 5.2 GHz whose bandwidth is on the order of 100 MHz. Recently, in [10], measurement campaigns have been performed in underground mines in the 2–5 GHz band but the results cannot be extrapolated to road and railway tunnels since the topology is quite different. In a mine gallery, roughness is very important, the typical width is 3 m, the geometry of the cross-section is not well defined and lastly, there are often many changes in the tunnel direction.
Furthermore, to increase the channel capacity in tunnels, space diversity both at the mobile and at the fixed base station can be introduced. However, good performances of multiple input multiple output (MIMO) techniques can be obtained under the condition of a small correlation between paths relating each transmitting and receiving antennas. This decorrelation is usually ensured by the multiple reflections on randomly distributed obstacles, giving often rise to a wide spread in the direction of arrival of the rays. On the contrary, a tunnel plays the role of an oversized waveguide and decorrelation can be due to the superposition of the numerous hybrid modes supported by the structure [11]. Experimental results at 900 MHz for a  MIMO configuration, are described in [12]. This paper shows that the antenna arrays must be put in the transverse plane of the tunnel to minimize the coupling between elements.
MIMO configuration, are described in [12]. This paper shows that the antenna arrays must be put in the transverse plane of the tunnel to minimize the coupling between elements.
The objective of this work is thus to extend the previous approaches by investigating the statistics of the electric field distribution in the 2.8–5 GHz frequency range in a tunnel environment for MIMO applications. Empirical formulas based on the experimental results are also proposed.
We proceed in two steps: (1) determination of the mean path loss and of the statistical distribution of the average field which can be received by the various antennas of an MIMO system. This first approach can thus be used to determine the average power related to the H matrix of an MIMO link, (2) field distribution and correlation in a transverse plane.
The paper is distributed as follows. Section 2 explains the experiments in detail and more specifically the environment and methodology of the measurements that has been followed. Section 3 investigates path loss and axial correlation while, in Section 4, field statistics in the transverse plane are analyzed. Section 5 deals with the transverse spatial correlation and Section 6 presents the principle of modeling the MIMO channel and gives an example of application. Finally, Section 7 summarizes the contributions of the present work and gives conclusions.
2. Environment, Measurement Equipment, and Methodology
2.1. Description of the Environment
The measurement campaign was performed in a 2-way tunnel, situated in the French Massif Central mountains. This straight tunnel, 3.4 km long, has a semicircular shape, as shown in Figure 1. The diameter of the cylindrical part is 8.6 m and the maximum height of the tunnel is 6.1 m. The tunnel was empty with no pipes, cables, or lights. However, every 100 m there are small safety zones, 1 m wide and few meters long, where an extinguisher is hung. It is difficult to estimate the roughness accurately but it is on the order of a centimetre. The tunnel was closed to traffic during the experiments, to make measurements in stationary conditions.
2.2. Measurement Equipment
Since we want to explore the channel response in a very wide frequency band (2.8–5 GHz), we have chosen to make measurements in the frequency domain rather than in the time domain, so as to get better accurate results. The complex channel transfer function between the transmitting (Tx) and receiving (Rx) antennas has thus been obtained by measuring the  parameter with a vector network analyzer (VNA Agilent E5071B). The Rx antenna is directly connected to one port of the VNA using a low attenuation coaxial cable, 4 m long, a 30 dB low-noise amplifier being inserted or not, depending on the received power. Using a coaxial cable to connect the Tx antenna to the other port of the VNA would lead to prohibitive attenuation, the maximum distance between Tx and Rx being 500 m. The signal of the Tx port of the VNA is thus converted to an optical signal which is sent through fibre optics, converted back to radio frequency and amplified. The signal feeding the vertical biconical transmitting (Tx) antenna has a power of 1 W. The phase stability of the fibre optics link has been checked and the calibration of the VNA takes amplifiers, cables, and optic coupler into account. The block diagram of the channel sounder is depicted in Figure 2.
parameter with a vector network analyzer (VNA Agilent E5071B). The Rx antenna is directly connected to one port of the VNA using a low attenuation coaxial cable, 4 m long, a 30 dB low-noise amplifier being inserted or not, depending on the received power. Using a coaxial cable to connect the Tx antenna to the other port of the VNA would lead to prohibitive attenuation, the maximum distance between Tx and Rx being 500 m. The signal of the Tx port of the VNA is thus converted to an optical signal which is sent through fibre optics, converted back to radio frequency and amplified. The signal feeding the vertical biconical transmitting (Tx) antenna has a power of 1 W. The phase stability of the fibre optics link has been checked and the calibration of the VNA takes amplifiers, cables, and optic coupler into account. The block diagram of the channel sounder is depicted in Figure 2.
The wideband biconical antennas (Electrometrics EM-6116) used in this experiment have nearly a flat gain, between 2 and 10 GHz. Indeed, the frequency response of the two antennas has been measured in an anechoic chamber, and the variation of the antenna gain was found to be less than 2 dB in our frequency range. Nevertheless, we have subtracted the antenna effect in the measurements, as it will be explained in Section 3.
It must also be emphasized that, in general, the radiation pattern of wideband antennas is also frequency dependent. This is not a critical point in our case since, in a tunnel, only waves impinging the tunnel walls with a grazing angle of incidence contribute to the total received power significantly. This means that, whatever the frequency, the angular spread of the received rays remains much smaller than the 3 dB beam width of the main antenna lobe in the E plane, equal to about 80°, the antenna being nearly omnidirectional in the H plane.
Since the channel transfer function may also strongly depend on the position of the antennas in the transverse plane of the tunnel, both Tx and Rx antennas were mounted on rails. The position mechanical systems are remote controlled, optic fibres connecting the step by step motors to the control unit.
2.3. Methodology
The channel frequency response has been measured for 1601 frequency points, equally spaced between 2.8 and 5 GHz, leading to a frequency step of 1.37 MHz.
The rails supporting the Tx and Rx antennas were put at a height of 1 m and centred on the same lane of this 2-lane tunnel. For each successive axial distance d, both the Tx and Rx antennas were moved in the transverse plane on a distance of 33 cm, with a spatial step of 3 cm, corresponding to half a wavelength at 5 GHz. A  transfer matrix is thus obtained, the configuration of the measurements being schematically described in Figrue 3. Fine spatial sampling was chosen for measurements in the transverse plane because, as recalled in the introduction, antenna arrays for MIMO applications have to be put in this plane to minimize correlation between array elements.
transfer matrix is thus obtained, the configuration of the measurements being schematically described in Figrue 3. Fine spatial sampling was chosen for measurements in the transverse plane because, as recalled in the introduction, antenna arrays for MIMO applications have to be put in this plane to minimize correlation between array elements.
Due to the limited time available for such an experiment and to operational constraints, it was not possible to extensively repeat such measurements for very small steps along the tunnel axis. In the experiments described in this paper, the axial step was chosen equal to 4 m when 50 m <d < 202 m and to 6 m when 202 m <d < 500 m. This is not critical because we are interested, in the axial direction, by the mean path loss and by the large-scale fluctuation of the average power received in the transverse plane. At each Tx and Rx position, 5 successive recordings of field variation versus frequency are stored and averaged.
It must be noted that in the case of a single input single output (SISO) link, a number of papers have already been published on the small-scale variation of a narrowband signal along the tunnel axis. For example, [13] describes results of experiments carried out in a wide tunnel at a frequency of 900 MHz. A summary of the measurement parameters and equipment characteristics is summarized in Table 1.
3. Path Loss and Correlation Along the Longitudinal Axis
3.1. Path Loss
The path loss is deduced from the measurement of the  scattering parameter. However, as briefly mentioned in the previous section, it can be more interesting to subtract the effects of the variation of the antenna characteristics with frequency by introducing a correction factor
scattering parameter. However, as briefly mentioned in the previous section, it can be more interesting to subtract the effects of the variation of the antenna characteristics with frequency by introducing a correction factor  . We have thus made preliminary measurements by putting the two biconical antennas, 1 m apart, in an anechoic room. Let
. We have thus made preliminary measurements by putting the two biconical antennas, 1 m apart, in an anechoic room. Let  be the scattering parameter measured in this configuration. The correction factor is thus given by
be the scattering parameter measured in this configuration. The correction factor is thus given by  , where
, where  means the average of x over the frequency band.
means the average of x over the frequency band.
The path loss in tunnel, taking this correction into account, is given by

Figure 4 shows the variation of  versus frequency, for
versus frequency, for  m. The fluctuation of the field amplitude is due to the combination in phase or out of phase of the various modes excited by the transmitting antenna, the phase of the propagation constant depending on frequency but also on the order of the hybrid modes propagating in the tunnel. To extract the variation of the mean path loss versus frequency, it is interesting to average such curves, obtained at any distance d, for the various transverse positions of the antennas. Furthermore, one can also average over few frequencies, considering a frequency bandwidth smaller than the channel coherence bandwidth. In this example, the coherence bandwidth being on the order of 10 MHz,
m. The fluctuation of the field amplitude is due to the combination in phase or out of phase of the various modes excited by the transmitting antenna, the phase of the propagation constant depending on frequency but also on the order of the hybrid modes propagating in the tunnel. To extract the variation of the mean path loss versus frequency, it is interesting to average such curves, obtained at any distance d, for the various transverse positions of the antennas. Furthermore, one can also average over few frequencies, considering a frequency bandwidth smaller than the channel coherence bandwidth. In this example, the coherence bandwidth being on the order of 10 MHz,  was averaged over 7 frequencies around f, the frequency step being 1.37 MHz, and over the 144 successive combinations of the transverse positions of the Tx and Rx antennas. The average value
was averaged over 7 frequencies around f, the frequency step being 1.37 MHz, and over the 144 successive combinations of the transverse positions of the Tx and Rx antennas. The average value  is also plotted in Figure 4.
is also plotted in Figure 4.
The curves "measurements" in Figure 5 represent the variation of  versus axial distance at 3 and 5 GHz. The path loss, at 3 GHz, corresponding to free-space conditions, has been also plotted. We see that, in this frequency range, the path loss is only slightly dependent on frequency.
versus axial distance at 3 and 5 GHz. The path loss, at 3 GHz, corresponding to free-space conditions, has been also plotted. We see that, in this frequency range, the path loss is only slightly dependent on frequency.
To deduce from these curves a simple theoretical model of the mean path loss  , these curves must be smoothed again by introducing a running mean over the axial distance. To get a very simple approximate analytical expression of
, these curves must be smoothed again by introducing a running mean over the axial distance. To get a very simple approximate analytical expression of  , it is assumed that
, it is assumed that  is the product of two functions, one depending on f and one depending on d [14].
is the product of two functions, one depending on f and one depending on d [14].
Furthermore, it is usually expressed in terms of two path loss exponents,  and
and  which indicate the rate at which the path loss decreases with frequency and distance, respectively, [15]. This leads to
which indicate the rate at which the path loss decreases with frequency and distance, respectively, [15]. This leads to

The constant  and the path loss exponents have been determined by minimizing the mean square error between the measurements and the model. The following values were found:
and the path loss exponents have been determined by minimizing the mean square error between the measurements and the model. The following values were found:  dB,
dB,  , and
, and  . The corresponding curves for 3 and 5 GHz have also been plotted in Figure 5. It must be outlined that all these values were deduced from measurements between 50 and 500 m and consequently, they are valid only in this range of axial distance.
. The corresponding curves for 3 and 5 GHz have also been plotted in Figure 5. It must be outlined that all these values were deduced from measurements between 50 and 500 m and consequently, they are valid only in this range of axial distance.
It can be interesting to compare this value of  to those already published in the literature and corresponding to attenuation factors measured for ultra-wideband systems in indoor environments. However, in this case, the range is much smaller, typically below 50 m. In line of sight (LOS) conditions, values from 1.3 to 1.7 were reported by [16, 17], while for non-LOS,
to those already published in the literature and corresponding to attenuation factors measured for ultra-wideband systems in indoor environments. However, in this case, the range is much smaller, typically below 50 m. In line of sight (LOS) conditions, values from 1.3 to 1.7 were reported by [16, 17], while for non-LOS,  may reach 2 to 4 as mentioned in [18, 19]. The small value that we have obtained comes from the guiding effect of the tunnel.
may reach 2 to 4 as mentioned in [18, 19]. The small value that we have obtained comes from the guiding effect of the tunnel.
The comparison between  and the predicted path loss
and the predicted path loss  shows that the difference in their values is characterized by a standard deviation
shows that the difference in their values is characterized by a standard deviation  dB.
dB.  can thus be modeled by (2) and by adding a random variable
can thus be modeled by (2) and by adding a random variable  with zero mean and standard deviation
with zero mean and standard deviation  :
:

3.2. Axial Correlation
One can expect that the variation of the average received power between one transverse plane and another will depend on the distance d, high-order propagating modes suffering important attenuation at large distances. To study this point, we have calculated, for a given frequency, the amplitude  of the complex correlation coefficient between the
of the complex correlation coefficient between the  transfer matrix elements measured at a distance d and the matrix elements measured at the distance
transfer matrix elements measured at a distance d and the matrix elements measured at the distance  , d varying between 50 m and 500 m. Let us recall that the step
, d varying between 50 m and 500 m. Let us recall that the step  is equal 4 m while 50 m <d < 202 m and 6 m when 202 m <d < 500 m.
is equal 4 m while 50 m <d < 202 m and 6 m when 202 m <d < 500 m.
Curves in Figure 6 give the variation of  for three frequencies: 3, 4, and 5 GHz. As one can expect from the modal theory, the correlation is an increasing function of distance. At 3 GHz, for example, the correlation between 2 receiving arrays, 4 m apart, varies from 0.6 at 50 m, to reach an average value of 0.9 at a distance of 200 m. If we now compare results obtained at 3 and 5 GHz, we see that the correlation increases less rapidly at 5 GHz, because high-order modes suffer less attenuation. By examining the shape of these curves, we observe two regions: the first one, at short distance from the transmitter, where the correlation increases nearly linearly, and the other where the average value of the correlation does not vary appreciably. A two-slope model seems thus well suited to fit the average variation of the correlation function.
for three frequencies: 3, 4, and 5 GHz. As one can expect from the modal theory, the correlation is an increasing function of distance. At 3 GHz, for example, the correlation between 2 receiving arrays, 4 m apart, varies from 0.6 at 50 m, to reach an average value of 0.9 at a distance of 200 m. If we now compare results obtained at 3 and 5 GHz, we see that the correlation increases less rapidly at 5 GHz, because high-order modes suffer less attenuation. By examining the shape of these curves, we observe two regions: the first one, at short distance from the transmitter, where the correlation increases nearly linearly, and the other where the average value of the correlation does not vary appreciably. A two-slope model seems thus well suited to fit the average variation of the correlation function.
In Figure 6, the three vertical lines correspond to the positions of the breakpoint between the two slopes, for the three frequencies, respectively. This breakpoint thus occurs at distance  from the transmitter and by plotting all curves for frequencies between 2.8 and 5 GHz, the following empirical formula giving has been obtained:
from the transmitter and by plotting all curves for frequencies between 2.8 and 5 GHz, the following empirical formula giving has been obtained:

At the breakpoint and beyond this distance, the average correlation between the fields received by the array elements, 6 m apart, is equal to  , with a standard deviation
, with a standard deviation  , this result remaining valid in all the frequency range. In the first zone, that is, for
, this result remaining valid in all the frequency range. In the first zone, that is, for  , the average variation of
, the average variation of  is modelled by
is modelled by

the standard deviation  being also equal to 0.06.
being also equal to 0.06.
This leads to the following expression for modeling the variation of the correlation coefficient along the tunnel axis:

4. Field Distribution in the Transverse Plane
4.1. Field Distribution Function
In the transverse plane, the field distribution was first studied by considering, for a given axial distance d, the  possible combinations of the Tx and Rx antennas, and 7 close frequencies, within a 10 MHz band, as earlier explained. This has been done for various frequency bands between 2.8 and 5 GHz. We have compared the measured data to those given by a Rayleigh, Weibull, Rician, Nakagami and Lognormal distribution, and then using the Kolmogorov-Smirnov [20] test to decide what distribution best fits the experimental results. A Rice distribution appears to be the optimum one, whatever the frequency. The mathematical expression of its probability density function (PDF) is given by
possible combinations of the Tx and Rx antennas, and 7 close frequencies, within a 10 MHz band, as earlier explained. This has been done for various frequency bands between 2.8 and 5 GHz. We have compared the measured data to those given by a Rayleigh, Weibull, Rician, Nakagami and Lognormal distribution, and then using the Kolmogorov-Smirnov [20] test to decide what distribution best fits the experimental results. A Rice distribution appears to be the optimum one, whatever the frequency. The mathematical expression of its probability density function (PDF) is given by

In this formula,  is the modified Bessel function of the first kind with order zero and
is the modified Bessel function of the first kind with order zero and  and
and  are parameters to be adjusted. The first order moment is expressed as
are parameters to be adjusted. The first order moment is expressed as

 being a Laguerre polynomial.
being a Laguerre polynomial.
Before explaining how the two parameters of the Rice distribution have been found, let us recall that, in the mobile communication area, a Rice distribution usually characterizes the field distribution in line of sight (LOS) conditions and in presence of a multipath propagation. Usually a K factor is introduced and defined as the ratio of signal power in dominant component, corresponding to the power of the direct ray, over the scattered, reflected power. One can follow the same approach by defining a K factor in a given receiving zone which is, in our case, defined by the segment 33 cm long in the transverse plane of the tunnel, along which measurements were carried out.
4.2. Ricean  Factor
Factor
Knowing the  matrix whose elements are the
matrix whose elements are the  complex values for successive positions of the Tx and Rx antennas in the transverse plane, one can calculate K at a distance d and a frequency f, from the following expression:
complex values for successive positions of the Tx and Rx antennas in the transverse plane, one can calculate K at a distance d and a frequency f, from the following expression:

It must be clearly outlined that, in a tunnel, the K factor cannot be easily interpreted. Indeed, there is no contribution of random components to the received power, the position of the 4 reflecting walls being invariant. K could be related to richness in terms of propagation modes having a significant power in the receiving transverse plane, a high number of modes giving rise to a high fluctuating field. However, quantifying the relationship between K and mode richness is not easy since the field fluctuation depends not only on the amplitude of the modes but also on their relative phase velocity. In a tunnel, one can conclude that K just gives an indication on the relative range of variation of the received power in a given zone.
Curves in Figure 7 have been plotted for 2 frequencies: 3 and 5 GHz. In the transverse zone of investigation (33 cm), for distances smaller than 200 m, the K factor is below −15 dB, which means that the received power strongly varies in the transverse plan, nearly following a Rayleigh distribution. However, K increases with distance and reaches 0 dB or more beyond 400 m, the constant part of the distribution becoming equal to or greater than the random part.
This increase of K is due to the fact that the contribution of high-order modes becomes less important leading to less fluctuation of the transverse field. The same interpretation based on the modes can be made to interpret the influence of frequency on the K values. The variation of K is of course related to the variation of the correlation coefficient along the tunnel axis, as described in the previous section.
By following the same approach as for the path loss, described in Section 3, and thus by averaging K over groups of 7 frequencies and over 144 successive combinations of the transverse positions of the transverse positions of the Tx and Rx antennas, an empirical expression of the average K factor in terms of frequency and distance can be found. It is given by

The best fit between the results given by (10) and those extracted from the measurements was obtained for the values of the parameters given in Table 2. The standard deviation between (10) and the measured K is given by  .
.
The curves labelled "model" in Figure 7 have been obtained by applying (10) and the above values for the parameters.
Let X be a random variable of zero mean. To completely describe the model, we can add to  such a random variable with a standard deviation of
such a random variable with a standard deviation of  and labeled
and labeled  :
:

4.3. Determination of the Ricean Parameters and Modeling of the Field Variation in the Transverse Plane
 is related to the field distribution parameters of the Rice distribution by
is related to the field distribution parameters of the Rice distribution by

The mean value of  is deduced from (10) for a given frequency and distance, and by assuming a mean value of 1 of the amplitude of the field distribution
is deduced from (10) for a given frequency and distance, and by assuming a mean value of 1 of the amplitude of the field distribution  , the field distribution parameters ν and
, the field distribution parameters ν and  can be calculated. Note that mean value of the field would be determined by the large-scale fading, and fast variations around the mean value by the Rice distribution. Therefore,
can be calculated. Note that mean value of the field would be determined by the large-scale fading, and fast variations around the mean value by the Rice distribution. Therefore,  can be computed using (8) and (12):
can be computed using (8) and (12):

By knowing  , ν is immediately deduced from (12). As an example, curves (a) and (b) in Figure 8 compare the PDFs deduced from the measurements to those assuming a Rice distribution, for
, ν is immediately deduced from (12). As an example, curves (a) and (b) in Figure 8 compare the PDFs deduced from the measurements to those assuming a Rice distribution, for  m and
m and  GHz, and
GHz, and  m and
m and  GHz, respectively. We see the rather good agreement between measurements and the empirical formulation; the confidence level of the Smirnoff-Kolmogorov test remaining below 0.05.
GHz, respectively. We see the rather good agreement between measurements and the empirical formulation; the confidence level of the Smirnoff-Kolmogorov test remaining below 0.05.
5. Transverse Spatial Correlation
The knowledge of the spatial correlation in the transverse plane is of special interest for MIMO systems. It is assumed, for simplicity, that the correlations at the transmitter and at the receiver are separable [21]. Furthermore, since the Rx and Tx antenna arrays are situated in the same transverse zone of the tunnel, one can expect that the correlation statistics are the same for the Tx site and for the Rx site and thus, in the following, they are not differentiated.
For each axial distance d, and for each frequency f, the amplitude of the complex correlation function  was deduced from the
was deduced from the  channel matrix, whose elements are associated to the successive positions of the Tx and Rx antennas in the transverse plane. Let s be the spacing between two receiving points. Figure 9 shows, for
channel matrix, whose elements are associated to the successive positions of the Tx and Rx antennas in the transverse plane. Let s be the spacing between two receiving points. Figure 9 shows, for  GHz, the variation of
GHz, the variation of  versus the axial distanceand for different values of s: 3, 9, 21, and 33 cm.
versus the axial distanceand for different values of s: 3, 9, 21, and 33 cm.
 is of course a decreasing function of the antenna spacing. Furthermore, for a given spacing, the correlation in the transverse plane increases when the axial distance increases, at least until the end of a zone, named A in Figure 9, occurring at a point called "breakpoint trans." This remark is connected to the comments made in Section 4 concerning the axial correlation, where we have outlined that, when the axial distance increases, the high-order modes are more and more attenuated, leading to a less fluctuating electromagnetic field. Beyond the "breakpoint trans" (zone B in Figure 9),
is of course a decreasing function of the antenna spacing. Furthermore, for a given spacing, the correlation in the transverse plane increases when the axial distance increases, at least until the end of a zone, named A in Figure 9, occurring at a point called "breakpoint trans." This remark is connected to the comments made in Section 4 concerning the axial correlation, where we have outlined that, when the axial distance increases, the high-order modes are more and more attenuated, leading to a less fluctuating electromagnetic field. Beyond the "breakpoint trans" (zone B in Figure 9),  keeps an average high value, even if local decreases are observed. The local decreases can be explained by the field pattern in the transverse plane of the tunnel. Indeed, this pattern does not present translation symmetry since it results from the combining of many modes, both in amplitude and in phase.
keeps an average high value, even if local decreases are observed. The local decreases can be explained by the field pattern in the transverse plane of the tunnel. Indeed, this pattern does not present translation symmetry since it results from the combining of many modes, both in amplitude and in phase.
By analyzing results in the whole frequency range, it appears that the width of zone A slightly increases with frequency, as it occurred in the case of the longitudinal correlation (Section 4). Again, using all measured frequencies, an empirical formula giving the position of the "breakpoint_trans" point is given by

In zone B, one can calculate the mean value  (s, zone B, f) by averaging
(s, zone B, f) by averaging  over the axial distance d. The results are the curves plotted in Figure 10, versus frequency and for different values of s: 3, 9, 21, and 33 cm.
over the axial distance d. The results are the curves plotted in Figure 10, versus frequency and for different values of s: 3, 9, 21, and 33 cm.
It appears that  (s, zone B, f) is nearly frequency independent and that an empirical formula fitting the experimental results can be obtained:
(s, zone B, f) is nearly frequency independent and that an empirical formula fitting the experimental results can be obtained:

The difference between (15) and the measured correlation is a random variable of zero mean and standard deviation  :
:

The modeling of the  in zone A assumes an average linear variation with distance. The adequate formula in this zone is
in zone A assumes an average linear variation with distance. The adequate formula in this zone is

In this formula, the implicit dependence on frequency comes from the value of  . The standard deviation around this value is nearly frequency independent and is modeled by
. The standard deviation around this value is nearly frequency independent and is modeled by

Finally, for a given antenna spacing, the correlation between two antenna elements is modeled by

6. Full Model
The previous sections have proposed empirical formulas, based on experimental results, to model the path loss and the field fluctuation and correlation in a transverse plane. These formulas can be applied to randomly generate the transfer matrices H of an MIMO link in a straight tunnel having an arched cross-section, which is the shape of most road and railway tunnels. The transmitting and receiving arrays are supposed to be linear arrays, whose axes are horizontal and situated in the transverse plane of the tunnel, this configuration being quite usual. An approach based on the Kronecker model [21] was chosen for its simplicity.
To determine the various elements of H, the following steps can be followed:
-
(1)
define the system parameters, such as frequency, distance between the transmitter and the receiver, number of array elements at the transmitter and at the receiver, element spacing and number of snapshots, corresponding to the number of realizations to be simulated;
-
(2)
determine a value for the path loss
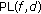 using (3);
using (3); -
(3)
compute a K factor from (11). We recall that in (3) and in (11), the value given by the model is the sum of two terms: a deterministic one plus a random variable whose standard deviation is known;
-
(4)
knowing K and
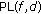 , the elements of a
, the elements of a  matrix, having the same size as H, are randomly chosen in a normalized Ricean distribution;
matrix, having the same size as H, are randomly chosen in a normalized Ricean distribution; -
(5)
as mentioned in Section 4, it was assumed that the correlations between either the transmitting elements or the receiving elements follow the same distribution. The terms of the correlation matrices at the transmitting and receiving sites,
 and
and  , are thus deduced from (19).
, are thus deduced from (19).
The Kronecker model leads to

To give an example of application of this formula, let us consider a  MIMO system at 4 GHz, an array element spacing of 0.8
MIMO system at 4 GHz, an array element spacing of 0.8  (6 cm at 4 GHz) and a distance d between the transmitter and the receiver of 250 m.
(6 cm at 4 GHz) and a distance d between the transmitter and the receiver of 250 m.
The channel capacity of a MIMO system for a given channel realization H can be computed as [22]

where  is the
is the  identity matrix,
identity matrix,  is the transpose conjugate operation and SNR is the signal-to-noise ratio at the receiver. The channel capacity C was calculated by assuming a fixed SNR equal to 10 dB. A constant SNR was chosen because we want to emphasize the influence of correlation and field distribution in the transverse plane. To compute the capacity assuming a fixed transmitting power, the contribution of the path loss must be added, which is straightforward.
is the transpose conjugate operation and SNR is the signal-to-noise ratio at the receiver. The channel capacity C was calculated by assuming a fixed SNR equal to 10 dB. A constant SNR was chosen because we want to emphasize the influence of correlation and field distribution in the transverse plane. To compute the capacity assuming a fixed transmitting power, the contribution of the path loss must be added, which is straightforward.
The model was applied by considering 1000 realizations and the cumulative probability density function of the capacity is plotted in Figure 11 (curve "model"). To be able to compare this distribution to experimental results, a large number of measured values are needed. To increase this number we have thus calculated the capacity not only at 4 GHz, but also for all frequencies within a 100 MHz band around 4 GHz. We see in Figure 11, the rather good agreement between results deduced from the experiments (curve "measurements") and those given by the model.
7. Conclusion
The statistics of the electromagnetic field variation in a tunnel has been deduced from measurements made in an arched tunnel, which is the usual shape of road and railway tunnels, and in a frequency range extending from 2.8 to 5 GHz. Both the methodology of the experiments and the analysis were aimed at predicting the performance of an MIMO link in a wide frequency band.
It was shown, by subtracting the antenna effect, that the path loss is not strongly dependent on frequency and that the attenuation constant keeps small values, the tunnel behaving as a low-loss guiding structure. Along the investigated transverse axis of the tunnel, over 33 cm long, the small-scale fading follows a Ricean distribution. However, for distances between the transmitting and receiving antennas up to 200 m, theK factor is below −15 dB, meaning that the field is nearly Rayleigh distributed. It also appeared that K is an increasing function of distance, reaching 0 dB at about 400 m.
Empirical formulas to model the main propagation characteristics were proposed and applied to generate transfer matrices of an MIMO link.
References
Yamaguchi Y, Abe T, Sekiguchi T: Radio wave propagation loss in the VHF to microwave region due to vehicles in tunnels. IEEE Transactions on Electromagnetic Compatibility 1989, 13(1):87-91.
Lienard M, Degauque P: Natural wave propagation in mine environments. IEEE Transactions on Antennas and Propagation 2000, 48(9):1326-1339. 10.1109/8.898765
Didascalou D, Maurer J, Wiesbeck W: Subway tunnel guided electromagnetic wave propagation at mobile communications frequencies. IEEE Transactions on Antennas and Propagation 2001, 49(11):1590-1596. 10.1109/8.964095
Yang X, Lu Y: Research on propagation characteristics of millimeter wave in tunnels. International Journal of Infrared and Millimeter Waves 2007, 28(10):901-909. 10.1007/s10762-007-9268-y
Zhang YP, Hwang Y: Characterization of UHF radio propagation channels in tunnel environments for microcellular and personal communications. IEEE Transactions on Vehicular Technology 1998, 47(1):283-296. 10.1109/25.661054
Zhang YP, Zheng GX, Sheng JH: Radio propagation at 900 MHz in underground coal mines. IEEE Transactions on Antennas and Propagation 2001, 49(5):757-762. 10.1109/8.929630
Briso-Rodriguez C, Cruz JM, Alonso JI: Measurements and modeling of distributed antenna systems in railway tunnels. IEEE Transactions on Vehicular Technology 2007, 56(5, part 2):2870-2879.
Wang T-S, Yang C-F: Simulations and measurements of wave propagations in curved road tunnels for signals from GSM base stations. IEEE Transactions on Antennas and Propagation 2006, 54(9):2577-2584. 10.1109/TAP.2006.880674
Ching GS, Ghoraishi M, Lertsirisopon N, et al.: Analysis of DSRC service over-reach inside an arched tunnel. IEEE Journal on Selected Areas in Communications 2007, 25(8):1517-1525.
Boutin M, Benzakour A, Despins CL, Affes S: Radio wave characterization and modeling in underground mine tunnels. IEEE Transactions on Antennas and Propagation 2008, 56(2):540-549.
Molina-Garcia-Pardo J-M, Lienard M, Degauque P, Dudley DG, Juan-Llàcer L: Interpretation of MIMO channel characteristics in rectangular tunnels from modal theory. IEEE Transactions on Vehicular Technology 2008, 57(3):1974-1979.
Liénard M, Degauque P, Baudet J, Degardin D: Investigation on MIMO channels in subway tunnels. IEEE Journal on Selected Areas in Communications 2003, 21(3):332-339. 10.1109/JSAC.2003.809627
Lienard M, Degauque P: Propagation in wide tunnels at 2 GHz: a statistical analysis. IEEE Transactions on Vehicular Technology 1998, 47(4):1322-1328. 10.1109/25.728522
Molisch AF: Ultrawideband propagation channels-theory, measurement, and modeling. IEEE Transactions on Vehicular Technology 2005, 54(5):1528-1545. 10.1109/TVT.2005.856194
Rappaport TS: Wireless Communications. Prentice-Hall, Englewood Cliffs, NJ, USA; 1996.
Ghassemzadeh SS, Jana R, Rice CW, Turin W, Tarokh V: Measurement and modeling of an ultra-wide bandwidth indoor channel. IEEE Transactions on Communications 2004, 52(10):1786-1796. 10.1109/TCOMM.2003.820755
Keignart J, Daniele N: Channel sounding and modeling for indoor UWB communications. Proceedings of International Workshop on Ultra Wideband Systems (IWUWBS '03), June 2003, Oulu, Finland
Cassioli D, Win MZ, Molisch AF: The ultra-wide bandwidth indoor channel: from statistical model to simulations. IEEE Journal on Selected Areas in Communications 2002, 20(6):1247-1257. 10.1109/JSAC.2002.801228
Hovinen V, Hämäläinen M, Tesi R, Hentilä L, Laine N: A proposal for a selection of indoor UWB path loss model. Wisair, Tel Aviv, Israel; 2002.http://grouper.ieee.org/groups/802/15/pub/2002/Jul02
Papoulis A, Pillai SU: Probability, Random Variables and Stochastic Processes. 4th edition. McGraw-Hill, Boston, Mass, USA; 2002.
Kermoal JP, Schumacher L, Pedersen KI, Mogensen PE, Frederiksen F: A stochastic MIMO radio channel model with experimental validation. IEEE Journal on Selected Areas in Communications 2002, 20(6):1211-1226. 10.1109/JSAC.2002.801223
Foschini GJ, Gans MJ: On limits of wireless communications in a fading environment when using multiple antennas. Wireless Personal Communications 1998, 6(3):311-335. 10.1023/A:1008889222784
Acknowledgments
This work has been supported by the European FEDER funds, the Region Nord-Pas de Calais, and the French ministry of research, in the frame of the CISIT project.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Molina-Garcia-Pardo, JM., Lienard, M. & Degauque, P. Propagation in Tunnels: Experimental Investigations and Channel Modeling in a Wide Frequency Band for MIMO Applications. J Wireless Com Network 2009, 560571 (2009). https://doi.org/10.1155/2009/560571
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/560571




 between two antennas for
between two antennas for  m and path loss
m and path loss  averaged over the transverse positions of the antennas and over 7 frequencies in a 10 MHz band.
averaged over the transverse positions of the antennas and over 7 frequencies in a 10 MHz band.

 Factor
Factor

 m and
m and  GHz, (b)
GHz, (b)  m and
m and  GHz.
GHz.

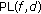 using (3);
using (3);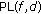 , the elements of a
, the elements of a  matrix, having the same size as H, are randomly chosen in a normalized Ricean distribution;
matrix, having the same size as H, are randomly chosen in a normalized Ricean distribution; and
and  , are thus deduced from (19).
, are thus deduced from (19).
 MIMO system, for a frequency of 4 GHz and for a distance of 250 m.
MIMO system, for a frequency of 4 GHz and for a distance of 250 m.