- Research Article
- Open access
- Published:
Joint Throughput Maximization and Fair Uplink Transmission Scheduling in CDMA Systems
EURASIP Journal on Wireless Communications and Networking volume 2009, Article number: 564692 (2009)
Abstract
We study the fundamental problem of optimal transmission scheduling in a code-division multiple-access wireless system in order to maximize the uplink system throughput, while satisfying the users quality-of-service (QoS) requirements and maintaining fairness among them. The corresponding problem is expressed as a weighted throughput maximization problem, under certain power and QoS constraints, where the weights are the control parameters reflecting the fairness constraints. With the introduction of the power index capacity, it is shown that this optimization problem can be converted into a binary knapsack problem, where all the corresponding constraints are replaced by the power index capacities at some certain system power index. A two-step approach is followed to obtain the optimal solution. First, a simple method is proposed to find the optimal set of users to receive service for a given fixed target system load, and then the optimal solution is obtained as a global search within a certain range. Furthermore, a stochastic approximation method is presented to effectively identify the required control parameters. The performance evaluation reveals the advantages of our proposed policy over other existing ones and confirms that it achieves very high throughput while maintains fairness among the users, under different channel conditions and requirements.
1. Introduction
The continuous growth in traffic volume and the emergence of new services have begun to change the structure and requirements of wireless networks. Future mobile communication systems will be characterized by high throughput, integration of services, and flexibility [1–5]. With the demand for high data rate and support of multiple quality of service (QoS), the transmission scheduling plays a key role in the efficient resource allocation process in wireless systems. The transmission scheduling determines the time instances that a mobile user may receive service, as well as the resources that should be allocated to support the requested service, in order to make the resource distribution fair and efficient.
The fundamental problem of scheduling the users transmission and allocating the available resources in a realistic uplink code-division multiple-access (CDMA) wireless system that supports multirate multimedia services, with efficiency and fairness, is investigated and analyzed in this paper. A transmission scheduling method which achieves the maximum system throughput under the constraints of satisfying certain users QoS requirements and maintaining throughput fairness among them is provided and evaluated.
1.1. Related Work and Motivation
A class of scheduling schemes, namely, the opportunistic scheduling schemes, has been proven to be an effective approach to improve the system throughput by utilizing the multiuser diversity effect [6, 7] in wireless communications. Specifically, for a system with many users that have independent varying channels, with high probability there is a user with channel much stronger than its average SNR requirement. Therefore, the system throughput may be maximized by choosing the user with "relatively best" channel for transmission at a given slot. However, some fairness constraints must be imposed on the scheduling policies to ensure the fair resource allocation.
It has been shown in [8] that scheduling users one-by-one can result in higher system throughput for high data rate traffic in the CDMA downlink. However, this work does not exploit the time-varying channel conditions. In [7, 9], a high-speed data rate scheme (HDR) is introduced, where the base station schedules the downlink transmission of a single user at a given time slot with the data rates and slot lengths varying according to the specific channel condition. In [10–12], a transmission scheduling scheme for multiple users, which considers both the channel condition and queueing delay/length, is proposed and shown to be throughput optimal if it is feasible. However, the fairness issue is not explicitly addressed in that work. In [13–15], a framework for opportunistic scheduling that maximizes the system performance by exploiting the time-varying channel conditions of wireless networks is presented. Three categories of scheduling problems—the temporal fairness, utilitarian fairness, and minimum-performance guarantee scheduling—are studied and optimal solutions are given.
Although the downlink transmission assignment is important for several applications, the efficient uplink transmission scheduling plays an important role as well, especially with the prevailing of multimedia communications and applications. It has been argued that the downlink scheduling method is not suitable to be applied to the uplink transmission scheduling, where simultaneous transmissions may result in higher throughput [16, 17]. The uplink transmission scheduling problem is more complicated and requires further consideration of additional elements to make the corresponding scheduling policies feasible [18]. The achievable throughput in such a case depends not only on the service access time, but also on the transmission powers and the corresponding users interference. In addition, multiple users can be scheduled simultaneously to transmit in the same time slot, which is a major difference from the wireline and TDMA-like scheduling schemes, making the respective scheduling processes either inapplicable or inefficient in the CDMA environment. The simple temporal fairness scheduling, where the main resource to be shared is the time, fails to provide rational fairness in this case. As a result, the throughput optimal and fair uplink transmission scheduling problem needs to jointly consider multiple factors such as access time, transmission power, channel conditions, and number of users to be scheduled at the same time. Heuristic approaches to address the problem of short-term fairness and demonstrate the tradeoff between fairness and throughput under some special cases have been introduced in [19–21].
Furthermore, how to maximize the throughput of uplink CDMA system was first analyzed in [16]. The sole purpose of uplink throughput maximization can be achieved by choosing the "best"  users in terms of their received power, when they transmit at their maximum power. However, such throughput maximization does not consider fairness, that is, the equal opportunity for all users to receiving service despite their channel conditions. Therefore, among the objectives of our approach in this paper is to identify the actual "best" users that should transmit in order to maximize the throughput, when the fairness constraints are introduced and respected.
users in terms of their received power, when they transmit at their maximum power. However, such throughput maximization does not consider fairness, that is, the equal opportunity for all users to receiving service despite their channel conditions. Therefore, among the objectives of our approach in this paper is to identify the actual "best" users that should transmit in order to maximize the throughput, when the fairness constraints are introduced and respected.
In [22], several scenarios of scheduling uplink CDMA transmission with voice and data services are analyzed. With the number of voice users and their corresponding transmission rates fixed, that work attempted to maximize the throughput of data service. It was shown that when the synchronization overhead is reasonable, a smaller number of simultaneous transmission users achieve higher system throughput and at the same time lower the average transmission power. However, in this case the achievable throughput is affected by the "weakest link." Therefore, this approach can be regarded only as a static analysis that considers the relationship between the performance and the number of users chosen for transmission. The problem of identifying the actual set of users to transmit based on their channel conditions, which may reduce the impact of the "weakest link", has not yet been investigated and is one of the main objectives of our paper.
In addition, the problem of uplink CDMA scheduling is further complicated by the fact that the conventional concept of capacity used in the wireline networks, for example, total bandwidth of the physical media, is not directly applicable in the CDMA systems. In this case, the actual system capacity is not fixed and known in advance, since it is a function of several parameters such as the number of users, the channel conditions, and the transmission powers.
Therefore, in summary the main contributions of this paper are as follows. (1) Jointly consider the factors of channel capacity, number of users and their interference, transmit power, and fairness requirements. (2) Formulate an optimization problem that stresses the fairness requirement under time-varying wireless environment and proves the existence of an optimal solution based on all constraints. (3) Exploit the power index concept and power index capacity, as a novel and effective way, to treat the fairness issue in the transmission scheduling policy under the considered uncertain and dynamic environment. (4) Devise a scheduling policy that achieves throughput fairness among the users and optimal system throughput under certain constraints.
1.2. Paper Outline
The rest of the paper is organized as follows. In Section 2, the system model that is used throughout our analysis is described, and the problem of the uplink scheduling in CDMA systems is rigorously formulated as a multiconstraint optimization problem. It is demonstrated that this problem can be expressed as a weighted throughput maximization problem, under certain power and QoS constraints, where the weights are the control parameters that reflect fairness constraints. Based on the concept of power index capacity, this optimization problem is converted into a simpler linear knapsack problem in Section 3.1, where all the corresponding constraints are replaced by the users power index capacities at some certain system power index. The optimal solution of the latter problem is identified in Sections 3.2 and 3.3, while in Section 3.4, a stochastic approximation method is presented in order to effectively identify the required control parameters. Section 4 contains the performance evaluation of the proposed method, along with some numerical results and discussion, and finally Section 5 concludes the paper.
2. System Model and Problem Formulation
In this paper, we consider a single cell DS-CDMA system with  backlogged users at time slot
backlogged users at time slot  . The users channel conditions are assumed to change according to some stationary stochastic process, while the uplink transmission rate is assumed to be adjustable with the variable spreading gain technique [23]. Each user
. The users channel conditions are assumed to change according to some stationary stochastic process, while the uplink transmission rate is assumed to be adjustable with the variable spreading gain technique [23]. Each user  is associated with some preassigned weight
is associated with some preassigned weight  according to its QoS requirement. In the following for simplicity in the presentation, we omit the notation of the specific slot
according to its QoS requirement. In the following for simplicity in the presentation, we omit the notation of the specific slot  from the notations and definitions we introduce. Let us denote by
from the notations and definitions we introduce. Let us denote by  the transmission rate of user
the transmission rate of user  in the slot under consideration. We assume that the chip rate
in the slot under consideration. We assume that the chip rate  for all mobiles is fixed, and hence the spreading gain
for all mobiles is fixed, and hence the spreading gain  of user
of user  is defined as
is defined as  . Let us also denote by
. Let us also denote by  the required signal-to-interference and noise ratio (SINR) level of user
the required signal-to-interference and noise ratio (SINR) level of user  , by
, by  the corresponding channel gain, and by
the corresponding channel gain, and by  the user
the user  transmission power at a given slot, which, however, is limited by the maximum power value
transmission power at a given slot, which, however, is limited by the maximum power value  . Therefore, the received SINR
. Therefore, the received SINR  for a user
for a user  is given by
is given by

where  is the one-sided power spectral density of additive white Gaussian noise (AWGN), and
is the one-sided power spectral density of additive white Gaussian noise (AWGN), and  determines the proportion of the interference from other users received power. Without loss of generality in the following, we assume
determines the proportion of the interference from other users received power. Without loss of generality in the following, we assume  . Obviously, to meet the SINR requirement, the received SINR
. Obviously, to meet the SINR requirement, the received SINR  has to be larger than the corresponding threshold
has to be larger than the corresponding threshold  , that is,
, that is,  . In the following, we assume perfect power control in the system under consideration, while users are scheduled to transmit at the beginning of every fixed-length slot. The objective of the optimal scheduling policy
. In the following, we assume perfect power control in the system under consideration, while users are scheduled to transmit at the beginning of every fixed-length slot. The objective of the optimal scheduling policy  is to find the optimal number of allowable users and their transmission rates, which achieves the maximum system throughput while maintaining the fairness property.
is to find the optimal number of allowable users and their transmission rates, which achieves the maximum system throughput while maintaining the fairness property.
2.1. Problem Formulation
Let  denote the total throughput in slot
denote the total throughput in slot  . Our objective function is to maximize the expectation of
. Our objective function is to maximize the expectation of  by selecting the optimal transmit power vector
by selecting the optimal transmit power vector  and transmit rate vector
and transmit rate vector  that is,
that is,

subject to specific SINR, maximum transmit power, and fairness constraints as follows:

where  denotes the mean throughput of user
denotes the mean throughput of user  in the corresponding backlogged period. It has been shown in [15, 24] that the above-constrained optimization problem can be considered as equivalent to the following problem (4), where
in the corresponding backlogged period. It has been shown in [15, 24] that the above-constrained optimization problem can be considered as equivalent to the following problem (4), where  is the minimal value among all
is the minimal value among all  , that is,
, that is,  . In (4), we transform the objective function (2) into finding the optimal transmit powers and rates that maximize the minimal normalized average rate
. In (4), we transform the objective function (2) into finding the optimal transmit powers and rates that maximize the minimal normalized average rate  . Therefore,
. Therefore,

Apparently, the solution of the above problem will finally make  for
for  since one can always reduce its throughput for the benefit of other users in order to maximize
since one can always reduce its throughput for the benefit of other users in order to maximize  . With the constraint
. With the constraint  , the objective function then is generalized to
, the objective function then is generalized to

where  is an arbitrary positive number. Here the crucial observation [24] is that the optimal scheduling policy will be the one that maximizes the sum of weighted throughputs and equalizes the normalized throughput. The maximization of mean-weighted rate in (5) is obtained by the maximization of the weighted rate in every slot, that is,
is an arbitrary positive number. Here the crucial observation [24] is that the optimal scheduling policy will be the one that maximizes the sum of weighted throughputs and equalizes the normalized throughput. The maximization of mean-weighted rate in (5) is obtained by the maximization of the weighted rate in every slot, that is,  for every slot
for every slot  . In conclusion, to obtain the optimal uplink throughput while keeping fairness, we must solve the following problem:
. In conclusion, to obtain the optimal uplink throughput while keeping fairness, we must solve the following problem:



The fairness constraint, that is,  , is represented by the choice of
, is represented by the choice of  . By adjusting the value of
. By adjusting the value of  , the user will get more or less opportunities to transmit data, and hence the corresponding normalized throughput is balanced. As we discuss later in this paper, the value of
, the user will get more or less opportunities to transmit data, and hence the corresponding normalized throughput is balanced. As we discuss later in this paper, the value of  can be approximated by a stochastic approximation algorithm, which has already found its application in [14, 15] under similar situations. Note that since we assume perfect power control in the CDMA system under consideration, only the equality case of (7) is considered here.
can be approximated by a stochastic approximation algorithm, which has already found its application in [14, 15] under similar situations. Note that since we assume perfect power control in the CDMA system under consideration, only the equality case of (7) is considered here.
The following Proposition 1 states that the optimal solution is achieved when a user either transmits at full power or does not transmit at all.
Proposition 1.
The optimal solution that maximizes the weighted throughput of problem (6) is such that

Proof.
In order to minimize the multiple access interference, users transmit with the minimum required power to meet the required threshold  . Therefore, we consider the equality case of constraint (7). To maintain exactly the threshold
. Therefore, we consider the equality case of constraint (7). To maintain exactly the threshold  for user
for user  , the achievable transmit rate is represented as
, the achievable transmit rate is represented as

The objective function then becomes

Differentiating twice with respect to the transmit power of a user  , we obtain
, we obtain

Since  is positive number, obviously (12) is nonnegative, while the objective function is a convex function of
is positive number, obviously (12) is nonnegative, while the objective function is a convex function of  . Hence, the optimal solution of this problem is that the transmit power obtains the value of its boundary, that is, either 0 or
. Hence, the optimal solution of this problem is that the transmit power obtains the value of its boundary, that is, either 0 or  .
.
In Section 3, the corresponding optimization problem is transformed to an equivalent problem of a simpler form, which facilitates the identification of the optimal solution. However, in the following we first introduce the concept of power index capacity which is used to represent the corresponding constraints, under the problem transformation.
2.2. Power Index Capacity
It has been shown in [25] that by solving the constraints (7) and (8), the following inequality must be satisfied if there exists a feasible power assignment  that meets the QoS requirements:
that meets the QoS requirements:

where

is defined as the power index of user  [26]. Relation (13) is the necessary and sufficient condition such that a power and rate solution is feasible under constraints (7) and (8) [25].
[26]. Relation (13) is the necessary and sufficient condition such that a power and rate solution is feasible under constraints (7) and (8) [25].
Let us regard  as the actual system load, which is the sum of power indices assigned to all backlogged users, while we assume that there is a target system load
as the actual system load, which is the sum of power indices assigned to all backlogged users, while we assume that there is a target system load  . It should be noted that
. It should be noted that  here is not fixed but has value
here is not fixed but has value  . The meaning and motivation for the definition of the target system load
. The meaning and motivation for the definition of the target system load  are that the system will attempt to provide the appropriate scheduling in order to make the actual system load
are that the system will attempt to provide the appropriate scheduling in order to make the actual system load  reach the target load (however, it serves as an upper bound and cannot be exceeded). For an arbitrarily selected
reach the target load (however, it serves as an upper bound and cannot be exceeded). For an arbitrarily selected  in the range of
in the range of  , there exist two possible cases concerning the relationship between the actual system load
, there exist two possible cases concerning the relationship between the actual system load  and the target system load. When considering small values for the target system load
and the target system load. When considering small values for the target system load  , the system can easily make the actual system load
, the system can easily make the actual system load  reach the target load under consideration, that is,
reach the target load under consideration, that is,  . On the other hand, when
. On the other hand, when  is large, especially when it approaches to 1, it may be impossible for the actual achievable system load
is large, especially when it approaches to 1, it may be impossible for the actual achievable system load  to reach
to reach  due to the limitation imposed by (13)). Let us assume that in time slot
due to the limitation imposed by (13)). Let us assume that in time slot  the maximum system load this system can achieve based on all users channel states and all possible user schedulings is
the maximum system load this system can achieve based on all users channel states and all possible user schedulings is  . We will now consider the two cases mentioned above, that is,
. We will now consider the two cases mentioned above, that is,  and
and  .
.
2.2.1. Target Load Is Less than or Equal to Maximum System Load
If we assume  , then the system load can achieve the target load,
, then the system load can achieve the target load,  . Therefore, (13) can be rewritten as follows:
. Therefore, (13) can be rewritten as follows:

For each individual user, there is a limitation on the maximum power index that it can reach, given by (15)

2.2.2. Target Load Is Larger than Maximum System Load
If the target load is larger than the maximum system load, that is,  , it means there will be no feasible transmission power solution in (7) and (8) to achieve this target load and therefore the relationship in (15) does not hold any more. In this case, we simply apply the power index restriction of (16) to each user. The consequence is that the final achieved system load becomes
, it means there will be no feasible transmission power solution in (7) and (8) to achieve this target load and therefore the relationship in (15) does not hold any more. In this case, we simply apply the power index restriction of (16) to each user. The consequence is that the final achieved system load becomes  since
since  .
.
In fact, unless all possible transmission user sets are searched, it is unknown in advance whether or not the actual system load  can reach the chosen
can reach the chosen  . Therefore, applying (16) to the case
. Therefore, applying (16) to the case  unifies the definition of the power index range, within which a user can be assigned a feasible power index without knowing the value of
unifies the definition of the power index range, within which a user can be assigned a feasible power index without knowing the value of  . One key principle and rule regarding the algorithm proposed in this paper is to assign to an individual user a power index that is less than or equal to its power index capacity. In the power index assignment algorithm described in Section 3.2, the situation where
. One key principle and rule regarding the algorithm proposed in this paper is to assign to an individual user a power index that is less than or equal to its power index capacity. In the power index assignment algorithm described in Section 3.2, the situation where  may occur. However, it should be noted here that as proven by Theorem 1 later in the paper, the global optimal solution must be the one satisfying
may occur. However, it should be noted here that as proven by Theorem 1 later in the paper, the global optimal solution must be the one satisfying  . The target load range where
. The target load range where  is then not possible to be the optimal solution. The intentionally introduced restriction of (16) in the case of
is then not possible to be the optimal solution. The intentionally introduced restriction of (16) in the case of  allows the algorithm to rule out such values of
allows the algorithm to rule out such values of  due to the fact that
due to the fact that  in this case.
in this case.
2.2.3. Definition of Power Index Capacity
Hence, given the system load  the maximum possible power index
the maximum possible power index  a user can accept in (15) is determined by the maximum transmit power
a user can accept in (15) is determined by the maximum transmit power  and the channel gain
and the channel gain  .
.
Definition 1.
In a CDMA system with  backlogged users at time slot
backlogged users at time slot  , given the target system power index
, given the target system power index  , the maximum power index that does not violate (13) for a single user whose channel gain is
, the maximum power index that does not violate (13) for a single user whose channel gain is  is defined as the power index capacity (PIC)
is defined as the power index capacity (PIC)  of this user.
of this user.
From (15), it can be easily found that the PIC of user  is
is

Note that in (17) the power index capacity is limited by the target system power index. This is reasonable since a power index capacity that is greater than  will have no practical meaning and application. Furthermore, since our focus in this paper is to find an optimal scheduling policy as well as the optimal system load
will have no practical meaning and application. Furthermore, since our focus in this paper is to find an optimal scheduling policy as well as the optimal system load  , the value of
, the value of  in (17) is not determined in advance.
in (17) is not determined in advance.
Intuitively, the power index represents the relationship between the transmission power and the corresponding interference that is caused to other users. If we considered that the total system power index is fixed to  , larger power index
, larger power index  for user
for user  indicates that it has relatively higher signal-to-interference ratio compared to the other users with smaller power index, while at the same time it causes more interference to them. Accordingly, users with high-power indices may lower their transmission power to reduce the interference they may cause, which in turn means that they will have smaller power index to limit the intracell interference of the system, and therefore satisfy (13) that guarantees the existence of a feasible transmission power solution.
indicates that it has relatively higher signal-to-interference ratio compared to the other users with smaller power index, while at the same time it causes more interference to them. Accordingly, users with high-power indices may lower their transmission power to reduce the interference they may cause, which in turn means that they will have smaller power index to limit the intracell interference of the system, and therefore satisfy (13) that guarantees the existence of a feasible transmission power solution.
3. Problem Transformation and Optimal Solution
3.1. Problem Transformation
The corresponding constraints in terms of the power index can be represented as follows:




Note that in the objective function we represent the rate  as a function of power index
as a function of power index  , where
, where

which converts the power index into transmission rate and can be easily derived from (14) by replacing  with
with  .
.
In the following, let  denote the set that contains all the power and rate vectors that satisfy constraints (7) and (8) and
denote the set that contains all the power and rate vectors that satisfy constraints (7) and (8) and  . The elements
. The elements  and
and  represent the transmit power and rate of the
represent the transmit power and rate of the  th user in the
th user in the  th vector. Similarly, we define another set
th vector. Similarly, we define another set  containing the power and rate vectors
containing the power and rate vectors  that satisfy constraints (19), (20), and (21). By definition, it is obvious that any power and rate vector
that satisfy constraints (19), (20), and (21). By definition, it is obvious that any power and rate vector  is feasible. However, since in constraint (21),
is feasible. However, since in constraint (21),  may take a value, that is, close to 1 , the required transmit power could also accordingly become larger than maximum allowable transmit power
may take a value, that is, close to 1 , the required transmit power could also accordingly become larger than maximum allowable transmit power  if we simply look at the result from (15). The following proposition states that if perfect power control is assumed, for any rate (or power index) vector that satisfies constraints (19), (20), and (21), there always exists a feasible transmit power vector.
if we simply look at the result from (15). The following proposition states that if perfect power control is assumed, for any rate (or power index) vector that satisfies constraints (19), (20), and (21), there always exists a feasible transmit power vector.
Proposition 2.
If the power index assignment for all  backlogged users satisfies constraints (19), (20), and (21), there always exists a feasible transmit power assignment, that is,
backlogged users satisfies constraints (19), (20), and (21), there always exists a feasible transmit power assignment, that is,  for
for  .
.
Proof.
Let vector  be the power index vector that satisfies constraints (19), (20), and (21). Denote
be the power index vector that satisfies constraints (19), (20), and (21). Denote  the sum of all power indices in vector
the sum of all power indices in vector  . From the definition of power index capacity, the power index capacity of each user is
. From the definition of power index capacity, the power index capacity of each user is  and
and  . Based on Definition 1 and (17), we have the following relation:
. Based on Definition 1 and (17), we have the following relation:

Hence, for any user  , the transmit rate may be chosen within range
, the transmit rate may be chosen within range

which still satisfies the above inequality and proves this proposition. The power control of the CDMA system will choose the minimal transmit power, that meets the required SINR.
The following proposition proves that the two sets  and
and  contain the same elements, which means that (19), (20), (21) and (7), (8) impose the same constraints over our problem.
contain the same elements, which means that (19), (20), (21) and (7), (8) impose the same constraints over our problem.
Proposition 3.
Any vector  is also included in set
is also included in set  , while any vector
, while any vector  is also included in set
is also included in set  .
.
Proof.
Suppose that  , and therefore it satisfies constraints (7), (8). It is apparent that
, and therefore it satisfies constraints (7), (8). It is apparent that  . Since, as shown earlier, constraints (7), and (8) can also be represented by (13) [25],
. Since, as shown earlier, constraints (7), and (8) can also be represented by (13) [25],  also satisfies (13). Using function (22), we can convert the rate vector
also satisfies (13). Using function (22), we can convert the rate vector  into the corresponding power index vector
into the corresponding power index vector  . Let
. Let  . For a feasible power and rate vector, with known
. For a feasible power and rate vector, with known  (
( [25]), we can find each user power index capacity
[25]), we can find each user power index capacity  . Since
. Since  satisfies (13), based on Proposition 2 and the definition of power index capacity, we conclude that
satisfies (13), based on Proposition 2 and the definition of power index capacity, we conclude that  . That means that the assigned powers and rates in
. That means that the assigned powers and rates in  also satisfy the constraints (19), (20), and (21). Therefore,
also satisfy the constraints (19), (20), and (21). Therefore,  .
.
Let us consider vector  . As before, the rate vector part can be converted to corresponding power index vector
. As before, the rate vector part can be converted to corresponding power index vector  . Let
. Let  and hence
and hence  due to constraints (19), (20), and (21). Note that for the case where
due to constraints (19), (20), and (21). Note that for the case where  ,
,  . Based on the previous discussion, we can easily conclude that the power vector is feasible. Therefore,
. Based on the previous discussion, we can easily conclude that the power vector is feasible. Therefore,

which satisfies (13)), for user  ,
,  . Therefore,
. Therefore,  .
.
The above proposition shows that the optimal solution can also be obtained with the new constraints since they define the same solution set. Please note that, as mentioned before, the fairness constraints in the original problem are replaced by parameters  . The choice of the proper values of
. The choice of the proper values of  that maintain fairness is discussed in detail later in this paper.
that maintain fairness is discussed in detail later in this paper.
Among the new constraints, the right-hand sides of inequalities (19) and (20) are not fixed values, but are functions of the selected target system load  . Hence, whether or not the final solution is feasible also depends on the choice of
. Hence, whether or not the final solution is feasible also depends on the choice of  . For any value of
. For any value of  , there could be many feasible solutions among which one will be the optimal. Moreover, there must exist an optimal system load
, there could be many feasible solutions among which one will be the optimal. Moreover, there must exist an optimal system load  that can achieve the overall best solution. It is natural to regard the objective
that can achieve the overall best solution. It is natural to regard the objective  as the function of system load
as the function of system load  ,
,  , and thus
, and thus  is the local optimal result at some specific
is the local optimal result at some specific  . The maximum
. The maximum  is achieved when
is achieved when  . The ultimate objective of the proposed method is to find this optimal
. The ultimate objective of the proposed method is to find this optimal  and the optimal power index assignment vector under it.
and the optimal power index assignment vector under it.
In Sections 3.2 and 3.3, we propose a two-step approach to solve the optimization problem (17)–(20). More specifically, in the first step (Section 3.2), we assume a fixed  and then given that fixed parameter
and then given that fixed parameter  we propose a simple method (greedy algorithm) trying to find the optimal set of users to receive service. However, this optimality is not a global optimality. In general, as mentioned before,
we propose a simple method (greedy algorithm) trying to find the optimal set of users to receive service. However, this optimality is not a global optimality. In general, as mentioned before,  could get any value within the interval
could get any value within the interval  . The global optimal solution can be obtained when parameter
. The global optimal solution can be obtained when parameter  is chosen to be the optimal one
is chosen to be the optimal one  . The actual objective of the second step of our approach (Section 3.3) is to find this optimal
. The actual objective of the second step of our approach (Section 3.3) is to find this optimal  , by which the global optimal set of users that will be scheduled to receive service can be identified.
, by which the global optimal set of users that will be scheduled to receive service can be identified.
3.2. Greedy Algorithm for a Given System Load
Before obtaining the best system load, we first discuss how to find the local best solution. Assuming that the value of  is known, the right-hand sides of (19) and (20) can be determined. Combining the two constraints together, we can express the optimization problem (18) by replacing
is known, the right-hand sides of (19) and (20) can be determined. Combining the two constraints together, we can express the optimization problem (18) by replacing  with
with  ,
,  as follows:
as follows:

Note that (26) is a nonlinear continuous knapsack problem with the  taking continuous values between 0 and 1. In general, solving this type of problem is proven to be difficult or even impossible in some cases [27]. However, Proposition 1 limits the transmit power of a user
taking continuous values between 0 and 1. In general, solving this type of problem is proven to be difficult or even impossible in some cases [27]. However, Proposition 1 limits the transmit power of a user  , to either
, to either  or
or  for the optimal solution. This condition provides a possible method to solve the above nonlinear knapsack problem. Without loss of generality, we suppose that the optimal solution is when the first
for the optimal solution. This condition provides a possible method to solve the above nonlinear knapsack problem. Without loss of generality, we suppose that the optimal solution is when the first  users transmit at their maximum power,
users transmit at their maximum power,  ,
,  . The optimal system load is
. The optimal system load is  . The following theorem states that the power index of an individual user is equal to its power index capacity under
. The following theorem states that the power index of an individual user is equal to its power index capacity under  , that is,
, that is,  .
.
Theorem 1.
Let the optimal solution allow  users to transmit at their maximum power and the system achieves the system load
users to transmit at their maximum power and the system achieves the system load  . The power index that an individual user received in this case is equal to its power index capacity, that is,
. The power index that an individual user received in this case is equal to its power index capacity, that is,  .
.
Proof.
For those users whose transmit powers are zero, the corresponding power index capacities are also zero. Therefore, their power indices are zero as well. Without loss of generality, we assume that the  users under consideration are identified as follows:
users under consideration are identified as follows:  . Based on Proposition 1, we have
. Based on Proposition 1, we have

Performing some manipulations in these  equations, we have
equations, we have

Letting  , we obtain
, we obtain  as
as

From the definition of power index capacity, we find that  .
.
With reference to the optimal solution of problem (26), we can prove the following theorem.
Theorem 2.
The optimal solution of the constrained optimization problem (26) can be obtained by solving the following linear 0-1 knapsack problem:

Proof.
Since  for user
for user  , we present the objective function of (26) as follows:
, we present the objective function of (26) as follows:

Based on Proposition 1, we know that the optimal solution is achieved when the transmit power of a user  is either
is either  or
or  . According to Theorem 1, in terms of power index that means that users are assigned either their power index capacity or 0 for the chosen system load
. According to Theorem 1, in terms of power index that means that users are assigned either their power index capacity or 0 for the chosen system load  . In the above relation (31), the solution for
. In the above relation (31), the solution for  is either 1 or 0. Therefore, we can modify (31) as follows without changing the final optimal solution:
is either 1 or 0. Therefore, we can modify (31) as follows without changing the final optimal solution:

where  .
.
Instead of solving for the optimal solution of the above integer knapsack problem (30), which is in principle NP-hard, we utilize a greedy algorithm (GA) in order to obtain an approximate solution. Let  denote the result achieved by the approximate solution, while
denote the result achieved by the approximate solution, while  and
and  denote the corresponding results of the optimal solutions for the integer and continuous knapsack problems, respectively. It has been proven that
denote the corresponding results of the optimal solutions for the integer and continuous knapsack problems, respectively. It has been proven that  [28]. Furthermore, let
[28]. Furthermore, let

which is a constant value for an individual user. Let us further suppose that all backlogged users are sorted in descending order according to  , that is,
, that is,  for
for  . If it is not the case, these values can be sorted in
. If it is not the case, these values can be sorted in  time through an efficient procedure. Thus, the optimal continuous solution of problem (30) is given by
time through an efficient procedure. Thus, the optimal continuous solution of problem (30) is given by

An algorithm that finds the critical point  within
within  time in a system with
time in a system with  users is provided in [28]. Based on solution (34), the greedy algorithm (GA) obtains the approximate solution
users is provided in [28]. Based on solution (34), the greedy algorithm (GA) obtains the approximate solution  as follows:
as follows:

where

It has been shown in [28] that in worst case  . Let
. Let  represent the result that corresponds to the integer solution of (32) when
represent the result that corresponds to the integer solution of (32) when  is assigned a value from
is assigned a value from  , and
, and  be the result when
be the result when  . From the definition of
. From the definition of  , we know that
, we know that  is the maximum value among all
is the maximum value among all  , that is,
, that is,  . Based on Proposition 1 and the analysis in the previous subsection, it is easy to find that
. Based on Proposition 1 and the analysis in the previous subsection, it is easy to find that 
 . Therefore, when the optimal system power index
. Therefore, when the optimal system power index  is chosen,
is chosen,  . Since
. Since  and the equality
and the equality  holds only when
holds only when  , and the optimal solution can be obtained.
, and the optimal solution can be obtained.
3.3. Optimal System Load
As we discussed in the last subsection the optimal solution of problem (26) depends on the selected system load  . Relation (17) shows that the power index capacity increases as
. Relation (17) shows that the power index capacity increases as  decreases. At the first point when
decreases. At the first point when  , the power index capacity reaches its largest value and then it decreases linearly following the value of
, the power index capacity reaches its largest value and then it decreases linearly following the value of  . Although a smaller value of
. Although a smaller value of  may increase the single user power index capacity at some range, the finally achieved objective function could be low due to the small system load
may increase the single user power index capacity at some range, the finally achieved objective function could be low due to the small system load  . On the other hand, setting large
. On the other hand, setting large  reduces the individual user power index capacity as (17) indicates. The consequence of smaller power index capacity is that more users are required to share
reduces the individual user power index capacity as (17) indicates. The consequence of smaller power index capacity is that more users are required to share  , and probably a small objective function should be used due to the concavity of function
, and probably a small objective function should be used due to the concavity of function  that converts the power index to throughput. Therefore, whether or not the objective function reaches its maximum value depends not only on the value of the system load
that converts the power index to throughput. Therefore, whether or not the objective function reaches its maximum value depends not only on the value of the system load  , but also on how it is shared among the candidate users. There must exist an optimal value of system load
, but also on how it is shared among the candidate users. There must exist an optimal value of system load  that can achieve the maximum weighted rate.
that can achieve the maximum weighted rate.
Let the power index vector  denote the optimal solution, which can be found through the method described in the previous section for a given specific value of
denote the optimal solution, which can be found through the method described in the previous section for a given specific value of  . Apparently,
. Apparently,  is a function of
is a function of  . The objective function (18) is the sum of individual weighted rates that are obtained from
. The objective function (18) is the sum of individual weighted rates that are obtained from  using function
using function  . Therefore,
. Therefore,  can also be regarded as a function of
can also be regarded as a function of  . Let
. Let  be the function that gives the maximum value of the sum of weighted rates at
be the function that gives the maximum value of the sum of weighted rates at  . Then the original optimization problem can be rewritten as follows:
. Then the original optimization problem can be rewritten as follows:

The optimal solution  of the above problem and its corresponding power index assignment by (34) with
of the above problem and its corresponding power index assignment by (34) with  provides the final optimal solution of (18).
provides the final optimal solution of (18).
Problem (37) is a simple unconstrained maximization problem that searches for the maximum  within the interval
within the interval  . The disadvantage of (37) is that it does not have an explicit expression. Hence, algorithms that rely on the first- or second-order derivatives will not be applicable in this case. Therefore, the searching process depends on the result of (34). Note that every time when a new value of
. The disadvantage of (37) is that it does not have an explicit expression. Hence, algorithms that rely on the first- or second-order derivatives will not be applicable in this case. Therefore, the searching process depends on the result of (34). Note that every time when a new value of  is chosen, the order of
is chosen, the order of  may be different from that of previous
may be different from that of previous  .
.
The time of calculating the best result for a newly chosen  , including the time of reordering the users (if needed), is easily obtained as
, including the time of reordering the users (if needed), is easily obtained as  if
if  is assumed to be large enough. Moreover, there are many possible local maximum points within the range
is assumed to be large enough. Moreover, there are many possible local maximum points within the range  . The final optimal
. The final optimal  must be a global best value. Although in [29] many searching algorithms on how to locate the minimum/maximum solution within a range are described, to make these algorithms effective there must be only one extreme point in the specified range. However, in general it is not possible to know the range which contains only the global optimal value. Thus, an exhaustive search within
must be a global best value. Although in [29] many searching algorithms on how to locate the minimum/maximum solution within a range are described, to make these algorithms effective there must be only one extreme point in the specified range. However, in general it is not possible to know the range which contains only the global optimal value. Thus, an exhaustive search within  would be needed. However, the following proposition provides a lower bound
would be needed. However, the following proposition provides a lower bound  with respect to the searching range instead of 0 in order to restrict the corresponding feasible searching range.
with respect to the searching range instead of 0 in order to restrict the corresponding feasible searching range.
Proposition 4.
The lower bound of the feasible searching range is given by

Proof.
With the decrease of the target system load  , the individual power index, provided by (14)), will keep increasing till
, the individual power index, provided by (14)), will keep increasing till  reaches the point
reaches the point  for user
for user  , that is
, that is  . With respect to user
. With respect to user  , if
, if  its power index
its power index  .
.  is given by
is given by  , which varies with different users since their
, which varies with different users since their  are not likely the same. Let
are not likely the same. Let  be the minimum among all
be the minimum among all  's. Once
's. Once  all backlogged users will have the same power index capacities
all backlogged users will have the same power index capacities  . Define a small increment
. Define a small increment  and let
and let  . Apparently, for all users their power indices will all have small increment
. Apparently, for all users their power indices will all have small increment  such that
such that  . Maintaining the previous power index assignment and giving
. Maintaining the previous power index assignment and giving  to any backlogged user will help increase the objective function (18). We hence can keep adding
to any backlogged user will help increase the objective function (18). We hence can keep adding  to
to  till it reaches
till it reaches  , which proves this proposition.
, which proves this proposition.
Since the optimal  can reside between
can reside between  and
and  , we need to calculate a series of sample values after every interval
, we need to calculate a series of sample values after every interval  . Apparently, the smaller the
. Apparently, the smaller the  the more samples we get and thereby the more accurate is the obtained result. On the other hand, it also increases the required computational time and power.
the more samples we get and thereby the more accurate is the obtained result. On the other hand, it also increases the required computational time and power.
Therefore, in practice we only use reasonably small  in order to reduce the corresponding computational power and complexity, while still obtain a good approximation of the optimal solution. It should be noted though that in theory when
in order to reduce the corresponding computational power and complexity, while still obtain a good approximation of the optimal solution. It should be noted though that in theory when  becomes infinitely small the above methodology can be used to find the optimal solution. Specifically, there exists an algorithm with complexity of
becomes infinitely small the above methodology can be used to find the optimal solution. Specifically, there exists an algorithm with complexity of  that guarantees the finding of the optimal solution, however its high complexity limits its applicability for real-time computations and can be used only for benchmarking purposes. Let us assume that the order in (34) is known and fixed. Under this condition, there are only
that guarantees the finding of the optimal solution, however its high complexity limits its applicability for real-time computations and can be used only for benchmarking purposes. Let us assume that the order in (34) is known and fixed. Under this condition, there are only  possible results satisfying the optimal condition in Proposition 1, that is, try the maximum transmission power in the fixed order with number of users from 1 to
possible results satisfying the optimal condition in Proposition 1, that is, try the maximum transmission power in the fixed order with number of users from 1 to  . The maximum result is the optimal one. For any two users in the possible system load range from
. The maximum result is the optimal one. For any two users in the possible system load range from  , their order of
, their order of  will change at most three times. Therefore, there are totally
will change at most three times. Therefore, there are totally  order changes for
order changes for  users. Every order change requires first the sorting operation and then the comparison operation that have complexity of
users. Every order change requires first the sorting operation and then the comparison operation that have complexity of  and
and  respectively, which makes the overall complexity of this method
respectively, which makes the overall complexity of this method  .
.
The optimal algorithm is described as follows.
-
(1)
Find the
 points of target system load,
points of target system load, 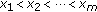 , between
, between  where the users change their orders in
where the users change their orders in  . Such points represent actually any point that for any two users
. Such points represent actually any point that for any two users  and
and  ,
,  , which is,
, which is,  (39)
(39)
Based on the definition of power index capacity in (17), the above equation will have at most three solutions.
-
(2)
Once the order is fixed, sort all
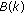 users by
users by  in descending order. The value
in descending order. The value 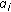 can be calculated using any number between
can be calculated using any number between 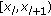 since the order will be the same within this range.
since the order will be the same within this range. -
(3)
Perform
 rounds of calculation of objective function (6). In round
rounds of calculation of objective function (6). In round  , let the largest
, let the largest  users transmit with their largest transmit powers.
users transmit with their largest transmit powers. -
(4)
Compare the result of round (
 ) to that of round
) to that of round  . If the result in round (
. If the result in round (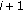 ) is less than round
) is less than round  , then stop the calculation. In that case, the result of round
, then stop the calculation. In that case, the result of round  is the best result in this order between
is the best result in this order between 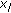 and
and 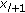 .
. -
(5)
The largest result obtained in step (4) is the global optimal solution.
Once the order is fixed in the range  at step (2), the method provided in Section 3.2 that finds the best local solution can be applied here, which will provide the largest
at step (2), the method provided in Section 3.2 that finds the best local solution can be applied here, which will provide the largest  ,
,  , users with this fixed order. The only difference is that the target system load is not provided directly by a specific known value
, users with this fixed order. The only difference is that the target system load is not provided directly by a specific known value  , but lies within a specific range. Based on Proposition 1, according to which the users allowed to transmit will use their maximum transmission power, we perform
, but lies within a specific range. Based on Proposition 1, according to which the users allowed to transmit will use their maximum transmission power, we perform  rounds of calculation in step (3) and compare the results to find the optimal
rounds of calculation in step (3) and compare the results to find the optimal  users.
users.
3.4. Fairness Conditions
As mentioned before, fairness is controlled by the vector  . When changing the values of
. When changing the values of  , we are actually pursuing a set of optimal fixed values
, we are actually pursuing a set of optimal fixed values  that balance the rate of users with varying channel conditions and hence keep fairness. Since we do not know in advance the exact distribution of the channel conditions, and the number of users may also change, it is difficult to obtain vector
that balance the rate of users with varying channel conditions and hence keep fairness. Since we do not know in advance the exact distribution of the channel conditions, and the number of users may also change, it is difficult to obtain vector  in advance. Therefore, a real-time algorithm is required that is capable of converging
in advance. Therefore, a real-time algorithm is required that is capable of converging  toward
toward  , while maintaining the asymptotic fairness. Stochastic approximation algorithm has been proven to be effective in estimating such parameters. Note that this algorithm has been implemented in [14, 15] in order to solve similar problems. Generally, the stochastic approximation algorithm is a recursive procedure for finding the root of a real-value function
, while maintaining the asymptotic fairness. Stochastic approximation algorithm has been proven to be effective in estimating such parameters. Note that this algorithm has been implemented in [14, 15] in order to solve similar problems. Generally, the stochastic approximation algorithm is a recursive procedure for finding the root of a real-value function  . In many practical cases, the form of function
. In many practical cases, the form of function  is unknown. Therefore, the result with the input variable
is unknown. Therefore, the result with the input variable  cannot be obtained directly. Instead, the observations of the results, sometimes with noise, will be taken. It has been proven that the root of
cannot be obtained directly. Instead, the observations of the results, sometimes with noise, will be taken. It has been proven that the root of  can be estimated with the observation
can be estimated with the observation  by the following procedure:
by the following procedure:

where  ,
,  . We can simply let
. We can simply let  . In most situations, the value of
. In most situations, the value of  may not be directly available, but instead the
may not be directly available, but instead the  , where
, where  is the observation noise. In this case, the above approximation approach still applies, with the observed value replaced by
is the observation noise. In this case, the above approximation approach still applies, with the observed value replaced by  . The convergence of
. The convergence of  to the root requires
to the root requires  .
.
Here, we define our function  as follows:
as follows:

whose root  will make
will make  which satisfies the fairness condition (3). The noise observation
which satisfies the fairness condition (3). The noise observation  in our case is:
in our case is:

It is easy to prove that the mean of noise  . Therefore, the value of
. Therefore, the value of  is then recursively obtained by
is then recursively obtained by

However,  need to know the mean of total system throughput
need to know the mean of total system throughput  . We use a smoothed value
. We use a smoothed value  to approximate
to approximate  and update
and update  as follows:
as follows:

where  is the smooth factor which determines how the estimated
is the smooth factor which determines how the estimated  follows the change of actual achieved system throughput. In the remaining of the paper, throughout the performance evaluation of our approach, the value
follows the change of actual achieved system throughput. In the remaining of the paper, throughout the performance evaluation of our approach, the value  is chosen. The numerical results presented in Sections 4.2.2 and 4.2.3, with respect to the convergence of
is chosen. The numerical results presented in Sections 4.2.2 and 4.2.3, with respect to the convergence of  's and the achievable fairness, demonstrate that such a method is very effective in approximating the optimal values of
's and the achievable fairness, demonstrate that such a method is very effective in approximating the optimal values of  and therefore controlling and maintaining fairness.
and therefore controlling and maintaining fairness.
4. Performance Evaluation
In this section, we evaluate the performance of the proposed method in terms of the achievable fairness and throughput, via modeling and simulation. Furthermore, to better understand the performance of the proposed scheduling algorithm-in the following we refer to as throughput maximization and fair scheduling (MAX-FAIR)—we compare it with the maximum throughput (MAX) scheme [16], which achieves the maximum total uplink throughput by allowing only the best  users in terms of their received power to transmit, and with the HDR algorithm [7, 9], which is a single user scheduling algorithm. The principles and operation of HDR basically refer to a proportional fair scheduling scheme, which can be used in the uplink scheduling to demonstrate the one-at-a-time proportional fair scheduling. Following the HDR principles the transmission of a single user at a given time slot is scheduled, with the data rates and slot lengths varying according to the specific channel condition. In the MAX scheme parameter,
users in terms of their received power to transmit, and with the HDR algorithm [7, 9], which is a single user scheduling algorithm. The principles and operation of HDR basically refer to a proportional fair scheduling scheme, which can be used in the uplink scheduling to demonstrate the one-at-a-time proportional fair scheduling. Following the HDR principles the transmission of a single user at a given time slot is scheduled, with the data rates and slot lengths varying according to the specific channel condition. In the MAX scheme parameter,  is determined by iteratively comparing the throughput of best
is determined by iteratively comparing the throughput of best  users,
users,  , where
, where  is the total number of users. The throughput achieved by MAX scheme is regarded as the upper bound throughput in the uplink CDMA scheduling. On the other hand, since HDR achieves temporal fairness, we consider it here to mainly observe the difference between temporal fairness and throughput fairness and their corresponding advantages in specific cases.
is the total number of users. The throughput achieved by MAX scheme is regarded as the upper bound throughput in the uplink CDMA scheduling. On the other hand, since HDR achieves temporal fairness, we consider it here to mainly observe the difference between temporal fairness and throughput fairness and their corresponding advantages in specific cases.
4.1. Model and Assumptions
Throughout our numerical study, we consider a single cell DS-CDMA multirate system with multiple active users. All active users are continuously backlogged during the simulation and generate packets with average size of 320 bytes. The maximum transmission power is assumed the same for all users, that is,  , while the system chip rate is
, while the system chip rate is  as defined in IS-95 and the required SINR is
as defined in IS-95 and the required SINR is  dB for data service, the same for all users. The transmission time is divided into 1 millisecond equal length slots, which is the algorithm scheduling interval, while the simulation lasts for
dB for data service, the same for all users. The transmission time is divided into 1 millisecond equal length slots, which is the algorithm scheduling interval, while the simulation lasts for  slots.
slots.
To study the impact of the channel condition variations on the system throughput and fairness performance, we model the channels through an 8-state Markov-Rayleigh fading channel model [30]. According to this model, the channel has equal steady-state probabilities of being in any of the eight states. We also assume that the coherent time is much larger than the length of a time-slot, hence the channel state is assumed to be constant within a time slot. At the beginning of each time slot, the channel model decides to transit to a new state, which can only be itself or one of its neighbor states, that is, from state  to
to 
 or
or  . Table 1 summarizes the state transition probabilities for all the eight states.
. Table 1 summarizes the state transition probabilities for all the eight states.
Furthermore, four different cases with respect to the ranges of the average SNRs that are assigned to the various users are considered. Specifically, Table 2 presents the corresponding ranges and lists the assignment of the average SNRs for each user for a seven-user scenario, under all these cases. The four different cases represent four different scenarios with respect to the SNR as follows (from top to bottom): large SNR range with low SNR users, low SNR, middle SNR, and high SNR. In the next subsection, we evaluate the performance of MAX-FAIR, MAX, and HDR methods under all four cases and compare their corresponding achieved throughput and fairness.
In most of the numerical results presented in the next subsection, unless otherwise is explicitly indicated, all users are assumed to have the same weight. Such a scenario allows us to better understand and compare the achievable performances of the various scheduling schemes, when users have different channel conditions. However, the operation and effectiveness of the proposed MAX-FAIR policy is also demonstrated in an environment, where users present different weights.
4.2. Numerical Results and Discussion
The numerical results presented in Sections 4.2.1 and 4.2.2 refer mainly to the impact of some of the parameters associated with the proposed MAX-FAIR algorithm on its operation and achievable performance and allow us to obtain a better understanding of its operational characteristics and properties. Then in Sections 4.2.3 and 4.2.4, comparative results about the achievable throughput and fairness of the MAX-FAIR, MAX and HDR algorithms are presented.
4.2.1. Finite System Power Index Samples
Figure 1 shows the sensitivity of the weighted throughput achieved by the MAX-FAIR algorithm as a function of the number of samples used to obtain these values. The last point in the horizontal axis corresponds to the optimal value. It should be noted that in the vertical axis, the depicted weighted throughputs are normalized over the optimal value. Moreover, the different curves provided in this figure correspond to different combinations of the SNR ranges and the number of active users. As can be seen, the more samples we choose, the closer is the obtained maximum value to the optimal value, which clearly presents the tradeoff between the accuracy and the required computational power, as discussed before in Section 3.3. For instance, we observe that in the cases with small SNR range (e.g., [0,1] dB), even 20 samples are sufficient to get satisfactory results, while for the cases with larger SNR range (e.g., [−3,3] dB), more samples may be required.
Furthermore, as it can be observed from this figure, for the case of [0,1] dB, the larger the number of active users in the system, the less sensitive is the achievable maximum result to the number of samples (i.e., the slope of the corresponding curve becomes smoother as the number of active users increases). On the other hand, when there are users with high SNR values (e.g., [−3,3] dB), the increasing number of active users makes the achieved throughput drop slightly for small number of samples. This difference in the system behavior is closely related to a different number of simultaneously served users, under different SNR ranges and channel conditions, as depicted by the different observed service patterns in Figure 2.
Specifically, in Figure 2, we present the probabilities of the number of simultaneously served users in each scheduling cycle. For this experiment, we consider 40 backlogged users in the system and perform 200 trials. In each trial, users are randomly assigned the SNRs in the designated SNR range, following the 8-state model [30] described in Section 4.1. We observe that when there are users having high SNR values, for example, in the cases of [−3,3] dB and [2,4] dB, only a small number of users (at most 2 in this experiment), are served concurrently. However, in the case that all users have small SNR values, for example, in the case of [−4,−2] dB, the number of simultaneously served users increases significantly (it is distributed between 4 and 17 in our case as can be seen by Figure 2). Such user distribution indicates that in the case that a single user cannot consume all the system resources (e.g., the case where users have low SNR values), more users will be scheduled simultaneously in order to achieve a more efficient resource utilization and as a result increase the total system throughput. This also demonstrates the advantage of our proposed scheduling algorithm over the one-by-one scheduling algorithms that have been proposed in literature. As a result, with respect to Figure 1, for the case of [0,1] dB, multiple users are scheduled to reach the maximal throughput. Increasing the number of active users enables the system to schedule more available candidates to achieve higher throughput, and therefore the achievable result is less sensitive to the number of samples. However, for the case [−3,3] dB at most only 1 or 2 users are scheduled for simultaneous transmission. In the following experiments and numerical results, we adopt the accuracy of 100 samples, which is sufficient to reach 95% of the optimal-weighted throughput.
4.2.2. Parameter Convergence by Stochastic Approximation
As described in Sections 2.1 and 3.4, parameters  's are used to represent the fairness constraints in our optimization problem formulation. Figure 3 shows the dynamic change of parameters
's are used to represent the fairness constraints in our optimization problem formulation. Figure 3 shows the dynamic change of parameters  's as the system and time evolve, for two different cases that correspond to two different SNR ranges. A seven-user scenario is considered, while for demonstration purposes for each case the corresponding values of only two representative users are presented—one user with strong channel and one user with weak channel. As mentioned before, all the users are assigned the same weight in order to more clearly demonstrate the influence of the channel conditions on
's as the system and time evolve, for two different cases that correspond to two different SNR ranges. A seven-user scenario is considered, while for demonstration purposes for each case the corresponding values of only two representative users are presented—one user with strong channel and one user with weak channel. As mentioned before, all the users are assigned the same weight in order to more clearly demonstrate the influence of the channel conditions on  's. It can be seen by this figure that the converged values of
's. It can be seen by this figure that the converged values of  's have the effect of compensating users with the weak channels and reducing the priority of users with strong channels in the scheduling policy. In fact, the converged values of
's have the effect of compensating users with the weak channels and reducing the priority of users with strong channels in the scheduling policy. In fact, the converged values of  's will make both users (weak and strong) to gain proper system resources and therefore achieve fair throughput. Please note that it is the relative values of
's will make both users (weak and strong) to gain proper system resources and therefore achieve fair throughput. Please note that it is the relative values of  's that control the priority of accessing the system resources, and not their absolute values. Furthermore, it should be noted that the lower the average SNR of a weak user, the larger the gap between the weak user and a strong user, which has negative impact on the achievable system throughput, as we will see in the following subsection.
's that control the priority of accessing the system resources, and not their absolute values. Furthermore, it should be noted that the lower the average SNR of a weak user, the larger the gap between the weak user and a strong user, which has negative impact on the achievable system throughput, as we will see in the following subsection.
4.2.3. Throughput and Fairness Performance
Figure 4 shows the average throughputs of all the users under the MAX-FAIR, MAX, and HDR methods, for a seven-user scenario where the average SNR range is [−3,3] dB and the corresponding average SNR assignments to the seven users are as shown in Table 2. In order to better demonstrate the tradeoff between the computational complexity and the achievable throughput of MAX-FAIR approach, we obtained the corresponding results under two different cases with respect to the number of power index samples (i.e., 20 and 100 samples). As observed in this figure the MAX-FAIR with 100 power index samples achieves slightly higher throughput, however it requires five times the computational power of the MAX-FAIR with 20 power index samples.
When compared to other two scheduling schemes, MAX-FAIR presents the best throughput-fairness performance (balances the achievable throughput of all users) despite the variable channel conditions of the different users, which indicates that the fairness is well maintained under the proposed scheduling algorithm. As mentioned before in the paper, the main objective of HDR is to achieve temporal fairness. Therefore, under HDR scheduling each user throughput is closely related to its channel conditions. That is why in Figure 4 we observe that users 1, 2, and 3 have smaller throughput than users 4, 5, and 6, while user 7 has the largest throughput under the HDR scheme. Under the MAX algorithm, user 7 consumes most of the system resources and achieves much higher throughput than the rest of the users due to the fact that the objective of MAX algorithm is to achieve the highest possible total system throughput, without however considering the fairness issue. In Figure 5, we further measure and evaluate the fairness performance by the standard deviation of the average throughput under all the four different SNR cases. Among the three algorithms, MAX-FAIR algorithm has the smallest deviation for all the different cases under consideration, while the corresponding values change only slightly from case to case. We also find that in general the standard deviation increases as the SNRs become higher. This happens because small fluctuation of  results in larger throughput change, if all the users have higher SNR levels.
results in larger throughput change, if all the users have higher SNR levels.
Figure 6 compares the corresponding average system throughputs of the three algorithms under evaluation, for the different SNR ranges (cases). As we expected, MAX-FAIR outperforms HDR in most cases due to the simultaneous scheduling of multiple users, as has been demonstrated in Figure 2, and consequently results in higher resource utilization. However, in the case of SNR range of [−3,3] dB, MAX-FAIR achieves slightly lower throughput than the HDR. The reason of that resides in the different fairness criteria considered and satisfied in these two algorithms, namely, the throughput fairness and temporal fairness. If we examine again Figure 3, we notice that users that have low average SNR (−3 dB) (e.g., users 1, 2, and 3) finally converge to a high  , which enables them to have equal opportunity to transmit under the MAX-FAIR scheduling policy. Due to their weak channel conditions, their average throughputs will be low and hence the total system throughput will become lower because of the satisfaction of the throughput fairness constraint. However, as explained before since access time is not the only resource to be shared among the users in these systems, considering throughput fairness instead of temporal fairness is more meaningful in these systems and environments, despite the slightly lower total throughput that can be achieved in some cases under this consideration. One possible alternative solution is to relax the fairness constraint if the QoS permits it. Our experiments have demonstrated that after relaxing fairness to 85% of its original requirement, the MAX-FAIR catches up and outperforms the HDR.
, which enables them to have equal opportunity to transmit under the MAX-FAIR scheduling policy. Due to their weak channel conditions, their average throughputs will be low and hence the total system throughput will become lower because of the satisfaction of the throughput fairness constraint. However, as explained before since access time is not the only resource to be shared among the users in these systems, considering throughput fairness instead of temporal fairness is more meaningful in these systems and environments, despite the slightly lower total throughput that can be achieved in some cases under this consideration. One possible alternative solution is to relax the fairness constraint if the QoS permits it. Our experiments have demonstrated that after relaxing fairness to 85% of its original requirement, the MAX-FAIR catches up and outperforms the HDR.
In order to obtain a more in-depth understanding of the MAX-FAIR fairness operation, in Figure 7, we present the achieved average throughputs for all the seven users under MAX-FAIR scheme, for a scenario where the SNR range is assumed to be [−3,3] dB, and the users are assigned different weights. The different weights can be considered as the mapping of different QoS requirements. In this scenario, users 1 and 4 have weight 1, users 2 and 5 have weight 2, while users 3, 6, and 7 have weight 4. Figure 7 demonstrates that the MAX-FAIR successfully schedules the transmissions and distributes the resources so that the various users achieve throughput according to their corresponding assigned weights. Specifically users with weights 2 and 4 obtain, respectively, two times and four times the throughput achieved by users with weight 1. In this figure, we also present (on the right-hand side vertical axis) the converged values of parameters  's. Here, the different values of
's. Here, the different values of  's reflect both the channel condition variations and the weight differences. Please note that the relationship between
's reflect both the channel condition variations and the weight differences. Please note that the relationship between  and weight is not linear due to the nonlinearity between the allocated resources and throughput.
and weight is not linear due to the nonlinearity between the allocated resources and throughput.
4.2.4. Number of Users
Figure 8 shows the achieved total system throughput under MAX and MAX-FAIR algorithms as a function of the number of backlogged users, for the case where the users SNRs are located within [0,1] dB range. Please note that as mentioned before MAX algorithm provides the maximum uplink transmission throughput without considering the fairness property, and therefore is assumed to provide the upper bound throughput in uplink scheduling. From this figure, we can clearly observe the great advantage of the proposed MAX-FAIR approach and its ability to achieve very high throughput, while still maintaining fairness. When the number of backlogged users reaches a certain level, for example, 35 in this experiment, the throughput becomes flat for both MAX-FAIR and MAX, which means that the chances of improving the throughput by opportunistic scheduling with multiple users have been fully utilized.
5. Conclusions
In this paper, the CDMA uplink throughput maximization problem, while maintaining throughput fairness among the various users, was considered. It was shown that such a problem can be expressed as a weighted throughput maximization problem, under certain power and QoS requirements, where the weights are the control parameters that reflect the fairness constraints. A stochastic approximation method was presented in order to effectively identify the required control parameters. The numerical results presented in the paper, with respect to the convergence of the control parameters and the achievable fairness, demonstrated that this method is very effective in approximating the optimal values and therefore controlling and maintaining fairness. Furthermore, the concept of power index capacity was used to represent all the corresponding constraints by the users power index capacities at some certain system power index. Based on this, the optimization problem under consideration was converted into a binary knapsack problem, where the optimal solution can be obtained through a global search within a specific range.
The performance of the proposed policy in terms of the achievable fairness and throughput was obtained via modeling and simulation and was compared with the performances of other scheduling algorithms. The corresponding results revealed the advantages of the proposed policy over other existing scheduling schemes and demonstrated that it achieves very high throughput, while satisfies the QoS requirements and maintains fairness among the users, under different channel conditions and requirements.
References
Adachi F, Sawahashi M, Suda H: Wideband DS-CDMA for next-generation mobile communications systems. IEEE Communications Magazine 1998, 36(9):56-69. 10.1109/35.714618
Wong KD, Varma VK: Supporting real-time IP multimedia services in UMTS. IEEE Communications Magazine 2003, 41(11):148-155. 10.1109/MCOM.2003.1244935
Berezdivin R, Breinig R, Topp R: Next generation wireless communications concepts and technologies. IEEE Communications Magazine 2002, 40(3):108-116. 10.1109/35.989768
Sollenberger NR, Seshadri N, Cox R: The evolution of IS-136 TDMA for third-generation wireless services. IEEE Personal Communications 1999, 6(3):8-18. 10.1109/98.772974
Ramis J, Carrasco L, Femenias G, Riera-Palou F: Scheduling algorithms for 4G wireless networks. IFIP International Federation for Information Processing 2007, 245: 264-276.
Viswanath P, Tse DNC, Laroia R: Opportunistic beamforming using dumb antennas. IEEE Transactions on Information Theory 2002, 48(6):1277-1294. 10.1109/TIT.2002.1003822
Bender P, Black P, Grob M, Padovani R, Sindhushayana N, Viterbi A: CDMA/HDR: a bandwidth-efficient high-speed wireless data service for nomadic users. IEEE Communications Magazine 2000, 38(7):70-77. 10.1109/35.852034
Berggren F, Kim S-L, Jäntti R, Zander J: Joint power control and intracell scheduling of DS-CDMA nonreal time data. IEEE Journal on Selected Areas in Communications 2001, 19(10):1860-1870. 10.1109/49.957302
Jalali A, Padovani R, Pankaj R: Data throughput of CDMA-HDR a high efficiency-high data rate personal communication wireless system. Proceedings of the 51st IEEE Vehicular Technology Conference (VTC '00), May 2000, Tokyo, Japan 3: 1854-1858.
M. Andrews, K. Kumaran, K. Ramanan, A. Stolyar, P.Whiting, and R. Vijayakumar, “CDMA data QoS scheduling on the forward link with variable channel conditions,” Bell Labs Technical Memorandum 10009626-000404-05TM, Bell Labs, Paris, France, April 2000.
Andrews M, Kumaran K, Ramanan K, Stolyar A, Whiting P, Vijayakumar R: Providing quality of service over a shared wireless link. IEEE Communications Magazine 2001, 39(2):150-154. 10.1109/35.900644
Shakkottai S, Stolyar A: Scheduling for multiple flows sharing a time-varying channel: the exponential rule. Bell Labs, Paris, France; 2000.
Liu X, Chong EKP, Shroff NB: Transmission scheduling for efficient wireless utilization. Proceedings of the 20th Annual Joint Conference of the IEEE Computer and Communications Societies (INFOCOM '01), April 2001, Anchorage, Alaska, USA 2: 776-785.
Liu X, Chong EKP, Shroff NB: A framework for opportunistic scheduling in wireless networks. Computer Networks 2003, 41(4):451-474. 10.1016/S1389-1286(02)00401-2
Liu Y, Knightly E: Opportunistic fair scheduling over multiple wireless channels. Proceedings of the 22nd Annual Joint Conference on the IEEE Computer and Communications Societies (INFOCOM '03), March 2003, San Francisco, Calif, USA 2: 1106-1115.
Jafar SA, Goldsmith A: Adaptive multirate CDMA for uplink throughput maximization. IEEE Transactions on Wireless Communications 2003, 2(2):218-228. 10.1109/TWC.2003.808958
Xu L, Shen X, Mark JW: Dynamic bandwidth allocation with fair scheduling for WCDMA systems. IEEE Wireless Communications 2002, 9(2):26-32. 10.1109/MWC.2002.998522
Li C, Papavassiliou S: Fair channel-adaptive rate scheduling in wireless networks with multirate multimedia services. IEEE Journal on Selected Areas in Communications 2003, 21(10):1604-1614. 10.1109/JSAC.2003.815596
Cho J, Hong D: Tradeoff analysis of throughput and fairness on CDMA packet downlinks with location-dependent QoS. IEEE Transactions on Vehicular Technology 2005, 54(1):259-271. 10.1109/TVT.2004.836895
Kulkarni SS, Rosenberg C: Opportunistic scheduling policies for wireless systems with short term fairness constraints. Proceedings of IEEE Global Telecommunications Conference (GLOBECOM '03), December 2003, San Francisco, Calif, USA 1: 533-537.
Li C, Papavassiliou S: Opportunistic scheduling with short term fairness in wireless communication systems. Proceedings of the Conference on Information Sciences and Systems (CISS '04), March 2004, Princeton, NJ, USA 167-172.
Ramakrishna S, Holtzman JM: A scheme for throughput maximization in a dual-class CDMA system. IEEE Journal on Selected Areas in Communications 1998, 16(6):830-844. 10.1109/49.709447
Ottosson T, Svensson A: On schemes for multirate support in DS-CDMA systems. Wireless Personal Communications 1998, 6(3):265-287. 10.1023/A:1008844314164
Borst S, Whiting P: Dynamic rate control algorithms for HDR throughput optimization. Proceedings of the 20th Annual Joint Conference of the IEEE Computer and Communications Societies (INFOCOM '01), April 2001, Anchorage, Alaska, USA 2: 976-985.
Sampath A, Kumar PS, Holtzman JM: Power control and resource management for a multimedia CDMA wireless system. Proceedings of the 6th IEEE International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC '95), September 1995, Toronto, Canada 1: 21-25.
Li C, Papavassiliou S: Joint throughput maximization and fair scheduling in uplink DS-CDMA systems. Proceedings of IEEE/Sarnoff Symposium on Advances in Wired and Wireless Communication, April 2004, Princeton, NJ, USA 193-196.
Hochbaum DS: A nonlinear Knapsack problem. Operations Research Letters 1995, 17(3):103-110. 10.1016/0167-6377(95)00009-9
Martello S, Toth P: Knapsack Problems: Algorithms and Computer Implementations. John Wiley & Sons, New York, NY, USA; 1990.
Miller R: Optimization: Foundations and Applications.. John Wiley & Sons, New York, NY, USA; 2000.
Wang H, Moayeri N: Finite-state Markov channel—a useful model for radio communication channels. IEEE Transactions on Vehicular Technology 1995, 44(1):163-171. 10.1109/25.350282
Acknowledgment
This work has been partially supported by EC EFIPSANS Project (INFSO-ICT-215549).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Papavassiliou, S., Li, C. Joint Throughput Maximization and Fair Uplink Transmission Scheduling in CDMA Systems. J Wireless Com Network 2009, 564692 (2009). https://doi.org/10.1155/2009/564692
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/564692
 points of target system load,
points of target system load, 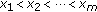 , between
, between  where the users change their orders in
where the users change their orders in  . Such points represent actually any point that for any two users
. Such points represent actually any point that for any two users  and
and  ,
,  , which is,
, which is, 
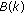 users by
users by  in descending order. The value
in descending order. The value 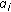 can be calculated using any number between
can be calculated using any number between 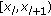 since the order will be the same within this range.
since the order will be the same within this range. rounds of calculation of objective function (6). In round
rounds of calculation of objective function (6). In round  , let the largest
, let the largest  users transmit with their largest transmit powers.
users transmit with their largest transmit powers. ) to that of round
) to that of round  . If the result in round (
. If the result in round (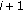 ) is less than round
) is less than round  , then stop the calculation. In that case, the result of round
, then stop the calculation. In that case, the result of round  is the best result in this order between
is the best result in this order between 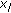 and
and 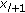 .
.


 's for different users and different SNR ranges (MAX-FAIR).
's for different users and different SNR ranges (MAX-FAIR).



