- Research Article
- Open access
- Published:
Feedforward Data-Aided Phase Noise Estimation from a DCT Basis Expansion
EURASIP Journal on Wireless Communications and Networking volume 2009, Article number: 568570 (2009)
Abstract
This contribution deals with phase noise estimation from pilot symbols. The phase noise process is approximated by an expansion of discrete cosine transform (DCT) basis functions containing only a few terms.We propose a feedforward algorithm that estimates the DCT coefficients without requiring detailed knowledge about the phase noise statistics. We demonstrate that the resulting (linearized) mean-square phase estimation error consists of two contributions: a contribution from the additive noise, that equals the Cramer-Rao lower bound, and a noise independent contribution, that results from the phase noise modeling error. We investigate the effect of the symbol sequence length, the pilot symbol positions, the number of pilot symbols, and the number of estimated DCT coefficients on the estimation accuracy and on the corresponding bit error rate (BER). We propose a pilot symbol configuration allowing to estimate any number of DCT coefficients not exceeding the number of pilot symbols, providing a considerable performance improvement as compared to other pilot symbol configurations. For large block sizes, the DCT-based estimation algorithm substantially outperforms algorithms that estimate only the time-average or the linear trend of the carrier phase.
1. Introduction
Phase noise refers to random perturbations in the carrier phase, caused by imperfections in both transmitter and receiver oscillators. Compensation of this phase noise is critical since these disturbances can considerably degrade the system performance. The phase noise process typically has a low-pass spectrum [1]. A description of the characteristics of oscillator phase noise is given in [2]. Discrete-time processes that have a bandwidth which is considerably less than the sampling frequency can often be modeled as an expansion of suitable basis functions, that contains only a few terms. Such a basis expansion has been successfully applied in the context of channel estimation and equalization in wireless communications, where the coefficients of the channel impulse response are low-pass processes with a bandwidth that is limited by the Doppler frequency [3–5]. Several methods trying to tackle the phase noise problem exist.
-
(i)
Designing oscillators operating at low-phase noise reduces the need of accurate phase noise compensation algorithms. This, however, leads to expensive oscillators which are difficult to integrate on chip [6–8].
-
(ii)
Phase noise can be tracked by means of a feedback algorithm that operates according to the principle of the phase-locked loop (PLL). As feedback algorithms give rise to rather long acquisition transients, they are not well suited to burst transmission systems [9, 10].
-
(iii)
The observation interval is divided into subintervals and a feedforward algorithm is used to estimate within each subinterval the local time-average (or the linear trend) of the phase [9–11]. This corresponds to approximating the phase noise by a function that is constant (or linear) within each subinterval. Such algorithms avoid the long acquisition transients encountered with feedback algorithms. However, in order that the piecewise constant (or linear) approximation of the phase noise be accurate, the subintervals should be short, in which case a high sensitivity to additive noise occurs.
-
(iv)
Recently, iterative joint estimation and decoding/detection algorithms have been proposed that make use of the a priori statistics of the phase noise process. A factor graph approach for the estimation of the Markov-type phase noise has been presented in [12, 13], while in [14, 15] sequential Monte Carlo methods combined with Kalman filtering are used to perform detection in the presence of phase noise. These algorithms are computationally rather complex, prevent the use of off-the-shelf decoders, and assume detailed knowledge about the phase noise statistics at the receiver. Less complex iterative phase noise estimation algorithms based on Wiener filtering have been presented in [16], but still require knowledge about the phase noise autocorrelation function at the receiver.
In this contribution, we apply the basis expansion model to the problem of phase noise estimation from pilot symbols only, using the orthogonal basis functions from the discrete cosine transform (DCT). In contrast to the case of channel estimation, the phase noise does not enter the observation model in a linear way. Section 2 presents the system description which includes the observation model and a general phase noise model. Also, the phase noise estimation algorithm, based on the estimation of only a few DCT coefficients, is derived. Section 3 contains the performance analysis of the proposed algorithm in terms of the mean-square error (MSE) of the phase estimate. The behavior of the linearized model in the frequency domain is examined in Section 4. Analysis results are confirmed by computer simulations in Section 5, which consider both the mean-square phase estimation error and the associated bit error rate (BER) degradation. Section 6 gives a complexity analysis of our algorithm. Conclusions are drawn in Section 7.
2. System Description
We consider the transmission of a block of K data symbols over an AWGN channel that is affected by phase noise. The resulting received signal is represented as

where the index  refers to the
refers to the  th symbol interval of length
th symbol interval of length  ,
,  is a sequence of data symbols with symbol energy
is a sequence of data symbols with symbol energy  , the additive noise
, the additive noise  is a sequence of i.i.d. zero-mean circularly symmetric complex-valued Gaussian random variables with
is a sequence of i.i.d. zero-mean circularly symmetric complex-valued Gaussian random variables with  , and
, and  is a time-varying phase noise process with
is a time-varying phase noise process with 

 correlation matrix
correlation matrix  . The symbol sequence
. The symbol sequence  contains
contains  known pilot symbols at positions
known pilot symbols at positions  , with constant magnitude
, with constant magnitude  . From the observation of the received signal at the pilot symbol positions
. From the observation of the received signal at the pilot symbol positions  , an estimate
, an estimate  of the time-varying phase
of the time-varying phase  is to be produced. This phase estimate will be used to rotate the received signal before data detection, that is, the detection of the data symbols is based on
is to be produced. This phase estimate will be used to rotate the received signal before data detection, that is, the detection of the data symbols is based on  . The detector is designed under the assumption of perfect carrier synchronization, that is,
. The detector is designed under the assumption of perfect carrier synchronization, that is,  . For uncoded transmission, the detection algorithm reduces to symbol-by-symbol detection:
. For uncoded transmission, the detection algorithm reduces to symbol-by-symbol detection:

with A denoting the symbol constellation. The phase  can be represented as a weighed sum of
can be represented as a weighed sum of  basis functions over the interval
basis functions over the interval  :
:

As  is essentially a low-pass process, it can be well approximated by the weighed sum of a limited number
is essentially a low-pass process, it can be well approximated by the weighed sum of a limited number of suitable basis functions:
of suitable basis functions:

In this contribution, we make use of the orthonormal discrete cosine transform (DCT) basis functions, that are defined as

Hence, from (3),  is the
is the  th DCT coefficient of
th DCT coefficient of  . As
. As  has its energy concentrated near the frequencies
has its energy concentrated near the frequencies  and
and  , the DCT basis functions are well suited to represent a low-pass process by means of a small number of basis functions.
, the DCT basis functions are well suited to represent a low-pass process by means of a small number of basis functions.
In the following, we produce from the observation  at the pilot symbol positions
at the pilot symbol positions  , with
, with  , an estimate
, an estimate  of the coefficients
of the coefficients  , with
, with  , using the phase model (4) with equality. The final estimate
, using the phase model (4) with equality. The final estimate  is obtained by computing the inverse DCT of
is obtained by computing the inverse DCT of  :
:

However, as (4) is not an exact model of the true phase  , the phase estimate is affected not only by the additive noise contained in the observation, but also by a phase noise modeling error. Considering the observations (1) at instants
, the phase estimate is affected not only by the additive noise contained in the observation, but also by a phase noise modeling error. Considering the observations (1) at instants  , and assuming that (4) holds with equality, we obtain
, and assuming that (4) holds with equality, we obtain

where for  and
and  is a
is a 

 diagonal matrix with
diagonal matrix with

and  with
with  . The
. The  vectors
vectors  ,
,  and
and  can be viewed as resulting from subsampling
can be viewed as resulting from subsampling  ,
,  and
and  at the instants
at the instants  that correspond to the pilot symbol positions. Similarly, the
that correspond to the pilot symbol positions. Similarly, the  th column of the
th column of the  matrix
matrix  is obtained by subsampling the
is obtained by subsampling the  th DCT basis function
th DCT basis function  . Maximum likelihood estimation of
. Maximum likelihood estimation of  from
from  results in
results in

As  enters the observation
enters the observation  in a nonlinear way, the ML estimate is not easily obtained. Therefore, we resort to a suboptimum ad hoc estimation of
in a nonlinear way, the ML estimate is not easily obtained. Therefore, we resort to a suboptimum ad hoc estimation of  , which is based on the argument (angle) of the complex-valued observations. However, as the function
, which is based on the argument (angle) of the complex-valued observations. However, as the function  reduces the argument of
reduces the argument of  to an interval
to an interval  , taking
, taking  might give rise to phase wrapping, especially when the time-average of
might give rise to phase wrapping, especially when the time-average of  is close to
is close to  or
or  . In order to reduce the probability of phase wrapping, we first rotate the observation
. In order to reduce the probability of phase wrapping, we first rotate the observation  over an angle
over an angle  that is close to the time-average of
that is close to the time-average of  , then we estimate the DCT coefficients of the fluctuation
, then we estimate the DCT coefficients of the fluctuation  and finally we compute the phase estimate
and finally we compute the phase estimate  . We select
. We select

and construct  with
with

We obtain an estimate  of the DCT coefficients of the fluctuation
of the DCT coefficients of the fluctuation  through a least-squares fit
through a least-squares fit  , yielding
, yielding

In order that  exists, we need
exists, we need  . Finally, the phase estimate is given by
. Finally, the phase estimate is given by

where  and
and  . Note from (13) that the estimation algorithm does not need specific knowledge about the phase noise process. As
. Note from (13) that the estimation algorithm does not need specific knowledge about the phase noise process. As  from (11) can be viewed as a noisy version of
from (11) can be viewed as a noisy version of  , the phase estimate
, the phase estimate  from (13), or, equivalently, the phase estimate
from (13), or, equivalently, the phase estimate  from (6), can be interpreted as an interpolated version of the subsampled noisy phase trajectory. The estimation of the phase trajectory involves the inversion of the
from (6), can be interpreted as an interpolated version of the subsampled noisy phase trajectory. The estimation of the phase trajectory involves the inversion of the  matrix
matrix  , which depends on the pilot symbol positions
, which depends on the pilot symbol positions  . Now, we point out that the pilot symbol positions can be selected such that
. Now, we point out that the pilot symbol positions can be selected such that  is diagonal, or, equivalently, that the
is diagonal, or, equivalently, that the  columns of the
columns of the  matrix
matrix  are orthogonal. Such selection of
are orthogonal. Such selection of  avoids the need for matrix inversion in (12). Denoting by
avoids the need for matrix inversion in (12). Denoting by  the orthonormal DCT basis functions of length
the orthonormal DCT basis functions of length  , it is easily verified that selecting
, it is easily verified that selecting  such that
such that

gives rise to

so that

with  denoting the
denoting the 

 identity matrix. Equations (12) and (13) then reduce to
identity matrix. Equations (12) and (13) then reduce to


In order that all  from (14) be integer,
from (14) be integer,  must be an odd multiple of
must be an odd multiple of  , that is,
, that is,  , yielding
, yielding  . The resulting pilot symbol configuration is suited for estimating any number of DCT coefficients not exceeding
. The resulting pilot symbol configuration is suited for estimating any number of DCT coefficients not exceeding  . When
. When  is not an odd multiple of
is not an odd multiple of  , rounding the right-hand side of (14) to the nearest integer gives rise to pilot symbol positions that still yield an essentially diagonal matrix
, rounding the right-hand side of (14) to the nearest integer gives rise to pilot symbol positions that still yield an essentially diagonal matrix  in which case the simplified equations (17) and (18) can still be used.
in which case the simplified equations (17) and (18) can still be used.
3. Performance Analysis
As the observation vector  is a nonlinear function of the carrier phase, an exact analytical performance analysis is not feasible. Instead, we will resort to a linearization of the argument function in (11) in order to obtain tractable results.
is a nonlinear function of the carrier phase, an exact analytical performance analysis is not feasible. Instead, we will resort to a linearization of the argument function in (11) in order to obtain tractable results.
Linearization of the argument function yields

for  , where
, where  is a sequence of i.i.d. zero-mean Gaussian random variables with variance
is a sequence of i.i.d. zero-mean Gaussian random variables with variance  . Note that (19) incorporates the true phase
. Note that (19) incorporates the true phase  instead of the approximate model (4), so that our performance analysis will take the modeling error into account. In order that the linearization in (19) be valid, we need
instead of the approximate model (4), so that our performance analysis will take the modeling error into account. In order that the linearization in (19) be valid, we need  (because
(because  ) and
) and  ; hence, the phase noise fluctuations should not cause phase wrapping and
; hence, the phase noise fluctuations should not cause phase wrapping and  should be sufficiently large. Substituting (19) into (13) yields
should be sufficiently large. Substituting (19) into (13) yields

where  ,
,  and the
and the  matrix
matrix  is such that its
is such that its  th row has a
th row has a  at the
at the  th column and zeroes elsewhere
th column and zeroes elsewhere  . The estimation error resulting from (20) is given by
. The estimation error resulting from (20) is given by

where  denotes the
denotes the  identity matrix. If the model (4) was exact, we would have
identity matrix. If the model (4) was exact, we would have  and
and  , yielding
, yielding

in which case the estimation error would be caused only by the additive noise.
As a performance measure of the estimation algorithm, we consider the mean-square error (MSE), defined as

Substituting (21) into (23) yields

where

The first term in (24) denotes the contribution from the additive noise, whereas the second term in (24) constitutes an MSE floor, caused by the phase noise modeling error. The phase noise statistics affect the MSE floor through the autocorrelation matrix  . The MSE floor decreases with increasing
. The MSE floor decreases with increasing  (because the modeling error is reduced when more DCT coefficients are taken into account), whereas the additive noise contribution to the MSE increases with
(because the modeling error is reduced when more DCT coefficients are taken into account), whereas the additive noise contribution to the MSE increases with  (because
(because  parameters need to be estimated). Hence, there is an optimum value of
parameters need to be estimated). Hence, there is an optimum value of  that minimizes the MSE.
that minimizes the MSE.
From the nonlinear observation model (7), which assumes that (4) holds with equality, we compute the Cramer-Rao lower bound on the MSE (23) resulting from any unbiased estimate  of the DCT coefficients of
of the DCT coefficients of  :
:

In (26),  denotes the Fisher information matrix related to the estimation of
denotes the Fisher information matrix related to the estimation of  from (7), which is found to be
from (7), which is found to be

Combining (26) with (27) yields the following performance bound:

Comparison of (24) and (28) indicates that our ad hoc algorithm (13) yields the minimum possible (over all unbiased estimates) noise contribution to the MSE (assuming that the linearization of the observation model is valid).
When the pilot symbol positions  are selected according to (14), the Cramer-Rao bound (28) reduces to
are selected according to (14), the Cramer-Rao bound (28) reduces to

which indicates that the sensitivity to additive noise increases with the number ( ) of estimated DCT coefficients.
) of estimated DCT coefficients.
4. Frequency-Domain Analysis
After linearization, (20) relates the phase estimate  to the actual phase
to the actual phase  and the additive noise
and the additive noise  . In the absence of additive noise, the estimator can be viewed as a linear system that transforms
. In the absence of additive noise, the estimator can be viewed as a linear system that transforms  into
into  by means of the transfer matrix
by means of the transfer matrix  . In order to analyze this system in the frequency domain, we consider an input
. In order to analyze this system in the frequency domain, we consider an input  with
with  , that is,
, that is,  contains only the frequency
contains only the frequency  . We investigate the mean-square error
. We investigate the mean-square error  between the input
between the input  and the output
and the output  ;
;  is given by (25), with
is given by (25), with  replaced by
replaced by  , where the superscript
, where the superscript  indicates conjugate transpose.
indicates conjugate transpose.
As  is periodic in
is periodic in  with period
with period  , the same periodicity holds for
, the same periodicity holds for  . Assuming the pilot symbol positions are according to (14) with
. Assuming the pilot symbol positions are according to (14) with  and
and  , Figure 1 shows
, Figure 1 shows  as a function of
as a function of  , with
, with  in the interval
in the interval  and
and  . The behavior of
. The behavior of  is explained by noting that subsampling
is explained by noting that subsampling  at the instants
at the instants  (with spacing
(with spacing  ) gives rise to aliasing. Frequencies
) gives rise to aliasing. Frequencies  and
and  yield the same subsampled phase trajectory. In the following discussion, the intervals
yield the same subsampled phase trajectory. In the following discussion, the intervals  and
and  are defined as
are defined as  and
and  , respectively; note that
, respectively; note that  .
.
-
(i)
As the first
 basis functions of the DCT transform cover the frequency interval
basis functions of the DCT transform cover the frequency interval 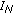 , we get
, we get 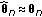 and
and 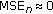 when
when 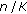 is in
is in 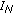 .
. -
(ii)
When
 is in the interval
is in the interval 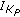 , but outside
, but outside  , we get
, we get 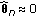 and
and 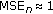 .
. -
(iii)
Suppose
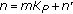 , with
, with  and
and  in
in  , because of aliasing,
, because of aliasing, 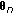 is interpreted as
is interpreted as 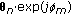 with
with  . When
. When 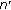 is in the interval
is in the interval 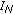 , we get
, we get 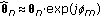 . The resulting estimation error is the sum of two complex exponentials with frequencies
. The resulting estimation error is the sum of two complex exponentials with frequencies 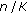 and
and  , yielding
, yielding  . When
. When 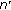 is not in
is not in  , we get
, we get 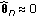 and
and  .
.
It follows from Figure 1 that the estimator can be viewed as a low-pass system with bandwidth  . Basically, the frequency components
. Basically, the frequency components  of
of  with
with  are tracked by the estimator, whereas the components with
are tracked by the estimator, whereas the components with  contribute to the MSE.
contribute to the MSE.
5. Simulation Results
In this section, we assess the performance of the proposed technique in terms of the MSE of the phase estimate and the resulting BER degradation by means of computer simulations. In our simulations, we will consider two types of phase noise, that is, Wiener phase noise and first-order phase noise. The (discrete time) first-order phase noise process  can be viewed as the output of a one-pole filter driven by white Gaussian noise:
can be viewed as the output of a one-pole filter driven by white Gaussian noise:

where  is a sequence of i.i.d. zero-mean Gaussian random variables with variance
is a sequence of i.i.d. zero-mean Gaussian random variables with variance  . The corresponding phase noise power spectrum and phase noise variance are given by
. The corresponding phase noise power spectrum and phase noise variance are given by


The approximations in (31) and (32) hold for  and
and  . It follows from (31) that
. It follows from (31) that  is the
is the  frequency of the power spectrum. The first-order phase noise models the phase instabilities of an oscillator signal that results from a phase-locked loop (PLL) circuit. The (discrete-time) Wiener phase noise
frequency of the power spectrum. The first-order phase noise models the phase instabilities of an oscillator signal that results from a phase-locked loop (PLL) circuit. The (discrete-time) Wiener phase noise  is described by the following system equation:
is described by the following system equation:

where the initial phase noise value  is uniformly distributed in
is uniformly distributed in  and
and  has the same meaning as in (30). Hence,
has the same meaning as in (30). Hence,  can be viewed as the output of an integrator with a white noise input. From (33), it follows that the variance of the Wiener phase noise increases linearly with the time index
can be viewed as the output of an integrator with a white noise input. From (33), it follows that the variance of the Wiener phase noise increases linearly with the time index  , which indicates that the process is nonstationary.
, which indicates that the process is nonstationary.
Comparing (33) and (30), it follows that the Wiener phase noise can be interpreted as a limiting case of first-order phase noise, in the limit for  . Hence, one can formally define the Wiener phase noise spectrum as the limit of the first-order spectrum (31); for
. Hence, one can formally define the Wiener phase noise spectrum as the limit of the first-order spectrum (31); for  ,
,

where the approximation in (34) holds for  . Note that the Wiener phase noise spectrum becomes unbounded at
. Note that the Wiener phase noise spectrum becomes unbounded at  , which is a consequence of the variance increasing linearly with time. In contrast, the complex envelope
, which is a consequence of the variance increasing linearly with time. In contrast, the complex envelope  of the oscillator signal can be shown to be a stationary process (with [1, the Lorentzian power spectrum]). The Wiener phase noise model is often used to describe the phase noise process of a free-running oscillator, although also more elaborate models exist, involving a phase noise spectrum that consists of a sum of terms of the form
of the oscillator signal can be shown to be a stationary process (with [1, the Lorentzian power spectrum]). The Wiener phase noise model is often used to describe the phase noise process of a free-running oscillator, although also more elaborate models exist, involving a phase noise spectrum that consists of a sum of terms of the form  [10, 17–19]. In order to reduce the strong low-frequency components of the phase noise resulting from a free-running oscillator, the oscillator is often incorporated in a PLL circuit; a first-order PLL gives rise to the first-order phase noise process (30) [17].
[10, 17–19]. In order to reduce the strong low-frequency components of the phase noise resulting from a free-running oscillator, the oscillator is often incorporated in a PLL circuit; a first-order PLL gives rise to the first-order phase noise process (30) [17].
Figure 2 shows the first-order phase noise power spectrum, normalized by its value  at
at  , as a function of the normalized frequency
, as a function of the normalized frequency  , with
, with  ; also displayed is the Wiener phase noise power spectrum (normalized by the same
; also displayed is the Wiener phase noise power spectrum (normalized by the same  ). As for both types of phase noise, the same value of
). As for both types of phase noise, the same value of  has been used, both spectra have the same high-frequency content.
has been used, both spectra have the same high-frequency content.
In the following simulations, Wiener phase noise is assumed, unless noted otherwise. First, we assume transmission of a block of length  symbols, consisting of
symbols, consisting of  uncoded QPSK data symbols and
uncoded QPSK data symbols and  constant-energy pilot symbols that are inserted into the sequence according to (14).
constant-energy pilot symbols that are inserted into the sequence according to (14).
-
(i)
Figure 3 shows the MSE of the phase estimate in the absence of phase noise as a function of
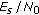 when
when 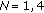 and
and  DCT coefficients are estimated; in addition, these simulation results are compared to the corresponding CRB (29). We observe that the CRB is achieved for sufficiently high values of
DCT coefficients are estimated; in addition, these simulation results are compared to the corresponding CRB (29). We observe that the CRB is achieved for sufficiently high values of  . For small
. For small  , the MSE exceeds the CRB, which is in agreement with the fact that the linearized observation model from (19) is no longer accurate in the low-SNR region. Furthermore, it is confirmed that the contribution from the additive noise to the MSE is proportional to the number of estimated coefficients
, the MSE exceeds the CRB, which is in agreement with the fact that the linearized observation model from (19) is no longer accurate in the low-SNR region. Furthermore, it is confirmed that the contribution from the additive noise to the MSE is proportional to the number of estimated coefficients 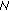 .
.
-
(ii)
Figure 4 shows the MSE as a function of
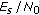 for
for  and
and 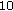 , but this time in the presence of Wiener phase noise with
, but this time in the presence of Wiener phase noise with 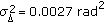 (which corresponds to "strong" phase noise, with
(which corresponds to "strong" phase noise, with 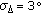 ). We observe an MSE floor in the high-
). We observe an MSE floor in the high-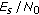 region, which can be reduced by increasing the number
region, which can be reduced by increasing the number  of estimated coefficients. Figure 4 also confirms that for low
of estimated coefficients. Figure 4 also confirms that for low  , the MSE increases when
, the MSE increases when 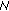 increases. This high-
increases. This high-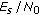 and low-
and low-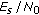 behaviors indicate that for given
behaviors indicate that for given 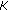 ,
, 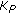 , and
, and 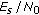 , the MSE can be minimized by proper selection of
, the MSE can be minimized by proper selection of 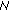 .
.
-
(iii)
Figure 5 shows the bit error rate (BER) as a function of
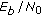 (
(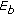 is the energy per transmitted bit,
is the energy per transmitted bit, 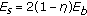 for QPSK) for
for QPSK) for 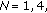 and
and 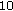 . The reference BER curve corresponds to a system with perfect synchronization and no pilot symbols
. The reference BER curve corresponds to a system with perfect synchronization and no pilot symbols  . We observe that for low
. We observe that for low  , it is sufficient to estimate only the time-average of the phase (i.e.,
, it is sufficient to estimate only the time-average of the phase (i.e., 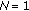 ). Estimating a higher number of DCT coefficients can lead to a worse BER performance for low
). Estimating a higher number of DCT coefficients can lead to a worse BER performance for low 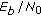 because the MSE of the phase estimate due to additive noise increases with
because the MSE of the phase estimate due to additive noise increases with  . At high
. At high  , a BER floor occurs which decreases with increasing
, a BER floor occurs which decreases with increasing 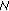 , so in this region it becomes beneficial to estimate more than just one DCT coefficient. Hence, the optimal number of estimated coefficients
, so in this region it becomes beneficial to estimate more than just one DCT coefficient. Hence, the optimal number of estimated coefficients  will depend on the operating
will depend on the operating  .
.
-
(iv)
Figure 6 compares the BER degradations at
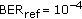 resulting from Wiener phase noise and first-order phase noise; the value of
resulting from Wiener phase noise and first-order phase noise; the value of  is the same for both phase noise processes, such that the Wiener phase noise spectrum and first-order phase noise spectrum are the same for large
is the same for both phase noise processes, such that the Wiener phase noise spectrum and first-order phase noise spectrum are the same for large 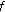 . (The BER degradation caused by some impairment is characterized by the increase (in dB) of
. (The BER degradation caused by some impairment is characterized by the increase (in dB) of  (as compared to the case of no impairment) needed to maintain the BER at a specified reference level.) As the 3 dB frequency
(as compared to the case of no impairment) needed to maintain the BER at a specified reference level.) As the 3 dB frequency  of the first-order phase noise is less than
of the first-order phase noise is less than 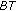 , the frequency contents of the Wiener phase noise and the first-order phase noise outside the estimator bandwidth are essentially the same, and the corresponding BER curves are nearly coincident; this is in agreement with the analysis from Section 4, where we showed that the low-frequency components of the phase noise practically do not contribute to the phase error. It is also confirmed that there is an optimum value of
, the frequency contents of the Wiener phase noise and the first-order phase noise outside the estimator bandwidth are essentially the same, and the corresponding BER curves are nearly coincident; this is in agreement with the analysis from Section 4, where we showed that the low-frequency components of the phase noise practically do not contribute to the phase error. It is also confirmed that there is an optimum value of  that minimizes the BER degradation; this optimum
that minimizes the BER degradation; this optimum 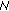 increases with
increases with 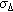 .
.
Next, we study the influence of the pilot symbol positions in the symbol sequence, assuming Wiener phase noise with  . The following scenarios are considered (see Figure 7), with
. The following scenarios are considered (see Figure 7), with  .
.
-
(i)
The pilot symbols are inserted according to (14) (SCEN1).
-
(ii)
All pilot symbols are located in the middle of the sequence (SCEN2).
-
(iii)
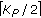 pilot symbols are inserted at the beginning of the sequence, the remaining
pilot symbols are inserted at the beginning of the sequence, the remaining  pilot symbols are placed at the end (SCEN3).
pilot symbols are placed at the end (SCEN3). -
(iv)
The
 pilot symbols are placed equidistantly at positions
pilot symbols are placed equidistantly at positions  (SCEN4).
(SCEN4). -
(v)
We divide the total number of 15 pilot symbols into 3 clusters of 5 consecutive pilot symbols each. The 3 clusters are centered at the positions (14) that correspond to
 (SCEN5).
(SCEN5). -
(vi)
We divide the total number of 15 pilot symbols into 5 clusters of 3 consecutive pilot symbols each. The 5 clusters are centered at the positions (14) that correspond to
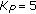 (SCEN6).
(SCEN6).
Figure 8 shows the BER for each scenario with  . We observe that SCEN2 and SCEN3 lead to essentially the same BER performance, that turns out to be very poor. The BER resulting from SCEN5 is slightly better, but still poor. Much better BER performance is obtained for SCEN1, SCEN4, and SCEN6, with SCEN1 yielding the best performance. The poor performance resulting from SCEN2, SCEN3, and SCEN5 comes from the poor conditioning of the
. We observe that SCEN2 and SCEN3 lead to essentially the same BER performance, that turns out to be very poor. The BER resulting from SCEN5 is slightly better, but still poor. Much better BER performance is obtained for SCEN1, SCEN4, and SCEN6, with SCEN1 yielding the best performance. The poor performance resulting from SCEN2, SCEN3, and SCEN5 comes from the poor conditioning of the  matrix
matrix  , yielding very large values when computing the inverse of
, yielding very large values when computing the inverse of  . As the DCT basis functions
. As the DCT basis functions  change only slowly with
change only slowly with  , SCEN2 yields a matrix
, SCEN2 yields a matrix  with nearly identical rows, so it behaves like a matrix of rank 1. Similarly, the matrices
with nearly identical rows, so it behaves like a matrix of rank 1. Similarly, the matrices  that correspond to SCEN3 and SCEN5 behave like matrices of ranks 2 and 3, respectively. Hence, when the pilot symbols are placed in a number of clusters that are less than the number (
that correspond to SCEN3 and SCEN5 behave like matrices of ranks 2 and 3, respectively. Hence, when the pilot symbols are placed in a number of clusters that are less than the number ( ) of DCT coefficients to be estimated, poor performance results. For SCEN1, SCEN4, and SCEN6, the number of pilot symbol clusters exceeds
) of DCT coefficients to be estimated, poor performance results. For SCEN1, SCEN4, and SCEN6, the number of pilot symbol clusters exceeds  ; the corresponding matrices
; the corresponding matrices  are full-rank (rank = 4), and good performance results. Note that SCEN1 and SCEN4 can cope with values of
are full-rank (rank = 4), and good performance results. Note that SCEN1 and SCEN4 can cope with values of  up to
up to  , whereas SCEN6 cannot handle values of
, whereas SCEN6 cannot handle values of  in excess of 5.
in excess of 5.
In the following, we investigate the influence of the number of pilot symbols on the MSE and the BER. The constant-energy pilot symbols are inserted into the data sequence according to (14). For (14) to hold, the block length  should be an odd multiple of the number of pilot symbols
should be an odd multiple of the number of pilot symbols  . We assume a total block length
. We assume a total block length  and simulate the BER and MSE for
and simulate the BER and MSE for  . Figure 9 shows the BER degradation at
. Figure 9 shows the BER degradation at  with respect to the reference system, for a fixed ratio
with respect to the reference system, for a fixed ratio  and various values of the block length
and various values of the block length  . The BER degradation
. The BER degradation  due to the insertion of pilot symbols (which amounts to
due to the insertion of pilot symbols (which amounts to  for
for  ) is included. The following observation can be made.
) is included. The following observation can be made.
-
(i)
For given block size
 , there is an optimum number
, there is an optimum number  of DCT coefficients to be estimated that minimizes the BER degradation. This is consistent with the observation that the MSE of the phase estimate can be minimized by a suitable choice of
of DCT coefficients to be estimated that minimizes the BER degradation. This is consistent with the observation that the MSE of the phase estimate can be minimized by a suitable choice of 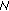 .
. -
(ii)
For very small
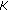 ,
, 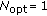 . The optimum value
. The optimum value 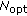 increases with increasing
increases with increasing  because more DCT coefficients are needed to model the phase fluctuations when
because more DCT coefficients are needed to model the phase fluctuations when 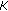 gets larger. Keeping
gets larger. Keeping  yields very large degradations when
yields very large degradations when 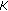 increases.
increases. -
(iii)
The BER degradation that corresponds to
 exhibits a (broad) minimum as a function of
exhibits a (broad) minimum as a function of 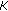 . As long as the fluctuation of
. As long as the fluctuation of  about its time-average is small, so that linearization of the argument function in (11) applies, the degradation decreases with increasing
about its time-average is small, so that linearization of the argument function in (11) applies, the degradation decreases with increasing  because the number
because the number  of noisy observations of the phase noise increases when the ratio
of noisy observations of the phase noise increases when the ratio  is fixed. However, for too large
is fixed. However, for too large  the fluctuation of the Wiener phase noise is so large that linearization is no longer valid (for Wiener phase noise, we need
the fluctuation of the Wiener phase noise is so large that linearization is no longer valid (for Wiener phase noise, we need 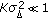 for the linearization to be accurate) and the resulting degradation increases with increasing
for the linearization to be accurate) and the resulting degradation increases with increasing  .
.
For the considered scenario, the minimum degradation occurs at  and amounts to about
and amounts to about  . When the actual block size
. When the actual block size  exceeds
exceeds  , the degradation can be limited by dividing the block in subblocks of at most
, the degradation can be limited by dividing the block in subblocks of at most  symbols, and estimating the phase trajectory for each subblock separately.
symbols, and estimating the phase trajectory for each subblock separately.
Figure 10 shows the BER degradation when (1)  and
and  and (2)
and (2)  and
and  , for the following phase noise estimation algorithms.
, for the following phase noise estimation algorithms.
-
(i)
The proposed DCT-based algorithm with pilot symbol placement according to SCEN1 (14) and selection of the optimum
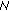 .
. -
(ii)
Estimation of only the time-average of the phase noise, with the pilot symbols arranged according to SCEN3.
-
(ii)
(iii)The method from Luise et al. [11], with the pilot symbols arranged according to SCEN3. The phase noise over the total symbol block is approximated as a linear interpolation between the average phase values over the first and the second pilot symbol clusters.
We observe that estimating only the time-average or the linear trend of the phase noise yields poor BER performance, except for small  . For
. For  , the DCT-based algorithm also estimates the time-average only (because
, the DCT-based algorithm also estimates the time-average only (because  is optimum for
is optimum for  ); we observe that SCEN3 (with pilot symbols at positions
); we observe that SCEN3 (with pilot symbols at positions  and
and  ) performs slightly better than the DCT-based algorithm (with pilot symbols at positions
) performs slightly better than the DCT-based algorithm (with pilot symbols at positions  and
and  ) for
) for  . However, when the block length is increased, the DCT algorithm that estimates multiple DCT coefficients outperforms both SCEN3 and Luise et al. and leads to a BER degradation that decreases with increasing K until an optimal value for
. However, when the block length is increased, the DCT algorithm that estimates multiple DCT coefficients outperforms both SCEN3 and Luise et al. and leads to a BER degradation that decreases with increasing K until an optimal value for  is reached.
is reached.
6. Complexity Analysis
In order to assess the complexity of the proposed algorithm, we determine the number of complex multiplications required per symbol interval. The calculation of the second term in (18) requires the highest number of computations. This term can be evaluated in the following ways.
-
(1)
In a first approach,
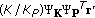 is calculated via two matrix multiplications: first
is calculated via two matrix multiplications: first  (dimension
(dimension 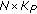 ) and
) and  (dimension
(dimension  ) are multiplied and then
) are multiplied and then  (dimension
(dimension  )and
)and  (dimension
(dimension 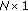 ) are multiplied. The resulting complexity is of the order
) are multiplied. The resulting complexity is of the order 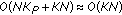 , with the approximation holding for
, with the approximation holding for 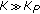 . Hence, the complexity per symbol interval amounts to
. Hence, the complexity per symbol interval amounts to  .
. -
(2)
In a second approach,
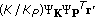 is calculated via a single-matrix multiplication:
is calculated via a single-matrix multiplication:  (dimension
(dimension  ) and
) and 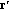 (dimension
(dimension 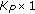 ) are multiplied. Taking into account that
) are multiplied. Taking into account that  can be computed offline, the resulting complexity per symbol is
can be computed offline, the resulting complexity per symbol is 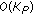 . As
. As 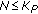 , the first approach is to be preferred over the second approach.
, the first approach is to be preferred over the second approach. -
(3)
The third approach exploits the fact that
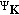 and
and  are submatrices of
are submatrices of 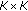 and
and  DCT transform matrices, respectively. Hence, the two matrix multiplications from the first approach can be replaced by an inverse DCT transform (size
DCT transform matrices, respectively. Hence, the two matrix multiplications from the first approach can be replaced by an inverse DCT transform (size 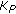 ) followed by a DCT transform (size
) followed by a DCT transform (size 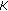 ). As
). As 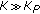 , the complexity of the size-
, the complexity of the size- DCT dominates. The DCT of a vector
DCT dominates. The DCT of a vector  of length
of length  can be obtained by calculating the discrete Fourier transform (DFT) of its even expansion
can be obtained by calculating the discrete Fourier transform (DFT) of its even expansion  (note that the even expansion has length
(note that the even expansion has length  ). As the FFT algorithm used for calculating the DFT of length
). As the FFT algorithm used for calculating the DFT of length  has a computational complexity
has a computational complexity 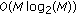 , the complexity of the size-
, the complexity of the size-  DCT is
DCT is  , yielding a complexity per symbol interval of
, yielding a complexity per symbol interval of 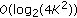 .
.
The complexity per symbol interval of the phase noise estimation method used by Benvenuti et al. [11] is about  . Figure 11 shows the order of complexity as a function of the block length
. Figure 11 shows the order of complexity as a function of the block length  , for the proposed algorithm (approaches 1 and 3) and for Luise et al. algorithm; the result related to the first approach in the proposed algorithm corresponds to taking for each K the value of N that is optimum for
, for the proposed algorithm (approaches 1 and 3) and for Luise et al. algorithm; the result related to the first approach in the proposed algorithm corresponds to taking for each K the value of N that is optimum for  . Luise et al. algorithm has a smaller complexity than the proposed algorithm, but the latter algorithm outperforms the former, especially when the phase noise is strong. For the proposed algorithm, we notice that matrix multiplication according to the first approach leads to the lowest computational complexity for
. Luise et al. algorithm has a smaller complexity than the proposed algorithm, but the latter algorithm outperforms the former, especially when the phase noise is strong. For the proposed algorithm, we notice that matrix multiplication according to the first approach leads to the lowest computational complexity for  . As
. As  becomes larger than
becomes larger than  , calculation via FFT (third approach) is less complex. At the point
, calculation via FFT (third approach) is less complex. At the point  yielding minimum BER degradation (see Figure 9), the first and third approaches give rise to the same complexity.
yielding minimum BER degradation (see Figure 9), the first and third approaches give rise to the same complexity.
7. Conclusions and Remarks
In this contribution, we have considered an ad hoc feedforward data-aided phase noise estimation algorithm that is based on the estimation of only a few  coefficients of the DCT basis expansion of the time-varying phase. The algorithm does not require detailed knowledge about the phase noise statistics. Linearization of the observation model has indicated that the mean-square error of the resulting estimate consists of an additive noise contribution (that increases with
coefficients of the DCT basis expansion of the time-varying phase. The algorithm does not require detailed knowledge about the phase noise statistics. Linearization of the observation model has indicated that the mean-square error of the resulting estimate consists of an additive noise contribution (that increases with  ) and an MSE floor caused by the phase noise modeling error (that decreases with
) and an MSE floor caused by the phase noise modeling error (that decreases with  ). The noise contribution coincides with the Cramer-Rao lower bound.
). The noise contribution coincides with the Cramer-Rao lower bound.
These analytical findings have been confirmed by means of computer simulations. The influence of the position and number  of pilot symbols inserted into the symbol sequence has been investigated. Computer simulations were carried out for several pilot symbol configurations. Arranging the pilot symbols according to (14), such that the subsampled DCT basis functions remain orthogonal, reduces the BER degradation as compared to the case of a preamble/postamble or midamble pilot symbol arrangement with estimation of only the time-average; in addition, the configuration (14) allows to estimate up to
of pilot symbols inserted into the symbol sequence has been investigated. Computer simulations were carried out for several pilot symbol configurations. Arranging the pilot symbols according to (14), such that the subsampled DCT basis functions remain orthogonal, reduces the BER degradation as compared to the case of a preamble/postamble or midamble pilot symbol arrangement with estimation of only the time-average; in addition, the configuration (14) allows to estimate up to  DCT coefficients with a reduced computational complexity. The BER degradation can be minimized by a suitable choice of block length
DCT coefficients with a reduced computational complexity. The BER degradation can be minimized by a suitable choice of block length  , the number
, the number  of pilot symbols, and the number
of pilot symbols, and the number  of DCT coefficients to be estimated.
of DCT coefficients to be estimated.
The considered DCT-based phase estimation algorithm makes use of the energy associated with the pilot symbols only. Further research will involve the incorporation of the DCT-based algorithm in an iterative phase noise estimation algorithm that exploits soft decisions about the data symbols, so that the resulting algorithm benefits from the energy associated with the data symbols as well. The performance and complexity of such an iterative algorithm will be investigated and compared to other iterative algorithms (such as those from [12–16]).
References
Demir A, Mehrotra A, Roychowdhury J: Phase noise in oscillators: a unifying theory and numerical methods for characterization. IEEE Transactions on Circuits and Systems I 2000, 47(5):655-674. 10.1109/81.847872
Parker TE: Characteristics and sources of phase noise in stable oscillators. Proceedings of the 41st Annual Frequency Control Symposium, May 1987, Philadelphia, Pa, USA 99-110.
Giannakis GB, Tepedelenlioglu C: Basis expansion models and diversity techniques for blind identification and equalization of time-varying channels. Proceedings of the IEEE 1998, 86(10):1969-1986. 10.1109/5.720248
Tugnait JK, Luo W: Blind space-time multiuser channel estimation in time-varying DS-CDMA systems. IEEE Transactions on Vehicular Technology 2006, 55(1):207-218. 10.1109/TVT.2005.861209
Rousseaux O, Leus G, Moonen M: Estimation and equalization of doubly selective channels using known symbol padding. IEEE Transactions on Signal Processing 2006, 54(3):979-990.
Nallatamby J-C, Prigent M, Vaury E, Laloue A, Camiade M, Obregon J: Low phase noise operation of microwave oscillator circuits. IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control 2000, 47(2):411-420. 10.1109/58.827428
Mukherjee J: Optimizing MOSFET channel width for low phase noise in LC oscillators. Proceedings of the 50th Midwest Symposium on Circuits and Systems (MWSCAS '07), August 2007, Montreal, Canada 610-613.
Jung DY, Park CS:Power efficient Ka-band low phase noise VCO in 0.13
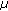 m CMOS. Electronics Letters 2008, 44(10):628-630. 10.1049/el:20080527
m CMOS. Electronics Letters 2008, 44(10):628-630. 10.1049/el:20080527Meyr H, Moeneclaey M, Fechtel S: Digital Communication Receivers: Synchronization, Channel Estimation, and Signal Processing, Wiley Series in Telecommunications and Signal Processing. John Wiley & Sons, New York, NY, USA; 1998.
Mengali U, D'Andrea AN: Synchronization Techniques for Digital Receivers. Plenum Press, New York, NY, USA; 1997.
Benvenuti L, Giugno L, Lottici V, Luise M: Code-aware carrier phase noise compensation on turbo-coded spectrally-efficient high-order modulations. Proceedings of the 8th International Workshop on Signal Processing for Space Communications (SPSC '03), September 2003, Catania, Italy 177-184.
Colavolpe G, Barbieri A, Caire G: Algorithms for iterative decoding in the presence of strong phase noise. IEEE Journal on Selected Areas in Communications 2005, 23(9):1748-1757.
Dauwels J, Loeliger H-A: Phase estimation by message passing. Proceedings of the IEEE International Conference on Communications (ICC '04), June 2004, Paris, France 1: 523-527.
Panayirci E, Cirpan H, Moeneclaey M: A sequential Monte Carlo method for blind phase noise estimation and data detection. Proceedings of the 13th European Signal Processsing Conference (EUSIPCO '05), September 2005, Antalya, Turkey
Panayırcı E, Çırpan HA, Moeneclaey M, Noels N: Blind-phase noise estimation in OFDM systems by sequential Monte Carlo method. European Transactions on Telecommunications 2006, 17(6):685-693. 10.1002/ett.1143
Godtmann S, Hadaschik N, Pollok A, Ascheid G, Meyr H: Iterative code-aided phase noise synchronization based on the LMMSE criterion. Proceedings of the 8th IEEE Signal Processing Advances in Wireless Communications (SPAWC '07), June 2007, Helsinki, Finland 1-5.
Petrovic D, Rave W, Fettweis G: Effects of phase noise on OFDM systems with and without PLL: characterization and compensation. IEEE Transactions on Communications 2007, 55(8):1607-1616.
ETSI : Digital video broadcasting (dvb), second generation framing structure, channel coding and modulation systems for broadcasting, interactive services, news gathering and other broadband satellite applications.
Abhayawardhana VS, Wassell IJ: Common phase error correction with feedback for OFDM in wireless communication. Proceedings of the IEEE Global Telecommunications Conference (GLOBECOM '02), November 2002, Taipei, Taiwan 1: 651-655.
acknowledgments
The authors wish to acknowledge the activity of the Network of Excellence in Wireless COMmunications (NEWCOM++) of the European Commission (Contract no. 216715) that motivated this work. This work is also supported by the FWO Project G.0047.06 Advanced space-time processing techniques for communication through multiantenna systems in realistic mobile channels.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Bhatti, J., Moeneclaey, M. Feedforward Data-Aided Phase Noise Estimation from a DCT Basis Expansion. J Wireless Com Network 2009, 568570 (2009). https://doi.org/10.1155/2009/568570
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/568570

 for
for  and
and  .
. basis functions of the DCT transform cover the frequency interval
basis functions of the DCT transform cover the frequency interval 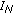 , we get
, we get 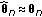 and
and 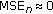 when
when 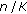 is in
is in 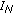 .
. is in the interval
is in the interval 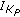 , but outside
, but outside  , we get
, we get 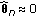 and
and 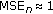 .
.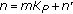 , with
, with  and
and  in
in  , because of aliasing,
, because of aliasing, 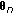 is interpreted as
is interpreted as 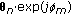 with
with  . When
. When 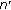 is in the interval
is in the interval 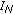 , we get
, we get 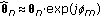 . The resulting estimation error is the sum of two complex exponentials with frequencies
. The resulting estimation error is the sum of two complex exponentials with frequencies 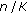 and
and  , yielding
, yielding  . When
. When 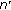 is not in
is not in  , we get
, we get 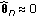 and
and  .
.
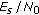 when
when 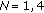 and
and  DCT coefficients are estimated; in addition, these simulation results are compared to the corresponding CRB (29). We observe that the CRB is achieved for sufficiently high values of
DCT coefficients are estimated; in addition, these simulation results are compared to the corresponding CRB (29). We observe that the CRB is achieved for sufficiently high values of  . For small
. For small  , the MSE exceeds the CRB, which is in agreement with the fact that the linearized observation model from (19) is no longer accurate in the low-SNR region. Furthermore, it is confirmed that the contribution from the additive noise to the MSE is proportional to the number of estimated coefficients
, the MSE exceeds the CRB, which is in agreement with the fact that the linearized observation model from (19) is no longer accurate in the low-SNR region. Furthermore, it is confirmed that the contribution from the additive noise to the MSE is proportional to the number of estimated coefficients 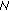 .
.
 .
.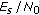 for
for  and
and 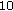 , but this time in the presence of Wiener phase noise with
, but this time in the presence of Wiener phase noise with 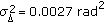 (which corresponds to "strong" phase noise, with
(which corresponds to "strong" phase noise, with 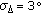 ). We observe an MSE floor in the high-
). We observe an MSE floor in the high-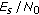 region, which can be reduced by increasing the number
region, which can be reduced by increasing the number  of estimated coefficients. Figure
of estimated coefficients. Figure  , the MSE increases when
, the MSE increases when 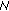 increases. This high-
increases. This high-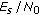 and low-
and low-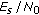 behaviors indicate that for given
behaviors indicate that for given  ,
, 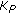 , and
, and 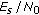 , the MSE can be minimized by proper selection of
, the MSE can be minimized by proper selection of 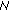 .
.
 is present
is present
 .
.
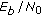 (
(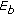 is the energy per transmitted bit,
is the energy per transmitted bit, 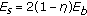 for QPSK) for
for QPSK) for 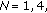 and
and 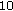 . The reference BER curve corresponds to a system with perfect synchronization and no pilot symbols
. The reference BER curve corresponds to a system with perfect synchronization and no pilot symbols  . We observe that for low
. We observe that for low  , it is sufficient to estimate only the time-average of the phase (i.e.,
, it is sufficient to estimate only the time-average of the phase (i.e., 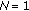 ). Estimating a higher number of DCT coefficients can lead to a worse BER performance for low
). Estimating a higher number of DCT coefficients can lead to a worse BER performance for low 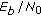 because the MSE of the phase estimate due to additive noise increases with
because the MSE of the phase estimate due to additive noise increases with  . At high
. At high  , a BER floor occurs which decreases with increasing
, a BER floor occurs which decreases with increasing 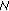 , so in this region it becomes beneficial to estimate more than just one DCT coefficient. Hence, the optimal number of estimated coefficients
, so in this region it becomes beneficial to estimate more than just one DCT coefficient. Hence, the optimal number of estimated coefficients  will depend on the operating
will depend on the operating  .
.
 is present.
is present. .
.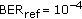 resulting from Wiener phase noise and first-order phase noise; the value of
resulting from Wiener phase noise and first-order phase noise; the value of  is the same for both phase noise processes, such that the Wiener phase noise spectrum and first-order phase noise spectrum are the same for large
is the same for both phase noise processes, such that the Wiener phase noise spectrum and first-order phase noise spectrum are the same for large 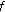 . (The BER degradation caused by some impairment is characterized by the increase (in dB) of
. (The BER degradation caused by some impairment is characterized by the increase (in dB) of  (as compared to the case of no impairment) needed to maintain the BER at a specified reference level.) As the 3 dB frequency
(as compared to the case of no impairment) needed to maintain the BER at a specified reference level.) As the 3 dB frequency  of the first-order phase noise is less than
of the first-order phase noise is less than 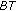 , the frequency contents of the Wiener phase noise and the first-order phase noise outside the estimator bandwidth are essentially the same, and the corresponding BER curves are nearly coincident; this is in agreement with the analysis from Section 4, where we showed that the low-frequency components of the phase noise practically do not contribute to the phase error. It is also confirmed that there is an optimum value of
, the frequency contents of the Wiener phase noise and the first-order phase noise outside the estimator bandwidth are essentially the same, and the corresponding BER curves are nearly coincident; this is in agreement with the analysis from Section 4, where we showed that the low-frequency components of the phase noise practically do not contribute to the phase error. It is also confirmed that there is an optimum value of  that minimizes the BER degradation; this optimum
that minimizes the BER degradation; this optimum 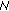 increases with
increases with 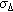 .
.
 for Wiener phase noise and first-order phase noise with
for Wiener phase noise and first-order phase noise with  . (1)
. (1)  ; (2)
; (2)  .
.  .
.
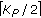 pilot symbols are inserted at the beginning of the sequence, the remaining
pilot symbols are inserted at the beginning of the sequence, the remaining  pilot symbols are placed at the end (SCEN3).
pilot symbols are placed at the end (SCEN3). pilot symbols are placed equidistantly at positions
pilot symbols are placed equidistantly at positions  (SCEN4).
(SCEN4). (SCEN5).
(SCEN5).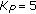 (SCEN6).
(SCEN6).
 .
.
 as function of
as function of
 for various
for various
 and fixed pilot symbol ratio
and fixed pilot symbol ratio
 and
and
 .
.
 , there is an optimum number
, there is an optimum number  of DCT coefficients to be estimated that minimizes the BER degradation. This is consistent with the observation that the MSE of the phase estimate can be minimized by a suitable choice of
of DCT coefficients to be estimated that minimizes the BER degradation. This is consistent with the observation that the MSE of the phase estimate can be minimized by a suitable choice of 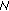 .
.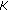 ,
, 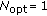 . The optimum value
. The optimum value 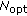 increases with increasing
increases with increasing  because more DCT coefficients are needed to model the phase fluctuations when
because more DCT coefficients are needed to model the phase fluctuations when 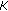 gets larger. Keeping
gets larger. Keeping  yields very large degradations when
yields very large degradations when 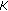 increases.
increases. exhibits a (broad) minimum as a function of
exhibits a (broad) minimum as a function of 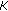 . As long as the fluctuation of
. As long as the fluctuation of  about its time-average is small, so that linearization of the argument function in (11) applies, the degradation decreases with increasing
about its time-average is small, so that linearization of the argument function in (11) applies, the degradation decreases with increasing  because the number
because the number  of noisy observations of the phase noise increases when the ratio
of noisy observations of the phase noise increases when the ratio  is fixed. However, for too large
is fixed. However, for too large  the fluctuation of the Wiener phase noise is so large that linearization is no longer valid (for Wiener phase noise, we need
the fluctuation of the Wiener phase noise is so large that linearization is no longer valid (for Wiener phase noise, we need 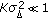 for the linearization to be accurate) and the resulting degradation increases with increasing
for the linearization to be accurate) and the resulting degradation increases with increasing  .
.
 as function of
as function of  . (1)
. (1)  and
and  ; (2)
; (2)  and
and  .
.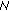 .
.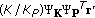 is calculated via two matrix multiplications: first
is calculated via two matrix multiplications: first  (dimension
(dimension 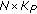 ) and
) and  (dimension
(dimension  ) are multiplied and then
) are multiplied and then  (dimension
(dimension  )and
)and  (dimension
(dimension 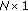 ) are multiplied. The resulting complexity is of the order
) are multiplied. The resulting complexity is of the order 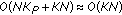 , with the approximation holding for
, with the approximation holding for 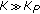 . Hence, the complexity per symbol interval amounts to
. Hence, the complexity per symbol interval amounts to  .
.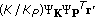 is calculated via a single-matrix multiplication:
is calculated via a single-matrix multiplication:  (dimension
(dimension  ) and
) and 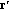 (dimension
(dimension 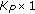 ) are multiplied. Taking into account that
) are multiplied. Taking into account that  can be computed offline, the resulting complexity per symbol is
can be computed offline, the resulting complexity per symbol is 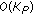 . As
. As 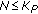 , the first approach is to be preferred over the second approach.
, the first approach is to be preferred over the second approach.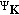 and
and  are submatrices of
are submatrices of 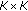 and
and  DCT transform matrices, respectively. Hence, the two matrix multiplications from the first approach can be replaced by an inverse DCT transform (size
DCT transform matrices, respectively. Hence, the two matrix multiplications from the first approach can be replaced by an inverse DCT transform (size 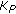 ) followed by a DCT transform (size
) followed by a DCT transform (size 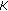 ). As
). As 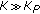 , the complexity of the size-
, the complexity of the size- DCT dominates. The DCT of a vector
DCT dominates. The DCT of a vector  of length
of length  can be obtained by calculating the discrete Fourier transform (DFT) of its even expansion
can be obtained by calculating the discrete Fourier transform (DFT) of its even expansion  (note that the even expansion has length
(note that the even expansion has length  ). As the FFT algorithm used for calculating the DFT of length
). As the FFT algorithm used for calculating the DFT of length  has a computational complexity
has a computational complexity 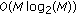 , the complexity of the size-
, the complexity of the size-  DCT is
DCT is  , yielding a complexity per symbol interval of
, yielding a complexity per symbol interval of 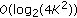 .
.
 m CMOS. Electronics Letters 2008, 44(10):628-630. 10.1049/el:20080527
m CMOS. Electronics Letters 2008, 44(10):628-630. 10.1049/el:20080527