- Research Article
- Open access
- Published:
A Time-Variant MIMO Channel Model Directly Parametrised from Measurements
EURASIP Journal on Wireless Communications and Networking volume 2009, Article number: 687238 (2009)
Abstract
This paper presents the Random-Cluster Model (RCM), a stochastic time-variant, frequency-selective, propagation-based MIMO channel model that is directly parametrised from measurements. Using a fully automated algorithm, multipath clusters are identified from measurement data without user intervention. The cluster parameters are then used to define the propagation environment in the RCM. In this way, the RCM provides a direct link between MIMO channel measurements and MIMO channel modelling. For validation, we take state-of-the-art MIMO measurements, and parametrise the RCM exemplarly. Using three different validation metrics, namely, mutual information, channel diversity, and the novel Environment Characterisation Metric, we find that the RCM is able to reflect the measured environment remarkably well.
1. Introduction
Multiple-input multiple-output technology (MIMO) [1] made its way in the recent years from an information-theoretic shooting star [2] to actual products on the mass market [3, 4]. Currently the 3GPP [5] is standardising MIMO for the next generation's mobile communications, what is called Long Term Evolution (LTE) as well as IEEE is standardising MIMO for WiMAX [6]. Already information theory told that the promise of increased spectral efficiency of MIMO systems is only available when the radio channel permits, but this seems to have faded out of people's memory.
Despite this fact, numerous algorithms were developed, mostly considering ideal uncorrelated i.i.d. Rayleigh fading channels between the transmit and receive antennas, which is only true in rich-scattering environments with sufficiently large antenna spacings at both transmitter and receiver. Otherwise, the performance of the algorithms deteriorates. To reach the goal of gigabit transmissions over the wireless link, one needs to include the knowledge of the actual channel into the algorithms. Thus, an accurate model of the propagation channel is paramount.
One can distinguish between three different types of MIMO channel models: (i) channel models for developing signal-processing algorithms, for example, [7, 8]. These models describe the radio channel by the correlations between the different links, established between individual antenna elements. This makes the model mathematically tractable, yet inaccurate when it comes to reflecting real-world propagation conditions, because current correlation-based models always base on the Rayleigh-fading (or, to some extent, Ricean fading) assumption. While the so-called "Kronecker" model [7] is favoured by many people because it can be treated by random-matrix theory [9], the Weichselberger Model [8] shows a much better fit to measurement data [10, 11]. (ii) channel models for MIMO deployment in a given environment, for example, ray-tracing [12, 13]. These models try to predict MIMO conditions given a map (or floor plan) for optimal positioning of MIMO-enabled base stations, which comes with high demands on computational power and accuracy of environment data bases; (iii) channel models for testing of algorithms and systems, for example, [14–16]. These models typically represent a certain kind of propagation scenario (like indoor offices, or outdoor picocells), without considering a specific propagation environment. This is achieved by modelling the propagation environment in a stochastic way. Such models usually have a medium complexity and represent realistic channels very well, however a closed-form expression of the channel model, as in the first case, does not exist. The major difference between these models is their ability to describe time variation.
A time-variant channel is an essential feature of mobile communications. The 3GPP Spatial Channel Model (SCM) [14] is well suited for simulating random-access communications. It models the channel in blocks (so-called "drops"), during which the channel only undergoes Doppler fading, but after a drop, the channel changes completely. This assumption makes it impossible to test signal processing algorithms that track the channel parameters between different snapshots. Additionally, the abrupt changes between the drops are challenging for hardware testing using channel simulators, since the device under test and the channel model need to be synchronized. A major improvement is the WINNER II geometry-based stochastic channel model [15], which includes a smooth transition between drops. This smooth transition is only provided by the full implementation of the WINNER II model. The popular down-scaled version "clustered-delay line" does not provide the basis to track the channel! The COST 273 MIMO channel model [16, Chapter 6.8] does not use the concept of drops, but intrinsically models the channel in a smooth way. While the user is moving through a randomly-generated map, he is illuminated via groups of different propagation paths depending on his location on this map. When the receiver moves out of a certain region "visibility region", a particular group of paths fades out, and vice versa. Unfortunately, the COST 273 model is not yet completely parametrised, nor fully implemented.
1.1. Contribution
In this paper, we present the novel Random-Cluster Model (RCM), a geometry-based stochastic MIMO channel model for time-variant frequency-selective channels. The application of the RCM focuses on algorithm and system testing, yet it is parametrised directly from measurements.
The Random-Cluster Model uses multipath clusters to model the radio channel. Generally, multipath clusters can be seen as groups of propagation paths having similar parameters. We concisely define a cluster by its mathematical description provided in Section 2.2. Clusters allow to characterise the propagation environment in a compact way using much less parameters than characterisation by individual multipath components (MPCs). This data reduction is the primary purpose for using clusters in radio channel models. Clusters were first only observed in delay domain by Saleh and Valenzuela [17]. Their concept was extended to the joint angle-of-arrival/delay domain in [18]. Recently [19] developed a test to prove the existence or non-existence of clusters in propagation path estimates from channel measurements, showing that clusters indeed exist independent of the authors' view. We were able to match clusters to real-world scattering objects [20].
Several innovations were necessary to construct the RCM, some of which have been introduced in conference papers. First, to accurately parametrise the RCM, automatic clustering techniques are necessary. The first semiautomatic approach for clustering MIMO channel data was introduced in [21]. We gradually extended these ideas by a meaningful joint clustering approach [22], a power-weighted clustering algorithm [23], a criterion to decide on the number of clusters, a reasonable initial guess, and the ability to track clusters over multiple time-variant snapshots [24]. The mere fact that clusters can be tracked demonstrates that clustering makes sense showing that they obviously stem from scattering objects. The automatic parametrisation by identifying clusters without user intervention turned out to be essential to process a large amount of multiantenna measurement data.
Regarding the ability to describe time-variant channels, the RCM is capable to model random-access channels, and, in addition, to cover continuous transmission in a time-variant environment as well by creating smoothly time-variant channel realisations. A major innovation of the RCM is the concept of linearly moving clusters. In this article, we will use the RCM to model smoothly time-variant channels. (A first description of the RCM, modelling random-access channels only was provided in [25], and [26] briefly outlines the ideas of using clusters for time-variant channel modelling.)
The RCM is a stochastic MIMO channel model, yet it is parametrised directly from measurements. By double-directional MIMO channel measurements in a specific environment, a single multivariate pdf of the cluster parameters is created, which is representative for the electromagnetic wave propagation in this environment. The parameters of a single realisation are drawn from this distribution. In this way, the RCM is a stochastic channel model, deriving its parameters directly from measurements.
The complexity of the RCM should be divided into (i) the parametrisation complexity and (ii) the execution complexity. Regarding the parametrisation complexity, the RCM is parametrised automatically from measurements, even if the number of parameters appears to be high. The execution complexity of the RCM is governed by the calculation of the channel matrix, as in all other prominent physical channel models [27]. It adds up to  real operations, where
real operations, where  denotes the number of MPCs,
denotes the number of MPCs,  and
and  denote the number of transmit and receive antennas, respectively, and
denote the number of transmit and receive antennas, respectively, and  denotes the number of frequency samples, for which the channel matrix is calculated.
denotes the number of frequency samples, for which the channel matrix is calculated.
The ultimate challenge for any channel model is its comparison to measurements. We will describe the extensive validation of the RCM against measurements using three different validation metrics: (i) mutual information [2], (ii) channel diversity [28], and (iii) the novel Environment Characterisation Metric [29]. We find that the RCM is able to reflect the measured time-variant environment noticeably well. Additionally, we will demonstrate why the popular mutual information "capacity" is a poor validation metric for time variant MIMO channel models.
1.2. Organisation
This article is organised as follows. Section 2 provides a first overview of the features of the Random Cluster Model. Section 2.1 outlines the structure of the RCM, Section 2.2 details the description of the environment by multipath clusters. The initialisation of the model is provided in Section 2.3, and details on the implementation of the time variance are given in Section 2.4. Section 3 describes the model validation by first outlining the validation framework. We then introduce the validation metrics used in Section 3.2, followed by the validation results in Section 3.3. Finally, Section 4 concludes the article. In Appendix , we provide an overview of the measurements used for parametrisation and validation.
2. The Random-Cluster Model
The RCM is based on the concept of multipath clusters. The most significant feature of the RCM is that it is parametrised directly from channel measurements by an automatic procedure. In this way, the RCM is specific to the environment; it closes the gap between channel measurements and channel modelling. Nonetheless it is a stochastic model as we will clarify shortly.
The novel approach of the RCM is to describe the time-variant geometry of the channel completely by statistical cluster parameters. Clusters provide a compact way of describing the underlying propagation environment. To accurately parametrise the clusters, we extract their parameters from measurements. An important feature of the MIMO channel also reflected by the model is the coupling between propagation paths in space and time, also known as the double-directional MIMO channel model [30]. To enable time-variance, clusters may move, relative to the Tx or Rx. By this, the RCM creates correlated snapshots in time of the propagation environment.
Summarising, the model has the following properties. It is
-
(i)
cluster-based,
-
(ii)
propagation-based, but stochastic,
-
(iii)
double-directional,
-
(iv)
time-variant.
What the RCM Provides
The main focus of the RCM is link-level simulation, for both algorithm testing and device testing. It is well suited to reflect time-variant scenarios that are similar, but not equal to the ones measured before. A major feature is that the parametrisation of the RCM, directly derived from measurements, is achieved automatically. In this way it perfectly fills the gap between channel sounding and channel simulation. Typical applications include testing in specifically challenging channel situations, or in specific application scenarios.
In contrast to "playback simulations" [31] where previously recorded impulse response data from a channel sounder are used to directly model the environment, the RCM is neither fixed in bandwidth, antenna array parameters, or simulation duration.
What the RCM Does Not Provide
By the way it is parametrised, the RCM is very specific in reflecting a certain type of environment. Being rooted in the COST 273 model [16, Chapter 6.8], one might think that the RCM is an all-purpose model. The model user will be warned that it does not perform like this. Many aspects that make a model very general have been intentionally omitted in the RCM in order to reduce complexity, for example, a dedicated path loss calculation, or a description of general environments.
For scenarios close to the measured ones, the RCM will still perform better than other (even standardised) models available, but proper parametrisation is always necessary.
The RCM is definitely not intended for supporting MIMO deployment. Since the model does not include any geometry, it is not suited for predicting the properties of the electromagnetic field in specific locations on a map, particularly not in environments that were not measured before.
2.1. General Model Structure
In the following we describe the RCM by its flow diagram shown in Figure 1. The RCM consists of two major parts: the initialisation, and the implementation of smooth time variation:
-
(1)
During initialisation, a first snapshot of the scenario is generated from the environment parameter function.
-
(2)
The implementation of the smooth time variation is split in two parts: (i) moving the clusters introduces small-scale changes to the environment and generates the Doppler-induced fading; (ii) the birth/death-process accounts for shadowing and large-scale changes.
Both of these parts rely on an accurate parametrisation of the environment. In the next paragraphs we will first detail how the environment is described. Subsequently we will explain the model flow step by step.
2.2. Environment Description—Multipath Clusters
Multipath clusters are the basis for the RCM. Each cluster is described by a number of parameters (Table 1), which are stacked into the cluster parameter vector  . We distinguish between the cluster location parameters (mean delay, azimuth and elevation positions), cluster spread parameters (delay spread, angular spreads), cluster power parameters (power of the cluster and power of the snapshot in which the cluster exists), cluster number parameters (number of paths within the cluster, average number of coexisting clusters in the same snapshot), and cluster movement parameters (change rates of the cluster location and power parameters, and cluster lifetime).
. We distinguish between the cluster location parameters (mean delay, azimuth and elevation positions), cluster spread parameters (delay spread, angular spreads), cluster power parameters (power of the cluster and power of the snapshot in which the cluster exists), cluster number parameters (number of paths within the cluster, average number of coexisting clusters in the same snapshot), and cluster movement parameters (change rates of the cluster location and power parameters, and cluster lifetime).
 .
.A time-variant environment may contain transitions between different propagation conditions, for example, from LOS to NLOS and back. Clusters in these propagation conditions have quite different properties. Different propagation conditions are mainly reflected by two simple parameters: the snapshot power and the number of clusters. These two parameters are included in the set of cluster parameters, being cluster selection parameters. They label clusters for specific propagation conditions in a statistical way.
2.2.1. Geometrical Interpretation
A straight-forward extension of a MIMO channel description by single, discrete MPCs, is the usage of multipath clusters.
Clusters are able to describe a double-directional wave-propagation environment in the same way as multipath components do. Figure 2 illustrates this concept. A cluster represents a unique link between the transmitter and the receiver having a certain power, a certain direction of departure, direction of arrival, and delay. Extending the concept of a single MPC, a cluster shows a certain spread in its parameters, describing the size of the cluster in space.
This leads to a significant reduction in the number of parameters. One cluster describing a manifold of multipath components showing similar propagation parameters is described by only 21 parameters (see Table 1), while a single MPC already needs 12 parameters (such seemingly large numbers of parameters are necessary for a time-variant description of clusters and propagation paths).
When we look at a cluster that stems from multiple bounces of an electromagnetic wave on its way from Tx to Rx, Figure 2 shows how a cluster appears when perceived from Tx and Rx separately. The cluster splits up in two parts. For single-bounce scattering, these two parts of a cluster overlap physically. For a direct path (line-of-sight), the cluster contains only a strong, single path. From the cluster parameters, one cannot deduct whether the cluster stems from single or from multiple-bounces scattering. From a modelling perspective concentrating on clusters, however, this knowledge is redundant (the same applies to MIMO modelling by multipath components). Note that we are using multiple clusters to describe the multipath structure of the radio channel, but Figure 2 shows just one cluster.
2.2.2. Environment pdf
In a measured environment, different kinds of clusters occur. We regard the parameters of these clusters as an ensemble of a multivariate distribution, which we call the environment pdf, (we use the established statistical notation, where  is the argument of the pdf of the random vector
is the argument of the pdf of the random vector  ),
),

The environment pdf characterises the multipath structure in a specific measured environment. In this way, the environment is completely parametrised by a description that is purely statistical. In some cases, this multivariate distribution may be multimodal and does not necessarily follow a simple closed-form distribution.
2.2.3. Parametrisation
The parameters of the RCM are characterized by the environment pdf, which can conveniently be estimated from MIMO channel measurements in a straight-forward way.
-
(1)
MIMO channel measurements provide multiple impulse responses of the scenario. While the channel sounder continuously records frequency-selective MIMO channel matrices at each time instant "snapshots", the transmitter is moved to capture the time-variant properties of the scenario.
-
(2)
Propagation paths are estimated from each snapshot of the channel measurements using a high-resolution parameter estimation. For this purpose we used the Initialization-and-Search-Improved SAGE (ISIS) estimator [32] to estimate
 paths from every measured snapshot.
paths from every measured snapshot. -
(3)
We identify and track clusters in these propagation paths using the fully automatic framework presented in [24]. This framework has the following key features.
-
(a)
The initial guess algorithm identifies the cluster locations by separating clusters as far as possible in the parameter space while taking already existing clusters from previous snapshots into account. The number of clusters is estimated by a power-threshold criterion.
-
(b)
The clustering is optimized using the KPowerMeans algorithm [23], which makes clusters as compact as possible. This is achieved by including the concept of path power into the classic KMeans algorithm and by enabling joint clustering by appropriate scaling of the input data.
-
(c)
Clusters are tracked using a Kalman filter between snapshots, where a probabilistic cluster fitting criterion decides whether a cluster has actually moved or has to be regarded as new.
-
(a)
As a result we obtain the parameters of all clusters in the measured environment, as described in Table 1. The change-rate parameters and cluster lifetimes are determined by the tracking of the clusters. Typical examples of the change-rate parameters and more discussion about their physical interpretation are provided in [33].
-
(1)
We estimate the environment pdf from all identified clusters using a kernel density estimator (KDE) [34].
The KDE approximates the underlying distribution by a sum of kernels. In this way, even multimodal distributions can be described easily. As result, the environment pdf can be written as

where  and
and  denote the mean and covariance of the
denote the mean and covariance of the  th kernel, and
th kernel, and  denotes the number of kernels used.
denotes the number of kernels used.
To parametrise the environment pdf for the RCM, we use Gaussian kernels, hence a Gaussian mixture pdf, such that

where  denotes the dimension of the cluster parameter vector. We used Gaussian kernels for their low complexity and analytical tractability. Furthermore, Gaussian kernels manage to describe all kinds of (continuous) pdfs with low error [35].
denotes the dimension of the cluster parameter vector. We used Gaussian kernels for their low complexity and analytical tractability. Furthermore, Gaussian kernels manage to describe all kinds of (continuous) pdfs with low error [35].
The kernel parameters  and
and  need to be estimated. The input data for this estimation are the identified clusters from a measurement route.
need to be estimated. The input data for this estimation are the identified clusters from a measurement route.
A straight-forward way to find the kernel parameters is to choose the  equal to the total number of identified clusters. Each individual identified cluster is used as (mean) parameter for an individual kernel. The variances of the kernel can then be estimated using the minimum average mean integrated squared error (AMISE) criterion [35]. This parametrisation approach is the most accurate one, although the number of kernels may become quite large.
equal to the total number of identified clusters. Each individual identified cluster is used as (mean) parameter for an individual kernel. The variances of the kernel can then be estimated using the minimum average mean integrated squared error (AMISE) criterion [35]. This parametrisation approach is the most accurate one, although the number of kernels may become quite large.
Of course, the obtained environment pdf is very specific to the measured environment since it is directly parametrised from measurements.
Figure 3 shows four different two-dimensional cuts of the same environment pdf, which was evaluated from a measurement run at 2.55 GHz in the office environment, described in the appendix. These two-dimensional pdfs are colour coded from black (low probability) to white (high probability).
It becomes obvious that the environment pdf is indeed a multimodal distribution, strongly depending on which parameters are observed. For example, Figure 3(a) demonstrates that clusters with large mean delay usually have weaker power, which was to be expected. Additionally, Figure 3(b) details from which Rx directions clusters with stronger power appear. Some of the cluster parameters are even intrinsically correlated. For instance, Figures 3(c)-3(d) show that there is a correlation between the cluster azimuth spreads. Additional values of the environment pdf can be found in [33, 36].
2.3. RCM Initialisation
The initialisation procedure generates the first snapshot of the model.
2.3.1. Drawing Initial Cluster Parameters
The environment pdf  provides a description for all kinds of clusters that were identified in the environment. To actually generate a snapshot, the momentary propagation condition of the environment must be selected. This is done by determining the intended snapshot power and the number of clusters (which are the cluster selection parameters). Their joint distribution function is contained in the environment pdf.
provides a description for all kinds of clusters that were identified in the environment. To actually generate a snapshot, the momentary propagation condition of the environment must be selected. This is done by determining the intended snapshot power and the number of clusters (which are the cluster selection parameters). Their joint distribution function is contained in the environment pdf.
Thus, we draw cluster parameters in a stepwise procedure.
-
(i)
First, we obtain the pdf of the number of clusters,
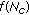 , by marginalizing the environment pdf to the number of clusters, which is done by integrating the environment pdf over the other dimensions. Then the actual number of clusters for the first snapshot,
, by marginalizing the environment pdf to the number of clusters, which is done by integrating the environment pdf over the other dimensions. Then the actual number of clusters for the first snapshot, 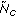 , is determined by drawing a random sample from this pdf. Since the number of clusters must be an integer number, the ceiling of the drawn value is assigned to
, is determined by drawing a random sample from this pdf. Since the number of clusters must be an integer number, the ceiling of the drawn value is assigned to 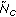 .
. -
(ii)
Then, we obtain the pdf of the snapshot power (given the number of clusters) by conditioning the environment pdf on the chosen number of clusters
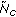 , and marginalising it to the snapshot power. From this marginal distribution
, and marginalising it to the snapshot power. From this marginal distribution  , the intended snapshot power,
, the intended snapshot power, 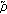 , is determined by drawing a random sample from this pdf. This intended snapshot is only used as a selection criterion for the clusters to be drawn in the next steps. In general, the sum power of the clusters will not exactly match the intended snapshot power.
, is determined by drawing a random sample from this pdf. This intended snapshot is only used as a selection criterion for the clusters to be drawn in the next steps. In general, the sum power of the clusters will not exactly match the intended snapshot power. -
(iii)
Finally, to select a specific type of clusters, the environment pdf is conditioned on both the number of clusters and on the intended snapshot power,
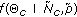 . From this final distribution, we draw
. From this final distribution, we draw  cluster parameter sets
cluster parameter sets 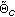 .
.
These parameters are drawn from a multivariate sum-of-Gaussian distribution, which sometimes leads to invalid parameters because of the Gaussian tails. For this reason, the drawn spread parameters and the mean delay are lower-bounded by zero, the number of paths within a cluster is rounded to the next larger integer and lower bounded by one, and the drawn cluster lifetime is rounded to the closest integer value larger or equal to one. In this way, we can retain the low-complexity kernel density estimation but still create valid cluster parameters for the model.
These (post-processed) cluster parameters specify the multipath structure of the initial snapshot.
2.3.2. Placing Multipath Components within the Clusters
-
(1)
In every cluster
 , the corresponding number of paths (which is an initial cluster parameter drawn before),
, the corresponding number of paths (which is an initial cluster parameter drawn before),  , is placed as follows. Every path is described by the path parameters: complex amplitude (
, is placed as follows. Every path is described by the path parameters: complex amplitude (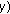 , total delay (
, total delay ( , and the azimuth and elevation of arrival and departure, respectively, (
, and the azimuth and elevation of arrival and departure, respectively, (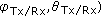 .
.
The delay is drawn from a Gaussian distribution with its mean and variance given in the cluster parameters. Similarly, the angular parameters are drawn from a wrapped Gaussian distribution [37] (in the wrapped Gaussian distribution, all realisations are mapped to their principal value in  ), where the mean and variance are again determined in the cluster parameters (Table 1). All paths within a cluster show the same amplitude,
), where the mean and variance are again determined in the cluster parameters (Table 1). All paths within a cluster show the same amplitude,  , determined by the total cluster power and the number of paths within a cluster, and have a random phase, which is drawn from a uniform distribution
, determined by the total cluster power and the number of paths within a cluster, and have a random phase, which is drawn from a uniform distribution  .
.
After having placed paths in all clusters, the propagation environment of the initial snapshot is completely specified by its multipath structure.
2.3.3. Generating the MIMO Channel Matrix "System Model"
To calculate the MIMO channel matrix, we use the common approach of a bandwidth filter and antenna filters [38].
The time-dependent MIMO channel transfer matrix is calculated from the multipath structure as

at a certain frequency bin  equidistantly spaced on a limited bandwidth between
equidistantly spaced on a limited bandwidth between  , where
, where  denotes the carrier frequency and
denotes the carrier frequency and  the simulated bandwidth. The antenna array patterns are described in
the simulated bandwidth. The antenna array patterns are described in  , and the subset
, and the subset  denotes the
denotes the  th path in cluster
th path in cluster  . This calculation dominates the computational complexity of the model (a low-complexity implementation of this equation is also available in [39]).
. This calculation dominates the computational complexity of the model (a low-complexity implementation of this equation is also available in [39]).
For the exemplary implementation of the RCM that we validated (see Section 3), we imply an  MIMO configuration with uniform linear arrays at both link ends, a bandwidth of 20 MHz, and 32 frequency bins. The centre frequency was set to either 2.55 GHz or to 5.25 GHz matching the measurement. An
MIMO configuration with uniform linear arrays at both link ends, a bandwidth of 20 MHz, and 32 frequency bins. The centre frequency was set to either 2.55 GHz or to 5.25 GHz matching the measurement. An  configuration provides a much tougher test whether a model renders the spatial environment properties correctly than the
configuration provides a much tougher test whether a model renders the spatial environment properties correctly than the  or
or  configurations envisaged for LTE. By including the actual antenna array pattern, the RCM can easily be extended to arbitrary array configurations other than ULAs.
configurations envisaged for LTE. By including the actual antenna array pattern, the RCM can easily be extended to arbitrary array configurations other than ULAs.
2.4. Implementation of the Time Variation
After the generation of the initial snapshot, the RCM generates channels correlated in time. The implementation of the time variation, based on the novel idea of linearly moving clusters, is an integral part of the model. In this way, both stationary and nonstationary time-variant channels can be modelled.
2.4.1. Time Bases
We distinguish between small-scale and large-scale time variations. Small-scale variations, which introduce fading, take place every sampling instant. Large-scale variations, reflecting changes in the propagation structure, occur in less frequent intervals.
For this reason, the RCM distinguishes between two time bases: the sampling time interval,  , and the cluster-lifetime interval,
, and the cluster-lifetime interval,  , where
, where  . Cluster lifetimes,
. Cluster lifetimes,  , are multiples of
, are multiples of  (see Table 1).
(see Table 1).
2.4.2. Large-Scale Variation—Cluster Birth/Death Process
In time-variant scenarios, where at least one of the transceivers is moving, the propagation conditions can change significantly. To introduce these large-scale changes into the model, we included a cluster birth/death process.
This birth/death process is motivated from observations in measurements, where clusters smoothly show up, exist over a period of time, and eventually fade away. We reflect this behaviour in our model by three parameters: (i) the cluster lifetime, responsible for the cluster death, (ii) a cluster birth pdf, and (iii) a fade-in/fade-out coefficient.
The lifetime of each cluster is already intrinsically defined in the cluster parameters (see Table 1), which was drawn from the environment pdf when the cluster was created. Cluster death is implemented by decreasing the lifetime of each cluster in every cluster lifetime interval,  . Dying clusters are fading out during the next cluster lifetime interval.
. Dying clusters are fading out during the next cluster lifetime interval.
An additional probability mass function (pmf), describing the number of cluster births per cluster lifetime interval, is also extracted from the measurements. The extraction method and examples of extracted parameters are provided in [33]. According to this pmf, a number of new clusters are drawn every cluster lifetime interval. After drawing the number of new clusters, the actual parameters of these new clusters are drawn in the same way as described in the initialisation procedure in Section 2.3.1. New-born clusters fade in during the next cluster lifetime interval.
The appearance or disappearance of clusters is done exponentially in the small-scale updates, controlled by the cluster fade-in/fade-out coefficient  . Empirical evaluations showed that a maximum cluster attenuation of 10 dB provides best results, hence
. Empirical evaluations showed that a maximum cluster attenuation of 10 dB provides best results, hence  .
.
Note that our approach is different from using "visibility regions" [40], which cannot be used since we do not consider the actual geometry of the environment.
2.4.3. Small-Scale Variation—Cluster Movement
The RCM models small-scale changes by the movement of the clusters in parameter space. In every sampling time interval, the parameters of the paths within a cluster are linearly incremented. These increments are provided in the cluster parameters  of the respective cluster (see Table 1).
of the respective cluster (see Table 1).
The update equations of the  th path in the
th path in the  th cluster for a moving station with speed
th cluster for a moving station with speed  (in wavelengths per second) are given as
(in wavelengths per second) are given as

In this way, clusters are moving in delay (causing Doppler shifts) and in angles, and they smoothly change their power. The speed  is a scalar defining how fast clusters move. The "direction" of movement is defined by the cluster movement parameters.
is a scalar defining how fast clusters move. The "direction" of movement is defined by the cluster movement parameters.
These small-scale changes intrinsically introduce correlated fading. This repeated update inherently creates a Doppler spectrum, where each individual path contributes with its Doppler shift  (equal for all paths within a cluster). Of course, linear movement is just a first-order approximation of the true movement of clusters, a more complex method can be found in [41]. However, the model validation will show that modelling movements linearly is sufficient to accurately reflecting the time-variant propagation environment.
(equal for all paths within a cluster). Of course, linear movement is just a first-order approximation of the true movement of clusters, a more complex method can be found in [41]. However, the model validation will show that modelling movements linearly is sufficient to accurately reflecting the time-variant propagation environment.
Whenever a cluster is fading in or fading out due to the birth/death process, the path weights,  , are additionally updated over the course of one cluster-lifetime interval by
, are additionally updated over the course of one cluster-lifetime interval by

3. Model Validation
Validation is paramount, it scrutinises whether a model reflects important properties of the propagation channel. Particularly for MIMO channels, models need to reflect the spatial structure of the channel correctly.
We validated the RCM against MIMO channel measurements carried out with an Elektrobit Propsound CS wideband channel sounder at two centre frequencies of 2.55 GHz and 5.25 GHz. Details about the measurements and the validated scenarios are presented in Appendix . For validation we will use three different validation metrics reflecting the spatial structure of the channels.
3.1. Validation Framework
We use the following procedure to validate the RCM (Figure 4).
-
(1)
Perform radio channel measurements in representative scenarios and estimate propagation paths [32] from the measurements for every snapshot of the channel.
-
(2)
Parametrise the RCM (see Section 2.2.3).
-
(3)
Generate reference channels by applying the system model (see Section 2.3.3) to the estimated paths parameters.
-
(4)
Generate smoothly time-variant modelled channels by invoking the RCM.
-
(5)
Compare the modelled channels with the reference channels according to the cdf of different validation metrics.
3.2. Validation Metrics
Before detailing the validation results, we present the different validation metrics. We concentrate on the validation of the spatial properties of the modelled channels.
3.2.1. Mutual Information
For the purpose of comparison with literature we take mutual information (MI) for model validation [42, 43]. (Quite frequently the term "capacity" is misused for mutual information.) However, we will show later in this section that MI has an intrinsic disadvantage, which disqualifies it as a good metric for validating the double-directional multipath structure of a time-varying channel.
We use the narrowband MI at frequency  and time
and time  , which is defined as
, which is defined as

where  denotes the normalised channel matrix, hence
denotes the normalised channel matrix, hence  . We use the normalisation to keep the receive SNR constant, which corresponds to perfect power control at the Tx. In this case, the channel transfer matrix at every time instant is normalized separately as
. We use the normalisation to keep the receive SNR constant, which corresponds to perfect power control at the Tx. In this case, the channel transfer matrix at every time instant is normalized separately as

where  denotes the number of frequencies. Then, the validation metric reflects the spatial structure of the channel best. We chose an SNR of 10 dB for the following validation evaluations. For creating a cdf, we use all time realisations and frequencies as our ensemble of samples.
denotes the number of frequencies. Then, the validation metric reflects the spatial structure of the channel best. We chose an SNR of 10 dB for the following validation evaluations. For creating a cdf, we use all time realisations and frequencies as our ensemble of samples.
The deficiencies of MI as a validation metric will now be demonstrated by a meaningful example. This example will also highlight the difference between average MI and ergodic capacity.
In Figure 5(a) we consider a single snapshot measured in the cafeteria environment (see Appendix ). This snapshot is described by a number of propagation paths with their parameters power, AoA, AoD, and delay. We now calculate the channel matrix of this scenario using the system model (4). Then, we create further channel realisations by just changing the phases of the paths randomly, but do not alter any other parameter. This method was introduced in [44] to generate multiple MIMO fading realisations from a single measurement. Note that this does not change the spatial structure of the channel at all. Finally, we calculate the MI for all these realisations according to (8).
Figure 5(b) shows the cdf of the so-computed MI. The MI varies considerably, even though the spatial structure of the channel remains the same. The reason for this effect is the fading created by randomly changing the phases of the paths. One can see that mutual information fails to reflect the spatial structure of a single realisation of an environment. A validation metric reflecting the spatial structure should provide one unique result, and not a wide-spread distribution. For this reason, MI is not suited to assess whether a channel model provides a correct spatial representation of the scenario or not.
As the spatial structure determines which gains the channel offers, the RCM strives to reflect the spatial structure as accurately as possible. Thus, also the validation metric should be specific to the spatial structure. Nevertheless, as MI is frequently used for validating MIMO channel models, we will also use MI in this paper, for reasons of comparison, but point out its deficiencies in the results.
3.2.2. Environment Characterisation Metric
The Environment Characterisation Metric (ECM) [29] is directly applied to the path parameters rather than to the channel matrix. This section shortly describes the significance of the ECM. For better readability, we will (i) enumerate all paths in each time instant from  , disregarding cluster structures for the time being, and (ii) skip the time index
, disregarding cluster structures for the time being, and (ii) skip the time index  in the following derivations whenever it is redundant.
in the following derivations whenever it is redundant.
The metric copes with path parameters in different units (angles and delay). For every path  , the angular data is transformed into its coordinates on the unit sphere for both Rx and Tx. For angles of arrival the transformation is given as
, the angular data is transformed into its coordinates on the unit sphere for both Rx and Tx. For angles of arrival the transformation is given as

for angles at the Tx it reads similarly. The delays are scaled by the maximum expected delay that occurs in the considered snapshots [45], hence  . So, every path is now described by seven dimensionless parameters collected in
. So, every path is now described by seven dimensionless parameters collected in

and by its power  . When considering only azimuthal propagation, the
. When considering only azimuthal propagation, the  -direction must be excluded. (Since the elevation estimation from our data was not trustworthy, we excluded elevation in the validation.)
-direction must be excluded. (Since the elevation estimation from our data was not trustworthy, we excluded elevation in the validation.)
The environment characterization metric (ECM) is defined as the empirical covariance matrix of the path parameter vector  ,
,

with the mean parameter vector given as  .
.
The ECM has the following properties [29].
-
(i)
The metric is system independent as it is calculated from the propagation paths directly. Additionally, the metric is independent of the phases of the propagation paths.
-
(ii)
The main diagonal contains the directional spreads (comparable to the azimuth and elevation spreads) at Rx and Tx, and the (normalized) rms delay spread. In this way, the ECM jointly represents the spatial structure, and wideband properties of the channel.
-
(iii)
The trace
 is the sum of the directional spreads [46] at Rx and Tx plus the (normalized) delay spread.
is the sum of the directional spreads [46] at Rx and Tx plus the (normalized) delay spread. -
(iv)
The determinant
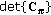 describes the volume spanned in the parameter space.
describes the volume spanned in the parameter space.
We use the ECM for the following two purposes.
-
(1)
Validating the spatio-temporal multipath structure: the singular values of the ECM (SV-ECM) can be interpreted as the fingerprint of the scenario, by which one can judge the compactness of the paths in the channel. Assuming that the parameters of all paths span a multidimensional ellipsoid, the SVs describe the lengths of the main axes of this ellipsoid. In this way, it transforms the traditional view of individual parameter spread values into a joint-spread approach. These properties make the SV-ECM genuinely suited for comparing channels. Calculating the SV-ECM for the example shown in Figure 5(a), the snapshot would result in the same values of the SV-ECM, no matter which phases the paths have. This demonstrates that the SV-ECM is a consistent metric, reflecting the multipath structure of the channel.
-
(2)
Validating the time-variance: the rate of change of the ECM shows how strongly the parametric channel changes between two neighbouring time instants. To quantify the rate of change between two ECM matrices of adjacent snapshots, we use the Frobenius inner matrix product [47] as
 (12)
(12)where
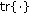 denotes the matrix trace operator, and
denotes the matrix trace operator, and  denotes the Frobenius matrix norm. The Frobenius inner product quantifies how similar the eigenvectors of the two matrix arguments are. For collinear matrices, we have
denotes the Frobenius matrix norm. The Frobenius inner product quantifies how similar the eigenvectors of the two matrix arguments are. For collinear matrices, we have 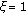 , while for orthogonal matrices,
, while for orthogonal matrices, 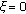 .
.
3.2.3. Diversity Measure
Spatial diversity describes the number of independent fading links between the Tx and Rx antenna arrays. In a full-diversity system, where all links between the Tx and Rx arrays are independent, one observes a spatial diversity of  [48]. This diversity is directly linked with the uncoded bit-error ratio (BER) performance of MIMO systems [1].
[48]. This diversity is directly linked with the uncoded bit-error ratio (BER) performance of MIMO systems [1].
Channel correlation reduces this diversity significantly. Ivrlac and Nossek provided the Diversity Measure [28], a way to quantify the available diversity directly from the MIMO channels without taking the detour via BER simulations. We will use this measure to quantify the diversity in both the measured and the modelled channels, and subsequently compare the results.
The Diversity Measure  of a MIMO system described by a channel matrix
of a MIMO system described by a channel matrix  with channel correlation matrix
with channel correlation matrix  is given by
is given by

Invoking the channel correlation matrix implicitly assumes the channel to be stationary over the time period of a sliding window. We want to bring to attention that the channel correlation matrix used here is entirely different from the path covariance matrix used as ECM in (11). To estimate samples of the channel correlation matrix, we chose a sliding window over  snapshots and all frequencies, that is,
snapshots and all frequencies, that is,

with  defined in (4). These estimated correlation matrices for all time instants are taken as ensemble to obtain the cdf of (13).
defined in (4). These estimated correlation matrices for all time instants are taken as ensemble to obtain the cdf of (13).
3.3. Validation Results
This paper presents validation results for two particularly interesting scenarios, (i) a measurement route in an office scenario, without line of sight between transmitter and receiver, and (ii) a route within a cafeteria (large room) mostly with LOS between transmitter and receiver (see Figure 11 in Appendix ). The Tx was moved through the rooms while the Rx was placed at a fixed position. The cafeteria scenario is a particularly challenging one, difficult to represent by any MIMO channel model, as it is a combination of two totally different propagation environments, depending on whether the LOS between Rx and Tx is blocked or not. For validation we generated smoothly-time varying channels using the RCM and used the three validation metrics described in the previous paragraphs. The validation of more scenarios can be found in [36, Chapter 4].
First, we use the ECM to validate the spatiotemporal multipath structure. Figure 6 compares the SV-ECM of the modelled paths with those identified directly from measurements "reference channels", both at 2.55 GHz and at 5.25 GHz, neglecting elevation. The ECM offers five SVs, shown as dashed lines (RCM) and solid lines (measurements). We observe that, judging from the ECM, the multipath structure is quite similar at the two carrier frequencies in both scenarios. The NLOS office scenario is much better matched at 2.55 GHz than at 5.25 GHz. At 5.25 GHz, the third and fourth SV-ECM of the modelled channels obviously have a positive bias. The reason for this poor match is an environment pdf that has little variation, particularly in the cluster receive azimuth position domain. This leads to reduced randomness when drawing the parameters of the scenarios, resulting in steeper SV-ECM cdfs. Considering the cafeteria scenario, there is much stronger variability, but still the environment is represented quite well. In both scenarios, the smallest SV-ECM of the modelled channels has a significant negative bias. We found the reason for this to be outlier paths that were estimated from the measurement, but these are not modelled by the RCM.
In a second step, we use the collinearity between two ECM matrices to validate the time variance. Figure 7 quantifies how strongly the channels change from snapshot to snapshot. In detail, the figure shows the cdfs of the ECM distances evaluated between all two adjacent time instants for both the modelled channels and the reference channels. A value of  indicates that the channels did not change, while smaller numbers indicate changes in the multipath structure.
indicates that the channels did not change, while smaller numbers indicate changes in the multipath structure.
In the NLOS office scenario, where the SNR of the measurement was only average, we observe that the model has a slightly lower number of small changes than the reference channels (rightmost part of Figure 7(a)). This is due to the path parameter estimation algorithm, which always estimates a number of outlier paths that appear at random in any single time snapshot. In the cafeteria scenario, we observe much stronger changes than in the office scenario due to the changes in the LOS part of the environment. The measurement SNR was high, so random outliers were no problem, as the rightmost part of the curves show. Between the outage probabilities of  and
and  , the model fits the measurement very well, which is the statistically relevant part. The few much larger changes that are observed in the measurements occur during the abrupt transition from LOS to NLOS.
, the model fits the measurement very well, which is the statistically relevant part. The few much larger changes that are observed in the measurements occur during the abrupt transition from LOS to NLOS.
Next, we present the validation using mutual information. Figure 8 shows the cdf of the evaluated mutual information for both modelled and reference channels at both carrier frequencies. We observe that the MI of the modelled channels have a negative bias in both scenarios. This could be already expected from the ECM validation, where the spreading of the paths (strongest SV-ECM) was also slightly too low. We discourage the use of MI for validating the spatial structure of the radio channel, since MI is influenced by both spatial structure and fading.
Finally, Figure 9 compares the Diversity Measure values of the modelled channels with the reference channels. In both scenarios, diversity is slightly overmodelled. While this is also a common effect of analytical channel models, there is no connection here. It may also happen that the RCM undermodels diversity. This result could also have been expected from the MI cdfs, where the cdf of the modelled channels showed a sligtly steeper slope than the cdf of the reference channels.
4. Conclusions
The presented Random-Cluster Model is well able to reflect the spatial properties of measured time-variant MIMO channels, even if the properties of the environment are varying between LOS and NLOS. By its direct parametrisation from measurement data, the RCM is specific to the measured environment. Since the RCM is propagation-based, the RCM is also scalable in carrier frequency, in bandwidth, and in its antenna array configuration. Still, it is a stochastic model. The propagation environment is described using a multivariate pdf of the cluster parameters. Depending on the accuracy of the estimation of this pdf from measurements, the parametrisation complexity is scalable. Time variance is implemented by linear cluster movement. Using the recommended clustering algorithm in combination with a Kernel Density Estimator, the RCM is parametrised automatically without user interaction.
Validation showed a close fit between the channels modelled by the RCM, and reference channels obtained from the measurements. Even though the RCM was only successfully validated against indoor measurements, the model structure is also well suited to represent outdoor radio channels, when adapting the parameters, respectively. This renders the RCM to be ideally suited to model particularly interesting propagation conditions that were measured before.
References
Paulraj AJ, Gore DA, Nabar RU, Bölcskei H: An overview of MIMO communications—a key to gigabit wireless. Proceedings of the IEEE 2004, 92(2):198-218. 10.1109/JPROC.2003.821915
Telatar IE: Capacity of multi-antenna Gaussian channels. AT&T Bell Laboratories, Murray Hill, NJ, USA; 1995.
3GPP—The 3rd Generation Partnership Project 2008, http://www.3gpp.org
IEEE 802.16 working group on broadband wireless access standards 2008, http://wirelessman.org
Shiu D-S, Foschini GJ, Gans MJ, Kahn JM: Fading correlation and its effect on the capacity of multielement antenna systems. IEEE Transactions on Communications 2000, 48(3):502-513. 10.1109/26.837052
Weichselberger W, Herdin M, Özcelik H, Bonek E: A stochastic MIMO channel model with joint correlation of both link ends. IEEE Transactions on Wireless Communications 2006, 5(1):90-100.
Edelman A, Rao NR: Random matrix theory. Acta Numerica 2005, 14: 233-297.
Wood LC, Hodgkiss WS: MIMO channel models and performance metrics. Proceedings of IEEE Global Telecommunications Conference (GLOBECOM '07), November 2007, Washington, DC, USA 3740-3744.
Wyne S, Molisch AF, Almers P, Eriksson G, Karedal J, Tufvesson F: Outdoor-to-indoor office MIMO measurements and analysis at 5.2 GHz. IEEE Transactions on Vehicular Technology 2008, 57(3):1374-1386.
Fügen T, Maurer J, Kuhnert C, Wiesbeck W: A modelling approach for multiuser MIMO systems including spatially-colored interference. Proceedings of IEEE Global Telecommunications Conference (GLOBECOM '04), November-December 2004, Dallas, Tex, USA 2: 938-942.
Degli-Esposti V, Guiducci D, de'Marsi A, Azzi P, Fuschini F: An advanced field prediction model including diffuse scattering. IEEE Transactions on Antennas and Propagation 2004, 52(7):1717-1728. 10.1109/TAP.2004.831299
Spatial channel model for Multiple Input Multiple Output (MIMO) simulations 3GPP, Valbonne, France; 2003.
Kyösti P, Meinilä J, Hentilä L, et al.: WINNER II channel models (d1.1.2v1.1). November 2007, http://www.ist-winner.org
Correia L (Ed): Mobile Broadband Multimedia Networks. Academic Press, San Diego, Calif, USA; 2006.
Saleh A, Valenzuela R: A statistical model for indoor multipath propagation. IEEE Journal on Selected Areas in Communications 1987, 5(2):128-137.
Spencer QH, Jeffs BD, Jensen MA, Swindlehurst AL: Modeling the statistical time and angle of arrival characteristics of an indoor multipath channel. IEEE Journal on Selected Areas in Communications 2000, 18(3):347-360. 10.1109/49.840194
Xiao H, Burr AG, Hentilä L, Kyösti P: Statistical technique to identify clusters from multi-dimensional measurement data. Proceedings of the 2nd European Conference on Antennas and Propagation (EuCAP '07), November 2007, Edinburgh, UK 1-7.
Galdo GD, Czink N, Haardt M: Cluster spatial localization from high-resolution parameter estimation. Proceedings of IEEE/ITG Workshop on Smart Antennas (WSA '06), March 2006, Ulm, Germany 1-7.
Salo J, Salmi J, Czink N, Vainikainen P: Automatic clustering of nonstationary MIMO channel parameter estimates. Proceedings of the 2nd International Conference on Telecommunications (ICT '05), May 2005, Cape Town, South Africa
Czink N, Cera P, Salo J, Bonek E, Nuutinen J-P, Ylitalo J: Improving clustering performance using multipath component distance. Electronics Letters 2006, 42(1):33-35. 10.1049/el:20063917
Czink N, Cera P, Salo J, Bonek E, Nuutinen J-P, Ylitalo J: A framework for automatic clustering of parametric MIMO channel data including path powers. Proceedings of IEEE Vehicular Technology Conference (VTC '06), September 2006, Montreal, Canada 114-118.
Czink N, Tian R, Wyne S, et al.: Tracking time-variant cluster parameters in MIMO channel measurements. Proceedings of the 2nd International Conference on Communications and Networking in China (ChinaCom '07), August 2007, Shanghai, China 1147-1151.
Czink N, Bonek E, Hentilä L, Nuutinen J-P, Ylitalo J: A measurement-based random-cluster MIMO channel model. Proceedings of IEEE Antennas and Propagation International Symposium, June 2007, Honolulu, Hawaii, USA 5363-5366.
Czink N, Bonek E, Ylitalo J, Zemen T: Measurement-based time-variant MIMO channel modelling using clusters. Proceedings of the 29th General Assembly of the International Union of Radio Science (URSI '08), August 2008, Chicago, Ill, USA
Kyösti P, Jämsä T: Complexity comparison of MIMO channel modelling methods. Proceedings of the 4th IEEE Internatilonal Symposium on Wireless Communication Systems (ISWCS '07), October 2007, Trondheim, Norway 219-223.
Ivrlac MT, Nossek JA: Quantifying diversity and correlation in Rayleigh fading MIMO communication systems. Proceedings of the 3rd IEEE International Symposium on Signal Processing and Information Technology (ISSPIT '03), December 2003, Darmstadt, Germany 158-161.
Czink N, Galdo GD, Yin X, Bonek E, Ylitalo J: A novel environment characterization metric for clustered MIMO channels: used to validate a SAGE parameter estimator. Wireless Personal Communications 2008, 46(1):83-98. 10.1007/s11277-007-9357-1
Steinbauer M, Molisch AF, Bonek E: The double-directional radio channel. IEEE Antennas and Propagation Magazine 2001, 43(4):51-63. 10.1109/74.951559
Kolu J, Nuutinen J-P, Jämsä T, Ylitalo J, KyÖsti P: Playback simulations of measured MIMO radio channels. In COST 273, TD(04)110. COST, Gothenburg, Sweden; June 2004.
Fleury BH, Tschudin M, Heddergott R, Dahlhaus D, Pedersen KI: Channel parameter estimation in mobile radio environments using the SAGE algorithm. IEEE Journal on Selected Areas in Communications 1999, 17(3):434-450. 10.1109/49.753729
Czink N, Tian R, Wyne S, et al.: Cluster parameters for time-variant MIMO channel models. Proceedings of the 2nd European Conference on Antennas and Propagation (EuCAP '07), November 2007, Edinburgh, UK 1-8.
Ihler A: Kernel Density Estimation Toolbox for MATLAB (R13). July 2007, http://ttic.uchicago.edu/~ihler/code
Scott DW: Multivariate Density Estimation. John Wiley & Sons, New York, NY, USA; 1992.
Czink N: The random-cluster model—a stochastic MIMO channel model for broadband wireless communication systems of the 3rd generation and beyond, Ph.D. dissertation. Technische Universität Wien, Vienna, Austria; FTW Dissertation Series, December 2007
Mardia KV, Jupp PE: Directional Statistics. John Wiley & Sons, New York, NY, USA; 2000.
Almers P, Bonek E, Burr A, et al.: Survey of channel and radio propagation models for wireless MIMO systems. EURASIP Journal on Wireless Communications and Networking 2007, 2007:-19.
Kaltenberger F, Zemen T, Üeberhuber CW: Low-complexity geometry-based MIMO channel simulation. EURASIP Journal on Advances in Signal Processing 2007, 2007:-17.
Asplund H, Glazunov AA, Molisch AF, Pedersen KI, Steinbauer M: The COST 259 directional channel model—part II: macrocells. IEEE Transactions on Wireless Communications 2006, 5(12):3434-3450.
Wallace JW, Jensen MA: Time-varying MIMO channels: measurement, analysis, and modeling. IEEE Transactions on Antennas and Propagation 2006, 54(11):3265-3273.
Erceg V, Schumacher L, Kyritsi P, et al.: TGn channel models. IEEE P802.11, Geneva, Switzerland; 2004.http://grouper.ieee.org/groups/802/11/
Kyösti P, Laselva D, Hentilä L, Jämsä T: Validating IST-WINNER indoor MIMO radio channel model. IST Mobile and Wireless Summit, June 2006, Mykonos, Greece
Molisch AF, Steinbauer M, Toeltsch M, Bonek E, Thomä RS: Capacity of MIMO systems based on measured wireless channels. IEEE Journal on Selected Areas in Communications 2002, 20(3):561-569. 10.1109/49.995515
Steinbauer M, Özcelik H, Hofstetter H, Mecklenbräuker CF, Bonek E: How to quantify multipath separation. IEICE Transactions on Electronics 2002, E85-C(3):552-557.
Fleury BH: First- and second-order characterization of direction dispersion and space selectivity in the radio channel. IEEE Transactions on Information Theory 2000, 46(6):2027-2044. 10.1109/18.868476
Golub G, van Loan C: Matrix Computations. 3rd edition. The Johns Hopkins University Press, London, UK; 1996.
Oestges C, Clerckx B: MIMO Wireless Communications. Academic Press, London, UK; 2007.
Elektrobit EB Propsim 2008, http://www.propsim.com
Hentilä L, Kyösti P, Ylitalo J, Zhao X, Meinilä J, Nuutinen J-P: Experimental characterization of multi-dimensional parameters at 2.45 and 5.25 GHz indoor channels. Proceedings of the Wireless Personal Multimedia Communications (WPMC '05), September 2005, Aalborg, Denmark 254-258.
Fleury BH, Jourdan P, Stucki A: High-resolution channel parameter estimation for MIMO applicationsusing the SAGE algorithm. Proceedings of the International Zurich Seminar on Broadband Communications, February 2002, Zurich, Switzerland 1-9.
Acknowledgments
This work was partly carried out in the frameworks of the European Projects NEWCOM, COST 273, and COST 2100. The authors thank Elektrobit for partly funding the Ph.D. work of N. Czink and for providing the measurement equipment. The authors gratefully acknowledge the help of Veli-Matti Holappa and Mikko Alatossava during the measurement campaign. The Telecommunications Research Center Vienna (ftw.) is supported by the Austrian Government and the City of Vienna within the competence centre programme COMET.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
A. Channel Measurements
This appendix describes the channel measurement equipment and the investigated scenarios.
A.1. Equipment
We employed a wideband radio channel sounder, EB Propsound CS [49], which utilizes periodic pseudorandom binary signals. The sounder is described in more detail in [50]. In sounding, M-sequences with adjustable code lengths are transmitted and multiplexed by switching the transmit and receive antennas. The spread spectrum signal has 100 Mchip/s chip rate and switches through all the antennas with the cycle rates presented in Table 2. Thus, sequential radio channel measurement between all possible TX and RX antenna pairs is achieved. The number of antenna elements used is inversely proportional to the cycle rate. The sounder was operated in burst-mode, that is, after four measuring cycles there was a break to allow real-time data transfer to the hard disk unit. During the measurements, a real-time display of the received impulse responses (IRs) could be monitored from the control laptop computer. In addition to basic data handling features, the post-processing tools include the ISIS (Initialization and Search Improved SAGE) software to identify individual MPCs by a super-resolution SAGE algorithm employing maximum likelihood techniques for parameter estimation [51].
 .
.The selected antenna arrays (Figure 10) are able to capture largely the spatial characteristics of the radio channel at both link-ends. The 2.55 GHz array (Figure 10(a)) used at the TX consists of 28 dual-polarized patch elements. The elements are positioned in a way that allows channel probing in the full azimuth domain. The upper ring of antenna elements in the ODA was not operative on one link end, so elevation information was not extracted from the measurements. Figure 10(b) shows the uniform circular array with  monopoles used at the RX end at 2.55 GHz. It supports full azimuth direction probing but not the elevation. At 5.25 GHz both TX and RX had 25 element patch arrays shown in Figure 10(c). Their properties are similar to the 2.55 GHz patch array. Table 3 shows the azimuth and elevation coverage of the antennas.
monopoles used at the RX end at 2.55 GHz. It supports full azimuth direction probing but not the elevation. At 5.25 GHz both TX and RX had 25 element patch arrays shown in Figure 10(c). Their properties are similar to the 2.55 GHz patch array. Table 3 shows the azimuth and elevation coverage of the antennas.
All antennas had been calibrated in an anechoic chamber. The signal model on which SAGE is based is using the measured array pattern data for calculating the angles of impinging or outgoing waves. In the calibration process, the antenna pattern of each single element was measured in amplitude and phase over azimuth and elevation, resulting in an azimuth/elevation matrix. This measurement was done for both horizontal and vertical polarisation. To minimize the interference of WLAN and Bluetooth, one center frequency for the measurements was chosen to be 2.55 GHz. Still, there seems to have been (spurious) radiation from these devices above 2.45 GHz, so we had to expect an enhanced noise floor in the IRs. The ensuing smaller dynamic range resulted in a smaller number of paths that ISIS could extract from the measurement. At the other center frequency of 5.25 GHz we did not observe any interference.
A.2. Scenarios
We took measurements on 28 different routes [36], of which we analyse two particularly interesting ones in this paper. The outer walls of the building were reinforced concrete or brick-stone walls, while inside walls were mostly of plasterboard with internal metal mounts.
The first measurement, NLOS throughout, was done in an office environment, where the receiver was fixed in the corridor and the transmitter was moved along a route in an office (Figure 11(a)).
The second measurement, predominantly LOS, was recorded in a cafeteria with metal tables and chairs. The receiver was fixed on a table, and the transmitter was moved along a route in the room. The Tx-Rx distance variation was large, and the LOS between transmitter and receiver was sometimes shadowed by an elevator (Figure 11(b)). People were moving randomly in the environment.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Czink, N., Zemen, T., Nuutinen, JP. et al. A Time-Variant MIMO Channel Model Directly Parametrised from Measurements. J Wireless Com Network 2009, 687238 (2009). https://doi.org/10.1155/2009/687238
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/687238


 paths from every measured snapshot.
paths from every measured snapshot.
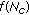 , by marginalizing the environment pdf to the number of clusters, which is done by integrating the environment pdf over the other dimensions. Then the actual number of clusters for the first snapshot,
, by marginalizing the environment pdf to the number of clusters, which is done by integrating the environment pdf over the other dimensions. Then the actual number of clusters for the first snapshot, 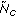 , is determined by drawing a random sample from this pdf. Since the number of clusters must be an integer number, the ceiling of the drawn value is assigned to
, is determined by drawing a random sample from this pdf. Since the number of clusters must be an integer number, the ceiling of the drawn value is assigned to 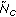 .
.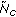 , and marginalising it to the snapshot power. From this marginal distribution
, and marginalising it to the snapshot power. From this marginal distribution  , the intended snapshot power,
, the intended snapshot power, 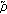 , is determined by drawing a random sample from this pdf. This intended snapshot is only used as a selection criterion for the clusters to be drawn in the next steps. In general, the sum power of the clusters will not exactly match the intended snapshot power.
, is determined by drawing a random sample from this pdf. This intended snapshot is only used as a selection criterion for the clusters to be drawn in the next steps. In general, the sum power of the clusters will not exactly match the intended snapshot power.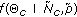 . From this final distribution, we draw
. From this final distribution, we draw  cluster parameter sets
cluster parameter sets 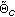 .
. , the corresponding number of paths (which is an initial cluster parameter drawn before),
, the corresponding number of paths (which is an initial cluster parameter drawn before),  , is placed as follows. Every path is described by the path parameters: complex amplitude (
, is placed as follows. Every path is described by the path parameters: complex amplitude (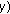 , total delay (
, total delay ( , and the azimuth and elevation of arrival and departure, respectively, (
, and the azimuth and elevation of arrival and departure, respectively, (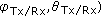 .
.

 is the sum of the directional spreads [
is the sum of the directional spreads [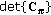 describes the volume spanned in the parameter space.
describes the volume spanned in the parameter space.
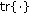 denotes the matrix trace operator, and
denotes the matrix trace operator, and  denotes the Frobenius matrix norm. The Frobenius inner product quantifies how similar the eigenvectors of the two matrix arguments are. For collinear matrices, we have
denotes the Frobenius matrix norm. The Frobenius inner product quantifies how similar the eigenvectors of the two matrix arguments are. For collinear matrices, we have 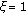 , while for orthogonal matrices,
, while for orthogonal matrices, 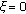 .
.

 seconds). NLOS office scenarioCafeteria scenario
seconds). NLOS office scenarioCafeteria scenario


 ODA, 2.55 GHz
ODA, 2.55 GHz UCA, 2.55 GHz
UCA, 2.55 GHz ODA, 5.25 GHz
ODA, 5.25 GHz