- Research Article
- Open access
- Published:
Antenna Selection for MIMO Systems with Closely Spaced Antennas
EURASIP Journal on Wireless Communications and Networking volume 2009, Article number: 739828 (2009)
Abstract
Physical size limitations in user equipment may force multiple antennas to be spaced closely, and this generates a considerable amount of mutual coupling between antenna elements whose effect cannot be neglected. Thus, the design and deployment of antenna selection schemes appropriate for next generation wireless standards such as 3GPP long term evolution (LTE) and LTE advanced needs to take these practical implementation issues into account. In this paper, we consider multiple-input multipleoutput (MIMO) systems where antenna elements are placed side by side in a limited-size linear array, and we examine the performance of some typical antenna selection approaches in such systems and under various scenarios of antenna spacing and mutual coupling. These antenna selection schemes range from the conventional hard selection method where only part of the antennas are active, to some newly proposed methods where all the antennas are used, which are categorized as soft selection. For the cases we consider, our results indicate that, given the presence of mutual coupling, soft selection can always achieve superior performance as compared to hard selection, and the interelement spacing is closely related to the effectiveness of antenna selection. Our work further reveals that, when the effect of mutual coupling is concerned, it is still possible to achieve better spectral efficiency by placing a few more than necessary antenna elements in user equipment and applying an appropriate antenna selection approach than plainly implementing the conventional MIMO system without antenna selection.
1. Introduction
The multiple-input multiple-output (MIMO) architecture has been demonstrated to be an effective means to boost the capacity of wireless communication systems [1], and has evolved to become an inherent component of various wireless standards, including the next-generation cellular systems 3GPP long term evolution (LTE) and LTE advanced. For example, the use of a MIMO scheme was proposed in the LTE standard, with possibly up to four antennas at the mobile side, and four antennas at the cell site [2]. In MIMO systems, antenna arrays can be exploited in two different ways, which are [3]: diversity transmission and spatial multiplexing. However, in either case, one main problem involved in the implementation of MIMO systems is the increased complexity, and thus the cost. Even though the cost for additional antenna elements is minimal, the radio frequency (RF) elements required by each antenna, which perform the microwave/baseband frequency translation, analog-to-digital conversion, and so forth, are usually costly.
These complexity and cost concerns with MIMO have motivated the recent popularity of antenna selection (AS)—an attractive technique which can alleviate the hardware complexity, and at the same time capture most of the advantages of MIMO systems. In fact, for its low user equipment (UE) complexity, AS (transmit) is currently being considered as a baseline of the single-user transmit diversity techniques in the LTE uplink which is a MIMO single carrier frequency division multiple access (SC-FDMA) system [4]. Further, when it comes to the RF processing manner, AS can be categorized into two groups: (1) hard selection, where only part of the antennas are active and the selection is implemented in the RF domain by means of a set of switchs (e.g., [5–7]); (2) soft selection, where all the antennas are active and a certain form of transformation is performed in the RF domain upon the received signals across all the antennas (e.g., [8–10]).
A considerable amount of research efforts have been dedicated to the investigation of AS, and have solidly demonstrated the theoretical benefits of AS (see [3] for a tutorial treatment). However, previous works largely ignore the hardware implementation issues related to AS. For instance, the physical size of UE such as mobile terminals and mobile personal assistants, are usually small and invariable, and the space allocated for an antenna array is limited. Such limitation makes the close spacing between antenna elements a necessity, inevitably leading to mutual coupling [11], and correlated signals. These issues have caught the interest of some researchers, and the capacity of conventional MIMO systems (without AS) under the described limitations and circumstances was investigated, among others, in [12–17]. To give an example, the study in [12] shows that as the number of receive antenna elements increases in a fixed-length array, the system capacity firstly increases to saturate shortly after the mutual coupling reaches a certain level of severeness; and drops after that.
Form factors of UE limit the performance promised by MIMO systems, and can further affect the proper functionality of AS schemes. These practical implementation issues merit our attention when designing and deploying AS schemes for the 3GPP LTE and LTE advanced technologies. There exist some interesting works, such as [18, 19] which consider AS in size sensitive wireless devices to improve the system performance. But in general, results, conclusions, and ideas on the critical implementation aspects of AS in MIMO systems still remain fragmented. In this paper, through electromagnetic modeling of the antenna array and theoretical analysis, we propose a comprehensive study of the performance of AS, to seek more effective implementation of AS in size sensitive UE employing MIMO where both mutual coupling and spatial correlation have a strong impact. In this process, besides the hybrid selection [5–7], a conventional yet popular hard AS approach, we are particularly interested in examining the performance potential of some typical soft AS schemes, including the FFT-based selection [9] and the phase-shift-based selection [10], that are very appealing but seem not to have attracted much attention so far. At the meantime, we also intend to identify the operational regimes of these representative AS schemes in the compact antenna array MIMO system. For the cases we consider, we find that in the presence of mutual coupling, soft AS can always achieve superior performance as compared to hard AS. Moreover, effectiveness of these AS schemes is closely related to the interelement spacing. For example, hard AS works well only when the interelement spacing is no less than a half wavelength.
Additionally, another goal of our study is to address a simple yet very practical question which deals with the cost-performance tradeoff in implementation: as far as mutual coupling is concerned, can we achieve better spectral efficiency by placing a few more than necessary antenna elements in size sensitive UE and applying a certain adequate AS approach than plainly implementing the conventional MIMO system without AS? Further, if the answer is yes, how would we decide the number of antenna elements for placement and the AS method for deployment? Our work will provide answers to the above questions, and it turns out the solution is closely related to identifying the saturation point of the spectral efficiency.
This paper is organized as follows. In Section 2, we introduce the network model for the compact MIMO system and characterize the input-output relationship by taking into account the influence of mutual coupling. In Section 3, we describe the hard and soft AS schemes that will be used in our study, and also estimate their computational complexity. In Section 4, we present the simulation results. We discuss our main findings in Section 5, and finally conclude this paper in Section 6.
2. Network Model for Compact MIMO
We consider a MIMO system with  transmit and
transmit and  receive antennas (
receive antennas ( ,
,  ). We assume antenna elements are placed in a side-by-side configuration along a fixed length at each terminal (transmitter and receiver), as shown in Figure 1. Other types of antenna configuration are also possible, for example, circular arrays [11]. But it is noted that, the side-by-side arrangement exhibits larger mutual coupling effects since the antennas are placed in the direction of maximum radiation [11, page 474]. Thus, the side-by-side configuration is more suitable to our study. We define
). We assume antenna elements are placed in a side-by-side configuration along a fixed length at each terminal (transmitter and receiver), as shown in Figure 1. Other types of antenna configuration are also possible, for example, circular arrays [11]. But it is noted that, the side-by-side arrangement exhibits larger mutual coupling effects since the antennas are placed in the direction of maximum radiation [11, page 474]. Thus, the side-by-side configuration is more suitable to our study. We define  and
and  as the aperture lengths for transmitter and receiver sides, respectively. In particular, we are more interested in the case that
as the aperture lengths for transmitter and receiver sides, respectively. In particular, we are more interested in the case that  is fixed and small, which corresponds to the space limitation of the UE. We denote
is fixed and small, which corresponds to the space limitation of the UE. We denote  as the dipole length,
as the dipole length,  as the dipole radius, and
as the dipole radius, and  (
( ) as the side-by-side distance between the adjacent dipoles at the receiver (transmitter) side. Thus, we have
) as the side-by-side distance between the adjacent dipoles at the receiver (transmitter) side. Thus, we have  and
and  .
.
A simplified network model (as compared to [13, 14], e.g.) for transmitter and receiver sides is depicted in Figure 2. Figure 3 illustrates a direct conversion receiver that connects the output signals in Figure 2, where LNA denotes the low-noise amplifier, LO denotes the local oscillator, and ADC denotes the analog-to-digital converter. For the ease of the following analysis, we assume that in the circuit setup, all the antenna elements at the receiver side are grounded through the load impedance  ,
,  (cf. Figure 2), regardless of whether they will be selected or not. In fact,
(cf. Figure 2), regardless of whether they will be selected or not. In fact,  constitute a simple matching circuit. Such matching circuit is necessary as it can enhance the efficiency of power transfer from the generator to the load [20, Chapter 11]. We also assume that the input impedance of each LNA in Figure 3 which is located very close to the antenna element to amplify weak received signals, is high enough such that it has little measurable effect on the receive array's output voltages. This assumption is necessary to facilitate the analysis of the network model. However, it is also very reasonable because this ensures that the input of the amplifier will neither overload the source of the signal nor reduce the strength of the signal by a substantial amount [21].
constitute a simple matching circuit. Such matching circuit is necessary as it can enhance the efficiency of power transfer from the generator to the load [20, Chapter 11]. We also assume that the input impedance of each LNA in Figure 3 which is located very close to the antenna element to amplify weak received signals, is high enough such that it has little measurable effect on the receive array's output voltages. This assumption is necessary to facilitate the analysis of the network model. However, it is also very reasonable because this ensures that the input of the amplifier will neither overload the source of the signal nor reduce the strength of the signal by a substantial amount [21].
Let us firstly consider the transmitter side, which can be regarded as a coupled  port network with
port network with  terminals. We define
terminals. We define  and
and  as the vectors of terminal currents and voltages, respectively, and they are related through
as the vectors of terminal currents and voltages, respectively, and they are related through

where  denotes the impedance matrix at the transmitter side. The
denotes the impedance matrix at the transmitter side. The  -th entry of
-th entry of  , when
, when  , denotes the mutual impedance between two antenna elements, and is given by [20, Chapter 21.2]:
, denotes the mutual impedance between two antenna elements, and is given by [20, Chapter 21.2]:

where

In the above expression,  denotes the characteristic impedance of the propagation medium, and can be calculated by
denotes the characteristic impedance of the propagation medium, and can be calculated by  , where
, where  and
and  denote permittivity and permeability of the medium, respectively. Likewise,
denote permittivity and permeability of the medium, respectively. Likewise,  denotes the propagation wavenumber of an electromagnetic wave propagating in a dielectric conducting medium, and can be computed through
denotes the propagation wavenumber of an electromagnetic wave propagating in a dielectric conducting medium, and can be computed through  , where
, where  is the angular frequency. Finally
is the angular frequency. Finally  ,
,  and
and  are defined as
are defined as

When  ,
,  is the self-impedance of a single antenna element, and can also be obtained from (2) by simply redefining
is the self-impedance of a single antenna element, and can also be obtained from (2) by simply redefining  ,
,  and
and  as follows:
as follows:

Thus, the self-impedance for an antenna element with  and
and  for example, is approximately
for example, is approximately

Further, let us consider an example that  antenna elements of such type are equally spaced over a linear array of length
antenna elements of such type are equally spaced over a linear array of length  . The impedance matrix
. The impedance matrix  is given by
is given by

For  , the terminal voltage
, the terminal voltage  can be related to the source voltage
can be related to the source voltage  via the source impedance
via the source impedance  by
by  . Define
. Define  , and
, and  . Then, from Figure 2, we can obtain the following results:
. Then, from Figure 2, we can obtain the following results:  and
and  . Therefore, the relationship between terminal voltages
. Therefore, the relationship between terminal voltages  and source voltages
and source voltages  can be written in matrix form as
can be written in matrix form as  Similar to [12], we choose
Similar to [12], we choose  , which roughly corresponds to a conjugate match in the presence of mild coupling. In the case of uncoupling in the transmitter side,
, which roughly corresponds to a conjugate match in the presence of mild coupling. In the case of uncoupling in the transmitter side,  is diagonal, and its diagonal elements are all the same. Consequently,
is diagonal, and its diagonal elements are all the same. Consequently,  is also diagonal, and its diagonal element can be denoted as
is also diagonal, and its diagonal element can be denoted as  . To accommodate the special case of zero mutual coupling where
. To accommodate the special case of zero mutual coupling where  is equal to
is equal to  , in our model we modify the relationship between
, in our model we modify the relationship between  and
and  into
into

where  .
.
Denote  as the vector of open circuited voltages induced across the receiver side antenna array, and
as the vector of open circuited voltages induced across the receiver side antenna array, and  as the voltage vector across the output of the receive array. Since we assumed high-input impedance of these LNAs, a similar network analysis can be carried out at the receiver side and will yield
as the voltage vector across the output of the receive array. Since we assumed high-input impedance of these LNAs, a similar network analysis can be carried out at the receiver side and will yield

where  .
.  is the mutual impedance matrix at the receiver side, and
is the mutual impedance matrix at the receiver side, and  is a diagonal matrix with its
is a diagonal matrix with its  th entry given by
th entry given by  ,
,  .
.  is given by
is given by  It is noted that the approximate conjugate match [12] is also assumed at the receiver side, so that the load impedance matrix
It is noted that the approximate conjugate match [12] is also assumed at the receiver side, so that the load impedance matrix  is diagonal with its entry given by
is diagonal with its entry given by  , for
, for  .
.
In frequency-selective fading channels, the effectiveness of AS is considerably reduced [3], which in turn makes it difficult to observe the effect of mutual coupling. Therefore, we focus our attention solely on flat fading MIMO channels. The radiated signal  is related to the received signal
is related to the received signal  through
through

where  is a
is a  complex Gaussian matrix with correlated entries. To account for the spatial correlation effect and the Rayleigh fading, we adopt the Kronecker model [22, 23]. This model uses an assumption that the correlation matrix, obtained as
complex Gaussian matrix with correlated entries. To account for the spatial correlation effect and the Rayleigh fading, we adopt the Kronecker model [22, 23]. This model uses an assumption that the correlation matrix, obtained as  with
with  being the operator stacking the matrix
being the operator stacking the matrix  into a vector columnwise, can be written as a Kronecker product, that is,
into a vector columnwise, can be written as a Kronecker product, that is,  , where
, where  and
and  are respectively, the receive and transmit correlation matrices, and
are respectively, the receive and transmit correlation matrices, and  denotes the Kronecker product. This implies that the joint transmit and receive angle power spectrum can be written as a product of two independent angle power spectrum at the transmitter and receiver. Thus, the correlated channel matrix
denotes the Kronecker product. This implies that the joint transmit and receive angle power spectrum can be written as a product of two independent angle power spectrum at the transmitter and receiver. Thus, the correlated channel matrix  can be expressed as
can be expressed as

where  is a
is a  matrix whose entries are independent identically distributed (i.i.d) circular symmetric complex Gaussian random variables with zero mean and unit variance. The
matrix whose entries are independent identically distributed (i.i.d) circular symmetric complex Gaussian random variables with zero mean and unit variance. The  -th entry of
-th entry of  or
or  is given by
is given by  [24], where
[24], where  is the zeroth order Bessel function of the first kind, and
is the zeroth order Bessel function of the first kind, and  denotes the distance between the
denotes the distance between the  ,
, -th antenna elements.
-th antenna elements.
Therefore, based on (8)–(11), the output signal vector  at the receiver can be expressed in terms of the input signal
at the receiver can be expressed in terms of the input signal  at the transmitter through
at the transmitter through

where  can be regarded as a compound channel matrix which takes into account both the Rayleigh fading in wireless channels and the mutual coupling effect at both transmitter and receiver sides, and
can be regarded as a compound channel matrix which takes into account both the Rayleigh fading in wireless channels and the mutual coupling effect at both transmitter and receiver sides, and  is the thermal noise. For simplicity, we assume uncorrelated noise at the receiving antenna element ports. For the case where correlated noise is considered, readers are referred to [16, 17].
is the thermal noise. For simplicity, we assume uncorrelated noise at the receiving antenna element ports. For the case where correlated noise is considered, readers are referred to [16, 17].
3. Hard and Soft AS for Compact MIMO
We describe here some typical hard and soft AS schemes that we will investigate, assuming the compact antenna array MIMO system described in Section 2. For hard AS, we focus only on the hybrid selection method [5–7]. For soft AS, we study two typical schemes: the FFT-based selection [9] which embeds fast Fourier transform (FFT) operations in the RF chains, and the phase-shift-based selection [10] which uses variable phase shifters adapted to the channel coefficients in the RF chains. For simplicity, we only consider AS at the receiver side with  antennas being chosen out of the
antennas being chosen out of the  available ones, and we focus on a spatial multiplexing transmission.
available ones, and we focus on a spatial multiplexing transmission.
We assume that the propagation channel is flat fading and quasistatic, and is known at the receiver. We also assume that the power is uniformly allocated across all the  transmit antennas, that is,
transmit antennas, that is,  . We denote the noise power as
. We denote the noise power as  , and the nominal signal-to-noise ratio (SNR) as
, and the nominal signal-to-noise ratio (SNR) as  . Then assuming some codes that approach the Shannon limit quite closely are used, the spectral efficiency (in bits/s/Hz) of this
. Then assuming some codes that approach the Shannon limit quite closely are used, the spectral efficiency (in bits/s/Hz) of this  full-complexity (FC) compact MIMO system without AS could be calculated through [1]
full-complexity (FC) compact MIMO system without AS could be calculated through [1]

It is worth noting that the length limits of transmit and receive arrays,  and
and  , enter into the compound channel matrix
, enter into the compound channel matrix  in a very complicated way. It is thus difficult to find a close-form analytical relationship between
in a very complicated way. It is thus difficult to find a close-form analytical relationship between  and
and  (
( ). Consequently, using Monte Carlo simulations to evaluate the performance of spectral efficiency becomes a necessity.
). Consequently, using Monte Carlo simulations to evaluate the performance of spectral efficiency becomes a necessity.
To avoid detailed system configurations and to make the performance comparison as general and as consistent as possible, we only use the spectral efficiency as the performance of interest. Moreover, all these AS schemes we study here are merely to optimize the spectral efficiency, not other metrics. Since each channel realization renders a spectral efficiency value, the ergodic spectral efficiency and the cumulative distribution function (CDF) of the spectral efficiency will be both meaningful. We will then consider them as performance measures for our study.
3.1. Hybrid Selection
This selection scheme belongs to the conventional hard selection, where  out of
out of  receive antennas are chosen by means of a set of switches in the RF domain (e.g., [5–7]). Figure 4(a) illustrates the architecture of the hybrid selection at the receiver side. As all the antenna elements at the receiver side are presumed grounded through the load impedance
receive antennas are chosen by means of a set of switches in the RF domain (e.g., [5–7]). Figure 4(a) illustrates the architecture of the hybrid selection at the receiver side. As all the antenna elements at the receiver side are presumed grounded through the load impedance  ,
,  , the mutual coupling effect will be always present at the receiver side. However, this can facilitate the channel estimation and allow us to extract rows from
, the mutual coupling effect will be always present at the receiver side. However, this can facilitate the channel estimation and allow us to extract rows from  for subset selection. Otherwise, the mutual coupling effect will vary with respect to the selected antenna subsets. For convenience, we define
for subset selection. Otherwise, the mutual coupling effect will vary with respect to the selected antenna subsets. For convenience, we define  as the
as the  selection matrix, which extracts
selection matrix, which extracts  rows from
rows from  that are associated with the selected subset of antennas. We further define
that are associated with the selected subset of antennas. We further define  as the collection of all possible selection matrices, whose cardinality is given by
as the collection of all possible selection matrices, whose cardinality is given by  . Thus, the system with hybrid selection delivers a spectral efficiency of
. Thus, the system with hybrid selection delivers a spectral efficiency of

Optimal selection that leads to  requires an exhaustive search over all
requires an exhaustive search over all  subsets of
subsets of  , which is evident by (14). Note that
, which is evident by (14). Note that

Then, the matrix multiplication in (14) has a complexity of  . Calculating the matrix determinant in (14) requires a complexity of
. Calculating the matrix determinant in (14) requires a complexity of  . Thus, we can conclude that optimal selection requires about
. Thus, we can conclude that optimal selection requires about  complex additions/multiplications. This estimated complexity for optimal selection can be deemed as an upper bound of the complexity of any hybrid AS scheme, since there exist some suboptimal but reduced complexity algorithms, such as the incremental selection and the decremental selection algorithms in [7].
complex additions/multiplications. This estimated complexity for optimal selection can be deemed as an upper bound of the complexity of any hybrid AS scheme, since there exist some suboptimal but reduced complexity algorithms, such as the incremental selection and the decremental selection algorithms in [7].
3.2. FFT-based Selection
As for this soft selection scheme (e.g., [9]), a  -point FFT transformation (phase-shift only) is performed in the RF domain firstly, as shown in Figure 4(b), where information across all the receive antennas will be utilized. After that, a hybrid-selection-like scheme is applied to extract
-point FFT transformation (phase-shift only) is performed in the RF domain firstly, as shown in Figure 4(b), where information across all the receive antennas will be utilized. After that, a hybrid-selection-like scheme is applied to extract  out of
out of  information streams. We denote
information streams. We denote  as the
as the  unitary FFT matrix with its
unitary FFT matrix with its  th entry given by:
th entry given by:

Accordingly, this system delivers a spectral efficiency of

The only difference between (14) and (17) is the  -point FFT transformation. Such FFT transformation requires a computational complexity of
-point FFT transformation. Such FFT transformation requires a computational complexity of  . If we assume
. If we assume  , then the computational complexity of optimal selection that achieves
, then the computational complexity of optimal selection that achieves  can be estimated as
can be estimated as  , which is the worst-case complexity.
, which is the worst-case complexity.
3.3. Phase-Shift Based Selection
This is another type of soft selection scheme (e.g., [10]) that we consider throughout this study. Its architecture is illustrated in Figure 4(c). Let us denote  as one
as one  matrix whose elements are nonzero and restricted to be pure phase-shifters, that we will fully define in what follows. There exists some other work such as [25] that also considers the use of tunable phase shifters to increase the total capacity of MIMO systems. However, in Figure 4(c), the matrix
matrix whose elements are nonzero and restricted to be pure phase-shifters, that we will fully define in what follows. There exists some other work such as [25] that also considers the use of tunable phase shifters to increase the total capacity of MIMO systems. However, in Figure 4(c), the matrix  that performs phase-shift implementation in the RF domain essentially serves as a
that performs phase-shift implementation in the RF domain essentially serves as a  -to-
-to- switch with
switch with  output streams. Additionally, unlike the FFT matrix,
output streams. Additionally, unlike the FFT matrix,  might not be unitary, and hence the resulting noise can be colored. Finally, this system's spectral efficiency can be calculated by [10]
might not be unitary, and hence the resulting noise can be colored. Finally, this system's spectral efficiency can be calculated by [10]

Let us define the singular value decomposition (SVD) of  as
as  , where
, where  and
and  are
are  ,
,  unitary matrices representing the left and right singular vector spaces of
unitary matrices representing the left and right singular vector spaces of  , respectively;
, respectively;  is a nonnegative and diagonal matrix, consisting of all the singular values of
is a nonnegative and diagonal matrix, consisting of all the singular values of  . In particular, we denote
. In particular, we denote  as the
as the  th largest singular value of
th largest singular value of  , and
, and  as the left singular vector of
as the left singular vector of  associated with
associated with  . Thus one solution to the phase shift matrix
. Thus one solution to the phase shift matrix  can be expressed as [10, Theorem 2]:
can be expressed as [10, Theorem 2]:

where  gives the phase angles, in radians, of a matrix with complex elements,
gives the phase angles, in radians, of a matrix with complex elements,  denotes the element-by-element exponential of a matrix.
denotes the element-by-element exponential of a matrix.
The overall cost for calculating the SVD of  is around
is around  [26, Lecture 31]. Computing the matrix multiplication in (19) requires a complexity around the order of
[26, Lecture 31]. Computing the matrix multiplication in (19) requires a complexity around the order of  . The matrix determinant has an order of complexity of
. The matrix determinant has an order of complexity of  . Therefore, the phase-shift-based selection requires around
. Therefore, the phase-shift-based selection requires around  complex additions/multiplications.
complex additions/multiplications.
4. Simulations
Our simulations focus on the case when AS is implemented only on the receiver side, but mutual coupling and spatial correlation are accounted for at both terminals. However, in order to examine the mutual coupling effect on AS at the receiving antenna array, we further assume  equally-spaced antennas at the transmitter array, and the interelement spacing
equally-spaced antennas at the transmitter array, and the interelement spacing  is fixed at
is fixed at  . This large spacing is chosen to make the mutual coupling effect negligible at the transmitting terminal. For the receiver terminal, we fix the array length
. This large spacing is chosen to make the mutual coupling effect negligible at the transmitting terminal. For the receiver terminal, we fix the array length  at
at  . We choose
. We choose  and
and  for all the dipole elements. Each component in the impedance matrices
for all the dipole elements. Each component in the impedance matrices  and
and  is computed through (2) which analytically expresses the self and mutual impedance of dipole elements in a side-by-side configuration. Finally, we fix the nominal SNR at
is computed through (2) which analytically expresses the self and mutual impedance of dipole elements in a side-by-side configuration. Finally, we fix the nominal SNR at  dB.
dB.
As algorithm efficiency is not a focus in this paper, for both hybrid and FFT-based selection methods, we use the exhaustive search approach to find the best antenna subset. For the phase-shift-based selection, we compute the phase shift matrix  through (19) given each
through (19) given each  . For each scenario of interest, we generate
. For each scenario of interest, we generate  random channel realizations, and study the performance in terms of the ergodic spectral efficiency and the CDF of the spectral efficiency.
random channel realizations, and study the performance in terms of the ergodic spectral efficiency and the CDF of the spectral efficiency.
4.1. Ergodic Spectral Efficiency of Compact MIMO
In Figure 5 we plot the ergodic spectral efficiency of a compact MIMO system for various  . The solid line in Figure 5 depicts the ergodic spectral efficiency when mutual coupling and spatial correlation is considered at both terminals. Also for the purpose of comparison, we include a dashed line which denotes the performance when only spatial correlation is considered at both sides, and a dash-dot line which corresponds to the case when only the simplest i.i.d Gaussian propagation channel is assumed in the system. It is clearly seen that mutual coupling in the compact MIMO system seriously decreases the system's spectral efficiency. Moreover, in accord with the observation in [12], our results also indicate that as the number of receive antenna elements increases, the spectral efficiency will firstly increase, but after reaching the maximum value (approximately around
. The solid line in Figure 5 depicts the ergodic spectral efficiency when mutual coupling and spatial correlation is considered at both terminals. Also for the purpose of comparison, we include a dashed line which denotes the performance when only spatial correlation is considered at both sides, and a dash-dot line which corresponds to the case when only the simplest i.i.d Gaussian propagation channel is assumed in the system. It is clearly seen that mutual coupling in the compact MIMO system seriously decreases the system's spectral efficiency. Moreover, in accord with the observation in [12], our results also indicate that as the number of receive antenna elements increases, the spectral efficiency will firstly increase, but after reaching the maximum value (approximately around  in Figure 5), further increase in
in Figure 5), further increase in  would result in a decrease of the achieved spectral efficiency. It is also worth noting that when
would result in a decrease of the achieved spectral efficiency. It is also worth noting that when  , the interelement spacing at the receiver side,
, the interelement spacing at the receiver side,  , is equal to
, is equal to  , which probably is the most widely adopted interelement spacing in practice. Thus, results in Figure 5 basically indicate that, by adding a few more elements and squeezing the interelement spacing down from
, which probably is the most widely adopted interelement spacing in practice. Thus, results in Figure 5 basically indicate that, by adding a few more elements and squeezing the interelement spacing down from  , it is possible to achieve some increase in the spectral efficiency, even in the presence of mutual coupling. But it is also observed that such increase is limited and relatively slow as compared to the spatial-correlated only case, and the spectral efficiency will saturate very shortly.
, it is possible to achieve some increase in the spectral efficiency, even in the presence of mutual coupling. But it is also observed that such increase is limited and relatively slow as compared to the spatial-correlated only case, and the spectral efficiency will saturate very shortly.
4.2. Ergodic Spectral Efficiency of Compact MIMO with AS
To study the performance of the ergodic spectral efficiency with regard to the number of selected antennas  for a compact MIMO system using AS, we consider three typical scenarios, namely,
for a compact MIMO system using AS, we consider three typical scenarios, namely,  in Figure 6,
in Figure 6,  in Figure 7, and
in Figure 7, and  in Figure 8. In each figure, we plot the performance of the hybrid selection, FFT-based selection, and phase-shift-based selection. Additionally, we also depict in each figure the ergodic spectral efficiency of the reduced full-complexity (RFC) MIMO, denoted as
in Figure 8. In each figure, we plot the performance of the hybrid selection, FFT-based selection, and phase-shift-based selection. Additionally, we also depict in each figure the ergodic spectral efficiency of the reduced full-complexity (RFC) MIMO, denoted as  , where only
, where only  receive antennas are distributed in the linear array and no AS is deployed. In Figure 6, it is observed that
receive antennas are distributed in the linear array and no AS is deployed. In Figure 6, it is observed that  , which in particular indicates the following:
, which in particular indicates the following:
-
(1)
Soft AS always performs no worse than hard AS. The phase-shift-based selection performs strictly better than the FFT-based selection.
-
(2)
With the same number of RF chains, the system with AS performs strictly better than the RFC system.
Interestingly, these conclusions that hold for this compact antenna array case are also generally true for MIMO systems without considering the mutual coupling effect (e.g., [10]). But a cross-reference to the results in Figure 5 can help understand this phenomenon. In Figure 5, it is shown that when  increases from
increases from  to
to  , the ergodic spectral efficiency of the compact MIMO system behaves nearly the same as that of MIMO systems without considering the mutual coupling effect. Therefore, it appears natural that when AS is applied to the compact MIMO system with
, the ergodic spectral efficiency of the compact MIMO system behaves nearly the same as that of MIMO systems without considering the mutual coupling effect. Therefore, it appears natural that when AS is applied to the compact MIMO system with  , similar conclusions can be obtained. It is also interesting that the FFT-based selection performs almost exactly the same as the hybrid selection.
, similar conclusions can be obtained. It is also interesting that the FFT-based selection performs almost exactly the same as the hybrid selection.
Next we increase the number of placed antenna elements to  , at which the compact MIMO system achieves the highest spectral efficiency (cf. Figure 5). We observe some different results in Figure 7, which are
, at which the compact MIMO system achieves the highest spectral efficiency (cf. Figure 5). We observe some different results in Figure 7, which are  . These results tell the following.
. These results tell the following.
-
(1)
Soft AS always outperforms hard AS. The phase-shift-based selection delivers the best performance among all these three AS schemes.
-
(2)
The phase-shift-based selection performs better than the RFC system when
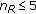 . The FFT-based selection performs better than the RFC system when
. The FFT-based selection performs better than the RFC system when  . The advantage of using the hybrid selection is very limited.
. The advantage of using the hybrid selection is very limited.
We further increase the number of antennas to  . Now the mutual coupling effect becomes more severe, and different conclusions are demonstrated in Figure 8. It is observed that
. Now the mutual coupling effect becomes more severe, and different conclusions are demonstrated in Figure 8. It is observed that  , indicating the following.
, indicating the following.
-
(1)
Soft AS performs strictly better than hard AS.
-
(2)
The phase-shift-based selection performs better than the FFT-based selection when
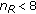 . After that, there is not much performance difference between them.
. After that, there is not much performance difference between them.
Also, similar to what we have observed in Figures 6 and 7, in terms of the ergodic spectral efficiency, none of the systems with AS outperforms the FC system with  receive antennas (and thus
receive antennas (and thus  RF chains). However, as for the RFC system with only
RF chains). However, as for the RFC system with only  antennas (and thus
antennas (and thus  RF chains), in Figure 8 we observe the following.
RF chains), in Figure 8 we observe the following.
-
(1)
The RFC system always performs better than the hybrid selection. The hybrid selection seems futile in this case.
-
(2)
The phase-shift-based selection performs better than the RFC system when
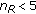 . The benefit of the FFT-based selection is very limited, and it seems not worth implementing.
. The benefit of the FFT-based selection is very limited, and it seems not worth implementing.
This indicates that due to the strong impact of mutual coupling in this compact MIMO system, only the phase-shift-based selection is still effective, but only for a limited range of numbers of the available RF chains. More specifically, when  it is best to use the phase-shift-based selection, otherwise the RFC system with
it is best to use the phase-shift-based selection, otherwise the RFC system with  antennas when
antennas when  . Further increase in the number of RF chains, however, will not lead to a corresponding increase in the spectral efficiency, as demonstrated in Figure 5.
. Further increase in the number of RF chains, however, will not lead to a corresponding increase in the spectral efficiency, as demonstrated in Figure 5.
For the purpose of comparison, we also plot the ergodic spectral efficiency of the phase-shift-based selection scheme in Figure 9, by extracting the corresponding curves from Figures 6–8. We find that by placing a few more antenna elements in the limited space so that the interelement spacing is less than  , for example,
, for example,  in Figure 9, the phase-shift-based selection approach can help boost the system spectral efficiency through selecting the best elements. In fact, the achieved performance is better than that of the conventional MIMO system without AS. This basically answers the question we posed in Section 1 that is related to the cost-performance tradeoff in implementation. However, further squeezing the interelement spacing will decrease the performance and bring no performance gain, as can be seen from the case of
in Figure 9, the phase-shift-based selection approach can help boost the system spectral efficiency through selecting the best elements. In fact, the achieved performance is better than that of the conventional MIMO system without AS. This basically answers the question we posed in Section 1 that is related to the cost-performance tradeoff in implementation. However, further squeezing the interelement spacing will decrease the performance and bring no performance gain, as can be seen from the case of  in Figure 9.
in Figure 9.
4.3. Spectral Efficiency CDF of Compact MIMO with AS
In Figure 10, we investigate the CDF of the spectral efficiency for compact MIMO systems with  . We consider the case of
. We consider the case of  in (Figure 10(a)) and
in (Figure 10(a)) and  in (Figure 10(b). We use dotted lines to denote the compact MIMO systems with AS, and dark solid lines for the FC compact MIMO systems (without AS). We also depict the spectral efficiency CDF-curves of the RFC systems of
in (Figure 10(b). We use dotted lines to denote the compact MIMO systems with AS, and dark solid lines for the FC compact MIMO systems (without AS). We also depict the spectral efficiency CDF-curves of the RFC systems of  and
and  in Figures 10(a) and 10(b), respectively in gray solid lines. As can be seen in Figure 10(a), soft AS schemes, that is, the phase-shift-based and FFT-based AS methods, perform pretty well as expected, but the hybrid selection performs even worse than the RFC system with
in Figures 10(a) and 10(b), respectively in gray solid lines. As can be seen in Figure 10(a), soft AS schemes, that is, the phase-shift-based and FFT-based AS methods, perform pretty well as expected, but the hybrid selection performs even worse than the RFC system with  without AS. When we increase
without AS. When we increase  to 6, as shown in Figure 10(b), the performance difference between hard and soft AS schemes, or between the phase-shift-based and the FFT-based selection methods, is quite small. But none of these systems with various AS schemes outperform the RFC system of
to 6, as shown in Figure 10(b), the performance difference between hard and soft AS schemes, or between the phase-shift-based and the FFT-based selection methods, is quite small. But none of these systems with various AS schemes outperform the RFC system of  without AS, which is consistent with what we have observed in Figure 7.
without AS, which is consistent with what we have observed in Figure 7.
These results clearly indicate that when the mutual coupling effect becomes severe, the advantage of using AS can be greatly reduced, which however, is usually very pronounced in MIMO systems where only spatial correlation is considered at both terminals, as shown for example in Figure 11. On the other hand, it is also found that the spectral efficiency of a RFC system without AS, which is usually the lower bound spectral efficiency to that of MIMO systems with AS (as illustrated by an example of Figure 11), can become even superior to the counterpart when mutual coupling is taken into account (as shown in Figure 10 for instance). However, it should be noted that this phenomenon is closely related to the network model that we adopt in Section 2. In such model, we have assumed that all the antenna elements are grounded through the impedance  , regardless of whether they will be selected or not. Thus, for MIMO systems with
, regardless of whether they will be selected or not. Thus, for MIMO systems with  receive elements and with a certain AS scheme, the mutual coupling impact at the receiver side comes from all these
receive elements and with a certain AS scheme, the mutual coupling impact at the receiver side comes from all these  elements, and is stronger than that of a RFC system with only
elements, and is stronger than that of a RFC system with only  receive elements.
receive elements.
5. Discussions
In our study, we also test different scenarios by varying the length of linear array  , for example, we choose
, for example, we choose  ,
,  , and so forth. For brevity, we leave out these simulation results here, but summarize our main findings as follows.
, and so forth. For brevity, we leave out these simulation results here, but summarize our main findings as follows.
Suppose the ergodic spectral efficiency of a compact antenna array MIMO system saturates at  . Our simulation results (e.g., Figure 5) indicate that
. Our simulation results (e.g., Figure 5) indicate that

where  rounds the number inside to the nearest integer less than or equal to it. We also have
rounds the number inside to the nearest integer less than or equal to it. We also have  for the sake of deploying AS. Our simulations reveal that the interelement spacing is closely related to the functionality of AS schemes. For the cases we study, the conclusion is the following:
for the sake of deploying AS. Our simulations reveal that the interelement spacing is closely related to the functionality of AS schemes. For the cases we study, the conclusion is the following:
-
(1)
When
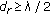 , both soft and hard selection methods are effective, but the selection gains vary with respect to
, both soft and hard selection methods are effective, but the selection gains vary with respect to  . Particularly, the phase-shift-based selection delivers the best performance among these tested schemes. Performance of the FFT-based selection and the hybrid selection appears undistinguishable.
. Particularly, the phase-shift-based selection delivers the best performance among these tested schemes. Performance of the FFT-based selection and the hybrid selection appears undistinguishable. -
(2)
When
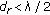 , there exist two situations:
, there exist two situations:-
(a)
When
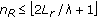 , the selection gain of the phase-shift-based selection still appears pronounced, but tends to become smaller when
, the selection gain of the phase-shift-based selection still appears pronounced, but tends to become smaller when 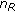 approaches
approaches  . The advantage of using the FFT-based selection is quite limited. The hybrid selection seems rather futile.
. The advantage of using the FFT-based selection is quite limited. The hybrid selection seems rather futile. -
(b)
When
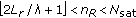 , neither soft nor hard selection seems effective. This suggests that AS might be unnecessary. Instead, we can simply use a RFC system with
, neither soft nor hard selection seems effective. This suggests that AS might be unnecessary. Instead, we can simply use a RFC system with 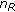 RF chains by equally distributing the elements over the limited space.
RF chains by equally distributing the elements over the limited space.
-
(a)
It is noted that in all these cases we examine, soft AS always has a superior performance over hard selection. This is because soft selection tends to use all the information available, while hard selection loses some additional information by selecting only a subset of the antenna elements. Our simulation results also suggest that, if hard selection is to be used, it is necessary to maintain  . Otherwise, the strong mutual coupling effect could render this approach useless. Further, if the best selection gain for system spectral efficiency is desired, one can place
. Otherwise, the strong mutual coupling effect could render this approach useless. Further, if the best selection gain for system spectral efficiency is desired, one can place  or so elements along the limited-length linear array, use
or so elements along the limited-length linear array, use  or less RF chains, and apply the phase-shift-based selection method. Therefore, it becomes crucial to identify the saturation point
or less RF chains, and apply the phase-shift-based selection method. Therefore, it becomes crucial to identify the saturation point  . This in turn requires the electromagnetic modeling of the antenna array that can take into account the mutual coupling effect.
. This in turn requires the electromagnetic modeling of the antenna array that can take into account the mutual coupling effect.
6. Conclusion
In this paper, we proposed a study of some typical hard and soft AS methods for MIMO systems with closely spaced antennas. We assumed antenna elements are placed linearly in a side-by-side fashion, and we examined the mutual coupling effect through electromagnetic modeling of the antenna array and theoretical analysis. Our results indicate that, when the interelement spacing is larger or equal to one half wavelength, selection gains of these tested soft and hard AS schemes will be very pronounced. However, when the number of antennas to be placed becomes larger and the interelement spacing becomes smaller than a half wavelength, only the phase-shift-based selection remains effective and this is only true for a limited number of available RF chains. The same conclusions however, are not observed for the case of hard selection. Thus it seems necessary to maintain the interelement spacing no less than one half wavelength when the hard selection method is desired. On the other hand, if the best selection gain for system spectral efficiency is desired, one can employ a certain number of elements for which the compact MIMO system attains its maximum ergodic spectral efficiency, use  or less RF chains, and deploy the phase-shift-based selection method. This essentially indicates, if the cost-performance tradeoff in implementation is concerned, by placing a few more than necessary antenna elements so that the system spectral efficiency reaches saturation and deploying the phase-shift-based selection approach, we can achieve better performance in terms of system spectral efficiency than the conventional MIMO system without AS. Overall, our study provides novel insight into the deployment of AS in future generation wireless systems, including the 3GPP LTE and LTE advanced technologies.
or less RF chains, and deploy the phase-shift-based selection method. This essentially indicates, if the cost-performance tradeoff in implementation is concerned, by placing a few more than necessary antenna elements so that the system spectral efficiency reaches saturation and deploying the phase-shift-based selection approach, we can achieve better performance in terms of system spectral efficiency than the conventional MIMO system without AS. Overall, our study provides novel insight into the deployment of AS in future generation wireless systems, including the 3GPP LTE and LTE advanced technologies.
References
Foschini GJ, Gans MJ: On limits of wireless communications in a fading environment when using multiple antennas. Wireless Personal Communications 1998, 6(3):311-335. 10.1023/A:1008889222784
Overview of 3GPP Release 8 V0.0.3 November 2008, http://www.3gpp.org/Release-8
Molisch AF, Win MZ: MIMO systems with antenna selection. IEEE Microwave Magazine 2004, 5(1):46-56. 10.1109/MMW.2004.1284943
Kotecha J: LTE:MIMO Techniques in 3GPP-LTE. Freescale Semiconductor, June 2008
Win MZ, Winters JH: Analysis of hybrid selection/maximal-ratio combining in Rayleigh fading. IEEE Transactions on Communications 1999, 47(12):1773-1776. 10.1109/26.809693
Molisch AF, Win MZ, Winter JH: Reduced-complexity transmit/receive-diversity systems. IEEE Transactions on Signal Processing 2003, 51(11):2729-2738. 10.1109/TSP.2003.818211
Gorokhov A, Gore DA, Paulraj AJ: Receive antenna selection for MIMO spatial multiplexing: theory and algorithms. IEEE Transactions on Signal Processing 2003, 51(11):2796-2807. 10.1109/TSP.2003.818204
Collin L, Berder O, Rostaing P, Burel G: Soft vs. hard antenna selection based on the minimum distance for MIMO systems. Proceedings of the 38th Asilomar Conference on Signals, Systems and Computers, November 2002, Grove, Calif, USA 2: 1369-1373.
Molisch AF, Zhang X: FFT-based hybrid antenna selection schemes for spatially correlated MIMO channels. IEEE Communications Letters 2004, 8(1):36-38. 10.1109/LCOMM.2003.822512
Zhang X, Molisch AF, Kung S-Y: Variable-phase-shift-based RF-baseband codesign for MIMO antenna selection. IEEE Transactions on Signal Processing 2005, 53(11):4091-4103.
Balanis CA: Antenna Theory: Analysis and Design. 3rd edition. John Wiley & Sons, New York, NY, USA; 2005.
Janaswamy R: Effect of element mutual coupling on the capacity of fixed length linear arrays. IEEE Antennas and Wireless Propagation Letters 2002, 1: 157-160.
Waldschmidt C, Schulteis S, Wiesbeck W: Complete RF system model for analysis of compact MIMO arrays. IEEE Transactions on Vehicular Technology 2004, 53(3):579-586. 10.1109/TVT.2004.825788
Wallace JW, Jensen MA: Mutual coupling in MIMO wireless systems: a rigorous network theory analysis. IEEE Transactions on Wireless Communications 2004, 3(4):1317-1325. 10.1109/TWC.2004.830854
Abouda AA, Häggman SG: Effect of mutual coupling on capacity of MIMO wireless channels in high SNR scenario. Progress in Electromagnetics Research 2006, 65: 27-40.
Gans MJ: Channel capacity between antenna arrays—part I: sky noise dominates. IEEE Transactions on Communications 2006, 54(9):1586-1592.
Gans MJ: Channel capacity between antenna arrays—part II: amplifier noise dominates. IEEE Transactions on Communications 2006, 54(11):1983-1992.
Xu Z, Sfar S, Blum RS: On the importance of modeling the mutual coupling for antenna selection for closely-spaced arrays. Proceedings of IEEE Conference on Information Sciences and Systems (CISS '06), March 2006, Princeton, NJ, USA 1351-1355.
Lu D, So DKC, Brown AK: Receive antenna selection scheme for V-BLAST with mutual coupling in correlated channels. Proceedings of IEEE International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC '08), September 2008, Cannes, France 1-5.
Orfanidis SJ: Electromagnetic Waves and Antennas. Rutgers University, Piscataway, NJ, USA; 2004.
Hewes J: Impedance and reactance. The Electronics Club, February 2008, http://www.kpsec.freeuk.com/imped.htm
Kermoal JP, Schumacher L, Pedersen KI, Mogensen PE, Frederiksen F: A stochastic MIMO radio channel model with experimental validation. IEEE Journal on Selected Areas in Communications 2002, 20(6):1211-1226. 10.1109/JSAC.2002.801223
Oestges C, Clerckx B, Vanhoenacker-Janvier D, Paulraj AJ: Impact of fading correlations on MIMO communication systems in geometry-based statistical channel models. IEEE Transactions on Wireless Communications 2005, 4(3):1112-1120.
Shiu D-S, Foschini GJ, Gans MJ, Kahn JM: Fading correlation and its effect on the capacity of multielement antenna systems. IEEE Transactions on Communications 2000, 48(3):502-513. 10.1109/26.837052
Nakaya Y, Toda T, Hara S, Takada J-I, Oishi Y: Incorporation of RF-adaptive array antenna into MIMO receivers. Proceedings of IEEE Topical Conference on Wireless Communication Technology (WCT '03), October 2003, Honolulu, Hawaii, USA 297-298.
Trefethen LN, Bau D III: Numerical Linear Algebra. SIAM, Philadelphia, Pa, USA; 1997.
Acknowledgments
This material is based on research supported by the Air Force Research Laboratory under agreement FA9550-09-1-0576, by the National Science Foundation under Grant CCF-0829958, and by the U.S. Army Research Office under Grant W911NF-08-1-0449. The authors would like to thank Dr. Dmitry Chizhik and Dr. Dragan Samardzija of Bell Laboratories, Alcatel-Lucent for the helpful discussions on the modeling and implementation issues.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Yang, Y., Blum, R.S. & Sfar, S. Antenna Selection for MIMO Systems with Closely Spaced Antennas. J Wireless Com Network 2009, 739828 (2009). https://doi.org/10.1155/2009/739828
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/739828


 compact MIMO system.
compact MIMO system.



 ) with mutual coupling at both transmitter and receiver sides.
) with mutual coupling at both transmitter and receiver sides.
 and
and  .
.
 and
and  .
.
 and
and  .
.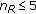 . The FFT-based selection performs better than the RFC system when
. The FFT-based selection performs better than the RFC system when  . The advantage of using the hybrid selection is very limited.
. The advantage of using the hybrid selection is very limited.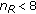 . After that, there is not much performance difference between them.
. After that, there is not much performance difference between them.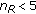 . The benefit of the FFT-based selection is very limited, and it seems not worth implementing.
. The benefit of the FFT-based selection is very limited, and it seems not worth implementing.
 .
.
 and
and  . (a) (
. (a) ( )(b) (
)(b) ( )
)
 ,
,  , and mutual coupling is not considered. (a) (
, and mutual coupling is not considered. (a) ( ) (b) (
) (b) ( )
)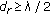 , both soft and hard selection methods are effective, but the selection gains vary with respect to
, both soft and hard selection methods are effective, but the selection gains vary with respect to  . Particularly, the phase-shift-based selection delivers the best performance among these tested schemes. Performance of the FFT-based selection and the hybrid selection appears undistinguishable.
. Particularly, the phase-shift-based selection delivers the best performance among these tested schemes. Performance of the FFT-based selection and the hybrid selection appears undistinguishable.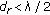 , there exist two situations:
, there exist two situations: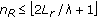 , the selection gain of the phase-shift-based selection still appears pronounced, but tends to become smaller when
, the selection gain of the phase-shift-based selection still appears pronounced, but tends to become smaller when 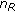 approaches
approaches  . The advantage of using the FFT-based selection is quite limited. The hybrid selection seems rather futile.
. The advantage of using the FFT-based selection is quite limited. The hybrid selection seems rather futile.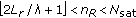 , neither soft nor hard selection seems effective. This suggests that AS might be unnecessary. Instead, we can simply use a RFC system with
, neither soft nor hard selection seems effective. This suggests that AS might be unnecessary. Instead, we can simply use a RFC system with 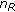 RF chains by equally distributing the elements over the limited space.
RF chains by equally distributing the elements over the limited space.