- Research Article
- Open access
- Published:
Optimal and Fair Resource Allocation for Multiuser Wireless Multimedia Transmissions
EURASIP Journal on Wireless Communications and Networking volume 2009, Article number: 801613 (2009)
Abstract
This paper presents an optimal and fair strategy for multiuser multimedia radio resource allocation (RRA) based on coopetition, which suggests a judicious mixture of competition and cooperation. We formulate the co-opetition strategy as sum utility maximization at constraints from both Physical (PHY) and Application (APP) layers. We show that the maximization can be solved efficiently employing the well-defined Layering as Optimization Decomposition (LOD) method. Moreover, the coopetition strategy is applied to power allocation among multiple video users, and evaluated through comparing with existing- competition based strategy. Numerical results indicate that, the co-opetition strategy adapts the best to the changes of network conditions, participating users, and so forth. It is also shown that the coopetition can lead to an improved number of satisfied users, and in the meanwhile provide more flexible tradeoff between system efficiency and fairness among users.
1. Introduction
Radio resource allocation (RRA) for multimedia services has drawn a lot of attention because of its capability of offering an efficient way to handle the resources. In previous research, much attention has been paid to system efficiency improvement, that is, maximizing system utility [1–8]. It is shown that the Nash Bargaining Solution (NBS), a well-defined notion in game theory, can be used to maximize the sum of Peak Signal-to-Noise Ratios (PSNRs) in rate allocation for collaborative video transmissions [1]. Optimal resource allocation for multiuser wireless transmissions is studied in [2] from an information theoretic perspective, and it is shown that sum rate maximization (SRM) is suboptimal when taking video quality into account. This work has been extended to joint power and subcarrier allocation for mutiuser video transmission in multi-carrier systems [3]. In [4], Application (APP), MAC, and Physical (PHY) layers are jointly optimized using Cross-Layer Design (CLD) for streaming video delivery in a multiuser wireless environments, and two objective functions are introduced, that is, minimizing the sum of mean square error (MSE) of all video users, maximizing the sum of PSNRs. As a continuous work of [4, 5] proposed an application-driven cross-layer optimization strategy and discussed the challenges in CLD for multiuser multimedia services. Two Layering, as Optimization Decomposition (LOD) methods, dual decomposition and gradient projection-based decomposition, are used in [6, 7] for downlink utility maximization (DUM) assuming utility functions at APP layer are concave, increasing, and differentiable. The maximization of weighted sum of data rates in cross-layer resource allocation is addressed in [8], and an improved conjugate gradient method under given power constraint is presented as well.
In the work mentioned above, all the resource allocation methods try to maximize the global utility function. There are also several resource allocations that run in a distributive way, for instance, ReSerVation Protocol (RSVP) was used to allocate bandwidth among multiple multimedia streams over internet based on the Traffic SPECifications (TSPECs) [9]; air time fairness allocates transmission time proportionally to TSPECs to eliminate the passive impact of cross-layer strategies employed in different transmitters [10]. Proportional fairness was introduced [11] to allocate resources based on users' rate requirements, and further applied to rate controlling [12]. In [1], the Kalai-Smorodinsky Bargaining Solution (KSBS) was used to allocate rates amongst multiple video users such that the utility achieved by each user is proportional to the maximum utility achievable.
Both maximization based and distributive policies work in a competitive way as explained by the following two examples. Utility maximization can actually be viewed as a process in which all users compete for resources according to the criteria that the Highest Quality Improvement the Highest Possibility Resources (HQIHPR) [2]. Using KSBS, users compete for resources to make efficient use of the resource and achieve higher utility. The disadvantage of these competitive policies is that they do not consider user's quality of service (QoS) satisfication degree, meaning that they are not suitable for multimedia services. To address this disadvantage, we propose an optimal and fair policy for multimedia resource allocation, which introduces a judicious mixture of competition and cooperation, such that user's QoS satisfication degree is taken into account. The idea behind this judicious mixture is Co-opetition, a concept from economic [13]. Co-opetition has been employed in decentralized resource management [14] and collaborative multimedia resource allocation in our preliminary work [15]. It is shown that co-opetition can provide better tradeoff between system efficiency and fairness.
Main contribution of this paper relies on the proposal of a novel co-opetition strategy for RRA in multimedia services, which is both optimal and fair. In this paper, optimal represents sum utility maximization (SUM) subject to the constraints on individual utility. It is worth to mention that the value of optimal sum utility might be smaller than that achieved by the unconstrained SUM, due to the constraints. Fair is defined to describe that, compared to unconstrained SUM, our strategy can result in fairer resource allocation. The additional fairness from our strategy comes from the individual utility constraint. Recall that the unconstrained SUM allocates resources in a competitive way, which has no constraint on individual utility. Our co-opetition strategy suggests a judicious mixture of competition and cooperation in resource allocation. We formulate the co-opetition strategy mathematically and solve it efficiently using LOD method. This mathematical formulation would help to get a better insight into the essential of competition and cooperation behaviors of users in RRA. We apply our strategy to wireless resource allocation for multiuser video transmissions and evaluate its performance by comparing with existing competition based mechanisms.
The rest of this paper is organized as follows. In Section 2, we formulate the co-opetition strategy, and in Section 3 we implement it by employing LOD method. In Section 4, we apply the co-opetition strategy to power allocation amongst multiple video users together with numerical results for performance evaluation. Conclusion is drawn in Section 5.
2. Problem Setup
We consider RRA over a downlink transmission with  users. We assume that the resource available at PHY layer is denoted by
users. We assume that the resource available at PHY layer is denoted by  . Denote
. Denote  as the rate region achievable at PHY layers, and assume that
as the rate region achievable at PHY layers, and assume that  is convex and compact. Convexity assumption means that time-sharing mode is enabled at PHY layer. Let
is convex and compact. Convexity assumption means that time-sharing mode is enabled at PHY layer. Let  denote the user
denote the user  's utility function, which is assumed to be concave, increasing, and differentiable. An example of utility is PSNR for video services [16]. Each user has a minimum desired rate, denoted by
's utility function, which is assumed to be concave, increasing, and differentiable. An example of utility is PSNR for video services [16]. Each user has a minimum desired rate, denoted by  , which should be at least guaranteed. That means
, which should be at least guaranteed. That means

otherwise, user  would not be served. A competition strategy should be employed to develop our co-opetition strategy. In this paper, we focus on optimization-based strategy, that is, sum utility maximization (SUM). Investigation based on distributive and competition-based strategies will be accommodated in our future work. For SUM, system utility function
would not be served. A competition strategy should be employed to develop our co-opetition strategy. In this paper, we focus on optimization-based strategy, that is, sum utility maximization (SUM). Investigation based on distributive and competition-based strategies will be accommodated in our future work. For SUM, system utility function  is defined as
is defined as

where  . Hence, SUM can be written as
. Hence, SUM can be written as

To allow co-opetition, we first define the notion of satisfied user. A user is called satisfied user if its achieved QoS is above or equal to predefined QoS threshold,  . Then the basic idea of co-opetition can be described as follows. During the process of RRA, in which all users compete for resources to achieve SUM, users who have achieved
. Then the basic idea of co-opetition can be described as follows. During the process of RRA, in which all users compete for resources to achieve SUM, users who have achieved  stop competing temporarily, until all resources have been allocated or all users have been satisfied. Denote rate required by user
stop competing temporarily, until all resources have been allocated or all users have been satisfied. Denote rate required by user  to achieve
to achieve  with
with  , and denote
, and denote  as
as  . We distinguish the following two cases.
. We distinguish the following two cases.
(1)If  , co-opetition allocates resources such that the minimum utility of all users is
, co-opetition allocates resources such that the minimum utility of all users is  , that is,
, that is,  .
.
(2)If  , co-opetition allocates resources such that the maximum utility of all users is
, co-opetition allocates resources such that the maximum utility of all users is  , that is,
, that is,  .
.
Thus, our co-opetition strategy reads

Introducing  provides better tradeoff between system efficiency and fairness. For example, for video services in which PSNR is chosen as a QoS metric,
provides better tradeoff between system efficiency and fairness. For example, for video services in which PSNR is chosen as a QoS metric,  can be set corresponding to
can be set corresponding to  dB, above which user could achieve good video quality and user's video satisfaction degree increases very slowly as PSNR increases. In this case, rate, which can translate to resources at PHY layer, is more important to unsatisfied users. In the following, we investigate how the LOD method is used to solve (4) efficiently.
dB, above which user could achieve good video quality and user's video satisfaction degree increases very slowly as PSNR increases. In this case, rate, which can translate to resources at PHY layer, is more important to unsatisfied users. In the following, we investigate how the LOD method is used to solve (4) efficiently.
3. LOD Method
LOD is a well-defined technique for network utility maximization (NUM) by decomposing the NUM into a set of subproblems coupled with each other. Each subproblem is associated with a protocol layer, in which it can be solved separately [17].
3.1. Rewrite Co-Opetition Strategy
We assume it is known whether  can be achieved or not. In the case of
can be achieved or not. In the case of  ,
,  translates into
translates into  , and
, and  translates into
translates into  otherwise. We also assume that
otherwise. We also assume that

always satisfies. Then constraints in (4) can be rewritten as

where  (In the case of
(In the case of  , total resource available cannot guarantee all users the minimum resource required, and some users will deny to be served. In this paper, we assume the minimum resource of all users can be always guaranteed, that is,
, total resource available cannot guarantee all users the minimum resource required, and some users will deny to be served. In this paper, we assume the minimum resource of all users can be always guaranteed, that is,  .). We observe that, no matter
.). We observe that, no matter  or not, the constraint has the same form of
or not, the constraint has the same form of

with  . Hence, (4) can be rewritten as
. Hence, (4) can be rewritten as

3.2. Dual Decomposition
To solve (8) with LOD, (8) is firstly modified by introducing an additional variable  , then the primal function (8) reads
, then the primal function (8) reads

After introducing the Lagrangian factors

the Lagrangian function of (9) is written as

with  . Thus, the dual function is
. Thus, the dual function is

The maximization in (9) can be solved by searching the optimum  and
and  such that the dual function is minimized, that is,
such that the dual function is minimized, that is,

Based on the analysis afore, (A.2) can be decomposed into two subproblems as

where


For given  and
and  , the above two-maximization can be solved independently at APP layer for (15) and at PHY layer for (16). So far, we have transformed the original maximization, (8), into its dual problem.
, the above two-maximization can be solved independently at APP layer for (15) and at PHY layer for (16). So far, we have transformed the original maximization, (8), into its dual problem.
3.3. Solving (13), (15) and (16)
As mentioned above, for each fixed  and
and  , (15) and (16) have to be solved. Denote
, (15) and (16) have to be solved. Denote  as the item to be maximized in (15), that is,
as the item to be maximized in (15), that is,

Then  is continuous and differentiable, and further denote
is continuous and differentiable, and further denote  as set of
as set of  such that
such that

Then (15) can be solved via efficiently selecting the optimum  , such that
, such that

Maximization of (16) refers to weighted sum rate maximization (WSRMax) at constraint of maximizing individual rate for certain PHY layer setup.  is a general constraint usually corresponding to given power or bandwidth.
is a general constraint usually corresponding to given power or bandwidth.  can be translated into individual constraint. Recall that,
can be translated into individual constraint. Recall that,  is assumed to be convex and compact, thus the domain of (16), denoted with
is assumed to be convex and compact, thus the domain of (16), denoted with  ,
,

is also convex and compact. WSRMax over  is a well-researched problem and there are many efficient solutions for a wide range of PHY layer setups [3, 8, 18].
is a well-researched problem and there are many efficient solutions for a wide range of PHY layer setups [3, 8, 18].
Hereafter, we assume that for each  and
and  , (15) and (16) can be solved efficiently. Then the optimum
, (15) and (16) can be solved efficiently. Then the optimum  and
and  can be determined, for example, using either sub-gradient method, cutting plane method or ellipsoid method [19]. In Section 5, we would show how to solve (13), (15) and (16) more concretely through power allocation.
can be determined, for example, using either sub-gradient method, cutting plane method or ellipsoid method [19]. In Section 5, we would show how to solve (13), (15) and (16) more concretely through power allocation.
3.4. Determining whether 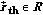 or Not
or Not
Note that is  not necessarily achievable. Whether
not necessarily achievable. Whether  or not can be determined by userwisely computing the minimum resource required to achieve
or not can be determined by userwisely computing the minimum resource required to achieve  . Fortunately again there are several solutions available for different scenarios. For example, in [20] a generic procedure, CLARA, was presented for cross-layer resource minimization subject to a set of constraints on the overall QoS. [21] proposed an iterative algorithm which monotonically converges to the unique allocation with optimal sum power efficiency. This is actually another hot topic as opposed to utility maximization in this paper, namely, cost minimization to achieve certain QoS.
. Fortunately again there are several solutions available for different scenarios. For example, in [20] a generic procedure, CLARA, was presented for cross-layer resource minimization subject to a set of constraints on the overall QoS. [21] proposed an iterative algorithm which monotonically converges to the unique allocation with optimal sum power efficiency. This is actually another hot topic as opposed to utility maximization in this paper, namely, cost minimization to achieve certain QoS.
3.5. Summery of LOD Method
In this Section, we have mapped our co-opetition strategy, (4), to a standard constrained optimization over convex domain, that is, (8). Moreover, importantly, through applying the LOD, many well-researched solutions are available which make our co-opetition strategy more applicable. Finally, since the resource allocation in this paper can be formulated as a convex optimization, the LOD method has worst-case polynomialtime complexity [17]. It will be shown that the LOD method converges within limited iterations. Figure 1 is a brief description to apply the co-opetition strategy. We investigate how co-opetition can be applied to power allocation in detail.
4. RRA Using Co-Opetition
In this Section, we first describe the system scenario, and then illustrate the co-opetition strategy in detail. Finally, numerical results are presented for performance evaluation through comparing with competition-based strategy.
4.1. System Setup
We consider downlink  -user video transmission in a cell with a base-station (BS) which acts as the central spectrum manager (CSM). At APP layer, users transmit same or different video sequences. We choose PSNR as user's utility as it is the only widely accepted video QoS metric and choose the rate-distortion (RD) model proposed in [16] to describe user's average RD behavior as this model applies well to the state-of-the-art video encoder [22]. Then user's utility can be defined as
-user video transmission in a cell with a base-station (BS) which acts as the central spectrum manager (CSM). At APP layer, users transmit same or different video sequences. We choose PSNR as user's utility as it is the only widely accepted video QoS metric and choose the rate-distortion (RD) model proposed in [16] to describe user's average RD behavior as this model applies well to the state-of-the-art video encoder [22]. Then user's utility can be defined as

where  and
and  are sequence parameters, which are dependent on video sequence characteristics, such as spatial and temporal resolution, delay constraints as well as the percentage of INTRA coded macro-blocks [1, 16].
are sequence parameters, which are dependent on video sequence characteristics, such as spatial and temporal resolution, delay constraints as well as the percentage of INTRA coded macro-blocks [1, 16].  is the minimum rate that should be at least guaranteed for user
is the minimum rate that should be at least guaranteed for user  , therefore in this work we assume that
, therefore in this work we assume that  .
.
At PHY layer, the BS has limited transmit power,  . Let
. Let  represent the power allocated to all the users, thus we have
represent the power allocated to all the users, thus we have  . Each user is assumed to experience an AWGN channel, whose capacity,
. Each user is assumed to experience an AWGN channel, whose capacity,  , is given by
, is given by

where  and
and  denote bandwidth available and receiver noise power, respectively.
denote bandwidth available and receiver noise power, respectively.
It is assumed that private information of each user, including  , are sent to CSM, where power allocation is made. Then CSM sends back the decision of power allocated to each user. Note that, more complicated PHY layer setups can also be taken into account, such as multicarrier and multiple antennas systems over Rayleigh fading channels. However, employing simple PHY layer setup would help to highlight the focus of this paper, investigating optimal and fair criteria for RRA. It is worth mentioning that the co-opetition strategy can be easily extended to other scenarios.
, are sent to CSM, where power allocation is made. Then CSM sends back the decision of power allocated to each user. Note that, more complicated PHY layer setups can also be taken into account, such as multicarrier and multiple antennas systems over Rayleigh fading channels. However, employing simple PHY layer setup would help to highlight the focus of this paper, investigating optimal and fair criteria for RRA. It is worth mentioning that the co-opetition strategy can be easily extended to other scenarios.
4.2. Co-Opetition Strategy
4.2.1. Co-Opetition Formulation
According to the common sense in the field of video signal processing, the PSNR threshold can be set to different values, such as 40 dB, 35 dB, or 32 dB, representing perfect, good and acceptable video quality, respectively. The PSNR threshold can also be set dynamically according to the total resources available, the number of users, and so forth. As an illustration, we choose QoS threshold as PSNR = 35 dB corresponding to good video quality, that is,  dB in (4). Denote
dB in (4). Denote  as
as  representing power required by users to achieve PSNR of 35 dB. Using co-opetition strategy, if
representing power required by users to achieve PSNR of 35 dB. Using co-opetition strategy, if  (
( means calculating the sum of all members in
means calculating the sum of all members in  , i.e.,
, i.e.,  .), the lower and upper bounds of achievable PSNR are set at
.), the lower and upper bounds of achievable PSNR are set at  dB and
dB and  , respectively, and
, respectively, and  and
and  dB otherwise. Correspondingly, when we have
dB otherwise. Correspondingly, when we have  , lower and upper bounds of rates are
, lower and upper bounds of rates are  and
and  , respectively, and
, respectively, and  and
and  otherwise. In this paper, it is easy to calculate
otherwise. In this paper, it is easy to calculate  corresponding to PSNR threshold, for both (21) and (22) are invertible and monotonic increasing functions. Thus, given PSNR threshold,
corresponding to PSNR threshold, for both (21) and (22) are invertible and monotonic increasing functions. Thus, given PSNR threshold,  or not can be easily determined, and consequently, both
or not can be easily determined, and consequently, both  and
and  are known.
are known.
Given each user's utility definition in (21) and (22), system utility writes

where  refers to as
refers to as  . We assume that capacity approaching channel codes is employed at PHY layer. Then our co-opetition strategy writes
. We assume that capacity approaching channel codes is employed at PHY layer. Then our co-opetition strategy writes

where  . Note that (24) has the same form as (8). The first constraint on the sum of the power (24) corresponds to
. Note that (24) has the same form as (8). The first constraint on the sum of the power (24) corresponds to  in (8).
in (8).
4.2.2. The Implement of Co-Opetition
Using LOD, maximization of (24) can be decomposed into

where  , and
, and

where  is defined as the upper bound of transmit power of user
is defined as the upper bound of transmit power of user  corresponding to
corresponding to  .
.
The optimum variable of (25),  , can be obtained by simply making the partial derivative of
, can be obtained by simply making the partial derivative of and let it equal to 0,
and let it equal to 0,

Then we have

where 
As mentioned in Section 3.3, (26) can be solved at PHY layer by the weighted sum rate maximization with the constraints of total and individual power. Note that  in (22) is concave and increasing with respect to
in (22) is concave and increasing with respect to  , thus the item to be maximized in (26) is also concave increasing. The domain of (26) is formed by two linear inequalities, each of which forms a convex domain together with
, thus the item to be maximized in (26) is also concave increasing. The domain of (26) is formed by two linear inequalities, each of which forms a convex domain together with  . Thus the domain of (26) is also convex, and (26) is accessible to conventional convex optimization techniques, such as feasible direction method and projected gradient method. In this paper the feasible increasing direction method is employed (see the Appendix for details).
. Thus the domain of (26) is also convex, and (26) is accessible to conventional convex optimization techniques, such as feasible direction method and projected gradient method. In this paper the feasible increasing direction method is employed (see the Appendix for details).
So far, given fixed  , two subproblems, (25) and (26), have been solved. We denote the optimal values of them with
, two subproblems, (25) and (26), have been solved. We denote the optimal values of them with  and
and  , respectively. In the following, the optimum
, respectively. In the following, the optimum  , denoted by
, denoted by  , will be determined such that the sum of
, will be determined such that the sum of  and
and  is minimized, that is,
is minimized, that is,

Note that, the dual function might not be differentiable or, in other words, (29) is not accessible to classical computational method, such as steepest descent method. In this paper we employ the sub-gradient method, which applies to both differentiable and nondifferentiable dual functions. Much like the feasible increasing direction method, sub-gradient method also searches the optimal  and
and  iteratively. The main iteration writes
iteratively. The main iteration writes

where  is the step-size which can be set as constant, and
is the step-size which can be set as constant, and  denotes the sub-gradient at
denotes the sub-gradient at  . Note that,
. Note that,  at
at  rightly forms a sub-gradient, so the sub-gradient can be obtained almost without any cost.
rightly forms a sub-gradient, so the sub-gradient can be obtained almost without any cost.
4.3. Numerical Results
In this subsection, the proposed co-opetition strategy (co-opetition) is evaluated by comparing with the strategy proposed in [1], which allocates resources using the Nash bargaining Solution of Same bargaining Power (NBS_SP). For the sake of comparison, we use the same test sequences as those in [1], and we list the parameters in Table I for reader's convenience.
4.3.1. Comparison in Terms of Individual PSNR
In this experiment we focus on individual PSNRs in the case of two users. At APP layer, user 1 transmits Foreman sequence of CIF resolution at 30 Hz, and user 2 transmits Mobile sequence of CIF resolution at 30 Hz. At PHY layer, we set the bandwidth to  = 250 kHz, and let the receiver noise power to be
= 250 kHz, and let the receiver noise power to be  and
and  for user 1 and user 2, respectively. Total transmit power
for user 1 and user 2, respectively. Total transmit power  varies from 50 to 800. Figure 2 shows the individual PSNRs achieved by these two schemes. If NBS_SP is employed, user 1 can achieve higher PSNR that user 2 or, in other words, it is very hard for user 2 to achieve satisfying video quality (PSNR
varies from 50 to 800. Figure 2 shows the individual PSNRs achieved by these two schemes. If NBS_SP is employed, user 1 can achieve higher PSNR that user 2 or, in other words, it is very hard for user 2 to achieve satisfying video quality (PSNR  35). In the case of
35). In the case of  , user 1 can always be satisfied. Note in this case, user 1's video satisfaction degree increases very slowly as the PSNR increases, but significantly for user 2. Taking this observation into account, co-opetition imposes individual constraint on each user (see (4). For example, with
, user 1 can always be satisfied. Note in this case, user 1's video satisfaction degree increases very slowly as the PSNR increases, but significantly for user 2. Taking this observation into account, co-opetition imposes individual constraint on each user (see (4). For example, with  , which can not satisfy two users simultaneously, co-opetition decreases user 1's PSNR to 35 dB, and consequently, user 2's PSNR achieves an improvement about 1 dB. If have
, which can not satisfy two users simultaneously, co-opetition decreases user 1's PSNR to 35 dB, and consequently, user 2's PSNR achieves an improvement about 1 dB. If have  , user 2's PSNR is improved such that user 2 is just satisfied. Note, in these two cases, co-opetiton keeps user 1 satisfied, while user 2 either be satisfied or achieve much QoS improvement. It is worth to mention that, under a given total transmit power constraint, NBS_SP can achieve higher total PSNR of two users than that in co-opetition. This is because the NBS_SP maximizes the sum of PSNRs without taking the individual PSNR constraints into account. The co-opetition works in quite a different way. It maximizes the sum of PSNRs under the constraints of individual PSNR. Therefore, the co-opetition is not only optimal (As stated in Section 1, in this paper the optimal means sum utility maximization under certain constraints, differing from unconstrained optimization.) , but also fairer than NBS_SP. This argument is further verified with other experiments
, user 2's PSNR is improved such that user 2 is just satisfied. Note, in these two cases, co-opetiton keeps user 1 satisfied, while user 2 either be satisfied or achieve much QoS improvement. It is worth to mention that, under a given total transmit power constraint, NBS_SP can achieve higher total PSNR of two users than that in co-opetition. This is because the NBS_SP maximizes the sum of PSNRs without taking the individual PSNR constraints into account. The co-opetition works in quite a different way. It maximizes the sum of PSNRs under the constraints of individual PSNR. Therefore, the co-opetition is not only optimal (As stated in Section 1, in this paper the optimal means sum utility maximization under certain constraints, differing from unconstrained optimization.) , but also fairer than NBS_SP. This argument is further verified with other experiments
4.3.2. Comparison in Terms of the Number of Satisfied Users and Minimum PSNRs
We study a more complicated scenario with nine users, each transmitting a sequence randomly selected from Table 1. They also experience different receiver noises randomly generated from 0 to 25. Figure 3 shows the number of satisfied users and the minimum PSNRs achieved by NBS_SP and co-opetition. We observe that, the co-opetition always outperforms the NBS_SP. For example, in the case of  , co-opetition can make all users satisfied, but only 6 users satisfied by NBS_SP. With respect to the minimum PSNR, which is an important criteria evaluating system in the worst case, improvement of around 6 dB can be achieved when
, co-opetition can make all users satisfied, but only 6 users satisfied by NBS_SP. With respect to the minimum PSNR, which is an important criteria evaluating system in the worst case, improvement of around 6 dB can be achieved when  . Note that, NBS_SP can only make minimum PSNRs from about 25 dB to 29 dB, corresponding to poor video quality, while above 32 dB for co-opetition leading to acceptable video quality. Recall that, the co-opetition implies a judicious mixture of competition and cooperation. Through competition, the best system efficiency can be achieved. However, pure competition, for example, NBS_SP, might make very high PSNRs for some users, for example, users transmitting simple video content or having good channel quality, but low PSNRs for the others. This disadvantage is eliminated by co-copetition through introducing cooperation among users. Again, this experiment indicates that co-opetition provides a good tradeoff between system efficiency and fairness.
. Note that, NBS_SP can only make minimum PSNRs from about 25 dB to 29 dB, corresponding to poor video quality, while above 32 dB for co-opetition leading to acceptable video quality. Recall that, the co-opetition implies a judicious mixture of competition and cooperation. Through competition, the best system efficiency can be achieved. However, pure competition, for example, NBS_SP, might make very high PSNRs for some users, for example, users transmitting simple video content or having good channel quality, but low PSNRs for the others. This disadvantage is eliminated by co-copetition through introducing cooperation among users. Again, this experiment indicates that co-opetition provides a good tradeoff between system efficiency and fairness.
Plot of the number of satisfied users (a) and minimum PSNRs (b) achieved by co-opetition and NBS_SP in the case of nine users. Id of sequences transmitted are 3, 6, 1, 3, 5, 1, 3, 2, 2, respectively. These sequences are randomly selected from Table 1. Bandwidth  is set to 400 KHz for all users, and the receiver noise power are set to 16, 7, 5, 1, 19, 12, 24, 12, 11, respectively, again by random generation.
is set to 400 KHz for all users, and the receiver noise power are set to 16, 7, 5, 1, 19, 12, 24, 12, 11, respectively, again by random generation.
4.3.3. Adaptive Co-Opetiton Strategy
In previous experiments, the threshold PSNR is fixed to be 35 dB. In order to consider more fairness in resource allocation, adaptive threshold can be employed. As an illustration, we present a simple method to set the threshold PSNR. More optimal and fair scheme for determining the threshold PSNR will be investigated in our future work. We employ PSNR = 32 dB, 34 dB and 36 dB to represent acceptable, good and very good quality, respectively. Denote resources required by the three levels with  , then threshold PSNR,
, then threshold PSNR,  , can be determined as follows
, can be determined as follows

where  is denote as total resources available.
is denote as total resources available.
Same system setup as that in previous experiment is used. We observe from Figure 4(a) that, co-opetition employing adaptive  still outperforms the NBS_SP. Moreover, adaptive
still outperforms the NBS_SP. Moreover, adaptive  is more concerned with fairness than that using fixed threshold. For example, in the case of low resource, for example,
is more concerned with fairness than that using fixed threshold. For example, in the case of low resource, for example,  ,
,  = 32 dB is selected. Consequently, an improvement of about 3 dB and 2 dB can be achieved for the minimum PSNRs compared to NBS_SP and co-opetition using fixed threshold (see Figure 3(b)), respectively. Note, these improvements are significantly important for users having low PSNRs. Although these improvements come from further decreasing the maximum achievable PSNR, it can provide fairer resource allocation. For instance, in Figure 4(a), it is very easy for all users to achieve similar quality level using co-opetition. Moreover,
= 32 dB is selected. Consequently, an improvement of about 3 dB and 2 dB can be achieved for the minimum PSNRs compared to NBS_SP and co-opetition using fixed threshold (see Figure 3(b)), respectively. Note, these improvements are significantly important for users having low PSNRs. Although these improvements come from further decreasing the maximum achievable PSNR, it can provide fairer resource allocation. For instance, in Figure 4(a), it is very easy for all users to achieve similar quality level using co-opetition. Moreover,  can also be set to a very high level, for example, 36 dB in the case of
can also be set to a very high level, for example, 36 dB in the case of  . An important advantage of this is that all users can be guaranteed high video quality, but cannot by fixed PSNR threshold and NBS_SP.
. An important advantage of this is that all users can be guaranteed high video quality, but cannot by fixed PSNR threshold and NBS_SP.
Plot of the number of satisfied users (a) and minimum PSNRs (b) achieved by NBS_SP and adaptive co-opetition. System setup is the same as that of Figure 3. 32 dB, 34 dB, and 36 dB refer to PSNR thresholds corresponding to different  .
.
4.3.4. Optimality Verification
Our co-opetition is also optimal. As stated in Section 1, optimal means sum utility maximization (SUM) under individual constraints. The optimality is verified by experimental analysis in the case of two users. Results of two examples of them are shown in Figure 5(a) and Figure 5(b). System setup is the same as that in Figure 2. The optimal average PSNRs are achieved by exhaustive search. Recall that the LOD method consists of inner and outer iterations. In each inner iteration, the power allocation is initiated corresponding to  for Figure 5(a) and
for Figure 5(a) and  for Figure 5(b). In the outer iteration, the values of
for Figure 5(b). In the outer iteration, the values of  and
and  are initialized randomly. Figures 5(a) and 5(b) show the results of outer iterations.
are initialized randomly. Figures 5(a) and 5(b) show the results of outer iterations.
From these two figures, we can see that our strategy is optimal under individual constraints. In Figure 2,  cannot satisfy two users simultaneously. Therefore the PSNR of user 1 is pegged at the threshold PSNR = 35 dB. The optimal average PSNR can be achieved after 14 iterations. In Figure 5(b),
cannot satisfy two users simultaneously. Therefore the PSNR of user 1 is pegged at the threshold PSNR = 35 dB. The optimal average PSNR can be achieved after 14 iterations. In Figure 5(b),  can make satisfying PSNR for both the two users. We observe that, user 2's PSNR has only little fluctuation, and converges to the threshold. At the optimal power allocation, both the two users' PSNRs are above or equal to the threshold. All these coincide with the results in Figure 2.
can make satisfying PSNR for both the two users. We observe that, user 2's PSNR has only little fluctuation, and converges to the threshold. At the optimal power allocation, both the two users' PSNRs are above or equal to the threshold. All these coincide with the results in Figure 2.
4.3.5. Summarization
To summarize, threshold PSNR plays importantly in adaptive/nonadaptive co-opetition strategies. It provides radio resource allocation (RRA) with more flexible tradeoff between system efficiency and fairness among users.
5. Conclusion
In this paper, we have presented an optimal and fair co-opetition strategy for multiuser multimedia RRA. Following contributions and conclusions have been made and drawn
-
(1)
We formulate the co-opetition strategy as sum utility maximization under constraints from both APP and PHY layers. APP layer constraints imply that co-opetition takes the QoS satisfaction degree into account in RRA.
-
(2)
We show that the co-opetition strategy can be implemented efficiently through applying the LOD method. Therefore the co-opetition strategy can easily apply to real time multimedia services.
-
(3)
We apply the co-opetition strategy to power allocation among multiple video users. Numerical results indicate that co-opetition can result in an improved number of satisfied users and significant improvement in minimum PSNRs as well. A simple method for adaptively determining threshold PSNR is also presented, such that fairer resource allocation can be achieved.
-
(4)
We conclude that co-opetition, that is, mixture of cooperation and competition, is more applicable to multiuser multimedia RRA than pure competition based strategy. Co-opetition strategy is not only optimal, but also fair.
Our future work is to design more feasible co-opetition strategy for different system setups, including multicarrier and multiple antennas systems. We also wish to extend our preliminary work to future heterogenous network, in which users not necessarily run in a collaborative way.
Algorithm 1: Feasible increasing direction method.
1: Set  and
and  , Precision
, Precision 
Repeat:
2: Determine  using(A.1)
using(A.1)
3: Determine  according (A.4) and(A.5)
according (A.4) and(A.5)
4: Determine  using(A.6)
using(A.6)
5: Compute  using(A.8)
using(A.8)
Until:  .
.
References
Park H, van der Schaar M: Bargaining strategies for networked multimedia resource management. IEEE Transactions on Signal Processing 2007, 55(7, part 1):3496-3511.
Shen C, van der Schaar M: Optimal resource allocation in wireless multiaccess video transmissions. Proceedings of the IEEE International Conference on Communications (ICC '07), June 2007, Glasgow, UK 4581-4586.
Su Y, van der Schaar M: Multiuser multimedia resource allocation over multicarrier wireless networks. IEEE Transactions on Signal Processing 2008, 56(5):2102-2116.
Choi L-U, Kellerer W, Steinbach E: On cross-layer design for streaming video delivery in multiuser wireless environments. EURASIP Journal on Wireless Communications and Networking 2006, 2006:-10.
Khan S, Peng Y, Steinbach E, Sgroi M, Kellerer W: Application-driven cross-layer optimization for video streaming over wireless networks. IEEE Communications Magazine 2006, 44(1):122-130.
Brehmer J, Utschick W: A decomposition of the downlink utility maximization problem. Proceedings of the 41st Annual Conference on Information Sciences and Systems (CISS '07), March 2007, Baltimore, Md, USA 437-441.
Brehmer J, Utschick W: Utility maximization strategies in the multi-user MIMO downlink. Proceedings of the 1st International Workshop on Cross Layer Design (IWCLD '07), September 2007, Jinan, China 86-90.
Böhnke R, Kammeyer K-D: Weighted sum rate maximization for the MIMO-downlink using a projected conjugate gradient algorithm. Proceedings of the 1st International Workshop on Cross Layer Design (IWCLD '07), September 2007, Jinan, China 82-85.
Zhang L, Deering S, Estrin D, Shenker S, Zappala D: RSVP: a new resource reservation protocal. IEEE Network 1993, 7(5):8-18. 10.1109/65.238150
van der Schaar M, Shankar N S: Cross-layer wireless multimedia transmission: challenges, principles, and new paradigms. IEEE Wireless Communications 2005, 12(4):50-58. 10.1109/MWC.2005.1497858
Kelly F: Charging and rate control for elastic traffic. European Transactions on Telecommunications 1997, 8(1):33-37. 10.1002/ett.4460080106
Kelly FP, Maulloo AK, Tan D: Rate control for communication networks: shadow prices, proportional fairness and stability. Journal of the Operational Research Society 1998, 49(3):237-252.
Brandenburger AM, Nalebuff BJ: Co-Opetition: A Revolution Mindset That Combines Competition and Cooperation: The Game Theory Strategy That's Changing the Game of Business. Currency Doubleday, New York, NY, USA; 1997.
Larcher A, Sun H, van der Shaar M, Ding Z, et al.: Decentralized transmission strategy for delay-sensitive applications over spectrum agile network. Proceedings of International Packet Video Workshop, December 2004, Irvine, Calif, USA
Guan Z, Yuan D, Zhang H: Novel coopetition paradigm based on bargaining theory or collaborative multimedia resource management. Proceedings of the 9th Annual IEEE International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC '08), September 2008, Cannes, France 1-5.
Stuhlmüller K, Fürber N, Link M, Girod B: Analysis of video transmission over lossy channels. IEEE Journal on Selected Areas in Communications 2000, 18(6):1012-1032. 10.1109/49.848253
Chiang M, Low SH, Calderbank AR, Doyle JC: Layering as optimization decomposition: a mathermatical theory of netowrk architectures. Proceedings of the IEEE 2007, 95(1):255-312 .
Shi S, Schubert M, Boche H: Weighted sum-rate optimization for multiuser MIMO systems. Proceedings of the 41st Annual Conference on Information Sciences and Systems (CISS '07), March 2007, Baltimore, Md, USA 425-430.
Goffin J-L, Vial J-P: Convex nondifferentiable optimization: a survey focussed on the analytic center cutting plane method. Logilab, University of Geneva, Geneva, Switzerland; 1999.
Nossek JA: CLARA: cross layer assisted resource allocation—theory and applications. Proceedings of the 1st IEEE International Workshop on Cross Layer Design (IWCLD '07), September 2007, Jinan, China
Yates RD: A framework for uplink power control in cellular radio systems. IEEE Journal on Selected Areas in Communications 1995, 13(7):1341-1347. 10.1109/49.414651
Andreopoulos Y, Munteanu A, Barbarien J, van der Schaar M, Cornelis J, Schelkens P: In-band motion compensated temporal filtering. Signal Processing: Image Communication 2004, 19(7):653-673. 10.1016/j.image.2004.05.007
Acknowledgment
This work was supported by NSFC (No. 60672036, No. 60832008) and Key Project of Provincial Scientific Foundation of Shandong (No. Z2008G01).
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
Feasible Increasing Direction Method
Feasible Increasing direction method iteratively searches the optimum variable,  , by in each iteration selecting a feasible increasing direction and update step size. Denote
, by in each iteration selecting a feasible increasing direction and update step size. Denote  as power allocation in the
as power allocation in the  iteration, then
iteration, then  satisfies the constraints in (26). Denote
satisfies the constraints in (26). Denote  ,
,  as the direction and step size employed in the
as the direction and step size employed in the  iteration, then
iteration, then  and
and  can be determined as follows.
can be determined as follows.
Denote  as the item to be maximized in (26), then the gradient of
as the item to be maximized in (26), then the gradient of  at
at  , denoted with
, denoted with  , writes
, writes

where

If  is strictly feasible, that is,
is strictly feasible, that is,

then set

Otherwise, denote  as set of indexes of active constraints, for example, if
as set of indexes of active constraints, for example, if  , then
, then  .
.  refers to
refers to  . Then
. Then  can be obtained by solving following maximization through linear programming,
can be obtained by solving following maximization through linear programming,

If  , then
, then  is optimal. Otherwise, compute
is optimal. Otherwise, compute  by solving following one-dimension maximization,
by solving following one-dimension maximization,

where

Given  and
and  ,
,  can be set as
can be set as

Then the feasible increasing direction method can be summarized in Algorithm 1.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Guan, Z., Yuan, D. & Zhang, H. Optimal and Fair Resource Allocation for Multiuser Wireless Multimedia Transmissions. J Wireless Com Network 2009, 801613 (2009). https://doi.org/10.1155/2009/801613
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/801613
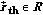 or Not
or Not

 , 30 Hz), user 2: Mobile (CIF,
, 30 Hz), user 2: Mobile (CIF,  30 Hz).
30 Hz).


 , 30 Hz), user 2: Mobile (CIF,
, 30 Hz), user 2: Mobile (CIF,  , 30 Hz). (a):
, 30 Hz). (a):  and (b):
and (b):  .
.