- Research Article
- Open access
- Published:
Ergodic Capacity for the SIMO Nakagami-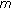 Channel
Channel
EURASIP Journal on Wireless Communications and Networking volume 2009, Article number: 802067 (2009)
Abstract
This paper presents closed-form expressions for the ergodic channel capacity of SIMO (single-input and multiple output) wireless systems operating in a Nakagami- fading channel. As the performance of SIMO channel is closely related to the diversity combining techniques, we present closed-form expressions for the capacity of maximal ratio combining (MRC), equal gain combining (EGC), selection combining (SC), and switch and stay (SSC) diversity systems operating in Nakagami-
fading channel. As the performance of SIMO channel is closely related to the diversity combining techniques, we present closed-form expressions for the capacity of maximal ratio combining (MRC), equal gain combining (EGC), selection combining (SC), and switch and stay (SSC) diversity systems operating in Nakagami- fading channels. Also, the ergodic capacity of a SIMO system in a Nakagami-
fading channels. Also, the ergodic capacity of a SIMO system in a Nakagami- fading channel without any diversity technique is derived. The latter scenario is further investigated for a large amount of receive antennas. Finally, numerical results are presented for illustration.
fading channel without any diversity technique is derived. The latter scenario is further investigated for a large amount of receive antennas. Finally, numerical results are presented for illustration.
1. Introduction
In recent years, the use of multiantenna systems provides large spectral efficiency for wireless communications in the presence of multipath fading environments. Multiple antennas can be used at the transmitter (MISO), the receiver (SIMO), or at both of them (MIMO). A SIMO system can be viewed as an antenna diversity scheme (diversity in space). Also, diversity combining is known to be a powerful technique to improve system performance in the presence of fading [1].
Several papers have been published regarding the capacity of SIMO systems operating in Nakagami environments. In [2], the channel capacity of a SIMO system in a Nakagami-m fading channel is presented with the assumption that all links between transmit and receive antennas are independent and identically distributed (i.i.d.). In [3], capacity with MRC and optimal power and rate adaptation is presented while in [4] Shannon capacity with MRC is derived. In both of them, the assumption that all links are correlated and not identically distributed Nakagami holds. In [5], capacity of Nakagami-m multipath fading channels with MRC was studied for different power and rate adaptation policies. Also, simple capacity formulas for correlated SIMO Nakagami-m channels were derived in [6]. In [7], an analytical expression for the capacity of SIMO systems over nonidentically independent Nakagami-m channels was derived. Significant work has been done in [8], where ergodic capacities of MRC, EGC, SC, and SSC of dual branch diversity systems are presented in closed-form expressions. The capacity expressions were obtained by assuming correlated and identically distributed Nakagami-m links.
In this paper, we examine the ergodic capacity of a SIMO system operating in independent Nakagami-m channels. Specifically we derive closed-form expressions for the ergodic capacity of dual EGC, SC, and SSC systems. For the EGC and SSC cases, we extend the work in [8] by allowing the parameter m of the Nakagami-m distribution to take noninteger values. Moreover for the SSC case, a compact and quite flexible formula of the ergodic capacity for integer values of m is presented. For the SC case, we present a new expression for the ergodic capacity with the assumption that the Nakagami branches are not identical. Finally, we present for the first time in international literature the ergodic capacity of a SIMO system without using any diversity combining technique over independent nonidentical Nakagami-m branches. In addition, it is shown that when the number of receive antennas is large, the ergodic capacity of such a system can be very well approximated by the ergodic capacity of a Rayleigh channel.
The remaining of this paper is organized as follows. Section 2 introduces a SIMO system. Section 3 examines the ergodic capacity for each diversity scheme and for the case where none of diversity technique is applied. Section 4 presents some results, and Section 5 draws the conclusion.
2. System Description
Consider a SIMO system with  receive antennas operating in independent Nakagami-m channels. The total power of the complex transmitted signal at a symbol period is constrained to be
receive antennas operating in independent Nakagami-m channels. The total power of the complex transmitted signal at a symbol period is constrained to be  . The received signal vector
. The received signal vector  at a random symbol period, assuming that the channel is constant over a symbol period, is given in a baseband representation as
at a random symbol period, assuming that the channel is constant over a symbol period, is given in a baseband representation as

where  is the
is the  complex channel-gain vector (
complex channel-gain vector ( means matrix transposition),
means matrix transposition),  is the
is the  complex antenna-gain vector, and n is the
complex antenna-gain vector, and n is the  zero-mean complex additive white Gaussian (AWGN) vector with i.i.d. entries and variance
zero-mean complex additive white Gaussian (AWGN) vector with i.i.d. entries and variance  . The received signal can be written as
. The received signal can be written as

where  ,
,  and
and  . Thus, the received signal-to-noise ratio (SNR)
. Thus, the received signal-to-noise ratio (SNR)  over a symbol period is
over a symbol period is

Assuming that the fading process is ergodic, the ergodic channel capacity is

where  is the bandwidth of the channel,
is the bandwidth of the channel,  denotes the ensemble average over
denotes the ensemble average over  , and
, and  is the probability density function (PDF) of the SNR
is the probability density function (PDF) of the SNR  .
.
3. Ergodic Channel Capacity
For all the cases listed below, we will assume that all links between transmitter and receivers  are Nakagami-m distributed. From [9], their PDF is
are Nakagami-m distributed. From [9], their PDF is

where  is the Gamma function [10, eqution (8.310.1)],
is the Gamma function [10, eqution (8.310.1)],  , and
, and  .
.
3.1. Ergodic Channel Capacity of Nakagami-m Fading Channel with MRC
Taking into account the above system description and assuming that the receiver has full channel state information (CSI), we choose the phases  of
of  , appeared in (2), as
, appeared in (2), as  . Also we choose
. Also we choose  . This means that all the signals at the receiver can be added cophasely and weighted according to the channel gain. Thus, (3) becomes
. This means that all the signals at the receiver can be added cophasely and weighted according to the channel gain. Thus, (3) becomes

This SNR arises from the MRC diversity technique [1, equation (9.1)]. Substituting the PDF of (6) in (4) gives the ergodic capacity of the Nakagami-m fading channel using MRC. Closed-form expressions have been presented in [3, equation (20)], [4, equation (16)] for the general case where links are correlated and not identically Nakagami-m distributed. If the links follow i.i.d. Nakagami-m variables, the referred equations reduce to [2, equation (36)]. When the parameter  of i.i.d Nakagami-m branches takes integer values, the ergodic capacity is given by [5, equation (26)]. A good approximation for the ergodic capacity, where links are independent and not identically distributed, was given in [7, equation (16)]. Also a useful expression for the PDF of
of i.i.d Nakagami-m branches takes integer values, the ergodic capacity is given by [5, equation (26)]. A good approximation for the ergodic capacity, where links are independent and not identically distributed, was given in [7, equation (16)]. Also a useful expression for the PDF of  for correlated and not identically distributed links can be found in [11, equation (18)].
for correlated and not identically distributed links can be found in [11, equation (18)].
3.2. Ergodic Channel Capacity of Nakagami-m Fading Channel with Coherent EGC
Taking into account the system description discussed in Section 2 and assuming that the receiver has full CSI, we choose phases  and modulus
and modulus  , appeared in (2), as
, appeared in (2), as  ,
,  for all
for all  . Thus (3) becomes
. Thus (3) becomes

This SNR arises using the coherent EGC diversity technique [1, equation (9.188)]. Substituting the PDF of (7) in (4) gives the ergodic capacity of the Nakagami-m fading channel using coherent EGC diversity technique. Finding analytically the PDF of (7) and consequently the channel capacity seems to be a very difficult problem. In [12], the sum of i.i.d Nakagami-m variables was studied.
The PDF of the sum of two i.i.d. Nakagami-m variables is given by [12, equation (4)]. From [13, page 130], we obtain the PDF transformation  for two random variables
for two random variables  ,
,  related as
related as  . Using that PDF transformation in (7) (here
. Using that PDF transformation in (7) (here  ) with the help of [12, equation (4)], we calculate the PDF of the SNR
) with the help of [12, equation (4)], we calculate the PDF of the SNR  . Thus, the PDF of the SNR of a dual branch EGC system over i.i.d. Nakagami-m fading channels can be written as
. Thus, the PDF of the SNR of a dual branch EGC system over i.i.d. Nakagami-m fading channels can be written as

where  is the average received SNR, and
is the average received SNR, and  denotes the confluent hypergeometric series, as in [10, equation (9.21.1)]. Closed-form expressions for the capacity of a dual branch equal gain combiner with correlated identically distributed Nakagami-m branches have been presented in [8, equation (8)]. In the following paragraph, we extend that ergodic capacity expression for i.i.d. Nakagami-m branches where the Nakagami parameter m is not necessarily an integer.
denotes the confluent hypergeometric series, as in [10, equation (9.21.1)]. Closed-form expressions for the capacity of a dual branch equal gain combiner with correlated identically distributed Nakagami-m branches have been presented in [8, equation (8)]. In the following paragraph, we extend that ergodic capacity expression for i.i.d. Nakagami-m branches where the Nakagami parameter m is not necessarily an integer.
The ergodic capacity of a dual-branch EGC system over i.i.d. Nakagami-m fading channels ( and
and  ) is given by (see Appendix A)
) is given by (see Appendix A)

where  is a generalized hypergeometric series, [10, equation (9.14.1)], and
is a generalized hypergeometric series, [10, equation (9.14.1)], and  denotes the digamma function, [10, equation (8.36.1)]. For integer values of the parameter m, (9) is reduced to (see Appendix A)
denotes the digamma function, [10, equation (8.36.1)]. For integer values of the parameter m, (9) is reduced to (see Appendix A)

where  is the upper incomplete gamma function, as in [10, equation (8.350.2)]. Taking into account [12, equations (8), (9) and (10)] and following the same procedure as in Appendix A (derivation of (9), (10)), we can derive the ergodic capacity of an equal gain combiner for three, four, and M i.i.d Nakagami-m branches. However it is impractical for the purpose of this paper to present all those tedious mathematical formulations. Nevertheless the impact of diversity on the capacity can be clearly depicted by using two branch schemes.
is the upper incomplete gamma function, as in [10, equation (8.350.2)]. Taking into account [12, equations (8), (9) and (10)] and following the same procedure as in Appendix A (derivation of (9), (10)), we can derive the ergodic capacity of an equal gain combiner for three, four, and M i.i.d Nakagami-m branches. However it is impractical for the purpose of this paper to present all those tedious mathematical formulations. Nevertheless the impact of diversity on the capacity can be clearly depicted by using two branch schemes.
3.3. Ergodic Channel Capacity of Nakagami-m Fading Channel with SC
We assume a combiner that chooses the branch with the highest SNR (or equivalently with the strongest signal assuming equal noise power among the branches). Thus, we choose the antenna gains appearing in (2) as  if
if  for all
for all  and 0 otherwise. Thus, (3) becomes
and 0 otherwise. Thus, (3) becomes

This is the widely known SC diversity technique as in [1, Chapter (9.8)]. The PDF of the SNR of two correlated identically distributed Nakagami-m channels is given in [1, equation (9.235)], and the resulting ergodic capacity for m integer is presented in [8, equation (19)].
From [14, equation (14)] and using the PDF transformation  for two random variables
for two random variables  ,
,  related as
related as  (here
(here  ), we can calculate the PDF of the SNR of two independent and not identically distributed Nakagami-m branches as follows:
), we can calculate the PDF of the SNR of two independent and not identically distributed Nakagami-m branches as follows:

where  ,
,  , and
, and  is the lower incomplete gamma function, [10, equation (8.350.1)].
is the lower incomplete gamma function, [10, equation (8.350.1)].
In order to find the ergodic capacity of a dual SC system, we have to solve the integral resulting by substituting (12) in (4). Unfortunately, this integral cannot be solved analytically when the Nakagami parameters  ,
,  take noninteger values. But, assuming that
take noninteger values. But, assuming that  ,
,  take integer values, the ergodic capacity of a dual-branch SC system over independent nonidentically distributed Nakagami-m fading channels is given by (see Appendix A)
take integer values, the ergodic capacity of a dual-branch SC system over independent nonidentically distributed Nakagami-m fading channels is given by (see Appendix A)

If the branches are identically distributed ( and
and  ), (13) reduces to
), (13) reduces to

3.4. Ergodic Channel Capacity of Nakagami-m Fading Channel with SSC
We consider a diversity system, for which, when the SNR of the currently connected branch falls below a predetermined threshold, the receiver switches to and stays with another branch, regardless of whether the SNR of that branch is above or below the predetermined threshold. This is the widely known SSC diversity technique as in [1, page 419]. In particular, we choose the antenna gains appearing in (2) as  if the SNR at the
if the SNR at the  branch is above a predetermined threshold
branch is above a predetermined threshold  and 0 otherwise. If the SNR at the
and 0 otherwise. If the SNR at the  branch is below the predetermined threshold
branch is below the predetermined threshold  , then we choose randomly an
, then we choose randomly an  where
where  ,
,  .
.
The PDF of the resulting SNR of a dual-branch SSC system over two i.i.d. Nakagami-m channels is given in [1, equation (9.276)]

where  .
.
The ergodic capacity of a dual-branch SSC system over i.i.d. Nakagami-m fading channels is given by (see Appendix A)

where  is Meijer's-
is Meijer's- function as defined in [10, page 1032]. For integer values of the parameter m, (16) is reduced to (see Appendix A)
function as defined in [10, page 1032]. For integer values of the parameter m, (16) is reduced to (see Appendix A)

3.5. Ergodic Channel Capacity of Nakagami-m Fading Channel with No Diversity Combining Technique
We suppose that the receiver has no CSI and no complexity (cannot make any signal processing). Thus, the system operates without any diversity technique used. Thus,  for all i and the random variable
for all i and the random variable  (appearing in (3)) is a sum of Nakagami-m random phase vectors. Consequently, (3) becomes
(appearing in (3)) is a sum of Nakagami-m random phase vectors. Consequently, (3) becomes

In order to find the PDF of (18), the PDF of the modulus of the sum of Nakagami-m random phase vectors is necessary. In [15], that PDF was derived for integer values of the Nakagami parameter m. Using that result, we write the modulus of the sum of Nakagami-m random phase vectors as a sum of weighted Nakagami-m PDFs (see Appendix B).
Thus, using in (18) the PDF transformation  for two random variables
for two random variables  ,
,  related as
related as  (here
(here  ), we can derive with the help of (B.6) the PDF of the SNR as a sum of weighted gamma PDFs, that is,
), we can derive with the help of (B.6) the PDF of the SNR as a sum of weighted gamma PDFs, that is,

where  is the PDF of a gamma-distributed random variable as in [13, page 87]. The ergodic channel capacity of a SIMO system without any diversity technique, over independent nonidentically distributed Nakagami-m branches, is given by (see Appendix A)
is the PDF of a gamma-distributed random variable as in [13, page 87]. The ergodic channel capacity of a SIMO system without any diversity technique, over independent nonidentically distributed Nakagami-m branches, is given by (see Appendix A)

Herein we will examine the case that the number of receive antennas is large. In that case the random variable  (appearing in (3)) tends to be a complex Gaussian random variable, according to the Central Limit Theorem [13, page 278], that is,
(appearing in (3)) tends to be a complex Gaussian random variable, according to the Central Limit Theorem [13, page 278], that is,

where  and
and  are the quadrature components of a Nakagami-m vector which follow the PDF according to [16, equation (6)]. That PDF has zero mean, and its variance equals to
are the quadrature components of a Nakagami-m vector which follow the PDF according to [16, equation (6)]. That PDF has zero mean, and its variance equals to  . According to the Central Limit Theorem,
. According to the Central Limit Theorem,  and
and  are zero mean Gaussian random variables with variance
are zero mean Gaussian random variables with variance  . Thus,
. Thus,  can be approximated by a Rayleigh distribution, as defined in [13, page 90], with its parameter
can be approximated by a Rayleigh distribution, as defined in [13, page 90], with its parameter  . Taking into account the random variables transformation
. Taking into account the random variables transformation  in (18), the resulting SNR follows an exponential distribution [13, page 85], that is,
in (18), the resulting SNR follows an exponential distribution [13, page 85], that is,

where  . Substituting (22) in (4) and using Theorem 3, we obtain
. Substituting (22) in (4) and using Theorem 3, we obtain

Thus, when L is large (asymptotic analysis), the ergodic capacity of the SIMO system can be approximated by the simple formula of (23), which is in fact the capacity of a Rayleigh channel [2, equations (21), (22)].
4. Results
Figure 1 shows the capacity per unit bandwidth for a dual branch MRC system over i.i.d. Nakagami-m fading channels (see [2, equation (36)]) for the case  ,
,  . Also, channel capacity without any diversity technique (see (20)) and SISO channel capacity (see [2, equation (21)]) are presented for comparison. It is clear that MRC improves the capacity of a SIMO Nakagami-m fading channel. It is also remarkable that channel capacity with none diversity technique is much greater than SISO capacity.
. Also, channel capacity without any diversity technique (see (20)) and SISO channel capacity (see [2, equation (21)]) are presented for comparison. It is clear that MRC improves the capacity of a SIMO Nakagami-m fading channel. It is also remarkable that channel capacity with none diversity technique is much greater than SISO capacity.
Figure 2 shows the capacity per unit bandwidth for a dual branch EGC system over i.i.d. Nakagami-m fading channels (see (10)) for the same parameter set as in Figure 1. Again, channel capacity without any diversity technique and SISO channel capacity are presented for comparison. It is obvious that EGC improves the capacity of a SIMO Nakagami-m fading channel.
Figure 3 shows the capacity per unit bandwidth for a dual branch SC system over independent Nakagami-m fading channels (see (13)) for the same parameter set as in Figures 1 and 2. Channel capacity without any diversity technique and SISO channel capacity are presented for comparison. We can see that SC performs slightly better than the case of none diversity technique.
Figure 4 shows the capacity per unit bandwidth for a dual branch SSC system over independent Nakagami-m fading channels (see (17)), for the same parameter set as in Figures 1, 2, and 3. The optimum adaptive switching threshold was determined as in [8, equation (31)] and was found  . Channel capacity without any diversity technique and SISO channel capacity are presented for comparison. It is clear that SSC improves the capacity of a SIMO Nakagami-m fading channel, but the case of none diversity technique performs slightly better than SSC. This is because SSC does not exploit both branches simultaneously. Essentially, SSC cannot have diversity gain. It simply uses one branch which has a smaller possibility to fall below a predetermined threshold (as it hops to the other).
. Channel capacity without any diversity technique and SISO channel capacity are presented for comparison. It is clear that SSC improves the capacity of a SIMO Nakagami-m fading channel, but the case of none diversity technique performs slightly better than SSC. This is because SSC does not exploit both branches simultaneously. Essentially, SSC cannot have diversity gain. It simply uses one branch which has a smaller possibility to fall below a predetermined threshold (as it hops to the other).
Figure 5 shows the capacity per unit bandwidth for a five and a dual branch system where none diversity technique is used. Each branch is assumed to be independent and is characterized as Nakagami-m fading channel with parameters  and
and  . Figure 5 shows that (23) gives a very good approximation of (20) for the channel capacity of a SIMO Nakagami-m fading channel even with
. Figure 5 shows that (23) gives a very good approximation of (20) for the channel capacity of a SIMO Nakagami-m fading channel even with  receive antennas.
receive antennas.
5. Conclusions
We have investigated the ergodic capacity of a SIMO system operating in a Nakagami-m fading channel. We have derived a closed-form expression for the ergodic capacity of a dual branch EGC system over i.i.d Nakagami-m branches, where the Nakagami parameter m can be any real number with  . Also, a closed-form formula is presented for m integer. A simple closed-form expression for the ergodic capacity of a dual SC diversity system operating in two independent but not identically distributed Nakagami-m branches has been derived. For that case, we have assumed that the Nakagami parameters
. Also, a closed-form formula is presented for m integer. A simple closed-form expression for the ergodic capacity of a dual SC diversity system operating in two independent but not identically distributed Nakagami-m branches has been derived. For that case, we have assumed that the Nakagami parameters  take integer values. A closed-form expression for the ergodic capacity of a dual SSC diversity system operating in two i.i.d. Nakagami-m branches has been derived for the case where the Nakagami parameter m can be any real number with
take integer values. A closed-form expression for the ergodic capacity of a dual SSC diversity system operating in two i.i.d. Nakagami-m branches has been derived for the case where the Nakagami parameter m can be any real number with  . Also, a simple closed-form formula is presented for m integer. It was observed that all diversity combining techniques that are considered in this paper provide improvement to the capacity of Nakagami-m fading channels. Finally, the ergodic capacity of a SIMO system without any diversity technique has been presented in a closed-form expression. For that case, we have assumed
. Also, a simple closed-form formula is presented for m integer. It was observed that all diversity combining techniques that are considered in this paper provide improvement to the capacity of Nakagami-m fading channels. Finally, the ergodic capacity of a SIMO system without any diversity technique has been presented in a closed-form expression. For that case, we have assumed  independent but not identically distributed Nakagami-m branches, where the parameters
independent but not identically distributed Nakagami-m branches, where the parameters  take integer values. It was shown that when the number of receive antennas is large (
take integer values. It was shown that when the number of receive antennas is large ( ), the ergodic capacity of a SIMO system without any diversity technique can be very well approximated by the capacity of a Rayleigh fading channel.
), the ergodic capacity of a SIMO system without any diversity technique can be very well approximated by the capacity of a Rayleigh fading channel.
References
Simon MK, Alouini M-S: Digital Communications over Fading Channels. John Wiley & Sons, New York, NY, USA; 2005.
Zheng F, Kaiser T: On the channel capacity of multiantenna systems with nakagami fading. EURASIP Journal on Applied Signal Processing 2006, 2006:-11.
Alouini M-S, Abdi A, Kaveh M: Sum of gamma variates and performance of wireless communication systems over Nakagami-fading channels. IEEE Transactions on Vehicular Technology 2001, 50(6):1471-1480. 10.1109/25.966578
Karagiannidis GK, Sagias NC, Tsiftsis TA:Closed-form statistics for the sum of squared Nakagami-
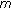 variates and its applications. IEEE Transactions on Communications 2006, 54(8):1353-1359.
variates and its applications. IEEE Transactions on Communications 2006, 54(8):1353-1359.Alouini M-S, Goldsmith AJ: Capacity of Nakagami multipath fading channels. Proceedings of the 47th IEEE Vehicular Technology Conference (VTC '97), May 1997, Phoenix, Ariz, USA 1: 358-362.
Zhang QT, Liu DP: Simple capacity formulas for correlated SIMO Nakagami channels. Proceedings of the 57th IEEE Vehicular Technology Conference (VTC '03), April 2003, Jeju, Korea 1: 554-556.
Magableh AM, Matalgah MM:Capacity of SIMO systems over non-identically independent Nakagami-
 channels. IEEE Sarnoff Symposium (SARNOFF '07), April-May 2007, Princeton, NJ, USA 1-5.
channels. IEEE Sarnoff Symposium (SARNOFF '07), April-May 2007, Princeton, NJ, USA 1-5.Khatalin S, Fonseka JP:Capacity of correlated Nakagami-
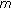 fading channels with diversity combining techniques. IEEE Transactions on Vehicular Technology 2006, 55(1):142-150. 10.1109/TVT.2005.861206
fading channels with diversity combining techniques. IEEE Transactions on Vehicular Technology 2006, 55(1):142-150. 10.1109/TVT.2005.861206Nakagami M:The
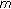 -distribution—a general formula on intensity distribution of rapid fading. Statistical Methods in Radio Wave Propagation 1962, 40: 757-768.
-distribution—a general formula on intensity distribution of rapid fading. Statistical Methods in Radio Wave Propagation 1962, 40: 757-768.Gradshteyn IS, Ryzhik IM: Table of Integrals, Series and Products. 7th edition. Academic Press, New York, NY, USA; 2007.
Win MZ, Winters JH: On maximal ratio combining in correlated Nakagami channels withunequal fading parameters and SNRs among branches: an analytical framework. Proceedings of IEEE Wireless Communications and Networking Conference (WCNC '99), September 1999, New Orleans, La, USA 1058-1064.
Dharmawansa P, Rajatheva N, Ahmed K:On the distribution of the sum of Nakagami-
 random variables. IEEE Transactions on Communications 2007, 55(7):1407-1416.
random variables. IEEE Transactions on Communications 2007, 55(7):1407-1416.Papoulis A: Probability, Random Variables and Stohastic Processes. 4th edition. McGraw-Hill, New York, NY, USA;
Fedele G, Izzo L, Tanda M: Dual diversity reception of M-ary DPSK signals over Nakagami fading channels. Proceedings of the 6th IEEE International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC '95), September 1995, Toronto, Canada 3: 1195-1201.
Karagiannidis GK:A closed-form solution for the distribution of the sum of Nakagami-
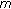 random phase vectors. IEEE Communications Letters 2006, 10(12):828-830.
random phase vectors. IEEE Communications Letters 2006, 10(12):828-830.Fraidenraich G, Leveque O, Cioffi JM:On the MIMO channel capacity for the Nakagami-
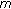 Channel. Proceedings of IEEE Global Telecommunication Conference (GLOCOM '07), November 2007, Washington, DC, USA 3612-3616.
Channel. Proceedings of IEEE Global Telecommunication Conference (GLOCOM '07), November 2007, Washington, DC, USA 3612-3616.Prudnikov AP, Brychkov YA, Marichev OI: Integrals and Series. Volume 1. Gordon and Breach Science, Amsterdam, The Netherlands; 1986.
Abramovitz M, Stegun IA: Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. 9th edition. Dover, New York, NY, USA; 1972.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendices
A
Theorem 1.
One has

for  ,
,  and
and  .
.
Theorem 2.
One has

for  ,
,  and
and  .
.
Theorem 3.
One has

Proof of Theorem 1.
We define  . With a change of variables we have
. With a change of variables we have

We write the term  to its Taylor series expansion as
to its Taylor series expansion as  , and (A.4) becomes
, and (A.4) becomes

The integral of (A.5) is solved by Mathematica Toolbox as

Substituting (A.6) in (A.5), we obtain (A.1).
Proof of Theorem 2.
Using partial integration and [10, equation (8.356.4)], the integral  can be written as
can be written as

If  is an integer (
is an integer ( ), using [10, equation (8.352.7)], (A.7) becomes
), using [10, equation (8.352.7)], (A.7) becomes

The integral of (A.8) can be written with the help of [10, equation (1.111)] as

and by the definition of the upper incomplete gamma function [10, equation (8.350.2)], (A.9) becomes

Replacing (A.10) in (A.8), we have that

Reversing the double sum of (A.11) and using [10, equation (8.352.4)], we obtain (A.2).
Proof of Theorem 3.
We set  in (A.8) and we have
in (A.8) and we have

Solving the integral in the second part of (A.12) with the help of [10, equation (8.353.3)], we obtain (A.3).
Derivation of (9) and (10)
Substituting (8) in (4) and replacing the confluent hypergeometric function of (8) with its infinite series representation [10, equation (9.210.1)], we obtain after some manipulations

The integral appearing in (A.13) was solved in [17, equation (2.6.23.4)]. Using this result, after some manipulations, (9) is derived. If  in (A.13) is an integer, we evaluate the integral of (A.13) by using Theorem 3 and after some manipulations, (10) arises.
in (A.13) is an integer, we evaluate the integral of (A.13) by using Theorem 3 and after some manipulations, (10) arises.
Derivation of (13)
Assuming that  and
and  take integer values, we are able to replace the lower incomplete gamma function
take integer values, we are able to replace the lower incomplete gamma function  , appearing in (12), with its finite sum representation [10, equation (8.352.1)]. Substituting (12) in (4) with the help of [10, equation (8.352.1)], we obtain after some manipulations
, appearing in (12), with its finite sum representation [10, equation (8.352.1)]. Substituting (12) in (4) with the help of [10, equation (8.352.1)], we obtain after some manipulations

Since  and
and  in (A.14) are integers, we use Theorem 3 of the current Appendix to solve the integral
in (A.14) are integers, we use Theorem 3 of the current Appendix to solve the integral  and finally, we obtain (13).
and finally, we obtain (13).
Derivation of (16) and (17)
Substituting (15) in (4), with the help of (A.4), we obtain

Using Theorem 1 to evaluate the integral  and considering that the integral
and considering that the integral  was solved in [17, equation (2.6.23.4)], from (A.15) we obtain (16).
was solved in [17, equation (2.6.23.4)], from (A.15) we obtain (16).
For integer values of the Nakagami parameter m in (A.15), we are able to use Theorems 2 and 3 to solve the integrals  and
and  , respectively. After some manipulations, from (A.15) we obtain (17).
, respectively. After some manipulations, from (A.15) we obtain (17).
Derivation of (20)
Replacing (19) in (4), we obtain after some manipulations

Using Theorem 3, we can solve the integral of (A.16) and finally we obtain (20).
B
If  is a sum of Nakagami-m random phase vectors, the PDF of its modulus has been derived in [15, equation (8)] as
is a sum of Nakagami-m random phase vectors, the PDF of its modulus has been derived in [15, equation (8)] as

where  and
and  is an operator defined as [15, equation (4)]
is an operator defined as [15, equation (4)]

with  ,
,  .
.  is the Pochhammer symbol, [18, equation (6.1.22)]. Reversing the multiple sum in (B.2), we can rewrite
is the Pochhammer symbol, [18, equation (6.1.22)]. Reversing the multiple sum in (B.2), we can rewrite  as
as

with the constraint that  and
and  . Thus,
. Thus,  is defined as
is defined as

Using the property  for the Pochhammer symbol, (B.4) can be written as
for the Pochhammer symbol, (B.4) can be written as

Substituting (B.3) in (B.1) with the help of (B.5) we obtain

which is, in fact, a sum of weighted Nakagami-m PDFs, as the author of [15] has noted.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Vagenas, E.D., Karadimas, P. & Kotsopoulos, S.A. Ergodic Capacity for the SIMO Nakagami-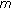 Channel.
J Wireless Com Network 2009, 802067 (2009). https://doi.org/10.1155/2009/802067
Channel.
J Wireless Com Network 2009, 802067 (2009). https://doi.org/10.1155/2009/802067
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/802067





 variates and its applications. IEEE Transactions on Communications 2006, 54(8):1353-1359.
variates and its applications. IEEE Transactions on Communications 2006, 54(8):1353-1359. channels. IEEE Sarnoff Symposium (SARNOFF '07), April-May 2007, Princeton, NJ, USA 1-5.
channels. IEEE Sarnoff Symposium (SARNOFF '07), April-May 2007, Princeton, NJ, USA 1-5.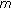 fading channels with diversity combining techniques. IEEE Transactions on Vehicular Technology 2006, 55(1):142-150. 10.1109/TVT.2005.861206
fading channels with diversity combining techniques. IEEE Transactions on Vehicular Technology 2006, 55(1):142-150. 10.1109/TVT.2005.861206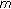 -distribution—a general formula on intensity distribution of rapid fading. Statistical Methods in Radio Wave Propagation 1962, 40: 757-768.
-distribution—a general formula on intensity distribution of rapid fading. Statistical Methods in Radio Wave Propagation 1962, 40: 757-768. random variables. IEEE Transactions on Communications 2007, 55(7):1407-1416.
random variables. IEEE Transactions on Communications 2007, 55(7):1407-1416.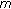 random phase vectors. IEEE Communications Letters 2006, 10(12):828-830.
random phase vectors. IEEE Communications Letters 2006, 10(12):828-830.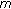 Channel. Proceedings of IEEE Global Telecommunication Conference (GLOCOM '07), November 2007, Washington, DC, USA 3612-3616.
Channel. Proceedings of IEEE Global Telecommunication Conference (GLOCOM '07), November 2007, Washington, DC, USA 3612-3616.