- Research Article
- Open access
- Published:
A Practical Scheme for Frequency Offset Estimation in MIMO-OFDM Systems
EURASIP Journal on Wireless Communications and Networking volume 2009, Article number: 821819 (2009)
Abstract
This paper deals with training-assisted carrier frequency offset (CFO) estimation in multiple-input multiple-output (MIMO) orthogonal frequency-division multiplexing (OFDM) systems. The exact maximum likelihood (ML) solution to this problem is computationally demanding as it involves a line search over the CFO uncertainty range. To reduce the system complexity, we divide the CFO into an integer part plus a fractional part and select the pilot subcarriers such that the training sequences have a repetitive structure in the time domain. In this way, the fractional CFO is efficiently computed through a correlation-based approach, while ML methods are employed to estimate the integer CFO. Simulations indicate that the proposed scheme is superior to the existing alternatives in terms of both estimation accuracy and processing load.
1. Introduction
Orthogonal frequency-division multiplexing (OFDM) is an attractive modulation technique for wideband wireless communications due to its robustness against multipath distortions and flexibility in allocating power and data rate over distinct subchannels. For these reasons, it is adopted in a variety of applications, including digital audio broadcasting (DAB), digital video broadcasting (DVB), and the IEEE 802.11a wireless local area network (WLAN) [1]. Combining OFDM with the multiple-input multiple-output (MIMO) technology is an effective solution to increase the capacity of practical commercial systems. The deployment of multiple antennas at both the transmitter and receiver ends can be exploited to improve reliability by means of space-time coding techniques and/or to increase the data rate through spatial multiplexing [2].
Similar to single-input single-output (SISO) OFDM, MIMO-OFDM is extremely sensitive to carrier frequency offsets (CFOs) induced by Doppler shifts and/or oscillator instabilities. The CFO destroys orthogonality among subcarriers and must be accurately estimated and compensated for to avoid severe error rate degradations [3]. While CFO recovery is a well-studied problem for single antenna systems, only few solutions are available for MIMO-OFDM. A blind kurtosis-based scheme is presented in [4], while a method for jointly estimating the CFO and MIMO channel is derived in [5] by placing null subcarriers and pilot tones across adjacent OFDM blocks. Unfortunately, these methods are quite complex as they require a large-point discrete Fourier transform (DFT) operation and a computationally demanding line search. Furthermore, they provide the CFO estimate upon observation of several OFDM blocks, and accordingly, are not suited for packet-oriented applications, where synchronization must be completed shortly after the reception of a packet. In order to achieve fast timing and frequency recovery, training sequences with a periodic structure are commonly employed in SISO-OFDM systems [6–8]. Extending this approach to MIMO-OFDM, however, is not straightforward as signals emitted from different antennas give rise to multistream interference (MSI) at the receiver station, which may degrade the accuracy of the synchronization algorithms. The detrimental effect of MSI can be alleviated by a careful design of the MIMO preambles. For instance, in [9], it is shown that the performance of the least-squares (LSs) channel estimator is optimized if the training sequences at different TX branches are orthogonal and shift-orthogonal for at least the channel length. To meet such requirement, a time-orthogonal design is employed in [10], where different TX antennas transmit their preambles over disjoint time intervals. In this way, however, the preamble length grows linearly with the number of TX branches, thereby, increasing the system overhead. The use of chirp-like polyphase sequences is suggested in [11], while a training block composed of repeated PN sequences with good cross-correlation properties is employed in [12]. In both cases, the CFO estimate is obtained by cross-correlating the repetitive parts of the received preambles in a way similar to SISO-OFDM. This approach is also adopted in [13, 14], where the pilot sequences are obtained by repeating Chu or Frank-Zadoff codes with a different cyclic shift applied at each TX antenna. Alternative criteria for MIMO-OFDM preamble design can be found in [15, 16].
A subspace-based method for CFO estimation in MIMO-OFDM has recently been proposed in [17]. In this scheme, pilot symbols at different transmit antennas are frequency-division multiplexed (FDM) and placed over equally spaced subcarriers. The resulting preambles are characterized by an inherent periodic structure in the time domain which can be effectively exploited at the receiver to separate signals arriving from different TX antennas. This approach is reminiscent of the multiple-signal-classification (MUSIC)-based frequency recovery scheme employed in [18] in the context of orthogonal frequency division multiple access (OFDMA). The main advantage with respect to [18] is that in [17], the CFO estimate is obtained with reduced complexity by looking for the roots of a real-valued polynomial function. A root-based approach is also adopted in [19] after writing the CFO metric in polynomial form.
In this paper, the repetitive slots-based CFO estimator discussed in [8] is extended to MIMO-OFDM transmissions. In order to enlarge the frequency acquisition range, however, we decompose the CFO into a fractional part plus an integer part. The fractional CFO is computed first by cross-correlating the repetitive segments of the received preambles in a way similar to [8], while the integer CFO is subsequently estimated by resorting to maximum likelihood (ML) methods. This results into an algorithm of affordable complexity which can estimate large CFOs and whose accuracy attains the relevant Cramer-Rao bound (CRB).
The rest of this paper is organized as follows. Section 2 describes the system model and introduces basic notation. In Section 3, we review the joint ML estimation of the CFO and MIMO channel, while Section 4 is devoted to the training sequences design and CFO recovery scheme. Simulation results are presented in Section 5 and some conclusions are drawn in Section 6.
Notation 1. Matrices and vectors are denoted by boldface letters, with  and
and  being the DFT matrix and identity matrix of order
being the DFT matrix and identity matrix of order  , respectively.
, respectively.  denotes an
denotes an  diagonal matrix with entries
diagonal matrix with entries  along its main diagonal, while
along its main diagonal, while  is the inverse of a square matrix
is the inverse of a square matrix  . We use
. We use  ,
,  ,
,  , and
, and  for expectation, complex conjugation, transposition, and Hermitian transposition, respectively. The notation
for expectation, complex conjugation, transposition, and Hermitian transposition, respectively. The notation  represents the Euclidean norm of the enclosed vector, while
represents the Euclidean norm of the enclosed vector, while  e
e  ,
,  and
and  stand for the real part, modulus, and principal argument of a complex number
stand for the real part, modulus, and principal argument of a complex number  . Finally,
. Finally,  denotes the (
denotes the ( )th entry of a matrix
)th entry of a matrix  while
while  is a trial value of the unknown parameter
is a trial value of the unknown parameter  .
.
2. System Model
We consider a MIMO-OFDM system with  transmitting and
transmitting and  receiving antennas. We denote by
receiving antennas. We denote by  the number of available subcarriers which are enumerated from
the number of available subcarriers which are enumerated from  to
to  and call
and call  the frequency domain pilot sequence at the
the frequency domain pilot sequence at the  th TX antenna. Before transmission, this sequence is converted in the time domain through an inverse discrete Fourier transform (IDFT) operation and a cyclic prefix (CP) of length
th TX antenna. Before transmission, this sequence is converted in the time domain through an inverse discrete Fourier transform (IDFT) operation and a cyclic prefix (CP) of length  is inserted to avoid inter-block interference (IBI). The signal emitted from the
is inserted to avoid inter-block interference (IBI). The signal emitted from the  th TX branch arrives at the
th TX branch arrives at the  th RX antenna after propagating through a multipath channel with discrete-time impulse response
th RX antenna after propagating through a multipath channel with discrete-time impulse response  , where
, where  is a design parameter that depends on the duration of the transmit/receive filters and on the channel delay spread. Since one single oscillator is used for frequency conversion at both ends of the wireless link, the same CFO is assumed for all transmit/receive antenna pairs. We denote by
is a design parameter that depends on the duration of the transmit/receive filters and on the channel delay spread. Since one single oscillator is used for frequency conversion at both ends of the wireless link, the same CFO is assumed for all transmit/receive antenna pairs. We denote by  the time domain samples available at the
the time domain samples available at the  th RX antenna and define
th RX antenna and define  diag
diag , where
, where  is the frequency offset normalized by the subcarrier spacing. Assuming ideal timing recovery and
is the frequency offset normalized by the subcarrier spacing. Assuming ideal timing recovery and  , we have
, we have

where  is an
is an  -dimensional vector of AWGN samples with zero-mean and variance
-dimensional vector of AWGN samples with zero-mean and variance  , while
, while 
 is the useful signal component, which is modeled as
is the useful signal component, which is modeled as

In (2), we have set  , where
, where  diag
diag collects the pilot sequence emitted by the
collects the pilot sequence emitted by the  th TX antenna, while
th TX antenna, while  is an
is an  matrix with entries
matrix with entries

In Section 3 we show how to exploit vectors  for jointly estimating the CFO
for jointly estimating the CFO  and the MIMO channel
and the MIMO channel  . In doing so, we adopt the FDM training sequences suggested in [17], which optimize the performance of the LS channel estimator thanks to their shift orthogonality properties [9]. Such sequences are expressed by
. In doing so, we adopt the FDM training sequences suggested in [17], which optimize the performance of the LS channel estimator thanks to their shift orthogonality properties [9]. Such sequences are expressed by

where  is a power of two not smaller than
is a power of two not smaller than  ,
,  are integer parameters satisfying
are integer parameters satisfying  and
and  are pilot symbols with constant modulus
are pilot symbols with constant modulus  . In this way, the total energy allocated to training amounts to
. In this way, the total energy allocated to training amounts to  and is equally split between the TX antennas.
and is equally split between the TX antennas.
3. Maximum Likelihood Frequency Estimation
Given the unknown parameters  , from (1), it turns out that vectors
, from (1), it turns out that vectors  are statistically independent and Gaussian distributed with mean
are statistically independent and Gaussian distributed with mean  and covariance matrix
and covariance matrix  . Hence, bearing in mind (2), the log-likelihood function (LLF) for
. Hence, bearing in mind (2), the log-likelihood function (LLF) for  takes the form
takes the form

As a consequence of the FDM property of the employed training sequences, we observe that  is the null matrix for any
is the null matrix for any  . Using this fact, after neglecting irrelevant terms independent of
. Using this fact, after neglecting irrelevant terms independent of  and
and  , we may rewrite the LLF as
, we may rewrite the LLF as

where we have borne in mind that  . The joint ML estimate of the unknown parameters is the location where
. The joint ML estimate of the unknown parameters is the location where  achieves its global maximum. After standard computations, the CFO estimate is found to be
achieves its global maximum. After standard computations, the CFO estimate is found to be

where

and  is the following Cholesky decomposition:
is the following Cholesky decomposition:

In the sequel, we refer to (7) as the maximum likelihood frequency estimator (MLFE). The following remarks are in order.
-
(1)
Observing that
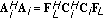 with rank
with rank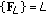 and rank
and rank 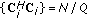 , it turns out that rank
, it turns out that rank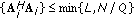 . Since
. Since 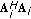 has dimensions
has dimensions  , a necessary condition for the existence of
, a necessary condition for the existence of  in the right-hand-side of (9) is that
in the right-hand-side of (9) is that 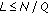 . On the other hand, from (4), it follows that
. On the other hand, from (4), it follows that  has entries
has entries  (10)
(10)and reduces to
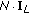 if
if 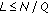 . In such a case, the frequency metric simplifies to
. In such a case, the frequency metric simplifies to (11)
(11) -
(2)
By invoking the asymptotic efficiency property of the MLFE, the frequency estimate (7) is expected to be unbiased with an accuracy that approaches the corresponding CRB for large data records and sufficiently high signal-to-noise ratios (SNRs). Using the LLF in (5), it is found that [19]:
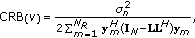 (12)
(12)where
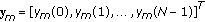 is an
is an 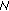 -dimensional vector with entries
-dimensional vector with entries (13)
(13)
4. Frequency Estimation with Reduced Complexity
4.1. Problem Formulation
Direct maximization of  in (8) undertakes heavy computational burden. One possible way to reduce the system complexity is indicated in [19], where
in (8) undertakes heavy computational burden. One possible way to reduce the system complexity is indicated in [19], where  is transformed into a real-valued polynomial function, and the CFO estimate is indirectly obtained by means of a polynomial rooting procedure. In this paper, we follow the alternative approach outlined in [8], by which a periodicity is first introduced in the MIMO training sequences, and CFO recovery is then accomplished by measuring the phase rotations between the repetitive parts of the received preambles. For this purpose, the sequences in (4) are modified so as to simultaneously satisfy the following constraints:
is transformed into a real-valued polynomial function, and the CFO estimate is indirectly obtained by means of a polynomial rooting procedure. In this paper, we follow the alternative approach outlined in [8], by which a periodicity is first introduced in the MIMO training sequences, and CFO recovery is then accomplished by measuring the phase rotations between the repetitive parts of the received preambles. For this purpose, the sequences in (4) are modified so as to simultaneously satisfy the following constraints:
-
(C1)
pilot symbols are equipowered, equispaced in the frequency domain and modulate distinct subcarriers at different TX antennas according to the FDM principle;
-
(C2)
each vector
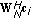 ??(
??( ) of time domain samples is obtained by the repetition of
) of time domain samples is obtained by the repetition of 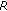 identical segments, where
identical segments, where  is some power of two.
is some power of two.
Condition C1 implies that the  preambles remain shift-orthogonal in the time domain, which is desirable to enhance the accuracy of the channel estimates, while condition C2 facilitates CFO recovery by ensuring that the preambles are periodic with period
preambles remain shift-orthogonal in the time domain, which is desirable to enhance the accuracy of the channel estimates, while condition C2 facilitates CFO recovery by ensuring that the preambles are periodic with period  .
.
To proceed further, let  be a power of two with
be a power of two with  . Then, it can be easily shown that C1 and C2 are simultaneously met if pilot symbols at each TX antenna are equispaced in the frequency domain at a distance of
. Then, it can be easily shown that C1 and C2 are simultaneously met if pilot symbols at each TX antenna are equispaced in the frequency domain at a distance of  subcarriers and their positions are shifted by
subcarriers and their positions are shifted by  subcarriers from one TX branch to the next. This amounts to putting
subcarriers from one TX branch to the next. This amounts to putting

where we set  to ensure that the total energy allocated to training is still
to ensure that the total energy allocated to training is still  . It is worth observing that the use of time-repetitive FDM training sequences for MIMO-OFDM has also been suggested in [16] to make the CRB of the frequency estimates independent of the channel realization. However, our design (14) is more general as it applies to any triple
. It is worth observing that the use of time-repetitive FDM training sequences for MIMO-OFDM has also been suggested in [16] to make the CRB of the frequency estimates independent of the channel realization. However, our design (14) is more general as it applies to any triple  whereas in [16], the number of subcarriers is constrained to be a multiple of
whereas in [16], the number of subcarriers is constrained to be a multiple of  . Recalling that in practical OFDM systems
. Recalling that in practical OFDM systems  is always a power of two, it turns out that the sequence design in [16] can only be adopted on condition that both
is always a power of two, it turns out that the sequence design in [16] can only be adopted on condition that both  and
and  are powers of two.
are powers of two.
As it is known, the use of OFDM preambles composed by  repetitive slots restricts the acquisition range of the CFO estimator to
repetitive slots restricts the acquisition range of the CFO estimator to  times the subcarrier spacing. To cope with such a drawback, we decompose
times the subcarrier spacing. To cope with such a drawback, we decompose  into a fractional part, less than
into a fractional part, less than  in magnitude, plus an integer part which is multiple of
in magnitude, plus an integer part which is multiple of  . The normalized CFO is thus rewritten as
. The normalized CFO is thus rewritten as

where  is an integer parameter referred to as the integer CFO (ICFO), while
is an integer parameter referred to as the integer CFO (ICFO), while  is the fractional CFO (FCFO) and belongs to the interval
is the fractional CFO (FCFO) and belongs to the interval  . Since the transmitted preambles remain periodic after passing through the channel (apart from the presence of thermal noise and from a phase shift induced by the CFO), each vector of received time domain samples can be decomposed into
. Since the transmitted preambles remain periodic after passing through the channel (apart from the presence of thermal noise and from a phase shift induced by the CFO), each vector of received time domain samples can be decomposed into  segments
segments  , with
, with

In(16),  is a
is a  -dimensional vector with elements
-dimensional vector with elements

while  are statistically independent Gaussian vectors with zero-mean and covariance matrix
are statistically independent Gaussian vectors with zero-mean and covariance matrix  .
.
4.2. Estimation of the Fractional CFO
Our first goal is the estimation of  based on the observations
based on the observations  . Inspection of (16) reveals that this task is complicated by the presence of the nuisance vectors
. Inspection of (16) reveals that this task is complicated by the presence of the nuisance vectors  . One possible approach is to consider such vectors as deterministic but unknown parameters and proceed to the joint ML estimation of the parameter set
. One possible approach is to consider such vectors as deterministic but unknown parameters and proceed to the joint ML estimation of the parameter set  , with
, with  . This approach has been used in [8] in the context of SISO-OFDM, and its extension to MIMO transmissions leads to the following FCFO metric:
. This approach has been used in [8] in the context of SISO-OFDM, and its extension to MIMO transmissions leads to the following FCFO metric:

where  is the
is the  —lag sample correlation function evaluated at the m th RX branch, that is,
—lag sample correlation function evaluated at the m th RX branch, that is,

The ML estimate of  is eventually found by locating the global maximum of
is eventually found by locating the global maximum of  . Unfortunately, no closed form solution is available except when
. Unfortunately, no closed form solution is available except when  . The more general case can be approached by an exhaustivesearch over the interval
. The more general case can be approached by an exhaustivesearch over the interval  which may be cumbersome in practice. For this reason, we suggest a suboptimal but simpler procedure which develops in two steps. In the first step a coarse FCFO estimate is obtained as
which may be cumbersome in practice. For this reason, we suggest a suboptimal but simpler procedure which develops in two steps. In the first step a coarse FCFO estimate is obtained as

The rationale behind the above expression is easily understood after substituting (16) into (19). This yields

where  is a zero-mean disturbance term collecting signal
is a zero-mean disturbance term collecting signal  noise and noise
noise and noise  noise interactions. Inspection of (21) reveals that, in the absence of noise, the right-hand-side of (20) is just the true FCFO. In order to improve the estimation accuracy,
noise interactions. Inspection of (21) reveals that, in the absence of noise, the right-hand-side of (20) is just the true FCFO. In order to improve the estimation accuracy,  is refined in the second step by looking for an estimate of the residual error
is refined in the second step by looking for an estimate of the residual error  . For this purpose, we let
. For this purpose, we let  and rewrite (18) in the following form:
and rewrite (18) in the following form:

where we have defined  and
and  . Setting to zero the derivative of (22) with respect to
. Setting to zero the derivative of (22) with respect to  and assuming that
and assuming that  is small enough such that
is small enough such that  , an estimate of
, an estimate of  can be computed in closed form as
can be computed in closed form as

The final FCFO estimate is given by

4.3. Estimation of the Integer CFO
If the normalized CFO is guaranteed to be less than  in magnitude, the quantity
in magnitude, the quantity  can be regarded as an estimate of
can be regarded as an estimate of  . Otherwise,
. Otherwise,  is expressed as in (15), and an estimate of the integer offset
is expressed as in (15), and an estimate of the integer offset  must be found. This problem is now addressed using ML methods.
must be found. This problem is now addressed using ML methods.
In order to compensate for the fractional offset  , the received samples at each RX branch are first counter-rotated at an angular speed
, the received samples at each RX branch are first counter-rotated at an angular speed  . This produces the
. This produces the  vectors
vectors  , with
, with

Substituting (1)-(2) into (25) and assuming ideal FCFO compensation, we obtain

where  is the noise contribution, which is statistically equivalent to
is the noise contribution, which is statistically equivalent to  . Vectors
. Vectors  are next used to get the joint ML estimate of
are next used to get the joint ML estimate of  . Bearing in mind (26), the corresponding LLF is found to be
. Bearing in mind (26), the corresponding LLF is found to be

by which, maximizing with respect to  , we obtain
, we obtain

Now, we observe that  is an
is an  matrix whose rank is not greater than
matrix whose rank is not greater than  . Hence, a necessary condition for the existence of
. Hence, a necessary condition for the existence of  is that
is that  . In such a case, if the pilot sequences are those defined in (14), we have
. In such a case, if the pilot sequences are those defined in (14), we have  so that (28) simplifies to
so that (28) simplifies to

The concentrated likelihood function for  is found by substituting (29) into the right-hand-side of (27). Neglecting irrelevant terms independent of
is found by substituting (29) into the right-hand-side of (27). Neglecting irrelevant terms independent of  , we obtain
, we obtain

and the ML estimate of  is computed as
is computed as

where  represents the largest expected value of
represents the largest expected value of  , which is determined by the stability of the transmitter and receiver oscillators. Recalling that
, which is determined by the stability of the transmitter and receiver oscillators. Recalling that  , after standard manipulations, we may put
, after standard manipulations, we may put  in the equivalent form
in the equivalent form

where  is the repetition with period
is the repetition with period  of the DFT of
of the DFT of  , that is,
, that is,

On the other hand, from (14), we see that symbols  are different from zero only when
are different from zero only when  , where
, where  are the indices of the pilot subcarriers at the
are the indices of the pilot subcarriers at the  th TX antenna. Function
th TX antenna. Function  can thus be rewritten as
can thus be rewritten as

Once the ICFO is obtained as indicated in (31), an estimate of the CFO is computed from (15) in the form

In the sequel, we refer to (35) as the reduced complexity frequency estimator (RCFE).
4.4. Remarks
(1) As mentioned previously, matrix  in (28) is nonsingular provided that
in (28) is nonsingular provided that  . Such condition is more restrictive than the constraint
. Such condition is more restrictive than the constraint  that was found in the previous section for MLFE. In particular, recalling that
that was found in the previous section for MLFE. In particular, recalling that  , it turns out that the maximum channel length that RCFE can manage is
, it turns out that the maximum channel length that RCFE can manage is  times smaller than for MLFE.
times smaller than for MLFE.
(2) Assuming for simplicity that the ICFO has been perfectly estimated, from (35), it follows that 
 . Since parameters
. Since parameters  are jointly estimated through ML methods, we expect that
are jointly estimated through ML methods, we expect that  asymptotically approaches the corresponding CRB. The latter is provided in [8] and reads
asymptotically approaches the corresponding CRB. The latter is provided in [8] and reads

where  denotes the average signal power at each RX branch, that is,
denotes the average signal power at each RX branch, that is,

The frequency MSE is thus given by

(3) The computational load of RCFE can be assessed as follows. Computing the correlations  in (19) requires a total of
in (19) requires a total of  real operations (additions plus multiplications) for each RX branch, while
real operations (additions plus multiplications) for each RX branch, while  operations are needed to obtain
operations are needed to obtain  in (23). Quantities
in (23). Quantities  in (33) are computed through an
in (33) are computed through an  -point DFT for each receiving antenna, with a corresponding complexity of
-point DFT for each receiving antenna, with a corresponding complexity of  . Finally, evaluating
. Finally, evaluating  in (34) needs additional
in (34) needs additional  operations for each
operations for each  . The overall complexity of RCFE is summarized in the first row of Table 1, where a distinction has been made between the FCFO and ICFO recovery tasks, and we have denoted by
. The overall complexity of RCFE is summarized in the first row of Table 1, where a distinction has been made between the FCFO and ICFO recovery tasks, and we have denoted by  the number of hypothesized ICFO values.
the number of hypothesized ICFO values.
(4) Our FCFO recovery algorithm is an improved version of the correlation-based frequency estimator (CBFE) proposed in [12]. Actually, both schemes employ training preambles composed by  repetitive parts and operate in two steps. A coarse estimate
repetitive parts and operate in two steps. A coarse estimate  is firstly computed by CBFE in a way similar to (20), and it is next refined by evaluating the quantity
is firstly computed by CBFE in a way similar to (20), and it is next refined by evaluating the quantity

The final CFO estimate is obtained as  and its MSE is given by [12]
and its MSE is given by [12]

Comparing this results with (38), we see that the loss (in dB) with respect to RCFE is  Log
Log , which approaches 1.25 dB for large values of
, which approaches 1.25 dB for large values of  . Furthermore, since no ICFO estimation is attempted in [12], the estimation range of CBFE is restricted to
. Furthermore, since no ICFO estimation is attempted in [12], the estimation range of CBFE is restricted to  , while RCFE can cope with CFOs as large as
, while RCFE can cope with CFOs as large as  . The overall complexity of CBFE is shown in the third line of Table 1. Compared to FCFO recovery by means of RCFE, the computational saving of CBFE is in the order of
. The overall complexity of CBFE is shown in the third line of Table 1. Compared to FCFO recovery by means of RCFE, the computational saving of CBFE is in the order of  .
.
5. Simulation Results
Computer simulations have been run to check and extend the analytical results of the previous sections. The simulation scenario is summarized as follows.
5.1. Simulation Model
The investigated MIMO-OFDM system has  subcarriers and operates in the 5 GHz frequency band. The signal bandwidth is 5 MHz, corresponding to a subcarrier distance of approximately
subcarriers and operates in the 5 GHz frequency band. The signal bandwidth is 5 MHz, corresponding to a subcarrier distance of approximately  kHz. The sampling period is
kHz. The sampling period is  microsecond, so that the useful part of each OFDM block has length
microsecond, so that the useful part of each OFDM block has length  millisecond. Each channel is characterized by
millisecond. Each channel is characterized by  independent Rayleigh fading taps with an exponentially decaying power delay profile
independent Rayleigh fading taps with an exponentially decaying power delay profile

In (41), the constant  is chosen such that the channel power is normalized to unity, that is,
is chosen such that the channel power is normalized to unity, that is,  . A new channel snapshot is generated at each simulation run and kept fixed over the training period. Vectors
. A new channel snapshot is generated at each simulation run and kept fixed over the training period. Vectors  are assumed to be statistically independent for different TX/RX antenna pairs. The training sequences employed by RCFE are given in (14), where we have set
are assumed to be statistically independent for different TX/RX antenna pairs. The training sequences employed by RCFE are given in (14), where we have set  and
and  . In this way, each TX antenna transmits a total of 32 pilot symbols which are randomly taken from a QPSK constellation with power
. In this way, each TX antenna transmits a total of 32 pilot symbols which are randomly taken from a QPSK constellation with power  . Parameters
. Parameters  and
and  are varied throughout simulations to assess their impact on the system performance.
are varied throughout simulations to assess their impact on the system performance.
Comparisons are made between RCFE, CBFE, and the polynomial-based frequency estimator (PBFE) proposed in [17]. This scheme employs the training sequences defined in (4) and performs initial ICFO recovery by maximizing the following cost function:

over the set 
 , with
, with  being the
being the  -point DFT of
-point DFT of  . After ICFO compensation, the fractional CFO is eventually estimated by looking for the roots of a real-valued polynomial function that is obtained by applying the MUSIC principle. As mentioned in [17], the estimation range of PBFE is
. After ICFO compensation, the fractional CFO is eventually estimated by looking for the roots of a real-valued polynomial function that is obtained by applying the MUSIC principle. As mentioned in [17], the estimation range of PBFE is  . Its computational requirement is mainly ascribed to the need for evaluating the correlation matrix of the received time domain samples and is summarized in the second row of Table 1.
. Its computational requirement is mainly ascribed to the need for evaluating the correlation matrix of the received time domain samples and is summarized in the second row of Table 1.
5.2. Performance Assessment
Figure 1 compares the performance of the fractional CFO estimators in terms of their MSE  versus the signal-to-noise ratio at each receiving antenna. The latter is defined as SNR
versus the signal-to-noise ratio at each receiving antenna. The latter is defined as SNR  , where
, where  is the noise power, and
is the noise power, and  is given in (37). Marks indicate simulation results, while solid lines are drawn to ease the reading of the graphs. The number of TX and RX antennas is
is given in (37). Marks indicate simulation results, while solid lines are drawn to ease the reading of the graphs. The number of TX and RX antennas is  and
and  , respectively. The same training sequences are used for both CBFE and RCFE, while PBFE employs the pilot design specified in (4) with
, respectively. The same training sequences are used for both CBFE and RCFE, while PBFE employs the pilot design specified in (4) with  and
and  . This means that the number of pilot symbols transmitted by each TX antenna is 32 for all the considered schemes. As suggested in [17], the pilot symbols
. This means that the number of pilot symbols transmitted by each TX antenna is 32 for all the considered schemes. As suggested in [17], the pilot symbols  for PBFE belong to a Chu sequence. The CFO is randomly generated at each simulation run with uniform distribution within the interval
for PBFE belong to a Chu sequence. The CFO is randomly generated at each simulation run with uniform distribution within the interval  , which corresponds to having
, which corresponds to having  and
and  . For the time being, we concentrate on the accuracy of the FCFO estimates and assume ideal ICFO recovery for both RCFE and PBFE. We use the average CRB to benchmark the performance of the considered schemes. The latter corresponds to the extended Miller and Chang bound (EMCB) [20] and is obtained by numerically averaging the right-hand-side of (12) with respect to the channel statistics. Inspection of Figure 1 reveals that RCFE outperforms the other schemes, and its accuracy is close to the EMCB at all investigated SNR values. As predicted by the theoretical analysis shown in (38) and (40), the loss of CBFE with respect to RCFE is approximately 1.25 dB. Looking at the system complexity, from Table 1, it turns out that in the considered scenario, RCFE requires a total of 57 500 operations for FCFO recovery, while PBFE and CBFE need 1 156 000 and 24 000 operations, respectively. Combining these figures with the results of Figure 1 indicates that RCFE is superior to PBFE in terms of both estimation accuracy and processing load, while CBFE is a valid solution when limiting the computational requirement is an issue of concern.
. For the time being, we concentrate on the accuracy of the FCFO estimates and assume ideal ICFO recovery for both RCFE and PBFE. We use the average CRB to benchmark the performance of the considered schemes. The latter corresponds to the extended Miller and Chang bound (EMCB) [20] and is obtained by numerically averaging the right-hand-side of (12) with respect to the channel statistics. Inspection of Figure 1 reveals that RCFE outperforms the other schemes, and its accuracy is close to the EMCB at all investigated SNR values. As predicted by the theoretical analysis shown in (38) and (40), the loss of CBFE with respect to RCFE is approximately 1.25 dB. Looking at the system complexity, from Table 1, it turns out that in the considered scenario, RCFE requires a total of 57 500 operations for FCFO recovery, while PBFE and CBFE need 1 156 000 and 24 000 operations, respectively. Combining these figures with the results of Figure 1 indicates that RCFE is superior to PBFE in terms of both estimation accuracy and processing load, while CBFE is a valid solution when limiting the computational requirement is an issue of concern.
Figure 2 illustrates the impact of the number of transmit antennas  on the accuracy of RCFE. The simulation scenario is the same as in Figure 1, except that now
on the accuracy of RCFE. The simulation scenario is the same as in Figure 1, except that now  or
or  . As it is seen, the frequency MSE is virtually independent of
. As it is seen, the frequency MSE is virtually independent of  and the same occurs for the EMCB. Such behavior can be ascribed to the fact that signals emitted by different TX antennas combine incoherently at each RX branch, so that higher values of
and the same occurs for the EMCB. Such behavior can be ascribed to the fact that signals emitted by different TX antennas combine incoherently at each RX branch, so that higher values of  do not result into a corresponding increase of the array gain. As it is known, array gain exploitation by means of multiple TX antennas requires channel knowledge at the transmitter in conjunction with suitable precoding techniques.
do not result into a corresponding increase of the array gain. As it is known, array gain exploitation by means of multiple TX antennas requires channel knowledge at the transmitter in conjunction with suitable precoding techniques.
Figure 3 shows how the performance of RCFE is affected by the number  of receiving antennas. In such a case,
of receiving antennas. In such a case, is fixed to three while
is fixed to three while  or
or  . As predicted by (38), the estimation accuracy improves with
. As predicted by (38), the estimation accuracy improves with  and this trend is also evident in the EMCB. The physical reason behind such SNR advantage is that the presence of multiple receiving antennas increases the length of the data record
and this trend is also evident in the EMCB. The physical reason behind such SNR advantage is that the presence of multiple receiving antennas increases the length of the data record  used for CFO recovery. This provides the system with an array gain of
used for CFO recovery. This provides the system with an array gain of  Log(
Log( ) dB.
) dB.
The performance of the ICFO estimators is illustrated in Figure 4 in terms of probability of failure  versus SNR. Comparisons are made between RCFE and PBFE using the same simulation setup of Figure 1. The RCFE metric defined in (34) is evaluated for
versus SNR. Comparisons are made between RCFE and PBFE using the same simulation setup of Figure 1. The RCFE metric defined in (34) is evaluated for  , while PBFE looks for the maximum of
, while PBFE looks for the maximum of  over the set
over the set  . In this way, the estimation range is
. In this way, the estimation range is  for RCFE and
for RCFE and  for PBFE. As it is seen, for SNR
for PBFE. As it is seen, for SNR  dB, the best performance is obtained with RCFE. From Table 1, it follows that the total number of operations needed to get the CFO estimate
dB, the best performance is obtained with RCFE. From Table 1, it follows that the total number of operations needed to get the CFO estimate  is 1 283 000 for PBFE and 252 500 for RCFE, thereby leading to a reduction of the processing load by a factor greater than 5. It is fair to say, however, that the complexity of PBFE can be controlled by a judicious design of parameter
is 1 283 000 for PBFE and 252 500 for RCFE, thereby leading to a reduction of the processing load by a factor greater than 5. It is fair to say, however, that the complexity of PBFE can be controlled by a judicious design of parameter  . Specifically, decreasing
. Specifically, decreasing  alleviates the computational requirement at the expense of a reduced CFO acquisition range.
alleviates the computational requirement at the expense of a reduced CFO acquisition range.
6. Conclusions
We have addressed the problem of training-assisted CFO recovery in MIMO-OFDM systems. To reduce the computational burden required by the exact ML solution, we have divided the CFO into a fractional part plus an integer part and have designed FDM pilot sequences that are periodic in the time domain. The fractional CFO is estimated in closed form by measuring the phase rotations between the repetitive parts of the received preambles, while the integer CFO is estimated in a joint fashion with the MIMO channel matrix by resorting to the ML principle. The proposed scheme has affordable complexity and exhibits improved performance with respect to existing alternatives. For these reasons, we believe that it provides an effective approach for frequency synchronization in beyond third generation (3G) wideband MIMO-OFDM transmissions.
References
Wireless LAN medium access control (MAC) and physical layer (PHY) specifications, higher speed physical layer extension in the 5 GHz band 1999.
Stüber GL, Barry JR, Mclaughlin SW, Li YE, Ingram MA, Pratt TG: Broadband MIMO-OFDM wireless communications. Proceedings of the IEEE 2004, 92(2):271-294. 10.1109/JPROC.2003.821912
Pollet T, van Bladel M, Moeneclaey M: BER sensitivity of OFDM systems to carrier frequency offset and Wiener phase noise. IEEE Transactions on Communications 1995, 43(234):191-193.
Yao Y, Giannakis GB: Blind carrier frequency offset estimation in SISO, MIMO, and multiuser OFDM systems. IEEE Transactions on Communications 2005, 53(1):173-183. 10.1109/TCOMM.2004.840623
Ma X, Oh M-K, Giannakis GB, Park D-J: Hopping pilots for estimation of frequency-offset and multiantenna channels in MIMO-OFDM. IEEE Transactions on Communications 2005, 53(1):162-172. 10.1109/TCOMM.2004.840663
Schmidl TM, Cox DC: Robust frequency and timing synchronization for OFDM. IEEE Transactions on Communications 1997, 45(12):1613-1621. 10.1109/26.650240
Morelli M, Mengali U: An improved frequency offset estimator for OFDM applications. IEEE Communications Letters 1999, 3(3):75-77. 10.1109/4234.752907
Ghogho M, Swami A, Ciblat P: Training design for CFO estimation in OFDM over correlated multipath fading channels. Proceedings of the 50th Annual IEEE Global Telecommunications Conference (GLOBECOM '07), November 2007, Washington, DC, USA 2821-2825.
Barhumi I, Leus G, Moonen M: Optimal training sequences for channel estimation in MIMO OFDM systems in mobile wireless channels. Proceedings of the International Zurich Seminar on Broadband Communications: Accessing, Transmission, Networking, February 2002, Zurich, Switzerland 441-446.
van Zelst A, Schenk TC: Implementation of a MIMO OFDM-based wireless LAN system. IEEE Transactions on Signal Processing 2004, 52(2):483-494. 10.1109/TSP.2003.820989
Mody AN, Stüber GL: Synchronization for MIMO OFDM systems. Proceedings of IEEE Global Telecommunicatins Conference (GLOBECOM '01), November 2001, San Antonio, Tex, USA 1: 509-513.
Yan C, Li S, Tang Y, Luo X: Frequency synchronization in MIMO OFDM system. Proceedings of the 60th IEEE Vehicular Technology Conference (VTC '04), September 2004, Los Angeles, Calif, USA 3: 1732-1734.
Schenk TCW, van Zelst A: Frequency synchronization for MIMO OFDM wireless LAN systems. Proceedings of the 58th IEEE Vehicular Technology Conference (VTC '03), October 2003, Orlando, Fla, USA 2: 781-785.
Zheng J, Han J, Lv J, Wu W: A novel timing and frequency synchronization scheme for MIMO OFDM system. Proceedings of the International Conference on Wireless Communications, Networking and Mobile Computing (WiCOM '07), September 2007, Shanghai, China 420-423.
Minn H, Al-Dhahir N, Li Y: Optimal training signals for MIMO OFDM channel estimation in the presence of frequency offset and phase noise. IEEE Transactions on Communications 2006, 54(10):1754-1759.
Ghogho M, Swami A: Training design for multipath channel and frequency-offset estimation in MIMO systems. IEEE Transactions on Signal Processing 2006, 54(10):3957-3965.
Jiang Y, Minn H, Gao X, You X, Li Y: Frequency offset estimation and training sequence design for MIMO OFDM. IEEE Transactions on Wireless Communications 2008, 7(4):1244-1254.
Cao Z, Tureli U, Yao Y-D: Deterministic multiuser carrier-frequency offset estimation for interleaved OFDMA uplink. IEEE Transactions on Communications 2004, 52(9):1585-1594. 10.1109/TCOMM.2004.833183
Jiang Y, You X, Gao X, Minn H: MIMO OFDM frequency offset estimator with low computational complexity. Proceedings of IEEE International Conference on Communications (ICC '07), June 2007, Glasgow, Scotland 5449-5454.
Gini F, Reggiannini R: On the use of Cramer-Rao-like bounds in the presence of random nuisance parameters. IEEE Transactions on Communications 2000, 48(12):2120-2126. 10.1109/26.891222
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Morelli, M., Moretti, M. & Imbarlina, G. A Practical Scheme for Frequency Offset Estimation in MIMO-OFDM Systems. J Wireless Com Network 2009, 821819 (2009). https://doi.org/10.1155/2009/821819
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/821819
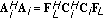 with rank
with rank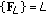 and rank
and rank 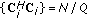 , it turns out that rank
, it turns out that rank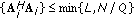 . Since
. Since 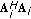 has dimensions
has dimensions  , a necessary condition for the existence of
, a necessary condition for the existence of  in the right-hand-side of (9) is that
in the right-hand-side of (9) is that 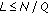 . On the other hand, from (4), it follows that
. On the other hand, from (4), it follows that  has entries
has entries 
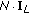 if
if 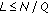 . In such a case, the frequency metric simplifies to
. In such a case, the frequency metric simplifies to
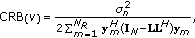
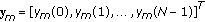 is an
is an 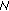 -dimensional vector with entries
-dimensional vector with entries
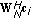 ??(
??( ) of time domain samples is obtained by the repetition of
) of time domain samples is obtained by the repetition of 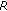 identical segments, where
identical segments, where  is some power of two.
is some power of two.
 = 3 and
= 3 and
 = 2.
= 2.

 = 2, 3, 4 and
= 2, 3, 4 and
 = 2.
= 2.

 = 3 and
= 3 and
 = 2, 3, 4.
= 2, 3, 4.

 = 3 and
= 3 and
 = 2.
= 2.