- Research Article
- Open access
- Published:
Secrecy Capacity of a Class of Broadcast Channels with an Eavesdropper
EURASIP Journal on Wireless Communications and Networking volume 2009, Article number: 824235 (2009)
Abstract
We study the security of communication between a single transmitter and many receivers in the presence of an eavesdropper for several special classes of broadcast channels. As the first model, we consider the degraded multireceiver wiretap channel where the legitimate receivers exhibit a degradedness order while the eavesdropper is more noisy with respect to all legitimate receivers. We establish the secrecy capacity region of this channel model. Secondly, we consider the parallel multireceiver wiretap channel with a less noisiness order in each subchannel, where this order is not necessarily the same for all subchannels, and hence the overall channel does not exhibit a less noisiness order. We establish the common message secrecy capacity and sum secrecy capacity of this channel. Thirdly, we study a class of parallel multireceiver wiretap channels with two subchannels, two users and an eavesdropper. For channels in this class, in the first (resp., second) subchannel, the second (resp., first) receiver is degraded with respect to the first (resp., second) receiver, while the eavesdropper is degraded with respect to both legitimate receivers in both subchannels. We determine the secrecy capacity region of this channel, and discuss its extensions to arbitrary numbers of users and subchannels. Finally, we focus on a variant of this previous channel model where the transmitter can use only one of the subchannels at any time. We characterize the secrecy capacity region of this channel as well.
1. Introduction
Information theoretic secrecy was initiated by Wyner in his seminal work [1], where he introduced the wiretap channel and established the capacity-equivocation region of the degraded wiretap channel. Later, his result was generalized to arbitrary, not necessarily degraded, wiretap channels by Csiszar and Korner [2]. Recently, many multiuser channel models have been considered from a secrecy point of view [3–22]. One basic extension of the wiretap channel to the multiuser environment is secure broadcasting to many users in the presence of an eavesdropper. In the most general form of this problem (see Figure 1), one transmitter wants to have confidential communication with an arbitrary number of users in a broadcast channel, while this communication is being eavesdropped by an external entity. Our goal is to understand the theoretical limits of secure broadcasting, that is, largest simultaneously achievable secure rates. Characterizing the secrecy capacity region of this channel model in its most general form is difficult, because the version of this problem without any secrecy constraints, is the broadcast channel with an arbitrary number of receivers, whose capacity region is open. Consequently, to have progress in understanding the limits of secure broadcasting, we resort to studying several special classes of channels, with increasing generality. The approach of studying special channel structures was also followed in the existing literature on secure broadcasting [8, 9].
The work in [9] first considers an arbitrary wiretap channel with two legitimate receivers and one eavesdropper, and provides an inner bound for achievable rates when each user wishes to receive an independent message. Secondly, [9] focuses on the degraded wiretap channel with two receivers and one eavesdropper, where there is a degradedness order among the receivers, and the eavesdropper is degraded with respect to both users (see Figure 2 for a more general version of the problem that we study). For this setting, the work in [9] finds the secrecy capacity region. This result is concurrently and independently obtained in this work as a special case, see Corollary 2, which is also published in a conference version in [23].
Another relevant work on secure broadcasting is [8] which considers secure broadcasting to  users using
users using  subchannels (see Figure 3) for two different scenarios. In the first scenario, the transmitter wants to convey only a common confidential message to all users, and in the second scenario, the transmitter wants to send independent messages to all users. For both scenarios, the work in [8] considers a subclass of parallel multireceiver wiretap channels, where in any given subchannel, there is a degradation order such that each receiver's observation (except the best one) is a degraded version of some other receiver's observation, and this degradation order is not necessarily the same for all subchannels. For the first scenario, the work in [8] finds the common message secrecy capacity for this subclass. For the second scenario, where each user wishes to receive an independent message, [8] finds the sum secrecy capacity for this subclass of channels.
subchannels (see Figure 3) for two different scenarios. In the first scenario, the transmitter wants to convey only a common confidential message to all users, and in the second scenario, the transmitter wants to send independent messages to all users. For both scenarios, the work in [8] considers a subclass of parallel multireceiver wiretap channels, where in any given subchannel, there is a degradation order such that each receiver's observation (except the best one) is a degraded version of some other receiver's observation, and this degradation order is not necessarily the same for all subchannels. For the first scenario, the work in [8] finds the common message secrecy capacity for this subclass. For the second scenario, where each user wishes to receive an independent message, [8] finds the sum secrecy capacity for this subclass of channels.
In this paper, our approach will be two-fold: first, we will identify more general channel models than considered in [8, 9] and generalize the results in [8, 9] to those channel models, and secondly, we will consider somewhat more specialized channel models than in [8] and provide more comprehensive results. More precisely, our contributions in this paper are as follows.
(1) We consider the degraded multireceiver wiretap channel with an arbitrary number of users and one eavesdropper, where users are arranged according to a degradedness order, and each user has a less noisy channel with respect to the eavesdropper, see Figure 2. We find the secrecy capacity region when each user receives both an independent message and a common confidential message. Since degradedness implies less noisiness [2], this channel model contains the subclass of channel models where in addition to the degradedness order users exhibit, the eavesdropper is degraded with respect to all users. Consequently, our result can be specialized to the degraded multireceiver wiretap channel with an arbitrary number of users and a degraded eavesdropper, see Corollary 2 and also [23]. The two-user version of the degraded multireceiver wiretap channel was studied and the capacity region was found independently and concurrently in [9].
(2) We then focus on a class of parallel multireceiver wiretap channels with an arbitrary number of legitimate receivers and an eavesdropper, see Figure 3, where in each subchannel, for any given user, either the user's channel is less noisy with respect to the eavesdropper's channel, or vice versa. We establish the common message secrecy capacity of this channel, which is a generalization of the corresponding capacity result in [8] to a broader class of channels. Secondly, we study the scenario where each legitimate receiver wishes to receive an independent message for another subclass of parallel multireceiver wiretap channels. For channels belonging to this subclass, in each subchannel, there is a less noisiness order which is not necessarily the same for all subchannels. Consequently, this ordered class of channels is a subset of the class for which we establish the common message secrecy capacity. We find the sum secrecy capacity for this class, which is again a generalization of the corresponding result in [8] to a broader class of channels.
(3) We also investigate a class of parallel multireceiver wiretap channels with two subchannels, two users, and one eavesdropper, see Figure 4. For the channels in this class, there is a specific degradation order in each subchannel such that in the first (resp., second) subchannel the second (resp., first) user is degraded with respect to the first (resp., second) user, while the eavesdropper is degraded with respect to both users in both subchannels. This is the model of [8] for  users and
users and  subchannels. This model is more restrictive compared to the one mentioned in the previous item. Our motivation to study this more special class is to provide a stronger and more comprehensive result. In particular, for this class, we determine the entire secrecy capacity region when each user receives both an independent message and a common message. In contrast, the work in [8] gives the common message secrecy capacity (when only a common message is transmitted) and sum secrecy capacity (when only independent messages are transmitted) of this class. We discuss the generalization of this result to arbitrary numbers of users and subchannels.
subchannels. This model is more restrictive compared to the one mentioned in the previous item. Our motivation to study this more special class is to provide a stronger and more comprehensive result. In particular, for this class, we determine the entire secrecy capacity region when each user receives both an independent message and a common message. In contrast, the work in [8] gives the common message secrecy capacity (when only a common message is transmitted) and sum secrecy capacity (when only independent messages are transmitted) of this class. We discuss the generalization of this result to arbitrary numbers of users and subchannels.
(4) We finally consider a variant of the previous channel model. In this model, we again have a parallel multireceiver wiretap channel with two subchannels, two users, and one eavesdropper, and the degradation order in each subchannel is exactly the same as in the previous item. However, in this case, the input and output alphabets of one subchannel are nonintersecting with the input and output alphabets of the other subchannel. Moreover, we can use only one of these subchannels at any time. We determine the secrecy capacity region of this channel when the transmitter sends both an independent message to each receiver and a common message to both receivers.
It is clear that all of the channel models we consider exhibit some kind of an ordered structure, where this ordered structure is in the form of degradedness in some channel models, and it is in the form of less noisiness in others. This common ordered structure in all channel models we considered implies that our achievability schemes and converse proofs use some common techniques. In particular, for achievability, we use stochastic encoding [2] in conjunction with superposition coding [24]; and for the converse proofs, we use outer bounding techniques in [1, 2], more specifically, the Csiszar-Korner identity, [2, Lemma 7].
2. Degraded Multireceiver Wiretap Channels
We first consider the generalization of Wyner's degraded wiretap channel to the case with many legitimate receivers. In particular, the channel consists of a transmitter with an input alphabet  ,
,  legitimate receivers with output alphabets
legitimate receivers with output alphabets  and an eavesdropper with output alphabet
and an eavesdropper with output alphabet  . The transmitter sends a confidential message to each user, say
. The transmitter sends a confidential message to each user, say  to the
to the  th user, in addition to a common message,
th user, in addition to a common message,  , which is to be delivered to all users. All messages are to be kept secret from the eavesdropper. The channel is assumed to be memoryless with a transition probability
, which is to be delivered to all users. All messages are to be kept secret from the eavesdropper. The channel is assumed to be memoryless with a transition probability  .
.
In this section, we consider a special class of these channels, see Figure 2, where users exhibit a certain degradation order, that is, their channel outputs satisfy the following Markov chain:

and each user has a less noisy channel with respect to the eavesdropper, that is, we have

for every  such that
such that  . In fact, since a degradation order exists among the users, it is sufficient to say that user 1 has a less noisy channel with respect to the eavesdropper to guarantee that all users do. Hereafter, we call this channel the degraded multireceiver wiretap channel with a more noisy eavesdropper. We note that this channel model contains the degraded multireceiver wiretap channel which is defined through the Markov chain:
. In fact, since a degradation order exists among the users, it is sufficient to say that user 1 has a less noisy channel with respect to the eavesdropper to guarantee that all users do. Hereafter, we call this channel the degraded multireceiver wiretap channel with a more noisy eavesdropper. We note that this channel model contains the degraded multireceiver wiretap channel which is defined through the Markov chain:

because the Markov chain in (3) implies the less noisiness condition in (2).
A  code for this channel consists of
code for this channel consists of  message sets,
message sets,  ,
,  , an encoder
, an encoder  ,
,  decoders, one at each legitimate receiver,
decoders, one at each legitimate receiver,  ,
,  . The probability of error is defined as
. The probability of error is defined as  . A rate tuple
. A rate tuple  is said to be achievable if there exists a code with
is said to be achievable if there exists a code with  and
and

where  denotes any subset of
denotes any subset of  . Hence, we consider only perfect secrecy rates. The secrecy capacity region is defined as the closure of all achievable rate tuples.
. Hence, we consider only perfect secrecy rates. The secrecy capacity region is defined as the closure of all achievable rate tuples.
The secrecy capacity region of the degraded multireceiver wiretap channel with a more noisy eavesdropper is given by the following theorem whose proof is provided in Appendix .
Theorem 1.
The secrecy capacity region of the degraded multireceiver wiretap channel with a more noisy eavesdropper is given by the union of the rate tuples  satisfying
satisfying

where  , and the union is over all probability distributions of the form
, and the union is over all probability distributions of the form

Remark 1.
Theorem 1 implies that a modified version of superposition coding can achieve the boundary of the capacity region. The difference between the superposition coding scheme used to achieve (5) and the standard one in [24], which is used to achieve the capacity region of the degraded broadcast channel, is that the former uses stochastic encoding in each layer of the code to associate each message with many codewords. This controlled amount of redundancy prevents the eavesdropper from being able to decode the message.
As stated earlier, the degraded multireceiver wiretap channel with a more noisy eavesdropper contains the degraded multireceiver wiretap channel which requires the eavesdropper to be degraded with respect to all users as stated in (3). Thus, we can specialize our result in Theorem 1 to the degraded multireceiver wiretap channel as given in the following corollary.
Corollary 2.
The secrecy capacity region of the degraded multireceiver wiretap channel is given by the union of the rate tuples  satisfying
satisfying

where  , and the union is over all probability distributions of the form
, and the union is over all probability distributions of the form

The proof of this corollary can be carried out from Theorem 1 by noting the following identity:

and the following Markov chains:

We acknowledge an independent and concurrent work regarding the degraded multireceiver wiretap channel. The work in [9] considers the two-user case and establishes the secrecy capacity region as well.
So far we have determined the entire secrecy capacity region of the degraded multireceiver wiretap channel with a more noisy eavesdropper. This class of channels requires a certain degradation order among the legitimate receivers which may be viewed as being too restrictive from a practical point of view. Our goal is to consider progressively more general channel models. Toward that goal, in the following section, we consider channel models where the users are not ordered in a degradedness or noisiness order. However, the concepts of degradedness and noisiness are essential in proving capacity results. In the following section, we will consider multireceiver broadcast channels which are composed of independent subchannels. We will assume some noisiness properties in these subchannels in order to derive certain capacity results. However, even though the subchannels will have certain noisiness properties, the overall broadcast channel will not have any degradedness or noisiness properties.
3. Parallel Multireceiver Wiretap Channels
Here, we investigate the parallel multireceiver wiretap channel where the transmitter communicates with  legitimate receivers using
legitimate receivers using  independent subchannels in the presence of an eavesdropper, see Figure 3. The channel transition probability of a parallel multireceiver wiretap channel is
independent subchannels in the presence of an eavesdropper, see Figure 3. The channel transition probability of a parallel multireceiver wiretap channel is

where  is the input in the
is the input in the  th subchannel where
th subchannel where  is the corresponding channel input alphabet,
is the corresponding channel input alphabet,  (resp.,
(resp.,  ) is the output in the
) is the output in the  th user's (resp., eavesdropper's)
th user's (resp., eavesdropper's)  th subchannel where
th subchannel where  (resp.,
(resp.,  ) is the
) is the  th user's (resp., eavesdropper's)
th user's (resp., eavesdropper's)  th subchannel output alphabet.
th subchannel output alphabet.
We note that the parallel multireceiver wiretap channel can be regarded as an extension of the parallel wiretap channel [21, 22] to the case of multiple legitimate users. Though the work in [21, 22] establishes the secrecy capacity of the parallel wiretap channel for the most general case, for the parallel multireceiver wiretap channel, obtaining the secrecy capacity region for the most general case seems to be intractable for now. Thus, in this section, we investigate special classes of parallel multireceiver wiretap channels. These channel models contain the class of channel models studied in [8] as a special case. Similar to [8], our emphasis will be on the common message secrecy capacity and the sum secrecy capacity.
3.1. The Common Message Secrecy Capacity
We first consider the simplest possible scenario where the transmitter sends a common confidential message to all users. Despite its simplicity, the secrecy capacity of a common confidential message (hereafter will be called the common message secrecy capacity) in a general broadcast channel is unknown.
The common message secrecy capacity for a special class of parallel multireceiver wiretap channels was studied in [8]. In this class of parallel multireceiver wiretap channels [8], each subchannel exhibits a certain degradation order which is not necessarily the same for all subchannels, that is, the following Markov chain is satisfied:

in the  th subchannel, where
th subchannel, where  is a permutation of
is a permutation of  . Hereafter, we call this channel the parallel degraded multireceiver wiretap channel.(In [8], these channels are called reversely degraded parallel channels. Here, we call them parallel degraded multireceiver wiretap channels to be consistent with the terminology used in the rest of the paper.) Although [8] established the common message secrecy capacity for this class of channels, in fact, their result is valid for the broader class in which we have either
. Hereafter, we call this channel the parallel degraded multireceiver wiretap channel.(In [8], these channels are called reversely degraded parallel channels. Here, we call them parallel degraded multireceiver wiretap channels to be consistent with the terminology used in the rest of the paper.) Although [8] established the common message secrecy capacity for this class of channels, in fact, their result is valid for the broader class in which we have either

or

valid for every  and for any
and for any  pair where
pair where  ,
,  . Thus, it is sufficient to have a degradedness order between each user and the eavesdropper in any subchannel instead of the long Markov chain between all users and the eavesdropper as in (12).
. Thus, it is sufficient to have a degradedness order between each user and the eavesdropper in any subchannel instead of the long Markov chain between all users and the eavesdropper as in (12).
Here, we focus on a broader class of channels where in each subchannel, for any given user, either the user's channel is less noisy than the eavesdropper's channel or vice versa. More formally, we have either

or

for all  and any
and any  pair where
pair where  ,
,  . Hereafter, we call this channel the parallel multireceiver wiretap channel with a more noisy eavesdropper. Since the Markov chain in (12) implies either (15) or (16), the parallel multireceiver wiretap channel with a more noisy eavesdropper contains the parallel degraded multireceiver wiretap channel studied in [8].
. Hereafter, we call this channel the parallel multireceiver wiretap channel with a more noisy eavesdropper. Since the Markov chain in (12) implies either (15) or (16), the parallel multireceiver wiretap channel with a more noisy eavesdropper contains the parallel degraded multireceiver wiretap channel studied in [8].
A  code for this channel consists of a message set,
code for this channel consists of a message set,  , an encoder,
, an encoder,  ,
,  decoders, one at each legitimate receiver
decoders, one at each legitimate receiver  . The probability of error is defined as
. The probability of error is defined as  where
where  is the
is the  th user's decoder output. The secrecy of the common message is measured through the equivocation rate which is defined as
th user's decoder output. The secrecy of the common message is measured through the equivocation rate which is defined as  . A common message secrecy rate,
. A common message secrecy rate,  , is said to be achievable if there exists a code such that
, is said to be achievable if there exists a code such that  , and
, and

The common message secrecy capacity is the supremum of all achievable secrecy rates.
The common message secrecy capacity of the parallel multireceiver wiretap channel with a more noisy eavesdropper is stated in the following theorem whose proof is given in Appendix .
Theorem 3.
The common message secrecy capacity,  , of the parallel multireceiver wiretap channel with a more noisy eavesdropper is given by
, of the parallel multireceiver wiretap channel with a more noisy eavesdropper is given by

where the maximization is over all distributions of the form  .
.
Remark 2.
Theorem 3 implies that we should not use the subchannels in which there is no user that has a less noisy channel than the eavesdropper. Moreover, Theorem 3 shows that the use of independent inputs in each subchannel is sufficient to achieve the capacity, that is, inducing correlation between channel inputs of subchannels cannot provide any improvement. This is similar to the results of [25, 26] in the sense that the work in [25, 26] established the optimality of the use of independent inputs in each subchannel for the product of two degraded broadcast channels.
As stated earlier, the parallel multireceiver wiretap channel with a more noisy eavesdropper encompasses the parallel degraded multireceiver wiretap channel studied in [8]. Hence, we can specialize Theorem 3 to recover the common message secrecy capacity of the parallel degraded multireceiver wiretap channel established in [8]. This is stated in the following corollary whose proof can be carried out from Theorem 3 by noting the Markov chain  .
.
Corollary 4.
The common message secrecy capacity of the parallel degraded multireceiver wiretap channel is given by

where the maximization is over all distributions of the form  .
.
3.2. The Sum Secrecy Capacity
We now consider the scenario where the transmitter sends an independent confidential message to each legitimate receiver, and focus on the sum secrecy capacity. We consider a class of parallel multireceiver wiretap channels where the legitimate receivers and the eavesdropper exhibit a certain less noisiness order in each subchannel. These less noisiness orders are not necessarily the same for all subchannels. Therefore, the overall channel does not have a less noisiness order. In the  th subchannel, for all
th subchannel, for all  , we have
, we have

where  is a permutation of
is a permutation of  . We call this channel the parallel multireceiver wiretap channel with a less noisiness order in each subchannel. We note that this class of channels is a subset of the parallel multireceiver wiretap channel with a more noisy eavesdropper studied in Section 3.1, because of the additional ordering imposed between users' subchannels. We also note that the class of parallel degraded multireceiver wiretap channels with a degradedness order in each subchannel studied in [8] is not only a subset of parallel multireceiver wiretap channels with a more noisy eavesdropper studied in Section 3.1 but also a subset of parallel multireceiver wiretap channels with a less noisiness order in each subchannel studied in this section.
. We call this channel the parallel multireceiver wiretap channel with a less noisiness order in each subchannel. We note that this class of channels is a subset of the parallel multireceiver wiretap channel with a more noisy eavesdropper studied in Section 3.1, because of the additional ordering imposed between users' subchannels. We also note that the class of parallel degraded multireceiver wiretap channels with a degradedness order in each subchannel studied in [8] is not only a subset of parallel multireceiver wiretap channels with a more noisy eavesdropper studied in Section 3.1 but also a subset of parallel multireceiver wiretap channels with a less noisiness order in each subchannel studied in this section.
A  code for this channel consists of
code for this channel consists of  message sets,
message sets,  , an encoder,
, an encoder,  ,
,  decoders, one at each legitimate receiver
decoders, one at each legitimate receiver  . The probability of error is defined as
. The probability of error is defined as  where
where  is the
is the  th user's decoder output. The secrecy is measured through the equivocation rate which is defined as
th user's decoder output. The secrecy is measured through the equivocation rate which is defined as  . A sum secrecy rate,
. A sum secrecy rate,  , is said to be achievable if there exists a code such that
, is said to be achievable if there exists a code such that  , and
, and

The sum secrecy capacity is defined to be the supremum of all achievable sum secrecy rates.
The sum secrecy capacity for the class of parallel multireceiver wiretap channels with a less noisiness order in each subchannel studied in this section is stated in the following theorem whose proof is given in Appendix .
Theorem 5.
The sum secrecy capacity of the parallel multireceiver wiretap channel with a less noisiness order in each subchannel is given by

where the maximization is over all input distributions of the form  and
and  denotes the index of the strongest user in the
denotes the index of the strongest user in the  th subchannel in the sense that
th subchannel in the sense that

for all  and any
and any  .
.
Remark 3.
Theorem 5 implies that the sum secrecy capacity is achieved by sending information only to the strongest user in each subchannel. As in Theorem 3, here also, the use of independent inputs for each subchannel is capacity-achieving, which is again reminiscent of the result in [25, 26] about the optimality of the use of independent inputs in each subchannel for the product of two degraded broadcast channels.
As mentioned earlier, since the class of parallel multireceiver wiretap channels with a less noisiness order in each subchannel contains the class of parallel degraded multireceiver wiretap channels studied in [8], Theorem 5 can be specialized to give the sum secrecy capacity of the latter class of channels as well. This result was originally obtained in [8]. This is stated in the following corollary. Since the proof of this corollary is similar to the proof of Corollary 4, we omit its proof.
Corollary 6.
The sum secrecy capacity of the parallel degraded multireceiver wiretap channel is given by

where the maximization is over all input distributions of the form  and
and  denotes the index of the strongest user in the
denotes the index of the strongest user in the  th subchannel in the sense that
th subchannel in the sense that

for all input distributions on  and any
and any  .
.
So far, we have considered special classes of parallel multireceiver wiretap channels for specific scenarios and obtained results similar to [8], only for broader classes of channels. In particular, in Section 3.1, we focused on the transmission of a common message, whereas in Section 3.2, we focused on the sum secrecy capacity when only independent messages are transmitted to all users. In the subsequent sections, we will specialize our channel model, but we will develop stronger and more comprehensive results. In particular, we will let the transmitter send both common and independent messages, and we will characterize the entire secrecy capacity region.
4. Parallel Degraded Multireceiver Wiretap Channels
We consider a special class of parallel degraded multireceiver wiretap channels with two subchannels, two users, and one eavesdropper. We consider the most general scenario where each user receives both an independent message and a common message. All messages are to be kept secret from the eavesdropper.
For the special class of parallel degraded multireceiver wiretap channels in consideration, there is a specific degradation order in each subchannel. In particular, we have the following Markov chain:

in the first subchannel, and the following Markov chain:

in the second subchannel. Consequently, although in each subchannel, one user is degraded with respect to the other one, this does not hold for the overall channel, and the overall channel is not degraded for any user. The corresponding channel transition probability is

If we ignore the eavesdropper by setting  , this channel model reduces to the broadcast channel that was studied in [25, 26].
, this channel model reduces to the broadcast channel that was studied in [25, 26].
A  code for this channel consists of three message sets,
code for this channel consists of three message sets,  ,
,  , one encoder
, one encoder  , two decoders one at each legitimate receiver
, two decoders one at each legitimate receiver  . The probability of error is defined as
. The probability of error is defined as  . A rate tuple
. A rate tuple  is said to be achievable if there exists a code such that
is said to be achievable if there exists a code such that  and
and

where  denotes any subset of
denotes any subset of  . The secrecy capacity region is the closure of all achievable secrecy rate tuples.
. The secrecy capacity region is the closure of all achievable secrecy rate tuples.
The secrecy capacity region of this parallel degraded multireceiver wiretap channel is characterized by the following theorem whose proof is given in Appendix .
Theorem 7.
The secrecy capacity region of the parallel degraded multireceiver wiretap channel defined by (28) is the union of the rate tuples  satisfying
satisfying

where the union is over all distributions of the form  .
.
Remark 4.
If we let the encoder use an arbitrary joint distribution  instead of the ones that satisfy
instead of the ones that satisfy  , this would not enlarge the region given in Theorem 7, because all rate expressions in Theorem 7 depend on either
, this would not enlarge the region given in Theorem 7, because all rate expressions in Theorem 7 depend on either  or
or  but not on the joint distribution
but not on the joint distribution  .
.
Remark 5.
The capacity-achieving scheme uses either superposition coding in both subchannels or superposition coding in one of the subchannels, and a dedicated transmission in the other one. We again note that this superposition coding is different from the standard one [24] in the sense that it associates each message with many codewords by using stochastic encoding at each layer of the code due to secrecy concerns.
Remark 6.
If we set  , we recover the capacity region of the underlying broadcast channel [26].
, we recover the capacity region of the underlying broadcast channel [26].
Remark 7.
If we disable one of the subchannels, say the first one, by setting  , the parallel degraded multireceiver wiretap channel of this section reduces to the degraded multireceiver wiretap channel of Section 2. The corresponding secrecy capacity region is then given by the union of the rate tuples
, the parallel degraded multireceiver wiretap channel of this section reduces to the degraded multireceiver wiretap channel of Section 2. The corresponding secrecy capacity region is then given by the union of the rate tuples  satisfying
satisfying

where the union is over all  . This region can be obtained through either Corollary 2 or Theorem 7 (by setting
. This region can be obtained through either Corollary 2 or Theorem 7 (by setting  and eliminating redundant bounds) implying the consistency of the results.
and eliminating redundant bounds) implying the consistency of the results.
Next, we consider the scenario where the transmitter does not send a common message, and find the secrecy capacity region.
Corollary 8.
The secrecy capacity region of the parallel degraded multireceiver wiretap channel defined by (28) with no common message is given by the union of the rate pairs  satisfying
satisfying

where the union is over all distributions of the form  .
.
Proof.
Since the common message rate can be exchanged with any user's independent message rate, we set  where
where  . Plugging these expressions into the rates in Theorem 7 and using Fourier-Moztkin elimination, we get the region given in the corollary.
. Plugging these expressions into the rates in Theorem 7 and using Fourier-Moztkin elimination, we get the region given in the corollary.
Remark 8.
If we disable the eavesdropper by setting  , we recover the capacity region of the underlying broadcast channel without a common message, which was found originally in [25].
, we recover the capacity region of the underlying broadcast channel without a common message, which was found originally in [25].
At this point, one may ask whether the results of this section can be extended to arbitrary numbers of users and parallel subchannels. Once we have Theorem 7, the extension of the results to an arbitrary number of parallel subchannels is rather straightforward. Let us consider the parallel degraded multireceiver wiretap channel with  subchannels, and in each subchannel, we have either the following Markov chain:
subchannels, and in each subchannel, we have either the following Markov chain:

or this Markov chain:

for any  . We define the set of indices
. We define the set of indices  (resp.,
(resp.,  ) as those where for every
) as those where for every  (resp.,
(resp.,  ), the Markov chain in (33) (resp., in (34)) is satisfied. Then, using Theorem 7, we obtain the secrecy capacity region of the channel with two users and
), the Markov chain in (33) (resp., in (34)) is satisfied. Then, using Theorem 7, we obtain the secrecy capacity region of the channel with two users and  subchannels as given in the following theorem which is proved in Appendix .
subchannels as given in the following theorem which is proved in Appendix .
Theorem 9.
The secrecy capacity region of the parallel degraded multireceiver wiretap channel with  subchannels, where each subchannel satisfies either (33) or (34), is given by the union of the rate tuples
subchannels, where each subchannel satisfies either (33) or (34), is given by the union of the rate tuples  satisfying
satisfying

where the union is over all distributions of the form  .
.
We are now left with the question whether these results can be generalized to an arbitrary number of users. If we consider the parallel degraded multireceiver wiretap channel with more than two subchannels and an arbitrary number of users, the secrecy capacity region for the scenario where each user receives a common message in addition to an independent message does not seem to be characterizable. Our intuition comes from the fact that, as of now, the capacity region of the corresponding broadcast channel without secrecy constraints is unknown [27]. However, if we consider the scenario where each user receives only an independent message, that is, there is no common message, then the secrecy capacity region may be found, because the capacity region of the corresponding broadcast channel without secrecy constraints can be established [27], although there is no explicit expression for it in literature. We expect this particular generalization to be rather straightforward, and do not pursue it here.
5. Sum of Degraded Multireceiver Wiretap Channels
We now consider a different multireceiver wiretap channel which can be viewed as a sum of two degraded multireceiver wiretap channels with two users and one eavesdropper. In this channel model, the transmitter has two nonintersecting input alphabets, that is,  with
with  , and each receiver has two nonintersecting alphabets, that is,
, and each receiver has two nonintersecting alphabets, that is,  with
with  for the
for the  th user,
th user,  , and
, and  with
with  for the eavesdropper. The channel is again memoryless with transition probability
for the eavesdropper. The channel is again memoryless with transition probability

where  ,
,  and
and  . Thus, if the transmitter chooses to use its first alphabet, that is,
. Thus, if the transmitter chooses to use its first alphabet, that is,  , the second user (resp. eavesdropper) receives a degraded version of user 1's (resp., user 2's) observation. However, if the transmitter uses its second alphabet, that is,
, the second user (resp. eavesdropper) receives a degraded version of user 1's (resp., user 2's) observation. However, if the transmitter uses its second alphabet, that is,  , the first user (resp. eavesdropper) receives a degraded version of user 2's (resp. user 1's) observation. Consequently, the overall channel is not degraded from any user's perspective, however, it is degraded from eavesdropper's perspective.
, the first user (resp. eavesdropper) receives a degraded version of user 2's (resp. user 1's) observation. Consequently, the overall channel is not degraded from any user's perspective, however, it is degraded from eavesdropper's perspective.
A  code for this channel consists of three message sets,
code for this channel consists of three message sets,  ,
,  , one encoder
, one encoder  and two decoders, one at each legitimate receiver,
and two decoders, one at each legitimate receiver,  . The probability of error is defined as
. The probability of error is defined as  . A rate tuple
. A rate tuple  is said to be achievable if there exists a code with
is said to be achievable if there exists a code with  and
and

where  denotes any subset of
denotes any subset of  . The secrecy capacity region is the closure of all achievable secrecy rate tuples.
. The secrecy capacity region is the closure of all achievable secrecy rate tuples.
The secrecy capacity region of this channel is given in the following theorem which is proved in Appendix .
Theorem 10.
The secrecy capacity region of the sum of two degraded multireceiver wiretap channels is given by the union of the rate tuples  satisfying
satisfying

where the union is over all  and distributions of the form
and distributions of the form  .
.
Remark 9.
This channel model is similar to the parallel degraded multireceiver wiretap channel of the previous section in the sense that it can be viewed to consist of two parallel subchannels, however, now the transmitter cannot use both subchannels simultaneously. Instead, it should invoke a time-sharing approach between these two so-called parallel subchannels ( reflects this concern). Moreover, superposition coding scheme again achieves the boundary of the secrecy capacity region, however, it differs from the standard one [24] in the sense that it needs to be modified to incorporate secrecy constraints, that is, it needs to use stochastic encoding to associate each message with multiple codewords.
reflects this concern). Moreover, superposition coding scheme again achieves the boundary of the secrecy capacity region, however, it differs from the standard one [24] in the sense that it needs to be modified to incorporate secrecy constraints, that is, it needs to use stochastic encoding to associate each message with multiple codewords.
Remark 10.
An interesting point about the secrecy capacity region is that if we drop the secrecy constraints by setting  , we are unable to recover the capacity region of the corresponding broadcast channel that was found in [26]. After setting
, we are unable to recover the capacity region of the corresponding broadcast channel that was found in [26]. After setting  , we note that each expression in Theorem 10 and its counterpart describing the capacity region [26] differ by exactly
, we note that each expression in Theorem 10 and its counterpart describing the capacity region [26] differ by exactly  . The reason for this is as follows. Here,
. The reason for this is as follows. Here,  not only denotes the time-sharing variable but also carries an additional information, that is, the change of the channel that is in use is part of the information transmission. However, since the eavesdropper can also decode these messages, the term
not only denotes the time-sharing variable but also carries an additional information, that is, the change of the channel that is in use is part of the information transmission. However, since the eavesdropper can also decode these messages, the term  , which is the amount of information that can be transmitted via changes of the channel in use, disappears in the secrecy capacity region.
, which is the amount of information that can be transmitted via changes of the channel in use, disappears in the secrecy capacity region.
6. Conclusions
In this paper, we studied secure broadcasting to many users in the presence of an eavesdropper. Characterizing the secrecy capacity region of this channel in its most general form seems to be intractable for now, since the version of this problem without any secrecy constraints is the broadcast channel with an arbitrary number of receivers, whose capacity region is open. Consequently, we took the approach of considering special classes of channels. In particular, we considered degraded multireceiver wiretap channels, parallel multireceiver wiretap channels with a more noisy eavesdropper, parallel multireceiver wiretap channels with less noisiness orderings in each subchannel, and parallel degraded multireceiver wiretap channels. For each channel model, we obtained either partial characterization of the secrecy capacity region or the entire region.
Appendices
A. Proof of Theorem 1
First, we show achievability, then provide the converse.
A.1. Achievability
Fix the probability distribution as

Codebook Generation
-
(i)
Generate
 length-
length- sequences
sequences 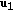 through
through  and index them as
and index them as  where
where  ,
, 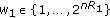 and
and  .
. -
(ii)
For each
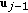 , where
, where  , generate
, generate  length-
length- sequences
sequences 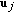 through
through 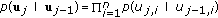 and index them as
and index them as 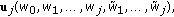 where
where 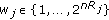 and
and 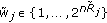 .
. -
(iii)
Finally, for each
 , generate
, generate  length-
length- sequences
sequences  through
through 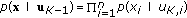 and index them as
and index them as  where
where  and
and  .
. -
(iv)
Furthermore, we set
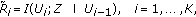 (A.2)
(A.2)where
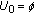 and
and  .
.
 ncoding
ncoding
Assume the messages to be transmitted are  . Then, the encoder randomly picks a set
. Then, the encoder randomly picks a set  and sends
and sends  .
.
Deco ing
ing
It is straightforward to see that if the following conditions are satisfied:

then all users can decode both the common message and the independent message directed to itself with vanishingly small error probability. Moreover, since the channel is degraded, each user, say the  th one, can decode all of the independent messages intended for the users whose channels are degraded with respect to the
th one, can decode all of the independent messages intended for the users whose channels are degraded with respect to the  th user's channel. Thus, these degraded users' rates can be exploited to increase the
th user's channel. Thus, these degraded users' rates can be exploited to increase the  th user's rate which leads to the following achievable region:
th user's rate which leads to the following achievable region:

where  and
and  . Moreover, after eliminating
. Moreover, after eliminating  , (A.4) can be expressed as
, (A.4) can be expressed as

where we used the fact that

where the second and the third equalities are due to the following Markov chain:

Equivocation C ulation
ulation
We now calculate the equivocation of the code described above. To that end, we first introduce the following lemma which states that a code satisfying the sum rate secrecy constraint fulfills all other secrecy constraints.
Lemma 11.
If the sum rate secrecy constraint is satisfied, that is,

then all other secrecy constraints are satisfied as well, that is,

where  denotes any subset of
denotes any subset of  .
.
Proof.
The proof of this lemma is as follows.





where (A.11) is due to the fact that we assumed that sum rate secrecy constraint (A.8) is satisfied and (A.13) follows from

which is a consequence of the fact that message sets are uniformly and independently distributed.
Hence, it is sufficient to check whether coding scheme presented satisfies the sum rate secrecy constraint.




where each term will be treated separately. Since given  ,
,  can take
can take  values uniformly, the first term is
values uniformly, the first term is


where the first equality follows from the following Markov chain:

The second term in (A.19) is



where (A.24) follows from the Markov chain in (A.22) and (A.25) can be shown by following the approach devised in [1]. We now bound the third term in (A.19). To that end, assume that the eavesdropper tries to decode  using the side information
using the side information  which is equivalent to decoding
which is equivalent to decoding  . Since
. Since  s are selected to ensure that the eavesdropper can decode them successively, see (A.2), then using Fano's lemma, we have
s are selected to ensure that the eavesdropper can decode them successively, see (A.2), then using Fano's lemma, we have

Thus, using (A.21), (A.25), and (A.26) in (A.19), we get


where (A.28) follows from the following, see (A.2) and (A.6),

A.2. Converse
First let us define the following auxiliary random variables:

which satisfy the following Markov chain:

To provide a converse, we will show

where  ,
,  . We show this in three steps. First, let us write down
. We show this in three steps. First, let us write down

The first term on the right-hand side of (A.33) is bounded as follows:










where (A.34) follows from Fano's lemma, (A.35) is obtained using Csiszar-Korner identity (see [2, Lemma 7]), and (A.36) is due to the fact that

which follows from the fact that each user's channel is less noisy with respect to the eavesdropper. Similarly, (A.38) follows from the fact that

which is a consequence of the fact that each user's channel is less noisy with respect to the eavesdropper's channel. Finally, (A.42) is due to the following Markov chain:

which is a consequence of the fact that the legitimate receivers exhibit a degradation order.
We now bound the terms of the summation in (A.33) for  . Let us use the shorthand notation,
. Let us use the shorthand notation,  , then
, then





where (A.47) follows from Fano's lemma, (A.48) is obtained through Csiszar-Korner identity, and (A.49) is a consequence of the fact that

which follows from the fact that each user's channel is less noisy with respect to the eavesdropper's channel. Finally, we bound the following term where we again use the shorthand notation  ,
,







where (A.53) follows from Fano's lemma, (A.54) is obtained by using Csiszar-Korner identity, and (A.55) follows from the fact that

which is due to the fact that each user's channel is less noisy with respect to the eavesdropper and (A.58) is due to the Markov chain:

which follows from the fact that the channel is memoryless. Finally, plugging (A.43), (A.51), and (A.59) into (A.33), we get

where  and
and  , and this concludes the converse.
, and this concludes the converse.
B. Proof of Theorem 3
Achievability of these rates follows from [8, Proposition 2]. We provide the converse. First let us define the following random variables:

where  ,
,  . Start with the definition
. Start with the definition







where (B.6) and (B.8) are due the following identities:

respectively, which are due to [2, Lemma 7]. Now, we will bound each summand in (B.8) separately. First, define the following variables:

Hence, the summand in (B.8) can be written as follows:








where (B.16) and (B.18) follow from the following identities:

respectively, which are again due to [2, Lemma 7]. Now, define the set of subchannels, say  , in which the
, in which the  th user is less noisy with respect to the eavesdropper. Thus, the summands in (B.18) for
th user is less noisy with respect to the eavesdropper. Thus, the summands in (B.18) for  are negative and by dropping them, we can bound (B.18) as follows:
are negative and by dropping them, we can bound (B.18) as follows:

Moreover, for  , we have
, we have


where both are due to the fact that for  , in this subchannel the
, in this subchannel the  th user is less noisy with respect to the eavesdropper. Therefore, adding (B.21) and (B.22) to each summand in (B.20), we get the following bound:
th user is less noisy with respect to the eavesdropper. Therefore, adding (B.21) and (B.22) to each summand in (B.20), we get the following bound:


where an equality follows from the following Markov chain:

which is a consequence of the facts that channel is memoryless and subchannels are independent. Finally, using (B.24) in (B.8), we get

which completes the proof.
C. Proof of Theorem 5
Achievability of Theorem 5 is a consequence of the achievability result for wiretap channels in [2]. We provide the converse proof here. We first define the function  which denotes the index of the strongest user in the
which denotes the index of the strongest user in the  th subchannel in the sense that
th subchannel in the sense that

for all  and any
and any  . Moreover, we define the following shorthand notations:
. Moreover, we define the following shorthand notations:

We first introduce the following lemma.
Lemma 12.
For the parallel multireceiver wiretap channel with less noisiness order, one has

Proof.
Consecutive uses of Csiszar-Korner identity [2], as in Appendix , yield

where each of the summand is negative, that is, we have

because  is the observation of the strongest user in the
is the observation of the strongest user in the  th subchannel, that is, its channel is less noisy with respect to all other users in the
th subchannel, that is, its channel is less noisy with respect to all other users in the  th subchannel. This concludes the proof of the lemma.
th subchannel. This concludes the proof of the lemma.
This lemma implies that

where the second inequality is due to Fano's lemma. Using (C.6), we get

where the first inequality follows from the fact that conditioning cannot increase entropy.
We now start the converse proof:


where (C.8) is a consequence of (C.7) and (C.9) is obtained via consecutive uses of the Csiszar-Korner identity [2] as we did in Appendix . We define the set of indices  such that for all
such that for all  , the strongest user in the
, the strongest user in the  th subchannel has a less noisy channel with respect to the eavesdropper, that is, we have
th subchannel has a less noisy channel with respect to the eavesdropper, that is, we have

for all  and any
and any  . Thus, we can further bound (C.9) as follows:
. Thus, we can further bound (C.9) as follows:




where (C.11) is obtained by dropping the negative terms, (C.12)-(C.13) are due to the following inequalities:

which come from the fact that for any  , the strongest user in the
, the strongest user in the  th subchannel has a less noisy channel with respect to the eavesdropper. Finally, we get (C.14) using the following Markov chain:
th subchannel has a less noisy channel with respect to the eavesdropper. Finally, we get (C.14) using the following Markov chain:

which is a consequence of the facts that channel is memoryless, and the subchannels are independent.
D. Proofs of Theorems 7 and 9
D.1. Proof of Theorem 7
We prove Theorem 7 in two parts, first achievability and then converse. Throughout the proof, we use the shorthand notations  ,
,  ,
,  .
.
D.1.1. Achievability
To show the achievability of the region given by (30), first we need to note that the boundary of this region can be decomposed into three surfaces as follows [26].
-
(i)
First surface:
 (D.1)
(D.1) -
(ii)
Second surface:
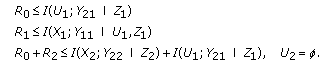 (D.2)
(D.2) -
(iii)
Third surface:
 (D.3)
(D.3)
We now show the achievability of these regions separately. Start with the first region.
Proposition 13.
The region defined by (D.1) is achievable.
Proof.
Fix the probability distribution

Co book Generation
book Generation
-
(i)
Split the private message rate of user 1 as
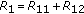 .
. -
(ii)
Generate
 length-
length- sequences
sequences  through
through 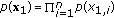 and index them as
and index them as  where
where 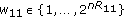 and
and 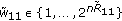 .
. -
(iii)
Generate
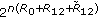 length-
length- sequences
sequences 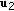 through
through  and index them as
and index them as  where
where 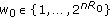 ,
,  and
and 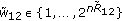 .
. -
(iv)
For each
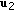 , generate
, generate 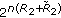 length-
length- sequences
sequences 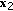 through
through  and index them as
and index them as  where
where 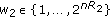 ,
,  .
. -
(v)
Furthermore, set the confusion message rates as follows:
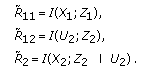 (D.5)
(D.5)
E coding
coding
If  is the message to be transmitted, then the receiver randomly picks
is the message to be transmitted, then the receiver randomly picks  and sends the corresponding codewords through each channel.
and sends the corresponding codewords through each channel.
D oding
oding
It is straightforward to see that if the following conditions are satisfied, then both users can decode the messages directed to themselves with vanishingly small error probability.

After eliminating  and
and  and plugging the values of
and plugging the values of  , we can reach the following conditions:
, we can reach the following conditions:

where we used the degradedness of the channel. Thus, we only need to show that this coding scheme satisfies the secrecy constraints.
Equivocation Computation
As shown previously in Lemma 11 of Appendix , checking the sum rate secrecy condition is sufficient:



We treat each term in (D.10) separately. The first term in (D.10) is

where the first equality is due to the independence of  and
and  , and the second equality is due the fact that both messages and confusion codewords are uniformly distributed. The second and the third terms in (D.10) are
, and the second equality is due the fact that both messages and confusion codewords are uniformly distributed. The second and the third terms in (D.10) are






where the equalities in (D.14) and (D.15) are due to the following Markov chains:

respectively, and the last inequality in (D.17) can be shown using the technique devised in [1]. To bound the last term in (D.10), assume that the eavesdropper tries to decode  using the side information
using the side information  and its observation. Since the rates of the confusion codewords are selected such that the eavesdropper can decode them given
and its observation. Since the rates of the confusion codewords are selected such that the eavesdropper can decode them given  (see (D.5)), using Fano's lemma, we get
(see (D.5)), using Fano's lemma, we get

for the third term in (D.10). Plugging (D.11), (D.17), and (D.19) into (D.10), we get

which completes the proof.
Achievability of the region defined by (D.2) follows due to symmetry. We now show the achievability of the region defined by (D.3).
Proposition 14.
The region described by (D.3) is achievable.
Proof.
Fix the probability distribution as follows:

Codebook Generation
-
(i)
Generate
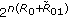 length-
length- sequences
sequences 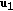 through
through 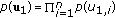 and index them as
and index them as  where
where  ,
,  .
. -
(ii)
For each
 , generate
, generate  length-
length- sequences
sequences  through
through  and index them as
and index them as  where
where  ,
,  .
. -
(iii)
Generate
 length-
length- sequences
sequences  through
through 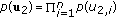 and index them as
and index them as 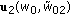 where
where 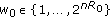 ,
, 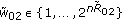 .
. -
(iv)
For each
 , generate
, generate  length-
length- sequences
sequences 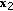 through
through 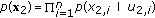 and index them as
and index them as  where
where 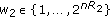 ,
, 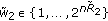 .
. -
(v)
Moreover, set the rates of confusion messages as follows:
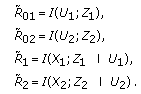 (D.22)
(D.22)
En oding
oding
Assume that the messages to be transmitted are  . Then, after randomly picking the tuple
. Then, after randomly picking the tuple  , corresponding codewords are sent.
, corresponding codewords are sent.
 ecoding
ecoding
Users decode  using their both observations. If
using their both observations. If  is the only message that satisfies
is the only message that satisfies

simultaneously for user  ,
,  is declared to be transmitted. Assume
is declared to be transmitted. Assume  is transmitted. The error probability for user
is transmitted. The error probability for user  can be bounded as
can be bounded as

using the union bound. Let us consider the following:

Similarly, we have

Thus, the probability of declaring that the  th message was transmitted can be bounded as
th message was transmitted can be bounded as

where the first equality is due to the independence of subchannels and codebooks used for each channel. Therefore, error probability can be bounded as

which vanishes if the following are satisfied:

After decoding the common message, both users decode their private messages if the rates satisfy


After plugging the values of  given by (D.22) into (D.29)–(D.31), one can recover the region described by (D.3) using the degradedness of the channel.
given by (D.22) into (D.29)–(D.31), one can recover the region described by (D.3) using the degradedness of the channel.
Equivocation Calculation
It is sufficient to check the sum rate constraint:




where each term will be treated separately. The first term is


where we first use the fact that  and
and  are independent given
are independent given  and secondly, we use the fact that messages are uniformly distributed. The second and third terms of (D.35) are
and secondly, we use the fact that messages are uniformly distributed. The second and third terms of (D.35) are




where the first equality is due to the independence of the subchannels. We now consider the last term of (D.35) for which assume that eavesdropper tries to decode  using the side information
using the side information  and its observation. Since the rates of the confusion messages are selected to ensure that the eavesdropper can decode
and its observation. Since the rates of the confusion messages are selected to ensure that the eavesdropper can decode  given
given  (see (D.22)), using Fano's lemma we have
(see (D.22)), using Fano's lemma we have

Plugging (D.37), (D.41), and (D.42) into (D.35), we have

which concludes the proof.
D.1.2. Converse
First let us define the following auxiliary random variables:

which satisfy the following Markov chains:

We remark that although  and
and  are correlated, at the end of the proof, it will turn out that selection of them as independent will yield the same region. We start with the common message rate:
are correlated, at the end of the proof, it will turn out that selection of them as independent will yield the same region. We start with the common message rate:





where (D.47) is due to Fano's lemma, the equality in (D.48) is due to the fact that the eavesdropper's channel is degraded with respect to the first user's channel. We bound each term in (D.50) separately. First term is





where (D.53) follows from the fact that conditioning cannot increase entropy and the equality in (D.54) is due to the following Markov chains:

both of which are due to the fact that subchannels are independent, memoryless, and degraded. We now consider the second term in (D.50),




where (D.58) follows from the following Markov chains:

both of which are due to the fact that subchannels are independent, memoryless, and degraded. Plugging (D.55) and (D.60) into (D.50), we get the following outer bound on the common rate.

Using the same analysis on the second user, we can obtain the following outer bound on the common rate as well.

We now bound the sum of independent and common message rates for each user,




where (D.64) is due to Fano's lemma, (D.65) is due to the fact that the eavesdropper's channel is degraded with respect to the first user's channel. Using (D.55), the first term in (D.67) can be bounded as

Thus, we only need to bound the second term of (D.67):







where (D.70) is due to the fact that conditioning cannot increase entropy, (D.71) is due to the following Markov chain:

and (D.73) follows from the fact that conditioning cannot increase entropy. Finally, (D.74) is due to the fact that each subchannel is memoryless. Hence, plugging (D.68) and (D.75) into (D.67), we get the following outer bound:

Similarly, for the second user, we can get the following outer bound:

We now bound the sum rates to conclude the converse:






where (D.80) follows from Fano's lemma, (D.81) is due to the fact that the eavesdropper's channel is degraded with respect to both users' channels, (D.83) is obtained by adding and subtracting  from the first term of (D.82). Now, we proceed as follows:
from the first term of (D.82). Now, we proceed as follows:



Adding  to (D.87), we get
to (D.87), we get




where the second term is zero as we show in what follows:

where we used the following Markov chain:

which is a consequence of the degradation orders that subchannels exhibit. Thus, (D.91) can be expressed as




where (D.95) follows from the following Markov chain:

which is due to the degradedness of the channel. Moreover, the second term in (D.97) is zero as we show in what follows:


where (D.100) follows from the following Markov chain:

Thus, (D.97) turns out to be

which can be further bounded as follows:




where (D.104) is due to the fact that conditioning cannot increase entropy, (D.105) is due to the following Markov chain:

Finally, (D.106) is due to our previous result in (D.75). We keep bounding terms in (D.84):







where (D.109) and (D.111) are due to the following Markov chains:

respectively, (D.113) follows from that conditioning cannot increase entropy and (D.114) is due to the following Markov chain:

which is a consequence of the fact that each subchannel is memoryless. Thus, we only need to bound  in (D.84) to reach the outer bound for the sum secrecy rate:
in (D.84) to reach the outer bound for the sum secrecy rate:






where (D.119) is due to the fact that conditioning cannot increase entropy, (D.120) and (D.121) follow from the following Markov chains:

respectively. Thus, plugging (D.106), (D.114), and (D.122) into (D.84), we get the following outer bound on the sum secrecy rate:

Following similar steps, we can also get the following one:

So far, we derived outer bounds, (D.62), (D.63), (D.77), (D.78), (D.124), (D.125), on the capacity region which match the achievable region provided. The only difference can be on the joint distribution that they need to satisfy. However, the outer bounds depend on either  or
or  but not on the joint distribution
but not on the joint distribution  . Hence, for the outer bound, it is sufficient to consider the joint distributions having the form
. Hence, for the outer bound, it is sufficient to consider the joint distributions having the form  . Thus, the outer bounds derived and the achievable region coincide yielding the capacity region.
. Thus, the outer bounds derived and the achievable region coincide yielding the capacity region.
D.2. Proof of Theorem 9
D.2.1. Achievability
To show the achievability of the region given in Theorem 9, we use Theorem 7. First, we group subchannels into two sets  where
where  contains the subchannels in which user
contains the subchannels in which user  has the best observation. In other words, we have the Markov chain:
has the best observation. In other words, we have the Markov chain:

for  and we have this Markov chain:
and we have this Markov chain:

for  .
.
We replace  with
with  ,
,  with
with  ,
,  with
with  ,
,  with
with  , and
, and  with
with  in Theorem 7. Moreover, if we select the pairs
in Theorem 7. Moreover, if we select the pairs  to be mutually independent, we get the following joint distribution:
to be mutually independent, we get the following joint distribution:

which implies that random variable tuples  are mutually independent. Using this fact, one can reach the expressions given in Theorem 9.
are mutually independent. Using this fact, one can reach the expressions given in Theorem 9.
D.2.2. Converse
For the converse part, we again use the proof of Theorem 7. First, without loss of generality, we assume  , and
, and  . We define the following auxiliary random variables:
. We define the following auxiliary random variables:

which satisfy the Markov chains:

Using the analysis carried out for the proof of Theorem 7, we get

where each term will be treated separately. The first term can be bounded as follows:



where (D.133) follows from the Markov chain:

which is due to the degradedness of the subchannels. To this end, we define the following auxiliary random variables:

which satisfy the Markov chains:

Thus, using these new auxiliary random variables in (D.134), we get

We now bound the second term in (D.131) as follows:






where (D.140) follows from the Markov chain:

which is a consequence of the degradedness of the subchannels, (D.141) and (D.142) follow from the fact that conditioning cannot increase entropy, and (D.143) is due to the Markov chain:

which is again a consequence of the degradedness of the subchannels. To this end, we define the following auxiliary random variables:

which satisfy the Markov chains:

Thus, using these new auxiliary random variables in (D.144), we get

Finally, using (D.138) and (D.149) in (D.131), we obtain

Due to symmetry, we also have

We now bound the sum of common and independent message rates. Using the converse proof of Theorem 7, we get

where, for the second term we already obtained, an outer bound given in (D.149). We now bound the first term:




where (D.154) follows from the fact that conditioning cannot increase entropy, and (D.155) is due to the following Markov chain:

which follows from the facts that channel is memoryless and subchannels are independent. Thus, plugging (D.149) and (D.156) into (D.152), we obtain

Due to symmetry, we also have

We now bound the sum secrecy rate. We first borrow the following outer bound from the converse proof of Theorem 7:


where, for the first and third terms, we already obtained outer bounds given in (D.156) and (D.149), respectively. We now bound the second term as follows:






where (D.163) follows from the Markov chain:

which is a consequence of the degradedness of the subchannels, (D.164) is obtained via using the definition of  given in (D.147), and (D.166) follows from the Markov chain:
given in (D.147), and (D.166) follows from the Markov chain:

which is due to the facts that channel is memoryless and subchannels are independent. Thus, plugging (D.149), (D.156), and (D.167) into (D.161), we get

Due to symmetry, we also have

Finally, we note that all outer bounds depend on the distributions  but not on any joint distributions of the tuples
but not on any joint distributions of the tuples  implying that selection of the pairs
implying that selection of the pairs  to be mutually independent is optimum.
to be mutually independent is optimum.
E. Proof of Theorem 10
We prove Theorem 10 in two parts; first, we show achievability, and then we prove the converse.
E.1. Achievability
Similar to what we have done to show the achievability of Theorem 7, we first note that boundary of the capacity region can be decomposed into three surfaces [26].
-
(i)
First surface:
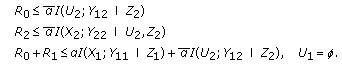 (E.1)
(E.1) -
(ii)
Second surface:
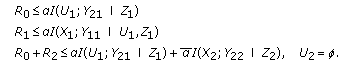 (E.2)
(E.2) -
(iii)
Third surface:
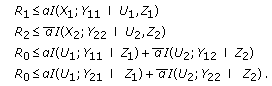 (E.3)
(E.3)
To show the achievability of each surface, we first introduce a codebook structure.
Codebook Structure
Fix the probability distribution as

-
(i)
Generate
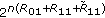 length-
length- sequences
sequences 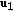 through
through  and index them as
and index them as  where
where  ,
, 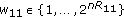 and
and 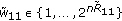 .
. -
(ii)
For each
 , generate
, generate 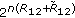 length-
length- sequences
sequences 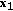 through
through  and index them as
and index them as  where
where  ,
, 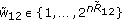 .
. -
(iii)
Generate
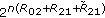 length-
length-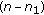 sequences
sequences  through
through  and index them as
and index them as  where
where 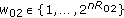 ,
,  and
and 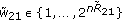 .
. -
(iv)
For each
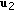 , generate
, generate  length-
length- sequences
sequences  through
through  and index them as
and index them as  where
where  ,
, 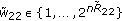 .
. -
(v)
We remark that this codebook uses first channel
 times and the other one
times and the other one 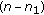 times. We define
times. We define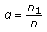 (E.5)
(E.5)and
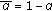 .
. -
(vi)
Furthermore, we set
 (E.6)
(E.6) (E.7)
(E.7) (E.8)
(E.8) (E.9)
(E.9) (E.10)
(E.10) (E.11)
(E.11)
Enc ding
ding
When the transmitted messages are  ,
,  , we randomly pick
, we randomly pick  ,
, and send corresponding codewords.
and send corresponding codewords.
Decodin
Using this codebook structure, we can show that all three surfaces which determine the boundary of the capacity region are achievable. For example, if we set  (that implies
(that implies  ) and
) and  , then we achieve the following rates with vanishingly small error probability:
, then we achieve the following rates with vanishingly small error probability:

Exchanging common message rate with user 1's independent message rate, one can obtain the first surface. Second surface follows from symmetry. For the third surface, we first set  . Moreover, we send common message in its entirety, that is, we do not use a rate splitting for the common message, hence we set
. Moreover, we send common message in its entirety, that is, we do not use a rate splitting for the common message, hence we set  ,
,  . In this case, each user, say the
. In this case, each user, say the  th one, decodes the common message by looking for a unique
th one, decodes the common message by looking for a unique  which satisfies
which satisfies

Following the analysis carried out in (D.24)-(D.29), the sufficient conditions for the common message to be decodable by both users can be found as

After decoding the common message, each user can decode its independent message if

Thus, the third surface can be achieved with vanishingly small error probability. As of now, we showed that all rates in the so-called capacity region are achievable with vanishingly small error probability, however we did not claim anything about the secrecy conditions which will be considered next.
Equivocation Calcula
To complete the achievability part of the proof, we need to show that this codebook structure also satisfies the secrecy conditions. For that purpose, it is sufficient to consider the sum rate secrecy condition:




where each term will be treated separately. The first term is



where the first equality is due to the Markov chain

The equality in (E.21) is due to the fact that  can take
can take  values uniformly, and given
values uniformly, and given  (resp.,
(resp.,  ),
),  (resp.,
(resp.,  ) can take
) can take  (resp.,
(resp.,  ) values with equal probability. To reach (E.22), we use the definitions in (E.6)–(E.11). We consider the second and third terms in (E.19):
) values with equal probability. To reach (E.22), we use the definitions in (E.6)–(E.11). We consider the second and third terms in (E.19):




where (E.24) is due to the fact that conditioning cannot increase entropy, (E.25) follows from the Markov chain:

and (E.27) can be shown using the technique devised in [1]. We bound the fourth term of (E.19). To this end, assume that the eavesdropper tries to decode  given side information
given side information  . Since the confusion message rates are selected as given in (E.6)-(E.9), the eavesdropper can decode them as long as this side information is available.Consequently, the use of Fano's lemma yields
. Since the confusion message rates are selected as given in (E.6)-(E.9), the eavesdropper can decode them as long as this side information is available.Consequently, the use of Fano's lemma yields

Finally, plugging (E.22),(E.27), and (E.29) into (E.19), we get

which completes the achievability part of the proof.
E.2. Converse
First, let us define the following auxiliary random variables:

where we assume that first channel is used  times. We again define
times. We again define

We note that the auxiliary random variables,  satisfy the Markov chains:
satisfy the Markov chains:

Similar to the converse of Theorem 7, here again,  and
and  can be arbitrarily correlated. However, at the end of converse, it will be clear that selection of them as independent would yield the same region. Start with the common message rate:
can be arbitrarily correlated. However, at the end of converse, it will be clear that selection of them as independent would yield the same region. Start with the common message rate:





where (E.35) is due to Fano's lemma, (E.36) is due to the fact that the eavesdropper's channel is degraded with respect to the first user's channel. Once we obtain (E.38), using the analysis carried out in the proof of Theorem 7, we can obtain the following bounds:


where (E.39) (resp., (E.40)) can be derived following the lines from (D.51) (resp., (D.57)) to (D.55) (resp., (D.60)). Thus, we have

and similarly, we can get

We now consider the sum of common and independent message rates:



where (E.43) is due to Fano's lemma, (E.44) follows from the fact that the eavesdropper's channel is degraded with respect to the first user's channel. The first term of (E.45) is already bounded in (E.39). The second term can be bounded as

which can be obtained following the lines from (D.69) to (D.75). Hence, plugging (E.39) and (E.46) into (E.45), we get

Similarly, we can obtain

Finally, we derive the outer bounds for the sum secrecy rate:





where in (E.49), we used Fano's lemma and (E.50) follows from the fact that the eavesdropper's channel is degraded with respect to both users' channels. We can again use the analysis carried out in the converse proof of Theorem 7 to bound (E.53). For example, following lines from (D.85) to (D.106), we can obtain

Similarly, if we follow the analysis from (D.108) to (D.114), we can get

and if we follow the lines from (D.117) to (D.122), we can get

Thus, plugging (E.54), (E.55), and (E.56) into (E.53), we get

Similarly, it can be shown that

So far, we derived outer bounds on the secrecy capacity region which match the achievable region. Hence, to claim that this is indeed the capacity region, we need to show that computing the outer bounds over all distributions of the form  yields the same region which we would obtain by computing over all
yields the same region which we would obtain by computing over all  . Since all the expressions involved in the outer bounds depend on either
. Since all the expressions involved in the outer bounds depend on either  or
or  but not on the joint distribution
but not on the joint distribution  , this argument follows, establishing the secrecy capacity region.
, this argument follows, establishing the secrecy capacity region.
References
Wyner A: The wire-tap channel. Bell System Technical Journal 1975, 54(8):1355-1387.
Csiszar I, Korner J: Broadcast channels with confidential messages. IEEE Transactions on Information Theory 1978, 24(3):339-348. 10.1109/TIT.1978.1055892
Tekin E, Yener A: The Gaussian multiple access wire-tap channel. IEEE Transactions on Information Theory 2008, 54(12):5747-5755.
Tekin E, Yener A: The general Gaussian multiple access and two-way wire-tap channels: achievable rates and cooperative jamming. IEEE Transactions on Information Theory 2008, 54(6):2735-2751.
Ekrem E, Ulukus S: On the secrecy of multiple access wiretap channel. Proceedings of the 46th Annual Allerton Conference on Communication, Control, and Computing, September 2008 1014-1021.
Liu R, Maric I, Spasojevic P, Yates RD: Discrete memoryless interference and broadcast channels with confidential messages: secrecy rate regions. IEEE Transactions on Information Theory 2008, 54(6):2493-2507.
Liu R, Poor HV: Secrecy capacity region of a multi-antenna Gaussian broadcast channel with confidential messages. IEEE Transactions on Information Theory 2009, 55(3):1235-1249.
Khisti A, Tchamkerten A, Wornell GW: Secure broadcasting over fading channels. IEEE Transactions on Information Theory 2008, 54(6):2453-2469.
Bagherikaram G, Motahari AS, Khandani AK: The secrecy rate region of the broadcast channel. Proceedings of the Allerton Conference on Communications, Control and Computing,, July 2008
Oohama Y: Relay channels with confidential messages. http://arxiv.org/abs/cs/0611125
Lai L, El Gamal H: The relay-eavesdropper channel: cooperation for secrecy. IEEE Transactions on Information Theory 2008, 54(9):4005-4019.
Yuksel M, Erkip E: The relay channel with a wire-tapper. Proceedings of the 41st Annual Conference on Information Sciences and Systems, March 2007
He X, Yener A: Cooperation with an untrusted relay: a secrecy perspective. submitted to IEEE Transactions on Information Theory
He X, Yener A: On the equivocation region of relay channels with orthogonal components. Proceedings of the Conference Record Asilomar Conference on Signals, Systems and Computers, November 2007 883-887.
Ekrem E, Ulukus S: Effects of cooperation on the secrecy of multiple access channels with generalized feedback. Proceedings of the Conference on Information Sciences and Systems, March 2008
Ekrem E, Ulukus S: Secrecy in cooperative relay broadcast channels. submitted to IEEE Transactions on Information Theory
Bloch M, Thangaraj A: Confidential messages to a cooperative relay. Proceedings of the IEEE Information Theory Workshop, May 2008
Liang Y, Poor HV: Generalized multiple access channels with confidential messages. IEEE Transactions on Information Theory 2008, 54(3):976-1002.
Liu R, Maric I, Yates RD, Spasojevic P: The discrete memoryless multiple access channel with confidential messages. Proceedings of the IEEE International Symposium on Information Theory, July 2006
Tang X, Liu R, Spasojevic P, Poor HV: Multiple access channels with generalized feedback and confidential messages. Proceedings of the IEEE Information Theory Workshop on Frontiers in Coding Theory, September 2007
Liang Y, Poor HV, Shamai S: Secure communication over fading channels. IEEE Transactions on Information Theory 2008, 54(6):2470-2492.
Li Z, Yates R, Trappe W: Secrecy capacity of independent parallel channels. Proceedings of the 44th Annual Allerton Conference on Communication, Control, and Computing, September 2006 841-848.
Ekrem E, Ulukus S: On secure broadcasting. Proceedings of the Asilomar Conference on Signals, Systems and Computers, October 2008
Cover T, Thomas J: Elements of Information Theory. 2nd edition. John Wiley & Sons; 2006.
Poltyrev GS: Capacity for a sum of certain broadcast channels. Problemy Peredachi Informatsii 1979, 15(2):40-44.
El Gamal A: Capacity of the product and sum of two unmatched broadcast channels. Problemy Peredachi Informatsii 1980, 16(1):3-23.
Goldsmith AJ, Effros M: The capacity region of broadcast channels with intersymbol interference and colored Gaussian noise. IEEE Transactions on Information Theory 2001, 47(1):219-240. 10.1109/18.904524
Acknowledgments
This work was supported by NSF Grants CCF 04-47613, CCF 05-14846, CNS 07-16311, and CCF 07-29127, and was presented in part at the 42nd Asilomar Conference on Signals, Systems and Computers, Pacific Grove, Calif, USA, October 2008 [23].
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Ekrem, E., Ulukus, S. Secrecy Capacity of a Class of Broadcast Channels with an Eavesdropper. J Wireless Com Network 2009, 824235 (2009). https://doi.org/10.1155/2009/824235
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/824235




 length-
length- sequences
sequences 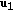 through
through  and index them as
and index them as  where
where  ,
, 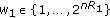 and
and  .
.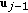 , where
, where  , generate
, generate  length-
length- sequences
sequences 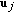 through
through 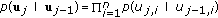 and index them as
and index them as 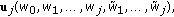 where
where 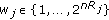 and
and 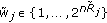 .
. , generate
, generate  length-
length- sequences
sequences  through
through 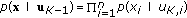 and index them as
and index them as  where
where  and
and  .
.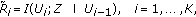
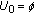 and
and  .
.
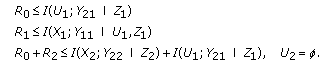

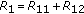 .
. length-
length- sequences
sequences  through
through 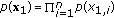 and index them as
and index them as  where
where 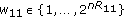 and
and 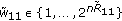 .
.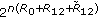 length-
length- sequences
sequences 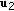 through
through  and index them as
and index them as  where
where 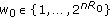 ,
,  and
and 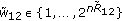 .
.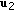 , generate
, generate 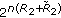 length-
length- sequences
sequences 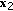 through
through  and index them as
and index them as  where
where 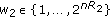 ,
,  .
.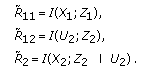
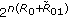 length-
length- sequences
sequences 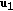 through
through 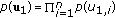 and index them as
and index them as  where
where  ,
,  .
. , generate
, generate  length-
length- sequences
sequences  through
through 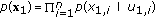 and index them as
and index them as  where
where 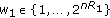 ,
, 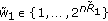 .
. length-
length- sequences
sequences 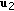 through
through 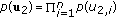 and index them as
and index them as 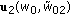 where
where 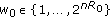 ,
, 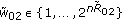 .
. , generate
, generate  length-
length- sequences
sequences 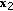 through
through 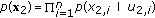 and index them as
and index them as  where
where 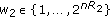 ,
, 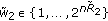 .
.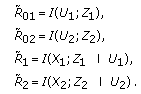
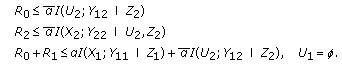
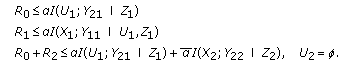
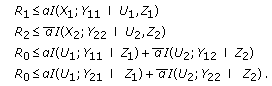
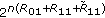 length-
length- sequences
sequences 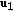 through
through  and index them as
and index them as  where
where  ,
, 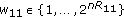 and
and 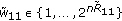 .
. , generate
, generate 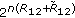 length-
length- sequences
sequences 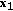 through
through  and index them as
and index them as  where
where  ,
, 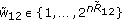 .
.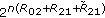 length-
length-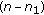 sequences
sequences  through
through  and index them as
and index them as  where
where 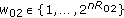 ,
,  and
and 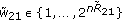 .
.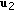 , generate
, generate 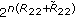 length-
length-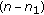 sequences
sequences  through
through 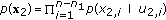 and index them as
and index them as 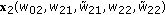 where
where  ,
, 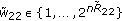 .
. times and the other one
times and the other one 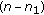 times. We define
times. We define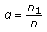
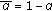 .
.




