- Research Article
- Open access
- Published:
Beamforming in Ad Hoc Networks: MAC Design and Performance Modeling
EURASIP Journal on Wireless Communications and Networking volume 2009, Article number: 839421 (2009)
Abstract
We examine in this paper the benefits of beamforming techniques in ad hoc networks. We first devise a novel MAC paradigm for ad hoc networks when using these techniques in multipath fading environment. In such networks, the use of conventional directional antennas does not necessarily improve the system performance. On the other hand, the exploitation of the potential benefits of smart antenna systems and especially beamforming techniques needs a prior knowledge of the physical channel. Our proposition performs jointly channel estimation and radio resource sharing. We validate the fruitfulness of the proposed MAC and we evaluate the effects of the channel estimation on the network performance. We then present an accurate analytical model for the performance of IEEE 802.11 MAC protocol. We extend the latter model, by introducing the fading probability, to derive the saturation throughput for our proposed MAC when the simplest beamforming strategy is used in real multipath fading ad hoc networks. Finally, numerical results validate our proposition.
1. Introduction
Ad hoc networks seem to be a promising solution for wireless access networks in beyond 3G system. Traditionally, the research in these networks assumes the use of omnidirectional antennas. In this case, while two nodes are communicating using a given channel, MAC protocols such as IEEE 802.11 require all other nodes in the vicinity to stay silent. With smart antennas, when two nodes are communicating, their neighbors may communicate simultaneously, depending on the directions or channels of transmission.
Mainly, the smart antenna systems can be classified into two kinds: switched beam systems and adaptive array systems. The switched beam systems comprise only basic switching between separate predefined beams. In adaptive array systems, signal-processing methods are used to increase the capacity and the coverage, to ameliorate the link quality and to improve the spatial reuse. Moreover, avoidance or suppression of interferences can be added to these systems. Clearly, adaptive systems are more beneficial but more complex than switched beam systems.
In one-hop communication systems (i.e., cellular networks), the use of smart antenna enables the network operators to enhance the wireless network capacity. In multihop networks, which are expected to experience an enormous traffic increase, exploiting the potential of these antennas improves the spectrum efficiency, extends the coverage range, and alleviates the interferences by taking advantage of the interference suppression capabilities. In fact, because of the higher gain, the transmission range is longer, which can lead to longer battery life, better connectivity, fewer hops, and lower latency. Furthermore, due to the narrower beamwidth, the interference is reduced (or canceled) and therefore, the throughput is increased. Interestingly, beamforming techniques have been proven as a promising solution to improve the performance of ad hoc networks. Using these techniques, the signal can be directed in some privileged directions or channels. Therefore, an increasing in per-link capacity as well as number of communicating nodes can be obtained.
In ad hoc networks, the nodes share the same physical channel. Thus, an efficient MAC protocol should be designed to control the channel access and decrease the amount of collisions. Although various MAC schemes have been extensively studied using omnidirectional antennas, they cannot be applied directly to networks where smart antennas are used. In the literature, a tremendous number of MAC schemes has been proposed to support the directivity [1–6]. Nevertheless, in order to improve the network performance, many authors consider some unrealistic assumptions (because of their cost or their infeasibility) such as:
-
(1)
locating the nodes by an external hardware as GPS [1],
-
(2)
splitting the main channel into two subchannels [2],
-
(3)
assuming that the signal strength is carried only by the Line-of-Sight (LOS) component between two nodes [7],
-
(4)
assuming a simplified antenna radiation pattern such as flat-top pattern or cone-sphere pattern [3].
As it can be seen, the proposed MAC protocols are so far from being realistic [7]. In fact, using external hardware may not be cost effective and also it may not be the appropriate solution in multipath environments. Likewise, using two channels, two transceivers are needed and the front-end becomes complex and expensive in cost and in power. On the other hand, the most enhanced directional antennas in the market cannot radiate power only in tight direction. Rather, they have significant side lobes. Moreover, directional antennas are typical for environments characterized by strong LOS components. Such assumption is not always valid. For example, in indoor environments a significant angular spread is expected and the performance of directional antennas may be worse than omnidirectional ones [7, 8].
Beside these unrealistic assumptions, another critical point has to be considered. In fact, the validation of the proposed paradigms has been carried out through discrete event simulators. The common characteristics of all these simulators are the lack of supporting the physical layer behavior (including the physical channel model [7]) and the huge simulation time. Thus, in addition to an enhanced MAC protocol, analytical models would be needed to overcome these problems. Although a considerable work is achieved to explore analytically the distributed coordination function (DCF) behavior of IEEE 802.11 MAC protocol [9], little work has been done when using smart antennas in ad hoc networks. Moreover, in the latter case, the properties of the physical channel such as multipath fading are not considered, and the smartness is treated as point-to-point directivity as we stated before.
In this work, we propose a MAC protocol with channel tracker algorithm for ad hoc networks when using beamforming techniques. Our proposition consists of implementing a proactive channel tracker algorithm in parallel with an enhanced MAC protocol to exploit the beamforming techniques to their fullest. For the sake of completeness, we explore in this work the importance of using smart antenna systems in ad hoc networks by using an analytical study. This paper is a continuation of earlier works [10, 11].
Our contribution can be outlined as follows. (a) We overview the pertinent works on the design and analytical modeling of MAC protocols in ad hoc networks when using smart antenna systems. (b) We propose a new MAC protocol (BMAC) using beamforming techniques. Besides, we use a channel tracker algorithm in order to estimate channel coefficients between nodes. (c) By simulation, we validate our proposition and we evaluate the overheads introduced by the channel tracker algorithm on the network. (d) We propose an accurate analytical model for evaluating the IEEE 802.11 performances. (e) We extend our latter proposition to support beamforming techniques.
Mainly, this paper will be divided into two complementary parts: the first one focuses on the MAC design, while the second deals with the analytical modeling of the performance of that design.
2. BMAC: A Novel MAC Design
2.1. Related Works
In the literature, two works attempt to survey MAC protocols in ad hoc networks when using smart antennas [12, 13]. In [12], the four-way handshaking of the IEEE 802.11 medium access is considered as the main criterion to categorize the surveyed MAC protocols. In [13], the authors classify the MAC protocols based on the access scheme which defines two major MAC categories: random access protocols and scheduled protocols. The first category represents an adequate solution for ad hoc networks and most of the works have been done using this scheme. These works are further classified into three groups: pure-RTS/CTS protocols, tone-based protocols, and other protocols using additional control packets.
A novel carrier sensing (CS) mechanism called directional virtual CS (DVCS) and a scheme estimating the nodes direction called angle of arrival (AoA) caching are proposed in [14]. The nodes update the AoA every time they receive a newer signal. In [15], the problem is alleviated by assuming that the gain in both omnidirectional mode and directional mode is the same. The control messages are sent in omnidirectional mode, while the data and the acknowledgment are exchanged using the beam receiving the highest power in the previous communication. In [16], a circular RTS is proposed to scan the medium. The authors in [17] propose a solution to overcome the hidden terminal problem. Moreover, they identify the transmitter and the receiver forbidden zones where the nodes are subject to interferences. In [1], the authors present another instances of hidden terminal; hidden terminal due to unheard RTS/CTS messages and hidden terminal due to the asymmetry in gain. They propose a multihop RTS MAC protocol to deal with these problems and to exploit the extended transmission range of directional antennas.
We note that these previous works have not fully exploited the benefits of adaptive arrays such as the ability to increase the spectrum efficiency, to extend the range of coverage and to form nulls in the directions of interferences. For these aims, little work has been done in literature. In [18], Yang proposed a MAC protocol called adaptive beamforming carrier sense multiple access/collision avoidance (ABF-CSMA/CA). In order to apply a directional RTS or CTS, a training sequence precedes these messages to estimate the channel. Another MAC protocol presented in [2] splits the main channel into two subchannels, with some predefined constraints.
2.2. BMAC Protocol
We propose a novel MAC protocol which performs channel gathering and medium sharing, jointly. Unlike other protocols, the Beamformed MAC (BMAC) does not require external devices to determine node locations. Our proposition is based on the channel and not on the position. The channel is estimated for further use when applying beamforming techniques, in order to couple the energy in the best way between the source and the destination and to restrain multiuser interferences. Thus, better connectivity and network capacity can be obtained. To prevent themselves from accessing pairs in communication sessions, the neighbors look up the updating frequency in their channel tables. If the tuple concerning a node is out of date then this node is considered busy.
The first algorithm in our proposition, called channel acquisition (CA), is proactive. In previous works, some authors assumed the availability of the destination location, others used AoA methods or external hardware as GPS to determine the node location. In indoor applications where a large angular spread is expected, the AoA methods may not be suitable to determine the positions of the nodes. Moreover, the potential of beamforming techniques will not be fully exploited if only the node location is known. For these reasons, we can see the importance to implement a proactive channel tracker algorithm in parallel with an enhanced MAC protocol to exploit the beamforming techniques to their fullest. This algorithm consists in transmitting a training sequence (pilot symbols) periodically each  (acquisition period). When receiving this training sequence, the channel to the corresponding node is estimated by applying the LMS algorithm [19]. Then, the channel coefficients and the node identifier are saved in a specific table called channel table.
(acquisition period). When receiving this training sequence, the channel to the corresponding node is estimated by applying the LMS algorithm [19]. Then, the channel coefficients and the node identifier are saved in a specific table called channel table.
The acquisition period  is calculated with respect to the coherence time
is calculated with respect to the coherence time  of the channel (
of the channel ( ). The coherence time is related to the maximum Doppler frequency:
). The coherence time is related to the maximum Doppler frequency:  where
where  is equal to
is equal to  ,
,  is the carrier frequency, and
is the carrier frequency, and  is the speed of light. Thus, low mobility (quasistatic) environments are the most suitable environments for our proposition. However, if the nodes are involved in a high-mobility scenario, the load of this algorithm may be unsupportable. As will be shown in the simulation and analytical results, wise choice of
is the speed of light. Thus, low mobility (quasistatic) environments are the most suitable environments for our proposition. However, if the nodes are involved in a high-mobility scenario, the load of this algorithm may be unsupportable. As will be shown in the simulation and analytical results, wise choice of  maintains an acceptable channel estimation for immediate use and alleviates the resulting overheads.
maintains an acceptable channel estimation for immediate use and alleviates the resulting overheads.
We note that if we apply the "on-demand" channel estimation procedure (which involves less overheads on the network), only the channel toward the destination will be available. In this case, we can improve the quality of service of the communication link between the source and the corresponding destination but we cannot alleviate the interferences since we do not have the estimation of the channels toward these interferences.
The second algorithm, called BMAC, is invoked when there is some data ready to be sent. The state diagram is presented in Figure 1, where CA is the channel acquisition, Bd is the beamformer (i.e., vector of weights) toward the destination, BRTS is the beamformed RTS, NN stands for neighbor nodes, and SNAV stands for specified NAV (i.e., NAV for a specified node).
Our MAC is based on IEEE 802.11 in order to ensure interoperability with current deployed WLAN modem. Under the assumption of using a half-duplex transceiver at each node, a packet exchange occurs as indicated in the state diagram. Some points have to be considered.
(i) When a packet comes from upper layers, the CA algorithm is interrupted for a packet exchange time (see the index  on Figure 1). Herein, different scenarios can be implemented depending on the application.
on Figure 1). Herein, different scenarios can be implemented depending on the application.
-
(1)
If the offered traffic load is sufficiently high, the network will be congested almost all the time. Consequently, the data packet will not have any priority over the training sequence (TS) packets and the data transmission will be interrupted each
 to transmit these sequences (if not, the estimated channel versions will be expired and the beamforming will not work properly). In this case, the amount of data lost by the omnidirectional transmission for the TS packets depends on the acquisition frequency.
to transmit these sequences (if not, the estimated channel versions will be expired and the beamforming will not work properly). In this case, the amount of data lost by the omnidirectional transmission for the TS packets depends on the acquisition frequency. -
(2)
If this is not the case, the CA algorithm can be stopped and the data transmission can proceed. Thus, the channel table for the nodes in the vicinity will be expired and the corresponding pair of nodes is considered busy.
(ii) Equipped with an antenna array of  elements, the source node calculates the transmit Bd weights in order to make nulls toward the
elements, the source node calculates the transmit Bd weights in order to make nulls toward the  high noisy neighbors (
high noisy neighbors ( is the degree of freedom) and to couple the energy toward the intended destination. These high noisy neighbors can be seen as the channels having the maximum energy (i.e., the potential interferences with respect to the current node). Then, a BRTS can be transmitted using the calculated Bd (see the index
is the degree of freedom) and to couple the energy toward the intended destination. These high noisy neighbors can be seen as the channels having the maximum energy (i.e., the potential interferences with respect to the current node). Then, a BRTS can be transmitted using the calculated Bd (see the index  on Figure 1).
on Figure 1).
Providing that an estimated channel version of all neighbor nodes is available, the zero forcing transmit beamforming algorithm is used. However, the traditional beamforming can be used. In the latter case, only the channel between the source and the destination will be used and the nulling capabilities cannot be exploited [20].
(iii) When receiving the BRTS control message, the nodes in the vicinity update their SNAV to prevent themselves from accessing this pair of nodes (source and destination). In fact, when using a Bd toward such destination, other nodes having near channels can receive the messages as well as this destination (see the index  on Figure 1).
on Figure 1).
(iv) When receiving the BRTS, the destination node calculates the exceeded power for further transmitted power correction and then it sends omnidirectional CTS (OCTS) message containing this correction factor. Using this parameter, the source can adjust the transmission power to a certain level in order to maintain prespecified link quality. By that, a simple power control mechanism is implemented and the energy is saved.
We note that, BCTS cannot be used in this scheme because the version of the estimated channel (estimated with omnidirectional antenna) which is available at the current destination, does not take into account the transmit Bd. To use BRTS and BCTS in the same scheme, we have to implement a joint adaptive beamforming between the source and the destination. This strategy will be time consuming and it is not appropriate for ad hoc networks. From a cross-layer point of view, any joint transmit receive beamforming (iterative optimization) will inundate the network by the overheads and will produce network instability [21] (see the index  on Figure 1).
on Figure 1).
(v) For receiving the OCTS message, the source can use the conjugate of the transmit Bd vector, namely, Bd*. It was shown in [22] that a strong network duality holds for TDD networks, in which the optimum receive Bds are the conjugates of the optimum transmit vectors (see the index  on Figure 1).
on Figure 1).
(vi) After the exchange of the control messages, the source uses the Bd vector toward the destination (Bd) to send the data packets. As we will see in the next section, the link capacity will be improved and a higher global capacity will be obtained due to the spatial reuse improvement.
(vii) Once the data transmission/reception is completed, an ACK is transmitted and a CA session is enabled, to inform the neighbors about the availability of this pair (see the index  on Figure 1).
on Figure 1).
(viii) If a tuple (i.e., for node B) in the channel table of a node A is not updated each  , where
, where  is a tradeoff factor, the node A assumes that node B is in a function mode and prevents itself from attempting to access this node, eliminating by that the deafness problem [23].
is a tradeoff factor, the node A assumes that node B is in a function mode and prevents itself from attempting to access this node, eliminating by that the deafness problem [23].
Finally, to summarize the main differences between our proposition and other propositions in the same context (i.e., DMAC [1]) we present in the following a brief comparison between BMAC and DMAC.
-
(1)
BMAC is channel-based however DMAC is position or location-based.
-
(2)
The BMAC works even in rich multipath scattering environment however DMAC shuts down if the angular spread is considerable. Moreover, if the sender and the receiver are not in LOS view, the performance of directional antenna may be worse than omnidirectional one.
-
(3)
The BMAC uses the adaptive beamforming techniques and not conventional directional antenna.
-
(4)
The radiation pattern of DMAC is very simplified and it is illustrated by a main lobe and by a small sphere representing the side lobes.
-
(5)
This simplified antenna radiation pattern is static. We mean that the node requires the position of the destination in order to steer the main lobe in the right direction. Moreover, this antenna radiation pattern imposes an aggressive simplification and the technological limits do not allow such "ideal" beam.
-
(6)
The BMAC is based on the Channel Acquisition subalgorithm to maintain an available channel estimation version for future use. This subalgorithm is exploited also as a virtual carrier sensing to prevent deafness and thus to avoid collision.
-
(7)
In DMAC the nodes location is determined by an external system.
-
(8)
DMAC does not perform power control (fixed beamwidth). In contrast, BMAC saves the energy by a simple optional power control mechanism.
-
(9)
DMAC uses DNAV (as DVCS) while BMAC uses SNAV as explained above.
-
(10)
The novelty of our proposition comes from both MAC and physical layer(application of beamforming techniques in ad hoc networks).
These points make the BMAC a realistic protocol. However DMAC (even if we assume that the determination of the nodes position is possible and the radiation pattern is feasible) will shut down in indoor application where the angle spread is expected to be very large.
2.3. Performances Evaluation of the BMAC Protocol
To evaluate the impact of the beamforming techniques and the channel-based protocol (BMAC) on ad hoc networks, we simulate through different random scenarios the three following MAC protocols: IEEE 802.11b (with omnidirectional antenna pattern), the basic DMAC [1] protocol (modified version of IEEE 802.11 MAC protocol to support pure directivity), and finally the BMAC. More attention will be focused on the BMAC to examine the effects of the tradeoff parameters  and
and  as well as channel evolution effects on the network performance. Note that
as well as channel evolution effects on the network performance. Note that  relates the acquisition period to the coherence time and
relates the acquisition period to the coherence time and  represents the tradeoff factor between the LOS and the non-LOS components of the channel.
represents the tradeoff factor between the LOS and the non-LOS components of the channel.
2.3.1. Simulation Model
In each scenario we use  nodes, each of which uses an antenna array equipped with
nodes, each of which uses an antenna array equipped with  elements.
elements.
Traffic Model
Firstly, to show the effectiveness of the BMAC, we used a high-traffic load model in order to put our network in a realistic congested condition. Using this traffic model, all the transmitters have always packets to send during the simulation. If the medium is available, they immediately perform a transmission. Otherwise, they push their packets in their stacks, and they wait until the medium becomes idle. Secondly, for channel-load evaluation purpose, we alleviate the network load and we simulate the BMAC in different environments: directive and nondirective environments, low-change and fast-change environments.
Channel Model
Many MAC protocols based on antenna directivity were proposed and performance improvements to the IEEE 802.11 MAC were shown. The propagation models used in these MAC are simplified and suitably do not take into account a certain number of physical phenomenon which can have an important impact on the network performance. The multipath propagation is one of these phenomenons. As we have seen, all the suggested protocols assume that the signal is carried out by the LOS path between two nodes.
Generally speaking, the path loss and the multipath fading are the most common characterizations of the channel. In this work, we characterize the radio propagation medium between each transmitter-receiver pair as a Ricean multipath channel. We assume a frequency flat fading channel where the coefficients between the transmitter and the receiver are collected in the  complex vector,
complex vector,  :
:

where  is the path loss,
is the path loss,  is the distance between the transmitter and the receiver,
is the distance between the transmitter and the receiver,  is a tradeoff factor between the LOS component and the random component of the channel (this parameter is equal to
is a tradeoff factor between the LOS component and the random component of the channel (this parameter is equal to  in our general simulation),
in our general simulation),  is the antenna array response for the main AoA,
is the antenna array response for the main AoA,  is a Gaussian random vector with zero mean and, the index
is a Gaussian random vector with zero mean and, the index  stands for the multipath effect. Note that we use a circular antenna array with
stands for the multipath effect. Note that we use a circular antenna array with  half wavelength spaced elements and we consider eight antenna elements in our simulations.
half wavelength spaced elements and we consider eight antenna elements in our simulations.
Signal Model
Assume that node  and node
and node  are in communication session. The signal received by node
are in communication session. The signal received by node  is given by
is given by

where  is the signal intended for node
is the signal intended for node  ,
,  is the channel vector between a predefined antenna element at node
is the channel vector between a predefined antenna element at node  and the antenna array at node
and the antenna array at node  ,
,  is the transpose conjugate of the weight vector described in the following section, and
is the transpose conjugate of the weight vector described in the following section, and  contains both background noise and interferences coming from another nodes in the vicinity.
contains both background noise and interferences coming from another nodes in the vicinity.
Beamforming Model
The simplest strategy to exploit the smartness of antenna arrays in ad hoc networks is to use standard beamforming, that is, to point the main lobe of the antenna array of the source in the direction of the destination. However, if the global CSI is available at the transmitter, it is possible to actively suppress the interferences as depicted in Figure 2. Beamforming algorithms can be formulated as centralized or decentralized game. In ad hoc networks and especially in civilian applications, where the available calculation power is moderate, a decentralized beamforming algorithm is preferred. In addition, because of the availability of all the channels toward the neighbors node, we will exploit only the zero-forcing algorithm in our work. In fact, the traditional beamforming does not perform interference rejection and therefore it is not so beneficial for ad hoc networks.
The zero-forcing algorithm performs interference cancellation by solving the following system:

where we concatenate the channels toward the destination and  high noisy neighbor nodes in the matrix
high noisy neighbor nodes in the matrix  .
.  stands for the gain vector toward these nodes. The first element of
stands for the gain vector toward these nodes. The first element of  is set to 1 and the others to
is set to 1 and the others to  where
where  is a small value chosen randomly in order to ensure the feasibility of the system (3). In receive mode and in order to avoid the noise amplification impairments, the MMSE algorithm can be used as a tradeoff between interference rejection and noise amplification.
is a small value chosen randomly in order to ensure the feasibility of the system (3). In receive mode and in order to avoid the noise amplification impairments, the MMSE algorithm can be used as a tradeoff between interference rejection and noise amplification.
2.3.2. Simulation Results
For our simulation, we use the OPNET Modeler [24]. The considered metrics are the average of the global one-hop throughput and the End-To-End delay. The simulation setup is summarized in Table 1.
We compare the performance of the simulated MAC protocols in randomly distributed topologies. Herein, the potential of beamforming techniques with respect to the simple directional antenna pattern is examined.
The results presented in Figure 3 show that BMAC outperforms both DMAC and IEEE in term of saturation throughput. As it can be seen, when the traffic load is light (left ellipsoid), the three MAC protocols show the same network performance. However, when a higher traffic load is experienced (right ellipsoid), the BMAC outperforms both DMAC and IEEE. This can be explained by the fact that the per-link capacity is improved by using beamforming techniques and the number of connections allowed by BMAC is greater than that allowed by DMAC and IEEE. Our proposition exploits effectively the wireless channel to improve the performance of ad hoc networks. The other MAC protocols based on the pure directivity show such performance in nonlinearly distributed scenarios where the directive component is dominant.
In order to see the effect of the channel components on the BMAC behaviors, we simulate this protocol in directive and very directive environments. Figure 4 presents the cumulative distribution function (CDF) of the End-To-End delay using different values of  . When
. When  , the medium is very directive and the BMAC performs worse than other cases. Here, we note that the use of the ETE delay is not intended to evaluate the performance of BMAC by itself, but only to show that the directive environment does not allow the BMAC to take full advantages from the smart antenna systems.
, the medium is very directive and the BMAC performs worse than other cases. Here, we note that the use of the ETE delay is not intended to evaluate the performance of BMAC by itself, but only to show that the directive environment does not allow the BMAC to take full advantages from the smart antenna systems.
As we have seen, the channel acquisition period is a function of the coherence time  , where
, where  is a tradeoff factor. In Figure 5, the BMAC is simulated for different values of
is a tradeoff factor. In Figure 5, the BMAC is simulated for different values of  . When the acquisition of the channel is done frequently (
. When the acquisition of the channel is done frequently ( ), the omnidirectional transmitted training sequence floods the network. For
), the omnidirectional transmitted training sequence floods the network. For  , the estimated channel version is out of date and the beamforming algorithms do not work correctly. In these two cases, the average one-hop throughput is affected and it provides moderate performances. Wise choice of
, the estimated channel version is out of date and the beamforming algorithms do not work correctly. In these two cases, the average one-hop throughput is affected and it provides moderate performances. Wise choice of  maintains an available channel estimation and alleviates the channel acquisition overheads. When
maintains an available channel estimation and alleviates the channel acquisition overheads. When  is between 1 and 3, the BMAC performs better and the average throughput is maximum.
is between 1 and 3, the BMAC performs better and the average throughput is maximum.
Since the goal is to examine the effect of the channel estimation overheads, Figure 6 plots the average one-hop throughput as function of the coherence time. If the environment changes significantly, the corresponding coherence time is small and the average throughput is moderate. Like wise, when the environment presents a slight evolution, the corresponding coherence time is high and the achieved throughput of BMAC is maximum.
In the sequel, we will access the performance of the BMAC through an analytical study. For this aim, we first bring out in the next section an accurate analytical model to evaluate the performances of the DCF scheme of IEEE 802.11 MAC protocol. Then, we extend the latter analytical model to access the performance of BMAC.
3. Analytical Modeling
As we stated in the introduction, most of the works in ad hoc networks with or without smart antenna systems have been validated by using discrete event simulators. In recent years, some analytical models have been proposed to analyze IEEE 802.11 MAC protocol behaviors. The work in [25] is a prominent work in this domain. Another attempts can be found in [26–28]. In [25], Bianchi evaluated the performance of the DCF scheme with the assumption of ideal channel conditions. This saturation throughput is defined as the limit reached by the system throughput as the offered load increase. Recall that in this basic work and under ideal channel condition, the packet is lost only in the case of collision. Furthermore, the authors assumed that the packets collide with constant and independent probability  called conditional collision probability. From a practical point of view, the problem is alleviated by skipping the impact of the finite-retry limits and some physical characteristics as the channel conditions and the antenna radiation pattern. Building up Bianchi's work, Wu et al. [26] dealt with one of the major limitations of the Markov model by including the finite retry limits. Ziouva and Antonakopoulos [27] introduced the concept of busy channel. Chatzimisios et al. [28] proposed a new performance analysis to calculate the packet delay and the packet drop probability.
called conditional collision probability. From a practical point of view, the problem is alleviated by skipping the impact of the finite-retry limits and some physical characteristics as the channel conditions and the antenna radiation pattern. Building up Bianchi's work, Wu et al. [26] dealt with one of the major limitations of the Markov model by including the finite retry limits. Ziouva and Antonakopoulos [27] introduced the concept of busy channel. Chatzimisios et al. [28] proposed a new performance analysis to calculate the packet delay and the packet drop probability.
So far, some works have been done to model analytically the effect of smart antennas on ad hoc networks. In [29], the author used a pie-slice antenna radiation pattern model and he neglected or simplified other physical parameters. In [30], many issues related to the deployment of directive antenna in ad hoc networks are discussed and analyzed. In this work, the transmission probabilities are taken independent from the MAC protocol. In [31], the authors suggested that the pie-slice models for the directional antenna exaggerate the system throughput. In [32], a MAC protocol exploiting the spatial diversity called SD-MAC is proposed. In this work, the authors extended a new approach to characterize the saturation throughput for multihop ad hoc networks using spatial diversity. The key feature in this work is the consideration of fading channels. As in [25], the packet loss probability (LP) due to collision is constant. Since fading can also occur, the packets can be lost without collision. Thus, the authors define the LP by  where
where  stands for the packet loss due to fading. Although the authors mention that the MIMO techniques and especially spatial diversity are used, they did not give an explicit expression of the packet LP that may coordinate with channel type and with the antenna array size. Furthermore, they suppose the availability of the channel sate information (CSI) without evaluating the effect or the cost of the channel estimation overheads on the network.
stands for the packet loss due to fading. Although the authors mention that the MIMO techniques and especially spatial diversity are used, they did not give an explicit expression of the packet LP that may coordinate with channel type and with the antenna array size. Furthermore, they suppose the availability of the channel sate information (CSI) without evaluating the effect or the cost of the channel estimation overheads on the network.
3.1. Modeling the IEEE 802.11 MAC Protocol
In this section, we propose a novel model combined with busy channel, retry limitation and nonsaturated condition. With improvements on the precedent models, our model adopts these three issues and brings out the new analytical throughput. We assume that the nodes in the network share the same physical properties and the number of nodes is fixed and finite.
For a given slot time  , let
, let  be the backoff stage and
be the backoff stage and  be the stochastic process representing the backoff window size. Thus, the bidimensional process
be the stochastic process representing the backoff window size. Thus, the bidimensional process  is a discrete-time Markov model, shown in Figure 7.
is a discrete-time Markov model, shown in Figure 7.
For retry limitation,  and
and  are set to represent the maximum retry limit in MAC layer and in Physical (PHY) layer, respectively. As specified in IEEE 802.11, contention window (CW) size of a stage
are set to represent the maximum retry limit in MAC layer and in Physical (PHY) layer, respectively. As specified in IEEE 802.11, contention window (CW) size of a stage  is
is  , when
, when  . If
. If  , the CW size is held as
, the CW size is held as  .
.  is the minimum contention window.
is the minimum contention window.
Here, we introduce an add-in state  representing the idle stage of a single node. The parameter
representing the idle stage of a single node. The parameter  represents the probability that a node has a consequent packet to transmit after a success or failed transmission. Correspondingly,
represents the probability that a node has a consequent packet to transmit after a success or failed transmission. Correspondingly,  is the probability that a node meets no new packet from upper layer and turns into the stage
is the probability that a node meets no new packet from upper layer and turns into the stage  to wait for new packets. At the waiting stage, a node keeps waiting slot by slot until it gets a new packet and moves into the backoff states.
to wait for new packets. At the waiting stage, a node keeps waiting slot by slot until it gets a new packet and moves into the backoff states.
For the convenience in demonstration, two intermediate points are involved between the idle stage and the backoff stages. They can be treated as two "pseudo states" for two instances in the function of nodes. The point named  after a transmission is the moment when a node is requiring new packets from upper layer. The other one named
after a transmission is the moment when a node is requiring new packets from upper layer. The other one named  before a transmission is the moment when a node is ready to send a new packet.
before a transmission is the moment when a node is ready to send a new packet.
In the Markov chain, the only nonnull one-step transition probabilities are expressed in (3.1). The first equation in (3.1) represents the basic function of backoff counter, CW decreases at each time slot. The second equation accounts for the fact that following a finished transmission, a node requires new packets from upper layer. In the third equation, when an unsuccessful transmission occurs at the backoff stage  , the backoff stage is increased to
, the backoff stage is increased to  , the new initial backoff value is uniformly chosen in the range
, the new initial backoff value is uniformly chosen in the range  :
:

The fourth equation models that a node will not decrease its CW when the backoff stage reaches  . Once the retransmission reaches the limit, no matter the current trial succeeds or fails, a node drops the present packet. The fifth equation shows that after a transmission, a node turns to the upper layer to obtain a new packet. The sixth equation describes that a node is ready to transmit if it has got a new packet. As shown in the seventh equation, a node is set to idle if it gets no new packet after a transmission, moreover, an idle node keeps waiting until there comes a new packet. Let
. Once the retransmission reaches the limit, no matter the current trial succeeds or fails, a node drops the present packet. The fifth equation shows that after a transmission, a node turns to the upper layer to obtain a new packet. The sixth equation describes that a node is ready to transmit if it has got a new packet. As shown in the seventh equation, a node is set to idle if it gets no new packet after a transmission, moreover, an idle node keeps waiting until there comes a new packet. Let  with
with  ,
,  be the stationary distribution of the chain. A closed-form solution can be obtained from this Markov chain. First, note that
be the stationary distribution of the chain. A closed-form solution can be obtained from this Markov chain. First, note that 
Due to the regularity of the chain, for each  , we have
, we have

with transitions in the chain, (5) can be simplified as  .
.
By using the normalization condition for stationary distribution, we have  . Therefore, the probability
. Therefore, the probability  that a node transmits in a randomly chosen slot time is shown in (6) and (7):
that a node transmits in a randomly chosen slot time is shown in (6) and (7):

and

Owing to the property of omnidirectional antenna, a node transmits with probability  while the others have to keep silence, we have
while the others have to keep silence, we have  . This latter equation and (7) represent a nonlinear system with two unknowns
. This latter equation and (7) represent a nonlinear system with two unknowns  and
and  , which can be solved by numerical methods.
, which can be solved by numerical methods.
Now, let  be the probability that there is at least one transmission in the considered period and
be the probability that there is at least one transmission in the considered period and  be the probability that a transmission is successful, given the probability
be the probability that a transmission is successful, given the probability  , we have
, we have

The throughput of the system can be deduced as follows:

where  is the average packets payload in a transmission,
is the average packets payload in a transmission,  is the time period for a successful transmission, and
is the time period for a successful transmission, and  is the time for a collision.
is the time for a collision.
Considering such a scenario, a node A is transmitting data to its destination with its backoff counter  ; the other nodes in the system remain silent and freeze their backoff counters due to the busy channel. Any backoff counter of silent nodes is
; the other nodes in the system remain silent and freeze their backoff counters due to the busy channel. Any backoff counter of silent nodes is  , otherwise a collision would have happened when more than one node reach the zero of backoff counter at the same time. According to the DCF specifications, after the transmission, all the nodes wait for a DIFS time and then continue the decrement in the backoff counters. Therefore, except node A, all the others can access the channel after a period
, otherwise a collision would have happened when more than one node reach the zero of backoff counter at the same time. According to the DCF specifications, after the transmission, all the nodes wait for a DIFS time and then continue the decrement in the backoff counters. Therefore, except node A, all the others can access the channel after a period  . Only when node A generates a new random backoff equal to zero for the next transmission, it will access again the channel after the period of one DIFS with a probability
. Only when node A generates a new random backoff equal to zero for the next transmission, it will access again the channel after the period of one DIFS with a probability  .
.
According to the standards in [9], the time periods for transmitting one packet and for a collision are  and
and  . Due to the different mechanisms, they are
. Due to the different mechanisms, they are

where  is the average length of general packet.
is the average length of general packet.
By considering the probability  , the durations of a successful transmission and a collision are
, the durations of a successful transmission and a collision are

Let  be the average length of a single packet,
be the average length of a single packet,  can be expressed as
can be expressed as

An extensive set of simulations (OPNET [24]) and numerical calculations validate this model by showing very accurate results in terms of normalized throughput. The parameter used in both simulation and numerical calculation are stated in Table 2 and the results are depicted in Figure 8.
3.2. Modeling the Performance of Ad Hoc Networks When Using the Simplest Beamforming Strategy
3.2.1. Preliminaries
The network consists of  nodes uniformly distributed in a square area, each of which has
nodes uniformly distributed in a square area, each of which has  neighboring nodes. That is, there are
neighboring nodes. That is, there are  nodes in the omnidirectional coverage zone of each node. We assume that all the nodes are equipped with
nodes in the omnidirectional coverage zone of each node. We assume that all the nodes are equipped with  half wavelength spaced antenna-elements. In this section, we derive the saturation throughput for ad hoc networks when using maximum ratio transmission technique. Our main contribution is concentrated on developing the packet LP due to fading when using a simple beamforming strategy. However, the model can be extended to other beamforming algorithms. Recall that, the channel state information is needed at the transmitter to properly generate the correspondent Bd. Based on the new accurate analytical model for IEEE 802.11 proposed in previous section, we derive also the saturation throughput of the BMAC using the developed packet LP. In summary, our work in this section is divided into two parts: the first one is about the determination of the packet LP due to fading by using both analytical and empirical studies. While in the second, we use this probability to calculate the saturation throughput of a simplified version of BMAC.
half wavelength spaced antenna-elements. In this section, we derive the saturation throughput for ad hoc networks when using maximum ratio transmission technique. Our main contribution is concentrated on developing the packet LP due to fading when using a simple beamforming strategy. However, the model can be extended to other beamforming algorithms. Recall that, the channel state information is needed at the transmitter to properly generate the correspondent Bd. Based on the new accurate analytical model for IEEE 802.11 proposed in previous section, we derive also the saturation throughput of the BMAC using the developed packet LP. In summary, our work in this section is divided into two parts: the first one is about the determination of the packet LP due to fading by using both analytical and empirical studies. While in the second, we use this probability to calculate the saturation throughput of a simplified version of BMAC.
3.2.2. Loss Probability Due to Fading
We perform this study under the assumption of perfect knowledge of the channel at the transmitter by using a channel estimation algorithm near to the one proposed in Section 2.2. We assume also that each node computes the Bd that mitigates the channel effect as the maximum ratio transmission [33]:

where  is the nonselective frequency channel coefficient between each antenna element and the destination. We assume an omnidirectional reception. Therefore, the LP due to fading for a given distance
is the nonselective frequency channel coefficient between each antenna element and the destination. We assume an omnidirectional reception. Therefore, the LP due to fading for a given distance  can be written as
can be written as

where  stands for the distribution function in term of probability density function (
stands for the distribution function in term of probability density function ( ) for the instantaneous signal to noise ratio
) for the instantaneous signal to noise ratio  at a given distance
at a given distance  , and the
, and the  stands for the packet error probability. The latter probability is relying on the bit error rate (
stands for the packet error probability. The latter probability is relying on the bit error rate ( ) for a given
) for a given  :
:

The  can be written as
can be written as  when using BPSK modulation.
when using BPSK modulation.  stands for the packet size. Note that, another modulation schemes can be used and the
stands for the packet size. Note that, another modulation schemes can be used and the  function changes accordingly.
function changes accordingly.
The  function depends on the beamforming strategy. Using the weight vector given in (13), the signal to noise ratio can be written as
function depends on the beamforming strategy. Using the weight vector given in (13), the signal to noise ratio can be written as

where  is the transmit signal power,
is the transmit signal power,  is the variance of the noise,
is the variance of the noise,  ,
,  is the FRIIS attenuation, and
is the FRIIS attenuation, and  follows a Gaussian distribution with zero mean and unit variance. This SNR obeys a scaled version of the
follows a Gaussian distribution with zero mean and unit variance. This SNR obeys a scaled version of the  distribution with
distribution with  degrees of freedom. Let
degrees of freedom. Let  . Thus,
. Thus,  can be written as
can be written as

where  stands for the gamma function. The theoretical and the empirical results are shown in Figure 9.
stands for the gamma function. The theoretical and the empirical results are shown in Figure 9.
After the determination of this probability with respect to the distance, the average packet loss due to the fading can be obtained. We note that we assume a uniform distribution of the distance between two nodes. Assuming that a set of nodes are uniformly distributed within the coverage zone  of a particular node, then the distribution function of the distance
of a particular node, then the distribution function of the distance  to this node is
to this node is  . Thus, the PDF of the distance between two nodes is given by
. Thus, the PDF of the distance between two nodes is given by  . Therefore, the average packet loss due to the fading can be calculated by
. Therefore, the average packet loss due to the fading can be calculated by  . In Figure 10, we plot the
. In Figure 10, we plot the  against the number of antennas
against the number of antennas  . As it can be expected, the greater the number of antennas is, the lower the probability of loss due to fading will be.
. As it can be expected, the greater the number of antennas is, the lower the probability of loss due to fading will be.
3.2.3. Saturation Throughput of the Beamformed MAC Protocol
Herein, we try to simplify the problem by assuming that the used beamforming algorithm is following the strategy presented by (13). However, if we use another specific algorithm [20] (as we presented in Section 2.3.1), the weights will be function of the channel coefficients and finally the SNR will obey to some other  function
function  . Furthermore, we assume that there is no interaction between the training sequence messages and the data messages. We analyze the throughput related to these two kinds of messages and finally we compute the effective saturation throughput by using the following approximation:
. Furthermore, we assume that there is no interaction between the training sequence messages and the data messages. We analyze the throughput related to these two kinds of messages and finally we compute the effective saturation throughput by using the following approximation:

where  (
( ) stands for the saturation throughput due to the data (training sequence) messages,
) stands for the saturation throughput due to the data (training sequence) messages,  represents the renewal period for a training sequence transmission and
represents the renewal period for a training sequence transmission and  is the acquisition period as defined in Section 2.2.
is the acquisition period as defined in Section 2.2.  is based on the saturation throughput for the basic access scheme of IEEE 802.11, without ACK and taking into account the probability of fading. Based on (7) and under the assumption of fixed backoff window (
is based on the saturation throughput for the basic access scheme of IEEE 802.11, without ACK and taking into account the probability of fading. Based on (7) and under the assumption of fixed backoff window ( = 0), the probability
= 0), the probability  is given by
is given by  , and the saturation throughput can be written as [25]
, and the saturation throughput can be written as [25]

where  is the duration of a time slot,
is the duration of a time slot,  is the probability to have at least one transmission in a given time slot time, and
is the probability to have at least one transmission in a given time slot time, and  is the probability of a successful transmission:
is the probability of a successful transmission:

In (19),  and
and  denote, respectively, the average time for successful transmission and failed transmission due to collision. They are calculated according to (11) and based on
denote, respectively, the average time for successful transmission and failed transmission due to collision. They are calculated according to (11) and based on  where
where  .
.  stands for the overheads. It is important to mention here that we transmit the training sequence in omnidirectional mode in order to estimate the channel coefficients without beamforming.
stands for the overheads. It is important to mention here that we transmit the training sequence in omnidirectional mode in order to estimate the channel coefficients without beamforming.
In the following and before computing the saturation throughput for data packets using beamforming techniques, two points have to be considered.
(i) The per-link performance enhancement due to the use of beamforming techniques is embedded in the LPF function. Higher number of antennas leads to lower LPF value, and then higher per-link capacity can be obtained. However, the performance improvement due to the spatial reuse will be modeled by a function called effective spatial reuse ( ) which denotes the number of simultaneous links that can coexist. Therefore, the number of stations that can be active at the same time will be
) which denotes the number of simultaneous links that can coexist. Therefore, the number of stations that can be active at the same time will be  .
.
In order to compute the average number of communication sessions that simultaneously coexist in the same neighborhood, we assume uniformly deployment of the  nodes in a disk. Recall that in this issue, we are based on the tight beamwidth of the transmit beamforming to estimate the number of links formed one by one by a transmitter localized at the center of the disk and a receiver localized at the edge. Taking into account that each node has an antenna array, we report in Figure 11 the null-to-null beamwidth (NNBW or
nodes in a disk. Recall that in this issue, we are based on the tight beamwidth of the transmit beamforming to estimate the number of links formed one by one by a transmitter localized at the center of the disk and a receiver localized at the edge. Taking into account that each node has an antenna array, we report in Figure 11 the null-to-null beamwidth (NNBW or  ) also called fire edge beamwidth.
) also called fire edge beamwidth.
Assuming now that a first node (say A) established a link among the  nodes. Therefore, the number of nodes that are eligible for another successful transmission will be
nodes. Therefore, the number of nodes that are eligible for another successful transmission will be  , where the second term represents the ratio of the surface occupied by the current directive communication to the whole disk surface. Then, the probability that one of these latter nodes establishes a link without disturbing the initial communicating node is
, where the second term represents the ratio of the surface occupied by the current directive communication to the whole disk surface. Then, the probability that one of these latter nodes establishes a link without disturbing the initial communicating node is  . For instance, we have two established links without overlapping of their radiation zones. Consequently, the result number of free nodes will be
. For instance, we have two established links without overlapping of their radiation zones. Consequently, the result number of free nodes will be  . A third link can be established with a probability of
. A third link can be established with a probability of  . Finally, the total number of links will be
. Finally, the total number of links will be  , where
, where  and
and  representing the first link. In Figure 11, we depict the ESR as a function of the antenna array size.
representing the first link. In Figure 11, we depict the ESR as a function of the antenna array size.
-
(ii)
The sources of loosing packets are three in our case:
-
(1)
loss due to fading given by
 ,
, -
(2)
loss due to collision represented by
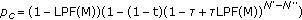 ,
, -
(3)
loss due to the mismatching between the estimated version of the channel and the real channel. In fact, under perfect estimation of the channel coefficients, the only error that may occur from the use of this estimated channel occurs in the adaptation between the coherence time and the acquisition period. In such case and based on the outdated channel coefficients, the calculated Bd that maximizes the diversity will be a scaled version of
 , where
, where  stands for estimated and the superscript
stands for estimated and the superscript  stands for transpose conjugate. Subsequently, weighting the real channel
stands for transpose conjugate. Subsequently, weighting the real channel 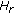 by this Bd will generate an additive factor that depends on the mismatching between the real channel and the estimated channel.
by this Bd will generate an additive factor that depends on the mismatching between the real channel and the estimated channel.
By simulation, we can determine the distribution function in this case. Figure 12 depicts the LPF when using an up-to-date or completely out-of-date estimated channel version in the beamforming algorithm. We notice that, the gap between the two curves represents the decrease in the SNR when inappropriate Bd is used.
Thus the  can be written as
can be written as

Therefore, substituting  by
by  in (7), we can obtain the probability of transmission in a generic time slot by using some numerical methods.
in (7), we can obtain the probability of transmission in a generic time slot by using some numerical methods.
Because of using the four way handshaking,  and
and  are calculated according to (11) and based on
are calculated according to (11) and based on  and
and  where
where

For notation simplicity, let  denote the loss probability due to fading and channel mismatching, that is
denote the loss probability due to fading and channel mismatching, that is  .
.
We consider the five events experienced by a typical user U [32] and we calculate the probability of each event based on  and
and  :
:
-
(i)
e1: U does not transmit and the medium is idle:
 (23)
(23)
-
(ii)
e2: U does not transmit and it detects a successfully transmission among other nodes:
 (24)
(24)
-
(iii)
e3: U does not transmit and it detects a collision among other nodes:
 (25)
(25)
-
(iv)
e4: U experiences a successful transmission:
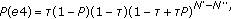 (26)
(26)
-
(v)
e5: U experiences a failed transmission:
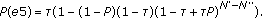 (27)
(27)
The average renewal period for each user is given by  where
where  ,
,  and
and  .
.
Finally, the total average throughput can be computed as:

where the use of  illustrates the fact that more than one transmission can coexist. This throughput represents the fraction of time where successful transmissions occurred.
illustrates the fact that more than one transmission can coexist. This throughput represents the fraction of time where successful transmissions occurred.
3.3. Numerical Example
Our model is evaluated through a numerical example using the parameters stated in Table 3.
In Figure 13, the saturation throughput with respect to the coherence time ( ) is plotted. Three antenna array systems are investigated (
) is plotted. Three antenna array systems are investigated ( ). As it can be seen, the saturation throughput increases as the number of antenna elements increases. This fact can be interpreted from two points of view: firstly, as the antenna array size increases, the loss due to fading decreases, and the links are more reliable. Secondly, a higher number of antenna elements enables more concurrent connections simultaneously, which increases significantly the system throughput. We observe also that the performance is moderate when the channel conditions change frequently (the coherence time is small). Using a 2-element antenna array, the performance presents slight changes when operating with low or high coherence time values. In this case, the throughput saturates approximately at
). As it can be seen, the saturation throughput increases as the number of antenna elements increases. This fact can be interpreted from two points of view: firstly, as the antenna array size increases, the loss due to fading decreases, and the links are more reliable. Secondly, a higher number of antenna elements enables more concurrent connections simultaneously, which increases significantly the system throughput. We observe also that the performance is moderate when the channel conditions change frequently (the coherence time is small). Using a 2-element antenna array, the performance presents slight changes when operating with low or high coherence time values. In this case, the throughput saturates approximately at  . On the other hand, when using an 8-element antenna array, the performance increases substantially and the saturation is approximately reached at
. On the other hand, when using an 8-element antenna array, the performance increases substantially and the saturation is approximately reached at  .
.
Moreover, we shed some light to evaluate the saturation throughput behavior with respect to the tradeoff factor  . Recall that, the acquisition period is related to the coherence time by the following factor:
. Recall that, the acquisition period is related to the coherence time by the following factor:  . Herein, we try to relate the simulation results with the numerical ones using an 8-element antenna array. In Figure 5, we have shown via simulation that the network presents the maximum performance when such optimal tradeoff factor is used. This optimality depends on the channel conditions and on the network parameters. In Figure 14, the result tends to have a maximum when
. Herein, we try to relate the simulation results with the numerical ones using an 8-element antenna array. In Figure 5, we have shown via simulation that the network presents the maximum performance when such optimal tradeoff factor is used. This optimality depends on the channel conditions and on the network parameters. In Figure 14, the result tends to have a maximum when  . This can be interpreted by the fact that when
. This can be interpreted by the fact that when  , the acquisition is frequent and the network will be overloaded by the training sequences. On the other hand, when
, the acquisition is frequent and the network will be overloaded by the training sequences. On the other hand, when  , the channel estimation is scarce and the beamforming techniques will not be fruitful. Note that the maximum value obtained here is close to that obtained with simulation and the analytical results are adequate with the simulation ones. These results show the effectiveness to choose an optimal value of
, the channel estimation is scarce and the beamforming techniques will not be fruitful. Note that the maximum value obtained here is close to that obtained with simulation and the analytical results are adequate with the simulation ones. These results show the effectiveness to choose an optimal value of  on the network performance.
on the network performance.
4. Conclusion
This work focused on exploring the benefits of smart antennas and especially beamforming techniques in multipath fading ad hoc networks. For this aim, we proposed a novel protocol, named BMAC, to adapt the MAC functionalities to the new antenna paradigm. The results show that, in quasistatic scenarios, the BMAC offers a high throughput and better quality of service than the conventional directional MAC. Moreover, we devised a new accurate model for analytical evaluation of the performance of ad hoc networks when simple beamforming technique is used. Finally, a numerical example shows that the numerical results cope with the simulation ones.
Beyond this work, we aim to design and analyze a more general MAC protocol to support MIMO links in ad hoc networks. For near scope, we aim to take into account the hidden terminal problem in the proposed analytical model.
References
Choudhury RR, Yang X, Ramanathan R, Vaidya NH: Using directional antennas for medium access control in ad hoc networks. Proceedings of the 8th ACM Annual International Conference on Mobile Computing and Networking (MobiCom '02), September 2002, Atlanta, Ga, USA 59-70.
Mundarath JC, Ramanathan P, Van Veen BD: NULLHOC: a MAC protocol for adaptive antenna array based wireless ad hoc networks in multipath environments. Proceedings of IEEE Global Telecommunications Conference (GLOBECOM '04), November 2004, Dallas, Tex, USA 5: 2765-2769.
Ramanathan R: On the performance of ad hoc networks with beamforming antennas. Proceedings of the 2nd ACM International Symposium on Mobile Ad Hoc Networking & Computing (MobiHoc '01), October 2001, Long Beach, Calif, USA 95-105.
Ramanathan R, Redi J, Santivanez C, Wiggins D, Polit S: Ad hoc networking with directional antennas: a complete system solution. IEEE Journal on Selected Areas in Communications 2005, 23(3):496-506.
Choudhury RR, Yang X, Ramanathan R, Vaidya NH: On designing MAC protocols for wireless networks using directional antennas. IEEE Transactions on Mobile Computing 2006, 5(5):477-491.
Singh A, Ramanathan P, Van Veen B: Spatial reuse through adaptive interference cancellation in multi-antenna wireless networks. Proceedings of IEEE Global Telecommunications Conference (GLOBECOM '05), November 2005, St. Louis, Mo, USA 5: 3092-3096.
Zorzi M, Zeidler J, Anderson A, et al.: Cross-layer issues in MAC protocol design for MIMO ad hoc networks. IEEE Wireless Communications 2006, 13(4):62-76. 10.1109/MWC.2006.1678167
Winters JH: Smart antenna techniques and their application to wireless ad hoc networks. IEEE Wireless Communications 2006, 13(4):77-83. 10.1109/MWC.2006.1678168
ANSI/IEEE std 802.11 : Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications. 1999.
Fakih K, Diouris JF, Andrieux G: BMAC: beamformed MAC protocol with channel tracker in MANET using smart antennas. Proceedings of the 9th European Conference on Wireless Technology (ECWT '06), September 2006, Manchester, UK 185-188.
Fakih K, Diouris J-F, Andrieux G: Analytical evaluation on the performance of ad hoc networks when using beamforming techniques. Proceedings of IEEE International Conference on Communications (ICC '08), May 2008, Beijing, China 2337-2342.
Robert Vilzmann CB: A survey on MAC protocols for ad hoc networks with directional antennas. Proceedings of 11th Networks and Applications towards a Ubiquitously Connected World: IFIP International Workshop on Networked Applications (EUNICE '05), July 2005, Madrid, Spain 187-200.
Dai H, Ng K-W, Wu M-Y: An overview of MAC protocols with directional antennas in wireless ad hoc networks. Proceedings of the 2nd International Conference on Wireless and Mobile Communications (ICWMC '06), July 2006, Bucharest, Romania 84.
Takai M, Martin J, Bagrodia R, Ren A: Directional virtual carrier sensing for directional antennas in mobile ad hoc networks. Proceedings of the 3rd ACM International Symposium on Mobile Ad Hoc Networking & Computing (MobiHoc '02), June 2002, Lausanne, Switzerland 183-193.
Nasipuri A, Ye S, You J, Hiromoto RE: A MAC protocol for mobile ad hoc networks using directional antennas. Proceedings of IEEE Wireless Communications and Networking Conference (WCNC '00), September 2000, Chicago, Ill, USA 3: 1214-1219.
Korakis T, Jakllari G, Tassiulas L: A MAC protocol for full exploitation of directional antennas in ad-hoc wireless networks. Proceedings of the 4th ACM International Symposium on Mobile Ad Hoc Networking & Computing (MobiHoc '03), June 2003, Annapolis, Md, USA 98-107.
Chen W-T, Ho T-W, Chen Y-C: An MAC protocol for wireless adhoc networks using smart antennas. Proceedings of the 11th International Conference on Parallel and Distributed Systems (ICPADS '05), July 2005, Fuduoka, Japan 1: 446-452.
Yang J, Li J, Sheng M: MAC protocol for mobile ad hoc network with smart antennas. Electronics Letters 2003, 39(6):555-557. 10.1049/el:20030337
Marzetta TL, Hochwald BM: Fast transfer of channel state information in wireless systems. IEEE Transactions on Signal Processing 2006, 54(4):1268-1278.
Swindlehurst AL, Peel C, Spencer Q: An Overview of Algorithms for Downlink Transmit Beamforming. Brigham Young University, Provo, Utah, USA; 2004.
Huang K, Andrews JG, Heath RW, Guo D, Berry RA: Spatial interference cancellation for mobile ad hoc networks: perfect CSI. Proceedings of IEEE Global Telecommunications Conference (GLOCOM '08), November-December 2008, New Orleans, La, USA 1-5.
Iltis RA, Kim S-J, Hoang DA: Noncooperative iterative MMSE beamforming algorithms for ad hoc networks. IEEE Transactions on Communications 2006, 54(4):748-759.
Choudhury RR, Vaidya NH: Deafness: a MAC problem in ad hoc networks when using directional antennas. Proceedings the 12th IEEE International Conference on Network Protocols (ICNP '04), October 2004, Berlin, Germany 283-292.
Opnet modeler http://www.opnet.com
Bianchi G: Performance analysis of the IEEE 802.11 distributed coordination function. IEEE Journal on Selected Areas in Communications 2000, 18(3):535-547. 10.1109/49.840210
Wu H, Peng Y, Long K, Cheng S, Ma J: Performance of reliable transport protocol over IEEE 802.11 wireless LAN: analysis and enhancement. Proceedings the 21st Annual Joint Conference of the IEEE Computer and Communications Societies (INFCOM '02), June 2002, New York, NY, USA 2: 599-607.
Ziouva E, Antonakopoulos T: CSMA/CA performance under high traffic conditions: throughput and delay analysis. Computer Communications 2002, 25(3):313-321. 10.1016/S0140-3664(01)00369-3
Chatzimisios P, Boucouvalas AC, Vitsas V, Vafiadis A, Economidis A, Huang P: A simple and effective backoff scheme for the IEEE 802.11 MAC protocol. Proceedings of the International Conference on Cybernetics and Information Technologies, Systems and Applications (CITSA '05), July 2005, Orlando, Fla, USA 1: 48-53.
Zander J: Slotted ALOHA multihop packet radio networks with directional antennas. Electronics Letters 1990, 26(25):2098-2100. 10.1049/el:19901351
Wang Y, Garcia-Luna-Aceves JJ: Directional collision avoidance in ad hoc networks. Performance Evaluation 2004, 58(2-3):215-241. 10.1016/j.peva.2004.07.012
Carvalho MM, Garcia-Luna-Aceves JJ: Modeling wireless ad hoc networks with directional antennas. Proceedings of the 25th IEEE International Conference on Computer Communications (INFOCOM '06), April 2006, Barcelona, Spain 1-12.
Hu M, Zhang J: MIMO ad hoc networks with spatial diversity: medium access control and saturation throughput. Proceedings of the 43rd IEEE Conference on Decision and Control (CDC '04), December 2004, Nassau, Bahamas 3: 3301-3306.
Lo TKY: Maximum ratio transmission. IEEE Transactions on Communications 1999, 47(10):1458-1461. 10.1109/26.795811
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Fakih, K., Diouris, JF. & Andrieux, G. Beamforming in Ad Hoc Networks: MAC Design and Performance Modeling. J Wireless Com Network 2009, 839421 (2009). https://doi.org/10.1155/2009/839421
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/839421

 to transmit these sequences (if not, the estimated channel versions will be expired and the beamforming will not work properly). In this case, the amount of data lost by the omnidirectional transmission for the TS packets depends on the acquisition frequency.
to transmit these sequences (if not, the estimated channel versions will be expired and the beamforming will not work properly). In this case, the amount of data lost by the omnidirectional transmission for the TS packets depends on the acquisition frequency.

 = 0. 5.
= 0. 5.







 ,
,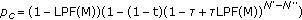 ,
, , where
, where  stands for estimated and the superscript
stands for estimated and the superscript  stands for transpose conjugate. Subsequently, weighting the real channel
stands for transpose conjugate. Subsequently, weighting the real channel 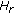 by this Bd will generate an additive factor that depends on the mismatching between the real channel and the estimated channel.
by this Bd will generate an additive factor that depends on the mismatching between the real channel and the estimated channel.



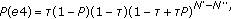
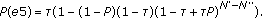

 .
.
 ,
,  .
.