- Research Article
- Open access
- Published:
Decentralising Multicell Cooperative Processing: A Novel Robust Framework
EURASIP Journal on Wireless Communications and Networking volume 2009, Article number: 890685 (2009)
Abstract
Multicell cooperative processing (MCP) has the potential to boost spectral efficiency and improve fairness of cellular systems. However the typical centralised conception for MCP incurs significant infrastructural overheads which increase the system costs and hinder the practical implementation of MCP. In Frequency Division Duplexing systems each user feeds back its Channel State Information (CSI) only to one Base Station (BS). Therefore collaborating BSs need to be interconnected via low-latency backhaul links, and a Control Unit is necessary in order to gather user CSI, perform scheduling, and coordinate transmission. In this paper a new framework is proposed that allows MCP on the downlink while circumventing the aforementioned costly modifications on the existing infrastructure of cellular systems. Each MS feeds back its CSI to all collaborating BSs, and the needed operations of user scheduling and signal processing are performed in a distributed fashion by the involved BSs. Furthermore the proposed framework is shown to be robust against feedback errors when quantized CSI feedback and linear precoding are employed.
1. Introduction
Cellular systems employing aggressive frequency reuse and especially full frequency reuse have recently attracted the attention due to the increasing demand for high quality and throughput wireless services (mobile Internet), together with the scarcity of radio spectrum. Although these systems lead to significant gains in spectrum usage, they incur important losses in cell throughput resulting from the increased amount of intercell interference (ICI). This mainly affects users located on the cell edge as they are more prone to ICI originating from neighbouring cells. Therefore ICI is a factor causing significant performance and fairness degradation in the network [1]. Furthermore ICI degrades performance of Multiple Input Multiple-Output (MIMO) systems; hence it impedes their deployment in a cellular context [2].
Multicell cooperative processing (MCP) has been recognized as an effective solution for ICI mitigation [1, 3, 4]. In MCP enabled systems BSs are grouped into cooperation clusters, each of which contains a subset of the network BSs. The BSs of each cluster exchange information and jointly process signals by forming virtual antenna arrays distributed in space. They can be seen as multiuser MIMO systems where the antennas are no longer collocated but remote. Notably, MCP has been shown to reduce ICI and boost performance; this especially suits the downlink as interference mitigation burdens the network infrastructure and not the receivers [3].
However, MCP comes at the cost of increased signaling and infrastructural overheads. On the downlink of cellular systems operating in Frequency Division Duplexing (FDD) mode, the overheads of MCP are related to the inherent need for Channel State Information (CSI) at the transmitter of multiuser MIMO systems and also to the distributed nature of collaborative BS processing [5]. The overheads related to MCP can be divided into two main categories.
Signaling Overheads
-
(i)
CSI estimation: users estimate a greater number of channel coefficients than a multiuser MIMO system, equal to the total number of cooperating antennas.
-
(ii)
CSI Feedback: feedback of the estimated high number of channel coefficients from users to BSs.
-
(iii)
Time synchronisation: collaborating BSs need to be tightly synchronised in time.
Infrastructural Overheads
-
(i)
Control Unit: the CU gathers CSI from the BSs, performs scheduling, and designs the transmission parameters according to the chosen transmission strategy.
-
(ii)
Low-latency backhaul links: collaborating BSs are connected with the CU via low-latency links in order to exchange CSI, scheduling decisions, and transmission parameters.
Note that the signaling overheads are independent of the architectural conception for MCP, whereas the infrastructural overheads mentioned above are related to the existing conception for the architecture of MCP.
A natural way for mitigating the aforementioned overheads is to limit the number of cooperating BSs per cluster. A simple technique that has been proposed is limited static clustering, where BS cooperation groups are of limited size and remain static; only neighbouring BSs collaborate [6, 7]. This has been shown to be a good trade-off between performance and overhead. However, even higher performance gains can be attained if the limited clusters are formed dynamically; in this case the cooperating BSs are not the neighbouring ones but rather the ones that interfere the most [8, 9]. In addition, ways of optimizing system performance under a constrained backhaul have been considered [10]. However, these contributions attempt mainly to mitigate the signaling overheads as they imply a CU per cooperation cluster and low-latency inter-BS links. In order to facilitate the deployment of MCP, it is desirable that the infrastructural overheads entailed by the existing conception for MCP (CU, low-latency backhaul links) are alleviated, and this aspect is not addressed in the abovementioned contributions.
According to the typical framework for MCP on the downlink of FDD systems, a Mobile Station (MS) estimates the channels related to the BSs of its cooperation cluster (CSI estimation). Then it feeds back to the BS of its cell (usually the one that it receives the maximum SNR from, defined as Master BS) either full or partial CSI (i.e., long-term or quantized CSI). Subsequently, the BS forwards this local information (CSI) to the CU of the cluster which gathers local CSI from all cooperating BSs. Local CSI for a BS is defined as the CSI related to the MSs belonging to its cell. Nonlocal CSI for a BS is defined as the CSI of the MSs belonging to different cells of the cooperation cluster. The CU selects the users to be served (scheduling phase) and calculates the transmission parameters which are then sent to the corresponding BSs for the transmission to take place (transmission phase). Therefore in the existing conception, a CU and the CU to BSs low-latency links are necessary [11–13], a fact which demands substantial changes to the current system architecture and a significant increase in costs.
In [14] a framework for decentralising MCP has been proposed which aims at keeping the necessary infrastructural overheads and costs for accommodating MCP to a minimum. It is assumed that each BS collects local together with nonlocal CSI; each MS sends its CSI estimate to all cooperating BSs. In this case, each BS can perform scheduling, and design the transmission parameters independently without the need of any CSI exchange with a central entity; the same scheduling decisions are made by each BS. The proposed framework has a potential sensitivity to feedback errors since MSs utilise several radio links in order to communicate their CSI to the collaborating BSs. This was not fully evaluated in [14] which only assumed unquantized (unlimited) feedback. However, limited feedback schemes are of practical importance [15]. Therefore in this paper a more realistic quantized feedback model is considered, and its sensitivity to feedback errors under the proposed framework is investigated. It is shown that the proposed decentralized framework is robust against feedback errors under a realistic digital feedback model.
The paper is structured in the following way: in Section 2 the system model is introduced. In Section 3 the linear precoding framework for transmission, together with the models for quantized feedback, and feedback errors are presented. In Section 4 the typical centralised conception for MCP is described while in Section 5 the proposed decentralised framework for MCP is discussed. In Section 6 numerical results are shown related to feedback errors proving the robustness of the decentralised MCP approach. The paper is concluded in Section 7.
2. System Model
A cellular system which comprises  base stations and
base stations and  mobile stations overall is considered. We consider the case of single-antenna BSs and MSs for simplicity, although our results can be easily generalized to the multiple antenna case. Downlink communication is taken into account, and frequency flat fading is assumed. The received signal of the
mobile stations overall is considered. We consider the case of single-antenna BSs and MSs for simplicity, although our results can be easily generalized to the multiple antenna case. Downlink communication is taken into account, and frequency flat fading is assumed. The received signal of the  th MS can be described as
th MS can be described as

where  represents the channel vector of the
represents the channel vector of the  th user,
th user,  is the vector containing the transmit antenna symbols, and
is the vector containing the transmit antenna symbols, and  is the independent complex circularly symmetric additive Gaussian noise coefficient. An average per antenna power constraint has been considered,
is the independent complex circularly symmetric additive Gaussian noise coefficient. An average per antenna power constraint has been considered,  for
for  . It is assumed that the system operates in FDD mode and that each MS
. It is assumed that the system operates in FDD mode and that each MS  obtains a perfect estimate of its own channel state
obtains a perfect estimate of its own channel state  . In addition, we consider delayless feedback links which are utilised by the MSs in order to feed back their CSI to the system infrastructure. The users feed back limited CSI (quantized CSI) which can be corrupted by errors introduced by the feedback channel.
. In addition, we consider delayless feedback links which are utilised by the MSs in order to feed back their CSI to the system infrastructure. The users feed back limited CSI (quantized CSI) which can be corrupted by errors introduced by the feedback channel.
In the case of single-cell processing (absence of BS cooperation), each MS receives useful signal only from one BS, usually the one providing the best long-term channel gain.  single antenna BSs are assumed; hence
single antenna BSs are assumed; hence  MSs are scheduled for transmission in each time slot. The vector of transmit symbols
MSs are scheduled for transmission in each time slot. The vector of transmit symbols  is mapped directly to the transmit antennas
is mapped directly to the transmit antennas  . Therefore the
. Therefore the  th MS receives the following signal when
th MS receives the following signal when  is its associated BS:
is its associated BS:

where  corresponds to the channel coefficient related to the useful signal and
corresponds to the channel coefficient related to the useful signal and  corresponds to the detrimental ICI. Thus the Signal to Interference plus Noise Ratio (SINR) of the user
corresponds to the detrimental ICI. Thus the Signal to Interference plus Noise Ratio (SINR) of the user  is
is

where  and
and  represent the respective power allocation levels. In this paper equal power allocation is considered across MSs for simplicity.
represent the respective power allocation levels. In this paper equal power allocation is considered across MSs for simplicity.
Notation. Lower and upper case boldface symbols denote vectors and matrices, respectively;  and
and  denote the transpose and the Hermitian transpose, respectively.
denote the transpose and the Hermitian transpose, respectively.  stands for the Euclidean norm of a vector,
stands for the Euclidean norm of a vector,  denotes the cardinality of a set,
denotes the cardinality of a set,  refers to the
refers to the  th element of a matrix diagonal, and
th element of a matrix diagonal, and  represents the complex space of
represents the complex space of  dimensions.
dimensions.  denotes the expectation operator, and
denotes the expectation operator, and  represents the angle between vectors
represents the angle between vectors  and
and  .
.
3. Linear Precoding for MCP
In MCP enabled networks each group of collaborating BSs forms a distributed antenna array. Therefore all the typical multiuser MIMO precoding techniques can be applied in order for the ICI to be mitigated. In this paper linear precoding is considered for MCP transmission as it provides a good trade-off between performance and complexity, and it is more robust to imperfect CSI compared to nonlinear schemes [15]. Furthermore linear precoding together with the more practical quantized feedback can be optimal under certain circumstances [16]. In addition to this, linear precoding scales optimally when a large number of MSs is available and opportunistic scheduling is employed [17].
Thus if  single-antenna BSs jointly perform linear precoding on the downlink, the BS antennas combine and serve at most
single-antenna BSs jointly perform linear precoding on the downlink, the BS antennas combine and serve at most  single-antenna mobile stations simultaneously. The complete channel matrix of the system is
single-antenna mobile stations simultaneously. The complete channel matrix of the system is

where  is the channel vector of the
is the channel vector of the  th MS. Let
th MS. Let  be the set of MSs scheduled to be served in a specific time slot, where
be the set of MSs scheduled to be served in a specific time slot, where  . Therefore
. Therefore  is the channel matrix related to these MSs. The vector of transmit symbols
is the channel matrix related to these MSs. The vector of transmit symbols  with power
with power  , where
, where  , is mapped to the transmit antennas as follows:
, is mapped to the transmit antennas as follows:

 is the precoding matrix of size
is the precoding matrix of size  which is a function of the received CSI of the scheduled users, and
which is a function of the received CSI of the scheduled users, and  is the beamforming vector corresponding to MS
is the beamforming vector corresponding to MS  . Therefore with linear precoding, the
. Therefore with linear precoding, the  th MS, where
th MS, where  , receives
, receives

The term  represents the detrimental ICI. In matrix notation the scheduled users receive
represents the detrimental ICI. In matrix notation the scheduled users receive

where  is the received signal vector and
is the received signal vector and  is a vector of independent complex circularly symmetric additive Gaussian noise components. The SINR
is a vector of independent complex circularly symmetric additive Gaussian noise components. The SINR  of the
of the  th MS is
th MS is

The term  corresponds to the intercell interference power.
corresponds to the intercell interference power.
Per-antenna power constraints are considered due to the fact that cooperating antennas are spatially distributed, and they cannot share their power. It is assumed that each antenna has an average power constraint, thus  for
for  . For equal power allocation
. For equal power allocation  , where
, where  is a column vector of 1s with dimension
is a column vector of 1s with dimension  , the elements of the power allocation vector must meet the following constraint [4]:
, the elements of the power allocation vector must meet the following constraint [4]:

Therefore the power allocation vector is

As a result, the SINR of the  th MS is
th MS is

With equal power allocation and an equal power constraint per BS,  for
for  , the expression for the power allocation vector (10) reduces to
, the expression for the power allocation vector (10) reduces to  .
.
The entity of the network responsible for user scheduling and precoder design receives an imperfect version  of the matrix H, due to quantization error (limited digital feedback) and to errors introduced by the feedback channel. The chosen precoding scheme is zero-forcing, where the precoding matrix inverts the imperfect channel matrix describing the received CSI. Hence the precoding matrix is
of the matrix H, due to quantization error (limited digital feedback) and to errors introduced by the feedback channel. The chosen precoding scheme is zero-forcing, where the precoding matrix inverts the imperfect channel matrix describing the received CSI. Hence the precoding matrix is

where  is a diagonal matrix that normalizes the columns of
is a diagonal matrix that normalizes the columns of  to unit norm. Note that other choices of linear precoding apart from zero-forcing (e.g., MMSE) can be considered [18]. The evaluation metric we are interested in is the ergodic achievable rate per cell:
to unit norm. Note that other choices of linear precoding apart from zero-forcing (e.g., MMSE) can be considered [18]. The evaluation metric we are interested in is the ergodic achievable rate per cell:

3.1. Quantized Limited Feedback
In the case of quantized limited feedback, for each user  there is a quantization codebook
there is a quantization codebook  consisting of
consisting of  vectors of unit norm, where
vectors of unit norm, where  is the number of feedback bits. This codebook is known both by the user and by the scheduling entity. Each MS after obtaining an estimate of its channel vector
is the number of feedback bits. This codebook is known both by the user and by the scheduling entity. Each MS after obtaining an estimate of its channel vector  (in this paper we assume a perfect estimate) quantizes its direction
(in this paper we assume a perfect estimate) quantizes its direction  to the vector from the codebook
to the vector from the codebook  that best approaches it, which is the one leading to the smallest angle separation [19–21]. Therefore
that best approaches it, which is the one leading to the smallest angle separation [19–21]. Therefore

where  results from the inner product rule. The quantity determining the efficiency of quantization is the quantization error defined as
results from the inner product rule. The quantity determining the efficiency of quantization is the quantization error defined as  . The codebook should be user specific in order to avoid multiple users quantizing their channel direction to the same vector.
. The codebook should be user specific in order to avoid multiple users quantizing their channel direction to the same vector.
After quantization, MS i feeds back to the system the index k in binary form which corresponds to the quantization vector that best describes its channel direction. Therefore this piece of information is defined as Channel Direction Information (CDI). The more the feedback bits are, the larger the quantization codebook is, which leads to a better approximation of the MS's channel direction. Apart from CDI, the scheduling entity needs some information regarding the channel quality of each user in order to be able to make user selection decisions; this is defined as Channel Quality Information (CQI). In this paper we consider the unquantized channel norm  as the fed back CQI which does not capture the interuser interference. This is because we are interested in investigating the precoding performance and not the efficiency of scheduling; therefore the consideration of more complex CQI metrics is unnecessary.
as the fed back CQI which does not capture the interuser interference. This is because we are interested in investigating the precoding performance and not the efficiency of scheduling; therefore the consideration of more complex CQI metrics is unnecessary.
A random codebook has been considered as optimization of the codebook design is beyond the scope of this paper. Thus the codebook is comprised of unit norm complex Gaussian random vectors,  and
and  .
.
Hence the concatenated quantized channel matrix of the system is  . The binary indices corresponding to the CSI vectors (lines of
. The binary indices corresponding to the CSI vectors (lines of  ) are fed back to the scheduling entity through one or several radio channels, depending on the MCP framework, that introduce errors. Therefore the concatenated channel possessed by the scheduling entity is
) are fed back to the scheduling entity through one or several radio channels, depending on the MCP framework, that introduce errors. Therefore the concatenated channel possessed by the scheduling entity is  , where
, where  is a function of the errors introduced by the feedback channel.
is a function of the errors introduced by the feedback channel.
3.2. Feedback Error Model
When quantized feedback is employed, each MS  feeds back a sequence of
feeds back a sequence of  bits,
bits,  ,
,  . These bits are the index of the vector in the employed codebook
. These bits are the index of the vector in the employed codebook  that best describes the CDI of a user in binary form. It is assumed that each transmitted bit
that best describes the CDI of a user in binary form. It is assumed that each transmitted bit  is received in error with probability
is received in error with probability  . Therefore
. Therefore

The probability of bit errors is considered to be identical and independent across different radio links. The received feedback can be protected from errors by the use of appropriate error correction techniques requiring the addition of a number of bits in the fed back sequence. However such consideration is beyond the scope of this paper which aims at examining the impact of feedback errors in the worst case scenario, when no error detection or correction schemes are employed.
4. Typical Centralised Framework for MCP
The typical conception for MCP entails that collaborating BSs are interconnected via low-latency backhaul links. These links are responsible for carrying the necessary signals that allow cooperating BSs to act jointly, perform user scheduling and design the transmission parameters for the scheduled users. Under a linear precoding framework these parameters are the beamforming weights applied by each BS antenna of the cooperation cluster. The entity coordinating this joint action is a Control Unit accommodated in each cooperation cluster. It gathers global user CSI and centrally performs MS scheduling and signal processing operations.
In this typical centralised framework for MCP, each MS is associated to a so-called Master or Anchor BS, and it conceptually belongs to its corresponding cell. There are three main phases in downlink communications of FDD systems that consider incorporating MCP [11–13].
-
(1)
Phase 1.
-
(i)
MSs estimate the CSI related to all cooperating BSs through downlink pilots. In this paper perfect channel estimation is assumed and thus each MS
 estimates the channel vector
estimates the channel vector  .
. -
(ii)
Incase limited digital feedback is employed, MSs quantize the direction of their channel estimate; that is, MS
 quantizes its channel direction
quantizes its channel direction  to
to  .
.
-
(i)
-
(2)
Phase 2.
-
(i)
MSs feedback their CSI (CDI and CQI) to their Master BS with the proper power and modulation and coding scheme (MCS) in order for the BS to be able to decode the information. All cooperating BSs gather local CSI, the CSI of the MSs belonging to their cells.
-
(ii)BSs
forward the local CSI to the CU of the cluster through the low-latency backhaul links. The CU collects global CSI
 affected by the errors on the feedback channel (Figure 1).
affected by the errors on the feedback channel (Figure 1).
-
(i)
-
(3)
Phase 3.
-
(i)
The CU schedules MSs based on global CSI
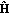 .
. -
(ii)
The CU designs the beamforming weights for each BS antenna and communicates them together with the scheduling decisions to the corresponding BSs for the transmission to take place.
-
(i)
This framework requires a significantly increased infrastructural cost comparing to the conventional cellular systems, as there is a demand for low-latency interbase links and a CU per cooperation cluster. Furthermore there is a need for an increased communication protocol complexity in order for these entities to interoperate properly. These facts inevitably imply changes in the current architecture of cellular systems in order for MCP to be enabled. However it is highly desirable that changes to the current structure of cellular systems are kept to a minimum when MCP capabilities are enabled.
In the centralised framework, each MS  utilises only one radio link to transmit the bit sequence describing its quantized CSI
utilises only one radio link to transmit the bit sequence describing its quantized CSI  , the link to the Master BS. Therefore if each bit faces an independent error probability per feedback link
, the link to the Master BS. Therefore if each bit faces an independent error probability per feedback link  (15), the probability that the
(15), the probability that the  th user's bit sequence
th user's bit sequence  is received in error by the scheduling entity (CU) is
is received in error by the scheduling entity (CU) is

where  denotes the binomial coefficient. The bit sequence is in error if at least one of its bits is in error; thus for a specific bit error probability
denotes the binomial coefficient. The bit sequence is in error if at least one of its bits is in error; thus for a specific bit error probability  , the more the feedback bits are, the more likely an error occurs. From this perspective it is of interest that the codebook size is kept as small as possible. However the smaller the codebook, the less accurately it can approach the actual channel state of the user, which leads to an inferior performance. Therefore a trade-off exists between the needed codebook precision and its size with respect to feedback errors.
, the more the feedback bits are, the more likely an error occurs. From this perspective it is of interest that the codebook size is kept as small as possible. However the smaller the codebook, the less accurately it can approach the actual channel state of the user, which leads to an inferior performance. Therefore a trade-off exists between the needed codebook precision and its size with respect to feedback errors.
5. Proposed Decentralised Framework for MCP
In order to face the setbacks of the typical centralized framework, we propose a framework that does not require centralised scheduling and transmission design, but still can achieve the same performance. One justification for centralised processing is that the involved BSs at each cooperation cluster are assumed to lack global user CSI  ; they only possess local CSI which is comprised of submatrices of
; they only possess local CSI which is comprised of submatrices of  ; MCP could be achieved in a decentralised fashion if each involved BS obtained global CSI. Taking this into account, we propose a framework for the downlink whose phases are as follows.
; MCP could be achieved in a decentralised fashion if each involved BS obtained global CSI. Taking this into account, we propose a framework for the downlink whose phases are as follows.
-
(1)
Phase 1 (identical with the centralised framework).
-
(i)
MSs estimate the CSI related to all cooperating BSs through downlink pilots. In this paper perfect channel estimation is assumed and thus each MS
 estimates the channel vector
estimates the channel vector 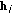 .
. -
(ii)
In case limited digital feedback is employed, MSs quantize the direction of their channel estimate; that is, MS
 quantizes its channel direction
quantizes its channel direction  to
to  .
.
-
(i)
-
(2)
Phase 2.
-
(i)
MSs feedback their CSI (CDI and CQI) to all cooperating BSs by utilising the radio links connecting them with the collaborating BSs. Each MS feeds back its CSI omnidirectionally, and this transmission is done with the proper power and MCS in order for all cluster BSs to be able to decode the information. All cooperating BSs gather global CSI, the CSI of the MSs of all cooperating cells (Figure 2).
-
(i)
-
(3)
Phase 3.
-
(i)
The BSs schedule MSs independently based on their acquired global CSI. Cluster BSs are synchronised and employ the same scheduling algorithm. In case there are no feedback errors, BSs receive the same input parameters (global CSI
 ), and the schedulers end up selecting exactly the same MSs. If feedback links introduce errors, the fed back CSI (CDI and CQI) needs to be protected by the use of appropriate techniques.
), and the schedulers end up selecting exactly the same MSs. If feedback links introduce errors, the fed back CSI (CDI and CQI) needs to be protected by the use of appropriate techniques. -
(ii)
Each BS designs the complete beamforming matrix and utilises the antenna weights corresponding to it; that is, BS
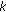 utilises for transmission the
utilises for transmission the 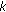 th line of the precoding matrix
th line of the precoding matrix 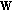 .
.
-
(i)
Under this framework, infrastructural costs and signaling protocol complexity are minimised when MCP is enabled as neither a CU per cluster nor the low latency links connecting it with the cooperating BSs are required. Hence, the structure of MCP enabled cellular networks can remain almost the same with the structure of the conventional cellular systems. Note that under this framework, radio feedback overhead remains the same, comparing to the conventional centralised framework, provided that the same resources are allocated to the terminal for feeding back its CSI by each cooperating BS.
In case errors are introduced to the fed back information, the decentralised framework can be more sensitive than the centralised one as error patterns can be different on each employed feedback link. In the centralised framework, each MS utilises only one radio link for feeding back its channel state information (CSI transmitted to the Master BS only); therefore there is only one error pattern affecting feedback information per MS in this case. In the decentralized framework MSs feed back their CSI to all cooperating BSs; thus each BS k might acquire a different version  of the global CSI
of the global CSI  .
.
Independent bit error probabilities on each feedback link increase the probability that the transmitted bit sequence of each user  ,
,  is received in error in at least one of the
is received in error in at least one of the  collaborating BSs. This probability is
collaborating BSs. This probability is

Hence feedback errors can potentially cause a further performance degradation to the decentralised framework than the centralised one compared to the no error case. Furthermore, it is interesting to investigate how close these two frameworks perform under the existence of feedback errors.
Let  be the set of the cooperating BSs, where
be the set of the cooperating BSs, where  . Independent bit error probabilities on each feedback link might result in the selection of different channel vectors by some of the
. Independent bit error probabilities on each feedback link might result in the selection of different channel vectors by some of the  base stations for a specific MS. For example it is possible for the received feedback of BS
base stations for a specific MS. For example it is possible for the received feedback of BS  that
that  , where
, where  ,
,  . A set of BSs
. A set of BSs  might receive a different CSI index than BS
might receive a different CSI index than BS  . This potential CSI discrepancy can lead to performance degradation of the decentralised framework (degradation on scheduling and precoding design). Therefore a good index for the discrepancy of the possessed CSI between the
. This potential CSI discrepancy can lead to performance degradation of the decentralised framework (degradation on scheduling and precoding design). Therefore a good index for the discrepancy of the possessed CSI between the  collaborating BSs is the probability of this discrepancy to occur. Consequently this is also an index of the performance gap between the two MCP frameworks. This probability of CSI discrepancy
collaborating BSs is the probability of this discrepancy to occur. Consequently this is also an index of the performance gap between the two MCP frameworks. This probability of CSI discrepancy  is given by the following expression:
is given by the following expression:

This is due to the fact that the fed back bit sequence remains identical across the  links if the same bits in sequence are either correct or in error. In this case there is no CSI discrepancy and the probability for this event to occur if
links if the same bits in sequence are either correct or in error. In this case there is no CSI discrepancy and the probability for this event to occur if  base stations collaborate and
base stations collaborate and  bits are transmitted is
bits are transmitted is  . Consequently the probability of discrepancy is
. Consequently the probability of discrepancy is  (18). The probability of CSI information discrepancy as a function of the number of feedback bits and the number of independent transmission links can be seen in Figures 3 (
(18). The probability of CSI information discrepancy as a function of the number of feedback bits and the number of independent transmission links can be seen in Figures 3 ( ) and 4 (
) and 4 ( ). It can be seen that the probability of CSI discrepancy heavily relies on the probability of bit error
). It can be seen that the probability of CSI discrepancy heavily relies on the probability of bit error  . Furthermore, the more the transmitted bits and the cooperating BSs, the more likely a CSI discrepancy occurs. In the physical layer, the bit error probability can be reduced by the use of advanced error correction techniques whereas the number of transmitted bits can be reduced by an intelligent codebook design. CSI discrepancy can also be prevented in the Medium Access Control (MAC) layer, when error detection is enabled, with the appropriate signaling techniques [22, Appendix B]. The impact of feedback errors is further evaluated in the following section.
. Furthermore, the more the transmitted bits and the cooperating BSs, the more likely a CSI discrepancy occurs. In the physical layer, the bit error probability can be reduced by the use of advanced error correction techniques whereas the number of transmitted bits can be reduced by an intelligent codebook design. CSI discrepancy can also be prevented in the Medium Access Control (MAC) layer, when error detection is enabled, with the appropriate signaling techniques [22, Appendix B]. The impact of feedback errors is further evaluated in the following section.
6. Numerical Results
In this section we evaluate the ergodic achievable rate performance of the proposed decentralised framework as a function of feedback errors, and we compare it with the typical centralised one. Three mutually interfering sectors of sectorised cells (the cell radius is 1 km) have been assumed to cooperate as this is a scenario of particular practical interest (see Figures 1 and 2). The channel coefficient between the  th MS and the
th MS and the  th sector is
th sector is

where  is the distance between the
is the distance between the  th MS and the
th MS and the  th sector,
th sector,  is the path-loss exponent and
is the path-loss exponent and  the path-loss constant. For the pathloss, the 3GPP Long Term Evolution (LTE) pathloss model has been used:
the path-loss constant. For the pathloss, the 3GPP Long Term Evolution (LTE) pathloss model has been used:

 is the corresponding log-normal coefficient which models large-scale fading (shadowing),
is the corresponding log-normal coefficient which models large-scale fading (shadowing),  , and
, and  is the complex Gaussian coefficient which models small-scale fading,
is the complex Gaussian coefficient which models small-scale fading,  .
.  is the sector antenna power gain as a function of the angle
is the sector antenna power gain as a function of the angle  in degrees, also following the LTE evaluation parameters:
in degrees, also following the LTE evaluation parameters:

We assume that each MS  obtains a perfect estimate of the channel vector associated to all cooperating BSs (
obtains a perfect estimate of the channel vector associated to all cooperating BSs ( ). This estimate is quantized and then fed back omnidirectionally (CDI and CQI feedback). In the centralised framework each MS's feedback is received only by its Master BS (Figure 1). In the decentralised framework all cooperating BSs receive the CSI feedback in order for the decentralised cooperation to take place (Figure 2). An important parameter which determines the BS transmission power is the System SNR which is the average SNR a user experiences at the edge of the cell without taking into account ICI.
). This estimate is quantized and then fed back omnidirectionally (CDI and CQI feedback). In the centralised framework each MS's feedback is received only by its Master BS (Figure 1). In the decentralised framework all cooperating BSs receive the CSI feedback in order for the decentralised cooperation to take place (Figure 2). An important parameter which determines the BS transmission power is the System SNR which is the average SNR a user experiences at the edge of the cell without taking into account ICI.
6.1. Codebook Size
When quantized feedback is employed, the number of feedback bits determines the performance of precoding. Notably the number of bits should increase linearly with the SNR and the number of transmit antennas [21]. However, the more the employed bits are the greater the probability of errors in the received CSI. This can be seen in Figures 5 and 6 where the ergodic capacity of the system with round-robin scheduling and limited feedback as a function of the available bits is plotted. This is for System SNR of 10 dB and 20 dB, respectively, and when random codebook is employed. Without any feedback errors, when system SNR is set to 10 dB, 16 bits provide a good approximation of the perfect CSI, whereas for system SNR equal to 20 dB (high power regime) 20 bits are approximately needed. Notably, MCP with quantized feedback needs more quantization bits compared to the conventional limited feedback multiuser MIMO systems since it is crucial that the achieved ergodic capacity is sufficiently above the capacity of the single-cell processing case.
A plot of the ergodic achievable rate as a function of the number of feedback bits for a random codebook when System SNR is 10 dB and round-robin scheduling is employed. The blue curves correspond to the case where the bit error probability is  , whereas for the red curves
, whereas for the red curves  . "Cent'' denotes the centralised framework and "Decent'' the decentralised one. It can be seen that with 16 bits we get relatively close to the performance of the perfect CSI case in the absence of feedback errors (black uppermost line).
. "Cent'' denotes the centralised framework and "Decent'' the decentralised one. It can be seen that with 16 bits we get relatively close to the performance of the perfect CSI case in the absence of feedback errors (black uppermost line).
A plot of the ergodic achievable rate as a function of the number of feedback bits for a random codebook when System SNR is 20 dB and round-robin scheduling is employed. The blue curves correspond to the case where the bit error probability is  , whereas for the red curves
, whereas for the red curves  . "Cent'' denotes the centralised framework and "Decent'' the decentralised one. It can be noted that we need at least 20 bits in order to approach the performance of the perfect CSI case in the absence of feedback errors (black uppermost line).
. "Cent'' denotes the centralised framework and "Decent'' the decentralised one. It can be noted that we need at least 20 bits in order to approach the performance of the perfect CSI case in the absence of feedback errors (black uppermost line).
6.2. Impact of Feedback Errors
Feedback errors inevitably degrade performance of both frameworks because some useful information is lost by the intervention of bit errors in the fed back CSI. This is because scheduling performance is degraded due to the corrupted CSI information, and also precoding matrix design is affected due to the same corrupted CSI. The decentralised framework can be more sensitive to scheduling degradation as imperfect CSI might result in a selection of different users by some of the cooperating BSs, depending on the scheduling algorithm employed, which will inevitably increase interuser interference. However, round-robin scheduling is robust to CSI feedback errors as scheduling decisions are not made based on CSI. This scheduling algorithm is selected for the present evaluation which focuses on the impact of feedback errors on the design of precoding matrices. Note that with the absence of feedback errors the performance of the two frameworks under any kind of scheduling and transmission strategy coincides.
In Figures 7 and 8 the ergodic capacity is plotted against the probability of bit errors  when MSs are scheduled in a round-robin fashion for system SNR of 10 and 20 dB, respectively. When the system SNR is 10 dB, 16 bits are chosen for feedback whereas at 20 dB, 20 feedback bits are considered. This increase in bits is justified by the higher power regime of operation which demands larger codebooks for guaranteeing low interuser interference. It can be seen that feedback errors have a much greater impact in the case of 20 bits which is justified by (16) and (17). Furthermore in the case of 20 bits the performance gap between the decentralised and centralised frameworks is increased, an increase justified by the greater probability of CSI discrepancy (18). Therefore a more intelligent codebook design can lead to a reduced number of feedback bits for the same performance targets and also provide better robustness against feedback errors. Generally, the centralised framework is a little more robust to feedback errors than the decentralised one, although for a bit error probability less than
when MSs are scheduled in a round-robin fashion for system SNR of 10 and 20 dB, respectively. When the system SNR is 10 dB, 16 bits are chosen for feedback whereas at 20 dB, 20 feedback bits are considered. This increase in bits is justified by the higher power regime of operation which demands larger codebooks for guaranteeing low interuser interference. It can be seen that feedback errors have a much greater impact in the case of 20 bits which is justified by (16) and (17). Furthermore in the case of 20 bits the performance gap between the decentralised and centralised frameworks is increased, an increase justified by the greater probability of CSI discrepancy (18). Therefore a more intelligent codebook design can lead to a reduced number of feedback bits for the same performance targets and also provide better robustness against feedback errors. Generally, the centralised framework is a little more robust to feedback errors than the decentralised one, although for a bit error probability less than  the difference is negligible. Furthermore the presented results reflect the case where no error detection/correction schemes have been employed. These schemes can significantly reduce the bit error probability
the difference is negligible. Furthermore the presented results reflect the case where no error detection/correction schemes have been employed. These schemes can significantly reduce the bit error probability  ; thus, they have the potential to eliminate the impact of feedback errors.
; thus, they have the potential to eliminate the impact of feedback errors.
7. Conclusion
Multicell Cooperative Processing promises significantly improved spectral efficiency and fairness for future cellular systems. However, this comes at the cost of increased infrastructural complexity and centralised processing related to the existing conception for MCP. According to this, cooperating BSs need to be connected to a Control Unit which plays the role of the cluster head. It gathers local CSI from the BSs, performs user scheduling, and designs the transmission parameters. In this paper a new framework has been proposed that allows MCP on the downlink to take place in a decentralised fashion; neither a CU is needed nor the low-latency backhaul links. Each BS receives CSI feedback from all the users of the cluster (global CSI) and designs transmission independently. The performance of the proposed framework has been evaluated under the realistic assumption of quantized limited feedback together with linear precoding and while feedback errors are introduced by the channel. It has been shown that the proposed scheme shows little degradation on the ergodic achievable sum-rate compared to the centralised alternative, which can be eliminated with a more intelligent codebook design and the addition of feedback protection schemes (error detection/correction). The decentralised framework allows MCP to be implemented with very few changes upon the current network architecture.
References
Karakayali MK, Foschini GJ, Valenzuela RA: Network coordination for spectrally efficient communications in cellular systems. IEEE Wireless Communications 2006, 13(4):56-61. 10.1109/MWC.2006.1678166
Catreux S, Driessen PF, Greenstein LJ: Simulation results for an interference-limited multiple-input multiple-output cellular system. IEEE Communications Letters 2000, 4(11):334-336. 10.1109/4234.892193
Shamai S, Zaidel BM: Enhancing the cellular downlink capacity via co-processing at the transmitting end. Proceedings of the IEEE Vehicular Technology Conference (VTC '01), May 2001, Rhodes, Greece 3: 1745-1749.
Zhang H, Dai H: Cochannel interference mitigation and cooperative processing in downlink multicell multiuser MIMO networks. EURASIP Journal on Wireless Communications and Networking 2004, 2004(2):222-235.
Spencer QH, Peel CB, Swindlehurst AL, Haardt M: An introduction to the multi-user MIMO downlink. IEEE Communications Magazine 2004, 42(10):60-67. 10.1109/MCOM.2004.1341262
Venkatesan S: Coordinating base stations for greater uplink spectral efficiency in a cellular network. Proceedings of the IEEE International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC '07), September 2007, Athens, Greece
Boccardi F, Huang H: Limited downlink network coordination in cellular networks. Proceedings of the IEEE International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC '07), September 2007, Athens, Greece
Papadogiannis A, Gesbert D, Hardouin E: A dynamic clustering approach in wireless networks with multi-cell cooperative processing. Proceedings of the IEEE International Conference on Communications (ICC '08), May 2008, Beijing, China 4033-4037.
Papadogiannis A, Bang HJ, Gesbert D, Hardouin E: Downlink overhead reduction for multi-cell cooperative processing enabled wireless networks. Proceedings of the IEEE International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC '08), September 2008, Cannes, France
Marsch P, Fettweis G: A framework for optimizing the downlink of distributed antenna systems under a constraint backhaul. Proceedings of the European Wireless Conference (EW '07), April 2007, Paris, France
Parkvall S, Dahlman E, Furuskar A, et al.: LTE-advanced—evolving LTE towards IMT-advanced. Proceedings of the IEEE Vehicular Technology Conference (VTC '08), September 2008, Calgary, Canada
Y. Song, L. Cai, K. Wu, and H. Yang, “Collaborative MIMO Based on Multiple Base Station Coordination,” Contribution to IEEE 802.16m, IEEE C802.16m-07/162, August 2007.
Alcatel Shanghai Bell, Alcatel Lucent, “Collaborative MIMO for LTE-A Downlink,” 3GPP TSG RAN WG1 Meeting 53bis, R1-082501,Warsaw, Poland, June-July 2008.
Papadogiannis A, Hardouin E, Gesbert D: A framework for decentralising multi-cell cooperative processing on the downlink. Proceedings of the 4th IEEE Broadband Wireless Access Workshop (BWA '08), December 2008, New Orleans, La, USA
Love DJ, Heath RW Jr., Lau VKN, Gesbert D, Rao BD, Andrews M: An overview of limited feedback in wireless communication systems. IEEE Journal on Selected Areas in Communications 2008, 26(8):1341-1365.
Jafar SA, Srinivasa S: On the optimality of beamforming with quantized feedback. IEEE Transactions on Communications 2007, 55(12):2288-2302.
Yoo T, Goldsmith A: On the optimality of multiantenna broadcast scheduling using zero-forcing beamforming. IEEE Journal on Selected Areas in Communications 2006, 24(3):528-541.
Peel CB, Hochwald BM, Swindlehurst AL: A vector-perturbation technique for near-capacity multiantenna multiuser communication—part I: channel inversion and regularization. IEEE Transactions on Communications 2005, 53(1):195-202. 10.1109/TCOMM.2004.840638
Kaltenberger F, Gesbert D, Knopp R, Kountouris M: Performance of multi-user MIMO precoding with limited feedback over measured channels. Proceedings of IEEE Global Communications Conference (GLOBECOM '08), December 2008, New Orleans, La, USA
Jindal N: MIMO broadcast channels with finite-rate feedback. IEEE Transactions on Information Theory 2006, 52(11):5045-5060.
Kountouris M, de Francisco R, Gesbert D, Slock DTM, Sälzer T: Efficient metrics for scheduling in MIMO broadcast channels with limited feedback. Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP '07), April 2007, Honolulu, Hawaii, USA 3: 109-112.
CELTIC WINNER+ deliverable : D1.4 Initial Report on Advanced Multiple Antenna Systems. January 2009, http://projects.celtic-initiative.org/winner+/deliverables_winnerplus.html
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Papadogiannis, A., Hardouin, E. & Gesbert, D. Decentralising Multicell Cooperative Processing: A Novel Robust Framework. J Wireless Com Network 2009, 890685 (2009). https://doi.org/10.1155/2009/890685
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/890685
 estimates the channel vector
estimates the channel vector  .
. quantizes its channel direction
quantizes its channel direction  to
to  .
. affected by the errors on the feedback channel (Figure
affected by the errors on the feedback channel (Figure 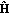 .
.
 estimates the channel vector
estimates the channel vector 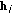 .
. quantizes its channel direction
quantizes its channel direction  to
to  .
. ), and the schedulers end up selecting exactly the same MSs. If feedback links introduce errors, the fed back CSI (CDI and CQI) needs to be protected by the use of appropriate techniques.
), and the schedulers end up selecting exactly the same MSs. If feedback links introduce errors, the fed back CSI (CDI and CQI) needs to be protected by the use of appropriate techniques.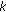 utilises for transmission the
utilises for transmission the 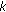 th line of the precoding matrix
th line of the precoding matrix 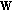 .
.

 in the decentralised framework as a function of the number of independent feedback links (equal to the number of involved BSs) and the number of feedback bits (18). The assumed bit error probability is
in the decentralised framework as a function of the number of independent feedback links (equal to the number of involved BSs) and the number of feedback bits (18). The assumed bit error probability is  .
.
 in the decentralised framework as a function of the number of independent feedback links (equal to the number of involved BSs) and the number of feedback bits (18). The assumed bit error probability is
in the decentralised framework as a function of the number of independent feedback links (equal to the number of involved BSs) and the number of feedback bits (18). The assumed bit error probability is  .
.


 for both the decentralised and the centralised frameworks, when System SNR = 10 dB and 16 bits are employed for quantization. In the decentralised case the CSI is fed back through 3 independent radio links.
for both the decentralised and the centralised frameworks, when System SNR = 10 dB and 16 bits are employed for quantization. In the decentralised case the CSI is fed back through 3 independent radio links.
 for both the decentralised and the centralised frameworks, when System SNR = 20 dB and 20 bits are employed for quantization. In the decentralised case the CSI is fed back through 3 independent radio links.
for both the decentralised and the centralised frameworks, when System SNR = 20 dB and 20 bits are employed for quantization. In the decentralised case the CSI is fed back through 3 independent radio links.