- Research Article
- Open access
- Published:
Mobility and Cooperation to Thwart Node Capture Attacks in MANETs
EURASIP Journal on Wireless Communications and Networking volume 2009, Article number: 945943 (2009)
Abstract
The nature of mobile ad hoc networks (MANETs), often unattended, makes this type of networks subject to some unique security issues. In particular, one of the most vexing problem for MANETs security is the node capture attack: an adversary can capture a node from the network eventually acquiring all the cryptographic material stored in it. Further, the captured node can be reprogrammed by the adversary and redeployed in the network in order to perform malicious activities. In this paper, we address the node capture attack in MANETs. We start from the intuition that mobility, in conjunction with a reduced amount of local cooperation, helps computing effectively and with a limited resource usage network global security properties. Then, we develop this intuition and use it to design a mechanism to detect the node capture attack. We support our proposal with a wide set of experiments showing that mobile networks can leverage mobility to compute global security properties, like node capture detection, with a small overhead.
1. Introduction
Ad hoc network can be deployed in harsh environments to fulfil law enforcement, search-and-rescue, disaster recovery, and other civil applications. Due to their nature, ad hoc networks are often unattended, hence prone to different kinds of novel attacks. For instance, an adversary could eavesdrop all the network communications. Further, the adversary might capture (i.e., remove) nodes from the network. These captured nodes can then be reprogrammed and deployed within the network area, for instance, to subvert the data aggregation or the decision making process in the network [1]. Also, the adversary could perform a sybil attack [2], where a single node illegitimately claims multiple identities also stolen from previously captured nodes. Another type of attack is the clone attack, where the node is first captured, then tampered with, reprogrammed, and finally replicated in the network. The former attack can be efficiently addressed with mechanism based on RSSI [3] or with authentication based on the knowledge of a fixed key set [4], while recent solutions have been proposed also for the detection of the clone attack [5, 6].
To think of a foreseeable application for node capture detection, note that recently the US Defense Advanced Research Projects Agency (DARPA) initiated a new research program to develop so-called LANdroids [7]: Smart robotic radio relay nodes for battlefield deployment. LANdroid mobile nodes are supposed to be deployed in hostile environment, establish an ad-hoc network, and provide connectivity as well as valuable information for soldiers that would later approach the deployment area. LANdroids might retain valuable information for a long time, until soldiers move close to the network. In the interim, the adversary might attempt to capture one of these nodes. We are not interested in the goals of the capture (that could be, e.g., to reprogram the node to infiltrate the network, or simply extracting the information stored in it); but on the open problem of how to detect the node capture that represents, as shown by the above-cited examples, a possible first step to jeopardize an ad hoc network. Indeed, an adversary has often to capture a node to tamper with—that is, to compromise its key set, or to reprogram it with malicious code—before being able to launch other more vicious, and may be still unknown, attacks. Node capture is one of the most vexing problems in ad hoc network security [8]. In fact, it is a very powerful attack and its detection is still an open issue. We believe that any solution to this problem has to meet the following requirements: (i) to detect the node capture as early as possible; (ii) to have a low rate of false positives—nodes which are believed to be captured and thus subject to a revocation process, but which were not actually taken by the adversary; (iii) to introduce a small overhead.
The solutions proposed so far are not satisfactory as for efficiency [8]. Also, while naïve centralized solutions can be applied to generic ad-hoc networks, they presents drawbacks like single point of failure and nonuniform energy consumption. These drawbacks do not make them appealing for ad hoc networks. Moreover, these networks often operates without the support of a base station. Efficient and distributed solutions to the node capture attack are of particular interest in this context.
To the best of our knowledge, there are no distributed solutions for the problem of detecting the node capture attack in Mobile Ad Hoc Networks (MANETs). Following a new interesting research thread that focuses on leveraging mobility to enforce security properties for wireless sensor and ad hoc networks [9, 10], we propose a new capture detection framework that leverages node mobility. We show that this approach can provide better performance compared to traditional solutions. Also, we show that using node cooperation in conjunction with node mobility can still improve the capture detection performance within specific network requirements.
The contribution of this paper is to provide a proof of concept: it is possible to leverage the emergent properties of mobile ad hoc networks via node mobility and node cooperation to design a node capture detection protocol. To this aim, we use the Random Waypoint Mobility Model (RWM) [11], an ideal mobility model which is simple and general enough (at least for some application scenarios) to explore our ideas. Furthermore, the result on any particular mobility model should depend not only from the model but also from the network setting, as pointed out in [12] for the delay-capacity tradeoff. Indeed, providing specific settings and evaluations for other models is out of the scope of this work.
Our solution is based on the simple observation that if node  will not remeet node
will not remeet node  within a period
within a period  , then it is possible that node
, then it is possible that node  has been captured. This observation is based on the fact that some time is required to the adversary to tamper with a sensor node. The time required by the adversary to perform such a type of attack was not investigated in the context of sensor network, until the work in [13]. In [13], the authors found out that node capture attacks (that give the adversary full control over a sensor node) are not so easy to implement, contrary to what was usually assumed in literature—indeed, among other requirements (e.g., expert knowledge and costly equipment), node tampering requires the removal of nodes from the network for a nonnegligible amount of time. In particular, while short attacks such as using plug-in devices can be performed in some 5 minutes, medium attacks that require (de-)soldering requires more than 30 minutes, and long attacks and very long attacks (e.g., erasing the security protection bits by UV light or invasive attack on electronic component) can require even some hours.
has been captured. This observation is based on the fact that some time is required to the adversary to tamper with a sensor node. The time required by the adversary to perform such a type of attack was not investigated in the context of sensor network, until the work in [13]. In [13], the authors found out that node capture attacks (that give the adversary full control over a sensor node) are not so easy to implement, contrary to what was usually assumed in literature—indeed, among other requirements (e.g., expert knowledge and costly equipment), node tampering requires the removal of nodes from the network for a nonnegligible amount of time. In particular, while short attacks such as using plug-in devices can be performed in some 5 minutes, medium attacks that require (de-)soldering requires more than 30 minutes, and long attacks and very long attacks (e.g., erasing the security protection bits by UV light or invasive attack on electronic component) can require even some hours.
We will build upon this intuition to provide a protocol that makes use of local cooperation and mobility to locally decide, with a certain probability, whether a node has been captured or not. Our proposed solution does not rely on any specific routing protocol: we resort to one-hop communications and to a sparing use of a message broadcasting primitive. These distinguished features help keep our protocol simple, efficient, and practically deployable, avoiding the use of sophisticated routing that can introduce complexity and overhead in the mobile setting. Furthermore, our experimental results demonstrate the effectiveness and the efficiency of our proposal. For instance, for a given energy budget, while the reference solution requires about 4000 seconds to detect node capture, our proposal requires less than 2000 seconds. We remark that the solution proposed in this paper is completely tunable: the capture detection time can be set as small as desired. However, a smaller detection time would imply an higher energy consumption.
The paper is organized as follows. Section 2 presents the related work in this area. Section 3 introduces the motivation and the framework of our proposal based on simple ad hoc network capabilities like node mobility and message broadcasting. Our specific proposal, the CMC Protocol, is then presented in Section 4, while in Section 5 we discuss the simulation results that give a qualitative idea of how mobility and node cooperation can be leveraged in order to decrease the node capture detection time. Finally, Section 6 reports some concluding remarks.
2. Related Work and Background
Mobility as a means to enforce security in mobile networks has been considered in [9]. Further, mobility has been considered in the context of routing [14] and of network property optimization [15]. In particular, the work in [14] leverages node mobility in order to disseminate information about destination location without incurring any communication overhead. In [15], the sink mobility is used to optimize the energy consumption of the whole network. A mobility-based solution for detecting the sybil attack has been recently presented in [10]. Finally, note that a few solutions exist for node failure detection in ad hoc networks [16–19]. However, such solutions assume a static network, missing a fundamental component of our scenario, as shown in what follows.
In this work, we use node mobility to cope with the node capture attack. As described in the following section, we specifically rely on the meeting frequencies between honest nodes to gather information about the absence of captured nodes. A property similar to that of node "remeeting" has been already considered in [20]. However, in [20], the authors investigate the time needed for a node to meet (for the first time) a fixed number of other nodes. This analysis is then used together with node mobility to achieve noninteractive recovery of missed messages. To the best of our knowledge no distributed solution leveraging node mobility has been proposed to detect the node capture attack in mobile ad-hoc and sensor networks.
While node capture attack is considered as major threat in many security solutions for WSN, to the best of our knowledge, it has not been directly addressed yet. However, some interest has been shown in modeling the node capture attack. In particular, in [21], both oblivious and smart node capture is considered for the design of a key management scheme for WSN. A deeper analysis on the modeling of the capture attack has been presented [22, 23]. In [22], it is shown how different greedy heuristics can be developed for node capture attacks and how minimum cost node capture attacks can be prevented in particular setting. In [23], the authors formalize node capture attacks using the vulnerability metric as a nonlinear integer programming minimization problem.
We recently published [24, 25]; the former arguments that mobility models have a relevant effect on the properties of the proposed algorithms, while the latter is a short contribution on the possibility to leverage network mobility for node capture detection. In particular, in [25] we presented the rationales for this type of approach and a preliminary solution to the problem. However, while the results given in [25] are encouraging, the specific solution proposed requires a high overhead to bound the number of false positives (wrongly revoked nodes). Note that, without this bounding mechanism, the number of false positives would be unacceptable. Furthermore, in [25] we did not study the feasibility of the new approach compared with other ones. In the present work, we leverage the intuition proposed in [25], which is the "remeeting" time between nodes, to design an efficient solution that leverages different levels of cooperation between nodes. In particular, we introduce a presence-proving mechanism used by allegedly captured nodes to show their actual presence in the network (i.e., eliminating the possibility of revoking a node which is present within the network). Further, we introduce a reference solution in order to quantify the quality of the proposed solutions. The proposed solutions are compared between them and with the reference solution. In particular, to have a fair comparison, we observed the detection time provided by the different protocols using the same energy budget. The result of our study confirms the intuition provided in [25]. Furthermore, it proves that within certain scenarios of node mobility, the proposed solutions provide a sensitive improvement over other possible approaches, such as the one based on classical message exchange.
Node mobility and node cooperation in a mobile ad hoc setting have been considered already in Disruption Tolerant Networks (DTNs) [26, 27]. However, such a message passing paradigm has not been used, so far, to support security. We leverage the concept introduced with DTN to cooperatively control the presence of a network node. Mobility to recover the secret state of a node has been recently introduced in [28, 29]. In this paper, we use one of the most common mobility patterns in literature, the Random Waypoint Mobility Model [11]. In this model, it is assumed that each node in the network acts independently: it selects a geographic destination in the deployment area (the way-point), it selects a speed uniformly at random in a given interval  , and then it moves toward the destination on a straight route at the selected speed. When at the way-point, it waits for some time, again selected uniformly at random from a given interval, and then the node repeats the process by choosing the next way-point. Some researchers have shown some problems related to this mobility model. One of the problems is that the average speed of the network tends to decrease during the life of the network itself and, if the minimum speed that can be selected by the nodes is zero, then average speed of the system converges to zero [30]. In the same paper, it is suggested to set the minimum speed to a value strictly greater than zero. In this case, the average speed of the system continues decreasing, but it converges to a nonzero asymptotic value. Other problems related to spatial node distribution have been considered by different authors [30, 31]. In the analysis presented in [14], "human speeds" are claimed to be a reasonable practical choice for mobile nodes. Note that the RWM might not be the best model to capture a "realistic" mobility scenario, as highlighted in [12]; however, the results achieved in this paper are meaningful as they are a proof of concept that mobility can be leveraged to enforce security properties; the provided protocols could be used in, and adapted to, more realistic mobility models.
, and then it moves toward the destination on a straight route at the selected speed. When at the way-point, it waits for some time, again selected uniformly at random from a given interval, and then the node repeats the process by choosing the next way-point. Some researchers have shown some problems related to this mobility model. One of the problems is that the average speed of the network tends to decrease during the life of the network itself and, if the minimum speed that can be selected by the nodes is zero, then average speed of the system converges to zero [30]. In the same paper, it is suggested to set the minimum speed to a value strictly greater than zero. In this case, the average speed of the system continues decreasing, but it converges to a nonzero asymptotic value. Other problems related to spatial node distribution have been considered by different authors [30, 31]. In the analysis presented in [14], "human speeds" are claimed to be a reasonable practical choice for mobile nodes. Note that the RWM might not be the best model to capture a "realistic" mobility scenario, as highlighted in [12]; however, the results achieved in this paper are meaningful as they are a proof of concept that mobility can be leveraged to enforce security properties; the provided protocols could be used in, and adapted to, more realistic mobility models.
In our proposed approach every node maintains its own clock. However, we require that clocks among nodes are just loosely synchronized. Note that there are a few solutions proposed in literature to provide loose time synchronization, like [32]. Therefore, in the following we will assume that skew and drift errors are negligible.
In our proposal, we also need to take into consideration the cost of broadcasting a message to all the nodes in the network. In [33], a classification of the different solutions for broadcasting scheme is provided: (i) Simple Flooding; (ii) probabilistic-based schemes; (iii) area-based schemes that assume location awareness; (iv) neighbor knowledge schemes that assume knowledge of two hop neighborhood.
Analyzing or comparing broadcasting cost is out of the scope of this paper. However, for a better comparison of the solutions proposed in this paper, we need to set a broadcast cost that will be expressed in terms of unicast messages. In fact, the overhead associated to the broadcasting varies with different network parameters (e.g., node density and communication radius). A deeper analysis on the overhead generated for different broadcasting protocols is presented in [34]. Also, note that probabilistic-based and neighbor-based protocols require a big overhead for a mobile network in order to know the network topology and neighborhood, respectively. Furthermore, the same argument can be considered for the localization protocol that is used in the area-based schemes. In the following, to embrace the more general case, we assume that nodes are not equipped with localization devices, like GPS. Finally, note that a message could be received more than once, for instance, because the receiver is in the transmission range of different rely nodes. However, in the following, we assume that a broadcasted message is received (then counted) only once for each node. A similar assumption is used, for example, in [34].
3. Node Capture Detection through Mobility and Cooperation
The aim of a capture detection protocol is to detect as soon as possible that a node has been removed from the network. In the following, we also refer to this event as a node capture. The protocol should be able to identify which is the captured node, so that its ID could be revoked from the network. Revocation is a fundamental feature—if the adversary reintroduces the captured (and possibly reprogrammed) node in the network, the node should not be able to take part to the network operations.
In the following, we first describe a simple distributed solution that does not exploit neither mobility nor cooperation among nodes; we use this solution as a reference solution to compare with our proposal. Then, we introduce the rationals we leverage to develop our protocol for node capture detection, detailed in the following section.
3.1. Reference Solution
To the best of our knowledge, no efficient and distributed solution leveraging mobility was proposed so far to cope with the node capture detection problem in Mobile Ad Hoc Network. However, a naïve solution that makes use of node communication capabilities can be easily figured out. We first describe this solution assuming the presence of a base station (BS); then, we will show how to relax this assumption. In the BS-based solution, each node periodically sends a message to the BS carrying some evidence of its own presence. In this way, the base station can witness for the presence of the claiming nodes. If a node does not send the claim of its presence to the BS within a given time range, the base station will revoke the corresponding node ID from the network (e.g., flooding the network with a revocation message). To remove the centralization point given by the presence of the BS, we require each node to notify its presence to any other node in the network. To achieve this goal, every  seconds a node sends a claim message advertising its presence to all the network nodes through a broadcast message. A node receiving this claim would restart a timeout set to
seconds a node sends a claim message advertising its presence to all the network nodes through a broadcast message. A node receiving this claim would restart a timeout set to  where
where  accounts for network propagation delay. Should the presence claim not be received before the timeout elapses, the revocation procedure would be triggered. However, note that if a node is required to store the ID of any other node as well as the receiving time of the received claim message,
accounts for network propagation delay. Should the presence claim not be received before the timeout elapses, the revocation procedure would be triggered. However, note that if a node is required to store the ID of any other node as well as the receiving time of the received claim message,  memory locations would be needed in every node. To reduce the memory requirement on node, it is possible to assume that the presence in the network of each node is tracked by a small subset of the nodes of the network. Hence, if a node is absent from the network for more than
memory locations would be needed in every node. To reduce the memory requirement on node, it is possible to assume that the presence in the network of each node is tracked by a small subset of the nodes of the network. Hence, if a node is absent from the network for more than  seconds, its absence can still be detected by a set of nodes.
seconds, its absence can still be detected by a set of nodes.
3.2. Our Approach
Our approach is based on the intuition that leveraging node mobility and cooperation helps node capture detection. We start from the following observation: if node  has detected a transmission originated by node
has detected a transmission originated by node  , at time
, at time  , we will say that a meeting occurred. Now, nodes
, we will say that a meeting occurred. Now, nodes  and
and  are mobile, so they will leave the communication range of each other after some time. However, we expect these two nodes to remeet again within a certain interval of time, or at least within a certain time interval with a certain probability. The solution can also be thought of as an exploitation of the opportunistic communication concept [27], like contact-based message delivery, to wireless ad hoc network security. In [25], the authors investigated how mobility can be used to detect a node capture and investigated the feasibility of mobility-based solutions. As a starting point, we analysed the remeeting probability through network simulation: the results comply with previous studies on delay in mobile ad hoc networks [12]. In Figure 1, we report on the simulation results on the probability that two nodes that had a meeting would not have a meeting again after
are mobile, so they will leave the communication range of each other after some time. However, we expect these two nodes to remeet again within a certain interval of time, or at least within a certain time interval with a certain probability. The solution can also be thought of as an exploitation of the opportunistic communication concept [27], like contact-based message delivery, to wireless ad hoc network security. In [25], the authors investigated how mobility can be used to detect a node capture and investigated the feasibility of mobility-based solutions. As a starting point, we analysed the remeeting probability through network simulation: the results comply with previous studies on delay in mobile ad hoc networks [12]. In Figure 1, we report on the simulation results on the probability that two nodes that had a meeting would not have a meeting again after  seconds. This probability has been evaluated for different values of the communication radius. In particular, we assume that the nodes are randomly deployed in a square area of
seconds. This probability has been evaluated for different values of the communication radius. In particular, we assume that the nodes are randomly deployed in a square area of  and that they move according to the random way-point mobility model. While the
and that they move according to the random way-point mobility model. While the  -axis indicates the time after the last meeting, the
-axis indicates the time after the last meeting, the  -axis indicates the probability that the two nodes have not remet yet. For example, assume that node
-axis indicates the probability that the two nodes have not remet yet. For example, assume that node  meets node
meets node  at time
at time  , then the probability that these two nodes have not met again after
, then the probability that these two nodes have not met again after  seconds is very close to
seconds is very close to  (for a sensing radius
(for a sensing radius  ).
).
In the following section, we propose a protocol that leverages node mobility to enhance node capture detection probability.
3.3. Assumptions and Notation
In the remaining of the paper, we assume a "smart" attacker model: it knows the detection protocol implemented in the network. This implies, for the reference solution, that a node  is captured just after node
is captured just after node  has broadcasted its presence claim message. The assumption at the base of our protocol is that if a node has been absent from the network for a given interval time (i.e., none can prove its presence in that interval) the node has been captured. It is worth noticing that also if a node is temporarily disconnected, a DTN-like routing mechanism [35] can be used to deliver a message to that node with some delay. For the aim of our protocol, we do not explicitly consider that interval time.
has broadcasted its presence claim message. The assumption at the base of our protocol is that if a node has been absent from the network for a given interval time (i.e., none can prove its presence in that interval) the node has been captured. It is worth noticing that also if a node is temporarily disconnected, a DTN-like routing mechanism [35] can be used to deliver a message to that node with some delay. For the aim of our protocol, we do not explicitly consider that interval time.
In the following we define a false-positive alarm as an alarm raised for a node that is actually present. One or more false-positive alarms can imply a false-positive detection, which corresponds to the revocation of a not captured node. Further, we refer to a false-negative detection as a captured node not actually revoked. However, we observe that using the presence-proving mechanism introduced in this paper (later discussed in Section 4), a node that is accused by a false-positive alarm would prove its presence, hence neutralizing the revoke. Furthermore, we observe that accordingly to our protocol, a node no longer active (e.g., destroyed or with run out batteries) would be revoked. However, there would be no false alarms and the overhead paid for the protocol would be just one network flooding. The flooding would allow every node in the network to be aware of the absence of the failed node—having a beneficial effect for other protocols such as routing. In general, we cannot distinguish if a node is not able to communicate with the other network nodes for a nonmalicious reason, or because it has been actually captured—our solution is conservative in this way, revoking such a node. It is out of the scope of this paper, and left as future work, to address the recovery of the former type of revoked nodes.
Another issue is Denial of Service (DoS). Indeed, since alarms are flooded in the network, it could be possible for a corrupted node to trigger false alarms so as to generate a DoS. This issue is out of the scope of this paper, however, for the sake of completeness, we sketch in the following a possible solution. The impact of false positives can be mitigated noticing that it could be possible, once the recovery mechanism detects a false alarm, to associate a failure tally to the node that raised the false alarm. If the tally exceeds a certain threshold, the appropriate action to isolate the misbehaving node could be take.
Further, we assume the existence of a failure-free node broadcasting mechanism [36]; and, finally, we point out that addressing node-to-node secure communications properties such as confidentiality, integrity, privacy, and authentication are out of the scope of this paper. However, note that a few solutions explicitly addressing these issues can be found in literature [4, 37, 38].
Table 1 resumes the intervals time notation used in this paper.
4. The Protocol
In this section, we describe our proposal for a node Capture detection protocol that leverages Mobility and Cooperation (CMC Protocol). Basically, each node  is given the task of witnessing for the presence of a specific set
is given the task of witnessing for the presence of a specific set  of other nodes (we will say that
of other nodes (we will say that  is tracking nodes in
is tracking nodes in  ). For each node
). For each node  that
that  gets into the communication range of,
gets into the communication range of,  sets a new time-out for
sets a new time-out for  with the value of the
with the value of the  's internal clock; the time out will expire after
's internal clock; the time out will expire after  seconds. The meeting nodes can also cooperate, exchanging information on the meeting time of nodes of interests, that is, nodes that are tracked by both
seconds. The meeting nodes can also cooperate, exchanging information on the meeting time of nodes of interests, that is, nodes that are tracked by both  and
and  . Note that node cooperation is an option that can be enabled or disabled in our protocol. If the time-out expires (i.e.,
. Note that node cooperation is an option that can be enabled or disabled in our protocol. If the time-out expires (i.e.,  and
and  did not remeet within
did not remeet within  seconds),
seconds),  floods the network with an alarm message. If node
floods the network with an alarm message. If node  does not prove its presence within
does not prove its presence within  seconds after the broadcasted alarm is flooded, every node in the network will revoke node
seconds after the broadcasted alarm is flooded, every node in the network will revoke node  . The detailed description of the CMC protocol follows.
. The detailed description of the CMC protocol follows.
4.1. Protocol Description
The CMC protocol is event-based; in particular, it is executed when the following holds.
-
(i)Node
 and node
and node  meet: this event triggers node
meet: this event triggers node  and node
and node  to execute
to execute 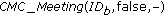 and CMC_Meeting
and CMC_Meeting respectively, if the cooperation parameter is set to false. Otherwise, node
respectively, if the cooperation parameter is set to false. Otherwise, node  executes CMC_Meeting
executes CMC_Meeting and node
and node 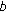 executes CMC_Meeting
executes CMC_Meeting . The function CMC_Meeting is also used in the cooperative scenario as a virtual meeting in order to update node presence information.
. The function CMC_Meeting is also used in the cooperative scenario as a virtual meeting in order to update node presence information. -
(ii)
The time-out related to node
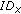 expires on node
expires on node  : node
: node  executes the procedure CMC_TimeOut
executes the procedure CMC_TimeOut .
. -
(iii)
Node
 eavesdrops a message
eavesdrops a message 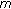 : node
: node  executes the procedure CMC_Receive(m).
executes the procedure CMC_Receive(m).
Algorithms 1, 2, and 3 show the corresponding pseudocode. The procedure CMC_Meeting, shown in Algorithm 1, is executed by both nodes involved in a meeting. In the case of a real meeting, the time is not specified, then the current node time  is used. However, when the procedure is invoked as a virtual meeting, a reference time (
is used. However, when the procedure is invoked as a virtual meeting, a reference time ( ) is also considered (lines 2, 3, and 4). When node
) is also considered (lines 2, 3, and 4). When node  meets node
meets node  , node
, node  checks if it is supposed to trace node
checks if it is supposed to trace node  (that is if
(that is if  ). This check is performed using the Trace function (line 5). It takes in input two node IDs, and provides a result pseudouniformly distributed in
). This check is performed using the Trace function (line 5). It takes in input two node IDs, and provides a result pseudouniformly distributed in  —where
—where  is the size of the wireless ad hoc network and
is the size of the wireless ad hoc network and  is the number of nodes tracked by each node. Node
is the number of nodes tracked by each node. Node  is to be tracked if and only if the result of the Trace function is one. A simple and efficient implementation of the function Trace can be found in [39], where it has been used in the context of pairwise key establishment. Assume now that
is to be tracked if and only if the result of the Trace function is one. A simple and efficient implementation of the function Trace can be found in [39], where it has been used in the context of pairwise key establishment. Assume now that  , then a further check on node
, then a further check on node  is performed (line 6). Indeed, node
is performed (line 6). Indeed, node  could be already revoked. Hence, each node stores a Revocation Table (
could be already revoked. Hence, each node stores a Revocation Table ( ) that lists the revoked nodes. If both previous tests (lines 5 and 6) succeed, then
) that lists the revoked nodes. If both previous tests (lines 5 and 6) succeed, then  calls the function Update that updates the information about the last meeting with node
calls the function Update that updates the information about the last meeting with node  (line 7). For example, if node
(line 7). For example, if node  meets
meets  at a given time
at a given time  , the function Update sets the information
, the function Update sets the information  in the
in the  (a Check Table stored in node
(a Check Table stored in node  memory). Node
memory). Node  uses a Time-out Table
uses a Time-out Table  to store and signal the following time-outs:
to store and signal the following time-outs:
Algorithm 1: . Node meeting event handler.
. Node meeting event handler.
Input:  : ID of the executing node.
: ID of the executing node.  : ID of the met node.
: ID of the met node.  : Current time of node
: Current time of node  .
.  : Check Table stored in node
: Check Table stored in node  memory.
memory.  : Revoked nodes table stored in node
: Revoked nodes table stored in node  memory.
memory.  : Time out table stored in node
: Time out table stored in node  memory.
memory.  : Alarm time.
: Alarm time.  : Time for the accused node to prove its presence.
: Time for the accused node to prove its presence.  : Boolean variable for cooperation option.
: Boolean variable for cooperation option.
-
1
begin
-
2
if NotSpecified (
 )then
)then -
3
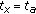 ;
; -
4
end
-
5
if Trace(
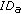 ,
,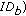 =
= then
then -
6
if Is-Not-Revoked (
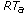 ,
,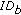 )then
)then -
7
Update (
 ,
,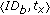 );
); -
8
UpdateTimeOut (
 ,
, );
); -
9
end
-
10
end
-
11
if
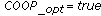 then
then -
12
foreach
 do
do -
13
If Is-Not-Revoked (
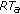 ,
, )then
)then -
14
If Trace (
 ) = 1then
) = 1then -
15
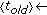 Look-Up (
Look-Up ( );
); -
16
 ;
; -
17
end
-
18
end
-
19
end
-
20
end
-
21
end
Algorithm 2: . Node Time Out event handler.
. Node Time Out event handler.
Input:  : ID of the executing node.
: ID of the executing node.  : ID of the node which time-out is expired.
: ID of the node which time-out is expired.  : Current time of node
: Current time of node  .
.  : Revoked nodes table stored in node
: Revoked nodes table stored in node  memory.
memory.  : Time out table stored in node
: Time out table stored in node  memory.
memory.  : Time for the accused node to prove its presence.
: Time for the accused node to prove its presence.
-
1
begin
-
2
if TimeOutKind(ALARM) then
-
3
Flooding (
 );
); -
4
UpdatingTimeOut (

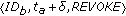 );
); -
5
else
-
6
RevokeNode (
 ,
, )
) -
7
end
-
8
end
Algorithm 3: . Received message event handler.
. Received message event handler.
Input:  : ID of the executing node.
: ID of the executing node.  : Current time of node
: Current time of node  .
.  : Received message.
: Received message.  : Revocation Table stored in node
: Revocation Table stored in node  memory.
memory.  : Time for the accused node to prove its presence.
: Time for the accused node to prove its presence.
-
1
begin
-
2
 ;
; -
3
if
 then
then -
4
if
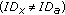 then
then -
5
if Is-Not-Revoked (
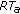 ,
,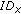 ) then
) then -
6
UpdateTimeOut (

 );
); -
7
end
-
8
else
-
9
Flooding (
 );
); -
10
end
-
11
end
-
12
if
 then
then
-
13
 (
( );
); -
14
end
-
15
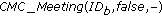 ;
; -
16
end
-
(i)
ALARM time-out, which is triggered after
 seconds are elapsed without remeeting node
seconds are elapsed without remeeting node  .,
., -
(ii)
REVOKE time-out, which is triggered after
 seconds are elapsed from receiving/triggering a node revocation for node
seconds are elapsed from receiving/triggering a node revocation for node 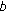 —assuming that in these
—assuming that in these  seconds no presence claim from
seconds no presence claim from  are received.
are received.
Then, for each meeting with non-revoked nodes in  , node
, node  removes any previous time-out for the met node and sets a new ALARM time-out for that node (line 8). Note that both the update functions (lines 7 and 8) do not perform any operation if the time argument
removes any previous time-out for the met node and sets a new ALARM time-out for that node (line 8). Note that both the update functions (lines 7 and 8) do not perform any operation if the time argument  is lower than the currently stored meeting time for the node
is lower than the currently stored meeting time for the node  : . This could happen in the case of a virtual meeting.
: . This could happen in the case of a virtual meeting.
If the cooperation option is set (COOP_opt=true in line 11), also the following steps are performed. For each not revoked node  traced by both node
traced by both node  and
and  (lines 12, 13, and 14), node
(lines 12, 13, and 14), node  sends a CLAIM message to
sends a CLAIM message to  carrying the meeting time between
carrying the meeting time between  and
and  . Each CLAIM message has the following format:
. Each CLAIM message has the following format:  , where
, where  is the sender of the claim message, CLAIM is the message type,
is the sender of the claim message, CLAIM is the message type,  is the ID of node
is the ID of node  the claim is related to, and the last parameter indicates the meeting time between
the claim is related to, and the last parameter indicates the meeting time between  and
and  . Another message type is ALARM, described in the following.
. Another message type is ALARM, described in the following.
CMC_TimeOut (Algorithm 2) is triggered when a time-out expires. If on node  an ALARM time-out expires for node
an ALARM time-out expires for node  , this means that node
, this means that node  did not meet node
did not meet node  for a time
for a time  . Then, node
. Then, node  floods the network with an alarm (Algorithm 2, line 3) and a new REVOKE time-out for node
floods the network with an alarm (Algorithm 2, line 3) and a new REVOKE time-out for node  is set. Each ALARM message has the following format:
is set. Each ALARM message has the following format:  , where
, where  is the sender of the claim message, ALARM notifies the message type, and
is the sender of the claim message, ALARM notifies the message type, and  is the ID of node
is the ID of node  the alarm is related to. When a REVOKE time-out expires, this means that after
the alarm is related to. When a REVOKE time-out expires, this means that after  seconds elapsed from the alarm triggering, no evidence of the presence in the network of the suspected captured node appeared. In this latter case, a node revocation procedure for node
seconds elapsed from the alarm triggering, no evidence of the presence in the network of the suspected captured node appeared. In this latter case, a node revocation procedure for node  is invoked by node
is invoked by node  .
.
CMC_Receive (Algorithm 3) is invoked when a message MSG is received. The fields of the message are assigned to local variables (line 2) and the type of the message is checked (line 3). Assume the message is of type ALARM: the executing node checks if the alarm is related to itself (line 4).
If the latter test fails, a further check is performed: the node checks whether the node  is not already revoked (line 5). If the check succeeds, a REVOKE time-out is set through an UpdateTimeOut procedure. Note that a REVOKE time-out for node
is not already revoked (line 5). If the check succeeds, a REVOKE time-out is set through an UpdateTimeOut procedure. Note that a REVOKE time-out for node  already should be in place, this procedure does not override the existing REVOKE time-out and simply returns. If the ALARM is related to the executing node itself (test performed at line 4 fails) node
already should be in place, this procedure does not override the existing REVOKE time-out and simply returns. If the ALARM is related to the executing node itself (test performed at line 4 fails) node  will flood the network with a presence CLAIM message (line 9). This measure prevents false-positive detection, that is, the revocation of nodes that are active in the network.
will flood the network with a presence CLAIM message (line 9). This measure prevents false-positive detection, that is, the revocation of nodes that are active in the network.
If the received message is of type CLAIM, this means that a node that was the target of an ALARM message is proving its presence; this message triggers a virtual meeting between  and the wrongly accused nodes (line 13). The overall result is that node
and the wrongly accused nodes (line 13). The overall result is that node  disables the REVOKE time-out for that node while restarting the ALARM time-out for the same node. These activities are also triggered when the COOP_opt is set (in fact, a CLAIM message is also sent in line 16, Algorithm 1). The objective of this invocation is to update the information on traced nodes via an information exchange with the met nodes.
disables the REVOKE time-out for that node while restarting the ALARM time-out for the same node. These activities are also triggered when the COOP_opt is set (in fact, a CLAIM message is also sent in line 16, Algorithm 1). The objective of this invocation is to update the information on traced nodes via an information exchange with the met nodes.
Finally, when  receives a message issued by node
receives a message issued by node  which is not originated within the protocol (e.g., it can be originated by the application layer), this message can be interpreted by the protocol as an evidence of the presence of node
which is not originated within the protocol (e.g., it can be originated by the application layer), this message can be interpreted by the protocol as an evidence of the presence of node  . Therefore, this can be interpreted as a special case of a node meeting, and the appropriate actions are triggered (line 15).
. Therefore, this can be interpreted as a special case of a node meeting, and the appropriate actions are triggered (line 15).
5. Simulations and Discussion
We performed simulations using a self-developed discrete event simulator. The simulator is written in C++ and implements the Random Waypoint Mobility Model. The events (nodes meeting, node arrival at its selected destination, and alarms time-out) are pushed to and pulled from an ideal time-line. Initially, nodes are assumed to be randomly deployed over a network area. Then, until the simulation ends, for each node, a random speed and destination location are randomly chosen (within the bounds set by the user): this implies to analyze and to order all the meeting events and the node arrival events with reference to the time-line. While the time goes by, the events on the time-line are processed. The events corresponding to node arrival are processed as previously described (choosing a destination, a node speed, and analyzing the new generated events). The node meeting events are processed as the core part of our detection protocol, for example, updating the time-out or sharing information with the met nodes. The alarms time-out expiring event generates the network flooding.
As for the energy model, we adopted the one proposed in [40]. To plot each point in the following graphs (as well as for Figure 1), we performed a set of experiments and reported the averaged results; the number of experiments has been set to achieve a confidence interval of  .
.
The comparison on the detection time between our protocol and the reference solution has been performed considering the energy cost. In particular, the energy cost has been expressed as a frequency of network flooding, as explained later.
5.1. Node Remeeting
In order to better understand how mobility and cooperation can speed up the capture detection process, we performed a first set of simulations to assess the frequency of node-to-node meetings. We considered a network of  nodes randomly deployed over a square area of
nodes randomly deployed over a square area of  . We used the random waypoint mobility model as the node mobility pattern. In particular, in our simulations we set the value for the minimum node speed greater than zero—this is a way to solve the decreasing average node speed problem of the random waypoint mobility model [8].
. We used the random waypoint mobility model as the node mobility pattern. In particular, in our simulations we set the value for the minimum node speed greater than zero—this is a way to solve the decreasing average node speed problem of the random waypoint mobility model [8].
The experiment was set in this way: we choose two nodes  and
and  ; when they meet, we set time at
; when they meet, we set time at  and continued following these nodes thorough their network evolution to experimentally determine how long it takes for these two nodes to meet again, in both the noncooperative and in the cooperative case. Crucially, in the cooperative scenario, if node
and continued following these nodes thorough their network evolution to experimentally determine how long it takes for these two nodes to meet again, in both the noncooperative and in the cooperative case. Crucially, in the cooperative scenario, if node  meets node
meets node  and sends to it all the information
and sends to it all the information  received during its last meeting with node
received during its last meeting with node  , this also accounts as a meeting between
, this also accounts as a meeting between  and
and  .
.
We performed the simulation for different values of sensing radius and average node speed both for the noncooperative and the cooperative scenario. The results are shown in Figure 2. The experiments support the following, simple intuitions: node cooperation increases the meeting probability; the higher is the sensing radius, the higher is the meeting probability; and the higher is the average node speed, the higher is the meeting probability. We used these results also to propose a reasonable value for the variable  to be used in the implementation of our proposal, for both the cooperative and noncooperative case.
to be used in the implementation of our proposal, for both the cooperative and noncooperative case.
5.2. Experimental Results
Parameters Tuning
As observed in previous work [25], all the protocols parameters are correlated, for example, increasing the average speed of the network would increase the number of meetings between nodes, hence reducing the number of false alarms. However, if we assume that parameters such as the network size, the nodes' mobility, and the network area are given, the main parameters that the network administrator can set is the alarm time  . In Figures 3(a) and 3(b) we show the influence of
. In Figures 3(a) and 3(b) we show the influence of  over the detection time and the rate of false positive alarms. We notice that increasing the alarm time also increases the detection time while decreasing the number of false positives. In particular, from Figure 3(a), we observe that the detection time increases linearly with
over the detection time and the rate of false positive alarms. We notice that increasing the alarm time also increases the detection time while decreasing the number of false positives. In particular, from Figure 3(a), we observe that the detection time increases linearly with  . Furthermore, we observe that the detection time using node cooperation is higher than the one without node cooperation. The motivation follows from the fact that without node cooperation nodes have stale information about the presence of the traced nodes. So, when a node is really captured, in the noncooperative scenario there will be some nodes that are already not meeting the captured node for a while. These nodes would raise the capture alarm before
. Furthermore, we observe that the detection time using node cooperation is higher than the one without node cooperation. The motivation follows from the fact that without node cooperation nodes have stale information about the presence of the traced nodes. So, when a node is really captured, in the noncooperative scenario there will be some nodes that are already not meeting the captured node for a while. These nodes would raise the capture alarm before  seconds elapses after the real node capture, hence decreasing the detection time with respect to the cooperative protocol. From Figure 3(a), we observe that the false alarms rate decreases exponentially with
seconds elapses after the real node capture, hence decreasing the detection time with respect to the cooperative protocol. From Figure 3(a), we observe that the false alarms rate decreases exponentially with  . Comparison between Figures 3(a) and 3(b) suggests that there is a tradeoff between the detection time and the number of false alarms. In order to give a straight and fair comparison between the proposed solutions (cooperative and noncooperative) and also with the reference solution, in the following section, we compare the detection time of the solutions on the basis of the overall energetic cost.
. Comparison between Figures 3(a) and 3(b) suggests that there is a tradeoff between the detection time and the number of false alarms. In order to give a straight and fair comparison between the proposed solutions (cooperative and noncooperative) and also with the reference solution, in the following section, we compare the detection time of the solutions on the basis of the overall energetic cost.
Energy-Driven Comparison
One of the key issues in ad hoc and sensor network is the energy consumption. Hence, we compared our proposal with the reference solution focusing on energy consumption. To provide an evaluation of our protocols in a manner that is device-independent, we chose to express the energy consumption in terms of generated messages. As for the energy devoted to computation, we considered the cost be negligible, as in [40].
The main communication cost of both our protocol and the reference solution is the number of flooding. The reference solution uses the flooding as a presence claim message while our protocol uses the flooding for both alarm broadcast and alarm-triggered presence notification; the latter flooding occurs when a node that has been erroneously advertised as possibly compromised sends (floods) a claim of its actual presence. To simplify our discussion, we assume that a network flooding corresponds to sending and to receiving a message by each network node. This is not always the case; actually, the load for broadcasting varies with different network parameters and the specific broadcasting protocol used [34]. However, this approximation is good enough to achieve our goal, that is, to show the qualitative improvement of our solution over the reference solution. To better appreciate the comparison with the reference solution—where a flooding occurs every time interval—in the following graphs, we report on the  -axis the time interval between two subsequent flooding, instead of the flooding frequency. Note that once the flooding interval is fixed, also the amount of required energy is fixed, and we can plot the performance of our protocol when using the same amount of energy, that is, the same amount of messages.
-axis the time interval between two subsequent flooding, instead of the flooding frequency. Note that once the flooding interval is fixed, also the amount of required energy is fixed, and we can plot the performance of our protocol when using the same amount of energy, that is, the same amount of messages.
In our simulation, we analyze how increasing the energy overhead affects the detection time. In other words, we fix the energy overhead at the same level for both protocols under evaluation, and measure which protocol achieves the best detection time.
Performance
To compare the performance of the proposed solution with the reference solution presented in Section 3.1, we implemented our protocol. In what follows, we fix a sensing radius of  . Since nodes in ad hoc settings could have strict memory constraints (e.g., in sensor network), in our simulations, we assume that each node traces a small number of other nodes. In fact, as a result of the pseudorandom function Trace (Algorithm 1, line 2) each node traces exactly 5 other network nodes. For the cooperative scenario, when two nodes
. Since nodes in ad hoc settings could have strict memory constraints (e.g., in sensor network), in our simulations, we assume that each node traces a small number of other nodes. In fact, as a result of the pseudorandom function Trace (Algorithm 1, line 2) each node traces exactly 5 other network nodes. For the cooperative scenario, when two nodes  and
and  meet, they exchange the information concerning the nodes tracked by both
meet, they exchange the information concerning the nodes tracked by both  and
and  ; we assume that this information can be contained in one message. Indeed, the number of shared traced nodes can be up to 5 (number of nodes traced by each node), but in practice, it turns out to be much smaller, on average (0.25 in our setting). We simulated our protocol with and without node cooperation, varying the alarm time from 250 to 8000 seconds and the average node speed from 5 m/s to 20 m/s. Figures 4(a) and 4(b) show the results of the simulation of our protocol without and with cooperation, respectively. Figure 4(a) shows the results when cooperation is switched off, for the two protocols and different speeds. On the
; we assume that this information can be contained in one message. Indeed, the number of shared traced nodes can be up to 5 (number of nodes traced by each node), but in practice, it turns out to be much smaller, on average (0.25 in our setting). We simulated our protocol with and without node cooperation, varying the alarm time from 250 to 8000 seconds and the average node speed from 5 m/s to 20 m/s. Figures 4(a) and 4(b) show the results of the simulation of our protocol without and with cooperation, respectively. Figure 4(a) shows the results when cooperation is switched off, for the two protocols and different speeds. On the  -axis, we fix the flooding interval for the reference solution protocol. In this way, the detection time is also fixed for the reference solution and it does not change when changing the speed. The quality of the detection for the reference solution is just linear: by doubling the flooding interval also the detection time doubles, while the energy cost halves. Figure 4(a) confirms our intuition: mobility with local cooperation can help computing global properties incurring in a small overhead.
-axis, we fix the flooding interval for the reference solution protocol. In this way, the detection time is also fixed for the reference solution and it does not change when changing the speed. The quality of the detection for the reference solution is just linear: by doubling the flooding interval also the detection time doubles, while the energy cost halves. Figure 4(a) confirms our intuition: mobility with local cooperation can help computing global properties incurring in a small overhead.
In this simulation scenario, for a reasonable speed of nodes, our protocol outperforms the reference solution. Take, as an example, a flooding interval of 50 seconds. From Figure 4(a), we can see that the detection time of the reference solution protocol is 5000 seconds. The performance of our protocol depends on the average speed of the system. If the average speed of the system is slow, for example, 5 m/s, then the detection time is more than 6000 seconds. However, if the network nodes move faster, then our solution improves over the reference solution. For instance, when the average speed is 20 m/s, the detection time is as low as 1600 seconds, much faster than the reference solution. From this experiment, it is also clear that the performance of our protocol depends on the average speed in the network: the faster the better. While the reference solution is an excellent solution for slow networks, for example, where nodes are carried by humans walking, our solution is the best for faster networks, and it is always the best when the energy overhead must be low. Now, we will switch cooperation on, and see that the performance of our protocol increases considerably, even though with some drawbacks when the energy budget is small.
Figure 4(b) describes the performance of our protocol when using cooperation. When the network flooding frequency is high, that is, network flooding interval is small, cooperation is very effective. Further, with cooperation, the performance of our protocol improves as the average speed of the nodes increases. In this case, our protocol is better than the reference solution even when starting from very high flooding frequency, that is, starting from systems that are very fast in detecting the node capture attack and that, consequently, have very high energy requirements. What is less intuitive is that cooperation is not useful when we move to more energy-saving systems. Take, as an example, a network where the average speed is 15 m/s. Our protocol is better than the reference solution whenever the design goal is to have a network with more energy available and to achieve a small detection time, that is, in Figure 4(b), whenever the flooding interval is smaller than 38 seconds. However, when considering a network with more stringent energy requirements, for example, when the flooding interval is 50 seconds, then it is simply not possible to reach such low energy costs by using cooperation. Cooperation has a cost, which is higher when the network is faster—indeed, in a faster network, the nodes meet more frequently, and thus cooperation is higher. In this case, the correct design guideline is to use our protocol with cooperation, if the objective is to have a system that is fast in detecting the node capture attack, though using more energy—in particular, in our example until a flooding interval of 38 seconds—and then to switch cooperation off, to get a cheaper protocol that can be used when the flooding interval can be larger.
As described in Figure 4(b), the limits of cooperation appear sooner in faster networks. This is intuitive, cooperation is more costly when nodes meet more often, and so the tradeoff moves toward noncooperation earlier. The implications of using mobility and local communications to compute global properties are not self-evident. If the network is fast enough, it is always better to use protocols like the one we propose rather than using static approaches like the reference solution. However, node cooperation flavored techniques, which appears to be effective in any case, have the result of making the information in the network spread faster, but at a cost.
5.3. Massive Attacks
In order to investigate the behavior of our protocol under a massive attack, we simulated the capture of 10% of the network nodes (10 out of 100) at the same time. We fixed the average speed at 15 m/s. Simulation results are shown in Figures 5(a) and 5(b) for the noncooperative and cooperative scenarios, respectively. For both cases, the figures show the result for one captured node and 10 captured nodes in a network of 100 nodes. From both figures, we can see that all the protocols, both the reference solution and our solution, with or without cooperation, are robust against massive attacks. Indeed, the small differences in performance do not justify a change in the defense strategy but for small intervals.
5.4. Other Mobility Patterns
We stress once again that the aim of this work is to give a proof of concept that both node mobility and node cooperation can help thwarting the node capture attack. Hence, to abstract from mobility details we choose to use the Random Waypoint Mobility Model. Mobility models based on randomly moving nodes may, for example, provide useful analytical approximations to the motion of vehicles that operate in dispatch mode or delivery mode [41]. It is important to note that the results obtained in this work are not directly applicable to others scenario-inspired mobility models [12]; for instance, while intermeeting time follows an exponential distribution under the RWM, intermeeting time is shown to be better approximated by a power-law distribution in some scenarios [12, 42]. However, it is also interesting to note that our solution allows the network to let autonomously emerge the subgroups of nodes that meet with higher frequency (communities). In fact, this can be done leveraging the false-positive alarm: if node  sends a high number of false alarms (further revoked by the accused node) related to node
sends a high number of false alarms (further revoked by the accused node) related to node  , this implies that
, this implies that  actually does not meet with
actually does not meet with  with "high" frequency. This information can be interpreted as if
with "high" frequency. This information can be interpreted as if  and
and  do not belong to the same community.
do not belong to the same community.
6. Conclusions
In this paper we have proposed, to the best of our knowledge, the first distributed solution to a major security threat in MANETs: the node capture attack. Our solution is based on the intuition that node mobility, together with local node cooperation, can be leveraged to design security protocols that are extremely effective and energy-efficient. We have also developed a protocol that, increasing the level of cooperation among nodes, makes global information flow faster in the network, even if at a cost in terms of energy. The experiments clearly show that leveraging mobility and cooperation helps in designing effective and efficient protocols. In particular, we also pointed out that there is critical speed necessary to induce enough information flow to make these new protocols outperform traditional ones, designed for static networks.
We believe that the ideas and protocols introduced in this paper pave the way for further research in the area; furthermore, even if specifically suited to address a major security threat, they could be also adopted in other scenarios to support other emergent properties as well.
References
Chan H, Perrig A, Song D: Random key predistribution schemes for sensor networks. Proceedings of the IEEE Symposium on Security and Privacy (S&P '03), September 2003
Newsome J, Shi E, Song D, Perrig A: The sybil attack in sensor networks: analysis & defenses. Proceedings of the 3rd International Conference on Information Processing in Sensor Networks (IPSN '04), April 2004
Demirbas M, Song Y: An RSSI-based scheme for sybil attack detection in wireless sensor networks. Proceedings of the International Symposium on a World of Wireless, Mobile and Multimedia Networks (WoWMoM '06), June 2006, New York, NY, USA 564-568.
Di Pietro R, Mancini LV, Mei A: Energy efficient node-to-node authentication and communication confidentiality in wireless sensor networks. Wireless Networks 2006, 12(6):709-721. 10.1007/s11276-006-6530-5
Conti M, Di Pietro R, Mancini LV, Mei A: A randomized, efficient, and distributed protocol for the detection of node replication attacks in wireless sensor networks. Proceedings of the International Symposium on Mobile Ad Hoc Networking and Computing (MobiHoc '07), 2007 80-89.
Parno B, Perrig A, Gligor VD: Distributed detection of node replication attacks in sensor networks. Proceedings of the IEEE Symposium on Security and Privacy (S&P '05), 2005
Information Processing Technology Office (IPTO) Defense Advanced Research Projects Agency (DARPA) BAA 07-46 LANdroids Broad Agency Announcement, 2007, http://www.darpa.mil/index.html
Perrig A, Stankovic J, Wagner D: Security in wireless sensor networks. Commununications of ACM 2004, 47(6):53-57. 10.1145/990680.990707
Capkun S, Hubaux J-P, Buttyán L: Mobility helps security in ad hoc networks. Proceedings of the International Symposium on Mobile Ad Hoc Networking and Computing (MobiHoc '03), 2003 46-56.
Piro C, Shields C, Levine BN: Detecting the sybil attack in mobile ad hoc networks. Proceedings of the 2nd International Conference on Security and Privacy in Communication Networks (SecureComm '06), 2006, Baltimore, Md, USA
Broch J, Maltz DA, Johnson DB, Hu Y-C, Jetcheva J: A performance comparison of multi-hop wireless ad hoc network routing protocols. Proceedings of the 4th Annual ACM/IEEE International Conference on Mobile Computing and Networking (MobiCom '98), 1998 85-79.
Sharma G, Mazumdar R, Shroff NB: Delay and capacity trade-offs in mobile ad hoc networks: a global perspective. Proceedings of the 25th Conference on Computer Communications (INFOCOM '06), 2006
Becher A, Becher E, Benenson Z, Dornseif M: Tampering with motes: real-world physical attacks on wireless sensor networks. Proceeding of the 3rd International Conference on Security in Pervasive Computing (SPC '06), 2006 104-118.
Grossglauser M, Vetterli M: Locating nodes with EASE: last encounter routing in ad hoc networks through mobility diffusion. Proceedings of the 22nd Annual Joint Conference of the IEEE Computer and Communications Societies (INFOCOM '03), 2003, San Francisco, Calif, USA
Luo J, Hubaux J-P: Joint mobility and routing for lifetime elongation in wireless sensor networks. Proceedings of the 24th Annual Joint Conference of the IEEE Computer and Communications Societies (INFOCOM '05), March 2005, Miami, Fla, USA
fan Hsin C, Liu M: A distributed monitoring mechanism for wireless sensor networks. Proceedings of the Workshop on Wireless Security (WiSe '02), 2002 57-66.
fan Hsin C, Liu M: Self-monitoring of wireless sensor networks. Computer Communications 2006, 29(4):462-476. 10.1016/j.comcom.2004.12.031
Hayashibara N, Cherif A, Katayama T: Failure detectors for large-scale distributed systems. Proceedings of the 21st IEEE Symposium on Reliable Distributed Systems (SRDS '02), October 2002, Suita, Japan
Ranganathan S, George AD, Todd RW, Chidester MC: Gossip-style failure detection and distributed consensus for scalable heterogeneous clusters. Cluster Computing 2001, 4(3):197-209. 10.1023/A:1011494323443
Curtmola R, Kamara S: A mechanism for communication-efficient broadcast encryption over wireless ad hoc networks. Electronic Notes in Theoretical Computer Science 2007, 171(1):57-69. 10.1016/j.entcs.2006.11.009
Huang D, Mehta M, Medhi D, Harn L: Location-aware key management scheme for wireless sensor networks. Proceedings of the 2nd ACM Workshop on Security of Ad Hoc and Sensor Networks (SASN '04), November 2004, Washington, DC, USA 29-42.
Tague P, Poovendran R: Modeling adaptive node capture attacks in multi-hop wireless networks. Ad Hoc Network 2007, 5(6):801-814. 10.1016/j.adhoc.2007.01.002
Tague P, Slater D, Rogers J, Poovendran R: Vulnerability of network traffic under node capture attacks using circuit theoretic analysis. Proceedings of the 27th IEEE International Conference on Computer Communications (INFOCOM '08), 2008 161-165.
Conti M, Di Pietro R, Gabrielli A, Mancini LV, Mei A: The quest for mobility models to analyse security in mobile ad hoc networks. Proceedings of the 7th International Conference on Wired/Wireless Internet Communications (WWIC '09), May 2009 85-96.
Conti M, Di Pietro R, Mancini LV, Mei A: Emergent properties: detection of the node-capture attack in mobile wireless sensor networks. Proceedings of the 1st ACM Conference on Wireless Network Security (WiSec '08), 2008 214-219.
Daly EM, Haahr M: Social network analysis for routing in disconnected delay-tolerant MANETs. Proceedings of the International Symposium on Mobile Ad Hoc Networking and Computing (MobiHoc '07), September 2007 32-40.
Sterbenz JPG, Krishnan R, Hain RR, et al.: Survivable mobile wireless networks: issues, challenges, and research directions. Proceedings of the 1st ACM Workshop on Wireless Security (WiSe '02), 2002, Atlanta, Ga, USA 31-40.
Di Pietro R, Mancini L, Soriente C, Spognardi A, Tsudik G: Data security in unattended sensor networks. IEEE Transactions on Computers 2009, 58(11):1500-1511.
Di Pietro R, Mancini L, Soriente C, Spognardi A, Tsudik G: Playing hide-and-seek with a focused mobile adversary in unattended wireless sensor networks. Ad Hoc Networks 2009, 7(8):1463-1475. 10.1016/j.adhoc.2009.04.002
Yoon J, Liu M, Noble B: Random waypoint considered harmful. Proceedings of the 22nd Annual Joint Conference of the IEEE Computer and Communications Societies, March 2003, San Franciso, Calif, USA 2: 1312-1321.
Hyytiä E, Lassila P, Virtamo J: Spatial node distribution of the random waypoint mobility model with applications. IEEE Transactions on Mobile Computing 2006, 5(6):680-694.
Sun K, Ning P, Wang C: Fault-tolerant cluster-wise clock synchronization for wireless sensor networks. IEEE Transactions on Dependable and Secure Computing 2005, 2(3):177-189. 10.1109/TDSC.2005.36
Williams B, Camp T: Comparison of broadcasting techniques for mobile ad hoc networks. Proceedings of the International Symposium on Mobile Ad Hoc Networking and Computing (MobiHoc '02), 2002 194-205.
Orecchia L, Panconesi A, Petrioli C, Vitaletti A: Localized techniques for broadcasting in wireless sensor networks. Proceedings of the Joint Workshop on Foundations of Mobile Computing (DIALM-POMC '04), October 2004, Philadelphia, Pa, USA
Burns B, Brock O, Levine BN: MORA routing and capacity building in disruption-tolerant networks. Ad Hoc Networks 2008, 6(4):600-620. 10.1016/j.adhoc.2007.05.002
Liu H, Wan P-J, Liu X, Yao F: A distributed and efficient flooding scheme using 1-hop information in mobile ad hoc networks. IEEE Transactions on Parallel and Distributed Systems 2007, 18(5):658-671.
Rahman SMM, Nasser N, Inomata A, Okamoto T, Mambo M, Okamoto E: Anonymous authentication and secure communication protocol for wireless mobile ad hoc networks. Security and Communication Networks 2008, 1(2):179-189. 10.1002/sec.4
Striki M, Baras J, Manousakis K: A robust, distributed TGDH-based scheme for secure group communications in MANET. Proceedings of the IEEE International Conference on Communications (ICC '04), May 2004
Di Pietro R, Mancini LV, Mei A: Efficient and resilient key discovery based on pseudo-random key pre-deployment. Proceedings of the IEEE International Parallel and Distributed Processing Symposium (IPDPS '04), 2004 2991-2998.
Wander A, Gura N, Eberle H, Gupta V, Shantz SC: Energy analysis of public-key cryptography for wireless sensor networks. Proceedings of the 3rd IEEE International Conference on Pervasive Computing and Communications Workshops (PERCOMW '05), 2005
Bandyopadhyay S, Coyle EJ, Falck T: Stochastic properties of mobility models in mobile ad hoc networks. IEEE Transactions on Mobile Computing 2007, 6(11):1218-1229.
Chaintreau A, Hui P, Diot C, Gass R, Scott J: Impact of human mobility on opportunistic forwarding algorithms. IEEE Transactions on Mobile Computing 2007, 6(6):606-620.
Acknowledgments
The authors would like to thank the anonymous reviewers for their helpful comments that helped to improve the quality of this paper. The authors are solely responsible for the views expressed in this paper, which do not necessarily reflect the position of supporting Organizations. This work was partly supported by: (1) the Spanish Ministry of Education through projects TSI2007-65406-C03-01 "E-AEGIS" and CONSOLIDER INGENIO 2010 CSD2007-0004 "ARES," (2) the Government of Catalonia under grant 2005 SGR 00446, and (3) the project APPLICAZIONI GOVERNATIVE LEGATE ALL'USO DEL PRS GALILEO (PRESAGO)—contract ASI I/030/07/0 starting September 6, 2007.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Conti, M., Di Pietro, R., Mancini, L.V. et al. Mobility and Cooperation to Thwart Node Capture Attacks in MANETs. J Wireless Com Network 2009, 945943 (2009). https://doi.org/10.1155/2009/945943
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/945943

 ,
,  m/s,
m/s,  m/s.
m/s. and node
and node  meet: this event triggers node
meet: this event triggers node  and node
and node  to execute
to execute 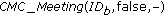 and CMC_Meeting
and CMC_Meeting respectively, if the cooperation parameter is set to false. Otherwise, node
respectively, if the cooperation parameter is set to false. Otherwise, node  executes CMC_Meeting
executes CMC_Meeting and node
and node 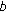 executes CMC_Meeting
executes CMC_Meeting . The function CMC_Meeting is also used in the cooperative scenario as a virtual meeting in order to update node presence information.
. The function CMC_Meeting is also used in the cooperative scenario as a virtual meeting in order to update node presence information.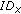 expires on node
expires on node  : node
: node  executes the procedure CMC_TimeOut
executes the procedure CMC_TimeOut .
. eavesdrops a message
eavesdrops a message 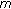 : node
: node  executes the procedure CMC_Receive(m).
executes the procedure CMC_Receive(m). )then
)then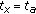 ;
;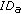 ,
,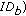 =
= then
then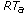 ,
,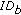 )then
)then ,
,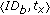 );
); ,
, );
);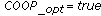 then
then do
do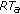 ,
, )then
)then ) = 1then
) = 1then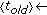
 );
); ;
; );
);
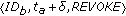 );
); ,
, )
) ;
; then
then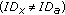 then
then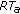 ,
,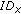 ) then
) then
 );
); );
); then
then
 (
( );
); ;
; seconds are elapsed without remeeting node
seconds are elapsed without remeeting node  .,
., seconds are elapsed from receiving/triggering a node revocation for node
seconds are elapsed from receiving/triggering a node revocation for node  —assuming that in these
—assuming that in these  seconds no presence claim from
seconds no presence claim from  are received.
are received.
 Without node cooperation,
Without node cooperation,  m/sWith node cooperation,
m/sWith node cooperation,  m/sWithout node cooperation,
m/sWithout node cooperation,  m/sWith node cooperation,
m/sWith node cooperation,  m/s
m/s

 ,
,  m. Without node cooperationUsing node cooperation
m. Without node cooperationUsing node cooperation
 ,
,  m,
m,  m/s. Without node cooperationUsing node cooperation
m/s. Without node cooperationUsing node cooperation