- Research Article
- Open access
- Published:
Network Modulation: An Algebraic Approach to Enhancing Network Data Persistence
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 141340 (2010)
Abstract
Large-scale distributed systems such as sensor networks usually experience dynamic topology changes, data losses, and node failures in various catastrophic or emergent environments. As such, maintaining data persistence in a scalable fashion has become critical and essential for such systems. The existing major efforts such as coding, routing, and traditional modulation all have their own limitations. In this work, we propose a novel network modulation (NeMo) approach to significantly improve the data persistence. Built on algebraic number theory, NeMo operates at the level of modulated symbols (so-called "modulation over modulation"). Its core notion is to mix data at intermediate network nodes and meanwhile guarantee the symbol recovery at the sink(s) without prestoring or waiting for other symbols. In contrast to the traditional thought that n linearly independent equations are needed to solve for n unknowns, NeMo opens a new regime to boost the convergence speed of achieving persistence. Different performance criteria (e.g., modulation and demodulation complexity, convergence speed, finite-bit representation, and noise robustness) have been evaluated in the comprehensive simulations and real experiments to show that the proposed approach is efficient to enhance the network data persistence.
1. Introduction
Today large-scale distributed systems are routinely deployed for many computing, detection, communication, and monitoring tasks. These systems are comprised of a large number of spatially distributed autonomous devices. Sensor networks, cellular networks, Wi-Fi, computational grids, data center, and peer-to-peer networks are among the typical examples of this type of systems with broad practical applications in both civilian and military areas. It is very common for these systems to incur data losses and node outages. For instance, sensor nodes may be short-lived due to limited energy resources or the failure in catastrophic/emergent environments. Also because of nodes' random placement, network topology is unknown and the sink location(s) may be unknown. Owing to all of these network uncertainties, how to safely and soundly deliver the data to the sink(s)—data persistence—becomes challenging and critical.
There are two major issues which have to be considered and resolved for enhancing data persistence in a large-scale distributed system. One is how to deliver the existing data to the sink(s) as soon as possible. This is an important metric to evaluate the performance of an algorithm targeting data persistence. Routing data to the sink(s) with the minimal transmission overhead (e.g., delay) is a straightforward solution to this issue. However, existing routing protocols such as [1–7] do not work appropriately due to lack of topology information, or they have to pay high communication and storage overhead when nodes are required to initiate data reading and transmission immediately without learning the network topology. The dynamics of network topology and unexpected node failures make things even worse.
The other issue is concerned with how to "back-up" data in the network so that if one node suddenly fails, its data can still survive in other places of the network. One natural approach is to adopt coding techniques. Recently, different coding techniques have been proposed (e.g., [8–13]) to increase data persistence. They show great improvement relative to the no coding case. However, there still exist several unsolved problems. For example, some coding techniques require the sink to collect enough packets to decode the next coded packet (see, e.g., [14]). This causes extra delay and decoding complexity at the sink and may be impractical for some applications with strict timeliness requirement such as sensor networks for catastrophe monitoring. Also the existing coding techniques are not flexible enough to incorporate new node joins and/or asynchronous nodes.
In this work, we view these two issues from a new angle: fast delivery can be interpreted as high transmission rate, while robustness to node failure or noise can be viewed as low error probability. This novel view makes enhancing data persistence analogous to achieving Shannon's capacity—the maximum error-free data rate over a channel [15]. In general, it is well known that there are two ways to achieve Shannon's capacity—coding and modulation. Recognizing this, it is not surprising to see that coding techniques can enhance data persistence. In addition, it becomes natural to introduce our approach—modulation.
Traditionally, there are two major categories of modulation schemes—analog and digital modulations. Analog modulation is applied continuously in response to the analog information signal, for example, frequency modulation (FM) for radio broadcasting. Clearly these modulation methods are not capable of incorporating the distributed digital data from sensors or other distributed autonomous devices. Digital modulation is a way to generate waveforms or symbols from a digital bit stream, for example, phase shift keying (PSK), quadrature amplitude modulation (QAM). However, these traditional digital modulation schemes are hard to "grow" when one node wants to combine two symbols (not bits) to a new symbol in a higher constellation. The symbols have to be demodulated back to bits and then the union of two sets of bits is modulated to a new symbol. Given the limited resources of a network node, this process may cost infeasibly high energy and memory consumption.
In this paper, we propose a novel approach that is referred to as network modulation (NeMo). NeMo is based on algebraic number theory to enhance data persistence. This approach adopts an algebraic way to "combine" symbols, which increases the information in a symbol while still guaranteeing the decodability at the sink. The core notion of NeMo is to mix the data at intermediate network nodes while allowing the sink to decode without prestored symbols.
Two different ways are proposed to modulate the symbols—nonregenerative NeMo and regenerative NeMo. They differ in the way that the newly received packet is processed. In the nonregenerative version, a node simply combines the incoming symbol with the local data. But the regenerative version demodulates the arrived symbol before combining it with the local data. Note that the modulation and demodulation of NeMo operate at the level of modulated symbols (called "modulation over modulation") and thus it can be independent from network layer. We formally prove that for both of these methods the symbol recovery is guaranteed at the sink and also carefully study all kinds of performance tradeoffs of them. Furthermore, we derive the upper bounds of the persistence curves with NeMo, which illustrate that our approach is more efficient than the existing Growth Codes (GCs) [13]. In addition, we propose solutions to several practical concerns such as packet header design and asynchronous node joins and failure.
The rest of this paper is organized as follows. We summarize the related works in Section 2 and formulate the problem and describe the network setting in Section 3. Section 4 introduces the basics of NeMo and the modulation and demodulation steps. Section 5 evaluates the performance of NeMo. Implementation issues are addressed and evaluated in Section 6. Section 7 presents the experiment results. Section 8 concludes the paper and proposes some future research directions.
2. Related Work
Distributed coding has been established as an effective paradigm to deliver high data persistence in networked systems. Like channel coding, its basic idea is to introduce data redundancy to the network. The redundancy spread over the network can help to recover the lost data in the presence of noise and node failure. Some distributed coding schemes have been developed for distributed storage systems to provide the reliable access to the data [8, 9, 11, 12], and for wireless sensor networks and peer-to-peer networks to deliver significant improvement in throughput [16–21] and reliability [13, 22–25]. Also, algebraic approach to network coding was introduced in [26] and this frame was extended to incorporate vector communication in linear deterministic networks [27].
However, most of the techniques in this area require accumulating a large number of codewords before decoding by using the traditional coding techniques such as Reed-Solomon [28], LT [29], Digital Fountain [14], LDPC [30], and turbo codes [31]. This is not desirable in a number of scenarios where resources are limited, nodes are subject to failure at anytime, or a smooth data persistence curve is required to provide low latency. In contrast, our NeMo can perform decoding instantaneously after receiving the data. Superposition coding is proposed to enhance the network throughput in MAC layer [32] by taking into account physical layer link information. However, symbol recovery is needed at each node and the data persistence is not considered.
Growth Codes (GCs) [13] is a recent major effort to maximize data persistence in a zero-configuration sensor network. Nodes exchange codewords with their neighbors while gradually increasing the codeword degree by combining received codewords with their own information. Liu et al. [23] generalized the GC scenario to include multisnapshots and general coding schemes. By associating a utility function with the recovered data, they design a joint coding and scheduling scheme to maximize the expected utility gain. Karande et al. [25] found that the random network coding outperforms GC in periphery monitoring topologies. Additionally, some other codes have been developed to provide unequal protection for prioritized data. For example, priority random linear codes [24] are proposed to partially recover more important subset of data when the whole recovery is impossible. Dimakis et al. [10] generalizes the GC analysis and investigates the design of fountain codes which provide good intermediate performance and unequal error protection for video streaming.
3. Problem Statement
In this section, for simplicity of illustration, we first present a description of a simple network model we will use to describe the design of NeMo. The model will be extended for a number of practical issues later in this paper. Then we define data persistence formally and formulate the problem we attack in this work.
3.1. Network Description
Our network model is similar to that considered in related works. It consists of a large sensor network with  sensors/nodes and
sensors/nodes and  sink. The network is zero-configuration such that nodes only sense their neighbors with whom they can communicate directly and do not know where the sink is. The network topology is random and can be altered. Typically the majority of the nodes cannot communicate with the sink directly. In addition, our initial study also makes the following assumptions:
sink. The network is zero-configuration such that nodes only sense their neighbors with whom they can communicate directly and do not know where the sink is. The network topology is random and can be altered. Typically the majority of the nodes cannot communicate with the sink directly. In addition, our initial study also makes the following assumptions:
-
(i)
every node has infinite processing power and memory;
-
(ii)
there is no node failure and data transmission error (e.g., channel fading or additive noise);
-
(iii)
each node takes only a single reading;
-
(iv)
all data packets have the same importance;
-
(v)
all nodes have the same transmission range;
-
(vi)
every node employs the same modulation technique and runs the same protocol;
-
(vii)
all nodes have half-duplex capability, that is, transmitting and receiving at different time slots (The work in [13] assumes full-duplex capacity. However, we believe half-duplex is more practical in the context. Our scheme also works for full-duplex scenario.)
The above assumptions construct a simple network model which is most appropriate to show the design principles and facilitate the analysis. Most of the assumptions are also adopted in the literature (see, e.g., [6, 13, 21, 25]). We will consider more practical network settings to address most of the above unrealistic assumptions in Section 6.
3.2. Problem Formulation
Data persistence is defined as the fraction of data generated within the system that eventually reaches the sink [13]. Now let us use a simple example to illustrate what makes NeMo unique to enhance the data persistence.
Example 1.
Suppose that there are two nodes (Node 1 and Node 2) with two readings/symbols,  and
and  for each. The network is two-hop from Node 1 to Node 2 and then to Sink (see Figure 1). The goal is to deliver both
for each. The network is two-hop from Node 1 to Node 2 and then to Sink (see Figure 1). The goal is to deliver both  and
and  to the sink. Without combining
to the sink. Without combining  and
and  at Node 2,
at Node 2,  hops are needed. We can do it in two hops if Node 2 can transmit a combination of
hops are needed. We can do it in two hops if Node 2 can transmit a combination of  and
and  ,
,  , in one slot. One question is: given two symbols, can we find an efficient approach to combine them as one symbol by guaranteeing identifiability at the sink side? For example, for BPSK modulated symbols
, in one slot. One question is: given two symbols, can we find an efficient approach to combine them as one symbol by guaranteeing identifiability at the sink side? For example, for BPSK modulated symbols  and
and  , that is,
, that is,  , when simple "adding"
, when simple "adding"  is applied, the possible values of
is applied, the possible values of  (known as constellation) are shown in the right subfigure of Figure 2. The
(known as constellation) are shown in the right subfigure of Figure 2. The  pair to generate
pair to generate  is depicted under the corresponding point of
is depicted under the corresponding point of  . From the figure, it is ready to see that the unique recovery of original readings is not guaranteed. For example, if
. From the figure, it is ready to see that the unique recovery of original readings is not guaranteed. For example, if  , the sink does not know which pair among
, the sink does not know which pair among  ,
,  , and
, and  was sent from Node 1 and Node 2. However, if we "smartly" combine
was sent from Node 1 and Node 2. However, if we "smartly" combine  and
and  as
as  the constellation of
the constellation of  is shown in the left subfigure of Figure 2. From the figure, we can see that one unique
is shown in the left subfigure of Figure 2. From the figure, we can see that one unique  is designated to every pair of
is designated to every pair of  and
and  . That means when the sink receives
. That means when the sink receives  , it can easily recover the original two symbols
, it can easily recover the original two symbols  and
and  . This shows that if we combine two symbols "smartly," symbol recovery is guaranteed.
. This shows that if we combine two symbols "smartly," symbol recovery is guaranteed.
Mathematically, we formulate the problem as follows. Suppose that  is the local symbol at Node 2 and
is the local symbol at Node 2 and  is a symbol newly received at Node 2. After linear combination, the symbol transmitted from this node to another node or sink is
is a symbol newly received at Node 2. After linear combination, the symbol transmitted from this node to another node or sink is

where  is the power normalizer, and
is the power normalizer, and  and
and  are two coefficients which are specified by modulation schemes. In general, we have
are two coefficients which are specified by modulation schemes. In general, we have

where  and
and  . The remaining question is how to choose
. The remaining question is how to choose  so that
so that  can be uniquely recovered from
can be uniquely recovered from  . This may look like an ill-posed problem—given one equation, how can one solve two or more unknowns? The key is that
. This may look like an ill-posed problem—given one equation, how can one solve two or more unknowns? The key is that  are not real or complex numbers, but belong to some lattice (e.g., all QAM symbols belong to complex Gaussian integer lattice). By appropriately choosing
are not real or complex numbers, but belong to some lattice (e.g., all QAM symbols belong to complex Gaussian integer lattice). By appropriately choosing  , it can be guaranteed that
, it can be guaranteed that  will be uniquely identified from
will be uniquely identified from  . We give the detailed design in the following sections.
. We give the detailed design in the following sections.
4. Design of NeMo
In this section, we briefly introduce algebraic number theory and describe our NeMo design based on it.
4.1. Terminology and Notation
In the following, we summarize some terminologies and corresponding notations which will be used in the rest of the paper.
Symbol
We adopt  's to denote the originally modulated symbols (before nodes exchange information), for example,
's to denote the originally modulated symbols (before nodes exchange information), for example,  -ary QAM. We call them OMsymbols. Multiple OM symbols can be modulated by NeMo into another symbol
-ary QAM. We call them OMsymbols. Multiple OM symbols can be modulated by NeMo into another symbol  called an NM symbol.
called an NM symbol.
Degree of an NM Symbol
The degree of an NM symbol  is the number of OM symbols employed to generate this symbol and is denoted as
is the number of OM symbols employed to generate this symbol and is denoted as  .
.
Maximum Degree of an NM Symbol
Due to computational power and memory size constraints, the degree of NM symbols is usually upper bounded. The maximum degree allowed is denoted as  .
.
Neighbor
The nodes within the transmission range of a node are called neighbors of this node.
Node ID
Node ID is a unique identity of a certain node in the network. It can be an IP address, or a geographic location.
Symbol Overlap
If two NM symbols contain some common OM symbols, we say these two symbols have some overlap.
Degree of a Modulator
It is defined as the length of the vector as in (2) from which the coefficients  's are drawn. We will see that the degree of a modulator is NOT always equal to the degree of the corresponding NM symbol.
's are drawn. We will see that the degree of a modulator is NOT always equal to the degree of the corresponding NM symbol.
4.2. Algebraic Number Theory for NeMo
Before we pursue the detailed modulation scheme, we need to introduce some basics of algebraic number theory which will be used to design NeMo.
Euler Numbers
Given an integer  , the Euler number
, the Euler number  of
of  is the cardinality of the set
is the cardinality of the set  , where
, where  stands for the greatest common divisor.
stands for the greatest common divisor.
As we mentioned, the key point of designing  in (2) is to make sure that when the OM symbols are linearly combined as an NM symbol, they can still be uniquely demodulated. There are different ways to design
in (2) is to make sure that when the OM symbols are linearly combined as an NM symbol, they can still be uniquely demodulated. There are different ways to design  . Here we are providing a systematic and general way based on algebraic number theory. For a given number of OM symbols
. Here we are providing a systematic and general way based on algebraic number theory. For a given number of OM symbols  , the design of has the following special structure
, the design of has the following special structure

where  is a scalar which will be designed as follows. The general design of
is a scalar which will be designed as follows. The general design of  only depends on the modulator's degree. It does not depend on the original modulation size (say
only depends on the modulator's degree. It does not depend on the original modulation size (say  -QAM or
-QAM or  -QAM).
-QAM).
For a given modulator degree  , select an integer
, select an integer  which is a multiple of
which is a multiple of  and
and  , where
, where  is a positive integer. The generator
is a positive integer. The generator (and thus
(and thus in ( 3 )) can be designed as
in ( 3 )) can be designed as

where
 is selected from
is selected from
 such that
such that
 , and
, and
 .
.
In the following, we provide one example to illustrate the design of  .
.
Example 2.
If  ,
,  , then we can select
, then we can select  , and the Euler number
, and the Euler number  . We can choose
. We can choose  such that
such that  . Hence,
. Hence,  .
.
Note that the choice of  is not unique. Different
is not unique. Different  choices for the same size
choices for the same size  may provide different performance in physical layer (see, e.g., [33]), but all of them achieve the same symbol identifiability. In Table 1, we list the design of
may provide different performance in physical layer (see, e.g., [33]), but all of them achieve the same symbol identifiability. In Table 1, we list the design of  with some commonly used values of
with some commonly used values of  . Although the choice of
. Although the choice of  is nonunique, in the following, we adopt the universal choice for all
is nonunique, in the following, we adopt the universal choice for all , that is,
, that is, .
.
 .
.4.3. The Basics of NeMo
Now we are ready to go into the design of NeMo. Note that, for simplicity we assume (i) each packet sent by a node consists of a packet header which includes the necessary information for network modulation (see Section 6 for its design) and one NM/OM symbol as the payload (the algorithm can be easily extended to multiple symbols), and (ii) time is divided into rounds as in [13]. In each round, a pair of nodes completes a packet exchange if no collision happens. The basic procedure is divided into three stages and works as follows.
Initialization
Every node has one packet ready if any.
Exchange
In each round, each node transmits its packet with probability  .
.
-
(a)
If a node decides to transmit the packet, it will randomly select a neighbor to forward the packet. The selected neighbor will receive the packet if it does not transmit in the meanwhile (recall that we assume half-duplex channel.). Otherwise the packet is dropped and the rest of the round becomes idle. Collision may also happen if a node is chosen for exchange by more than one neighboring nodes at the beginning of a round. Therefore, to summarize, for one node to successfully receive a packet from another node, three conditions must be met: (i) this node decides not to transmit; (ii) it is selected by another node to forward packets; and (iii) it is not selected by more than one node (if collision is considered).
-
(b)
Those nodes which successfully received packets will forward their stored packets back to the corresponding nodes to complete an exchange round.
Packet Processing
When a node receives a packet from its neighbor, it will first check the packet header. If the packet is completely new, that is, there is no overlap with the node's currently stored packet, the node will combine it into the stored packet (i.e., network modulation). If the newly received packet has some overlap with the stored one (judged from the packet header), then the newly received packet will be stored to replace the old one. In this case, the transmission pair of two nodes just exchanges their packets.
It is not hard to see that exchanging may bring some information loss if an old packet is replaced by the new one even when the old one has new OM symbols. However, here we consider a resource constrained environment (e.g., sensor networks) so that intermediate nodes may not be able to afford demodulating every NM symbol. We will discuss the variation in Section 4.6 when nodes can afford up to a certain level of demodulation cost. If the node is the sink, then it will demodulate the packet and save the data.
The aforementioned procedure works iteratively and after some rounds the full data persistence will be achieved at the sink. Next, we will describe how to process and modulate incoming packets in detail.
4.4. Network Modulation
Suppose that a node has an NM symbol  of degree
of degree  in the memory and receives a new NM symbol
in the memory and receives a new NM symbol  of degree
of degree  . The node will check the packet header first for symbol overlap. If they have overlap, the node's old packet will be replaced by the new one. If they have no overlap, the node will perform NeMo as follows.
. The node will check the packet header first for symbol overlap. If they have overlap, the node's old packet will be replaced by the new one. If they have no overlap, the node will perform NeMo as follows.
Case 1.
If  (i.e., both are OM symbols), then the modulation step is the same as the one in (2) with
(i.e., both are OM symbols), then the modulation step is the same as the one in (2) with  .
.
Case 2.
If  or
or  is greater than
is greater than  , we need to check the degrees of modulator for
, we need to check the degrees of modulator for  and
and  . Suppose that the degree of the modulator of
. Suppose that the degree of the modulator of  is
is  and that of
and that of  is
is  , the new NM symbol is then generated as
, the new NM symbol is then generated as

where  is the generator of
is the generator of  . After modulation,
. After modulation,  becomes an NM symbol with the degree of the modulator
becomes an NM symbol with the degree of the modulator  , but it only contains
, but it only contains  nonzero OM symbols.
nonzero OM symbols.
The proof for the symbol recovery of nonregenerative NeMo is given as follows. First, based on Cases 1 and 2, one can verify that all NM symbols have  's size
's size  , recursively.
, recursively.
Second, based on Example 2 in Section 4.2, the generator  for
for  is
is  and
and  provided
provided  . Given two degrees
. Given two degrees  and
and  , where
, where  ,
,  and
and  can be represented as
can be represented as

where  and
and  . Because we have
. Because we have  ,
,

Combining (7) and (6), by defining a new generator as  , we obtain that
, we obtain that  actually is a linear combination of
actually is a linear combination of  and
and  with modulator degree
with modulator degree  . According to Example 2 in Section 4.2, this new
. According to Example 2 in Section 4.2, this new  guarantees identifiability. Note that the degree of the modulator is greater than the degree of the NM symbol here.
guarantees identifiability. Note that the degree of the modulator is greater than the degree of the NM symbol here.
Next, we will illustrate how the sink demodulates the received packets to recover original OM symbols.
4.5. Network Demodulation
After explaining the modulation schemes of NeMo, we now define the demodulation of NeMo, that is, how to recover OM symbols from the received NM symbols at the sink.
Let us define an important concept—the effective degree of an NM symbol first. The set of demodulated OM symbols stored at the sink is denoted as  . A newly received NM symbol
. A newly received NM symbol  has degree
has degree  . The effective degree of
. The effective degree of  , denoted by
, denoted by  , is defined as the number of OM symbols that are contained in
, is defined as the number of OM symbols that are contained in  but not present in
but not present in  . The node IDs of associated OM symbols in
. The node IDs of associated OM symbols in  are contained in the packet header of
are contained in the packet header of  (see Section 6), we can compute the effective degree
(see Section 6), we can compute the effective degree  by simply comparing with the set
by simply comparing with the set  . Note that the packet header stores all the necessary information so that the modulation coefficients
. Note that the packet header stores all the necessary information so that the modulation coefficients  's can be derived and the adopted coefficients are known (see Section 6.1 for details).
's can be derived and the adopted coefficients are known (see Section 6.1 for details).
The demodulation proceeds as follows.
-
(i)
If
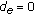 , the sink simply discards the packet with NM symbol
, the sink simply discards the packet with NM symbol  since all the OM symbols contained in
since all the OM symbols contained in  are known.
are known. -
(ii)
If
 , the only unknown OM symbol can be obtained by subtracting other demodulated OM symbols from
, the only unknown OM symbol can be obtained by subtracting other demodulated OM symbols from  .
. -
(iii)
If
 , we first cancel the known OM symbols from
, we first cancel the known OM symbols from  and obtain an NM symbol modulated by
and obtain an NM symbol modulated by  unknown symbols finally. Then, by exhaustively searching over all possible
unknown symbols finally. Then, by exhaustively searching over all possible  OM symbol vectors which have been saved in a look-up table, we can determine the rest unknown OM symbols. Due to the design of
OM symbol vectors which have been saved in a look-up table, we can determine the rest unknown OM symbols. Due to the design of  in Section 4.2, a
in Section 4.2, a  OM symbol vector can be uniquely determined given only one NM symbol.
OM symbol vector can be uniquely determined given only one NM symbol.
Note here, the demodulation of NeMo is different from the decoder of the GC in [13]. Instead of discarding the packets which contain more than one unknown symbol as in GC, NeMo is able to demodulate any number of unknown OM symbols through a look-up table. The demodulation complexity of NeMo is mainly determined by searching the look-up table. Suppose that the size of the constellation of OM symbol is  . Then, the complexity of the exhaustive search is
. Then, the complexity of the exhaustive search is  . The constellation size for OM symbols is typically small, for example, constellation size
. The constellation size for OM symbols is typically small, for example, constellation size  (BPSK) and
(BPSK) and  (QPSK) are usually adopted. Therefore, the demodulation complexity is mainly determined by the distribution of the effective degree of received NM symbol. Later we will use simulation to illustrate the distribution of the effective degrees at the sink.
(QPSK) are usually adopted. Therefore, the demodulation complexity is mainly determined by the distribution of the effective degree of received NM symbol. Later we will use simulation to illustrate the distribution of the effective degrees at the sink.
4.6. Regenerative NeMo
So far NeMo requires no demodulation at each node. Thus, in the following, we name it nonregenerative NeMo. However, this may be too pessimistic in some scenarios and cannot increase persistence "efficiently and aggressively" since it discards overlapping NM symbols even when they contain new OM symbols. In the following, we propose a variation of NeMo, namely regenerative NeMo, which is able to exploit the tradeoff between computational resources and performance.
In contrast to nonregenerative NeMo, in regenerative NeMo nodes will demodulate the NM symbol in each incoming packet into OM symbols (the demodulation procedure is the same as the one described in Section 4.5) and only keep the ones which have not been stored at the node. Note that here the nodes only store OM symbols. When a node decides to exchange packets, it will modulate all the OM symbols it stores into an NM symbol and send it to the randomly picked neighbor as

where  is the
is the  th entry of a vector with length
th entry of a vector with length  ,
,  is the power normalizer, and
is the power normalizer, and  's are the selected OM symbols.
's are the selected OM symbols.
Note that the demodulation complexity is determined by the degree of the NM symbols  . Therefore, a nonsink node may not be able to afford demodulating NM symbols with unbounded degrees and have to set a constraint on the maximal degree (denoted by
. Therefore, a nonsink node may not be able to afford demodulating NM symbols with unbounded degrees and have to set a constraint on the maximal degree (denoted by  ) of an NM symbol. With a
) of an NM symbol. With a  setting, the procedure of regenerative NeMo is modified as follows.
setting, the procedure of regenerative NeMo is modified as follows.
Suppose that a node receives an NM symbol  with effective degree
with effective degree  and it has
and it has  (
( ) OM symbols stored (including the local reading).
) OM symbols stored (including the local reading).
-
(i)
If
 , the node will discard the arrival since it does not have enough resource to afford demodulation of
, the node will discard the arrival since it does not have enough resource to afford demodulation of  .
. -
(ii)
If
 , the node demodulates
, the node demodulates  into
into 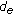 new OM symbols and then randomly replaces one OM symbol among the
new OM symbols and then randomly replaces one OM symbol among the  OM symbols received with its local reading. These
OM symbols received with its local reading. These 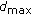 OM symbols will be saved in the memory and other symbols in the memory will be discarded.
OM symbols will be saved in the memory and other symbols in the memory will be discarded. -
(iii)
If
 and
and  , after demodulation, the node will randomly pick
, after demodulation, the node will randomly pick  symbols from the
symbols from the  nonlocal OM symbols, and save them with the local reading and
nonlocal OM symbols, and save them with the local reading and  newly received OM symbols. The other OM symbols in the memory are discarded.
newly received OM symbols. The other OM symbols in the memory are discarded. -
(iv)
Otherwise (
 ), the node just saves
), the node just saves  OM symbols in the memory.
OM symbols in the memory.
In any case, the node only stores up to  OM symbols in its memory. Whenever there is a chance for transmission, the node just modulates the OM symbols in its memory into one NM symbol as in (8) and sends it out.
OM symbols in its memory. Whenever there is a chance for transmission, the node just modulates the OM symbols in its memory into one NM symbol as in (8) and sends it out.
In summary, the general rules for regenerative NeMo are: (i) giving the newly received OM symbols and local reading higher priority to be stored and transmitted in the next round so that the new data have more chances to be circulated as soon as possible; and (ii) discarding the old OM symbols in the memory in order to limit storage space usage and search complexity.
We can further demodulate a subset of the incoming NM symbols selectively (e.g., random selection or thresholding on the degree of NM symbol) in order to achieve different tradeoffs between computational complexity and performance in different environments. In this sense, the nonregenerative version can be viewed as a special case of regenerative NeMo.
5. Performance Evaluations
We have introduced the proposed NeMo design with some assumptions described in Section 3.1. In this section, we adopt computer simulations to evaluate the performance of NeMo. For the sake of comparison, the performance of the GC in [13] is also provided.
5.1. Optimal Case
Let us first evaluate the optimal cases for NeMo, that is, the upper bound of the persistence performance. As shown in (5) and (8), NeMo combines two NM symbols with degrees  and
and  to generate a new NM symbol of degree
to generate a new NM symbol of degree  . Each node aggressively increases the degree of its NM symbol no matter nonregenerative or regenerative NeMo is adopted. Suppose at the current exchange round, all NM symbols at the nodes of the network have degree
. Each node aggressively increases the degree of its NM symbol no matter nonregenerative or regenerative NeMo is adopted. Suppose at the current exchange round, all NM symbols at the nodes of the network have degree  (or
(or  OM symbols). Then after one exchange round, the degree of all NM symbols will be increased to as high as
OM symbols). Then after one exchange round, the degree of all NM symbols will be increased to as high as  when the new arrival contains completely new symbols (denoted by optimal case). Assume at the beginning (round
when the new arrival contains completely new symbols (denoted by optimal case). Assume at the beginning (round  ), all nodes only have one OM symbol (or can be seen as NM symbol of degree
), all nodes only have one OM symbol (or can be seen as NM symbol of degree  ), the degree of all the NM symbols will become
), the degree of all the NM symbols will become  after
after  exchanges under the optimal case. Therefore the maximal number of OM symbols recovered at the sink after
exchanges under the optimal case. Therefore the maximal number of OM symbols recovered at the sink after  exchange rounds is
exchange rounds is  . Considering at most
. Considering at most  OM symbols exist in an
OM symbols exist in an  -node network, the upper bound of the persistence after
-node network, the upper bound of the persistence after  rounds is thus
rounds is thus  .
.
If we bound the degree of NM symbols at each node by  , the upper bound on the persistence after
, the upper bound on the persistence after  exchanges becomes
exchanges becomes

In Figure 3, we plot the optimal persistence curves with different  for a network of
for a network of  nodes. Different from GC, the optimal persistence curves with
nodes. Different from GC, the optimal persistence curves with  can increase faster than linear with slope
can increase faster than linear with slope  . For example, when
. For example, when  , the persistence rate is
, the persistence rate is  which increases with slope
which increases with slope  .
.
The numerical evaluation setup for our NeMo technique is described as follows. The network is generated by randomly distributing  nodes in a
nodes in a  square area. One sink node is also randomly placed in the network to collect the information but does not generate its own reading. Differing from the related works [13, 22, 25], we consider the sink as a normal node which does not send out any packets. Since no node knows where the sink is, the sink will not send out requests to its neighbors but simply wait for random deliveries. The radius of the neighborhood for each of these
square area. One sink node is also randomly placed in the network to collect the information but does not generate its own reading. Differing from the related works [13, 22, 25], we consider the sink as a normal node which does not send out any packets. Since no node knows where the sink is, the sink will not send out requests to its neighbors but simply wait for random deliveries. The radius of the neighborhood for each of these  nodes is
nodes is  . BPSK modulation is employed for OM symbols generated at each node. Also, symmetric link is assumed between each pair of nodes within the transmission range. On MAC layer, we adopt slotted transmissions (i.e., the time is divided into exchange rounds), and collisions are possible at each node but the sink can resolve collisions. The probability that each node transmits its packet at the beginning of each exchange round is fixed as
. BPSK modulation is employed for OM symbols generated at each node. Also, symmetric link is assumed between each pair of nodes within the transmission range. On MAC layer, we adopt slotted transmissions (i.e., the time is divided into exchange rounds), and collisions are possible at each node but the sink can resolve collisions. The probability that each node transmits its packet at the beginning of each exchange round is fixed as  .
.
Based on this network setup, we compare the data persistence obtained by simulating our NeMo, GC, and no coding on the network. No coding is a scheme in which nodes exchange an OM symbol or a codeword without any further modulation or coding. Because the network is random and the packet forwarding is random, the persistence actually is a random number. Therefore, we illustrate the persistence in both average (as in all other references) and outage performance which are important to quantify the statistical property of persistence. More than  realizations of the random network are simulated to obtain the average persistence performance, while over
realizations of the random network are simulated to obtain the average persistence performance, while over  realizations are simulated to depict outage persistence curves.
realizations are simulated to depict outage persistence curves.
5.2. Average Persistence
Synchronization Issue
When the sensor nodes are deployed in emergent scenarios, such as fires, floods, or earthquakes, they must start collecting and transmitting data quickly, having little chance to synchronize among themselves. Also different sensors may get their readings at different times. Thus, here we study the effects of synchronousness. For the same simulation setup as Section 5.1, we set the starting time of every node to be randomly selected from  to
to  . Figure 4 shows the persistence as a function of exchange rounds for nonregenerative NeMo, regenerative NeMo (no
. Figure 4 shows the persistence as a function of exchange rounds for nonregenerative NeMo, regenerative NeMo (no  and
and  ), and GC (with a scheduled sink) when the nodes are not synchronized (
), and GC (with a scheduled sink) when the nodes are not synchronized ( and
and  ). We can see the performance of GC degrades dramatically though we adopted "scheduled sink" as in [13]. Again, this is because the optimal degree distribution, which is hard-coded into the nodes before their deployment, cannot maximize the decoding probability at the sink while the degree of a codeword is increased. However, NeMo does not have any requirement on synchronization and is much less affected by the asynchronism.
). We can see the performance of GC degrades dramatically though we adopted "scheduled sink" as in [13]. Again, this is because the optimal degree distribution, which is hard-coded into the nodes before their deployment, cannot maximize the decoding probability at the sink while the degree of a codeword is increased. However, NeMo does not have any requirement on synchronization and is much less affected by the asynchronism.
Collision Effects
As in most related works such as [13, 22, 25], a full-duplex network with perfect collision resolution is considered, for example, one node can exchange with multiple nodes at the same time. Here, we use this full-duplex scenario as a benchmark on the performance study. We plot the data persistence of nonregenerative NeMo, regenerative NeMo (no  and
and  ), and the GC in Figure 5(a). From the figure, we observe that the data persistence of GC cannot reach one if the sink follows the same protocol as a normal node ("GC, normal sink"). This is because the sink is not always chosen by the neighbors to exchange packets and thus the optimal degree distribution proposed in [13] is violated. However, NeMo still reaches persistence
), and the GC in Figure 5(a). From the figure, we observe that the data persistence of GC cannot reach one if the sink follows the same protocol as a normal node ("GC, normal sink"). This is because the sink is not always chosen by the neighbors to exchange packets and thus the optimal degree distribution proposed in [13] is violated. However, NeMo still reaches persistence  fast even with this normal sink. Even when GC performs scheduling at the sink ("GC, scheduled sink") as in [13], NeMo outperforms GC with much faster convergence speed. Regenerative NeMo converges faster than nonregenerative NeMo because it more aggressively collects new symbols at the expense of higher complexity. Regenerative NeMo with a degree constraint
fast even with this normal sink. Even when GC performs scheduling at the sink ("GC, scheduled sink") as in [13], NeMo outperforms GC with much faster convergence speed. Regenerative NeMo converges faster than nonregenerative NeMo because it more aggressively collects new symbols at the expense of higher complexity. Regenerative NeMo with a degree constraint  (with a normal sink), which is more practical given resource constrained networks, also performs much better than GC (with a normal sink) and no coding scheme.
(with a normal sink), which is more practical given resource constrained networks, also performs much better than GC (with a normal sink) and no coding scheme.
Now, we come back to the more practical setup—half-duplex transmission with collision. Figure 5(b) compares different schemes where collisions may happen in every node (including sink). Compared with collision resolution case, the persistence curves converge slower than the case in Figure 5(a). NeMo is quite robust to collision. Usually, the "perfect no collision" case in Figure 5(a) is too optimistic, while the "collision at every node" case in Figure 5(b) is too pessimistic. In Figure 5(c), we consider that only the sink is capable to resolve collisions while other nodes cannot. Here, we can see that NeMo performs similarly to the other two cases and outperforms GC. In the following, we just adopt this network setup unless otherwise mentioned.
5.3. Outage Analysis
To show the bandwidth efficiency of our designs, we now investigate the outage performance. The outage probability is defined as the probability that the network persistence is less than a certain threshold. We consider nonregenerative and regenerative NeMo, and plot the outage probability versus exchange rounds in Figure 6 by fixing the threshold persistence as  . We do not plot the outage curve for GC because it cannot reach
. We do not plot the outage curve for GC because it cannot reach  persistence as we can see in Figure 5(c). For the fixed threshold persistence, the design represented by the curve on the left has better outage performance than the one associated with the curve on the right, since the left curve achieves zero outage probability with fewer exchanges. From Figure 6, we find that regenerative NeMo with
persistence as we can see in Figure 5(c). For the fixed threshold persistence, the design represented by the curve on the left has better outage performance than the one associated with the curve on the right, since the left curve achieves zero outage probability with fewer exchanges. From Figure 6, we find that regenerative NeMo with  has the worst outage performance. This is because the NM symbol degrees are limited by
has the worst outage performance. This is because the NM symbol degrees are limited by  , and thus introduce a large "tail" in the pdf of persistence. It is clear that regenerative NeMo (no
, and thus introduce a large "tail" in the pdf of persistence. It is clear that regenerative NeMo (no  ) achieves the best outage performance (i.e., decay fastest) since the nodes decode received NM symbols and retain the new information, while in nonregenerative NeMo some new information will be dropped.
) achieves the best outage performance (i.e., decay fastest) since the nodes decode received NM symbols and retain the new information, while in nonregenerative NeMo some new information will be dropped.
5.4. Complexity Analysis
Usually, network nodes (e.g., sensors) have limited computing power. In NeMo, nodes need to perform modulations and/or demodulations described in Section 4. If the modulation/demodulation complexity is high, the node may lack timely response and be drained fast. In this subsection, we analyze the complexity of modulation and demodulation schemes at the sink and the other nodes. The complexity is evaluated by counting the number of arithmetic operations required for modulation/demodulation.
5.4.1. At the Sink
Effective degree is an important indicator on the complexity of demodulation. We first plot the cdf of the effective degrees of received NM symbols at the sink in Figure 7(a). The  -axis represents the effective degree and
-axis represents the effective degree and  -axis denotes the corresponding percentage of the received symbols which have effective degrees less than or equal to this degree. From the figure, we can see that the probability to demodulate a symbol with high effective degree is really low, since for most packets (>90% for nonregenerative NeMo and >85% for regenerative NeMo) received at the sink the degree is less than or equal to
-axis denotes the corresponding percentage of the received symbols which have effective degrees less than or equal to this degree. From the figure, we can see that the probability to demodulate a symbol with high effective degree is really low, since for most packets (>90% for nonregenerative NeMo and >85% for regenerative NeMo) received at the sink the degree is less than or equal to  . The reason that regenerative NeMo has higher effective degree than nonregenerative NeMo is that regenerative NeMo increases the degree more aggressively. Furthermore, we find that upper bounding the degree of NM symbols by
. The reason that regenerative NeMo has higher effective degree than nonregenerative NeMo is that regenerative NeMo increases the degree more aggressively. Furthermore, we find that upper bounding the degree of NM symbols by  can further reduce the percentage of high degrees. Therefore, we claim that the complexity of demodulation scheme of NeMo is fairly low.
can further reduce the percentage of high degrees. Therefore, we claim that the complexity of demodulation scheme of NeMo is fairly low.
The sink node demodulates incoming packets and stores the demodulated OM symbols in the memory. These OM symbols are used to cancel the effect of known symbols on the received NM symbol  of degree
of degree  to get a new NM symbol
to get a new NM symbol  of effective degree
of effective degree  . This requires
. This requires  adding and multiplying operations. Then, we compare all possible
adding and multiplying operations. Then, we compare all possible  vectors with
vectors with  to find a unique symbol vector, where
to find a unique symbol vector, where  is a constellation size. For each comparison, the sink performs
is a constellation size. For each comparison, the sink performs  adding and multiplying operations. Thus,
adding and multiplying operations. Thus,  operations are needed to demodulate one NM symbol at the sink. The demodulation complexity at the sink for different
operations are needed to demodulate one NM symbol at the sink. The demodulation complexity at the sink for different  when BPSK is employed is plotted in Figure 7(b). As
when BPSK is employed is plotted in Figure 7(b). As  becomes large, the sink receives NM symbols with higher degree and hence the complexity becomes higher due to exhaustive search for demodulation.
becomes large, the sink receives NM symbols with higher degree and hence the complexity becomes higher due to exhaustive search for demodulation.
5.4.2. At the Other Nodes
Non-regenerative NeMo does not require to demodulate at each node. The demodulation complexity of regenerative NeMo is the same as that at the sink. Typically, the normal nodes have less computing resource than the sink so that they will have more limited degree constraint.
Next we compare the modulation complexity for regenerative and nonregenerative NeMo. For regenerative NeMo, the modulation complexity depends on the number of OM symbols in the memory of the node. As shown in (8),  multiplications and
multiplications and  additions are required to modulate
additions are required to modulate  OM symbols. For nonregenerative NeMo, suppose that we want to modulate two NM symbols each of which is of degree
OM symbols. For nonregenerative NeMo, suppose that we want to modulate two NM symbols each of which is of degree  and
and  , respectively. According to (5), the node only needs
, respectively. According to (5), the node only needs  adding and multiplying operation no matter what
adding and multiplying operation no matter what  and
and  are. The node performs
are. The node performs  additional adding and multiplying operation when it adds its own information. Figure 7(c) plots the complexity curves for both regenerative and nonregenerative versions. We find they are close to each other and climb up slowly with the increase of
additional adding and multiplying operation when it adds its own information. Figure 7(c) plots the complexity curves for both regenerative and nonregenerative versions. We find they are close to each other and climb up slowly with the increase of  . Figure 7(c) also includes a demodulation curve for comparison. We can see that the complexity of modulation is orders of magnitude smaller than that of demodulation. This confirms the intuition that regenerative NeMo consumes more computing resource and the NM degree needs to be limited.
. Figure 7(c) also includes a demodulation curve for comparison. We can see that the complexity of modulation is orders of magnitude smaller than that of demodulation. This confirms the intuition that regenerative NeMo consumes more computing resource and the NM degree needs to be limited.
6. Implementation Issues
To this point, we have presented the NeMo under the ideal case with the assumptions in Section 3.1. To implement NeMo in a real network, we have to deal with a number of limitations and requirements arisen from a resource-constrained environment. In this section, we carefully investigate and evaluate the major implementation issues including limited communication and storage usage, and node failure, making NeMo feasible for real world applications.
6.1. Packet Overhead
As stated in Section 4, nodes exchange packets with each other, and a packet includes a packet header and an NM symbol as the payload. Since the processing of received packets are different for regenerative and nonregenerative NeMo, the corresponding design of the packet header is also different.
For nonregenerative NeMo, to determine the coefficients that are adopted to modulate the NM symbol, the packet header must include the information to design the vector  in (3) and the positions of coefficients adopted, since not all the elements of
in (3) and the positions of coefficients adopted, since not all the elements of  are used to modulate OM symbols. Because
are used to modulate OM symbols. Because  is uniquely determined by the modulator degree
is uniquely determined by the modulator degree  as shown in Section 4.2 and
as shown in Section 4.2 and  is always selected as
is always selected as  for nonregenerative NeMo, we only need
for nonregenerative NeMo, we only need  bits in the header to determine
bits in the header to determine  (and thus
(and thus  ). To indicate which elements of
). To indicate which elements of  are used, we can put the indices of all the adopted coefficients into the header, requiring
are used, we can put the indices of all the adopted coefficients into the header, requiring  bits. Notice that in this way we record the ordering information of the used elements, which is important for demodulation at the sink. Alternatively, we can have a
bits. Notice that in this way we record the ordering information of the used elements, which is important for demodulation at the sink. Alternatively, we can have a  -bit bit-map to indicate whether an element of
-bit bit-map to indicate whether an element of  is adopted (e.g., "1" at the
is adopted (e.g., "1" at the  th bit means the
th bit means the  th element is adopted). But this way loses the ordering information. The node ID overhead is the same as the one in GC [13].
th element is adopted). But this way loses the ordering information. The node ID overhead is the same as the one in GC [13].
In general, the header design is not unique [13], we use the first two bits of the header to signify which format is used in this packet. Besides, we use the following  bits to represent
bits to represent  , which can support a maximum
, which can support a maximum  as
as  . The next
. The next  bits (or
bits (or  bits if
bits if  is set) are dedicated to signify the degree of the packet.
is set) are dedicated to signify the degree of the packet.
For regenerative NeMo, we do not need to provide the information of modulation coefficients, since the coefficients are uniquely determined by the degree of the packet. Therefore, only the node IDs are needed. So we only need to record the sequence of the related source node IDs in the packet header.
We simulate random networks in a  square area with the radius of the neighborhood of a node
square area with the radius of the neighborhood of a node  and compare the average length of packet headers for GC and NeMo. The average in bits is provided in Table 2. For all the schemes, the sink works as a normal node (not scheduled sink) as we described before. The average packet overhead for NeMo is obtained when persistence
and compare the average length of packet headers for GC and NeMo. The average in bits is provided in Table 2. For all the schemes, the sink works as a normal node (not scheduled sink) as we described before. The average packet overhead for NeMo is obtained when persistence  is achieved, while GC only achieves around
is achieved, while GC only achieves around  during the same time period.
during the same time period.
From Table 2, we can see that for all the schemes, the larger the network size, the longer the packet header. This is due to the increase of symbols in the modulation/coding. Among them the nonregenerative NeMo requires the longest header because both the source node IDs and the coefficients information need to be recorded. Furthermore, for the regenerative NeMo, the  setting suppresses the increase of the packet overhead a lot since the number of both source nodes and coefficients is upper bounded. We also find that with
setting suppresses the increase of the packet overhead a lot since the number of both source nodes and coefficients is upper bounded. We also find that with  the header does not increase much (from
the header does not increase much (from  to
to  ) when the network size is doubled. This is because the length becomes same for every transmission after the degree of an NM symbol reaches
) when the network size is doubled. This is because the length becomes same for every transmission after the degree of an NM symbol reaches  . Compared to GC, our nonregenerative NeMo has longer packet header in the time period of the simulation. However, considering the low persistence rate and much longer time GC requires to achieve the persistence
. Compared to GC, our nonregenerative NeMo has longer packet header in the time period of the simulation. However, considering the low persistence rate and much longer time GC requires to achieve the persistence  , the nonregenerative NeMo actually has the less total overhead.
, the nonregenerative NeMo actually has the less total overhead.
6.2. Waveform Storage and Noise Effect
To make NeMo work well in a resource-constrained system, memory usage is an important issue. Usually the distributed devices (e.g., a sensor) only have very limited memory space such that not all the received information can be stored. In other words, for practical implementation in a real network, we want the memory usage to be as few as possible. In the following, we discuss how the node stores its packet to maximize the efficiency of memory usage.
For nonregenerative NeMo, besides the coefficient and node ID information for constructing the packet header (discussed in Section 4.1) when transmitting, we need to store the NM symbol to be transmitted (as the payload). As shown in (5), NM symbols are complex numbers so that we need to apply finite bits with either floating-point arithmetic or fixed-point arithmetic to represent them. Although the precision is low, the fixed-point representation is usually preferred because of its simplicity on hardware implementation. Note that, no matter which representation is adopted, quantization noise is introduced. Furthermore, packet errors may be introduced and propagate in the network. We will show that only with a small number of bits, the NeMo works very well numerically.
The network setup is the same as that in Section 5. We adopt fixed-point arithmetics with  integer bits and
integer bits and  fractional bits to store NM symbols in the memory. Figure 8 depicts the error rate of recovered OM symbols at the sink as a function of exchange rounds when
fractional bits to store NM symbols in the memory. Figure 8 depicts the error rate of recovered OM symbols at the sink as a function of exchange rounds when  for nonregenerative NeMo. Three curves are plotted for
for nonregenerative NeMo. Three curves are plotted for  combinations
combinations  ,
,  , and
, and  , respectively. We find that for
, respectively. We find that for  and
and  combinations, the error rate increases quickly in the first a few rounds and keeps the same level after that. This means the quantization error does not deteriorate over time. We also find that with the increase of memory usage, the error rate decreases dramatically. When the fixed-point representation with
combinations, the error rate increases quickly in the first a few rounds and keeps the same level after that. This means the quantization error does not deteriorate over time. We also find that with the increase of memory usage, the error rate decreases dramatically. When the fixed-point representation with  combination is adopted, the performance is the same as that of the ideal case, that is, no error happens at the sink. Similar claims hold for regenerative NeMo.
combination is adopted, the performance is the same as that of the ideal case, that is, no error happens at the sink. Similar claims hold for regenerative NeMo.
Here, we reveal tradeoffs of NeMo on persistence rate, memory usage, and complexity. If more bits are adopted, the memory usage and complexity are higher, but persistence rate is also higher. The trigger of these tradeoffs is  . These also show that NeMo is independent from physical layer modulation once the waveforms are stored and operated as bits. Therefore, the selection of
. These also show that NeMo is independent from physical layer modulation once the waveforms are stored and operated as bits. Therefore, the selection of  should depend on the network resources (e.g., complexity, delay constraint), but not on the physical layer noise and link quality.
should depend on the network resources (e.g., complexity, delay constraint), but not on the physical layer noise and link quality.
6.3. Node Failure
We want to make our scheme effective and robust in a resource-constrained and disaster-prone environment. Here we evaluate our NeMo in two types of scenarios: (i) random failure, where every node randomly dies due to the limited resource (e.g., battery power); and (ii) regional failure, where the network or its parts may be destroyed or affected in some way. For example, in the event of fire, flood, or earthquake, the nodes in a certain region may stop functioning simultaneously.
6.3.1. Random Failure
Since transmissions consume much more power than receptions we assume the battery energy will be used up after a certain number of transmissions (denoted by  ). The simulation setup is the same as that in Section 5.
). The simulation setup is the same as that in Section 5.  is set to
is set to  and
and  , respectively. The persistence under this scenario is plotted in Figure 9(a). From the figure, we can see that when
, respectively. The persistence under this scenario is plotted in Figure 9(a). From the figure, we can see that when  , the NeMo (both nonregenerative and regenerative) is not impacted much since they converge very fast (close to persistence 1 before
, the NeMo (both nonregenerative and regenerative) is not impacted much since they converge very fast (close to persistence 1 before  rounds). When
rounds). When  , the achieved persistence decreases since a portion of symbols have not obtained the opportunity to propagate to the active areas. The
, the achieved persistence decreases since a portion of symbols have not obtained the opportunity to propagate to the active areas. The  constraint worsens the performance.
constraint worsens the performance.
6.3.2. Regional Failure
We simulate this scenario by disabling part of the network at the time of disaster. Suppose that  is the exchange round when the disaster happens, and the nodes within distance
is the exchange round when the disaster happens, and the nodes within distance  from a randomly located disaster center will stop functioning and all the links connecting them fail together. In Figure 9(b), we plot data persistence as a function of the disaster radius
from a randomly located disaster center will stop functioning and all the links connecting them fail together. In Figure 9(b), we plot data persistence as a function of the disaster radius  for
for  and
and  , respectively. Similar to the observed in the random case, when
, respectively. Similar to the observed in the random case, when  , both regenerative and nonregenerative NeMo (their curves are overlapped in the figure.) achieve the perfect persistence regardless of the disaster radius due to the fast convergence speed of NeMo. But if there is
, both regenerative and nonregenerative NeMo (their curves are overlapped in the figure.) achieve the perfect persistence regardless of the disaster radius due to the fast convergence speed of NeMo. But if there is  constraint, the achieved persistence decreases when the disaster radius increases. Again, we observe that more symbols are recovered at the sink for a disaster that happened at
constraint, the achieved persistence decreases when the disaster radius increases. Again, we observe that more symbols are recovered at the sink for a disaster that happened at  than that at
than that at  .
.
7. Experiment Results
We carry out an experiment with the software-defined radio (SDR) to demonstrate the feasibility of NeMo in practice. Both the transmitter and the receiver of SDR are implemented by RFX daughterboards as in [34], which is a Universal Software Radio Peripheral (USRP) [35]. Channel coding is not applied in this experiment. Signal processing modules such as modulation and demodulation are implemented in Matlab. The square-root raised cosine pulse shaping filter is adopted, and the symbol duration is
daughterboards as in [34], which is a Universal Software Radio Peripheral (USRP) [35]. Channel coding is not applied in this experiment. Signal processing modules such as modulation and demodulation are implemented in Matlab. The square-root raised cosine pulse shaping filter is adopted, and the symbol duration is  , where
, where  is the sampling period. Complex samples are passed to the transmitter, where they are converted to an analog signal by the digital to analog converter, upconverted to the carrier frequency
is the sampling period. Complex samples are passed to the transmitter, where they are converted to an analog signal by the digital to analog converter, upconverted to the carrier frequency  MHz, and then transmitted through a wireless channel. This process is inverted at the receiver.
MHz, and then transmitted through a wireless channel. This process is inverted at the receiver.
For the network setup,  sensors/nodes and one sink node are placed randomly in a
sensors/nodes and one sink node are placed randomly in a  square area as in Section 5. The radius of the neighborhood of each node is
square area as in Section 5. The radius of the neighborhood of each node is  . The OM symbols generated at each node is BPSK modulated as
. The OM symbols generated at each node is BPSK modulated as  or
or  . The slotted transmissions with collisions are considered. The probability that each node transmits its packet at the beginning of each exchange round is fixed as
. The slotted transmissions with collisions are considered. The probability that each node transmits its packet at the beginning of each exchange round is fixed as  . We set
. We set  for both nonregenerative and regenerative NeMo and assume that the sink operates as a normal node. Here we also give nonregenerative NeMo an upper bound on the modulation degree due to the unavoidable noise effect in the real environment.
for both nonregenerative and regenerative NeMo and assume that the sink operates as a normal node. Here we also give nonregenerative NeMo an upper bound on the modulation degree due to the unavoidable noise effect in the real environment.
The communications among the  nodes are simulated in Matlab, while the transmission from one neighbor (transmitter) to the sink (receiver) is implemented using two RFX
nodes are simulated in Matlab, while the transmission from one neighbor (transmitter) to the sink (receiver) is implemented using two RFX daughterboards. The average persistence of nonregenerative NeMo and regenerative NeMo is depicted in Figure 10. The performance of GC is also given as a reference. From the figure, we can see that both regenerative and nonregenerative NeMo approach persistence
daughterboards. The average persistence of nonregenerative NeMo and regenerative NeMo is depicted in Figure 10. The performance of GC is also given as a reference. From the figure, we can see that both regenerative and nonregenerative NeMo approach persistence  (even with
(even with  ) in a practical environment quickly, while GC only collects around
) in a practical environment quickly, while GC only collects around  information. This confirms our observation in simulation. We also compare the complexity of NeMo and GC in Table 3 by measuring the CPU time required to achieve persistence
information. This confirms our observation in simulation. We also compare the complexity of NeMo and GC in Table 3 by measuring the CPU time required to achieve persistence  ,
,  , and
, and  , respectively. Note that the computational time to generate the network and the neighbor list is not included. From the table we can see that regenerative NeMo in general consumes more time than nonregenerative NeMo because of the demodulation complexity at each node. GC requires less time to achieve low persistence thanks to its binary operations. As persistence increases, GC becomes comparable with NeMo since NeMo reaches higher persistence faster. In addition, GC never reaches persistence higher than
, respectively. Note that the computational time to generate the network and the neighbor list is not included. From the table we can see that regenerative NeMo in general consumes more time than nonregenerative NeMo because of the demodulation complexity at each node. GC requires less time to achieve low persistence thanks to its binary operations. As persistence increases, GC becomes comparable with NeMo since NeMo reaches higher persistence faster. In addition, GC never reaches persistence higher than  .
.
8. Conclusion
In this paper, we have proposed a new approach—network modulation (NeMo) to significantly enhance data persistence for large-scale distributed systems. Based on algebraic number theory, NeMo mixes data at intermediate network nodes and meanwhile guarantees the symbol recovery at the sink(s). In contrast to other existing methods, NeMo works for asynchronous nodes in heterogeneous networks, and also boosts data persistence over linear convergence speed. We have evaluated NeMo with different performance criteria (such as modulation and demodulation complexity, convergence speed, and memory usage). Both simulation and experiment results show effectiveness of NeMo. NeMo reveals a new regime for random network transmissions. Some future research directions include enhancing network lifetime by taking into account nodes with finite energy, designing NeMo for nodes with unequal importance and/or mobility, and investigating NeMo over wireless fading environments.
References
Heinzelman WR, Kulik J, Balakrishnan H: Adaptive protocols for information dissemination in wireless sensor networks. Proceedings of the 5th Annual ACM/IEEE International Conference on Mobile Computing and Networking (MOBICOM '99), August 1999, Seattle, Wash, USA 174-185.
Al-Karaki JN, Kamal AE: Routing techniques in wireless sensor networks: a survey. IEEE Wireless Communications 2004, 11(6):6-27. 10.1109/MWC.2004.1368893
Perkins C, Bhagwat P: Highly dynamic destination-sequenced distance-vector routing (DSDV) for mobile computers. Proceedings of the ACM Conference on Applications, Technologies, Architectures, and Protocols for Computer Communication (SIGCOMM '94), August-September 1994, London, UK 234-244.
Johnson D, Maltz D: Dynamic source routing in ad-hoc wireless networks. Proceedings of the ACM Conference on Applications, Technologies, Architectures, and Protocols for Computer Communication (SIGCOMM '96), August 1996, Stanford, Calif, USA 153-181.
Perkins C, Royer EM: Ad-hoc on-demand distance vector routing. Proceedings of the 2nd IEEE Workshop on Mobile Computing Systems and Applications, February 1999, New Orleans, La, USA 90-100.
Karp B, Kung HT: GPSR: greedy perimeter stateless routing for wireless networks. Proceedings of the 6th Annual International Conference on Mobile Computing and Networking (MOBICOM '00), August 2000, Boston, Mass, USA 243-254.
Das SM, Pucha H, Hu YC: MicroRouting: a scalable and robust communication paradigm for sparse ad hoc networks. Proceedings of the 19th IEEE International Parallel and Distributed Processing Symposium (IPDPS '05), April 2005, Denver, Colo, USA
Acedanski S, Deb S, Médard M, Koetter R: How good is random linear coding based distributed networked storage? Proceedings of the 1st Workshop on Network Coding, Theory, and Applications, April 2005, Riva del Garda, Italy
Dimakis AG, Godfrey PB, Wainwright MJ, Ramchandran K: Network coding for distributed storage systems. Proceedings of the 26th IEEE International Conference on Computer Communications (INFOCOM '07), May 2007, Anchorage, Alaska, USA 2000-2008.
Dimakis AG, Wang J, Ramchandran K: Unequal growth codes: intermediate performance and unequal error protection for video streaming. Proceedings of the IEEE Workshop on Multimedia Signal Processing, October 2007, Chania, Greece 107-110.
Dimakis AG, Prabhakaran V, Ramchandran K: Ubiquitous access to distributed data in large-scale sensor networks through decentralized erasure codes. Proceedings of the 4th International Symposium on Information Processing in Sensor Networks (IPSN '05), April 2005, Los Angeles, Calif, USA 111-117.
Jiang A: Network coding for joint storage and transmission with minimum cost. Proceedings of the IEEE International Symposium on Information Theory (ISIT '06), July 2006, Seattle, Wash, USA 1359-1363.
Kamra A, Misra V, Feldman J, Rubenstein D: Growth codes: maximizing sensor network data persistence. Proceedings of the ACM Conference on Applications, Technologies, Architectures, and Protocols for Computer Communication (SIGCOMM '06), September 2006, Pisa, Italy 255-266.
Byers JW, Luby M, Mitzenmacher M, Rege A: A digital fountain approach to reliable distribution of bulk data. Proceedings of the ACM Conference on Applications, Technologies, Architectures, and Protocols for Computer Communication (SIGCOMM '98), August-September 1998, Vancouver, Canada 56-67.
Shannon CE: A mathematical theory of communication. Bell System Technical Journal 1948, 27: 379-423, 623–656.
Ahlswede R, Cai N, Li S-YR, Yeung RW: Network information flow. IEEE Transactions on Information Theory 2000, 46(4):1204-1216. 10.1109/18.850663
Li S-YR, Yeung RW, Cai N: Linear network coding. IEEE Transactions on Information Theory 2003, 49(2):371-381.
Ho T, Koetter R, Médard M, Karger D, Effros M: The benefits of coding over routing in a randomized setting. Proceedings of IEEE International Symposium on Information Theory (ISIT '03), June-July 2003, Yokohama, Japan 227-234.
Wang D, Zhang Q, Liu J: Partial network coding: theory and application for continuous sensor data collection. Proceedings of the 14th IEEE International Workshop on Quality of Service (IWQoS '06), June 2006, New Haven, Conn, USA 93-101.
Katti S, Katabi D, Hu W, Rahul H, Médard M: The importance of being opportunistic: practical network coding for wireless environments. Proceedings of the Annual Allerton Conference on Communication, Control, and Computing, September 2005, Allerton, Ill, USA
Katti S, Rahul H, Hu W, Katabi D, Médard M, Crowcroft J: XORs in the air: practical wireless network coding. Proceedings of the ACM Conference on Applications, Technologies, Architectures, and Protocols for Computer Communication (SIGCOMM '06), September 2006, Pisa, Italy 243-254.
Munaretto D, Widmer J, Rossi M, Zorzi M: Network coding strategies for data persistence in static and mobile sensor networks. Proceedings of the International Workshop on Wireless Networks: Communication, Cooperation and Competition, April 2007, Limassol, Cyprus 1-8.
Liu J, Liu Z, Towsley D, Xia CH: Maximizing the data utility of a data archiving & querying system through joint coding and scheduling. Proceedings of the 6th International Symposium on Information Processing in Sensor Networks (IPSN '07), April 2007, Cambridge, Mass, USA 244-253.
Lin Y, Li B, Liang B: Differentiated data persistence with priority random linear codes. Proceedings of the IEEE International Conference on Distributed Computing Systems (ICDCS '07), June 2007, Toronto, Canada 47-47.
Karande S, Misra K, Radha H: Natural growth codes: partial recovery under random network coding. Proceedings of the 42nd Annual Conference on Information Sciences and Systems (CISS '08), March 2008, Princeton, NJ, USA 540-544.
Koetter R, Médard M: An algebraic approach to network coding. IEEE/ACM Transactions on Networking 2003, 11(5):782-795. 10.1109/TNET.2003.818197
Ebrahimi J, Fragouli C: Algebraic algorithms for vector network coding. 2010, http://infoscience.epfl.ch/record/144144
Wicker SB: Reed-Solomon Codes and Their Applications. IEEE Press, Piscataway, NJ, USA; 1994.
Luby M: LT codes. Proceedings of the IEEE Symposium on the Foundations of Computer Science (FOCS '02), November 2002, Vancouver, Canada 271-271.
Gallager RG: Low-density parity-check codes. IEEE Transactions on Information Theory 1962, 8(1):21-28. 10.1109/TIT.1962.1057683
Berrou C, Glavieux A, Thitimajshima P: Near Shannon limit error-correcting coding and encoding: turbo-codes. Proceedings of the IEEE International Conference on Communications (ICC '93), May 1993, Geneva, Switzerland 1064-1070.
Li L, Alimi R, Ramjee R, Shi J, Sun Y, Viswanathan H, Yang YR: Superposition coding for wireless mesh networks. Proceedings of the 13th Annual ACM International Conference on Mobile Computing and Networking (MobiCom '07), September 2007, Montreal, Canada 330-333.
Xin Y, Wang Z, Giannakis GB: Space-time diversity systems based on linear constellation precoding. IEEE Transactions on Wireless Communications 2003, 2(2):294-309. 10.1109/TWC.2003.808970
Katti S, Gollakota S, Katabi D: Embracing wireless interference: analog network coding. Proceedings of the ACM Conference on Applications, Technologies, Architectures, and Protocols for Computer Communication (SIGCOMM '07), August 2007, Kyoto, Japan 397-408.
Ettus Research LLC : Universal software radio peripheral. http://www.ettus.com/
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Ma, X., Choi, G. & Zhang, W. Network Modulation: An Algebraic Approach to Enhancing Network Data Persistence. J Wireless Com Network 2010, 141340 (2010). https://doi.org/10.1155/2010/141340
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/141340


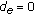 , the sink simply discards the packet with NM symbol
, the sink simply discards the packet with NM symbol  since all the OM symbols contained in
since all the OM symbols contained in  are known.
are known. , the only unknown OM symbol can be obtained by subtracting other demodulated OM symbols from
, the only unknown OM symbol can be obtained by subtracting other demodulated OM symbols from  .
. , we first cancel the known OM symbols from
, we first cancel the known OM symbols from  and obtain an NM symbol modulated by
and obtain an NM symbol modulated by  unknown symbols finally. Then, by exhaustively searching over all possible
unknown symbols finally. Then, by exhaustively searching over all possible  OM symbol vectors which have been saved in a look-up table, we can determine the rest unknown OM symbols. Due to the design of
OM symbol vectors which have been saved in a look-up table, we can determine the rest unknown OM symbols. Due to the design of  in Section 4.2, a
in Section 4.2, a  OM symbol vector can be uniquely determined given only one NM symbol.
OM symbol vector can be uniquely determined given only one NM symbol. , the node will discard the arrival since it does not have enough resource to afford demodulation of
, the node will discard the arrival since it does not have enough resource to afford demodulation of  .
. , the node demodulates
, the node demodulates  into
into 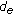 new OM symbols and then randomly replaces one OM symbol among the
new OM symbols and then randomly replaces one OM symbol among the  OM symbols received with its local reading. These
OM symbols received with its local reading. These 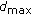 OM symbols will be saved in the memory and other symbols in the memory will be discarded.
OM symbols will be saved in the memory and other symbols in the memory will be discarded. and
and  , after demodulation, the node will randomly pick
, after demodulation, the node will randomly pick  symbols from the
symbols from the  nonlocal OM symbols, and save them with the local reading and
nonlocal OM symbols, and save them with the local reading and  newly received OM symbols. The other OM symbols in the memory are discarded.
newly received OM symbols. The other OM symbols in the memory are discarded. ), the node just saves
), the node just saves  OM symbols in the memory.
OM symbols in the memory.
 .s
.s





 and
and  ; (b) Regional failure when
; (b) Regional failure when  and
and  .
.