- Research Article
- Open access
- Published:
SSC Diversity Receiver over Correlated 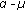 Fading Channels in the Presence of Cochannel Interference
Fading Channels in the Presence of Cochannel Interference
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 142392 (2010)
Abstract
This paper studies the performances of a dual-branch switched-and-stay combining (SSC) diversity receiver, operating over correlated  fading in the presence of cochannel interference (CCI). Very useful, novel, infinite series expressions are obtained for the output signal to interference ratio's (SIR's) probability density function (PDF) and cumulative distribution function (CDF). The performance analysis is based on an outage probability (OP) and an average bit error probability (ASEP) criteria. ASEP is efficiently evaluated for modulation schemes such as noncoherent frequency-shift keying (NCFSK) and binary differentially phase-shift keying (BDPSK). The effects of various parameters, such as input SIR unbalance, the level of correlation between received desired signals and interferences, nonlinearity of the environment, and fading severity on systems performances are graphically presented and analyzed.
fading in the presence of cochannel interference (CCI). Very useful, novel, infinite series expressions are obtained for the output signal to interference ratio's (SIR's) probability density function (PDF) and cumulative distribution function (CDF). The performance analysis is based on an outage probability (OP) and an average bit error probability (ASEP) criteria. ASEP is efficiently evaluated for modulation schemes such as noncoherent frequency-shift keying (NCFSK) and binary differentially phase-shift keying (BDPSK). The effects of various parameters, such as input SIR unbalance, the level of correlation between received desired signals and interferences, nonlinearity of the environment, and fading severity on systems performances are graphically presented and analyzed.
1. Introduction
Various techniques for reducing the fading effects and the influence of the cochannel interference (CCI) are used in wireless communication systems [1]. The two main goals of the diversity techniques are  upgrading the transmission reliability without increasing transmission power and bandwidth and
upgrading the transmission reliability without increasing transmission power and bandwidth and  increasing the channel capacity. Space diversity is an efficient method for amelioration of system's quality of service (QoS) when multiple receiver antennas are used. There are several principal types of combining techniques and division, that can be generally performed depending on the complexity restriction put on the communication system and the amount of channel state information available at the receiver.
increasing the channel capacity. Space diversity is an efficient method for amelioration of system's quality of service (QoS) when multiple receiver antennas are used. There are several principal types of combining techniques and division, that can be generally performed depending on the complexity restriction put on the communication system and the amount of channel state information available at the receiver.
However, switch and stay combining (SSC) is the least complex and can be used in conjunction with coherent, noncoherent, and differentially coherent modulation schemes. In general, with SSC diversity considered in this paper, the receiver selects a particular branch until its signal-to-noise ratio (SNR) drops below a predetermined threshold. When this happens, the combiner switches to another branch and stays there regardless of whether the SNR of that branch is above or below the predetermined threshold [1–3]. In fading environments as in cellular systems, where the level of CCI is sufficiently high as compared to the thermal noise, SSC selects a particular branch until its signal-to-interference ratio (SIR) drops below a predetermined threshold (SIR-based switched diversity). Then the combiner switches to another branch and stays there regardless of SIR of that branch. This type of diversity, in which switching is based on the SIR value, can be measured in real time both in base stations (uplink) and in mobile stations (downlink) using specific SIR estimators.
The multipath fading in wireless communications is modelled by several distributions including Weibull, Nakagami-m Hoyt, Rayleigh, and Rice. By considering two important phenomena inherent to radio propagation, namely, nonlinearity and clustering, the  -
- fading model was proposed and discussed in [4–7]. The model provides a very good fit to measured data over a wide range of fading conditions. The
fading model was proposed and discussed in [4–7]. The model provides a very good fit to measured data over a wide range of fading conditions. The  -
- distribution is written in terms of physicallybased fading parameters, namely,
distribution is written in terms of physicallybased fading parameters, namely,  and
and  . Roughly speaking,
. Roughly speaking,  is related to the nonlinearity of the environment, whereas
is related to the nonlinearity of the environment, whereas  is associated with the number of multipath clusters. The diversity reception over
is associated with the number of multipath clusters. The diversity reception over  -
- fading channels was previously discussed in [8–11].
fading channels was previously discussed in [8–11].
There is a number of papers concerning performance analysis of SSC receivers, for example, [12–15]. The performance analysis of SSC diversity receivers, operating over correlated Ricean fading satellite channels, can be found in [13], where the performance is evaluated based on a bunch of novel analytical formulae for the outage probability (OP), average symbol error probability (ASEP), channel capacity (CC), the amount of fading (AoF), and the average output SNR obtained in infinite series form. The similar performance analysis of the switched diversity receivers operating over correlated Weibull fading channels in terms of OP, ASEP, moments, and moment generating function (MGF) can be found in [14]. Reference [15] studies the performance of a dual-branch SSC diversity receiver with the switching decision based on SIR, operating over correlated Ricean fading channels in the presence of correlated Nakagami-m distributed CCI. Moreover to the best of author's knowledge, no analytical study of switch and stay combining involving assumed correlated  -
- fading for both desired signal and cochannel interference has been reported in the literature.
fading for both desired signal and cochannel interference has been reported in the literature.
In this paper, desired signal and CCI are considered to be affected by  -
- fading distribution, which is adequate for multipath waves, propagating in a nonhomogenous environment. An approach to the performance analyses of given SSC diversity receiver is presented. Effectiveness of any modulation scheme and the type of diversity used is studied thought evaluating the system's performance over the channel conditions. Infinite series expressions for probability distribution function (PDF) and cumulative distribution function (CDF) of the output SIR for SSC diversity are derived. Furthermore, infinite series expression for important performance measure, such as OP, is obtained. An OP is shown graphically for different system parameters. Using infinite series formulae, ASEP is efficiently evaluated for several modulation schemes such as noncoherent frequency-shift keying (NCFSK) and binary differentially phase-shift keying (BDPSK). This analysis has a high level of generality because
fading distribution, which is adequate for multipath waves, propagating in a nonhomogenous environment. An approach to the performance analyses of given SSC diversity receiver is presented. Effectiveness of any modulation scheme and the type of diversity used is studied thought evaluating the system's performance over the channel conditions. Infinite series expressions for probability distribution function (PDF) and cumulative distribution function (CDF) of the output SIR for SSC diversity are derived. Furthermore, infinite series expression for important performance measure, such as OP, is obtained. An OP is shown graphically for different system parameters. Using infinite series formulae, ASEP is efficiently evaluated for several modulation schemes such as noncoherent frequency-shift keying (NCFSK) and binary differentially phase-shift keying (BDPSK). This analysis has a high level of generality because  -
- fading distribution model includes as special cases other important distributions such as Weibull and Nakagami-m (therefore the one-sided Gaussian and Rayleigh are also special cases of it).
fading distribution model includes as special cases other important distributions such as Weibull and Nakagami-m (therefore the one-sided Gaussian and Rayleigh are also special cases of it).
2. System Model and Received Statistics
Independent fading assumes antenna elements in diversity systems to be placed sufficiently apart, which is not general case in practice due to insufficient spacing between antennas. When diversity system is applied on small terminals with multiple antennas, correlation arises between branches. Now, due to insufficient antennae spacing, desired signal envelopes  and
and  experience correlative
experience correlative  -
- fading, with joint distribution [5]:
fading, with joint distribution [5]:

Similarly, due to insufficient antennae spacing, envelopes of interference  and
and  are correlated with joint
are correlated with joint  -
- distribution [5]:
distribution [5]:

It is important to quote that  and
and  denote the desired and interfering signal power correlation coefficients defined as
denote the desired and interfering signal power correlation coefficients defined as  , and
, and  , respectively. For the desired signal with correlated envelopes
, respectively. For the desired signal with correlated envelopes  and the arbitrary power parameters
and the arbitrary power parameters  , connected with the nonlinearity of the environment,
, connected with the nonlinearity of the environment,  , explained in [5],
, explained in [5],  denote the
denote the  -root mean values of desired signal. Similarly
-root mean values of desired signal. Similarly  denote the
denote the  -root mean values of interferer signal. Parameters
-root mean values of interferer signal. Parameters  and
and  are associated with the number of multipath clusters through which desired and interference signals propagate, and they are defined in the terms of normalized variances as in [5, 11].
are associated with the number of multipath clusters through which desired and interference signals propagate, and they are defined in the terms of normalized variances as in [5, 11].  and
and  are, respectively, the covariance and variance operators, and
are, respectively, the covariance and variance operators, and  stands for Gamma function [16].
stands for Gamma function [16].  defines generalized Laguerre polynomial with the property of [17]
defines generalized Laguerre polynomial with the property of [17]

Let  and
and  represent the instantaneous SIR on the diversity branches, respectively [18]. The joint PDF of
represent the instantaneous SIR on the diversity branches, respectively [18]. The joint PDF of  and
and  and can be expressed by [18, 19]
and can be expressed by [18, 19]

Substituting (1), (2), and (3) in (4), we get

where  with
with

where  denotes
denotes  ,
,  denotes
denotes 


 denotes
denotes 
 , with
, with  denoting the Pochhammer symbol [16]. Derivation of this expression is presented in the appendix. Let
denoting the Pochhammer symbol [16]. Derivation of this expression is presented in the appendix. Let  represent the instantaneous SIR at the SSC output, and
represent the instantaneous SIR at the SSC output, and  the predetermined switching threshold for the both input branches. Following [20], the PDF of SIR is given by
the predetermined switching threshold for the both input branches. Following [20], the PDF of SIR is given by

where  , according to [20], can be expressed as
, according to [20], can be expressed as  . Moreover,
. Moreover,  can be expressed as infinite series
can be expressed as infinite series

 with
with  , being the Gaussian hypergeometric function [16], and
, being the Gaussian hypergeometric function [16], and

In the same manner, the  can be expressed as
can be expressed as

Similarly, the CDF of the SSC output SIR, that is, the  is given by [11, 20]
is given by [11, 20]

By substituting (5) in  and (10) in
and (10) in  and
and  can be expressed as the following infinite series, respectively,
can be expressed as the following infinite series, respectively,



with


The nested infinite sums in (8) and (12) converge for any defined value of the parameters  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  , and
, and  . Numbers of terms that need to be summed in (12) to achieve accuracy at the
. Numbers of terms that need to be summed in (12) to achieve accuracy at the  significant digit are presented in Table 1. As is shown in this table, the number of the terms that need to be summed to achieve a desired accuracy depends strongly on the correlation coefficient
significant digit are presented in Table 1. As is shown in this table, the number of the terms that need to be summed to achieve a desired accuracy depends strongly on the correlation coefficient  and
and  . The number of the terms increases as correlation coefficient increases. Convergence becomes slow and we need much more terms when
. The number of the terms increases as correlation coefficient increases. Convergence becomes slow and we need much more terms when  and
and  are higher and closer to 1. For the special cases of
are higher and closer to 1. For the special cases of  ,
,  , and for the special case of
, and for the special case of  ,
,  , we can evaluate CDF and PDF expressions for Weibull and for Nakagami-m desired signal and cochannel interference, respectively. This generality of CDF of output SIR for a number of fading distributions is the main contribution of our work.
, we can evaluate CDF and PDF expressions for Weibull and for Nakagami-m desired signal and cochannel interference, respectively. This generality of CDF of output SIR for a number of fading distributions is the main contribution of our work.
3. Outage Probability
Since OP is defined as probability that the instantaneous SIR of the system falls below a specified threshold value, it can be expressed in terms of the CDF of  , that is, as
, that is, as  , where
, where  is the specified threshold value. Using (11)–(15) the Pout performances results have been obtained. These results are presented in Figure 1, as the function of the normalized outage threshold (dB) for several values of
is the specified threshold value. Using (11)–(15) the Pout performances results have been obtained. These results are presented in Figure 1, as the function of the normalized outage threshold (dB) for several values of  ,
,  ,
,  ,
,  ,
,  , and
, and  . Normalized outage threshold (dB) is defined as being the average SIR's at the input branch of the balanced dual-branch switched-and-stay combiner, normalized by specified threshold value
. Normalized outage threshold (dB) is defined as being the average SIR's at the input branch of the balanced dual-branch switched-and-stay combiner, normalized by specified threshold value  . Results show that as the signal and interference correlation coefficients,
. Results show that as the signal and interference correlation coefficients,  and
and  , increase and normalized outage threshold decreases, OP increases.
, increase and normalized outage threshold decreases, OP increases.
4. Average Symbol Error Probability
The ASEP ( ) can be evaluated by averaging the conditional symbol error probability for a given SIR, that is,
) can be evaluated by averaging the conditional symbol error probability for a given SIR, that is,  , over the PDF of
, over the PDF of  , that is,
, that is,  [8]:
[8]:

where  depends on applied modulation scheme. For BDPSK and NCFSK modulation schemes the conditional symbol error probability for a given SIR threshold can be expressed by
depends on applied modulation scheme. For BDPSK and NCFSK modulation schemes the conditional symbol error probability for a given SIR threshold can be expressed by  , where
, where  for BDPSK and
for BDPSK and  for NCFSK [14]. Hence, substituting (7) into (17) gives the following ASEP expression for the considered dual-branch SSC receiver:
for NCFSK [14]. Hence, substituting (7) into (17) gives the following ASEP expression for the considered dual-branch SSC receiver:

Using the previously derived infinite series expressions, we present representative numerical performance evaluation results of the studied dual-branch SSC diversity receiver, such as ASEP in case of two modulation schemes, NCFSK and BDPSK. Applying (18) on BDPSK and NCFSK modulation schemes, the ASEP performance results have been obtained, for several values of  ,
,  ,
,  ,
,  ,
,  and
and  , as a function of the average SIRs at the input branches of the balanced dual-branch switched-and-stay combiner, that is,
, as a function of the average SIRs at the input branches of the balanced dual-branch switched-and-stay combiner, that is,  . These results are plotted in Figures 2 and 3. It is shown that while as the signal and interference correlation coefficients,
. These results are plotted in Figures 2 and 3. It is shown that while as the signal and interference correlation coefficients,  and
and  increase and the average SIR's at the at the input branches increase, the ASEP increases at the same time. Comparison of Figures 2 and 3 shows better performance of BDPSK modulation scheme versus NCFSK modulation scheme.
increase and the average SIR's at the at the input branches increase, the ASEP increases at the same time. Comparison of Figures 2 and 3 shows better performance of BDPSK modulation scheme versus NCFSK modulation scheme.
5. Conclusion
In this paper, the system performances of a dual-branch SSC diversity receiver over correlated  -
- channels are analyzed based on SIR. Fading between the diversity branches and between interferers is correlated and
channels are analyzed based on SIR. Fading between the diversity branches and between interferers is correlated and  -
- distributed. The complete statistics for the SSC output SIR is given in the infinite series expressions form, that is, PDF, CDF, and OP. Using these new formulae, ASEP was efficiently evaluated for some modulation schemes such as DPSK and NCFSK. The main contribution of this analysis for dualbranch signal combiner is that it has been done for a general case of
distributed. The complete statistics for the SSC output SIR is given in the infinite series expressions form, that is, PDF, CDF, and OP. Using these new formulae, ASEP was efficiently evaluated for some modulation schemes such as DPSK and NCFSK. The main contribution of this analysis for dualbranch signal combiner is that it has been done for a general case of  -
- (Generalized Gamma) distribution, which includes as special cases important other distributions such as Weibull and Nakagami-m (therefore, the One-Sided Gaussian and Rayleigh are also special cases of it), so our analysis has a high level of generality.
(Generalized Gamma) distribution, which includes as special cases important other distributions such as Weibull and Nakagami-m (therefore, the One-Sided Gaussian and Rayleigh are also special cases of it), so our analysis has a high level of generality.
References
Stuber GL: Mobile Communication. 2nd edition. Kluwer Academic Publishers, Boston, Mass, USA; 2001.
Lee WCY: Mobile Communications Engineering. Mc-Graw-Hill, New York, NY, USA; 2001.
Simon MK, Alouini MS: Digital Communication over Fading Channels. John Wiley & Sons, New York, NY, USA; 2005.
Yacoub MD:The
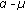 distribution: a physical fading model for the Stacy distribution. IEEE Transactions on Vehicular Technology 2007, 56(1):27-34.
distribution: a physical fading model for the Stacy distribution. IEEE Transactions on Vehicular Technology 2007, 56(1):27-34.De Souza RAA, Fraidenraich G, Yacoub MD:On the multivariate
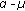 distribution with arbitrary correlation. Proceedings of International Telecommunications Symposium (ITS '06), September 2006, Fortaleza, Brazil 38-41.
distribution with arbitrary correlation. Proceedings of International Telecommunications Symposium (ITS '06), September 2006, Fortaleza, Brazil 38-41.Coulson AJ, Williamson AG, Vaughan RG: Improved fading distribution for mobile radio. IEE Proceedings: Communications 1998, 145(3):197-202. 10.1049/ip-com:19981991
Piboongungon T, Aalo VA, Iskander CD, Efthymoglou GP: Biyariate generalised gamma distribution with arbitrary fading parameters. Electronics Letters 2005, 41(12):709-710. 10.1049/el:20050435
Sagias NC, Mathiopoulos PT: Switched diversity receivers over generalized gamma fading channels. IEEE Communications Letters 2005, 9(10):871-873. 10.1109/LCOMM.2005.10026
Sagias NC, Karagiannidis GK, Mathiopoulos PT, Tsiftsis TA: On the performance analysis of equal-gain diversity receivers over generalized Gamma fading channels. IEEE Transactions on Wireless Communications 2006, 5(10):2967-2975.
Panić SR, Stefanović MČ, Mosić AV:Performance analyses of selection combining diversity receiver over
 Fading channels in the presence of co-channel interference. IET Communications 2009, 3(11):1769-1777. 10.1049/iet-com.2009.0023
Fading channels in the presence of co-channel interference. IET Communications 2009, 3(11):1769-1777. 10.1049/iet-com.2009.0023Bithas PS, Sagias NC, Tsiftsis TA: Performance analysis of dual-diversity receivers over correlated generalised Gamma fading channels. IET Communications 2008, 2(1):174-178. 10.1049/iet-com:20070207
Abu-Dayya AA, Beaulieu NC: Switched diversity on microcellular Ricean channels. IEEE Transactions on Vehicular Technology 1994, 43(4):970-976. 10.1109/25.330159
Bithas PS, Mathiopoulos PT: Performance analysis of SSC diversity receivers over correlated ricean fading satellite channels. EURASIP Journal on Wireless Communications and Networking 2007, 2007:-9.
Bithas PS, Mathiopoulos PT, Karagiannidis GK: Switched diversity receivers over correlated weibull fading channels. Proceedings of International Workshop on Satellite and Space Communications (IWSSC '06), September 2006, Madrid, Spain 143-147.
Bandjur DV, Stefanovic MC, Bandjur MV: Performance analysis of SSC diversity receiver over correlated Ricean fading channels in presence of co-channel interference. Electronics Letters 2008, 44(9):587-588. 10.1049/el:20080270
Gradshteyn I, Ryzhik I: Tables of Integrals, Series, and Products. Academic Press, London, UK; 1980.
, January 2009 http://mathworld.wolfram.com/
Karagiannidis GK: Performance analysis of SIR-based dual selection diversity over correlated Nakagami-m fading channels. IEEE Transactions on Vehicular Technology 2003, 52(5):1207-1216. 10.1109/TVT.2003.816612
Stefanović MČ, Milović DM, Mitić AM, Jakovljević MM: Performance analysis of system with selection combining over correlated Weibull fading channels in the presence of cochannel interference. International Journal of Electronics and Communications 2008, 62(9):695-700. 10.1016/j.aeue.2007.09.006
Ko Y-C: Analysis and optimization of switched diversity systems. IEEE Transactions on Vehicular Technology 2000, 49(5):1813-1831. 10.1109/25.892586
Author information
Authors and Affiliations
Corresponding author
Appendix
Substituting (1), (2), and (3) in (4) results in

 given as
given as
 denotes
denotes Let
Let  and
and  be the average SIRs at the first and second input branches of the dual-branch selection combiner. Then, the following integrals from the pervious expression can be presented in the form:
be the average SIRs at the first and second input branches of the dual-branch selection combiner. Then, the following integrals from the pervious expression can be presented in the form:

 . Finally, (12) can be written as
. Finally, (12) can be written as
 with
with
 can be written as
can be written as







Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Spalević, P.Ć., Panić, S.R., Dolićanin, Ć.B. et al. SSC Diversity Receiver over Correlated 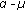 Fading Channels in the Presence of Cochannel Interference.
J Wireless Com Network 2010, 142392 (2010). https://doi.org/10.1155/2010/142392
Fading Channels in the Presence of Cochannel Interference.
J Wireless Com Network 2010, 142392 (2010). https://doi.org/10.1155/2010/142392
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/142392


 , for NCFSK modulation scheme and several values of
, for NCFSK modulation scheme and several values of  ,
,  ,
,  ,
,  ,
,  , and
, and  .
.
 , for BDPSK modulation scheme and several values of
, for BDPSK modulation scheme and several values of  ,
,  ,
,  ,
,  ,
,  , and
, and  .
.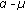 distribution: a physical fading model for the Stacy distribution. IEEE Transactions on Vehicular Technology 2007, 56(1):27-34.
distribution: a physical fading model for the Stacy distribution. IEEE Transactions on Vehicular Technology 2007, 56(1):27-34.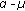 distribution with arbitrary correlation. Proceedings of International Telecommunications Symposium (ITS '06), September 2006, Fortaleza, Brazil 38-41.
distribution with arbitrary correlation. Proceedings of International Telecommunications Symposium (ITS '06), September 2006, Fortaleza, Brazil 38-41. Fading channels in the presence of co-channel interference. IET Communications 2009, 3(11):1769-1777. 10.1049/iet-com.2009.0023
Fading channels in the presence of co-channel interference. IET Communications 2009, 3(11):1769-1777. 10.1049/iet-com.2009.0023