- Research Article
- Open access
- Published:
Uplink Cross-Layer Scheduling with Differential QoS Requirements in OFDMA Systems
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 168357 (2010)
Abstract
Fair and efficient scheduling is a key issue in cross-layer design for wireless communication systems, such as 3GPP LTE and WiMAX. However, few works have considered the multiaccess of the traffic with differential QoS requirements in wireless systems. In this paper, we will consider an OFDMA-based wireless system with four types of traffic associated with differential QoS requirements, namely, minimum reserved rate, maximum sustainable rate, maximum latency, and tolerant jitter. Given these QoS requirements, the traffic scheduling will be formulated into a cross-layer optimization problem, which is convex fortunately. By separating the power allocation through the waterfilling algorithm in each user, this problem will further reduce to a kind of continuous quadratic knapsack problem in the base station which yields low complexity. It is then demonstrated that the proposed cross-layer method cannot only guarantee the application layer QoS requirements, but also minimizes the integrated residual workload in the MAC layer. To further enhance the ability of QoS assurance in heavily loaded scenario, a call admission control scheme will also be proposed. The simulation results show that the QoS requirements for the four types of traffic are guaranteed effectively by the proposed algorithms.
1. Introduction
Orthogonal frequency-division multiple access (OFDMA) offers a very attractive solution in providing high performance and flexible deployment for broadband wireless access network. In particular, OFDMA provides at more degrees of freedom for multiuser systems. The subcarriers can be allocated dynamically at different time instances to exploit the multiuser diversity [1] and frequency diversity [2], and adaptive power allocation can also be applied to further improve the power efficiency [3]. To enhance the efficiency and fairness, OFDMA also allows us to schedule time-domain resources, referred to as timeslots.
The typical OFDMA systems in wireless communications are 3GPP LTE-based cellular system [4] and IEEE 802.16 protocol-based WiMAX system [5]. These newly emerging systems provide a platform for applying the cross-layer resource allocation and scheduling technology. These systems are designed as a unified wireless access system to support multiple types of traffic, such as voice, data, audio/video, multimedia, interactive game, and Internet access. Thus, how to jointly use these technologies in the physical (PHY) layer and MAC layer to support the traffic with differential QoS requirements in the application layer is a central problem in OFDMA systems [6]. In this paper, we shall focus on this problem and use a cross-layer optimization methodology to provide a traffic scheduling method for supporting efficiently multiplexing services with a variety of QoS requirements.
Due to the stochastic nature of the traffic arrival process and the wireless channel, it is a challenging work to achieve fair and efficient resource allocation and QoS-guaranteed scheduling in OFDMA systems. In 1995, a joint-layer optimization perspective was proposed by Telatar and Gallager in [7]. Subsequently, Berry and Yeh put forward that the future wireless communication system design needs cross-layer optimization methodology [8]. They also discussed the cross-layer approach for wireless resource allocation in multiaccess and broadcasting queueing systems, respectively. Specifically, in order to collect all the parameters together in the uplinks, one may formulate the system as a multiaccess queueing system or generic switch model and consider the weighted sum of the queue lengths, which is often referred to as the integrated workload. More recently, Stolyar proved the optimality of the MaxWeight scheduling in [9]. In [10], Mandelbaum and Stolyar extended this method to the continuous strictly increasing convex function of the queue length and proved the optimality of  law scheduling. Based on the queueing theory and optimization method, Niyato and Hossain studied the radio resource management in IEEE 802.16 wireless broadband system [11]. An alternative method to incorporate concerns and constraints of various layers is to apply utility maximization formulation. In [12], Song et al. used this method to obtain a queue-aware and channel-aware scheduling algorithm, that is, transmit the traffic which minimizes the average delay. Based on the similar framework, Kulkarni and Rosenberg studied the opportunistic scheduling framework of multiple QoS requirements and short-term fairness in the system with multiple wireless interfaces [13]. In [14], Fu et al. solved the dual problems of maximizing expected throughput given limited energy and of minimizing expected energy given the minimum throughput constraint.
law scheduling. Based on the queueing theory and optimization method, Niyato and Hossain studied the radio resource management in IEEE 802.16 wireless broadband system [11]. An alternative method to incorporate concerns and constraints of various layers is to apply utility maximization formulation. In [12], Song et al. used this method to obtain a queue-aware and channel-aware scheduling algorithm, that is, transmit the traffic which minimizes the average delay. Based on the similar framework, Kulkarni and Rosenberg studied the opportunistic scheduling framework of multiple QoS requirements and short-term fairness in the system with multiple wireless interfaces [13]. In [14], Fu et al. solved the dual problems of maximizing expected throughput given limited energy and of minimizing expected energy given the minimum throughput constraint.
The above works have significantly enhanced the overall performance of wireless communications. However, they did not consider the scheduling problem of multiple types of traffic with differential QoS requirements, which is a practical scenario in OFDMA wireless access network. A typical OFDMA system, say IEEE 802.16 broadband wireless access network, has multiple independent users communicating with one base station (BS). There are four types of traffic in IEEE 802.16 protocol, namely, best effort service (BE), nonrealtime polling service (nrtPS), realtime polling service (rtPS), and unsolicited grant service (UGS) [5]. Any application-layer traffic must be classified into one of these types, and its QoS requirements can be described differentially by minimum reserved rate, maximum sustainable rate, maximum latency, and tolerant jitter. Thus, the arrival traffic of each user will be stored in different buffers and scheduled by a cross-layer scheduler in BS. Since the OFDMA-based PHY layer is timeslotted, every user should offer the traffic transmission request and its QoS parameters at the beginning of each timeslot. Given the constraints of QoS requirements and the instantaneous channel conditions, the scheduler allocates subcarriers, power, and timeslots, so as to transmit the traffic efficiently and guarantee the differential QoS requirements.
In this paper, the integrated residual workload method is introduced to cover the above considerations. By using this method, the resource allocation and traffic scheduling can be formulated into a cross-layer optimization problem under the transmission rate constraints, which is convex fortunately. Since the power allocation gives little advantage in terms of ergodic capacity [15], we decompose the power allocation from the original convex optimization problem through the water-filling algorithm in each user. The resulting optimization problem in BS, referred to as the time-frequency allocation problem, is fortunately a continuous quadratic knapsack problem with a generalized upper bound and an angular structure in the constraints. The knapsack problem (integer or continuous) has been studied for decades, which has often used to solve resource allocation problems in operational research, economics, military, and communications [16, 17]. According to the results in [18, 19], this time-frequency allocation problem can be solved with a low complexity. At this context, an integrated residual workload minimization (IRWM) algorithm and a heuristic call admission control (CAC) algorithm are proposed as a framework of the resource management scheme for future OFDMA-based wireless access networks. It is then demonstrated that the proposed cross-layer method cannot only guarantee the application layer QoS requirements, but also minimize the integrated residual workload in the MAC layer. The simulation results also verified that the QoS requirements for the four types of traffic are guaranteed effectively by the proposed scheduling algorithms.
The rest of the paper is organized as follows. Section 2 presents the system model and the QoS requirements. In Section 3, we present the cross-layer optimization problem and the problem decomposition. An optimal scheduling policy and a heuristic CAC algorithm is also presented in this section. Simulation results are presented in Section 4. Section 5 concludes this paper.
2. Cross-Layer Multiaccess Queuing Model
Consider an OFDMA system with multiple independent access users, where each user transmits four types of traffic to a BS. Then, each user has four queues, each of which corresponds to one type of traffic. In this system, each subcarrier can serve any queue, and each queue can be served by any subcarrier. Thus, the queues depend on each other and the subcarriers cannot be scheduled separately. Then, the uplink scheduling issue in this OFDMA system can be seen as a centralized cross-layer multiaccess queuing system, shown in Figure 1, which is also referred to as the generic switch model in [9].
2.1. QoS Parameters and Traffic Scheduling Framework
Similar to IEEE 802.16e protocol [5], the traffic supported by this OFDMA system is divided into four types, and a different traffic type has different QoS requirements. The QoS requirements supported include:
-
(i)
minimum reserved rate
 , denoted by
, denoted by  , which is the transmission rate that cannot be violated even the system is in congestion;
, which is the transmission rate that cannot be violated even the system is in congestion; -
(ii)
maximum sustainable rate
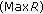 , denoted by
, denoted by  , which is the peak transmission rate allowed;
, which is the peak transmission rate allowed; -
(iii)
maximum latency
 , denoted by
, denoted by 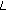 , which is the maximum sojourn time of the traffic in a queue;
, which is the maximum sojourn time of the traffic in a queue; -
(iv)
tolerant jitter (Tol
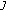 ), denoted by
), denoted by  , which is the maximum absolute value of the latency difference for the same type of traffic.
, which is the maximum absolute value of the latency difference for the same type of traffic.
We use  , to denote the set of traffic types (in this paper, the script symbol
, to denote the set of traffic types (in this paper, the script symbol  is used to denote a set, whose cardinality will be denoted by
is used to denote a set, whose cardinality will be denoted by  ), Then, the best effort (BE) service, denoted by
), Then, the best effort (BE) service, denoted by  , is used to support the best effort traffic, such as E-mail and file transfer. There are no explicit QoS requirements. The nonrealtime polling service (nrtPS), denoted by
, is used to support the best effort traffic, such as E-mail and file transfer. There are no explicit QoS requirements. The nonrealtime polling service (nrtPS), denoted by  , assures the uplink service flow receives transmission opportunities even during network congestion, such as Internet browsing and data transfer. The QoS requirements supported include
, assures the uplink service flow receives transmission opportunities even during network congestion, such as Internet browsing and data transfer. The QoS requirements supported include  and
and  . The realtime polling service (rtPS), denoted by
. The realtime polling service (rtPS), denoted by  , offers realtime uplink service flows that transport variable-size data packets, such as moving pictures experts group (MPEG) video, interactive game. The QoS requirements supported include
, offers realtime uplink service flows that transport variable-size data packets, such as moving pictures experts group (MPEG) video, interactive game. The QoS requirements supported include  ,
,  , and
, and  . The unsolicited grant service (UGS), denoted by
. The unsolicited grant service (UGS), denoted by  , offers realtime service flows that transport fixed-size data packets arriving periodically, such as T1/E1 and voice over IP without silence suppression. The QoS requirements supported include
, offers realtime service flows that transport fixed-size data packets arriving periodically, such as T1/E1 and voice over IP without silence suppression. The QoS requirements supported include  ,
,  (which is equal to
(which is equal to  ),
),  , and Tol
, and Tol .
.
In the interested OFDMA system, access user must negotiate the QoS requirements with BS before the traffic connection is established. The negotiation process determines the value of  ,
,  ,
,  , and
, and  for each type of traffic. Since this OFDMA system is timeslotted, then each user must provide the current value of the QoS parameters (including rate, latency, and jitter) and the traffic transmission request for each type of traffic at the beginning of every timeslot. Then, under the constraints of the QoS requirements and the channel conditions, BS determines which type and how much the traffic will be transmitted in this timeslot and allocates subcarrier, power, and time to them. Thus, the scheduling policy of BS is the central problem here. The cross-layer method proposed in the paper is an optimal resource allocation and scheduling method.
for each type of traffic. Since this OFDMA system is timeslotted, then each user must provide the current value of the QoS parameters (including rate, latency, and jitter) and the traffic transmission request for each type of traffic at the beginning of every timeslot. Then, under the constraints of the QoS requirements and the channel conditions, BS determines which type and how much the traffic will be transmitted in this timeslot and allocates subcarrier, power, and time to them. Thus, the scheduling policy of BS is the central problem here. The cross-layer method proposed in the paper is an optimal resource allocation and scheduling method.
2.2. Problem Formulation
In the OFDMA system, we assume BS has the perfect channel sate information (CSI), since it can be achieved through ranging, channel estimation, and the message interaction between BS and users [5]. According to [20], the instantaneous capacity of subcarrier  for user
for user  with adaptive modulation coding (AMC) mechanism is given by
with adaptive modulation coding (AMC) mechanism is given by

where  is the bandwidth of the subcarrier,
is the bandwidth of the subcarrier,  is the set of access users, and
is the set of access users, and  is the set of subcarriers. The parameter
is the set of subcarriers. The parameter  is calculated by
is calculated by

where  is the target bit error rate of the AMC mechanism. The instantaneous signal-to-noise ratio (SNR)
is the target bit error rate of the AMC mechanism. The instantaneous signal-to-noise ratio (SNR)  can be rewritten as
can be rewritten as

where  is the average SNR of the receiver in user
is the average SNR of the receiver in user  ,
,  is the proportion of the power allocated to subcarrier
is the proportion of the power allocated to subcarrier  of user
of user  , and
, and  is the corresponding channel gain which can be obtained by channel estimation [21]. Then, the channel condition of user
is the corresponding channel gain which can be obtained by channel estimation [21]. Then, the channel condition of user  is given by the vector
is given by the vector

The channel condition of the whole system is given by  , and its state space is denoted by
, and its state space is denoted by  . We also let
. We also let  ,
,  , and
, and  denote its state space.
denote its state space.
In the interested OFDMA system, a timeslot is divided into multiple parts which will be allocated to the traffic of different type in each user. Let  denote the generic traffic in
denote the generic traffic in  , which is the set of traffic for type
, which is the set of traffic for type  in user
in user  . Let
. Let  be the timeslot occupancy ratio of the subcarrier
be the timeslot occupancy ratio of the subcarrier  for the traffic
for the traffic  . Similar to the channel conditions of the OFDMA system, we let
. Similar to the channel conditions of the OFDMA system, we let  ,
,  , and
, and  denote its state space. Thus, the transmission rate of traffic
denote its state space. Thus, the transmission rate of traffic  can be given by
can be given by

As stated in last subsection, there is no explicit QoS requirement for the first type of traffic  . The QoS requirements of the second type of traffic
. The QoS requirements of the second type of traffic  is
is  and
and  , which indicate that
, which indicate that

where  can be calculated by (5). The QoS requirements of the third type of traffic
can be calculated by (5). The QoS requirements of the third type of traffic  include
include  ,
,  , and
, and  , which indicate that
, which indicate that

where  is the latency of the traffic
is the latency of the traffic  . In the timeslotted system, we have
. In the timeslotted system, we have

where  is the length of timeslot and
is the length of timeslot and  . The QoS requirements of the fourth type of traffic
. The QoS requirements of the fourth type of traffic  include
include  ,
,  ,
,  , and Tol
, and Tol , which indicate that
, which indicate that

where  has a similar relationship as (8), and
has a similar relationship as (8), and  is the jitter of the traffic
is the jitter of the traffic  . According to the definition,
. According to the definition,  is given by
is given by

where " " denotes
" denotes  was transmitted before
was transmitted before  .
.
3. Optimal Scheduling Policy
3.1. Cross-Layer Optimization Problem
The scheduling policy for this OFDMA system should transmit all the traffic as soon as possible, while guaranteeing the differential QoS requirements. As a cross-layer design problem, maximizing the spectrum efficiency is also an important consideration. Thus, we need to design a proper objective function to collect all the considerations. Similar to the methods in [9, 10, 13], the integrated residual workload is defined as follows.
Definition 1.
Let  be the set of traffic for type
be the set of traffic for type  in user
in user  and
and  be a continuous strictly increasing nonnegative convex function for
be a continuous strictly increasing nonnegative convex function for  and
and  . The integrated residual workload
. The integrated residual workload  at the end of the current timeslot is defined as
at the end of the current timeslot is defined as

where  is the length of timeslot,
is the length of timeslot,  is the transmission rate allocated to traffic
is the transmission rate allocated to traffic  .
.  is the function of the jitter
is the function of the jitter  , and
, and  is the function of the latency
is the function of the latency  . They are both the continuous strictly increasing nonnegative convex function, and they satisfy:
. They are both the continuous strictly increasing nonnegative convex function, and they satisfy:  if
if  ,
,  , then
, then  ,
,  ;
;  if
if  ,
,  , then
, then  ,
,  .
.
In this definition,  is the residual workload of the traffic
is the residual workload of the traffic  at the end of the current timeslot. Since the resource is allocated according to the transmission request, then we have
at the end of the current timeslot. Since the resource is allocated according to the transmission request, then we have  . Here,
. Here,  may have the form of
may have the form of  according to its definition. It represents the punishment to the residual traffic in the queue. Clearly,
according to its definition. It represents the punishment to the residual traffic in the queue. Clearly,  is increasing since there must be a greater punishment for more residual traffic. It can be seen that if
is increasing since there must be a greater punishment for more residual traffic. It can be seen that if  is small, the small increase will not affect the stability of the scheduling system, that is,
is small, the small increase will not affect the stability of the scheduling system, that is,  should be small at this time. However, if
should be small at this time. However, if  is large, a small increase may make the system unstable, that is,
is large, a small increase may make the system unstable, that is,  should be large. Thus,
should be large. Thus,  must be a convex function when
must be a convex function when  .
.  and
and  represent the punishment to the jitter and the latency, respectively. According to their properties,
represent the punishment to the jitter and the latency, respectively. According to their properties,

can satisfy the conditions in Definition 1, where  is the shape factor and
is the shape factor and  is the location parameter, which will be set to
is the location parameter, which will be set to  or
or  . Thus, the integrated residual workload represents the residual workload of four types and their QoS requirements of delay and jitter. Thus, the cross-layer scheduling algorithm proposed in this paper is to minimize the integrated residual workload.
. Thus, the integrated residual workload represents the residual workload of four types and their QoS requirements of delay and jitter. Thus, the cross-layer scheduling algorithm proposed in this paper is to minimize the integrated residual workload.
Before constructing the cross-layer optimization problem, we may do some preprocess on  in order to simplify the problem. Note that the purpose of the maximum transmission rate is to restrict some greedy traffic to occupy too much bandwidth. Thus, if we do some operations on
in order to simplify the problem. Note that the purpose of the maximum transmission rate is to restrict some greedy traffic to occupy too much bandwidth. Thus, if we do some operations on  to make the transmission rate cannot be greater than
to make the transmission rate cannot be greater than  , then a group of constraints can be eliminated. Let
, then a group of constraints can be eliminated. Let  be the transmission request after preprocess, then for every
be the transmission request after preprocess, then for every  and
and  , we have
, we have

where  is the indicator function, which is defined as
is the indicator function, which is defined as

On the other hand, except for the type of traffic  , other three types are burst traffic. Thus, at the beginning of some timeslot, the traffic transmission request
, other three types are burst traffic. Thus, at the beginning of some timeslot, the traffic transmission request  may be smaller than
may be smaller than  . Then, we need to do some operations on
. Then, we need to do some operations on  in order to eliminate this contradiction. Let
in order to eliminate this contradiction. Let  be the minimum rate after preprocess, then for every
be the minimum rate after preprocess, then for every  and
and  , we have
, we have

Finally, collecting the scheduling objectives, QoS requirements, and physical constraints together, we have the following optimization problem:

where  . In this formulation,
. In this formulation,  is the integrated residual workload after this time of traffic transmission. The constraints on
is the integrated residual workload after this time of traffic transmission. The constraints on  means one subcarrier can be shared by all the traffic, while the constraint on
means one subcarrier can be shared by all the traffic, while the constraint on  means, for each user, the sum of the power allocated to all subcarriers cannot exceed the total power constraint. If the traffic does not have a specific QoS requirement, the weighted function will be set to
means, for each user, the sum of the power allocated to all subcarriers cannot exceed the total power constraint. If the traffic does not have a specific QoS requirement, the weighted function will be set to  . The time average value of
. The time average value of  at epoch
at epoch  , denoted by
, denoted by  , is calculated as an exponentially weighted low-pass filter [22],
, is calculated as an exponentially weighted low-pass filter [22],

3.2. Problem Decomposition
Equation (16) represents a complicated nonlinear optimization problem. In this section, we will propose a method to solve this problem with low complexity. Firstly, the following theorem shows the problem represented by (16) is convex.
Theorem 2.
The problem represented by (16) is a convex optimization problem, whose solution can be given by

where  is the Lagrangian multiplier, and
is the Lagrangian multiplier, and  .
.
Proof.
Consider the definition of convex optimization problem in [23]. First, the feasible region of the optimization variables  and
and  constructs a convex polyhedron. Then, besides two groups of linear constraints, there are three groups of nonlinear constraints. Since a nonnegative weighted sum of convex functions is a convex function [23], then
constructs a convex polyhedron. Then, besides two groups of linear constraints, there are three groups of nonlinear constraints. Since a nonnegative weighted sum of convex functions is a convex function [23], then  is a concave function of
is a concave function of  and
and  according to (1), (3), and (5). Since
according to (1), (3), and (5). Since  is an increasing convex function,
is an increasing convex function,  is a convex function. Note that
is a convex function. Note that  and
and  are constants, for the delay and the jitter are known, then
are constants, for the delay and the jitter are known, then  is a convex function. Since this is a convex optimization problem, the solutions expressed in (18) can be derived from Karush-Kuhn-Tucker (KKT) condition directly.
is a convex function. Since this is a convex optimization problem, the solutions expressed in (18) can be derived from Karush-Kuhn-Tucker (KKT) condition directly.
Although the optimization problem represented by (16) is convex, the numerical algorithm for this problem still has a high computation complexity [23]. In the following, we will decompose this problem. The resulting problem enjoys a low complexity at a cost of trivial performance loss.
It should be noted that the layered optimization does not make big difference in terms of ergodic capacity [15]. Thus, we can decompose this problem into two steps: first, allocate subcarrier and timeslot to each type of traffic for every user; second, allocate power by using water-filling algorithm in each user. Since there are many works on the iterative implementation for water-filling [21], we only discuss the first step in detail. By using the equal power allocation and the quadratic objective function, the problem represented by (16) can be reduced to (19).

The resulting optimization problem in (19), referred to as the time-frequency allocation problem, is fortunately a continuous quadratic knapsack problem with a generalized upper bound and an angular structure in the constraints. The knapsack problem (integer or continuous) has been studied for decades, which has often been used to solve resource allocation problem in operational research, economics, military, and communications [16, 17]. According to the results in [16], we first form a Lagrangian relaxation with respect to the constraints 
 . The resulting Lagrangian subproblems then construct
. The resulting Lagrangian subproblems then construct  singly constrained convex problems, that is,
singly constrained convex problems, that is,

By using the vector  , this problem can be converted into the following form
, this problem can be converted into the following form

According to the algorithm proposed in [18, 19], this subproblem can be numerically solved efficiently.
3.3. Asymptotic Optimal Scheduling Policy
The feasible region of the problem represented by (19) might be an empty set, which means that the system may be unstable for some traffic transmission request and QoS requirements. The scheduling algorithm under which the system is stable is referred to as the stable scheduling algorithm (SSA). In order to discuss the stability of the scheduling algorithm, we define the static service split (SSS) scheduling algorithm which is similar to [9].
Definition 3.
For every channel state  , there is a fixed continuous probability measure
, there is a fixed continuous probability measure  , where
, where  is the timeslot allocation vector and
is the timeslot allocation vector and  is the power allocation vector. The SSS scheduling algorithm parameterized by the set of measures
is the power allocation vector. The SSS scheduling algorithm parameterized by the set of measures  . The average (or the long-term) service rate of traffic type
. The average (or the long-term) service rate of traffic type  in user
in user  is
is

Then,  is called the SSS algorithm.
is called the SSS algorithm.
Similar to [9], the simple observation shows that if  and the constrains
and the constrains  hold, then the SSS algorithm, allocating to each traffic the average rate, will make the system stable. This fact gives the condition on which the system is stable.
hold, then the SSS algorithm, allocating to each traffic the average rate, will make the system stable. This fact gives the condition on which the system is stable.
Lemma 4.
Let  be the minimum reserved rate, and
be the minimum reserved rate, and  ,
,  are the maximum latency and tolerant jitter, respectively. The sufficient condition for the existence of a SSA is for at least one SSS algorithm, the integrated residual workload
are the maximum latency and tolerant jitter, respectively. The sufficient condition for the existence of a SSA is for at least one SSS algorithm, the integrated residual workload  exists, and the following equations hold for every
exists, and the following equations hold for every  ,
,

From this lemma, one can define the scheduling algorithm stability region  as the QoS requirements set which satisfies Lemma 4. Then, the asymptotic properties of the optimization problem represented by (19) can be summarized as the following theorem.
as the QoS requirements set which satisfies Lemma 4. Then, the asymptotic properties of the optimization problem represented by (19) can be summarized as the following theorem.
Theorem 5.
If QoS parameters are in the scheduling algorithm stability region  , then the solution of the optimization problem represented by (19) satisfies the QoS requirements of (6), (7), and (9) when
, then the solution of the optimization problem represented by (19) satisfies the QoS requirements of (6), (7), and (9) when  , and minimizes the integrated residual workload
, and minimizes the integrated residual workload  .
.
Proof.
If the QoS requirements are in the region  , according to Lemma 4, the SSA must exist. So, the feasible domain of the optimization problem represented by (19) is not null. According to Theorem 2, the optimal solution of the problem represented by (19) exists. Because the arrival rate of traffic
, according to Lemma 4, the SSA must exist. So, the feasible domain of the optimization problem represented by (19) is not null. According to Theorem 2, the optimal solution of the problem represented by (19) exists. Because the arrival rate of traffic  is
is  , which is also the requesting rate, then
, which is also the requesting rate, then  is equal to
is equal to  as long as the optimal solution exists. According to the law of large numbers, the average rates in time are equal to their mathematical expectations, then (6), (7), and (9) hold.
as long as the optimal solution exists. According to the law of large numbers, the average rates in time are equal to their mathematical expectations, then (6), (7), and (9) hold.
The scheduling algorithm executes as in Algorithm 1: users offer traffic transmission requests and QoS parameters at the beginning of each timeslot, meanwhile the BS estimates the uplink wireless channel condition, then the BS solves the problem represented by (19) and sends the resource allocation results to all users. After receiving  , each user executes the water-filling algorithm independently to obtain
, each user executes the water-filling algorithm independently to obtain  . As this algorithm always tries to minimize the integrated residual workload, it will be referred to as the integrated residual workload minimization (IRWM) algorithm.
. As this algorithm always tries to minimize the integrated residual workload, it will be referred to as the integrated residual workload minimization (IRWM) algorithm.
Algorithm 1: IRWM algorithm.
 Receive the transmission request
Receive the transmission request  and the QoS parameters.
and the QoS parameters.
 for
for and
and  do
do
 if
if then
then

 .
.
 else if
else if then
then

 .
.
 end if
end if
 end for
end for
 Solve the optimization problem represented by (19).
Solve the optimization problem represented by (19).
 Transmit
Transmit  to every user.
to every user.
3.4. Heuristic Call Admission Control
For an OFDMA system in the heavily loaded scenario, the stability of the queues cannot always be assured. In this case, the optimization problem represented by (19) will have a null feasible region. To overcome this problem, we need to design a call admission control (CAC) mechanism. The algorithm based on this idea is listed as Algorithm 2. Join this heuristic CAC algorithm and the IRWM algorithm will form a cross-layer resource allocation and scheduling framework for OFDMA wireless networks supporting multiple types of traffic.
Algorithm 2: Heuristic CAC algorithm.
 Determine
Determine  ,
,  ,
,  and
and  for a specific
for a specific  and
and  .
.
 Add
Add  ,
,  and
and  to (19).
to (19).

 ,
,  .
.

 .
.
 if
if exists then
exists then
 Admit.
Admit.
 else
else
 Reject.
Reject.
 end if
end if
4. Simulation Results
The uplink scenario of one BS and  users is addressed in this section. The wireless channel between each user and the base station undergoes
users is addressed in this section. The wireless channel between each user and the base station undergoes  -path frequency selective fading. The OFDMA system considered has
-path frequency selective fading. The OFDMA system considered has  subcarriers, and the bandwidth for each subcarrier is
subcarriers, and the bandwidth for each subcarrier is  . The channel gains for different subcarriers are independent and identical distribution and the variance is
. The channel gains for different subcarriers are independent and identical distribution and the variance is  . The average SNR for the first four users are
. The average SNR for the first four users are  and
and  for the second user. The target BER of AMC mechanism is
for the second user. The target BER of AMC mechanism is  . If we allocate transmission power equally, then the channel capacity is about
. If we allocate transmission power equally, then the channel capacity is about  for the first four users and about
for the first four users and about  for the second four users. We consider the time duration of
for the second four users. We consider the time duration of  timeslots.
timeslots.
The ON-OFF model is used to generate the traffic for each user. The traffic parameters are listed in Table 1, where  is the exponential distribution with the average
is the exponential distribution with the average  . The total average arrival rate is
. The total average arrival rate is  , which is bigger than the channel capacity of the second group of users with equal power allocation. The QoS requirements are shown in Table 2. In these tables, the time unit is the length of timeslot
, which is bigger than the channel capacity of the second group of users with equal power allocation. The QoS requirements are shown in Table 2. In these tables, the time unit is the length of timeslot  , the traffic unit is bit and the transmission rate unit is bit/timeslot. In the objective function, we let
, the traffic unit is bit and the transmission rate unit is bit/timeslot. In the objective function, we let  be
be  . The weighted functions for the latency and the jitter have the form as (12), whose shape parameters are the
. The weighted functions for the latency and the jitter have the form as (12), whose shape parameters are the  and Tol
and Tol , respectively.
, respectively.
The simulation results for the second user are shown in Figures 2–7. From Figures 2–5, we can see that the average transmission rate is greater than the minimum rate or equal to the constant rate. So, the IRWM algorithm can guarantee the minimum reserved rate requirements. Figure 6 shows the latency of traffic type  . The largest traffic latency is about
. The largest traffic latency is about  , it does not exceed the maximum latency requirement
, it does not exceed the maximum latency requirement  . The latency of traffic type
. The latency of traffic type  is shown in Figure 7, which does not exceed the corresponding maximum value in Table 2 too. So, the IRWM algorithm can guarantee the maximum latency and the tolerant jitter requirements.
is shown in Figure 7, which does not exceed the corresponding maximum value in Table 2 too. So, the IRWM algorithm can guarantee the maximum latency and the tolerant jitter requirements.
For performance comparison, the heuristic scheme has also been simulated. In this scheme, the interleaved subcarrier allocation is used. The subcarriers are allocated to the traffic of type  first. Then, according to the traffic requirements and QoS parameters, the subcarriers are allocated to the traffic of types
first. Then, according to the traffic requirements and QoS parameters, the subcarriers are allocated to the traffic of types  and
and  , respectively. At last, the residual subcarriers are allocated to the traffic of type
, respectively. At last, the residual subcarriers are allocated to the traffic of type  . In this scheme, the maximum sustainable rates of traffic types
. In this scheme, the maximum sustainable rates of traffic types  and
and  are two critical parameters, which balance the transmission among traffic types
are two critical parameters, which balance the transmission among traffic types  ,
,  , and traffic type
, and traffic type  . If the maximum sustainable rate is too large, the traffic of type
. If the maximum sustainable rate is too large, the traffic of type  can nearly not get transmission opportunities, while if it is too small, the latency requirement of traffic types
can nearly not get transmission opportunities, while if it is too small, the latency requirement of traffic types  will be violated. In IRWM algorithm; however, there is no need to set the maximum sustainable rate manually, because the integrated residual workload can balance all the types of traffic automatically. The simulation results show that the proposed IRWM algorithm has a better performance. It has a greater transmission rate for traffic types of
will be violated. In IRWM algorithm; however, there is no need to set the maximum sustainable rate manually, because the integrated residual workload can balance all the types of traffic automatically. The simulation results show that the proposed IRWM algorithm has a better performance. It has a greater transmission rate for traffic types of  ,
,  , and
, and  . It also yields a smaller latency for the traffic type of
. It also yields a smaller latency for the traffic type of  . Therefore, the simulation results show that the differential QoS requirements of four types of traffic are guaranteed effectively by the proposed IRWM algorithm.
. Therefore, the simulation results show that the differential QoS requirements of four types of traffic are guaranteed effectively by the proposed IRWM algorithm.
5. Conclusion
The problem of uplink traffic scheduling with differential QoS requirements in OFDMA systems was addressed in this paper. A cross-layer optimization methodology, which jointly considers the traffic arrival process and the wireless channel conditions, was adopted to achieve better QoS for the users accessing to a common base station. In particular, we introduce the integrated residual workload to formulate the traffic scheduling problem into a convex optimization problem. By decomposing this problem into two steps, that is, a continuous quadratic knapsack problem in BS and a water-filling power allocation algorithm in each user, we presented a low-complexity algorithm referred to as the IRWM. Besides, a heuristic CAC scheme was proposed to avoid the sharply decreasing of QoS, when the system is in congestion. Both the theoretical analysis and the simulation results showed that the differential QoS requirements of the application layer are guaranteed effectively by the proposed algorithm in the MAC layer.
References
Ali SH, Lee K-D, Leung VCM: Dynamic resource allocation in OFDMA wireless metropolitan area networks. IEEE Wireless Communications 2007, 14(1):6-13.
Bai B, Chen W, Cao Z, Letaief KB: Max-matching diversity in OFDMA systems. IEEE Transactions on Communications 2010, 58(4):1161-1171.
Wong CY, Cheng RS, Letaief KB, Murch RD: Multiuser OFDM with adaptive subcarrier, bit, and power allocation. IEEE Journal on Selected Areas in Communications 1999, 17(10):1747-1758. 10.1109/49.793310
Sesia S, Toufik I, Baker M: LTE—The UMTS Long Term Evolution—From Theory to Practice. John Wiley & Sons, New York, NY, USA; 2009.
IEEE Std. 802.16eTM, IEEE Standard for Local and Metropolitan Area Networks, Part 16: Air Interface for Fixed and Mobile Broadband Wireless Access Systems, Amendment 2: Physical and Medium Access Control Layers for Combined Fixed and Mobile Operation in Licensed Bands and Corrigendum 1. IEEE Press, New York, NY, USA; 2005.
Andrews JG, Ghosh A, Muhamed R: Fundamentals of WiMAX—Understanding Broadband Wireless Networking. Prentice Hall, New York, NY, USA; 2007.
Telatar IE, Gallager RG: Combining queueing theory with information theory for multiaccess. IEEE Journal on Selected Areas in Communications 1995, 13(6):963-969. 10.1109/49.400652
Berry RA, Yeh EM: Cross-layer wireless resource allocation. IEEE Signal Processing Magazine 2004, 21(5):59-68. 10.1109/MSP.2004.1328089
Stolyar AL: Maxweight scheduling in a generalized switch: state space collapse and workload minimization in heavy traffic. Annals of Applied Probability 2004, 14(1):1-53. 10.1214/aoap/1075828046
Mandelbaum A, Stolyar AL: Scheduling flexible servers with convex delay costs: heavy-traffic optimality of the generalized c μ -rule. Operations Research 2004, 52(6):836-855. 10.1287/opre.1040.0152
Niyato D, Hossain E: A queuing-theoretic and optimization-based model for radio resource management in IEEE 802.16 broadband wireless networks. IEEE Transactions on Computers 2006, 55(11):1473-1488.
Song G, Li Y, Cimini Jr LJ, Zheng H: Joint channel-aware and queue-aware data scheduling in multiple shared wireless channels. Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC '04), March 2004, Atlanta, Ga, USA 3: 1939-1944.
Kulkarni SS, Rosenberg C: Opportunistic scheduling: generalizations to include multiple constraints, multiple interfaces, and short term fairness. Wireless Networks 2005, 11(5):557-569. 10.1007/s11276-005-3512-y
Fu A, Tsitsiklis JN: Optimal transmission scheduling over a fading channel with energy and deadline constraints. IEEE Transactions on Wireless Communications 2006, 5(2):630-641. 10.1109/TWC.2006.1603978
Goldsmith AJ, Varaiya PP: Capacity of fading channels with channel side information. IEEE Transactions on Information Theory 1997, 43(6):1986-1992. 10.1109/18.641562
Bretthauer KM, Shetty B: The nonlinear knapsack problem—algorithms and applications. European Journal of Operational Research 2002, 138(3):459-472. 10.1016/S0377-2217(01)00179-5
Patriksson M: A survey on the continuous nonlinear resource allocation problem. European Journal of Operational Research 2008, 185(1):1-46. 10.1016/j.ejor.2006.12.006
Pang J-S: A new and efficient algorithm for a class of portfolio selection problems. Operations Research 1980, 28(3):754-767, . 10.1287/opre.28.3.754
Bretthauer KM, Shetty B: Quadratic resource allocation with generalized upper bounds. Operations Research Letters 1997, 20(2):51-57. 10.1016/S0167-6377(96)00039-9
Goldsmith AJ, Chua S: Variable-rate variable-power MQAM for fading channels. IEEE Transactions on Communications 1997, 45(10):1218-1230. 10.1109/26.634685
Tse D, Viswanath D: Fundamentals of Wireless Communication. Cambridge University Press, New York, NY, USA; 2005.
Viswanath P, Tse DNC, Laroia R: Opportunistic beamforming using dumb antennas. IEEE Transactions on Information Theory 2002, 48(6):1277-1294. 10.1109/TIT.2002.1003822
Boyd S, Vandenberghe L: Convex Optimization. Cambridge University Press, New York, NY, USA; 2004.
Acknowledgment
This work is supported by NSFC key project under Grant no. 60832008, and RGC/NSFC project under Grant no. N_HKUST622/06.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Bai, B., Chen, W., Cao, Z. et al. Uplink Cross-Layer Scheduling with Differential QoS Requirements in OFDMA Systems. J Wireless Com Network 2010, 168357 (2010). https://doi.org/10.1155/2010/168357
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/168357

 , denoted by
, denoted by  , which is the transmission rate that cannot be violated even the system is in congestion;
, which is the transmission rate that cannot be violated even the system is in congestion;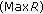 , denoted by
, denoted by  , which is the peak transmission rate allowed;
, which is the peak transmission rate allowed; , denoted by
, denoted by 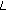 , which is the maximum sojourn time of the traffic in a queue;
, which is the maximum sojourn time of the traffic in a queue;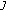 ), denoted by
), denoted by  , which is the maximum absolute value of the latency difference for the same type of traffic.
, which is the maximum absolute value of the latency difference for the same type of traffic.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.