- Research Article
- Open access
- Published:
Bit Error Rate Approximation of MIMO-OFDM Systems with Carrier Frequency Offset and Channel Estimation Errors
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 176083 (2010)
Abstract
The bit error rate (BER) of multiple-input multiple-output (MIMO) orthogonal frequency-division multiplexing (OFDM) systems with carrier frequency offset and channel estimation errors is analyzed in this paper. Intercarrier interference (ICI) and interantenna interference (IAI) due to the residual frequency offsets are analyzed, and the average signal-to-interference-and-noise ratio (SINR) is derived. The BER of equal gain combining (EGC) and maximal ratio combining (MRC) with MIMO-OFDM is also derived. The simulation results demonstrate the accuracy of the theoretical analysis.
1. Introduction
Spatial multiplexing multiple-input multiple-output (MIMO) technology significantly increases the wireless system capacity [1–4]. These systems are primarily designed for flat-fading MIMO channels. A broader band can be used to support a higher data rate, but a frequency-selective fading MIMO channel is met, and this channel experiences intersymbol interference (ISI). A popular solution is MIMO-orthogonal frequency-division multiplexing (OFDM), which achieves a high data rate at a low cost of equalization and demodulation. However, just as single-input single-output- (SISO-) OFDM systems are highly sensitive to frequency offset, so are MIMO-OFDM systems. Although one can use frequency offset correction algorithms [5–10], residual frequency offsets can still increase the bit error rate (BER).
The BER of SISO-OFDM systems impaired by frequency offset is analyzed in [11], in which the frequency offset is assumed to be perfectly known at the receiver, and, based on the intercarrier interference (ICI) analysis, the BER is evaluated for multipath fading channels. Many frequency offset estimators have been proposed [8, 12–14]. A synchronization algorithm for MIMO-OFDM systems is proposed in [15], which considers an identical timing offset and frequency offset with respect to each transmit-receive antenna pair. In [10], where frequency offsets for different transmit-receive antennas are assumed to be different, the Cramer-Rao lower bound (CRLB) for either the frequency offsets or channel estimation variance errors for MIMO-OFDM is derived. More documents on MIMO-OFDM channel estimation by considering the frequency offset are available at [16, 17].
However, in real systems, neither the frequency offset nor the channel can be perfectly estimated. Therefore, the residual frequency offset and channel estimation errors impact the BER performance. The BER performance of MIMO systems, without considering the effect of both the frequency offset and channel estimation errors, is studied in [18, 19].
This paper provides a generalized BER analysis of MIMO-OFDM, taking into consideration both the frequency offset and channel estimation errors. The analysis exploits the fact that for unbiased estimators, both channel and frequency offset estimation errors are zero-mean random variables (RVs). Note that the exact channel estimation algorithm design is not the focus of this paper, and the main parameter of interest is the channel estimation error. Many channel estimation algorithms developed for either SISO or MIMO-OFDM systems, for example, [20–22], can be used to perform channel estimation. The statistics of these RVs are used to derive the degradation in the receive SINR and the BER. Following [10], the frequency offset of each transmit-receive antenna pair is assumed to be an independent and identically distributed (i.i.d.) RV.
This paper is organized as follows. The MIMO-OFDM system model is described in Section 2, and the SINR degradation due to the frequency offset and channel estimation errors is analyzed in Section 3. The BER, taking into consideration both the frequency offset and channel estimation errors, is derived in Section 4. The numerical results are given in Section 5, and the conclusions are presented in Section 6.
Notation.  and
and  are transpose and complex conjugate transpose. The imaginary unit is
are transpose and complex conjugate transpose. The imaginary unit is  .
.  and
and  are the real and imaginary parts of
are the real and imaginary parts of  , respectively.
, respectively.  represents the angle of
represents the angle of  , that is,
, that is,  . A circularly symmetric complex Gaussian RV with mean
. A circularly symmetric complex Gaussian RV with mean  and variance
and variance  is denoted by
is denoted by  .
.  is the
is the  identity matrix, and
identity matrix, and  is the
is the  all-zero matrix.
all-zero matrix.  is the
is the  all-zero vector.
all-zero vector.  is the
is the  th entry of vector
th entry of vector  , and
, and  is the
is the  th entry of matrix
th entry of matrix  .
.  and
and  are the mean and variance of
are the mean and variance of  .
.
2. MIMO-OFDM Signal Model
Input data bits are mapped to a set of  complex symbols drawn from a typical signal constellation such as phase-shift keying (PSK) or quadrature amplitude modulation (QAM). The inverse discrete fourier transform (IDFT) of these
complex symbols drawn from a typical signal constellation such as phase-shift keying (PSK) or quadrature amplitude modulation (QAM). The inverse discrete fourier transform (IDFT) of these  symbols generates an OFDM symbol. Each OFDM symbol has a useful part of duration
symbols generates an OFDM symbol. Each OFDM symbol has a useful part of duration  seconds and a cyclic prefix of length
seconds and a cyclic prefix of length  seconds to mitigate ISI, where
seconds to mitigate ISI, where  is longer than the channel-response length. For a MIMO-OFDM system with
is longer than the channel-response length. For a MIMO-OFDM system with  transmit antennas and
transmit antennas and  receive antennas, an
receive antennas, an  vector
vector  represents the block of frequency-domain symbols sent by the
represents the block of frequency-domain symbols sent by the  th transmit antenna, where
th transmit antenna, where  . The time-domain vector for the
. The time-domain vector for the  th transmit antenna is given by
th transmit antenna is given by  , where
, where  is the total transmit power and
is the total transmit power and  is the
is the  IDFT matrix with entries
IDFT matrix with entries  for
for  . Each entry of
. Each entry of  is assumed to be i.i.d. RV with mean zero and unit variance; that is,
is assumed to be i.i.d. RV with mean zero and unit variance; that is,  for
for  and
and  .
.
The discrete channel response between the  th receive antenna and
th receive antenna and  th transmit antenna is
th transmit antenna is  , where
, where  is the maximum delay between the
is the maximum delay between the  th transmit and the
th transmit and the  th receive antennas, and
th receive antennas, and  . Uncorrelated channel taps are assumed for each antenna pair
. Uncorrelated channel taps are assumed for each antenna pair  ; that is,
; that is,  when
when  . The corresponding frequency-domain channel response matrix is given by
. The corresponding frequency-domain channel response matrix is given by  with
with  representing the channel attenuation at the
representing the channel attenuation at the  th subcarrier. In the sequel, the channel power profiles are normalized as
th subcarrier. In the sequel, the channel power profiles are normalized as  for all
for all  . The covariance of channel frequency response is given by
. The covariance of channel frequency response is given by

Note that if  and
and  are satisfied simultaneously, we assume that there is no correlation between
are satisfied simultaneously, we assume that there is no correlation between  and
and  . Otherwise the correlation between
. Otherwise the correlation between  and
and  is nonzero.
is nonzero.
In this paper,  and
and  are used to represent the initial phase and normalized frequency offset (normalized to the OFDM subcarrier spacing) between the oscillators of the
are used to represent the initial phase and normalized frequency offset (normalized to the OFDM subcarrier spacing) between the oscillators of the  -th transmit and the
-th transmit and the  th receive antennas. The frequency offsets
th receive antennas. The frequency offsets  for all
for all  are modeled as zero-mean i.i.d. RVs. (Multiple rather than one frequency offset are assumed in this paper, with each transmit-antenna pair being impaired by an independent frequency offset. This case happens when the distance between different transmit or receive antenna elements is large enough, and this big distance results in a different angle-of-arrive (AOA) of the signal received by each receive antenna element. In this scenario, once the moving speed of the mobile node is high, the Doppler Shift related to different transmit-receive antenna pair will be different.)
are modeled as zero-mean i.i.d. RVs. (Multiple rather than one frequency offset are assumed in this paper, with each transmit-antenna pair being impaired by an independent frequency offset. This case happens when the distance between different transmit or receive antenna elements is large enough, and this big distance results in a different angle-of-arrive (AOA) of the signal received by each receive antenna element. In this scenario, once the moving speed of the mobile node is high, the Doppler Shift related to different transmit-receive antenna pair will be different.)
By considering the channel gains and frequency offsets, the received signal vector can be represented as

where  ,
,  and
and  is a vector of additive white Gaussian noise (AWGN) with
is a vector of additive white Gaussian noise (AWGN) with  . Note that the channel state information is available at the receiver, but not at the transmitter. Consequently, the transmit power is equally allocated among all the transmit antennas.
. Note that the channel state information is available at the receiver, but not at the transmitter. Consequently, the transmit power is equally allocated among all the transmit antennas.
3. SINR Analysis in MIMO-OFDM Systems
This paper treats spatial multiplexing MIMO, where independent data streams are mapped to distinct OFDM symbols and are transmitted simultaneously from transmit antennas. The received vector  at the
at the  th receive antenna is thus a superposition of the transmit signals from all the
th receive antenna is thus a superposition of the transmit signals from all the  transmit antennas. When demodulating
transmit antennas. When demodulating  , the signals from the transmit antennas other than the
, the signals from the transmit antennas other than the  th transmit antenna constitute interantenna interference (IAI). The structure of MIMO-OFDM systems is illustrated in Figure 1, where
th transmit antenna constitute interantenna interference (IAI). The structure of MIMO-OFDM systems is illustrated in Figure 1, where  represents the subcarrier spacing.
represents the subcarrier spacing.
Here, we first assume that  and
and  for each
for each  have been estimated imperfectly; that is,
have been estimated imperfectly; that is,  and
and  , where
, where  and
and  are the estimation errors of
are the estimation errors of  and
and  (
( represents the estimation error of
represents the estimation error of  ), respectively. We also assume that each
), respectively. We also assume that each  is demodulated with a negligible error. After estimating
is demodulated with a negligible error. After estimating  , that is,
, that is,  ,
,  can be compensated for and
can be compensated for and  can be demodulated as
can be demodulated as

where  is derived from
is derived from  by replacing
by replacing  with
with  and
and  and
and  are the residual IAI and AWGN components of
are the residual IAI and AWGN components of  , respectively (When
, respectively (When  is large enough and the frequency offset is not too big (e.g.,
is large enough and the frequency offset is not too big (e.g.,  ), from the Central-Limit Theorem (CLT) [23, Page 59], the IAI can be approximated as Gaussian noise.).
), from the Central-Limit Theorem (CLT) [23, Page 59], the IAI can be approximated as Gaussian noise.).
3.1. SINR Analysis without Combining at Receive Antennas
The SINR is derived for the  th transmit signal at the
th transmit signal at the  th receive antenna. The signals transmitted by antennas other than the
th receive antenna. The signals transmitted by antennas other than the  th antenna are interference, which should be eliminated before demodulating the desired signal of the
th antenna are interference, which should be eliminated before demodulating the desired signal of the  th transmit antenna. Existing interference cancelation algorithms [24–27] can be applied here.
th transmit antenna. Existing interference cancelation algorithms [24–27] can be applied here.
Let us first define the parameters 
 ,
,  , and
, and 
 ,
,  . Based on (3), the
. Based on (3), the  th subcarrier
th subcarrier  of the
of the  th transmit antenna can be demodulated as
th transmit antenna can be demodulated as

where  is decomposed as
is decomposed as  , which is the ICI contributed by subcarriers other than the
, which is the ICI contributed by subcarriers other than the  th subcarrier of transmit antenna
th subcarrier of transmit antenna  . (The decomposition of ICI into the format of
. (The decomposition of ICI into the format of  is referred to [11].) We can easily prove that
is referred to [11].) We can easily prove that  and
and  are zero-mean RVs subject to the following assumptions.
are zero-mean RVs subject to the following assumptions.
-
(1)
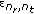 is an i.i.d. RV with mean zero and variance
is an i.i.d. RV with mean zero and variance  for all
for all 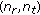 .
. -
(2)
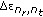 is an i.i.d. RV with mean zero and variance
is an i.i.d. RV with mean zero and variance 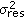 for each
for each  .
. -
(3)
 for each
for each  .
. -
(4)
 is an i.i.d. RV with mean zero and variance
is an i.i.d. RV with mean zero and variance 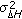 for each
for each 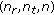 .
. -
(5)
 ,
, 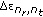 ,
, 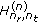 , and
, and  are independent of each other for each
are independent of each other for each 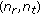 .
.
Given these assumptions, let us first define  as the interference contributed by the
as the interference contributed by the  th subcarrier of the interfering transmit antennas, that is, the co-subcarrier inter-antenna-interference (CSIAI), and define
th subcarrier of the interfering transmit antennas, that is, the co-subcarrier inter-antenna-interference (CSIAI), and define  as the ICI contributed by the subcarriers other than the
as the ICI contributed by the subcarriers other than the  th subcarrier of the interfering transmit antennas, that is, the intercarrier-interantenna interference (ICIAI). Then we derive
th subcarrier of the interfering transmit antennas, that is, the intercarrier-interantenna interference (ICIAI). Then we derive  and
and  as
as


where  is given by (1). The demodulation of
is given by (1). The demodulation of  is degraded by either
is degraded by either  or IAI (CSIAI plus ICIAI). In this paper, we assume that the integer part of the frequency offset has been estimated and corrected, and only the fractional part frequency offset is considered. Considering small frequency offsets, the following requirements are assumed to be satisfied:
or IAI (CSIAI plus ICIAI). In this paper, we assume that the integer part of the frequency offset has been estimated and corrected, and only the fractional part frequency offset is considered. Considering small frequency offsets, the following requirements are assumed to be satisfied:
-
(1)
 for all
for all  ,
, -
(2)
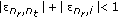 for all
for all 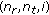 ,
, -
(3)
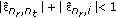 for all
for all 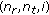 .
.
Condition 1 requires that each frequency offset should be much smaller than 1, and conditions 2 and 3 require that the sum of any two frequency offsets (and the frequency offset estimation results) should not exceed 1. The last two conditions are satisfied only if the estimation error does not exceed 0.5. If all these three conditions are satisfied simultaneously, we can represent  ,
,  ,
,  , and
, and  as
as




Therefore, the interference due to the  th subcarrier of transmit antennas (other than the
th subcarrier of transmit antennas (other than the  th transmit antenna, i.e., the interfering antennas) is
th transmit antenna, i.e., the interfering antennas) is


with  representing the higher-order item of
representing the higher-order item of  and
and  . It is easy to show that
. It is easy to show that  and
and  are zero-mean RVs and that their variances are given by
are zero-mean RVs and that their variances are given by


respectively. After averaging out frequency offset  , frequency offset estimation error
, frequency offset estimation error  , and channel estimation error
, and channel estimation error  for all
for all  , the average SINR of
, the average SINR of  (parameterized by only
(parameterized by only  ) is
) is

where  and
and  , independent of
, independent of  .
.
For signal demodulation in MIMO-OFDM, signal received in multiple receive antennas can be exploited to improve the receive SINR. In the following, equal gain combining (EGC) and maximal ratio combining (MRC) are considered.
3.2. SINR Analysis with EGC at Receive Antennas
In order to demodulate the signal transmitted by the  th transmit antenna, the
th transmit antenna, the  received signals are cophased and combined to improve the receiving diversity. Therefore, the EGC output is given by
received signals are cophased and combined to improve the receiving diversity. Therefore, the EGC output is given by

where  . After averaging out
. After averaging out  ,
,  , and
, and  for each
for each  , the average SINR of
, the average SINR of  is given by
is given by

When  is large enough, (17) can be further simplified as
is large enough, (17) can be further simplified as

3.3. SINR Analysis with MRC at Receive Antennas
In a MIMO-OFDM system with  receive antennas, based on the channel estimation
receive antennas, based on the channel estimation  for each
for each  , the received signal at all the
, the received signal at all the  receive antennas can be combined by using MRC, and therefore the combined output is given by
receive antennas can be combined by using MRC, and therefore the combined output is given by

where  . After averaging out
. After averaging out  ,
,  , and
, and  for each
for each  , the average SINR of
, the average SINR of  is
is

where we have defined  , and the noise part can be represented as
, and the noise part can be represented as  . When
. When  is large enough, (20) can be further simplified as
is large enough, (20) can be further simplified as

4. BER Performance
The BER as a function of SINR in MIMO-OFDM is derived in this section. We consider  -ary square QAM with Gray bit mapping. In the work of Rugini and Banelli [11], the BER of SISO-OFDM with frequency offset is developed. The BER analysis in [11] is now extended to MIMO-OFDM.
-ary square QAM with Gray bit mapping. In the work of Rugini and Banelli [11], the BER of SISO-OFDM with frequency offset is developed. The BER analysis in [11] is now extended to MIMO-OFDM.
As discussed in [11, 28, 29], the BER for the  th transmit antenna with the input constellation being
th transmit antenna with the input constellation being  -ary square QAM (Gray bit mapping) can be represented as
-ary square QAM (Gray bit mapping) can be represented as

where  and
and  are specified by signal constellation,
are specified by signal constellation,  is the average SINR of the
is the average SINR of the  th transmit antenna, and
th transmit antenna, and  is the error function (Please refer to [28] for the meaning of
is the error function (Please refer to [28] for the meaning of  and
and  .).
.).
Note that in MIMO-OFDM systems, the SINR at each subcarrier is an RV parameterized by the frequency offset and channel attenuation. In order to derive the average SINR of MIMO-OFDM systems, (22) should be averaged over the distribution of  as
as

where  ,
,  ,
,  , and
, and  . Since obtaining a close-form solution of (23) appears impossible, an infinite-series approximation of
. Since obtaining a close-form solution of (23) appears impossible, an infinite-series approximation of  is developed. In [11], the average is expressed as an infinite series of generalized hypergeometric functions.
is developed. In [11], the average is expressed as an infinite series of generalized hypergeometric functions.
From [30, page 939],  can be represented as an infinite series:
can be represented as an infinite series:

Therefore, (23) can be rewritten as

where  depends on the type of combining. Note that
depends on the type of combining. Note that  has been derived in Section 3 and that for the
has been derived in Section 3 and that for the  th subcarrier
th subcarrier  ,
,  ,
,  and
and  for each
for each  have been averaged out. Therefore,
have been averaged out. Therefore,  in (25) can be replaced by
in (25) can be replaced by  ; that is, the average BER can be expected over subcarrier
; that is, the average BER can be expected over subcarrier  (
( ), and finally
), and finally  can be simplified as
can be simplified as

where  is based on
is based on  instead of
instead of  . We first define
. We first define  and
and  , which will be used in the following subsections. We next give a recursive definition for
, which will be used in the following subsections. We next give a recursive definition for  for the following reception methods: (1) demodulation without combining, (2) EGC, and (3) MRC.
for the following reception methods: (1) demodulation without combining, (2) EGC, and (3) MRC.
Note that the SINR for each combining scenario (i.e., without combining, EGC, or MRC) is a function of the second-order statistics of the channel and frequency offset estimation errors (although the interference also comprises the fourth-order statistics of the frequency offset estimation errors, they are negligible as compared to the second-order statistics for small estimation errors). Any probability distribution with zero mean and the same variance will result in the same SINR. Therefore, the exact distributions need not be specified. However, when the BER is derived by using an infinite-series approximation, the actual distribution of the frequency offset estimation errors is required. In [31], it is shown that both the uniform distribution and Gaussian distribution are amenable to infinite-series solutions with closed-form formulas for the coefficients. In the following sections, the frequency offset estimation errors are assumed to be i.i.d. Gaussian RVs with mean zero and variance  [10].
[10].
4.1. BER without Receiving Combining
The BER measured at the  th receive antenna for the
th receive antenna for the  th transmit antenna can be approximated by (25) with
th transmit antenna can be approximated by (25) with  instead of
instead of  being used here; that is,
being used here; that is,

When  , we have
, we have  , as derived in Appendix A. The initial condition is given by
, as derived in Appendix A. The initial condition is given by

4.2. BER with EGC
For a MIMO-OFDM system with EGC reception, the average BER can be approximated by (25) with  instead of
instead of  being used here; that is,
being used here; that is,

Defining  ,
,  ,
,  , and
, and  , when
, when  , we have
, we have

as derived in Appendix B. The initial condition is given by

4.3. BER with MRC
For a MIMO-OFDM system with channel knowledge at the receiver, the receiving diversity can be optimized by using MRC, and the average BER can be approximated by (25) with  instead of
instead of  being used here; that is,
being used here; that is,

By defining  ,
,  with
with  is given by
is given by

as derived in Appendix C. The initial condition is given by

4.4. Complexity of the Infinite-Series Representation of BER
Infinite-series BER expression (27), (29), or (32) must be truncated in practice. The truncation error is negligible if the number of terms is large enough: Reference [31] shows that when the number of terms is as large as 50, the finite-order approximation is good. In this case, a total of  multiplication and
multiplication and  summation operations are needed to calculate the BER for each combining scheme.
summation operations are needed to calculate the BER for each combining scheme.
5. Numerical Results
Quasistatic MIMO wireless channels are assumed; that is, the channel impulse response is fixed over one OFDM symbol period but changes across the symbols. The simulation parameters are defined in Table 1.
The SINR degradation due to the residual frequency offsets is shown in Figure 2 for  and
and  10 dB. The SINR degradation increases with
10 dB. The SINR degradation increases with  . Because of IAI due to the multiple transmit antennas, the SINR performance of MIMO-OFDM with
. Because of IAI due to the multiple transmit antennas, the SINR performance of MIMO-OFDM with  is worse than that of SISO-OFDM, even though EGC or MRC is applied to exploit the receiving diversity. IAI in MIMO-OFDM can be suppressed by increasing the number of receive antennas. In this simulation, when
is worse than that of SISO-OFDM, even though EGC or MRC is applied to exploit the receiving diversity. IAI in MIMO-OFDM can be suppressed by increasing the number of receive antennas. In this simulation, when  , the average SINR with either EGC or MRC will be higher than that of SISO-OFDM system. For each MIMO scenario, MRC outperforms EGC.
, the average SINR with either EGC or MRC will be higher than that of SISO-OFDM system. For each MIMO scenario, MRC outperforms EGC.
The BER degradation due to the residual frequency offsets is shown in Figure 3 for  and
and  10 dB (
10 dB ( is the bit energy per noise per Hz). The BER for 4-phase PSK (QPSK) or 16QAM subcarrier modulation is considered. Just as with the case of SINR, the BER degrades with large
is the bit energy per noise per Hz). The BER for 4-phase PSK (QPSK) or 16QAM subcarrier modulation is considered. Just as with the case of SINR, the BER degrades with large  . For example, when
. For example, when  and
and  for QPSK (16QAM), a BER of
for QPSK (16QAM), a BER of  (
( ) or
) or  (
( ) is achieved with EGC or MRC at the receiver, respectively. When
) is achieved with EGC or MRC at the receiver, respectively. When  is increased to
is increased to  , a BER of
, a BER of  (
( ) or
) or  (
( ) can be achieved with EGC or MRC, respectively.
) can be achieved with EGC or MRC, respectively.
Figures 4 to 9 compare BERs of QPSK and 16QAM with different combining methods. Figures 4 and 5 consider SISO-OFDM. The BER is degraded due to the frequency offset and channel estimation errors. For a fixed channel estimation variance error  , a larger variance of frequency offset estimation error, that is,
, a larger variance of frequency offset estimation error, that is,  , implies a higher BER. For example, if
, implies a higher BER. For example, if  ,
,  20 dB and
20 dB and  , the BER with QPSK (16QAM) is about
, the BER with QPSK (16QAM) is about  (
( ); when
); when  increases to
increases to  , the BER with QPSK (16QAM) increases to
, the BER with QPSK (16QAM) increases to  (
( ).
).
IAI appears with multiple transmit antennas, and the BER will degrade as IAI increases. Note that since IAI cannot be totally eliminated in the presence of the frequency offset and channel estimation errors, a BER floor occurs at the high SNR. IAI can be reduced considerably by exploiting the receiving diversity by using either EGC or MRC, as shown in Figures 6, 7, 8, and 9. Without receiver combining, the BER is much worse than that in SISO-OFDM, simply because of the SINR degradation due to IAI. For example, when  and
and  , the BER with QPSK is about
, the BER with QPSK is about  when
when  , which is three times of that of SISO-OFDM (which is about
, which is three times of that of SISO-OFDM (which is about  ), as shown in Figure 6. For a given number of receive antennas, MRC can achieve a lower BER than that achieved with EGC, but the receiver requires accurate channel estimation. For example, in Figure 7, when
), as shown in Figure 6. For a given number of receive antennas, MRC can achieve a lower BER than that achieved with EGC, but the receiver requires accurate channel estimation. For example, in Figure 7, when  with
with  and 16QAM, the performance improvement of EGC (MRC) over that without combining is about 5.5 dB (6 dB), and that performance improvement increases to 7.5 dB (8.5 dB) if
and 16QAM, the performance improvement of EGC (MRC) over that without combining is about 5.5 dB (6 dB), and that performance improvement increases to 7.5 dB (8.5 dB) if  is increased to
is increased to  . By increasing the number of receive antennas to 4, this performance improvement is about 8.2 dB (9 dB) for EGC (MRC), with
. By increasing the number of receive antennas to 4, this performance improvement is about 8.2 dB (9 dB) for EGC (MRC), with  , or 11 dB (13.9 dB) for EGC (MRC), with
, or 11 dB (13.9 dB) for EGC (MRC), with  , as shown in Figure 9.
, as shown in Figure 9.
Our theoretical BER approximations are accurate at low SNR with/without diversity combining. However, the simulation and theory results diverge as the SNR increases, especially when  is large. For example, in Figure 9, with 16QAM, when (
is large. For example, in Figure 9, with 16QAM, when ( ,
,  ) and
) and  , about 1 dB difference exists between the simulation and the theoretical result for either EGC or MRC at high SNR. This discrepancy is due to several reasons. As the SNR increases, the system becomes interference limited. When
, about 1 dB difference exists between the simulation and the theoretical result for either EGC or MRC at high SNR. This discrepancy is due to several reasons. As the SNR increases, the system becomes interference limited. When  ,
,  , and
, and  are not large enough, the interferences may not be well approximated as Gaussian RVs with zero mean. In addition, with either EGC or MRC reception, the phase rotation or channel attenuation of the receive substreams should be estimated, and their estimation accuracy will also affect the combined SINR. The instant large phase or channel estimation error also contributes a deviation to the BER when using EGC or MRC.
are not large enough, the interferences may not be well approximated as Gaussian RVs with zero mean. In addition, with either EGC or MRC reception, the phase rotation or channel attenuation of the receive substreams should be estimated, and their estimation accuracy will also affect the combined SINR. The instant large phase or channel estimation error also contributes a deviation to the BER when using EGC or MRC.
6. Conclusions
The BER of MIMO-OFDM due to the frequency offset and channel estimation errors has been analyzed. The BER expressions for no combining, EGC, and MRC were derived. These expressions are in infinite-series form and can be truncated in practice. The simulation results show that the truncation error is negligible if the number of terms is large than 50.
Appendices
A. BER without Combining
Without loss of generality, the signal transmitted by the  th transmit antenna is assumed in this subsection to be demodulated at the
th transmit antenna is assumed in this subsection to be demodulated at the  th receive antenna. For each
th receive antenna. For each  ,
,  has a probability density function (PDF)
has a probability density function (PDF)  . When the number of receive antennas
. When the number of receive antennas  is larger than 2,
is larger than 2,  can be represented as
can be represented as

where  is defined in (15),
is defined in (15),  ,
,  , and
, and  . Equation (A.1) can be further derived as
. Equation (A.1) can be further derived as

From the last step of (A.1),  can be represented as a function of
can be represented as a function of  and
and  :
:

By resolving (A.3),  can be represented as
can be represented as

By replacing  in (A.2) with (A.4),
in (A.2) with (A.4),  can be finally simplified as
can be finally simplified as

B. BER of EGC
Without loss of generality, consider the demodulation of the signal transmitted by the  th transmit antenna. Define
th transmit antenna. Define

and  . As in Appendix A, when
. As in Appendix A, when  ,
,  can be represented as
can be represented as

where  ,
,  ,
,  , and
, and  . Equation (B.2) can be further simplified as
. Equation (B.2) can be further simplified as

From the last step of (B.2),  can be represented as a function of
can be represented as a function of  and
and  :
:

By resolving (B.4),  can be represented as
can be represented as

By replacing  in (B.3) with (B.5),
in (B.3) with (B.5),  can be finally simplified as
can be finally simplified as

C. BER of MRC
Without loss of generality, consider the demodulation of the signal transmitted by the  th transmit antenna. Define
th transmit antenna. Define  . When
. When  ,
,  can be represented as
can be represented as

where  and
and  . (C.1) can be further simplified as
. (C.1) can be further simplified as

From the last step of (C.1),  can be represented as a function of
can be represented as a function of  and
and  :
:

By resolving (C.3),  can be represented as
can be represented as

By replacing  in (C.2) with (C.4),
in (C.2) with (C.4),  can be finally simplified as
can be finally simplified as

References
Foschini GJ: Layered space-time architecture for wireless communication in a fading environment when using multi-element antennas. Bell Labs Technical Journal 1996, 1(2):41-59.
Foschini GJ, Gans MJ: On limits of wireless communications in a fading environment when using multiple antennas. Wireless Personal Communications 1998, 6(3):311-335. 10.1023/A:1008889222784
Goldsmith A, Jafar SA, Jindal N, Vishwanath S: Capacity limits of MIMO channels. IEEE Journal on Selected Areas in Communications 2003, 21(5):684-702. 10.1109/JSAC.2003.810294
Marzetta TL, Hochwald BM: Capacity of a mobile multiple-antenna communication link in rayleigh flat fading. IEEE Transactions on Information Theory 1999, 45(1):139-157. 10.1109/18.746779
Moose PH: Technique for orthogonal frequency division multiplexing frequency offset correction. IEEE Transactions on Communications 1994, 42(10):2908-2914. 10.1109/26.328961
Cui T, Tellambura C: Maximum-likelihood carrier frequency offset estimation for OFDM systems over frequency-selective fading channels. Proceedings of the IEEE International Conference on Communications, May 2005, Seoul, Korea 4: 2506-2510.
Minn H, Bhargava VK, Letaief KB: A robust timing and frequency synchronization for OFDM systems. IEEE Transactions on Wireless Communications 2003, 2(4):822-839.
Zhang Z, Zhao M, Zhou H, Liu Y, Gao J: Frequency offset estimation with fast acquisition in OFDM system. IEEE Communications Letters 2004, 8(3):171-173. 10.1109/LCOMM.2004.823423
Zhang Z, Jiang W, Zhou H, Liu Y, Gao J: High accuracy frequency offset correction with adjustable acquisition range in OFDM systems. IEEE Transactions on Wireless Communications 2005, 4(1):228-236.
Besson O, Stoica P: On parameter estimation of MIMO flat-fading channels with frequency offsets. IEEE Transactions on Signal Processing 2003, 51(3):602-613. 10.1109/TSP.2002.808102
Rugini L, Banelli P: BER of OFDM systems impaired by carrier frequency offset in multipath fading channels. IEEE Transactions on Wireless Communications 2005, 4(5):2279-2288.
Schmidl TM, Cox DC: Robust frequency and timing synchronization for OFDM. IEEE Transactions on Communications 1997, 45(12):1613-1621. 10.1109/26.650240
Morelli M, Mengali U: Improved frequency offset estimator for OFDM applications. IEEE Communications Letters 1999, 3(3):75-77. 10.1109/4234.752907
Ma X, Tepedelenlioǧlu C, Giannakis GB, Barbarossa S: Non-data-aided carrier offset estimators for OFDM with null subcarriers: identifiability, algorithms, and performance. IEEE Journal on Selected Areas in Communications 2001, 19(12):2504-2515. 10.1109/49.974615
Mody A, Stuber G: Synchronization for MIMO OFDM systems. Proceedings of IEEE Global Telecommunications Conference (GLOBECOM '01), November 2001, San Antonio, Tex, USA 1: 509-513.
Minn H, Al-Dhahir N, Li Y: Optimal training signals for MIMO OFDM channel estimation in the presence of frequency offset and phase noise. IEEE Transactions on Communications 2006, 54(10):1754-1759.
Ghogho M, Swami A: Training design for multipath channel and frequency-offset estimation in MIMO systems. IEEE Transactions on Signal Processing 2006, 54(10):3957-3965.
Loyka S, Gagnon F: Performance analysis of the V-BLASt algorithm: an analytical approach. IEEE Transactions on Wireless Communications 2004, 3(4):1326-1337. 10.1109/TWC.2004.830853
Loyka S, Gagnon F: V-BLAST without optimal ordering: analytical performance evaluation for rayleigh fading channels. IEEE Transactions on Communications 2006, 54(6):1109-1120. 10.1109/TCOMM.2006.876875
Li Y, Cimini LJ Jr., Sollenberger NR: Robust channel estimation for OFDM systems with rapid dispersive fading channels. IEEE Transactions on Communications 1998, 46(7):902-915. 10.1109/26.701317
Cui T, Tellambura C: Robust joint frequency offset and channel estimation for OFDM systems. Proceedings of the 60th IEEE Vehicular Technology Conference (VTC '04), September 2004, Los Angeles, Calif, USA 1: 603-607.
Minn H, Al-Dhahir N: Optimal training signals for MIMO OFDM channel estimation. IEEE Transactions on Wireless Communications 2006, 5(5):1158-1168.
Proakis JG: Digital Communications. 4th edition. McGraw-Hill, New York, NY, USA; 2001.
Dào DN, Tellambura C: Intercarrier interference self-cancellation space-frequency codes for MIMO-OFDM. IEEE Transactions on Vehicular Technology 2005, 54(5):1729-1738. 10.1109/TVT.2005.853477
Tang T, Heath RW Jr.: Space-time interference cancellation in MIMO-OFDM systems. IEEE Transactions on Vehicular Technology 2005, 54(5):1802-1816. 10.1109/TVT.2005.851299
Giangaspero L, Agarossi L, Paltenghi G, Okamura S, Okada M, Komaki S: Co-channel interference cancellation based on MIMO OFDM systems. IEEE Wireless Communications 2002, 9(6):8-17. 10.1109/MWC.2002.1160076
Stamoulis A, Diggavi SN, Al-Dhahir N: Intercarrier interference in MIMO OFDM. IEEE Transactions on Signal Processing 2002, 50(10):2451-2464. 10.1109/TSP.2002.803347
Cho K, Yoon D: On the general BER expression of one- and two-dimensional amplitude modulations. IEEE Transactions on Communications 2002, 50(7):1074-1080. 10.1109/TCOMM.2002.800818
Yang L-L, Hanzo L: Recursive algorithm for the error probability evaluation of M-QAM. IEEE Communications Letters 2000, 4(10):304-306. 10.1109/4234.880816
Gradshteyn IS, Ryzhik IM: Table of Integrals, Series, and Products. 5th edition. Academic Press, New York, NY, USA; 1994.
Zhang Z, Tellambura C: The effect of imperfect carrier frequency offset estimation on an OFDMA uplink. IEEE Transactions on Communications 2009, 57(4):1025-1030.
Zhang Z, Zhang W, Tellambura C: BER of MIMO-OFDM systems with carrier frequency offset and channel estimation errors. Proceedings of IEEE International Conference on Communications (ICC '07), June 2007, Glasgow, Scotland 5473-5477.
Acknowledgments
This paper has been presented in part at the IEEE Globecom 2007 [32]. Although the conference paper was a brief version of this journal paper and they have the same results and conclusion, this journal paper provides a more detailed proof to each result appeared in the IEEE ICC 2007 paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zhang, Z., Zhang, L., You, M. et al. Bit Error Rate Approximation of MIMO-OFDM Systems with Carrier Frequency Offset and Channel Estimation Errors. J Wireless Com Network 2010, 176083 (2010). https://doi.org/10.1155/2010/176083
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/176083

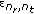 is an i.i.d. RV with mean zero and variance
is an i.i.d. RV with mean zero and variance  for all
for all 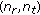 .
.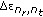 is an i.i.d. RV with mean zero and variance
is an i.i.d. RV with mean zero and variance 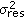 for each
for each  .
. for each
for each  .
. is an i.i.d. RV with mean zero and variance
is an i.i.d. RV with mean zero and variance 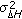 for each
for each 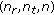 .
. ,
, 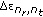 ,
, 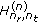 , and
, and  are independent of each other for each
are independent of each other for each 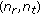 .
. for all
for all  ,
,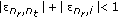 for all
for all 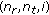 ,
,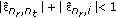 for all
for all 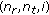 .
.


 ).
).

 ).
).

 ).
).

 ).
).

 ).
).

 ).
).