- Research Article
- Open access
- Published:
 -Net Approach to Sensor
-Net Approach to Sensor 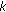 -Coverage
-Coverage
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 192752 (2009)
Abstract
Wireless sensors rely on battery power, and in many applications it is difficult or prohibitive to replace them. Hence, in order to prolongate the system's lifetime, some sensors can be kept inactive while others perform all the tasks. In this paper, we study the  -coverage problem of activating the minimum number of sensors to ensure that every point in the area is covered by at least
-coverage problem of activating the minimum number of sensors to ensure that every point in the area is covered by at least  sensors. This ensures higher fault tolerance, robustness, and improves many operations, among which position detection and intrusion detection. The
sensors. This ensures higher fault tolerance, robustness, and improves many operations, among which position detection and intrusion detection. The  -coverage problem is trivially NP-complete, and hence we can only provide approximation algorithms. In this paper, we present an algorithm based on an extension of the classical
-coverage problem is trivially NP-complete, and hence we can only provide approximation algorithms. In this paper, we present an algorithm based on an extension of the classical  -net technique. This method gives an
-net technique. This method gives an  -approximation, where
-approximation, where  is the number of sensors in an optimal solution. We do not make any particular assumption on the shape of the areas covered by each sensor, besides that they must be closed, connected, and without holes.
is the number of sensors in an optimal solution. We do not make any particular assumption on the shape of the areas covered by each sensor, besides that they must be closed, connected, and without holes.
1. Introduction
Coverage problems have been extensively studied in the context of sensor networks (see, e.g., [1–4]). The objective of sensor coverage problems is to minimize the number of active sensors, to conserve energy usage, while ensuring that the required region is sufficiently monitored by the active sensors. In an over-deployed network we can also seek  -coverage, in which every point in the area is covered by at least
-coverage, in which every point in the area is covered by at least  sensors. This ensures higher fault tolerance, robustness, and improves many operations, among which position detection and intrusion detection.
sensors. This ensures higher fault tolerance, robustness, and improves many operations, among which position detection and intrusion detection.
The  -coverage problem is trivially NP-complete, and hence we focus on designing approximation algorithms. In this paper, we extend the well-known
-coverage problem is trivially NP-complete, and hence we focus on designing approximation algorithms. In this paper, we extend the well-known  -net technique to our problem and present an
-net technique to our problem and present an  -factor approximation algorithm, where
-factor approximation algorithm, where  is the size of the optimal solution. The classical greedy algorithm for set cover [5], when applied to
is the size of the optimal solution. The classical greedy algorithm for set cover [5], when applied to  -coverage, delivers an
-coverage, delivers an  -approximation solution, where
-approximation solution, where  is the number of target points to be covered. Our approximation algorithm is an improvement over the greedy algorithm, since our approximation factor of
is the number of target points to be covered. Our approximation algorithm is an improvement over the greedy algorithm, since our approximation factor of  is independent of
is independent of  and of the number of target points.
and of the number of target points.
Instead of solving the sensor's  -coverage problem directly, we consider a dual problem, the
-coverage problem directly, we consider a dual problem, the  -hitting set. In the
-hitting set. In the  -hitting set problem, we are given sets and points, and we look for the minimum number of points that "hit" each set at least
-hitting set problem, we are given sets and points, and we look for the minimum number of points that "hit" each set at least  times (a set is hit by a point if it contains it). Brönnimann and Goodrich were the first [6] to solve the hitting set using the
times (a set is hit by a point if it contains it). Brönnimann and Goodrich were the first [6] to solve the hitting set using the  -net technique [7]. In this paper, we introduce a generalization of
-net technique [7]. In this paper, we introduce a generalization of  -nets, which we call
-nets, which we call  -nets. Using
-nets. Using  -nets with the Brönnimann and Goodrich algorithm's [6], we can solve the
-nets with the Brönnimann and Goodrich algorithm's [6], we can solve the  -hitting set, and hence the sensor's
-hitting set, and hence the sensor's  -coverage problem. Our main contribution is a way of constructing
-coverage problem. Our main contribution is a way of constructing  -nets by random sampling. A recent Infocom paper [8] uses
-nets by random sampling. A recent Infocom paper [8] uses  -nets to solve the
-nets to solve the  -coverage problem. However we believe that their result is fundamentally flawed (see Section 2.1 for more details). So, to the best of our knowledge, we are the first to give a correct extension of
-coverage problem. However we believe that their result is fundamentally flawed (see Section 2.1 for more details). So, to the best of our knowledge, we are the first to give a correct extension of  -nets for the
-nets for the  -coverage problem.
-coverage problem.
Paper Organization
The rest of the paper is organized as follow. The  -coverage problem is introduced in Section 2. Section 2.1 contains detailed discussion about related work. The
-coverage problem is introduced in Section 2. Section 2.1 contains detailed discussion about related work. The  -net approach is presented in Section 3.
-net approach is presented in Section 3.
2. Problem Formulation and Related Work
We start by defining the sensing region and then we will define the  -coverage problem with sensors. In the literature, sensing regions have been often modeled as disks. In this paper, we consider sensing regions of general shape, because this reflects a more realistic scenario.
-coverage problem with sensors. In the literature, sensing regions have been often modeled as disks. In this paper, we consider sensing regions of general shape, because this reflects a more realistic scenario.
Definition 1 (sensing region).
The sensing region of a sensor is the area "covered" by a sensor. Sensing regions can have any shape that is closed, connected, and without holes, as in Figure 1(a). Often, sensing regions are modeled as disks as in Figure 1(b), but we consider more general shapes.
Definition 2 (target points).
Target points are the given points in the 2D plane that we wish to cover using the sensors.
 -SC Problem
-SC Problem
Given a set of sensors with fixed positions and a set of target points, select the minimum number of sensors, such that each target point is covered (is contained in the selected sensing region) by at least  of the selected sensors.
of the selected sensors.
For simplicity, we have defined the above  -SC problem's objective as coverage of a set of given target points. However, as discussed later, our algorithms and techniques easily generalize to the problem of covering a given area.
-SC problem's objective as coverage of a set of given target points. However, as discussed later, our algorithms and techniques easily generalize to the problem of covering a given area.
Example 1.
Suppose we are given 4 sensors and 20 points as in Figure 2(a), and we want to select the minimum number of sensors to 2-cover all points. In this particular example, 2 sensors are not enough to 2-cover all points. Instead, 3 sensors suffice, as shown in Figure 2(b).
2.1. Related Work
In the recent years, there has been a lot of research done [1–3, 9] to address the coverage problem in sensor network. In particular, Slijepcevic and Potkonjak [3] design a centralized heuristic to select mutually exclusive sensor covers that independently cover the network region. In [2], Charkrabarty et al. investigate linear programming techniques to optimally place a set of sensors on a sensor field for a complete coverage of the field. In [10], Shakkottai et al. consider an unreliable sensor network, and derive necessary and sufficient conditions for the coverage of the region and connectivity of the network with high probability. In one of our prior works [1], we designed a greedy approximation algorithm that delivers a connected sensor cover within a logarithmic factor of the optimal solution; this work was later generalized to  -coverage in [11].
-coverage in [11].
Recently, Hefeeda and Bagheri [8] used the well-known  -net technique to solve the problem of
-net technique to solve the problem of  -covering the sensor's locations. However, we strongly believe that their result is fundamentally flawed. Essentially, they select a set of subsets of size
-covering the sensor's locations. However, we strongly believe that their result is fundamentally flawed. Essentially, they select a set of subsets of size  (called
(called  -flowers) represented by the center of their locations. However, their result is based on the following incorrect claim that if the centers of a set of
-flowers) represented by the center of their locations. However, their result is based on the following incorrect claim that if the centers of a set of  -flowers 1-cover a set of points
-flowers 1-cover a set of points  , then the set of sensors associated with the
, then the set of sensors associated with the  -flowers will
-flowers will  -cover
-cover  . In addition, in their analysis, they implicitly assume that an optimal solution can be represented as a disjoint union of
. In addition, in their analysis, they implicitly assume that an optimal solution can be represented as a disjoint union of  -flowers, which is incorrect. In this paper we present a correct extension of the
-flowers, which is incorrect. In this paper we present a correct extension of the  -net technique for the
-net technique for the  -coverage problem in sensor networks.
-coverage problem in sensor networks.
Two closely related problems to the sensor-coverage problem are set cover and hitting set problems. The area covered by a sensor can be thought as a set, which contains the points covered by that sensor. The hitting set problem is a "dual" of the set cover problem. In both set cover and hitting set problems, we are given sets and elements. While in set cover the goal is to select the minimum number of sets to cover all elements/points, in hitting set the goal is to select a subset of elements/points such that each set is hit. The classical result for set cover [5] gives an  -approximation algorithm, where
-approximation algorithm, where  is the number of target points to be covered. The same greedy algorithm also delivers a
is the number of target points to be covered. The same greedy algorithm also delivers a  -approximation solution for the
-approximation solution for the  -SC problem. In contrast, the result in this paper yields an
-SC problem. In contrast, the result in this paper yields an  -approximation algorithm for the
-approximation algorithm for the  -SC problem, where
-SC problem, where  is the optimal size (i.e., minimum number of sensors needed to provide
is the optimal size (i.e., minimum number of sensors needed to provide  -coverage of the given target points). Note that our approximation factor is independent of
-coverage of the given target points). Note that our approximation factor is independent of  and of the number of target points.
and of the number of target points.
Brönnimann and Goodrich [6] were the first to use the  -net technique [7] to solve the hitting set problem and hence the set cover with an
-net technique [7] to solve the hitting set problem and hence the set cover with an  -approximation, where
-approximation, where  is the size of the optimal solution. In this paper, we extend their
is the size of the optimal solution. In this paper, we extend their  -net technique to
-net technique to  -coverage. It is interesting to observe that our extension is independent of
-coverage. It is interesting to observe that our extension is independent of  and it gives an
and it gives an  -approximation also for
-approximation also for  -coverage. For the particular case of 1-coverage with disks, it is possible to build "small"
-coverage. For the particular case of 1-coverage with disks, it is possible to build "small"  -nets using the method of Matoušek, Seidel, and Welzl [12] and obtain a constant-factor approximation for the 1-hitting set problem. Their method [12] can be easily extended to
-nets using the method of Matoušek, Seidel, and Welzl [12] and obtain a constant-factor approximation for the 1-hitting set problem. Their method [12] can be easily extended to  -hitting set, and this would give a constant-factor approximation for the
-hitting set, and this would give a constant-factor approximation for the  -SC problem when the sensing regions are disks. However, in this paper we focus on sensing regions of arbitrary shapes and sizes, as long as they are closed, connected, and without holes.
-SC problem when the sensing regions are disks. However, in this paper we focus on sensing regions of arbitrary shapes and sizes, as long as they are closed, connected, and without holes.
Another related problem is the art gallery problem (see [13] for a survey) which is to place a minimum number of guards in a polygon so that each point in the polygon is visible from at least one of the guards. Guards may be looked upon as sensors with infinite range. However, in this paper, we focus on selecting already deployed sensor.
3. The  -Net-Based Approach
-Net-Based Approach
In this section, we present an algorithm based on the classical  -net technique, to solve the
-net technique, to solve the  -coverage problem. The classical
-coverage problem. The classical  -net technique is used to solve the hitting set problem, which is the dual of the set cover problem. The
-net technique is used to solve the hitting set problem, which is the dual of the set cover problem. The  -SC problem is essentially a generalization of the set cover problem—thus, we will extend the
-SC problem is essentially a generalization of the set cover problem—thus, we will extend the  -net technique to solve the corresponding generalization of the hitting set problem.
-net technique to solve the corresponding generalization of the hitting set problem.
3.1. Hitting Set Problem and the  -Net Technique
-Net Technique
We start by describing the use of the classical  -net technique to solve the traditional hitting set problem. We begin with a couple of formal definitions.
-net technique to solve the traditional hitting set problem. We begin with a couple of formal definitions.
Set Cover (SC); Hitting Set (HS)
Given a set of points  and a collection of sets
and a collection of sets  , the set cover (SC) problem is to select the minimum number of sets from
, the set cover (SC) problem is to select the minimum number of sets from  whose union contains (covers) all points in
whose union contains (covers) all points in  . The hitting set (HS) problem is to select the minimum number of points from
. The hitting set (HS) problem is to select the minimum number of points from  such that all sets in
such that all sets in  are "hit" (a set is considered hit, if one of its points has been selected).
are "hit" (a set is considered hit, if one of its points has been selected).
Note that HS is a dual of SC, and hence solving HS is sufficient to solve SC.
We now define  -nets. Intuitively, an
-nets. Intuitively, an  -net is a set of points that hits all large sets (but may not hit the smaller ones). For the overall scheme, we will assign weights to points, and use a generalized concept of weighted
-net is a set of points that hits all large sets (but may not hit the smaller ones). For the overall scheme, we will assign weights to points, and use a generalized concept of weighted  -nets that must hit all large-weighted sets.
-nets that must hit all large-weighted sets.
Definition 3 ( -Net; Weighted
-Net; Weighted  -Net).
-Net).
Given a set system  , where
, where  is a set of points and
is a set of points and  is a collection of sets, a subset
is a collection of sets, a subset  is an
is an  -net if for every set
-net if for every set  in
in  s.t.
s.t.  , we have that
, we have that  .
.
Given a set system  , and a weight function
, and a weight function  , define
, define  for
for  . A subset
. A subset  is a weighted
is a weighted -net for
-net for  if for every set
if for every set  in
in  s.t.
s.t.  , we have that
, we have that  .
.
Using  -Nets to Solve the Hitting Set Problem
-Nets to Solve the Hitting Set Problem
The original algorithm for solving hitting set problem using  -net was invented by Brönnimann and Goodrich [6]. Below, we give a high-level description of their overall approach (referred to as the BG algorithm), because it will help understand our own extension. We begin by showing how
-net was invented by Brönnimann and Goodrich [6]. Below, we give a high-level description of their overall approach (referred to as the BG algorithm), because it will help understand our own extension. We begin by showing how  -nets are related to hitting sets, and then, show how to use
-nets are related to hitting sets, and then, show how to use  -nets to actually compute hitting sets.
-nets to actually compute hitting sets.
Let us assume that we have a black-box to compute weighted  -nets, and that we know the optimal hitting set
-nets, and that we know the optimal hitting set  which is of size
which is of size  . Now, define a weight function
. Now, define a weight function  as
as  if
if  and
and  otherwise. Then, set
otherwise. Then, set  , and use the black-box to compute a weighted
, and use the black-box to compute a weighted  -net for
-net for  . It is easy to see that this weighted
. It is easy to see that this weighted  -net is actually a hitting set for
-net is actually a hitting set for  , since
, since  for all sets
for all sets  . There are known techniques [7] to compute weighted
. There are known techniques [7] to compute weighted  -nets of size
-nets of size  for set systems with a constant VC-dimension (defined later); thus, the above gives us an
for set systems with a constant VC-dimension (defined later); thus, the above gives us an  -approximate solution. For the particular case of disks, it is possible to construct
-approximate solution. For the particular case of disks, it is possible to construct  -nets of size
-nets of size  [12] and hence obtain a constant-factor approximation.
[12] and hence obtain a constant-factor approximation.
However, in reality, we do not know the optimal hitting set. So, we iteratively guess its size  , starting with
, starting with  and progressively doubling
and progressively doubling  until we obtain a hitting set solution (using the above approach). Also, to "converge" close to the
until we obtain a hitting set solution (using the above approach). Also, to "converge" close to the  above, we use the following scheme. We start with all weights set to 1. If the computed weighted
above, we use the following scheme. We start with all weights set to 1. If the computed weighted  -net is not a hitting set, then we pick one set in
-net is not a hitting set, then we pick one set in  that is not hit by it and double the weights of all points that it contains. Then, we iterate with the new weights. It can be shown that if the estimate of
that is not hit by it and double the weights of all points that it contains. Then, we iterate with the new weights. It can be shown that if the estimate of  is correct and using
is correct and using  , then we are guaranteed to find a hitting set using the previous approach after a certain number of iterations. Thus, if we do not find a hitting set after enough iterations, we double the estimate of
, then we are guaranteed to find a hitting set using the previous approach after a certain number of iterations. Thus, if we do not find a hitting set after enough iterations, we double the estimate of  and try again. It can be shown in [6] that the previous approach finds an
and try again. It can be shown in [6] that the previous approach finds an  -approximate hitting set in polynomial time for set systems with constant VC-dimension (defined below), where
-approximate hitting set in polynomial time for set systems with constant VC-dimension (defined below), where  is the size of the optimal hitting set.
is the size of the optimal hitting set.
VC-dimension
We end the description of the BG algorithm, with the definition of Vapnik- ervonenkis (VC) dimension of set systems. Informally, the VC-dimension of a set system
ervonenkis (VC) dimension of set systems. Informally, the VC-dimension of a set system  is a mathematical way of characterizing the "regularity" of the sets in
is a mathematical way of characterizing the "regularity" of the sets in  (with respect to the points
(with respect to the points  ) in the system. A bounded VC-dimension allows the construction of an
) in the system. A bounded VC-dimension allows the construction of an  -net through random sampling of large enough size. The VC-dimension is formally defined in terms of set shattering, as follows.
-net through random sampling of large enough size. The VC-dimension is formally defined in terms of set shattering, as follows.
Definition 4 (VC-dimension).
A set  is considered to be shattered by a collection of sets C if for each
is considered to be shattered by a collection of sets C if for each  , there exists a set
, there exists a set  such that
such that  . The VC-dimension of a set system
. The VC-dimension of a set system  is the cardinality of the largest set of points in
is the cardinality of the largest set of points in  that can be shattered by
that can be shattered by  .
.
In our case, the VC dimension is at most 23 as given by the following theorem by Valtr [14].
Theorem 1.
If  is compact and simply connected, then VC-dimension of the set system
is compact and simply connected, then VC-dimension of the set system  , where
, where  is a set of points and
is a set of points and  is a collection of sets, is at most 23.
is a collection of sets, is at most 23.
Note that for a finite collection of sensors, whose covering regions are compact and simply connected, the dual is compact and simply connected too.
3.2. 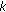 -Hitting Set Problem and the
-Hitting Set Problem and the  -Net Technique
-Net Technique
We now formulate the  -hitting set (
-hitting set ( -HS) problem, which is a generalization of the hitting set problem, normely, we want each set in the system to be hit by
-HS) problem, which is a generalization of the hitting set problem, normely, we want each set in the system to be hit by  selected points.
selected points.
Definition 5 ( -hitting set (
-hitting set ( -HS)).
-HS)).
Given a set system  , the
, the  -hitting set(
-hitting set( -HS) problem is to find the smallest subset of points
-HS) problem is to find the smallest subset of points  with at most one point for each sibling-set such that
with at most one point for each sibling-set such that  hits every set in
hits every set in  at least
at least  times.
times.
3.2.1. Connection between 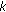 -HS and
-HS and  -SC Problem
-SC Problem
Note that the previous  -HS problem is the (generalized) dual of our sensor
-HS problem is the (generalized) dual of our sensor  -coverage problem (
-coverage problem ( -SC problem). Essentially, each point in the
-SC problem). Essentially, each point in the  -HS problem corresponds to a sensing region of a sensor, and each set in the
-HS problem corresponds to a sensing region of a sensor, and each set in the  -HS problem corresponds to a target point. In what followos, we describe how to solve the
-HS problem corresponds to a target point. In what followos, we describe how to solve the  -HS problem, which essentially solves our
-HS problem, which essentially solves our  -SC problem. To solve the
-SC problem. To solve the  -HS, we need to define and use a generalized notion of
-HS, we need to define and use a generalized notion of  -net.
-net.
Definition 6 (weighted  -net).
-net).
Suppose that  is a sibling-set system, and
is a sibling-set system, and  is a weight function. Define
is a weight function. Define  for
for  . A set
. A set  is a weighted
is a weighted -net for
-net for  if
if  , whenever
, whenever  and
and  .
.
Using  -Nets to Solve
-Nets to Solve  -HS
-HS
We can solve the  -HS problem using the BG algorithm [6], without much modification. However, we need an algorithm compute weighted
-HS problem using the BG algorithm [6], without much modification. However, we need an algorithm compute weighted  -nets. The below theorem states that an appropriate random sampling of about
-nets. The below theorem states that an appropriate random sampling of about  points from
points from  gives a
gives a  -net with high probability, if the set system
-net with high probability, if the set system  has a bounded VC-dimension. For the sake of clarity, we defer the proof of the following theorem.
has a bounded VC-dimension. For the sake of clarity, we defer the proof of the following theorem.
Theorem 2.
Let  be a weighted set system. For a given number
be a weighted set system. For a given number  , let
, let  be a subset of points of size
be a subset of points of size  picked randomly from
picked randomly from  with probability proportional to the total weight of the points in such subset.
with probability proportional to the total weight of the points in such subset.
Then, for

the subset  is a weighted
is a weighted  -sibling-net with probability at least
-sibling-net with probability at least  , where
, where  , and
, and  is the VC-dimension of the set system.
is the VC-dimension of the set system.
Now, based on the prevouise theorem, we can use the BG algorithm with some modifications to solve the  -HS problem. Essentially, we estimate the size
-HS problem. Essentially, we estimate the size  of an optimal
of an optimal  -HS (starting with 1 and iteratively doubling it), set
-HS (starting with 1 and iteratively doubling it), set  , and use Theorem 2 to compute a
, and use Theorem 2 to compute a  -net
-net  of size
of size  . Theorem 2 gives a
. Theorem 2 gives a  -net with high probability. It is possible to check efficiently if the obtained set is indeed a
-net with high probability. It is possible to check efficiently if the obtained set is indeed a  -net. If it is not, we can try again until we get one. On average, a small number of trials are sufficient to obtain a
-net. If it is not, we can try again until we get one. On average, a small number of trials are sufficient to obtain a  -net. If
-net. If  is indeed a
is indeed a  -hitting set, we stop; else, we pick a set in the system
-hitting set, we stop; else, we pick a set in the system  that is not
that is not  -hit and double the weight of all the points it contains. With the new weights, we iterate the process. It can be shown that within
-hit and double the weight of all the points it contains. With the new weights, we iterate the process. It can be shown that within  iterations of weight-doubling, we are guaranteed to get a
iterations of weight-doubling, we are guaranteed to get a  -HS solution if the optimal size of a
-HS solution if the optimal size of a  -HS is indeed
-HS is indeed  . See Appendix for the proof, which is similar to the one for BG in [6]. Thus, after
. See Appendix for the proof, which is similar to the one for BG in [6]. Thus, after  iterations, if we have not found a
iterations, if we have not found a  -HS, we can double our current estimate of
-HS, we can double our current estimate of  , and iterate. see Algorithm 1. The below theorem shows that the previous algorithm gives an
, and iterate. see Algorithm 1. The below theorem shows that the previous algorithm gives an  -approximate solution in polynomial time with high probability for general sets. The proof of the following theorem is again similar to that for the BG algorithm [6].
-approximate solution in polynomial time with high probability for general sets. The proof of the following theorem is again similar to that for the BG algorithm [6].
Algorithm 1: Solving  -HS problem using
-HS problem using  -nets. Since
-nets. Since  -HS is the dual of
-HS is the dual of  -SC, this algorithm also solves
-SC, this algorithm also solves  -SC (in
-SC (in  -SC,
-SC,  corresponds to the set of sensors, and C to the set of target points).
corresponds to the set of sensors, and C to the set of target points).
-
1
Given a set system
 .
. -
2
for (
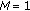 ;
;  ;
; 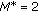 )
) -
3
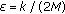
-
4
reset the weights of all points in
 to 1;
to 1; -
5
for (
 ;
;  ;
;  )
) -
6
Compute a
 -net
-net  of size
of size  using Theorem 2;
using Theorem 2; -
7
if each set in
 is
is 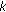 -hit by
-hit by 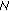 , return
, return 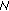 ;
; -
8
select a set in
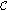 that is not
that is not  -hit, and double the weight of all the points in the set;
-hit, and double the weight of all the points in the set;
Theorem 3.
The algorithm described previous (Algorithm 1) runs in time  and gives a
and gives a  -approximate solution for the
-approximate solution for the  -HS problem for a general set systems
-HS problem for a general set systems  of constant VC-dimension, where
of constant VC-dimension, where  is the optimal size of a
is the optimal size of a  -HS.
-HS.
Proof.
The outer for loop, where  is doubled each time, is run at most
is doubled each time, is run at most  times. The inner for loop, where the weights are doubled for a set, is executed at most
times. The inner for loop, where the weights are doubled for a set, is executed at most  times. Computing a
times. Computing a  -net using Theorem 2 takes at most
-net using Theorem 2 takes at most  time, while the doubling-weight process may take up to
time, while the doubling-weight process may take up to  time.
time.
We now prove the approximation factor. An optimal algorithm would find a  -hitting set of size
-hitting set of size  . If the VC-dimension is a constant, the
. If the VC-dimension is a constant, the  -HS method of Theorem 2 finds a
-HS method of Theorem 2 finds a  -net of size
-net of size  . So if
. So if  , the size of the
, the size of the  -hitting set is
-hitting set is  , which is an
, which is an  -approximation.
-approximation.
Outline of Proof of Theorem 2
There are two challenges in generalizing the random-sampling technique of [7], namely, (i) sampling with replacement cannot be used, and (ii) weights must be part of the sampling process.
3.2.2. Challenges in Extending the Technique of [7] to  -Hitting Set
-Hitting Set
The classical method [7] of constructing a  -net consists of randomly picking a set
-net consists of randomly picking a set  of at least
of at least  points, for a certain
points, for a certain  , where each point is picked independently and randomly from the given set of points. This way of constructing a
, where each point is picked independently and randomly from the given set of points. This way of constructing a  -net may result in duplicate points in
-net may result in duplicate points in  , but the presence of duplicates does not cause a problem in the analysis. Thus, we can also construct weighted
, but the presence of duplicates does not cause a problem in the analysis. Thus, we can also construct weighted  -net easily by emulating weights using duplicated copies of the same point. The above described approach works well for 1-hitting set, partly because we do not count the number of times each set is hit. However, for the case of
-net easily by emulating weights using duplicated copies of the same point. The above described approach works well for 1-hitting set, partly because we do not count the number of times each set is hit. However, for the case of  -hitting set, when constructing a
-hitting set, when constructing a  -net, we need to ensure that the number of distinct points that hit each set is at least
-net, we need to ensure that the number of distinct points that hit each set is at least  . Thus, constructing a
. Thus, constructing a  -net by picking points independently at random (with duplicates) does not lead to correct analysis. Instead, we suggest a novel method to construct a weighted
-net by picking points independently at random (with duplicates) does not lead to correct analysis. Instead, we suggest a novel method to construct a weighted  -net
-net  by: (i) selecting a random subset of points (without duplicates) at once, and (ii) including the weights directly in the previous sampling process. To the best of our knowledge, we are the first one to propose this extension (as discussed before, [8] uses
by: (i) selecting a random subset of points (without duplicates) at once, and (ii) including the weights directly in the previous sampling process. To the best of our knowledge, we are the first one to propose this extension (as discussed before, [8] uses  -nets to solve sensor's
-nets to solve sensor's  -coverage, but their method is flawed).
-coverage, but their method is flawed).
Proof Sketch of Theorem 2
Let  be as given by (1), and let
be as given by (1), and let  be the subset of points randomly picked from
be the subset of points randomly picked from  as described in Theorem 2. After picking
as described in Theorem 2. After picking  , pick another set
, pick another set  (for the purposes of the below analysis) in the same way as
(for the purposes of the below analysis) in the same way as  . We now define two events
. We now define two events

where  and
and  . The proof consists of 3 major steps.
. The proof consists of 3 major steps.
-
(1)
First, we show that
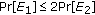 .
. -
(2)
Then, it is easier to bound the probability of
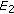
 (3)
(3) -
(3)
Finally, we have that
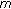 verifies
verifies 
The outline of each step follows.
( ) From the definition of conditional probability
) From the definition of conditional probability

So we just need to show that  . Let
. Let  (where
(where  's are pairwise different). Define the random variable
's are pairwise different). Define the random variable

Set  , and we have
, and we have  . It is possible to show that
. It is possible to show that  , and
, and  . Applying Chebyshev's inequality
. Applying Chebyshev's inequality

the result follows.
( ) We use an alternate view. Instead of picking
) We use an alternate view. Instead of picking  and then
and then  , pick
, pick  of size
of size  , then pick
, then pick  and set
and set  . It can be shown that the two views are equivalent. Now, define
. It can be shown that the two views are equivalent. Now, define

Since  and
and  are disjoint
are disjoint  and then
and then  if and only if
if and only if  . So we have that
. So we have that  happens only if
happens only if  . By counting the number of ways of choosing
. By counting the number of ways of choosing  s.t.
s.t.  , we can bound
, we can bound 

Since  depends only on the intersection
depends only on the intersection 

( ) it is similar to [7].
) it is similar to [7].
Please, refer to Appendix for the detailed proof.
Remark 1.
Note that the approximation factor of Theorem 3 could be improved, if we could design an algorithm to construct smaller  -nets. For instance, if we could construct a
-nets. For instance, if we could construct a  -net of size
-net of size  , then we would have a constant-factor approximation for the
, then we would have a constant-factor approximation for the  -HS problem. For the particular case of disks, it is easy to extend the method in [12] to build a
-HS problem. For the particular case of disks, it is easy to extend the method in [12] to build a  -net of size
-net of size  (see Appendix for more details). Essentially, it is enough to replace
(see Appendix for more details). Essentially, it is enough to replace  with
with  and the proof follows through. Also note that the dual of disks and points is also composed by disks and points.
and the proof follows through. Also note that the dual of disks and points is also composed by disks and points.
3.2.3. Distributed  -Net Approach
-Net Approach
Distributed implementation of the  -net algorithm requires addressing the following main challenges.
-net algorithm requires addressing the following main challenges.
-
(1)
We need to construct a
 -net, through some sort of distributed randomized selection.
-net, through some sort of distributed randomized selection. -
(2)
For each constructed
 -net
-net  , we need to verify in a distributed manner whether
, we need to verify in a distributed manner whether  is indeed a
is indeed a 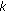 -coverage set (
-coverage set ( -hitting set in the dual).
-hitting set in the dual). -
(3)
If
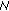 is not a
is not a 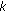 -coverage set, then we need to select one target point (a set in the dual) that is not
-coverage set, then we need to select one target point (a set in the dual) that is not 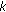 -covered by
-covered by  and double the weights of all the sensing regions covering it.
and double the weights of all the sensing regions covering it.
We address the previous challenges in the following manner. First, we execute the distributed algorithm in rounds, where a round corresponds to one execution of the inner for loop of Algorithm 1 (i.e., execution of the sampling algorithm for a particular set of weights and a particular estimate of  ). We implement rounds in a weakly synchronized manner using internal clocks. Now, for each of the previous challenges, we use the following solutions.
). We implement rounds in a weakly synchronized manner using internal clocks. Now, for each of the previous challenges, we use the following solutions.
-
(1)
Each sensor keeps an estimate of the total weight of the system and computes
 independently. To select
independently. To select  sensors, each sensor decides to select itself independently with a probability
sensors, each sensor decides to select itself independently with a probability 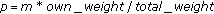 , resulting in selection of
, resulting in selection of  sensors (in expectation).
sensors (in expectation). -
(2)
Locally, verify
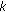 -coverage of the owned target points, by exchanging messages with near-by (that cover a common target point) sensors. If a target point owned by a sensor
-coverage of the owned target points, by exchanging messages with near-by (that cover a common target point) sensors. If a target point owned by a sensor 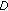 and its near-by sensors are all
and its near-by sensors are all  -covered for a certain number of rounds (e.g., 10), then
-covered for a certain number of rounds (e.g., 10), then  exits the algorithm.
exits the algorithm. -
(3)
Each sensor decides to select one of the owned target points with a probability of
 , which ensures that the expected number of selected target point is 1.
, which ensures that the expected number of selected target point is 1.
3.2.4. Generalizations to  -Coverage of an Area
-Coverage of an Area
The  -net approach can also be used to
-net approach can also be used to  -cover a given area, rather than a given set of target points (as required by the formulation of
-cover a given area, rather than a given set of target points (as required by the formulation of  -SC problem). Essentially, coverage of an area requires dividing the given area into "subregions" as in our previous work [1]; a subregion is defined as a set of points in the plane that are covered by the same set of sensing regions. The number of such subregions can be shown to be polynomial in the total number of sensing regions in the system. The algorithm described here can then be used without any other modification, and the performance guarantee still holds.
-SC problem). Essentially, coverage of an area requires dividing the given area into "subregions" as in our previous work [1]; a subregion is defined as a set of points in the plane that are covered by the same set of sensing regions. The number of such subregions can be shown to be polynomial in the total number of sensing regions in the system. The algorithm described here can then be used without any other modification, and the performance guarantee still holds.
4. Conclusions
In this paper, we studied the  -coverage problem with sensors, which is to select the minimum number of sensors so that each target point is covered by at least
-coverage problem with sensors, which is to select the minimum number of sensors so that each target point is covered by at least  of them. We provided an
of them. We provided an  -approximation, where
-approximation, where  is the number of sensors in an optimal solution. We introduced a generalization of the classical
is the number of sensors in an optimal solution. We introduced a generalization of the classical  -net technique, which we called
-net technique, which we called  -net. We gave a method to build
-net. We gave a method to build  -nets based on random sampling. We showed how to solve the sensor's
-nets based on random sampling. We showed how to solve the sensor's  -coverage problem with the Brönnimann and Goodrich algorithm [6] together with our
-coverage problem with the Brönnimann and Goodrich algorithm [6] together with our  -nets. We believe to be the first one to propose this extension.
-nets. We believe to be the first one to propose this extension.
As a future work, we would like to extend this technique to directional sensors. A directional sensor is a sensor that has associated multiple sensing regions, and its orientation determines its actual sensing region. The  -coverage problem with directional sensors is NP-complete and in [15] we proposed a greedy approximation algorithm. We believe that the use of
-coverage problem with directional sensors is NP-complete and in [15] we proposed a greedy approximation algorithm. We believe that the use of  -nets can give a better approximation factor for this problem.
-nets can give a better approximation factor for this problem.
Appendices
A. About the Number of Iterations of the Doubling Process
This appendix contains the proof that when  is equal to the size of the
is equal to the size of the  -hitting set, then
-hitting set, then  ,
,  iterations of the doubling process are enough to retrieve the optimal
iterations of the doubling process are enough to retrieve the optimal  -hitting set. This proof follows the lines of the one in [6], but with the additional parameter
-hitting set. This proof follows the lines of the one in [6], but with the additional parameter  .
.
Theorem 4.
If  ,
,  iterations of the internal for loop of Algorithm 1 are sufficient to find a
iterations of the internal for loop of Algorithm 1 are sufficient to find a  -hitting set.
-hitting set.
Proof.
Initially  . The set
. The set  selected at the end of the internal for loop satisfies
selected at the end of the internal for loop satisfies  , because the algorithm found a weighted
, because the algorithm found a weighted  -net. Doubling the weights of the elements in
-net. Doubling the weights of the elements in  adds a total of
adds a total of  new weight to the system. So
new weight to the system. So  grows at most by a
grows at most by a  factor at each iteration. Then, after
factor at each iteration. Then, after  iterations
iterations

Let  be the optimal
be the optimal  -hitting set. Initially we have
-hitting set. Initially we have  . Since
. Since  is a
is a  -hitting set, there are least
-hitting set, there are least  elements of
elements of  in each set of
in each set of  . So for any possible set
. So for any possible set  chosen in step 11, there are at least
chosen in step 11, there are at least  elements of
elements of  that are doubled. By the convexity of the function
that are doubled. By the convexity of the function  , the increase of
, the increase of  is minimal if the doublings are spread out over the elements of
is minimal if the doublings are spread out over the elements of  as evenly as possible. So after
as evenly as possible. So after  iterations, we have
iterations, we have

Since the weights are positive and  ,
,  . We need to find the largest
. We need to find the largest  for which
for which

can be true. Taking the log

and solving for 

where we used the fact that  for
for  . Since the expression on the RHS is
. Since the expression on the RHS is  for any possible value of
for any possible value of  , the theorem follows.
, the theorem follows.
B. Computing Weighted 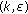 -Nets by Random Sampling
-Nets by Random Sampling
This appendix contains the proof of Theorem 2, which is an extension of the  -net theorem of Haussler and Welz [7]. As explained in Section 3.2, the two challenges in generalizing the random-sampling technique are that (i) sampling with replacement cannot be used, and (ii) weights must be part of the sampling process. Our contribution is a new method to obtain weighted
-net theorem of Haussler and Welz [7]. As explained in Section 3.2, the two challenges in generalizing the random-sampling technique are that (i) sampling with replacement cannot be used, and (ii) weights must be part of the sampling process. Our contribution is a new method to obtain weighted  -nets in which (i) we sample a subset of points at once (without duplicates), and (ii) we include the weights directly in the sampling process.
-nets in which (i) we sample a subset of points at once (without duplicates), and (ii) we include the weights directly in the sampling process.
We start by proving three lemmas, and then we will prove Theorem 2. Let  be as given by (1), and let
be as given by (1), and let  be the subset of points randomly picked from
be the subset of points randomly picked from  as described in Theorem 2. After picking
as described in Theorem 2. After picking  , pick another set
, pick another set  (for the purpose of the below analysis) in the same way as
(for the purpose of the below analysis) in the same way as  . We now define two events
. We now define two events

where  .
.
Intuitively,  is the event that
is the event that  does not
does not  -hit some set
-hit some set  , but
, but  has a "large" intersection with the set
has a "large" intersection with the set  (also remember that
(also remember that  is disjoint from
is disjoint from  ). Note that
). Note that  is a lower bound the average size of the intersection of
is a lower bound the average size of the intersection of  and
and  (as computed below).
(as computed below).
Lemma 1.
It holds that 
Proof.
 , because if
, because if  happens, then
happens, then  happens too. From the definition of conditional probability
happens too. From the definition of conditional probability

it suffices to show that  .
.
Let  (where the
(where the  's are pairwise different). Since
's are pairwise different). Since  happens, there is some set
happens, there is some set  s.t.
s.t.  and
and  . Therefore,
. Therefore,  is at least the probability that, for this
is at least the probability that, for this  ,
,  .
.
Let  be the random variable (r.v.)
be the random variable (r.v.)

Each subset  (resp.,
(resp.,  ) is picked with probability proportional to the sum of the weights of its elements, and each element can appear in
) is picked with probability proportional to the sum of the weights of its elements, and each element can appear in  (resp.,
(resp.,  ) subsets (because these are the ways of putting every other elements in the remaining positions). So the probability of picking one element depends only on its weight, and not on the other elements, which means that the elements are pairwise independent. So we have that
) subsets (because these are the ways of putting every other elements in the remaining positions). So the probability of picking one element depends only on its weight, and not on the other elements, which means that the elements are pairwise independent. So we have that

where  is a function that returns the weight of given set, which is defined as the sum of the weights of its elements.
is a function that returns the weight of given set, which is defined as the sum of the weights of its elements.
Let  . Clearly
. Clearly  . We have
. We have

To bound the deviation from the expectation, we use Chebyshev's inequality

Since  's are independent, the covariance is zero. So we get
's are independent, the covariance is zero. So we get

where we used the fact that for the 0-1 r.v.  ,
,  .
.
Applying Chebyshev's inequality

where in the last inequality we used the fact that

Finally we have that

Lemma 2.
It holds that  where
where  .
.
Proof.
The experiment of picking  and
and  can be viewed in an alternative way. Pick a subset
can be viewed in an alternative way. Pick a subset  of size
of size  at random (each subset is picked with probability proportional to the sum of the weights of its elements). Then, pick
at random (each subset is picked with probability proportional to the sum of the weights of its elements). Then, pick  as a subset of
as a subset of  of size
of size  at random (again with probability proportional to the sum of the weights of its elements). Finally, let
at random (again with probability proportional to the sum of the weights of its elements). Finally, let  . Note that this view is equivalent because the probability of picking any subset
. Note that this view is equivalent because the probability of picking any subset  is the same as before, (similarly for
is the same as before, (similarly for  ). This can be verified as follow. We are going to compute the probability of picking a certain subset
). This can be verified as follow. We are going to compute the probability of picking a certain subset  in both cases. In order to do this, we need to compute the sum of all possible sets of size
in both cases. In order to do this, we need to compute the sum of all possible sets of size  . Among all possible sets of size
. Among all possible sets of size  , each element appears in exactly
, each element appears in exactly  of them (because these are the ways of putting every other element in the remaining positions). Now, it is not necessary to know exactly in which set each element gives its contribution, but it is enough to know that it appears a total of
of them (because these are the ways of putting every other element in the remaining positions). Now, it is not necessary to know exactly in which set each element gives its contribution, but it is enough to know that it appears a total of  times. So, the sum of weight of all possible sets of size
times. So, the sum of weight of all possible sets of size  is
is  . Then
. Then

Now we are going to compute the probability of picking a subset  containing
containing  . This requires to determine the sum of the weights of all subsets of size
. This requires to determine the sum of the weights of all subsets of size  that contain
that contain  .
.  appears in
appears in  of them (as these are the number of ways of putting any other element in the remaining
of them (as these are the number of ways of putting any other element in the remaining  positions), and it gives a contribution of
positions), and it gives a contribution of  in each of them. Any other element can appear in any of the remaining
in each of them. Any other element can appear in any of the remaining  positions, for a total of
positions, for a total of  times (because fixed any element, the remaining
times (because fixed any element, the remaining  elements can be placed in any of the remaining
elements can be placed in any of the remaining  positions). So we get that
positions). So we get that

We also need to compute the probability of picking  from
from 

This requires to know  , which can be computed as
, which can be computed as

So,

Finally, it is easy to verify that

Let  , with
, with  , and define
, and define  . Since
. Since  and
and  are disjoint,
are disjoint,  , and then
, and then  is equivalent to
is equivalent to  . If
. If  , then
, then  does not happen, and it does not happen if
does not happen, and it does not happen if  either. Suppose that
either. Suppose that  , where
, where  , then we can pick
, then we can pick  as follow. We select
as follow. We select  elements among the points outside the intersection with
elements among the points outside the intersection with 

and the remaining  elements anywhere else
elements anywhere else

Their product can be bounded in the following way:

where in the last inequality we used the fact that

which can be proved by induction. The base case,  , is trivial. Assuming that the formula is valid for
, is trivial. Assuming that the formula is valid for  , we get
, we get

where in the last inequality we used the fact that  .
.
Using this fact, we can bound  . Recall that
. Recall that  happens only if
happens only if  . So
. So

For two sets  s.t.
s.t.  and
and  , the events
, the events  and
and  are the same. This is because the occurrence of
are the same. This is because the occurrence of  depends only on the intersection
depends only on the intersection  . The number of sets
. The number of sets  s.t.
s.t.  is unique at most
is unique at most  by Corollary 1 below. Then
by Corollary 1 below. Then

Lemma 3.
For any set system  , with
, with  and VC-dimension
and VC-dimension  ,
,  , where
, where  .
.
Proof.
See [16].
Given a set system  , for any subset of the points
, for any subset of the points  , let
, let  denote the projection of
denote the projection of  onto
onto  , that is, the set
, that is, the set  .
.
Corollary 1.
For any set system  , if
, if  , then
, then  has VC-dimension
has VC-dimension  , which implies
, which implies  .
.
Finally, we prove the main theorem.
B.1. Proof of Theorem 2
Combining Lemmas 1, 2, and 3

so we need to show that

which can be written as

or equivalently

Now we consider each part of the sum separately. From (1), it follows that

so it suffice to show that

If this inequality is valid for some value of  , then it is for any valid for any bigger value of
, then it is for any valid for any bigger value of  . So we just need to verify it for
. So we just need to verify it for  . Plugging in
. Plugging in  we get
we get

and this is equivalent to

which is definitely true.
C. Computing Small Weighted 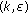 -Nets for Disks
-Nets for Disks
In this appendix we present a simple extension of [12] to build small weighted  -nets for disks. The original construction in [12] easily extends to
-nets for disks. The original construction in [12] easily extends to  -nets by replacing
-nets by replacing  with
with  . The proof presented here is simplified respect to the original one, because we consider only disks, instead of pseudodisks.
. The proof presented here is simplified respect to the original one, because we consider only disks, instead of pseudodisks.
The underlining idea is to pick points that are spaced apart, which hit all large enough disks. The strategy that we are going to use is to draw "colored" disks that contain a fixed number of points, and select points only on the border of the colored disks. The position and the size of colored disks depend on the input points, but not on the input disks. All colored disks, but one, will have exactly  input points, where
input points, where  . Each input point gets the color of the colored disks that covers it or remains uncolored if uncovered. After placing the colored disks, we compute a Dealaunay triangulation (DT) of the colored points. DT will have uni-colored, bi-colored, and tri-colored triangles. Triangles will have uni-colored and bi-colored edges. Let us define some terminology (see Figure 3).
. Each input point gets the color of the colored disks that covers it or remains uncolored if uncovered. After placing the colored disks, we compute a Dealaunay triangulation (DT) of the colored points. DT will have uni-colored, bi-colored, and tri-colored triangles. Triangles will have uni-colored and bi-colored edges. Let us define some terminology (see Figure 3).
Definition 7 (corridor; hall; sides; ends; corners).
-
(i)
Let a corridor be a maximal connected chain of bi-colored triangles in DT sharing bi-colored edges. In our construction, corridors are between two colored disks.
-
(ii)
Let a hall be a maximal group of adjacent tri-colored triangles (this is a generalization of the degenerate-corridors of [12]). In our construction, halls are between 3 or more disks, attached to the end of the corridors.
-
(iii)
Corridors are bounded by two chains of uni-colored edges, which we call sides, and two bi-colored edges, which we call ends.
-
(iv)
We call the endpoints of the sides the corners of the subcorridor. Note that one of the sides can degenerate in a single point, in which case there are 3 corners, instead of 4.
We start by describing the algorithm for the unweighted case, and we will show how to add weights afterwords. We are given  , a family
, a family  of disks, and a set
of disks, and a set  of
of  points in the plane. For simplicity assume that the points are in general position (i.e., no three points are collinear, and no four points are cocircular). Let define
points in the plane. For simplicity assume that the points are in general position (i.e., no three points are collinear, and no four points are cocircular). Let define  (the reason for this will be clear soon). Let
(the reason for this will be clear soon). Let  be disjoints subsets of
be disjoints subsets of  constructed in the following manner. From the boundary of
constructed in the following manner. From the boundary of  , "bite off" subsets of
, "bite off" subsets of  of size
of size  with the following properties.
with the following properties.
-
(i)
The union of all the
 subsets contains the boundary points of
subsets contains the boundary points of 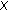 :
:  (where
(where  is the convex hull).
is the convex hull). -
(ii)
Each
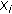 is representable as
is representable as  for some half-plane
for some half-plane 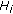 (or equivalently,
(or equivalently, 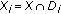 for some (large enough) disk
for some (large enough) disk  , and to simplify the proof we can think that
, and to simplify the proof we can think that  is bigger than any input disk).
is bigger than any input disk). -
(iii)
 for
for 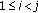 , and
, and 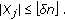
Now, consider the internal points of  , that are not part of any disk
, that are not part of any disk  . We are going to draw the largest number of disks of size
. We are going to draw the largest number of disks of size  to cover the internal points. Specifically, let
to cover the internal points. Specifically, let  be a maximal collection of disjoint subsets of
be a maximal collection of disjoint subsets of  satisfying
satisfying
-
(i)
 for some disk
for some disk 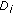 ,
, -
(ii)
 for
for 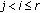 .
.
At this point, we have a total of  disks
disks  . For each
. For each  ,
,  , color the points of
, color the points of  with color
with color  , and call
, and call  the disk defining color
the disk defining color , or colored disk
, or colored disk . Let
. Let  be the set of colored points, and call the points in
be the set of colored points, and call the points in  colorless. Let DT be the Dealaunay triangulation of the set of colored points
colorless. Let DT be the Dealaunay triangulation of the set of colored points  . Break each corridor
. Break each corridor  into a minim number of subcorridors, that is, subchains of the chain of triangles that form
into a minim number of subcorridors, that is, subchains of the chain of triangles that form  , so that each subcorridor contains at most
, so that each subcorridor contains at most  colorless points. Let
colorless points. Let  be the set of the corners of all subcorridors. Clearly
be the set of the corners of all subcorridors. Clearly  . We are going to show that
. We are going to show that  is a the
is a the  -net for
-net for  that is, any disk of
that is, any disk of  that contains
that contains  points of
points of  also contains
also contains  points of
points of  . This construction is summarized in Algorithm 2.
. This construction is summarized in Algorithm 2.
Algorithm 2: Small  -nets for disks.
-nets for disks.
-
1
Let

-
2
Let
 be disjoints subsets of
be disjoints subsets of  with the following properties:
with the following properties: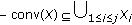 (where
(where 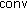 is the convex hull)
is the convex hull) each
each 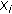 is representable as
is representable as 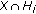 for some halfplane
for some halfplane (or equivalently,
(or equivalently, 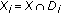 for some (large enough) This construction of subsets of
for some (large enough) This construction of subsets of 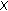 can be done by
can be done bydisk
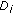 , and to simplify the proof we can think that
, and to simplify the proof we can think that 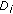 is bigger than any input disk)
is bigger than any input disk) for
for  , and
, and 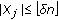
repeatedly "biting off" subsets of
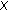 with halfplanes
with halfplanes -
3
Let
 be a maximal collection of disjoint subsets of
be a maximal collection of disjoint subsets of  satisfying:
satisfying: for some disk
for some disk 
 for
for 
-
4
For each
 ,
,  , color the points of
, color the points of  with color
with color  , and call
, and call 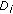 the disk defining color
the disk defining color , or colored disk
, or colored disk .
.Let
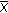 be the set of colored points, and call the points in
be the set of colored points, and call the points in  colorless;
colorless; -
5
Let DT be the Dealaunay triangulation of the set of colored points
 ;
; -
6
Break each corridor
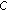 into a minim number of subcorridors, i.e. subchains of the chain of triangles
into a minim number of subcorridors, i.e. subchains of the chain of trianglesthat form
 , so that each subcorridor contains at most
, so that each subcorridor contains at most 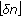 colorless points
colorless points -
7
Let
 be the set of the corners of all subcorridors. Clearly
be the set of the corners of all subcorridors. Clearly  ;
; -
8
Return
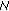 has the
has the 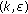 -net for
-net for  ;
;
First of all note that colorless points can only be in corridors and halls (because unicolored triangles are contained in the corresponding color-defining disks). Also, we can observe that any disk  containing no colored points contains less than
containing no colored points contains less than  points of
points of  . In fact, from the maximality of the construction, there cannot be colorless disks with
. In fact, from the maximality of the construction, there cannot be colorless disks with  points. Than we claim what follows.
points. Than we claim what follows.
Claim
There are at most  corridors in DT, and
corridors in DT, and 
Proof.
See [12]. Note that, since all  are disjoint, and all but maybe one contain
are disjoint, and all but maybe one contain  points, so
points, so  .
.
We now prove the  -net theorem for disks.
-net theorem for disks.
Theorem 5 ( -net theorem for disks).
-net theorem for disks).
Algorithm 2 creates a  -net of size
-net of size  for
for  , where
, where  is a set of points
is a set of points  in non-D-degenerate position (i.e., no three points are collinear, and no four points are cocircular), and D is a family of disks.
in non-D-degenerate position (i.e., no three points are collinear, and no four points are cocircular), and D is a family of disks.
Proof.
By claim  we have that the size of
we have that the size of  is
is  . So we only need to show that
. So we only need to show that  contains at least
contains at least  points in each input disk of size at least
points in each input disk of size at least  .
.
First of all, the case  is already proved in [12], so we focus on the case of
is already proved in [12], so we focus on the case of  .
.
For a generic input disk of size at least  , we are going to compute the minimum number of corners contributed by each intersecting region (colored disk, subcorridor, or hall), while assuming that it has the largest possible intersection. Also, we will pay attention not to count the same corner multiple times. If a colored disk is completely contained in an input disk, it will contribute for the biggest number of corners. So we should only consider colored disks that intersect the boundary of the input disk. We claim that the minimum contribution is given when the boundary of an input disk intersects an alternation of colored disks and corridors. In this case we should count 1 corner, for each colored disk/corridor. The only case in which (a part of) the boundary of the input disk does not intersect any colored disk is when it is contained inside a corridor. But this can only happen if there is a colored disk inside the input disk, but we already argued that this will give a higher contribution. The following is an upper bound on the number of intersecting points. There can be
, we are going to compute the minimum number of corners contributed by each intersecting region (colored disk, subcorridor, or hall), while assuming that it has the largest possible intersection. Also, we will pay attention not to count the same corner multiple times. If a colored disk is completely contained in an input disk, it will contribute for the biggest number of corners. So we should only consider colored disks that intersect the boundary of the input disk. We claim that the minimum contribution is given when the boundary of an input disk intersects an alternation of colored disks and corridors. In this case we should count 1 corner, for each colored disk/corridor. The only case in which (a part of) the boundary of the input disk does not intersect any colored disk is when it is contained inside a corridor. But this can only happen if there is a colored disk inside the input disk, but we already argued that this will give a higher contribution. The following is an upper bound on the number of intersecting points. There can be  points for the colored disk, plus another
points for the colored disk, plus another  points for the subcorridor on the side of the corner that we are counting, plus another
points for the subcorridor on the side of the corner that we are counting, plus another  points for the hall adjacent to them. This means that for
points for the hall adjacent to them. This means that for  points there is at least 1 corner. We are considering input disks of size at least
points there is at least 1 corner. We are considering input disks of size at least  , and this implies that there are at least
, and this implies that there are at least  points in each disk.
points in each disk.
Finally, we consider the weighted case. The construction is similar to the unweighted one, with the only difference that the colored disks contain  points, where
points, where  is the sum of the weights of all points. It is easy to see that the proof follows through.
is the sum of the weights of all points. It is easy to see that the proof follows through.
References
Gupta H, Zhou Z, Das SR, Gu Q: Connected sensor cover: self-organization of sensor networks for efficient query execution. IEEE/ACM Transactions on Networking 2006, 14(1):55-67.
Chakrabarty K, Iyengar SS, Qi H, Cho E: Grid coverage for surveillance and target location in distributed sensor networks. IEEE Transactions on Computers 2002, 51(12):1448-1453. 10.1109/TC.2002.1146711
Slijepcevic S, Potkonjak M: Power efficient organization of wireless sensor networks. Proceedings of the International Conveference of Communication (ICC '01), June 2001, Helsinki, Finland 2: 472-476.
Meguerdichian S, Koushanfar F, Qu G, Potkonjak M: Exposure in wireless ad-hoc sensor networks. Proceedings of the 7th Annual International Conference on Mobile Computing and Networking (MOBICOM '01), July 2001, Rome, Italy 139-150.
Cormen TH, Leiserson CE, Rivest RL, Stein C: Introduction to Algorithms. 2nd edition. MIT Press, Boston, Mass, USA; 2001.
Brönnimann H, Goodrich MT: Almost optimal set covers in finite VC-dimension. Discrete and Computational Geometry 1995, 14(1):463-479. 10.1007/BF02570718
Haussler D, Welzl E:
 -nets and simplex range queries. Discrete and Computational Geometry 1987, 2(1):127-151. 10.1007/BF02187876
-nets and simplex range queries. Discrete and Computational Geometry 1987, 2(1):127-151. 10.1007/BF02187876Hefeeda M, Bagheri M:Randomized
 -coverage algorithms for dense sensor networks. Proceedings of the 26th IEEE International Conference on Computer Communications (INFOCOM '07), May 2007 2376-2380.
-coverage algorithms for dense sensor networks. Proceedings of the 26th IEEE International Conference on Computer Communications (INFOCOM '07), May 2007 2376-2380.Ye F, Zhong G, Cheng J, Lu S, Zhang L: PEAS: a robust energy conserving protocol for long-lived sensor networks. Proceedings of the 23rd IEEE International Conference on Distributed Computing Systems (ICDCS '03), May 2003, Providence, RI, USA 28-37.
Shakkottai S, Srikant R, Shroff N: Unreliable sensor grids: coverage, connectivity and diameter. Proceedings of the 22nd Annual Joint Conference of the IEEE Computer and Communications Societies (INFOCOM '03), March-April 2003, San Francisco, Calif, USA 2: 1073-1083.
Zhou Z, Das S, Gupta H: Connected K-coverage problem in sensor networks. Proceedings of the 13th International Conference on Computer Communications and Networks (ICCCN '04), 2004 373-378.
Matousek J, Seidel R, Welzl E:How to net a lot with little: small
 -nets for disks and halfspaces. Proceedings of the 6th Annual Symposium on Computational Geometry (SCG '90), June 1990, Berkeley, Calif, USA 16-22.
-nets for disks and halfspaces. Proceedings of the 6th Annual Symposium on Computational Geometry (SCG '90), June 1990, Berkeley, Calif, USA 16-22.O'Rourke J: Art Gallery Theorems and Algorithms, International Series of Monographs on Computer Science. Volume 3. Oxford University Press, New York, NY, USA; 1987.
Valtr P: Guarding galleries where no point sees a small area. Israel Journal of Mathematics 1998, 104: 1-16. 10.1007/BF02897056
Fusco G, Gupta H: Selection and orientation of directional sensors for coverage maximization. Proceedings of the 6th Annual IEEE Conference on Sensor, Mesh and Ad Hoc Communications and Networks (SECON '09), June 2009, Rome, Italy
Alon N, Spencer JH:
 -nets and VC-dimensions of range spaces. In The Probabilistic Method. 2nd edition. Wiley-Interscience, New York, NY, USA; 2000:220-225.
-nets and VC-dimensions of range spaces. In The Probabilistic Method. 2nd edition. Wiley-Interscience, New York, NY, USA; 2000:220-225.
Acknowledgments
This work was supported in part by the NSF awards: 0713186, 0721701, 0721665.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Fusco, G., Gupta, H.  -Net Approach to Sensor
-Net Approach to Sensor  -Coverage.
J Wireless Com Network 2010, 192752 (2009). https://doi.org/10.1155/2010/192752
-Coverage.
J Wireless Com Network 2010, 192752 (2009). https://doi.org/10.1155/2010/192752
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/192752


 -SC problem. Suppose we are given 4 sensors of centers
-SC problem. Suppose we are given 4 sensors of centers  and 20 points as in (a). The problem is to select the minimum number of sensors to
and 20 points as in (a). The problem is to select the minimum number of sensors to  -cover all points. A possible solution for
-cover all points. A possible solution for  is shown in (b), where 3 sensors suffice to 2-cover all points.
is shown in (b), where 3 sensors suffice to 2-cover all points. -Net-Based Approach
-Net-Based Approach -Net Technique
-Net Technique -Hitting Set Problem and the
-Hitting Set Problem and the  -Net Technique
-Net Technique -HS and
-HS and  -SC Problem
-SC Problem .
.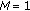 ;
;  ;
; 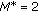 )
)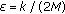
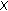 to 1;
to 1; ;
;  ;
; 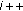 )
) -net
-net  of size
of size  using Theorem 2;
using Theorem 2; is
is 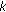 -hit by
-hit by 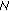 , return
, return 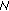 ;
; that is not
that is not  -hit, and double the weight of all the points in the set;
-hit, and double the weight of all the points in the set; -Hitting Set
-Hitting Set .
.

 verifies
verifies 
 -Net Approach
-Net Approach -net, through some sort of distributed randomized selection.
-net, through some sort of distributed randomized selection. -net
-net  , we need to verify in a distributed manner whether
, we need to verify in a distributed manner whether  is indeed a
is indeed a 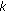 -coverage set (
-coverage set ( -hitting set in the dual).
-hitting set in the dual).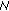 is not a
is not a 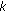 -coverage set, then we need to select one target point (a set in the dual) that is not
-coverage set, then we need to select one target point (a set in the dual) that is not 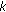 -covered by
-covered by  and double the weights of all the sensing regions covering it.
and double the weights of all the sensing regions covering it. independently. To select
independently. To select  sensors, each sensor decides to select itself independently with a probability
sensors, each sensor decides to select itself independently with a probability 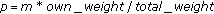 , resulting in selection of
, resulting in selection of  sensors (in expectation).
sensors (in expectation).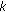 -coverage of the owned target points, by exchanging messages with near-by (that cover a common target point) sensors. If a target point owned by a sensor
-coverage of the owned target points, by exchanging messages with near-by (that cover a common target point) sensors. If a target point owned by a sensor 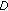 and its near-by sensors are all
and its near-by sensors are all  -covered for a certain number of rounds (e.g., 10), then
-covered for a certain number of rounds (e.g., 10), then  exits the algorithm.
exits the algorithm. , which ensures that the expected number of selected target point is 1.
, which ensures that the expected number of selected target point is 1. -Coverage of an Area
-Coverage of an Area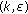 -Nets by Random Sampling
-Nets by Random Sampling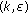 -Nets for Disks
-Nets for Disks
 subsets contains the boundary points of
subsets contains the boundary points of 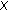 :
:  (where
(where  is the convex hull).
is the convex hull). is representable as
is representable as  for some half-plane
for some half-plane  (or equivalently,
(or equivalently, 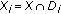 for some (large enough) disk
for some (large enough) disk  , and to simplify the proof we can think that
, and to simplify the proof we can think that  is bigger than any input disk).
is bigger than any input disk). for
for 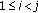 , and
, and 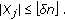
 for some disk
for some disk 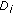 ,
, for
for 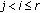 .
.
 be disjoints subsets of
be disjoints subsets of  with the following properties:
with the following properties: (where
(where  is the convex hull)
is the convex hull) each
each  is representable as
is representable as 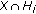 for some halfplane
for some halfplane (or equivalently,
(or equivalently, 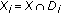 for some (large enough) This construction of subsets of
for some (large enough) This construction of subsets of  can be done by
can be done by , and to simplify the proof we can think that
, and to simplify the proof we can think that 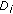 is bigger than any input disk)
is bigger than any input disk) for
for  , and
, and 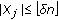
 with halfplanes
with halfplanes be a maximal collection of disjoint subsets of
be a maximal collection of disjoint subsets of  satisfying:
satisfying: for some disk
for some disk 
 for
for 
 ,
,  , color the points of
, color the points of  with color
with color  , and call
, and call 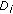 the disk defining color
the disk defining color , or colored disk
, or colored disk .
.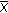 be the set of colored points, and call the points in
be the set of colored points, and call the points in  colorless;
colorless; ;
;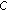 into a minim number of subcorridors, i.e. subchains of the chain of triangles
into a minim number of subcorridors, i.e. subchains of the chain of triangles , so that each subcorridor contains at most
, so that each subcorridor contains at most 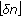 colorless points
colorless points be the set of the corners of all subcorridors. Clearly
be the set of the corners of all subcorridors. Clearly  ;
;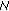 has the
has the  -net for
-net for  ;
; -nets and simplex range queries. Discrete and Computational Geometry 1987, 2(1):127-151. 10.1007/BF02187876
-nets and simplex range queries. Discrete and Computational Geometry 1987, 2(1):127-151. 10.1007/BF02187876 -coverage algorithms for dense sensor networks. Proceedings of the 26th IEEE International Conference on Computer Communications (INFOCOM '07), May 2007 2376-2380.
-coverage algorithms for dense sensor networks. Proceedings of the 26th IEEE International Conference on Computer Communications (INFOCOM '07), May 2007 2376-2380. -nets for disks and halfspaces. Proceedings of the 6th Annual Symposium on Computational Geometry (SCG '90), June 1990, Berkeley, Calif, USA 16-22.
-nets for disks and halfspaces. Proceedings of the 6th Annual Symposium on Computational Geometry (SCG '90), June 1990, Berkeley, Calif, USA 16-22. -nets and VC-dimensions of range spaces. In The Probabilistic Method. 2nd edition. Wiley-Interscience, New York, NY, USA; 2000:220-225.
-nets and VC-dimensions of range spaces. In The Probabilistic Method. 2nd edition. Wiley-Interscience, New York, NY, USA; 2000:220-225.