- Research Article
- Open access
- Published:
Efficient Vector-Based Forwarding for Underwater Sensor Networks
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 195910 (2010)
Abstract
Underwater Sensor Networks (UWSNs) are significantly different from terrestrial sensor networks in the following aspects: low bandwidth, high latency, node mobility, high error probability, and 3-dimensional space. These new features bring many challenges to the network protocol design of UWSNs. In this paper, we tackle one fundamental problem in UWSNs: robust, scalable, and energy efficient routing. We propose vector-based forwarding (VBF), a geographic routing protocol. In VBF, the forwarding path is guided by a vector from the source to the target, no state information is required on the sensor nodes, and only a small fraction of the nodes is involved in routing. To improve the robustness, packets are forwarded in redundant and interleaved paths. Further, a localized and distributed self-adaptation algorithm allows the nodes to reduce energy consumption by discarding redundant packets. VBF performs well in dense networks. For sparse networks, we propose a hop-by-hop vector-based forwarding (HH-VBF) protocol, which adapts the vector-based approach at every hop. We evaluate the performance of VBF and HH-VBF through extensive simulations. The simulation results show that VBF achieves high packet delivery ratio and energy efficiency in dense networks and HH-VBF has high packet delivery ratio even in sparse networks.
1. Introduction
Recently, underwater sensor networks have emerged as a very powerful technique for many applications in underwater environments, including monitoring, measurement, surveillance, and control [1–7]. Compared with traditional techniques in these application scenarios, underwater sensor networks enable people to perform underwater activities more accurately and timely in much wider areas.
Even though underwater sensor networks (UWSNs) share some common properties with terrestrial sensor networks, such as the large number of nodes and the limited energy supplies, UWSNs are significantly different from terrestrial sensor networks in many aspects: low bandwidth, high latency, node mobility (resulting in high network dynamics), high error probability, and three-dimensional network topology. These new features bring many challenges to the protocol design of UWSNs. In this paper, we tackle one fundamental problem in UWSNs: robust, scalable, and energy efficient routing. The unique features of UWSNs pose great challenges on its routing protocol design and make many existing routing protocols for terrestrial networks unsuitable.
1.1. Unique Features of UWSNs
UWSNs are significantly different from any terrestrial sensor networks in terms of the following aspects.
-
(i)
Low Bandwidth and High Latency in UWSNs. Acoustic channels (instead of RF channels) are used as the communication method since radio does not work well in water. The propagation speed of acoustic signals in water is about
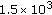 m/sec, which is five orders of magnitude lower than the radio propagation speed (
m/sec, which is five orders of magnitude lower than the radio propagation speed (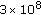 m/sec). Moreover, the available bandwidth of underwater acoustic channels is limited and dramatically depends on both transmission range and frequency. According to [8], nearly no research and commercial system can exceed 40
m/sec). Moreover, the available bandwidth of underwater acoustic channels is limited and dramatically depends on both transmission range and frequency. According to [8], nearly no research and commercial system can exceed 40 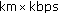 as the maximum attainable
as the maximum attainable 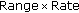 product.
product. -
(ii)
UWSNs Are Highly Dynamic. The underwater sensor networks we target are highly mobile networks where sensor nodes are not fixed and they will float with water currents. From empirical observations, underwater objects may move at the speed of 2-3 knots (or 3–6 kilometers per hour) in a typical underwater condition [6, 7]. This kind of mobility results in a highly dynamic network topology.
-
(iii)
UWSNs Are Highly Error-Prone. Underwater acoustic communication channels are significantly affected by many factors such as signal attenuation, noise, multipath, Doppler spread, and even water temperature. All these factors cause high bit-error and delay variance. Thus, communication links in UWSNs are highly error-prone. Moreover, sensor nodes are more vulnerable in harsh underwater environments. Compared with their terrestrial counterparts, underwater sensor networks have a higher node-failure rate and packet-loss probability.
-
(iv)
UWSNs Are Three-Dimensional. UWSNs are usually deployed in a three-dimensional space. This is different from the 2-dimensional deployment of most terrestrial sensor networks.
These characteristics of UWSNs bring up many new challenges and make the existing routing protocols for terrestrial sensor networks unsuitable here. For UWSNs, the routing protocols should be able to handle the node mobility and the unreliable communication links with high energy efficiency.
1.2. Routing Challenges in UWSNs
UWSNs are highly dynamic networks, which makes existing routing protocols for stationary or quasistationary networks unsuitable. In UWSNs, the mobility speed of nodes is around 1–3 meter per second, the acoustic signal propagate at 1500 meter/s, and the transmission range of the sensor nodes is less than 1 km. The low propagation speed of the acoustic signal and relatively highly mobile nodes cause the network topology change dramatically and dynamically. For example, when the distance between the sender and the receiver is large, it is possible that the network topology changes during the time the data packet traverses the networks. Many existing protocols for terrestrial networks are for relatively stable network topology. Generally, these protocols fall into two categories: proactive routing and reactive routing. In proactive routing protocols such as OLSR [9], TBRPE [10], and DSDV [11], routes need to be found and maintained prehand, which is quite expensive for UWSNs. On the other hand, in reactive protocols such as AODV [12] and DSR [13], the route discovery process is triggered by the communication demand at sources. In the phase of route discovery, the source seeks to establish a route toward the destination by flooding a route request message, which would be very costly in dynamic networks. Thus, these protocols are not suitable for UWSNs.
In UWSNs, nodes are usually powered by battery; thus energy efficiency is one of the major design concerns. Many energy efficient routing protocols for the terrestrial sensor networks, such as Directed Diffusion [14], Two-Tier-Data Dissemination (TTDD) [15], and GRAB [16], can not be applied in UWSN since they are mainly designed for stationary networks. Not much work has been done on the energy efficient routing protocols for such highly dynamic networks as UWSNs.
In addition, the unstable acoustic channel condition and the dynamic network topology of UWSNs make the conventional single path forwarding protocols very unreliable. Multipath routing [17, 18] which uses multiple paths simultaneously for data transmission is a promising technology here.
1.3. Contributions
We propose a novel routing protocol, called vector-based forwarding (VBF), to address the routing problem in UWSNs. VBF is an essentially geographic routing protocol, which is robust, scalable, and energy efficient. In VBF, the forwarding path is the vector from the source to the destination. No state information is required on the sensor nodes and only a small fraction of the nodes in the networks are involved in routing. Moreover, packets are forwarded along redundant and interleaved paths from the source to the destination; it is robust against packet loss and node failure. To enhance the performance of VBF in sparse networks, we propose a variant of VBF, called hop-by-hop VBF (HH-VBF). In HH-VBF, the forwarding path is the vector from forwarding nodes to the target instead of the one from the source to the target. HH-VBF is capable of finding a forwarding path even in a very sparse network. Further, we develop localized and distributed self-adaptation algorithms to improve the performance of VBF and HH-VBF. The self-adaptation algorithms allow the nodes to weigh the benefit to forward packets and reduce energy consumption by discarding low benefit packets. We evaluate the performance of VBF and HH-VBF through extensive simulations.
The rest of this paper is organized as follows. We first briefly review some related work in Section 2. Then, we present our VBF and HH-VBF protocol in Section 3. After that, we evaluate VBF and HH-VBF through simulations in Section 4. Finally, we conclude the paper in Section 5.
2. Related Work
In this section, we will review related work in both terrestrial networks and underwater networks.
2.1. Routing in Terrestrial Wireless Networks
Energy efficiency has long been recognized as one of the most important properties for terrestrial wireless networks. Many energy efficient routing protocols such as Directed Diffusion [14], Two-Tier Data Dissemination [15], GRAdient [16], Rumor routing [19], and SPIN [20], which aim for high energy efficiency, have been proposed in the last few years for terrestrial wireless networks. These protocols can achieve high energy efficiency in the terrestrial networks. However, they depend on the relatively stable neighborhood to form the routing path. If applying these protocols in UWSNs, it would be costly to maintain and recover the frequently broken routing path due to the node mobility.
Geographic routing protocols, which leverage the position information of each node to determine the forwarding path, have been investigated extensively for terrestrial wireless networks [21–26]. In [21], GPSR protocol, which always selects the node geographically closest to the destination of the target, is proposed. If GPSR cannot find any node closer to the destination of the packet than the forwarder, it adopts right-hand rule to forward the packet. Beacon-less routing algorithm (BLR) in [22] selects the next hop through Dynamic Forwarding Delay (DFD). Upon receiving a packet, each node computes its DFD value determined by its position. The node with the least DFD value forwards the packet. The Contention-based forwarding (CBF) protocol proposed in [23] selects the next hop by area-based suppression. In CBF, only nodes in an area called suppression area contend to forward the packet. The routing protocols proposed in [24, 25] take not only the position but also the quality of the link into consideration in selection of the next hop.
Since geographic routing protocols do not rely on the stable neighborhood to find the forwarding path, it is a very promising technique to address the routing issues in networks with dynamic topology. Our proposed VBF protocol is a kind of geographic routing protocols which is adapted to the unique underwater environment.
2.2. Routing in Underwater Networks
Much research work has been done in the last few years on the routing protocols for underwater networks. The challenges and state-of-art for the routing protocols in underwater networks have been discussed in detail in [5, 6]. A pioneering work is done in [27] on the routing protocol for underwater networks. In this work, a central master node is used to probe the network topology and do the route establishment. The authors of [28] propose a centralized routing algorithm for delay sensitive application and a distributed routing algorithm for delay-insensitive applications in three-dimensional underwater networks. In [29], the authors propose a novel method to improve the efficiency of the flood-based routing protocol in underwater sensor networks. Focus beam routing appears in [30], which dynamically establishes a route as the data packet traverses the network towards its final destinations. An adaptive routing protocol for underwater Delay Tolerant Networks (DTN) has been proposed in [31], which divides the network into multiple layers and every node adaptively finds its routes to the upper layer according to its past memory.
Different from all the above work, our VBF takes advantages of the location information to form one or multiple routing pipes from the source to the destination. Multiple routes might be used simultaneously in VBF to improve the reliability. At the same time, the self-adaption algorithm in VBF can greatly improve the energy efficiency. Thus, our VBF can achieve a good balance between the reliability and energy efficiency.
3. Vector-Based Forwarding Protocol (VBF)
In this section, we present our vector-based forwarding (VBF) protocol and its enhanced version, hop-by-hop vector-based forwarding (HH-VBF) protocol in details.
3.1. Overview of VBF
In sensor networks, energy constraint is a crucial factor since sensor nodes usually run on battery, and it is impossible or difficult to recharge them in most application scenarios. In underwater sensor networks, in addition to energy saving, the routing algorithms should be able to handle node mobility in an efficient way.
Vector-Based Forwarding (VBF) protocol meets these requirements successfully. We assume that each node in VBF knows its position information, which is provided by some location algorithms [32–37]. If there is no such localization service available, a sensor node can still estimate its relative position to the forwarding node by measuring its distance to the forwarder and the angle of arrival (AOA) and strength of the signal by being armed with some hardware device. This assumption is justified by the fact that acoustic directional antennae are of much smaller size than RF directional antennae due to the extremely small wavelength of sound. Moreover, underwater sensor nodes are usually larger than land-based sensors, and they have room for such devices. In this work, we assume that the position information can be calculated by measuring the AOA and strength of the signal.
In VBF, each packet carries the positions of the sender, the target, and the forwarder (i.e., the node which transmits this packet). The forwarding path is specified by the routing vector from the sender to the target. Upon receiving a packet, a node computes its relative position to the forwarder. Recursively, all the nodes receiving the packet compute their positions. If a node determines that it is sufficiently close to the routing vector (e.g., less than a predefined distance threshold), it puts its own computed position in the packet and continues forwarding the packet; otherwise, it simply discards the packet. In this way, all the packet forwarders in the sensor network form a "routing pipe": the sensor nodes in this pipe are eligible for packet forwarding, and those which are not close to the routing vector (i.e., the axis of the pipe) do not forward. Figure 1 illustrates the basic idea of VBF. In the figure, node  is the source, and node
is the source, and node  is the sink. The routing vector is specified by
is the sink. The routing vector is specified by  . Data packets are forwarded from
. Data packets are forwarded from  to
to  . Forwarders along the routing vector form a routing pipe with a precontrolled radius (i.e., the distance threshold, denoted by
. Forwarders along the routing vector form a routing pipe with a precontrolled radius (i.e., the distance threshold, denoted by  in this paper).
in this paper).
As we can see, like all other source routing protocols, VBF requires no state information at each node. Therefore, it is scalable to the size of the network. Moreover, in VBF, only the nodes along the forwarding path (specified by the routing vector) are involved in packet routing, thus saving the energy of the network.
3.2. The Basic VBF Protocol
VBF is a source routing protocol where each packet carries simple routing information. In a packet, there are three position fields, SP, TP, and FP, that is, the coordinates of the sender, the target, and the forwarder. In order to handle node mobility, each packet contains a RANGE field. When a packet reaches the area specified by its TP, this packet is flooded in an area controlled by the RANGE field. The forwarding path is specified by the routing vector from the sender to the target. Each packet also has a RADIUS field, which is a predefined threshold used by sensor nodes to determine if they are close enough to the routing vector and eligible for packet forwarding.
3.2.1. Sink-Initiated Query
There are two types of queries. One is location-dependent query. In this case, the sink is interested in some specific area and knows the location of the area. The other type is location independent query, when the sink wants to know some specific type of data regardless of its location. For example, the sink wants to know if there exist abnormal high temperatures in the network. Both of these two types of queries can be routed effectively by VBF.
For location dependent queries, the sink is interested in some specific area; so it issues an INTEREST query packet, which carries the coordinates of the sink and the target in the sink-based coordinate system. Each node which receives this packet calculates its own position and the distance to the routing vector. If the distance is less than RADIUS (i.e., the distance threshold), then this node updates the FP field of the packet and forwards it; otherwise, it discards this packet. For location-independent queries, the INTEREST packet may carry some invalid positions for the target. Upon receiving such packets, a node first checks if it has the data which the sink is interested in. If so, the node computes its position in the sink-based coordinate system, generates data packets, and sends back to the sink. Otherwise, it updates the FP field of the packet and further forwards it.
3.2.2. Source-Initiated Query
In some application scenarios, the source can initiate the query process. VBF also supports such source_initiated query. If a source senses some events and wants to inform the sink, it first broadcasts a DATA_READY packet. Upon receiving such packets, each node computes its own position in the source-based coordinate system, updates the FP field, and forwards the packet. Once the sink receives this packet, it calculates its position in the source-based coordinate system and transforms the position of the source into its own coordinate system. Then the sink can decide if it is interested in such data. If so, it may send out an INTEREST packet to the area where the source resides.
Handling Source Mobility
Since the source node keeps moving, its location calculated based on the old INTEREST packet might not be accurate any more. If no measure is taken to correct the source location, the actual forwarding path might get far away from the expected one; that is, the destination of the data forwarding path most probably misses the sink. We propose the following sink-assisted approach to solve this problem.
The source keeps sending packets to the sink, and the sink can utilize the source location information carried in the packets to determine if the source moves out of the targeted scope. For example, if the sink calculates its position as  based on the coordinates of the source,
based on the coordinates of the source,  , and its real position is
, and its real position is  , then the sink can calculate the relative position of the sink to the source as
, then the sink can calculate the relative position of the sink to the source as  . Therefore, the real position of the source is
. Therefore, the real position of the source is  . By comparing
. By comparing  and
and  , the sink can decide if the source moves out of the scope of the interested area. If so, the sink sends the SOURCE_DENY packet to the source using
, the sink can decide if the source moves out of the scope of the interested area. If so, the sink sends the SOURCE_DENY packet to the source using  . Once the source gets such packets, it stops sending data. At the same time, the sink initiates a new INTEREST query and finds a new source.
. Once the source gets such packets, it stops sending data. At the same time, the sink initiates a new INTEREST query and finds a new source.
3.3. The Self-Adaptation Algorithm for VBF
In the basic VBF protocol, all the nodes inside the routing pipe are qualified to forward packets. In dense networks, too many nodes might be involved in the data forwarding process. To save energy, it is desirable to adjust the forwarding policy based on the node density. However, due to the mobility of the nodes in the network, it is infeasible to determine the global node density. Moreover, it is inappropriate to measure the density at the transmission ends (i.e., the sender and the target) because of the low propagation speed of acoustic signals. We propose a self-adaptation algorithm for VBF to allow each node to estimate the density in its neighborhood (based on local information) and forward packets adaptively.
Desirableness Factor
We introduce the notion of desirableness factor to measure the "suitableness" of a node to forward packets.
Definition 1.
Given a routing vector  , where
, where  is the source and
is the source and  is the sink, for forwarder
is the sink, for forwarder  , the VBF desirableness factor,
, the VBF desirableness factor,  , of a node
, of a node  , is defined as
, is defined as  , where
, where  is the distance of
is the distance of  to the routing vector
to the routing vector  ,
,  is the distance between node
is the distance between node  and node
and node  and
and  is the angle between vector
is the angle between vector  and vector
and vector  .
.  is the transmission range and
is the transmission range and  is the radius of the "routing pipe" (i.e., the distance threshold).
is the radius of the "routing pipe" (i.e., the distance threshold).
Figure 2(a) depicts the various parameters used in the definition of desirableness factor. From the definition, we see that for any node close enough to the routing vector, that is,  , the desirableness factor of that this node is in the range of
, the desirableness factor of that this node is in the range of  . For a node, if its desirableness factor is large, it means that either its distance to the routing vector is large or it is not far away from the forwarder. In other words, it is not desirable for this node to continue forwarding the packet. On the other hand, if the desirableness factor of a node is
. For a node, if its desirableness factor is large, it means that either its distance to the routing vector is large or it is not far away from the forwarder. In other words, it is not desirable for this node to continue forwarding the packet. On the other hand, if the desirableness factor of a node is  , then this node is on both the routing vector and the edge of the transmission range of the forwarder. We call this node as the optimal node, and its position as the best position. For any forwarder, there is at most one optimal node and one best position. If the desirableness factor of a node is close to
, then this node is on both the routing vector and the edge of the transmission range of the forwarder. We call this node as the optimal node, and its position as the best position. For any forwarder, there is at most one optimal node and one best position. If the desirableness factor of a node is close to  , it means this node is close to the best position.
, it means this node is close to the best position.
The Algorithm
We propose a self-adaptation algorithm based on the concept of desirableness factor. This algorithm aims to select the most desirable nodes as forwarders. In this algorithm, when a node receives a packet, it first determines if it is close enough to the routing vector. If yes, the node then holds the packet for a time period related to its desirableness factor. In other words, each qualified node delays forwarding the packet by a time interval  , which is calculated as follows:
, which is calculated as follows:

where  is a predefined maximum delay,
is a predefined maximum delay,  is the propagation speed of acoustic signals in water, that is, 1500 m/s, and
is the propagation speed of acoustic signals in water, that is, 1500 m/s, and  is the distance between this node and the forwarder. In the above equation, the first term reflects the waiting time based on the node's desirableness factor: the more desirable (i.e., the smaller the desirableness factor), the less time to wait. The second term represents the additional time needed for all the nodes in the forwarder's transmission range to receive the acoustic signal from the forwarder.
is the distance between this node and the forwarder. In the above equation, the first term reflects the waiting time based on the node's desirableness factor: the more desirable (i.e., the smaller the desirableness factor), the less time to wait. The second term represents the additional time needed for all the nodes in the forwarder's transmission range to receive the acoustic signal from the forwarder.
During the delayed time period  , if a node receives duplicate packets from
, if a node receives duplicate packets from  other nodes, then this node has to compute its desirableness factors relative to these nodes,
other nodes, then this node has to compute its desirableness factors relative to these nodes,  , and the original forwarder,
, and the original forwarder,  . If
. If  , where
, where  is a predefined initial value of desirableness factor (
is a predefined initial value of desirableness factor ( ), then this node forwards the packet; otherwise, it discards the packet.
), then this node forwards the packet; otherwise, it discards the packet.
Essentially, the above self-adaptation algorithm gives higher priority to the desirable node to continue broadcasting the packet, and it also allows a less desirable node to have chances to reevaluate its "importance" in the neighborhood. After receiving the same packets from its neighbors, the less desirable node can measure its importance by computing its desirableness factor relative to its neighbors. If there are many more desirable nodes in the neighborhood, we exponentially reduce the probability of this node to forward the packet. That is, it is useless for this node to forward the packet anymore since many other more desirable nodes have forwarded the packet. In fact, if a node receives more than two duplicate packets during its waiting time, it is most likely that this node will not forward the packet no matter what initial value  takes. In this way, we can reduce the computation overhead by skipping the reevaluation of the desirableness factor.
takes. In this way, we can reduce the computation overhead by skipping the reevaluation of the desirableness factor.
From (1), we can see that the optimal node does not defer forwarding packets in the self-adaptation algorithm. Thus, we have the following lemma.
Lemma 2.
If there exists an optimal path from the sender to the target, that is, each node in the path is the optimal node for its upstream node, then the self-adaptation algorithm selects this path and entails no delay.
An Example
We illustrate VBF with self-adaptation in Figure 2(b). In this figure, the forwarding path is specified as the routing vector  from the source
from the source  to the sink
to the sink  . The node
. The node  is the current forwarder. There are three nodes, namely,
is the current forwarder. There are three nodes, namely,  ,
,  and
and  in its transmission range. Node
in its transmission range. Node  has the smallest desirableness factor among these nodes. Therefore,
has the smallest desirableness factor among these nodes. Therefore,  has the shortest delay time and sends out the packet first. As shown in this figure, node
has the shortest delay time and sends out the packet first. As shown in this figure, node  is most likely to discard the packet because it is in the transmission range of
is most likely to discard the packet because it is in the transmission range of  and it has to reevaluate the benefit to send the packet. Node
and it has to reevaluate the benefit to send the packet. Node  is out of the transmission range of
is out of the transmission range of  ; therefore, it also forwards the packet.
; therefore, it also forwards the packet.
3.4. Summary of VBF
We have described the basic VBF routing protocol and the self-adaptation algorithm. We can see that VBF addresses the mobility of nodes in the network effectively. The positioning of nodes is performed locally and no global synchronization required. VBF has no requirement for stable forward path. VBF is an energy efficient and scalable protocol.  In VBF, no state information is required for each node; therefore, it is scalable to the size of the network.
In VBF, no state information is required for each node; therefore, it is scalable to the size of the network.  In VBF, only the nodes close to the routing vector are involved in packet forwarding, and all other nodes are in idle state, thus saving energy. The self-adaptation algorithm helps to further reduce energy consumption by selecting more desirable nodes.
In VBF, only the nodes close to the routing vector are involved in packet forwarding, and all other nodes are in idle state, thus saving energy. The self-adaptation algorithm helps to further reduce energy consumption by selecting more desirable nodes.
VBF is also robust and less computationally demanding.  The success of data delivery is not dependent on the stable neighborhood, but on the node density. If there exists at least one path in the "routing pipe" specified by the routing vector, then the packet can be successfully delivered.
The success of data delivery is not dependent on the stable neighborhood, but on the node density. If there exists at least one path in the "routing pipe" specified by the routing vector, then the packet can be successfully delivered.  The computation demand on each node is appropriate for routing on-demand since only simple vector-related calculation is needed.
The computation demand on each node is appropriate for routing on-demand since only simple vector-related calculation is needed.
The routing pipe in VBF is determined by a predefined radius. In sparse networks, if no nodes lie within this pipe, then data packets cannot be forwarded to the sink even though paths may exist outside the pipe. In basic VBF, these paths will not be discovered and thus the delivery ratio will be severely affected. To improve the performance of VBF in sparse networks, we propose an enhanced version of VBF: Hop-by-hop Vector-based Forwarding (HH-VBF).
3.5. VBF Enhancement: Hop-by-Hop Vector-Based Forwarding (HH-VBF)
In HH-VBF, we redefine the routing virtual pipe to be a per-hop virtual pipe creation, instead of a unique pipe from the source to the sink. This hop-by-hop approach allows the expansion of the probability of finding a routing path in comparison with VBF. Consider a node  which receives a packet from the source or a forwarder node
which receives a packet from the source or a forwarder node  . Upon receipt of the packet, the node computes the vector from the sender
. Upon receipt of the packet, the node computes the vector from the sender  to the sink. In this way, the forwarding pipe changes each hop in the network, giving the name hop-by-hop vector-based forwarding (HH-VBF). After a receiver computes the vector from its sender to the sink, it calculates its distance to that vector. If this distance is smaller than the predefined threshold, it is eligible to forward the packet. We refer to such a node as a candidate forwarder for the packet.
to the sink. In this way, the forwarding pipe changes each hop in the network, giving the name hop-by-hop vector-based forwarding (HH-VBF). After a receiver computes the vector from its sender to the sink, it calculates its distance to that vector. If this distance is smaller than the predefined threshold, it is eligible to forward the packet. We refer to such a node as a candidate forwarder for the packet.
As in VBF, each candidate forwarder maintains a self-adaptation timer which depends on the desirableness factor. The timer represents the time the node holds the packet before forwarding it. We modify Definition 1 and get a new definition of the desirableness factor for HH-VBF.
Definition 3.
For a candidate forwarder  , the HH-VBF desirableness factor,
, the HH-VBF desirableness factor,  , of a node
, of a node  , is defined as
, is defined as

where  is the distance between node
is the distance between node  and node
and node  , and
, and  is the angle between
is the angle between  and
and  .
.  is the transmission range and
is the transmission range and  is the sink.
is the sink.
The self-adaption algorithm in HH-VBF is different from that in the VBF. As we recall, due to the effective packet suppression strategy adopted in VBF, only a few paths could be selected to forward packets. This may cause problems in sparse networks. To enhance the packet delivery ratio in sparse networks, we introduce some redundancy control in the self-adaption procedure for HH-VBF.
In HH-VBF, when a node receives a packet, it first holds the packet for some time period proportional to its desirableness factor (this is similar to VBF). Therefore, the node with the smallest desirableness factor will send the packet first. Following this way, each node in the neighborhood may hear the same packet multiple times. HH-VBF allows each node overhearing the duplicate packet transmissions to control the forwarding of this packet as follows: the node calculates its distances to the various vectors from the packet forwards to the sink. If the minimum one of these distances is still larger than a predefined minimum distance threshold  , this node will forward the packet; otherwise, it simply drops the packet. Obviously, the bigger
, this node will forward the packet; otherwise, it simply drops the packet. Obviously, the bigger  is, the more nodes will be allowed for packet forwarding. Thus, HH-VBF can control forwarding redundancy by adjusting
is, the more nodes will be allowed for packet forwarding. Thus, HH-VBF can control forwarding redundancy by adjusting  .
.
Each node that qualifies as a candidate forwarder delays the packet forwarding by an interval  which is computed the same way as in VBF. Then each node still uses the self-adaptation algorithm to limit the redundant packets.
which is computed the same way as in VBF. Then each node still uses the self-adaptation algorithm to limit the redundant packets.
Compared with the basic VBF, HH-VBF has two significant benefits:  more paths can be found for data delivery in sparse networks;
more paths can be found for data delivery in sparse networks;  HH-VBF is less sensitive to the routing pipe radius (i.e., the distance threshold). Correspondingly, we have the following two lemmas.
HH-VBF is less sensitive to the routing pipe radius (i.e., the distance threshold). Correspondingly, we have the following two lemmas.
Lemma 4.
Given the same routing pipe radius, if a packet is routable in VBF, then it must be routable in HH-VBF.
Proof.
If we can show that any routing-involved node in VBF is also involved in routing in HH-VBF, then we prove the lemma. Now, we assume that in HH-VBF, a node  is not involved in routing. This implies that in the network no path leading from the source to
is not involved in routing. This implies that in the network no path leading from the source to  gives the distance threshold. Thus, the source-to-sink routing pipe of the basic VBF protocol does not cover node
gives the distance threshold. Thus, the source-to-sink routing pipe of the basic VBF protocol does not cover node  ; that is,
; that is,  is not involved in routing. Using the contradiction method, we prove the lemma.
is not involved in routing. Using the contradiction method, we prove the lemma.
Lemma 4 indicates that HH-VBF is at least as reliable as VBF.
Lemma 5.
The valid range of routing pipe radius of HH-VBF is  , while the valid range of VBF is
, while the valid range of VBF is  , where
, where  is the node transmission range, and
is the node transmission range, and  is the network diameter (here one assumes that all nodes have the same transmission range).
is the network diameter (here one assumes that all nodes have the same transmission range).
Proof.
In HH-VBF, each node makes packet forwarding decisions based on its distance to the vector from its forwarder to the sink. If the distance is smaller than the predefined pipe radius, the node will forward the packet; otherwise it will discard the packet. In this way, when the pipe radius is bigger than the transmission range of the forwarder, those nodes which are outside the transmission range while still lie in the routing pipe are useless since they can not hear the packets from the forwarder. Thus, the valid range of routing pipe radius of HH-VBF is  , where
, where  is the transmission range.
is the transmission range.
In VBF, each node makes packet forwarding decisions based on its distance to the vector from the source to the sink. When the pipe radius is bigger than the transmission range, those nodes which are outside the transmission range of one forwarder while still lie in the routing pipe may hear packets from other forwarder. This means that they may be still eligible for packet forwarding. Thus, theoretically there is no upper limit for the pipe radius of VBF, while in practice, the valid range of routing pipe radius of VBF is  , where
, where  is the network diameter.
is the network diameter.
In VBF, the bigger the pipe radius, the higher successful data delivery ratio VBF can achieve, and the more optimal the paths VBF can select. Thus, for networks with different node densities, a proper pipe radius should be carefully chosen. While for HH-VBF, from Lemma 5, we can see that the biggest value of the pipe radius is  , which will clearly yield the highest successful data delivery ratio. Thus, in HH-VBF, we can eliminate the trouble of tuning the pipe radius by simply choosing the transmission range
, which will clearly yield the highest successful data delivery ratio. Thus, in HH-VBF, we can eliminate the trouble of tuning the pipe radius by simply choosing the transmission range  .
.
4. Performance Evaluation
In this section, we evaluate the performance of VBF and HH-VBF through extensive simulations in NS-2.
4.1. Simulation Settings
In our simulations, sensor nodes are randomly distributed in a 3D field of  . There are one data source and one sink. The source is fixed at location
. There are one data source and one sink. The source is fixed at location  near one corner of the field at the floor, while the sink is at location
near one corner of the field at the floor, while the sink is at location  near the opposite corner at the surface. Besides the source and the sink, all other nodes are mobile as follows: they can move in horizontal two-dimensional space, that is, in the X-Y plane (which is the most common mobility pattern in underwater applications [36]). Each node randomly selects a destination and moves toward that destination. Once the node arrives at the destination, it randomly selects a new destination and moves in a new direction. The sending rate is set to be one packet per 10 seconds, which is low to reduce interference among packets. For each simulation, the results are averaged over
near the opposite corner at the surface. Besides the source and the sink, all other nodes are mobile as follows: they can move in horizontal two-dimensional space, that is, in the X-Y plane (which is the most common mobility pattern in underwater applications [36]). Each node randomly selects a destination and moves toward that destination. Once the node arrives at the destination, it randomly selects a new destination and moves in a new direction. The sending rate is set to be one packet per 10 seconds, which is low to reduce interference among packets. For each simulation, the results are averaged over  times, with a randomly generated topology in each run. The total simulation time for each run is
times, with a randomly generated topology in each run. The total simulation time for each run is  seconds. We also implement a random access MAC protocol for UWSNs in ns2. In this MAC protocol, when a sender has packets to send, it first senses the channel. If the channel is free, it sends out its packets. If the channel is busy, it uses a back-off algorithm to contend the channel. The maximum number of back-offs is 4.
seconds. We also implement a random access MAC protocol for UWSNs in ns2. In this MAC protocol, when a sender has packets to send, it first senses the channel. If the channel is free, it sends out its packets. If the channel is busy, it uses a back-off algorithm to contend the channel. The maximum number of back-offs is 4.
As to the parameter in the physical layer, we set the parameters according to a commercial acoustic modem, LinkQuest UWM1000 [38]: the bit rate is  kbps; the transmission range is
kbps; the transmission range is  meters; the energy consumptions in sending mode, receiving mode and idle mode are
meters; the energy consumptions in sending mode, receiving mode and idle mode are  w,
w,  w, and
w, and  mw, respectively. Further, we set the packet size to
mw, respectively. Further, we set the packet size to  Bytes, the pipe radius to
Bytes, the pipe radius to  meters for VBF, and the predefined distance minimum threshold of HH-VBF,
meters for VBF, and the predefined distance minimum threshold of HH-VBF,  to
to  meters.
meters.
Performance Metrics
We propose three metrics: success rate, energy cost, and energy tax. Success rate is defined as the ratio of the number of packets successfully received by the sink to the number of packets generated by the source. Energy cost is measured by the total energy consumption of all the nodes in the network. Energy tax is defined as the average energy consumption for each successfully received packet.
4.2. Impact of Density and Mobility
We first investigate the impact of node density and mobility. In this set of experiments, all the mobile nodes have the same speed. We vary the mobility speed of each node from 0 m/s to 3 m/s and the number of nodes from 500 to 4000. The simulation results are plotted in Figures 3(a) and 3(b).
Figure 3(a) shows the success rate as the function of the number of nodes and the speed of nodes. When the node density is low, the success rate increases with density. However, when more than 4000 nodes are deployed in the space, the success rate remains above 90%. The success rate decreases slightly when the nodes are mobile; however, it is rather stable under different mobility speeds.
Figure 3(b) depicts the energy cost as the number of nodes and the speed of nodes vary. The energy cost increases when the number of nodes increases since more nodes are involved in packet forwarding. For the same number of nodes in the network, this figure also shows that the energy cost in static networks is slightly less than that in dynamic networks. However, the energy cost remains relatively stable as we vary the mobility speed of nodes in the network.
This set of simulation experiments have shown that in VBF, node speed has some impact on success rate and energy cost, but not significantly. It demonstrates that VBF could handle node mobility very effectively.
4.3. Impact of the Routing Pipe Radius
We test the impact of the routing pipe radius (i.e., the distance threshold) in this set of simulations. There are 2000 nodes in the network, and their speed is fixed at 1.5 m/s. We vary the radius from 0 meters to 200 meters. The results are shown in Figures 4(b) and 4(a).
From Figure 4(b), we can see that the success rate increases as the radius is lifted; meanwhile, as shown in Figure 4(a), more energy is consumed because more qualified nodes forward the packets. The curve in Figure 4(b) becomes flat when the radius exceeds 150 meters. This is caused by the topology of the network and the positions of the sink. The sink is located at the corner of a cube. It does not help to improve the success rate further once the radius exceeds some threshold since there are no nodes in routing pipe near the sink.
As shown in the above figures, the routing pipe radius does affect the given metrics greatly. In short, the bigger the radius is, the higher success rate VBF can achieve, the more energy VBF consumes, and the more optimal path VBF selects.
4.4. Effect of the Self-Adaptation Algorithm
In order to check the effect of the self-adaptation algorithm, we implement two versions of VBF, one is armed with self-adaptation algorithm, and the other is not. We compare the performance of these two implementations. In this set of simulation experiments, the speed of each node is fixed at 1.5 m/s, and the routing pipe radius is fixed at 100 m. The results are shown in Figures 5(a) and 5(b).
From Figure 5(a), we can see that even in a spare network, VBF with self-adaptation algorithm spends only half as much time as the one without self-adaptation algorithm. When the number of nodes increases, the difference between these two curves tends to increase, indicating that the self-adaptation algorithm can save more energy when the networks are densely deployed.
As shown in Figure 5(b), the success rate of VBF with self-adaptation is slightly less than the one without self-adaptation. However, the difference between these two curves tends to dwindle as the number of nodes increases. With more than 1000 nodes in the network, the difference is less than 5%. This result shows that the side effect of the self-adaptation algorithm diminishes in dense networks.
The results from this set of simulations show that the self-adaptation algorithm can save energy effectively, especially for dense networks. Even though the self-adaptation algorithm achieves this goal by introducing extra end-to-end delay and slightly reducing success rate, the success rate reduction is less than 10% in the sparse network case and the extra end-to-end delay is also limited. Furthermore, these side effects tend to disappear when the number of nodes increases.
4.5. Robustness of VBF
In this set of simulations, we evaluate the robustness of VBF against packet loss (or channel error) and node failure. In the experiments, the number of nodes is fixed at 1000, the radius is set 100 m, and the speed of nodes is set 0 m/s. In order to increase the density of the node deployment, we set the space to  . The source and the sink are located at (250.250,0) and (250,250,500), respectively.
. The source and the sink are located at (250.250,0) and (250,250,500), respectively.
The simulation results are shown in Figure 6. The  -axis is the error probability, which has different meanings. For the packet loss curve, node failure is set 0 and
-axis is the error probability, which has different meanings. For the packet loss curve, node failure is set 0 and  -axis is packet loss probability. For the node failure curve, packet loss is fixed at 0 and the
-axis is packet loss probability. For the node failure curve, packet loss is fixed at 0 and the  -axis is node failure probability. From this figure, we can see that VBF is robust against both packet loss and node failure. When the packet loss is as high as 50%, the success rate can still reach 90%. We also observe that VBF is more robust against packet loss since the packet in VBF is forwarded in interleaved forward paths. If a node does not receive a packet from one forwarding node, this node still has the chance to receive the same packet from another forwarding node since the forwarding paths in VBF are interleaved and redundant.
-axis is node failure probability. From this figure, we can see that VBF is robust against both packet loss and node failure. When the packet loss is as high as 50%, the success rate can still reach 90%. We also observe that VBF is more robust against packet loss since the packet in VBF is forwarded in interleaved forward paths. If a node does not receive a packet from one forwarding node, this node still has the chance to receive the same packet from another forwarding node since the forwarding paths in VBF are interleaved and redundant.
4.6. How HH-VBF Helps?
In this simulation setting, we compare the performance of VBF and HH-VBF in different network scenarios and show that HH-VBF can greatly improve the performance of VBF in sparse networks.
4.6.1. The Impact of Node Density
In this set of simulations, we examine the impact of node density. We fix the node speed at  (i.e., static networks) and change node density by varying the number of nodes deployed in the field from
(i.e., static networks) and change node density by varying the number of nodes deployed in the field from  to
to  . The results for success rate, energy cost, and energy tax are plotted in Figures 7(a), 7(b), and 7(c), respectively.
. The results for success rate, energy cost, and energy tax are plotted in Figures 7(a), 7(b), and 7(c), respectively.
From Figure 7(a), we can clearly observe the general trend of success rate for both VBF and HHVBF: with the increasing node density, the success rate is enhanced. This is intuitive: for any node in the network, as the network density becomes larger, more nodes will fall in its routing pipe (with fixed radius as the transmission range). In other words, more nodes are qualified for packet forwarding, as naturally leads to higher success rate. Future, we can see that the success rate of HH-VBF is significantly improved upon VBF, especially when the network is sparse. This observation is consistent with our early analysis: HH-VBF can find more paths for data delivery in sparse networks.
Figure 7(b) shows us that the energy cost of HH-VBF is higher than that of VBF, and the gap becomes more significant as the network gets denser. This is reasonable as the higher the node density, the more paths HH-VBF can find. We normalize the energy consumption, that is, compute the energy tax, and the results are illustrated in Figure 7(c). From this figure, we can observe that when the network is sparse, the normalized energy cost of HH-VBF is greatly lower than that of VBF. For example, when the number of nodes is  , the energy tax of HH-VBF is
, the energy tax of HH-VBF is  J/pkt, while the energy overhead of VBF is as high as
J/pkt, while the energy overhead of VBF is as high as  J/pkt. This is mainly because the data delivery ratio of VBF is extremely low (
J/pkt. This is mainly because the data delivery ratio of VBF is extremely low ( when the network size is
when the network size is  ). This further confirms that VBF is not good for sparse networks. On the other hand, when the network gets denser, VBF shows its advantage over HH-VBF: HH-VBF still tends to find more paths, while the delivery ratio has reached the maximum. In this case, more paths do not help to increase the success rate, but more energy cost will be introduced.
). This further confirms that VBF is not good for sparse networks. On the other hand, when the network gets denser, VBF shows its advantage over HH-VBF: HH-VBF still tends to find more paths, while the delivery ratio has reached the maximum. In this case, more paths do not help to increase the success rate, but more energy cost will be introduced.
4.6.2. The Impact of Node Mobility
In this set of simulations, we explore how node mobility impacts the performance of HH-VBF. We fix the network size at  (a relatively sparse network) and vary the node speed from
(a relatively sparse network) and vary the node speed from  to
to  m/s. Figures 8(a), 8(b), and 8(c) plot the results for the three metrics. From Figure 8(a), we can observe that the node mobility has different effects on the success rate of VBF and HH-VBF when the node speed is low. By conducting many additional simulation experiments, we find that this is mainly due to the randomness of network topology generation. For VBF, when node pattern changes from "static" to "mobile", the mobility actually helps to increase the chance that nonconnected paths become connected, while for HH-VBF, since there are more routing pipes in the network, light node mobility causes the chance that nonconnected paths become connected smaller. In fact, when the network is extremely sparse, for example, the network size is
m/s. Figures 8(a), 8(b), and 8(c) plot the results for the three metrics. From Figure 8(a), we can observe that the node mobility has different effects on the success rate of VBF and HH-VBF when the node speed is low. By conducting many additional simulation experiments, we find that this is mainly due to the randomness of network topology generation. For VBF, when node pattern changes from "static" to "mobile", the mobility actually helps to increase the chance that nonconnected paths become connected, while for HH-VBF, since there are more routing pipes in the network, light node mobility causes the chance that nonconnected paths become connected smaller. In fact, when the network is extremely sparse, for example, the network size is  in our simulations, the impact of light node mobility on HH-VBF has the same trend for VBF: the success rate is slightly enhanced. In addition, when we increase the number of simulation runs, the effect of node mobility is decreased (due to space limit, these results are not shown in in this paper). Furthermore, from Figure 8(a), we can see that as the node speed gets higher, the success rate of both VBF and HH-VBF becomes stable. This indirectly confirms that experiencing more topologies will help eliminate the difference caused by the topology randomness.
in our simulations, the impact of light node mobility on HH-VBF has the same trend for VBF: the success rate is slightly enhanced. In addition, when we increase the number of simulation runs, the effect of node mobility is decreased (due to space limit, these results are not shown in in this paper). Furthermore, from Figure 8(a), we can see that as the node speed gets higher, the success rate of both VBF and HH-VBF becomes stable. This indirectly confirms that experiencing more topologies will help eliminate the difference caused by the topology randomness.
Figures 8(b), 8(c), and 8(a) together convey the major information: both HH-VBF and VBF are robust to node mobility, while HH-VBF has much better performance (in terms of both success rate and energy tax) than VBF in sparse networks.
To summarize, we evaluate the performance of VBF under highly dynamic networks where almost all the nodes are mobile. The results show that VBF addresses the node mobility issue effectively and efficiently. In addition, these results also show that self-adaptation algorithm contributes significantly to save energy. Moreover, the simulation results show that VBF is robust against node failure and channel error. Additionally, our simulation results also prove that HH-VBF improves the success rate significantly and show significant improvement in sparse networks.
5. Conclusions
In this paper, we have proposed a vector-based forwarding (VBF) protocol to address the routing challenges in UWSNs. VBF is scalable, robust, and energy efficient.  Packets carry routing related information and no state information is required at nodes. Thus, it is scalable in terms of network size.
Packets carry routing related information and no state information is required at nodes. Thus, it is scalable in terms of network size.  In VBF, only those nodes in the routing pipe are involved in data forwarding. Therefore, it is energy efficient. Moreover, our self-adaptation algorithm allows a node to estimate its importance in its neighborhood and thus adjust its forwarding policy to save more energy.
In VBF, only those nodes in the routing pipe are involved in data forwarding. Therefore, it is energy efficient. Moreover, our self-adaptation algorithm allows a node to estimate its importance in its neighborhood and thus adjust its forwarding policy to save more energy.  VBF utilizes path redundancy (controlled by the routing pipe radius) to provide robustness against packet loss and node failure. To improve the performance of VBF in sparse networks, we propose an enhanced version of VBF, hop-by-hop vector-based forwarding (HH-VBF) protocol. HH-VBF adopts multiple forwarding vectors in the networks and, thus, improves the performance of VBF significantly in sparse networks. Our simulation results have demonstrated the promising performance of both VBF and HH-VBF.
VBF utilizes path redundancy (controlled by the routing pipe radius) to provide robustness against packet loss and node failure. To improve the performance of VBF in sparse networks, we propose an enhanced version of VBF, hop-by-hop vector-based forwarding (HH-VBF) protocol. HH-VBF adopts multiple forwarding vectors in the networks and, thus, improves the performance of VBF significantly in sparse networks. Our simulation results have demonstrated the promising performance of both VBF and HH-VBF.
References
Xie GG, Gibson J: A networking protocol for underwater acoustic networks. Department of Computer Science, Naval Postgraduate School, Monterey, Calif, USA; December 2000.
Proakis JG, Rice JA, Sozer EM, Stojanovic M: Shallow water acoustic networks. IEEE Communications Magazine 2001, 39(11):114-119. 10.1109/35.965368
Proakis JG, Sozer EM, Rice JA, Stojanovic M: Shallow water acoustic networks. IEEE Communications Magazines 2001, 39(11):114-119. 10.1109/35.965368
Akyildiz IF, Pompili D, Melodia T: Challenges for efficient communication in underwater acoustic sensor networks. ACM Sigbed Review 2004, 1(1):3-8.
Heidemann J, Ye W, Wills J, Syed A, Li Y: Research challenges and applications for underwater sensor networking. Proceedongs of the IEEE Wireless Communications and Networking Conference (WCNC '06), April 2006, Las Vegas, Nev, USA 1: 228-235.
Cui J-H, Kong J, Gerla M, Zhou S: The challenges of building scalable mobile underwater wireless sensor networks for aquatic applications. IEEE Network 2006, 20(3):12-18. 10.1109/MNET.2006.1637927
Kong J, Cui J-H, Wu D, Gerla M: Building underwater adhoc networks for large scale real-time aquatic applications. Proceedings of the IEEE Military Communication Conference (MILCOM '05), 2005
Kilfoyle DB, Baggeroer AB: State of the art in underwater acoustic telemetry. IEEE Journal of Oceanic Engineering 2000, 25(1):4-27. 10.1109/48.820733
Jacquet P, Mühlethaler P, Clausen T, Laouiti A, Qayyum A, Viennot L: Optimized link state routing protocol for Ad Hoc networks. Proceedings of the 5th IEEE International Multi Topic Conference (INMIC '01), 2001
Ogier R, Lewis M, Templin F: Topology dissemination based on reverse-path forwarding(TBRFP). IETF, Anaheim, Calif, USA; February 2004.
Perkins C, Bhagwat P: Highly dynamic destination-sequenced distance-vector (DSDV) routing for mobile computers. Proceedings of the ACM Conference on Communications Architectures, Protocols and Applications (SIGCOMM '94), August 1994, London, UK
Perkins CE, Royer E: Ad-Hoc on-demand distance vector routing. Proceedings of the IEEE Workshop on Mobile Computing Systems and Applications (WMCSA '99), February 1999, New Orleans, La, USA
Johnson DB, Maltz DA: Dynamic source routing in Ad Hoc wireless networks. In Mobile Computing, Kluwer International Series in Engineering and Computer Science. Volume 353. Kluwer Academic Publishers, Dodrecht, The Netherlands; December 1996:153-179. 10.1007/978-0-585-29603-6_5
Intanagonwiwat C, Govindan R, Estrin D: Directed diffusion: a scalable and roust communication paradigm for sensor networks. Proceedings of the 6th Annual International Conference on Mobile Computing and Networking (MOBICOM '00), August 2000, Boston, Mass, USA
Ye F, Luo H, Cheng J, Lu S, Zhang L: A two-tier data dissemination model for large-scale wireless sensor networks. Proceedings of the 8th Annual International Conference on Mobile Computing and Networking (MOBICOM '02), September 2002, Atlanta, Ga, USA
Ye F, Zhong G, Lu S, Zhang L: GRAdient broadcast: a robust data delivery protocol for large scale sensor networks. ACM Wireless Networks 2005, 11(3):285-298. 10.1007/s11276-005-6612-9
Marina M, Das S: On-demand multi path distance vector routing in ad hoc networks. Proceedings of International Conference on Network Protocols (ICNP '01), November 2001, Riverside, Calif, USA 11-14.
Leung R, Liu J, Poon E, Chan ALC, Li B: MP-DSR: a QoS-aware multi-path dynamic source routing protocol for wireless ad-hoc networks. Proceedings of IEEE International Conference on Local Computer Networks, 2001, Los Alamitos, Calif, USA
Braginsky D, Estrin D: Rumor routing algorithm for sensor networks. Proceedings of the ACM International Workshop on Wireless Sensor Networks and Applications (WSNA '02), September 2002, Atlanta, Ga, USA 22-31.
Heinzelman WR, Kulik J, Balakrishnan H: Adaptive protocols for information dissemination in wireless sensor networks. Proceedings of the 5th Annual ACM/IEEE International Conference on Mobile Computing and Networking (MOBICOM '99), August 1999, Seattle, Wash, USA
Karp B, Kung HT: GPSR: greedy perimeter stateless routing for wireless networks. Proceedings of the 6th Annual International Conference on Mobile Computing and Networking (MOBICOM '00), August 2000, Boston, Mass, USA 243-254.
Heissenbüttel M, Braun T, Bernoulli T, Wälchli M: BLR: beacon-less routing algorithm for mobile ad hoc networks. Elsevier's Computer Communication Journal 2003, 27(11):1076-1086.
Füßler H, Widmer J, Käsemann M, Mauve M, Hartenstein H: Contention-based forwarding for mobile ad hoc networks. Elsevier's Ad Hoc Networks 2003, 1(4):351-369. 10.1016/S1570-8705(03)00038-6
Seada K, Zuniga M, Helmy A, Krishnamachari B: Energy-efficient forwarding strategies for geographic routing in lossy wireless sensor networks. Proceedings of the 2nd International Conference on Embedded Networked Sensor Systems (SenSys '04), November 2004, Baltimore, Md, USA
Lee S, Bhattacharjee B, Banerjee S: Efficient geographic routing in multihop wireless networks. Proceedings of the 6th ACM International Symposium on Mobile Ad Hoc Networking and Computing (MobiHoc '05), May 2005
Niculescu D, Nath B: Trajectory based forwarding and its applications. Proceedings of the 9th Annual International Conference on Mobile Computing and Networking (MOBICOM '03), September 2003, San Diego, Calif, USA
Xie GG, Gibson JH: A network layer protocol for UANs to address propagation delay induced performance limitations. Prroceedings of the MTS/IEEE Oceans Conference, November 2001, Honolulu, Hawaii, USA 1-8.
Pompili D, Melodia T: Three-dimenisional routing in underwater acoustic sensor networks. Proceedings of the 2nd ACM International Workshop on Performance Evaluation of Wireless Ad Hoc, Sensor, and Ubiquitous Networks (WASUN '05), October 2005, Montreal, Calif, USA 214-221.
Goel A, Kannan AG, Katz I, Bartos R: Improving efficiency of a flooding-based routing protocol for underwater networks. Proceedings of the 3rd ACM International Workshop on Underwater Networks, September 2008, San Francisco, Calif, USA 91-94.
Jornet JM, Stojanovic M, Zorzi M: Focused beam routing protocol for underwater acoustic networks. Proceedings of the 3rd ACM International Workshop on Underwater Networks, September 2008, San Francisco, Calif, USA 75-81.
Guo Z, Colombi G, Wang B, Cui J-H, Maggiorinit D, Rossi GP: Adaptive routing in underwater delay/disruption tolerant sensor networks. Proceedings of the 5th IEEE Annual Conference on Wireless on Demand Network Systems and Services (WONS '08), January 2008, Bavaria, Germany 31-39.
Austin TC, Stokey RP, Sharp KM: PARADIGM: a buoybased system for AUV navigation and tracking. Proceedings of the MTS/IEEE Oceans Conference and Exhibition (Oceans '00), 2000, Providence, RI, USA 2: 935-938.
Zhang Y, Cheng L: A distributed protocol for multi-hop underwater robot positioning. Proceedings of the IEEE International Conference on Robotics and Biomimetics, August 2004
Garcia J-E: Ad hoc positioning for sensors in underwater acoustic networks. Proceedings of the MTS/IEEE Oceans Conference (Ocean '04), 2004 4: 2338-2340.
Kussat NH, Chadwell CD, Zimmerman R: Absolute positioning of an autonomous underwater vehicle using GPS and acoustic measurements. IEEE Journal of Oceanic Engineering 2005, 30(1):153-164. 10.1109/JOE.2004.835249
Zhou Z, Cui J-H, Zhou S: Localization for large-scale underwater sensor networks. Proceedings of the IFIP International Conferences on Networking, May 2007, Atlanta, Ga, USA 108-119.
Zhou Z, Cui J-H, Bagtzoglou A: Scalable localization with mobility prediction for underwater sensor networks. UCONN CSE Report July 2007., (UbiNet-TR07-01):
LinkQuest http://www.link-quest.com/
Xie P, Cui J-H, Lao L: VBF: vector-based forwarding protocol for underwater sensor networks. Proceedings of the IFIP Working Conference on Networking, May 2006, Coimbra, Portugal
Acknowledgments
This work is supported in part by the US National Science Foundation under CAREER Grant no. 0644190, Grant no. 0709005, Grant no. 0721834, Grant no. 0821597, and the US Office of Navy Research under YIP Grant no. N000140810864. Part of this work is presented in IFIP Networking'06 [39].
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Xie, P., Zhou, Z., Nicolaou, N. et al. Efficient Vector-Based Forwarding for Underwater Sensor Networks. J Wireless Com Network 2010, 195910 (2010). https://doi.org/10.1155/2010/195910
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/195910
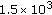 m/sec, which is five orders of magnitude lower than the radio propagation speed (
m/sec, which is five orders of magnitude lower than the radio propagation speed (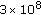 m/sec). Moreover, the available bandwidth of underwater acoustic channels is limited and dramatically depends on both transmission range and frequency. According to [
m/sec). Moreover, the available bandwidth of underwater acoustic channels is limited and dramatically depends on both transmission range and frequency. According to [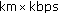 as the maximum attainable
as the maximum attainable 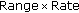 product.
product.






