- Research Article
- Open access
- Published:
On the Capacity of Hybrid Wireless Networks with Opportunistic Routing
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 202197 (2009)
Abstract
This paper studies the capacity of hybrid wireless networks with opportunistic routing (OR). We first extend the opportunistic routing algorithm to exploit high-speed data transmissions in infrastructure network through base stations. We then develop linear programming models to calculate the end-to-end throughput bounds from multiple source nodes to single as well as multiple destination nodes. The developed models are applied to study several hybrid wireless network examples. Through case studies, we investigate several factors that have significant impacts on the hybrid wireless network capacity under opportunistic routing, such as node transmission range, density and distribution pattern of base stations (BTs), and number of wireless channels on wireless nodes and base stations. Our numerical results demonstrate that opportunistic routing could achieve much higher throughput on both ad hoc and hybrid networks than traditional unicast routing (UR). Moreover, opportunistic routing can efficiently utilize base stations and achieve significantly higher throughput gains in hybrid wireless networks than in pure ad hoc networks especially with multiple-channel base stations.
1. Introduction
New portable devices, such as iPhone and PDAs, are increasingly equipped with strong communication and computation capabilities. They can host a wide range of applications, such as web browsing, audio/video streaming, and online gaming. Most devices have multiple radio interfaces and support different wireless protocols, such as Bluetooth, Wi-Fi, and 3G. It has become critical for such devices to efficiently utilize resources available in a hybrid wireless networking environment to achieve high data throughput and support bandwidth-intensive applications.
Recently, Opportunistic Routing (OR) was proposed to improve the throughput for ad-hoc networks. In this paper, we explore the gain of integrating OR with hybrid wireless networks that consist of ad hoc wireless nodes and base stations connected to a wireline infrastructure. We first extend the opportunistic routing algorithm to exploit high-speed data transmissions in infrastructure network through base stations. We then develop linear programming models to calculate the end-to-end throughput bounds from multiple source nodes to single as well as multiple destination nodes. The developed models are applied to study several hybrid wireless network examples. Through case studies, we investigate several factors that have significant impacts on the hybrid wireless network capacity under OR, such as density and distribution pattern of Base Stations, number of wireless channels on wireless nodes and BTs.
The contribution of this paper is fourfold.
-
(1)
We propose a simple method to extend OR to hybrid wireless networks. We develop new transmission cost metrics and forwarding priority rules to take into account candidate routes through BTs and infrastructure network.
-
(2)
We develop linear programming models to calculate end-to-end throughput bounds from multiple source nodes to single as well as multiple destination nodes.
-
(3)
We demonstrate through case studies that OR can efficiently utilize BTs and achieve significantly higher throughput gains in hybrid wireless networks than in pure ad-hoc networks. And the throughput gain of OR is also higher than that of UR in hybrid networks.
-
(4)
We systematically evaluate several factors determining the throughput gains of OR in hybrid wireless networks.
The rest of the paper is organized as follows. We briefly review the related works in Section 2. In Section 3, we present the extension of OR to hybrid wireless networks and the LP models to characterize the throughput bounds from multiple sources to single destination and from multiple sources to multiple destinations. Case studies on several example hybrid wireless networks are presented in Section 4. The paper is concluded in Section 5.
2. Background and Related Work
The throughput bound and capacity of ad-hoc and hybrid wireless networks have been studied extensively in the past. Well-known papers as in [1] and [2] developed analytical methods to calculate the capacity of mobile and ad-hoc networks. The works in [3–8] investigated the capacity of ad-hoc networks with infrastructure support in different cases and scenarios under UR. Recently, the topic Opportunistic Routing on ad-hoc networks attracted lots of interest [9–13]. In [12], the authors studied the opportunistic routing protocol ExOR, which dynamically chooses paths on a per-transmission basis in a wireless network to efficiently improve the throughput. To illustrate the idea of OR, in Figure 1,  wants to send packets to
wants to send packets to  .
.  ,
,  and
and  are closer to
are closer to  and are chosen as the candidate forwarders. After one broadcast from
and are chosen as the candidate forwarders. After one broadcast from  ,
,  ,
,  and
and  all receive the packet. Assuming that
all receive the packet. Assuming that  has the highest forwarding priority, so it will take over and broadcast the packet to its candidate forwarders
has the highest forwarding priority, so it will take over and broadcast the packet to its candidate forwarders  ,
,  and
and  . Assume that highest priority node
. Assume that highest priority node  misses the packet, so
misses the packet, so  will take over and forward the packet to its destination
will take over and forward the packet to its destination  . In [9], by integrating opportunistic routing with network coding, a new protocol MORE leads to significant throughput improvement in both unicast and multicast cases. In [10], the authors introduced the robust distribution opportunistic routing scheme based on ETX metric that can find the optimal path from source to destination. Authors of [13] conducted a systematic performance evaluation, taking into account node densities, channel qualities, and traffic rates to identify the cases when opportunistic routing makes sense. The recent work from Zeng et al. [14] proposed the method to calculate the maximum throughput between two end nodes with Opportunistic Routing in ad-hoc networks. The main focus of this paper is to study the throughput improvement of OR in hybrid wireless networks.
. In [9], by integrating opportunistic routing with network coding, a new protocol MORE leads to significant throughput improvement in both unicast and multicast cases. In [10], the authors introduced the robust distribution opportunistic routing scheme based on ETX metric that can find the optimal path from source to destination. Authors of [13] conducted a systematic performance evaluation, taking into account node densities, channel qualities, and traffic rates to identify the cases when opportunistic routing makes sense. The recent work from Zeng et al. [14] proposed the method to calculate the maximum throughput between two end nodes with Opportunistic Routing in ad-hoc networks. The main focus of this paper is to study the throughput improvement of OR in hybrid wireless networks.
3. Capacity of Hybrid Wireless Networks with OR
3.1. Network Model
We consider a hybrid wireless network consisting of wireless nodes and Wi-Fi Base Stations (BTs). Wireless nodes are equipped with radio interfaces and can communicate with each other through multihop ad-hoc transmissions. BTs are connected to the Internet using high bandwidth wireline connections. If a wireless node is within the coverage of a BT, it can communicate with the BT using single-hop infrastructure mode. Optionally, a wireless node might have a connection to a 3G base station that covers all wireless nodes under consideration. The optional 3G connection can be used as a control channel for nodes to exchange control information, such as the geographical locations of nodes. Packets can be transmitted using two transmission modes: ad-hoc mode and infrastructure mode. We assume that all nodes in the network are cooperative and forward each other's packets to their destinations with Opportunistic Routing. Here are some assumptions on hybrid wireless networks under study.
-
(i)
There are
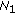 static wireless nodes randomly located in a square area. There are
static wireless nodes randomly located in a square area. There are  Wi-Fi Base Stations in the same area.
Wi-Fi Base Stations in the same area. -
(ii)
Wireless nodes are homogeneous. They have the same set of transmission rates and equivalent effective transmission ranges.
-
(iii)
Assume that the coverage areas of BTs do not overlap with each other. Each wireless node could connect to at most one BT.
-
(iv)
Source node transmits data with OR through relay nodes to destination. If the relay node is a wireless node, it uses OR to forward the packet to the next-hop node (relay or the final destination). If a relay node is a BT, it forwards the packet to the next-hop node through direct single-hop transmission.
-
(v)
Through a separate control channel (e.g., 3G), every node knows the geographical locations of its neighbors, base stations, and the destination node. Nodes then could differentiate the transmissions in wireless domain and wireline domain when making route selection over hybrid wireless network.
-
(vi)
We study two different models for data transmissions in hybrid wireless networks:
-
(1)
Single-Channel Model. In this model, all BT nodes and wireless nodes are equipped with a single radio interface. They use the same frequency spectrum to communicate with each other. In other words, infrastructure and ad-hoc transmissions share the same wireless channel. Wireless nodes use OR and BTs use UR to forward packets toward their destinations. Since every BT node only has a single wireless channel, it could communicate with no more than one wireless node at any given time.
-
(2)
Multiple-Channel Model. In this model, infrastructure and ad-hoc transmissions operate at nonoverlapping frequency ranges. Wireless nodes in the coverage of a BT can simultaneously communicate with the BT using infrastructure mode and other wireless nodes using ad-hoc mode. Moreover, every BT node has multiple wireless channels, and so it can communicate with multiple wireless nodes simultaneously. Wireless nodes use OR and BTs use UR to forward packets. If the Candidate Relay Set (CRS) of a wireless node consists of a BT and some wireless nodes, the wireless node simultaneously employs infrastructure and ad-hoc transmissions to push the same packet to the BT and wireless nodes, respectively.
-
(1)
3.2. Concurrent Transmitter Sets
The biggest challenge of studying the capacity of wireless networks is to model the conflicts between wireless links. The concept of Concurrent Transmitter Sets (CTSs) was proposed in [14] to calculate the end-to-end throughput in ad-hoc networks with OR. We extend the CTS concept to study the capacity of hybrid wireless networks.
With OR, a transmitter has multiple forwarding candidates in its Candidate Relay Set (CRS). Let all links from a transmitter to nodes in its CRS be links associated with that transmitter. In a hybrid wireless network, Conservative CTS (CCTS) is a set of transmitters (including the BTs) that when all of them are transmitting simultaneously, all links associated with them are still usable (no interfere with any other link [14]). However, such a requirement is too restrictive. Data from a transmitter can be forwarded to the next hop as long as one forwarding candidate in its CRS receives the data. To account for this, Greedy CTS (GCTS) is a set of transmitters (including the BTs) that when all of them are transmitting data simultaneously, at least one link associated with each transmitter is usable. This leads to the maximum end-to-end throughput. A maximal CCTS (GCTS) is a CCTS (GCTS) that is not a true subset of any another CCTS (GCTS).
For the single-channel model, infrastructure transmissions could interfere with ad-hoc transmissions. A BT cannot send and receive data with more than one wireless node at a particular time. For the multiple-channel model, BTs can send and receive data with multiple nodes simultaneously in infrastructure mode. Infrastructure transmissions have no conflict with ad-hoc transmissions. Due to the assumed nonoverlapped BT coverage areas, infrastructure transmissions of different BTs are also conflict-free. Data transmissions between BTs are in the wireline domain and will not interfere with any wireless transmissions. Consequently, directed links between BTs and directed links between a BT and its associated end nodes can be activated at anytime without introducing interference to any other link in the network. With the assumption of the number of wireless channels on each BT is big enough that it could send and receive data with all associated nodes simultaneously, all BT nodes can be included in all CTSs. An example of CTS is illustrated in Figure 2. A link  in the graph indicates node
in the graph indicates node  CRS of node
CRS of node  and they are in the transmission range of each other. Assume that source node
and they are in the transmission range of each other. Assume that source node  needs to send data to destination node
needs to send data to destination node  with the relays
with the relays  ,
,  and base stations
and base stations  ,
,  and
and  . We will find the CTSs for the two different models.
. We will find the CTSs for the two different models.
-
(1)
Single-Channel Model. Pairs of nodes
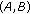 ,
, 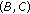 , and
, and 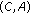 could not be included in the same CCTS. The reason is that two sets of links associated with each pair of nodes are not interference free. Also the pairs of of nodes
could not be included in the same CCTS. The reason is that two sets of links associated with each pair of nodes are not interference free. Also the pairs of of nodes 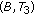 and
and 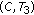 could not be included in the same CCTS because their links to node
could not be included in the same CCTS because their links to node 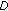 are not interference free. So the maximal Conservative CTSs in this case are
are not interference free. So the maximal Conservative CTSs in this case are 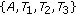 ,
, 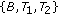 , and
, and  . The maximal Greedy CTSs in this case are exactly the same as the above maximal CCTSs. When all nodes in each of these GCTSs is transmitting simultaneously, usable links associated with each node are
. The maximal Greedy CTSs in this case are exactly the same as the above maximal CCTSs. When all nodes in each of these GCTSs is transmitting simultaneously, usable links associated with each node are 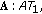

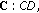
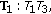
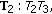 and
and 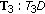 .
. -
(2)
MultiChannels Model. For Conservative CTSs, pairs of nodes
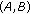 ,
, 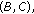 and
and 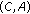 could not be included in the same CCTS. So the maximal CCTSs in this case are
could not be included in the same CCTS. So the maximal CCTSs in this case are 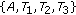 ,
, 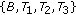 , and
, and  . On the other hand, for GCTSs, there are only pairs of nodes
. On the other hand, for GCTSs, there are only pairs of nodes  and
and  that could not be included in the same GCTS. It is because the only link
that could not be included in the same GCTS. It is because the only link 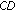 associated with node
associated with node 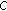 will be not usable whenever nodes
will be not usable whenever nodes  or
or 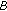 activated to transmit data. So the maximal Greedy CTSs in this case are
activated to transmit data. So the maximal Greedy CTSs in this case are  and
and 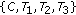 . When all nodes in each of these GCTSs is transmitting simultaneously, usable links associated with each node are
. When all nodes in each of these GCTSs is transmitting simultaneously, usable links associated with each node are 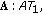
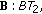
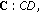

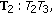 and
and  .
.
3.3. Opportunistic Routing Model
In OR, a transmitter selects neighbors "closer", that is, with lower transmission cost, to the destination as candidate forwarders in CRS. Forwarders in CRS are ranked based on their "closeness" to the destination. Since there is no preset route to a destination with OR, it is impossible to determine the accurate transmission cost from a node to a destination. In a pure ad-hoc network, one can use the geographic distance between a node  and destination node
and destination node  to measure the packet transmission cost from
to measure the packet transmission cost from  to
to  through ad-hoc network. For hybrid wireless networks, we propose a new metric that takes into account the low transmission cost through the infrastructure network. We assume that costs of the infrastructure transmissions between BTs are negligible. Then the cheapest transmission from
through ad-hoc network. For hybrid wireless networks, we propose a new metric that takes into account the low transmission cost through the infrastructure network. We assume that costs of the infrastructure transmissions between BTs are negligible. Then the cheapest transmission from  to
to  through infrastructure network is for
through infrastructure network is for  to transmit a packet destined to
to transmit a packet destined to  first to its closest BT,
first to its closest BT,  Then
Then  transmits the packet to a BT
transmits the packet to a BT  that is the closest to node
that is the closest to node  Finally,
Finally,  sends the packet to
sends the packet to  If
If  is directly covered by
is directly covered by  we use geographic distance
we use geographic distance  between
between  and
and  to estimate the transmission cost
to estimate the transmission cost  from
from  to
to  . If
. If  is not in the coverage of
is not in the coverage of  , we choose a node
, we choose a node  in
in  's coverage that is the closest to
's coverage that is the closest to  as a relay node. All packets from
as a relay node. All packets from  to
to  will be first sent to
will be first sent to  using the ad-hoc mode, then be relayed to
using the ad-hoc mode, then be relayed to  using the infrastructure mode. Consequently, the transmission cost is estimated as
using the infrastructure mode. Consequently, the transmission cost is estimated as  . Similarly, the transmission cost from
. Similarly, the transmission cost from  to
to  can be estimated as
can be estimated as  . The total transmission cost through the infrastructure network is then estimated as
. The total transmission cost through the infrastructure network is then estimated as  . The effective transmission cost
. The effective transmission cost  from
from  to
to  in the hybrid wireless network is the minimum of the cost of pure ad-hoc transmission and that of transmission through infrastructure:
in the hybrid wireless network is the minimum of the cost of pure ad-hoc transmission and that of transmission through infrastructure:

For the example in Figure 2, the source node is  and the destination node is
and the destination node is  . Assume that the geographic distances are
. Assume that the geographic distances are  = 9,
= 9,  = 5,
= 5,  = 7,
= 7,  = 5, and
= 5, and  = 7. The transmission cost using infrastructure network can be estimated as
= 7. The transmission cost using infrastructure network can be estimated as

So  = 8.
= 8.
In OR, a forwarding candidate is utilized to transmit a packet if and only if it receives the packet and all other candidates with higher priority in the CRS do not receive the packet. To study the capacity of OR, we need to calculate theeffective forwarding rate of a link between a transmitter  to each of its forwarding candidate
to each of its forwarding candidate  . Let
. Let  send data to its forwarding candidate set with rate
send data to its forwarding candidate set with rate  . Let
. Let  be the candidate forwarding set for
be the candidate forwarding set for  , and let
, and let  . The priority order to forward packets from
. The priority order to forward packets from  is
is  . Let
. Let  be the Packet Reception Ratio (PRR) between
be the Packet Reception Ratio (PRR) between  and
and 
 theoretically depends on distance between
theoretically depends on distance between  and
and  end node density around the position of nodes
end node density around the position of nodes  and
and  and the MAC scheduling scheme. Then the effective forwarding rate
and the MAC scheduling scheme. Then the effective forwarding rate  on link
on link  is
is

3.4. Throughput Bound to Single Destination
Given basic models studied in previous sections, we now proceed to study the capacity of hybrid wireless networks with OR. We start with the case that multiple sources send data to the same destination. As summarized in Table 1, there is a set  including
including  source nodes
source nodes  sending traffic to the same destination node
sending traffic to the same destination node  . From the original network, we create a connected graph
. From the original network, we create a connected graph  .
.  is the set of nodes, including end nodes and BT nodes.
is the set of nodes, including end nodes and BT nodes.  is the set of all available links, including ad-hoc links and infrastructure links. Let
is the set of all available links, including ad-hoc links and infrastructure links. Let  be the amount of traffic sent on link
be the amount of traffic sent on link  . We are interested in finding out the bound of end-to-end throughput from source nodes in
. We are interested in finding out the bound of end-to-end throughput from source nodes in  to
to  .
.
Assume that there are  maximal CTSs
maximal CTSs  . At any time, when a CTS is scheduled to transmit, nodes in the scheduled CTS could transmit packets simultaneously. Let
. At any time, when a CTS is scheduled to transmit, nodes in the scheduled CTS could transmit packets simultaneously. Let  be the time fraction that CTS
be the time fraction that CTS  is scheduled. We need to calculate the effective forwarding rate
is scheduled. We need to calculate the effective forwarding rate  for each link
for each link  under each CTS
under each CTS  . If a CCTS
. If a CCTS  is scheduled and
is scheduled and  , all links associated with
, all links associated with  are usable, and therefore
are usable, and therefore  , for all
, for all , which is calculated in (3); if
, which is calculated in (3); if  ,
,  . If a GCTS
. If a GCTS  is scheduled and node
is scheduled and node  , some links associated with
, some links associated with  maybe not usable. Let
maybe not usable. Let  be a binary variable for the usability of link
be a binary variable for the usability of link  under a GCTS
under a GCTS  , then we have
, then we have  , for all
, for all .
.
Let  be the sending rate from source
be the sending rate from source  toward the destination
toward the destination  . We have the following LP optimization formulation to characterize the throughput bound with single destination:
. We have the following LP optimization formulation to characterize the throughput bound with single destination:

subject to





Equation (4) is to find the maximum amount of traffic sent out from all the source nodes  to the destination. Constraint (5) specifies that the traffic on all links are none negative and there are no traffic from one node to its neighbor nodes that are not in its forwarding candidate set. Constraint (6) specifies flow conservation on all relay nodes. Constraint (7) specifies the flow conservations on all source nodes
to the destination. Constraint (5) specifies that the traffic on all links are none negative and there are no traffic from one node to its neighbor nodes that are not in its forwarding candidate set. Constraint (6) specifies flow conservation on all relay nodes. Constraint (7) specifies the flow conservations on all source nodes  . Constraint (8) states that no outgoing traffic from destination node
. Constraint (8) states that no outgoing traffic from destination node  . Constraint (9) preserves that only one CTS could be activated to transmit at any given time and the traffic assigned on each link is no more than the aggregate effective forwarding rate of that link during all active phases of CTSs. Depending on what types of CTSs we used as the input of the above formulation, we will get different bounds. Conservative CTS (CCTS) leads to conservative upper bound; Greedy CTS (GCTS) leads to optimistic upper bound of the end-to-end throughput.
. Constraint (9) preserves that only one CTS could be activated to transmit at any given time and the traffic assigned on each link is no more than the aggregate effective forwarding rate of that link during all active phases of CTSs. Depending on what types of CTSs we used as the input of the above formulation, we will get different bounds. Conservative CTS (CCTS) leads to conservative upper bound; Greedy CTS (GCTS) leads to optimistic upper bound of the end-to-end throughput.
3.5. Throughput Bound to Multiple Destinations
Based on the formulation for the single destination, we develop a model to calculate the throughput bound from multiple sources to multiple destinations in hybrid wireless networks. Suppose that there are a set  including
including  source nodes
source nodes  and a set
and a set  including
including  destination nodes
destination nodes  . In OR, at each node
. In OR, at each node  , there are different candidate forward sets for different destinations. Let
, there are different candidate forward sets for different destinations. Let  be the candidate forwarding set for destination node
be the candidate forwarding set for destination node  at node
at node  ,
,  with the priority order
with the priority order  . Similar to (3), for the
. Similar to (3), for the  -th forward candidate
-th forward candidate  in
in  , we can calculate the effective forwarding rate for destination
, we can calculate the effective forwarding rate for destination  on link
on link  as
as

Since CTS is also defined based on forwarding sets for all nodes, we need to include destination information into the definition of CTS. More specifically, a Conservative CTS (CCTS)  is a set of transmitter-destination pairs
is a set of transmitter-destination pairs  , such that all links
, such that all links  are usable when all transmitters in CCTS are active. Similarly, a Greedy CTS (GCTS)
are usable when all transmitters in CCTS are active. Similarly, a Greedy CTS (GCTS)  is a set of transmitter-destination pairs
is a set of transmitter-destination pairs  such that for each transmitter
such that for each transmitter  in GCTS, there exists at least one link
in GCTS, there exists at least one link 
 , that is usable when other transmitters in GCTS are active.
, that is usable when other transmitters in GCTS are active.
Similar to the single destination case, we need to calculate the effective forwarding rate  on each link
on each link  for destination
for destination  under each CTS
under each CTS  . If a CCTS
. If a CCTS  is scheduled and
is scheduled and  , all links from
, all links from  to nodes in
to nodes in  are usable, therefore
are usable, therefore 
 , which is calculated in (10); if
, which is calculated in (10); if  ,
,  . If a GCTS
. If a GCTS  is scheduled and
is scheduled and  , some links associated with
, some links associated with  maybe not usable. Let
maybe not usable. Let  be a binary variable for the usability of link
be a binary variable for the usability of link  under a GCTS
under a GCTS  , then we have
, then we have 
 .
.
Let  be the sending rate from source
be the sending rate from source  to the destination
to the destination  , and let
, and let  be the traffic on link
be the traffic on link  destined to
destined to  . We have the following LP optimization formulation to characterize the aggregate throughput bound:
. We have the following LP optimization formulation to characterize the aggregate throughput bound:

subject to





Similar to the single destination case, constraints (12), (13), (14), and (15) specify legitimate per-destination traffic flow on all links, relay nodes, source nodes, and destinations. Constraint (16) preserves that one CTS can be activated to transmit at any time; for each destination, the traffic assigned on each link is no more than total amount of traffic that could be delivered on that link during all active phases of CTSs.
4. Performance Evaluation
In this section, we apply models developed in the previous section to study the throughput bound and capacity of hybrid wireless networks with OR in three different cases: Single Source to Single Destination, Multiple Sources to Single Destination, and Multiple Sources to Multiple Destinations.
4.1. Methodology
We set up the case studies with different network sizes and different characteristics of the network in order to get the most accurate conclusions about the hybrid wireless network capacity. Based on the transmission range of transmitters, we developed a C++ program to calculate CTSs. Given node locations, the program calculates CTSs for both single-channel and multiple-channel models. The proposed LP method could be used for any type of packet loss model. For demonstration, we use a simple packet loss model on link  :
:  , where
, where  is the distance between
is the distance between  and
and  , and
, and  is the maximum transmission range. The node transmission rate is fixed at 10 packets/timeslot. We then calculate the effective forwarding rate on each link
is the maximum transmission range. The node transmission rate is fixed at 10 packets/timeslot. We then calculate the effective forwarding rate on each link  for each CTS. Then we use AMPL-CPLEX to solve the LP Problem to find the maximum throughput in each case. For each case study, we conduct multiple simulation runs and report the average of all runs.
for each CTS. Then we use AMPL-CPLEX to solve the LP Problem to find the maximum throughput in each case. For each case study, we conduct multiple simulation runs and report the average of all runs.
To understand the gain of OR in hybrid wireless networks, we also compare the performance of OR with that of hybrid unicast routing in the same network setting. To calculate the throughput bound of UR, we first build up the link conflict graph out of the original graph. In the conflict graph, each vertex corresponds to a link in the original graph. There is a link between two vertexes in the conflict graph if two corresponding links in the original graph interfere with each other. By finding all maximal independent sets of vertexes in the conflict graph, we can find the maximal sets of links in the original graph that can be activated at the same time. Assume that there are  maximal independent sets
maximal independent sets  . At any time, one set can be scheduled to transmit and all links in the scheduled set can transmit simultaneously. Let
. At any time, one set can be scheduled to transmit and all links in the scheduled set can transmit simultaneously. Let  be the time fraction that
be the time fraction that  is scheduled. The forwarding rate on link
is scheduled. The forwarding rate on link  is
is

Then, we can reuse the LP formulation from (4) to (9) and from (11) to (16) to calculate the capacity of hybrid wireless networks under either OR or UR routing method.
4.2. Single Source to Single Destination
At first, we run the case studies with a small network setting. The network area is  m. There are 8 wireless ad-hoc nodes. Nodes are located at the special positions as in Figure 3(a). Node 1 is the source, and node 8 is the destination. The initial radio range of nodes is 110 m. Source node and relay nodes send out packets with rate 10 packets/timeslot. We start the experiment with pure ad-hoc transmissions. Then BTs are added with different parameters and positions. From this setup, we calculate the maximum end to end throughput at 6 different cases of BT locations: Case 1: no BT; Case 2: one BT in position
m. There are 8 wireless ad-hoc nodes. Nodes are located at the special positions as in Figure 3(a). Node 1 is the source, and node 8 is the destination. The initial radio range of nodes is 110 m. Source node and relay nodes send out packets with rate 10 packets/timeslot. We start the experiment with pure ad-hoc transmissions. Then BTs are added with different parameters and positions. From this setup, we calculate the maximum end to end throughput at 6 different cases of BT locations: Case 1: no BT; Case 2: one BT in position  ; Case 3: two BTs in positions
; Case 3: two BTs in positions  and
and  ; Case 4: two BTs in positions
; Case 4: two BTs in positions  and
and  with the radio range of every node from now on increased to 120 m; Case 5: two BTs in position
with the radio range of every node from now on increased to 120 m; Case 5: two BTs in position  and
and  Case 6: two BTs in position
Case 6: two BTs in position  and
and  . We make the comparison between the OR and UR on the same network setting. The LP results of the bound of end-to-end throughput are showed on the Figure 3(b). First, we analyze throughput bound with OR. In ad-hoc mode, the bound of throughput from node 1 to node 8 is 0.3 packets/TS. All traffic is routed through the path 1
. We make the comparison between the OR and UR on the same network setting. The LP results of the bound of end-to-end throughput are showed on the Figure 3(b). First, we analyze throughput bound with OR. In ad-hoc mode, the bound of throughput from node 1 to node 8 is 0.3 packets/TS. All traffic is routed through the path 1 2
2 3
3

 8. The bottom necks on the maximum throughput path are the links: 2
8. The bottom necks on the maximum throughput path are the links: 2 3, 3
3, 3 4, 4
4, 4 5, 5
5, 5 6, 6
6, 6 7. In case 2, when one BT is added to the network, throughput bound starts gaining to 0.36 packets/TS since some additional traffic could be routed through infrastructure network over links 4
7. In case 2, when one BT is added to the network, throughput bound starts gaining to 0.36 packets/TS since some additional traffic could be routed through infrastructure network over links 4 In Case 3, when two BTs are located in the positions of
In Case 3, when two BTs are located in the positions of  and
and  , throughput bound increased to 1.0 packets/TS where more traffic could be routed through infrastructure network to get over "bottleneck" area. In case 4, when the radio range of each node is slightly increased, the throughput bound is increased to 1.65 packets/TS since the packet loss ratios on links are reduced. Consequently the effective forwarding rates on wireless links are increased. When the positions of two BTs are changed to positions
, throughput bound increased to 1.0 packets/TS where more traffic could be routed through infrastructure network to get over "bottleneck" area. In case 4, when the radio range of each node is slightly increased, the throughput bound is increased to 1.65 packets/TS since the packet loss ratios on links are reduced. Consequently the effective forwarding rates on wireless links are increased. When the positions of two BTs are changed to positions  and
and  in case 5, the throughput is increased to 4.1 packets/TS. This is because all traffic is routed through high bandwidth infrastructure network through link
in case 5, the throughput is increased to 4.1 packets/TS. This is because all traffic is routed through high bandwidth infrastructure network through link  . In case 6, two BTs are located in position
. In case 6, two BTs are located in position  and
and  , closer to the source and destination nodes. That helps to improve the bound of throughput from node 1 to node 8 to 5.14 packets/TS. All traffic is routed through the infrastructure network from the source to the destination in a single path.
, closer to the source and destination nodes. That helps to improve the bound of throughput from node 1 to node 8 to 5.14 packets/TS. All traffic is routed through the infrastructure network from the source to the destination in a single path.
When wireless nodes use UR to forward data, throughput gets through a single path from the source node to the destination node. The throughput bound on each case is Case 1: 0.3 packets/TS; Case 2: 0.3 packets/TS; Case 3: 0.47 packets/TS; Case 4: 1.06 packets/TS; Case 5: 4.09 packets/TS; Case 6: 5.14 packets/TS. Throughput bound of the network with OR will be higher than that with UR when the optimal solution uses more than one path to forward data toward the destination node. Therefore in cases 2, 3, 4, and 5, throughput gain with OR is higher than that with UR. But both routing methods get the same throughput bound for the cases 1 and 6. From the above results, we can see that infrastructure network could significantly increase the end-to-end throughput of ad-hoc network with OR. The numbers and locations of BTs are important and could significantly impact the end-to-end throughput. OR will outperform UR for the cases of using multipaths to get to the destination.
4.3. Multiple Sources to Single Destination
For the case of multiple sources and single destination, we studied two different settings. The first setting is to calculate the throughput bound with random demands, random nodes, and BTs positions. The second setting is to study the impact of BT distribution patterns on the throughput bound of the network. For each setting, we make comparisons between two different node models and between OR and UR.
There are 35 nodes randomly located in an area of  We randomly select 10 nodes as source nodes and one node as destination node. The radio range of nodes is 150 m. Source nodes and relay nodes send data with rate 10 packets/TS. We start with pure ad-hoc network and then add BTs randomly to the network. For the multiple-channel model, we assume that BTs have 4 wireless channels to communicate with wireless nodes.
We randomly select 10 nodes as source nodes and one node as destination node. The radio range of nodes is 150 m. Source nodes and relay nodes send data with rate 10 packets/TS. We start with pure ad-hoc network and then add BTs randomly to the network. For the multiple-channel model, we assume that BTs have 4 wireless channels to communicate with wireless nodes.
Figure 4 presents the throughput bound of hybrid wireless networks as the number of BTs increases. The figure shows the average values of 10 samples. From the figure, we see the growth trend of the throughput bound in random hybrid network as the number of base stations increases. When the number of base stations gets to 5, the throughput bound of hybrid wireless network outperforms the pure ad-hoc case by more than 170% for multiple-channel model and by 125% for single-channel model (4.88 and 3.54 packets/TS compared to 2.86 packets/TS in ad-hoc case). Due to the increased capacity of BTs, the throughput bound increases higher on multiple-channel model than single-channel model. Analyzing the results in details, we found that when the number of base stations is increased, the traffic routed through the pure ad-hoc network decreases and the traffic through the infrastructure network increases. As a result, the end-to-end throughput is improved. Also for either models, OR always gets significantly higher throughput than UR. The reason is that with multiple demands from multiple sources, at each hop, there are more chances for wireless nodes to forward packets through multinodes CRS under OR than a single relay node under UR. This makes the throughput bounds of OR much higher than UR.
For the second case study, we measure the throughput bound with the same network configuration as the first case but with three different BT distribution patterns: random distribution, regular distribution, and clustered distribution. For the regular distribution with  BTs, we evenly partition the whole area into
BTs, we evenly partition the whole area into  regions around the center of the area. One BT is placed at the center of each region. For the clustered distribution of BTs, we used a simple greedy scheme to add BTs one by one to the network at positions that could cover the highest number of uncovered wireless nodes. Again, we study the two models. Figure 5 shows the comparison of the throughput bounds under three BT distribution patterns with the single-channel model. With the same number of base stations deployed on the network, the throughput bound in regular distribution case is approximately as high as the throughput bound in the random distribution case, but higher than the throughput bound in the case of clustered distribution. This is because that, with the clustered BT distribution, many wireless nodes fall into the coverage of a same BT. Since each BT shares a single channel between ad-hoc transmission, the transmission through BT actually becomes the bottleneck and the bandwidth in the infrastructure network cannot be efficiently utilized. Meanwhile, for the multiple-channel model in Figure 6, the throughput bound in the case of clustered BT distribution is
regions around the center of the area. One BT is placed at the center of each region. For the clustered distribution of BTs, we used a simple greedy scheme to add BTs one by one to the network at positions that could cover the highest number of uncovered wireless nodes. Again, we study the two models. Figure 5 shows the comparison of the throughput bounds under three BT distribution patterns with the single-channel model. With the same number of base stations deployed on the network, the throughput bound in regular distribution case is approximately as high as the throughput bound in the random distribution case, but higher than the throughput bound in the case of clustered distribution. This is because that, with the clustered BT distribution, many wireless nodes fall into the coverage of a same BT. Since each BT shares a single channel between ad-hoc transmission, the transmission through BT actually becomes the bottleneck and the bandwidth in the infrastructure network cannot be efficiently utilized. Meanwhile, for the multiple-channel model in Figure 6, the throughput bound in the case of clustered BT distribution is  higher than the random and regular BT distributions. In the extreme case when number of base stations is 5, the throughput bound for 3 cases are 4.81, 5.14, and 5.81 packets/TS, respectively. The reason is that with clustered distribution, more wireless nodes can be covered with the same number of BTs, and with multiple channels, the transmissions through BTs are no longer bottleneck. This shows that the more nodes covered by BTs, the higher the throughput bound improvement. Also, in the studied case, due to random source nodes distribution, the regular BT distribution only slightly outperforms the random BT distribution.
higher than the random and regular BT distributions. In the extreme case when number of base stations is 5, the throughput bound for 3 cases are 4.81, 5.14, and 5.81 packets/TS, respectively. The reason is that with clustered distribution, more wireless nodes can be covered with the same number of BTs, and with multiple channels, the transmissions through BTs are no longer bottleneck. This shows that the more nodes covered by BTs, the higher the throughput bound improvement. Also, in the studied case, due to random source nodes distribution, the regular BT distribution only slightly outperforms the random BT distribution.
4.4. Multiple Sources to Multiple Destinations
For the case of Multiple Sources to Multiple Destinations, we set up a network area of  There are 10 nodes randomly placed in the area. We then configure 3 random pairs of source and destination nodes. The radio range of nodes is 150 m. Node transmission rate is 10 packets/TS. We start with pure ad-hoc network. We then gradually add BTs one by one to random locations of the network until 5 BTs are added. The throughput improvement result is shown in Figure 7. From this figure, we can see that the throughput bound increases as the number of base stations increases. Throughput bound for multiple-channel model is significantly higher than the single-channel model for both OR and UR. OR always got higher throughput bound than UR. For OR, the throughput bound with 5 BTs in case of multiple-channel model is 3.5 packets/TS, which is more than four times of the throughput bound of the pure ad-hoc case (0.79 packets/TS) and equals to 160% throughput bound in case of single-channel model.
There are 10 nodes randomly placed in the area. We then configure 3 random pairs of source and destination nodes. The radio range of nodes is 150 m. Node transmission rate is 10 packets/TS. We start with pure ad-hoc network. We then gradually add BTs one by one to random locations of the network until 5 BTs are added. The throughput improvement result is shown in Figure 7. From this figure, we can see that the throughput bound increases as the number of base stations increases. Throughput bound for multiple-channel model is significantly higher than the single-channel model for both OR and UR. OR always got higher throughput bound than UR. For OR, the throughput bound with 5 BTs in case of multiple-channel model is 3.5 packets/TS, which is more than four times of the throughput bound of the pure ad-hoc case (0.79 packets/TS) and equals to 160% throughput bound in case of single-channel model.
5. Conclusion
In this paper, we studied the throughput gain of OR routing schemes in hybrid wireless networks. We first extended OR to exploit the high-throughput routes over infrastructure network. We then developed linear programming models to characterize the capacity of hybrid wireless networks with OR. Our models calculate the end-to-end throughput bounds from multiple source nodes to single as well as multiple destination nodes. Through case studies on example hybrid wireless networks, we demonstrated the throughput gain of OR in hybrid wireless networking environment. The impacts of several factors on OR performance, such as the radio range of nodes, the density, and distribution pattern of BTs, were evaluated in the case studies. We also demonstrated that OR got higher throughput gain than UR in both ad-hoc and hybrid wireless networks, and single-channel and multiple-channel models. The current solving assumes simplified packet loss model. As a work for future direction, we will study the capacity of hybrid wireless networks with more realistic packet loss models. We used maximal CTS to calculate the throughput bounds. However it is time consuming to identify maximal CTS for large networks. We will study more efficient ways to model the conflicts between hybrid wireless links and characterize network capacity. We also plan to verify our capacity results using packet level simulations.
References
Gupta P, Kumar PR: The capacity of wireless networks. IEEE Transactions on Information Theory 2000, 46(2):388-404. 10.1109/18.825799
Grossglauser M, Tse D: Mobility increases the capacity of ad hoc wireless networks. Proceedings of the Annual Joint Conference of the IEEE Computer and Communications Societies (INFOCOM '01), 2001 3: 1360-1369.
Liu B, Liu Z, Towsley D: On the capacity of hybrid wireless networks. Proceedings of the Annual Joint Conference of the IEEE Computer and Communications Societies (INFOCOM '03), 2003 2: 1543-1552.
Kozat UC, Tassiulas L: Throughput capacity of random ad hoc networks with infrastructure support. Proceedings of the 9th Annual International Conference on Mobile Computing and Networking (MOBICOM '03), September 2003, San Diego, Calif, USA 55-65.
Agarwal A, Kumar PR: Capacity bounds for ad hoc and hybrid wireless networks. Computer Communication Review 2004, 34(3):71-81. 10.1145/1031134.1031143
Zemlianov A, de Veciana G: Capacity of ad hoc wireless networks with infrastructure support. IEEE Journal on Selected Areas in Communications 2005, 23(3):657-667.
Dai Q, Rong L, Hu H: Capacity, delay and mobility in hybrid wireless networks. Proceedings of the IEEE International Conference on Networking, Sensing and Control (ICNSC '08), 2008 271-276.
Liu B, Thiran P, Towsley D: Capacity of a wireless ad hoc network with infrastructure. Proceedings of the International Symposium on Mobile Ad Hoc Networking and Computing (MobiHoc '07) 2007, 239-246.
Chachulski S, Jennings M, Katti S, Katabi D: Trading structure for randomness in wireless opportunistic routing. Proceedings of the ACM SIGCOMM Conference on Computer Communications 2007, 169-180.
Dubois-Ferrire H, Grossglauser M, Vetterli M: Least-cost opportunistic routing. Proceedings of the Allerton Conference on Communication, Control, and Computing, September 2007, Monticello, Ill, USA
De Couto DSJ, Aguayo D, Bicket J, Morris R: A high-throughput path metric for multi-hop wireless routing. Proceedings of the 9th Annual International Conference on Mobile Computing and Networking (MOBICOM '03), September 2003, San Diego, Calif, USA 134-146.
Biswas S, Morris R: Opportunistic routing in multi-hop wireless networks. Proceedings of the 2nd Workshop on Hot Topics in Networks (HotNets '03), November 2003, Cambridge, Mass, USA
Shah RC, Wietholter S, Wolisz A, Rabaey JM: When does opportunistic routing make sense? Proceedings of the 3rd IEEE International Conference on Pervasive Computing and Communications Workshops (PerSens '05), March 2005 350-356.
Zeng K, Lou W, Zhai H: On end-to-end throughput of opportunistic routing in multirate and multihop wireless networks. Proceedings of the Annual Joint Conference of the IEEE Computer and Communications Societies (INFOCOM '08), April 2008, Phoenix, Ariz, USA 1490-1498.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Le, T., Liu, Y. On the Capacity of Hybrid Wireless Networks with Opportunistic Routing. J Wireless Com Network 2010, 202197 (2009). https://doi.org/10.1155/2010/202197
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/202197

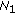 static wireless nodes randomly located in a square area. There are
static wireless nodes randomly located in a square area. There are  Wi-Fi Base Stations in the same area.
Wi-Fi Base Stations in the same area.
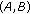 ,
, 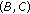 , and
, and 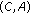 could not be included in the same CCTS. The reason is that two sets of links associated with each pair of nodes are not interference free. Also the pairs of of nodes
could not be included in the same CCTS. The reason is that two sets of links associated with each pair of nodes are not interference free. Also the pairs of of nodes 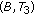 and
and 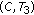 could not be included in the same CCTS because their links to node
could not be included in the same CCTS because their links to node 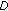 are not interference free. So the maximal Conservative CTSs in this case are
are not interference free. So the maximal Conservative CTSs in this case are 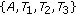 ,
, 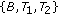 , and
, and  . The maximal Greedy CTSs in this case are exactly the same as the above maximal CCTSs. When all nodes in each of these GCTSs is transmitting simultaneously, usable links associated with each node are
. The maximal Greedy CTSs in this case are exactly the same as the above maximal CCTSs. When all nodes in each of these GCTSs is transmitting simultaneously, usable links associated with each node are 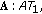

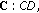
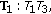
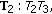 and
and 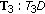 .
.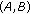 ,
, 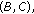 and
and 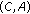 could not be included in the same CCTS. So the maximal CCTSs in this case are
could not be included in the same CCTS. So the maximal CCTSs in this case are 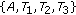 ,
, 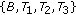 , and
, and  . On the other hand, for GCTSs, there are only pairs of nodes
. On the other hand, for GCTSs, there are only pairs of nodes  and
and  that could not be included in the same GCTS. It is because the only link
that could not be included in the same GCTS. It is because the only link 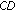 associated with node
associated with node 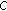 will be not usable whenever nodes
will be not usable whenever nodes  or
or 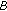 activated to transmit data. So the maximal Greedy CTSs in this case are
activated to transmit data. So the maximal Greedy CTSs in this case are  and
and 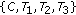 . When all nodes in each of these GCTSs is transmitting simultaneously, usable links associated with each node are
. When all nodes in each of these GCTSs is transmitting simultaneously, usable links associated with each node are 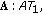
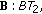
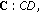

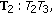 and
and  .
.



