- Research Article
- Open access
- Published:
A Linear Mixed-Effects Model of Wireless Spectrum Occupancy
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 203178 (2010)
Abstract
We provide regression analysis-based statistical models to explain the usage of wireless spectrum across four mid-size US cities in four frequency bands. Specifically, the variations in spectrum occupancy across space, time, and frequency are investigated and compared between different sites within the city as well as with other cities. By applying the mixed-effects models, several conclusions are drawn that give the occupancy percentage and the ON time duration of the licensed signal transmission as a function of several predictor variables.
1. Introduction
Spectrum measurement studies conducted by wireless communications researchers have shown that the utilization of licensed wireless spectrum is relatively low [1]. This is a result of the fact that frequency bands are exclusively licensed to specific services and entities on a command-and-control basis by regulatory agencies, for example, U.S. Federal Communications Commission (FCC), Industry Canada, and U.K. Office of Communications (OfCom). Although such a scheme is effective in protecting the rights of the incumbent license holders, a completely new strategy of spectrum allocation is needed in order to accommodate the increasing need for efficiently utilizing the wireless spectrum. This new strategy, called dynamic spectrum access (DSA), can be enabled by highly agile wireless platforms called cognitive radios [2]. Recently, as a significant step in this direction, the FCC has adopted the initial rules for the use of unlicensed devices in TV bands [3]. Consequently, there is a need to accurately assess and characterize wireless spectrum in order to facilitate the transition to this new spectrum allocation strategy.
Some of the earlier works aimeing at quantifying the spectrum usage within the context of DSA-oriented cognitive radio using actual real-time measurements have been reported in [1, 4]. A comprehensive summary of spectrum occupancy for New York City and several locations in Virginia were reported in [1]. Reference [4] presents similar results for locations in the state of Georgia. In particular, spectrum occupancy variations as a function of varying thresholds and across the different angles of arrival at the receiver were presented. In [5], a more thorough mathematical analysis based on continuous-time semi-Markov models is provided using spectrum measurement data of WLAN channels. More recently, closed-form probability distributions are presented for several fixed bandwidth signalling channels in [6] using the datasets presented in [1] whereas in [7], a comparison of the spectrum occupancy characteristics in four mid-size US cities is provided.
Spectrum measurement-based studies similar to those described above have also been conducted outside of the United States. In [8], spectrum occupancy for several bands in the frequency range from  MHz to
MHz to  MHz in urban Auckland, New Zealand is provided. In [9], four spectrum sensing methods have been proposed, and their performance is compared for UMTS uplink and GSM
MHz in urban Auckland, New Zealand is provided. In [9], four spectrum sensing methods have been proposed, and their performance is compared for UMTS uplink and GSM  uplink bands. In [10], a methodology has been developed to identify TV whitespace frequencies in the UK, using digital TV coverage maps in conjunction with a database containing their locations.
uplink bands. In [10], a methodology has been developed to identify TV whitespace frequencies in the UK, using digital TV coverage maps in conjunction with a database containing their locations.
Although the paradigm shift in wireless spectrum regulatory approaches is based on the assumption that the majority of wireless spectra are extensively underutilized by the incumbent license holders, who rely on several independently conducted measurement campaigns, there still exists a definite need to obtain a deeper understanding of this natural resource. By gaining insights into wireless spectrum occupancy characteristics, appropriate technical and legislative actions can be taken in order to support continued growth in the wireless sector. In this paper, we present a statistical analysis for the wireless spectrum occupancy across the spatial, temporal, and frequency dimensions using measurements collected in four mid-size US cities, namely, Rochester, NY; Buffalo, NY; Pittsburgh, PA; Worcester, MA. Although we have collected these measurements across several bands within the 88 MHz–3 GHz frequency range, results pertaining to only certain bands are presented for the purpose of brevity.
The rest of this paper is organized as follows. In Section 2, the measurement setup consisting of the hardware and software tools used to collect the data is described. Then, a description of the statistical results extracted from the measured data is presented in Section 3. A brief discussion of the linear mixed-effects model followed by its application to the collected measurement data is provided in Sections 4 and 5. Finally, we conclude the paper by highlighting the key conclusions in Section 4.
2. Spectrum Measurement Setup
In our measurement campaign, we used two antennas for scanning the low- and the high-frequency ranges. For the low-frequency range, from  MHz to
MHz to  MHz, we used a Diamond D-
MHz, we used a Diamond D- mini-Discone antenna with an operating frequency range of
mini-Discone antenna with an operating frequency range of  MHz. For the high-frequency range, from
MHz. For the high-frequency range, from  MHz to
MHz to  MHz, we used an Advanced Technical Materials (ATM)
MHz, we used an Advanced Technical Materials (ATM)  -
- -
- -
- horn antenna with an operating frequency range of
horn antenna with an operating frequency range of  GHz and an aperture of
GHz and an aperture of  . This helped us in observing the variation in spectrum usage across different angles of arrival. During our operation, one of these antennas is wired to an Agilent CSA series
. This helped us in observing the variation in spectrum usage across different angles of arrival. During our operation, one of these antennas is wired to an Agilent CSA series  spectrum analyzer with frequency range ranging from
spectrum analyzer with frequency range ranging from  kHz to
kHz to  GHz and consisting of a low-noise amplifier (LNA). We use an in-house software tool called SQUIRREL (Spectrum Query Utility Interface for Real-time Radio Electromagnetics) to communicate remotely with the spectrum analyzer via commands issued through a simple graphical user interface on a laptop. The GUI accepts details such as the center frequency, the span around the center frequency, and the resolution bandwidth. SQUIRREL communicates with the spectrum analyzer using TCL (Tool Command Language) over TCP/IP. After the sweep action is performed by the spectrum analyzer, the data points are returned to the GUI in a comma-spaced value format. In its current format, the GUI and the server are written in JAVA and can be deployed on a variety of operating systems and computers.
GHz and consisting of a low-noise amplifier (LNA). We use an in-house software tool called SQUIRREL (Spectrum Query Utility Interface for Real-time Radio Electromagnetics) to communicate remotely with the spectrum analyzer via commands issued through a simple graphical user interface on a laptop. The GUI accepts details such as the center frequency, the span around the center frequency, and the resolution bandwidth. SQUIRREL communicates with the spectrum analyzer using TCL (Tool Command Language) over TCP/IP. After the sweep action is performed by the spectrum analyzer, the data points are returned to the GUI in a comma-spaced value format. In its current format, the GUI and the server are written in JAVA and can be deployed on a variety of operating systems and computers.
The details about the locations and the dates of our spectrum measurement campaign are given in Table 1. We chose five locations which were at least a mile apart from each other, so that we would be able to capture the spatial variation as we go higher in frequency in the radio frequency (RF) spectrum. We measured usage activity across approximately  % of the wireless spectrum from
% of the wireless spectrum from  MHz to
MHz to  MHz. We omitted those bands in which the average usage has been previously reported to be extremely low. Thus, we focused on the remaining bands of interest. Also, in our measurement procedure, we sweep a particular frequency band, for example, Personal Communications Service (PCS) from
MHz. We omitted those bands in which the average usage has been previously reported to be extremely low. Thus, we focused on the remaining bands of interest. Also, in our measurement procedure, we sweep a particular frequency band, for example, Personal Communications Service (PCS) from  MHz to
MHz to  MHz, completely for a specific number of times and then proceed to the next band instead of scanning a wide frequency range. By performing the sweeps in this manner, our goal was to capture temporal variations over small periods of time. We chose a constant resolution bandwidth of
MHz, completely for a specific number of times and then proceed to the next band instead of scanning a wide frequency range. By performing the sweeps in this manner, our goal was to capture temporal variations over small periods of time. We chose a constant resolution bandwidth of  kHz, and the number of sweeps recorded per band per site is
kHz, and the number of sweeps recorded per band per site is  . Figure 1 provides a first-step summary of all the data points collected across all the frequencies in bins of
. Figure 1 provides a first-step summary of all the data points collected across all the frequencies in bins of  kHz. This plot which is a complementary cumulative distribution function shows the spectrum occupancy in each of the four cities as a function of energy.
kHz. This plot which is a complementary cumulative distribution function shows the spectrum occupancy in each of the four cities as a function of energy.
3. Spectrum Occupancy Characteristics
Figure 1 shows the trend in the occupancy irrespective of the cities, sites, time, and frequency. Although it serves the purpose of summarizing the measured results, a great deal of details remain hidden in the data with respect to both the occupancy characteristics over time, frequency, and space, and their dependance on other influencing factors. One way of analyzing the occupancy results is presented in [7] where we have provided occupancy values in percentages across different channels, along different angles of arrival and over several time sweeps as observed during the measurement duration. Another way of performing the analysis is from the point of associating the measured data with certain predictor variables in a linear mixed-effects model as we will explain below.
Due to the differences in the signal modulation involved as well as the differences in the bandwidths utilized by each channel, energy spectral densities corresponding to signals transmitted for different wireless services can be expected to be different. Thus, the four different wireless services analyzed, namely, paging, TV, WCS, and PCS correspond to four different predictor variables. Similarly, the four US cities are also predictor variables. Assuming that the spectrum usage is dependant on two other factors, namely, the time of the day and day of the week, they are incorporated as well. Due to the fact that our data corresponds to only four mid-size US cities, we do not claim that our model is a representative of all the mid-size US cities. This is the reason why although our model is not as general as we would like it to be, due to practical constraints involved, we, nevertheless, believe that it is indicative of the general trends in spectrum occupancy characteristics that can be expected in any typical US city. Moreover, we considered the population densities associated with the measurement sites as our random-effects term to reflect this fact. In the following sections, we provide more details regarding the occupancy values by grouping the appropriate collected data points as functions of several predictor variables. We now briefly explain the algorithm used to determine the presence/absence of the licensed user signal.
In order to show a comparison of the spectrum usage as a function of the variables mentioned above, an optimum threshold is computed using Otsu's gray-level thresholding algorithm [11] for each of the datasets. Otsu's optimum threshold provides a maximum separation between the two classes of data, namely, the signal and the noise (There are alternative approaches for computing the threshold, some of which are explained in [4]). Our primary motivation to use Otsu's thresholding algorithm is influenced by the nature of the data collected. Our measured data is in fact samples of energy spectral density (ESD) across a band of concentration and not time samples. We cannot apply traditional signal detection-based techniques due to total absence of phase information. Therefore, we detect the presence of the signal in the data purely from the point of view of separating data into two distinct distributions. The optimal threshold calculated using Otsu's algorithm is known to maximize the variance between the two classes of data, namely, the signal and the noise classes. Therefore, we employ this algorithm in our analysis.
In order to apply Otsu's algorithm, a matrix  is formed from the collected data points where the row
is formed from the collected data points where the row  contains data points over all the frequency locations in the band of interest during one particular time instant, and the column
contains data points over all the frequency locations in the band of interest during one particular time instant, and the column  represents the data points observed in that frequency bin over all time sweeps during the measurement process. The next step is to transform the contents of this matrix into gray-scale values by applying the procedure given by
represents the data points observed in that frequency bin over all time sweeps during the measurement process. The next step is to transform the contents of this matrix into gray-scale values by applying the procedure given by

Applying Otsu's algorithm to the matrix,  , gives the required optimum threshold, using which, all the values that are below are classified as noise and the rest as signal. Performing row-wise additions on the matrix,
, gives the required optimum threshold, using which, all the values that are below are classified as noise and the rest as signal. Performing row-wise additions on the matrix,  and dividing each element of the obtained column matrix with the total number of frequency locations give the percentage occupancy during the time period when the measurements were taken. We consider this percentage occupancy as the response variable which is a function of predictors such as the city, the site, the time of day during which the measurements were taken, weekday/weekend, and the specific wireless service corresponding to a particular frequency band, as mentioned previously. Before proceeding to fit the spectrum occupancy percentage as a function of these variables, we provide a brief overview of the linear mixed-effects model and explain its appropriateness in modeling the above-mentioned response variable.
and dividing each element of the obtained column matrix with the total number of frequency locations give the percentage occupancy during the time period when the measurements were taken. We consider this percentage occupancy as the response variable which is a function of predictors such as the city, the site, the time of day during which the measurements were taken, weekday/weekend, and the specific wireless service corresponding to a particular frequency band, as mentioned previously. Before proceeding to fit the spectrum occupancy percentage as a function of these variables, we provide a brief overview of the linear mixed-effects model and explain its appropriateness in modeling the above-mentioned response variable.
4. An Overview of the Linear Mixed-Effects Model
The normal linear model given by the equation:

explains the relationship between one or more independent variables, called regressor variables, and a dependent variable, called the response variable. The parameters of the model are called the regression coefficients, specified as  and the error variance, defined as
and the error variance, defined as  . The above model has one random-effect term, the error term
. The above model has one random-effect term, the error term  given by
given by

which is assumed to be independent and identically distributed (i.i.d.). Another important assumption is that the sample is drawn randomly from the population of interest. Usually, we set  =
= while
while  is either a constant or an intercept. Therefore, rewriting the model in matrix form yields
is either a constant or an intercept. Therefore, rewriting the model in matrix form yields

where we define the following variables:
-
(i)
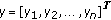 is the response vector;
is the response vector; -
(ii)
 is the model matrix;
is the model matrix; -
(iii)
 is the vector of regression coefficients;
is the vector of regression coefficients; -
(iv)
 is the vector of errors;
is the vector of errors; -
(v)
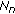 represents the n-variable multivariate normal distribution.
represents the n-variable multivariate normal distribution.
Estimating the parameters of the above model is a well known linear least squares problem. The estimate of the regression coefficient vector is given by the expression:

Several variants of the basic linear regression model of (2) are widely used in various areas of science. One such variant is the mixed-effect model. These models include additional random-effect terms and are appropriate in representing clustered, and therefore, dependent data arising when data are collected over time on the same entities; that is, these repeated measures data are generated by observing a number of entities repeatedly under differing experimental conditions, where the entities are assumed to constitute a random sample from a population of interest. Longitudinal data constitute a common type of repeated measures data, where the observations are ordered by time or position in space. In general, longitudinal data can be defined as repeated measures data where the observations within entities could not have been randomly assigned to the levels of a "treatment" of interest (usually time or position in space); hence, serial correlation results.
Writing the linear mixed-effect model of the form shown in (2) yields

where

Alternately, but equivalently, the above model can be written in matrix form as

where we define the following variables:
-
(i)
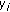 is the
is the  response variable for observations in the
response variable for observations in the  group;
group; -
(ii)
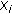 is the
is the  model vector for the fixed effects for observations in the
model vector for the fixed effects for observations in the 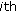 group;
group; -
(iii)
 is the
is the 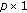 vector of fixed-effects coefficients for the
vector of fixed-effects coefficients for the 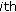 group;
group; -
(iv)
 is the
is the  model matrix for the random effects for observations in the
model matrix for the random effects for observations in the 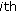 group;
group; -
(v)
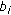 is the
is the 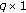 vector of random-effects coefficients for the
vector of random-effects coefficients for the 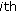 group;
group; -
(vi)
 is the
is the  variable of error for the
variable of error for the  group;
group; -
(vii)
 is the
is the  covariance matrix for the random-effects;
covariance matrix for the random-effects; -
(viii)
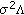 is the
is the  covariance matrix for the errors in the
covariance matrix for the errors in the  group.
group.
From the above representation, define  ,
,  and
and  When the variance components
When the variance components  and D are known, the standard estimators for
and D are known, the standard estimators for  and b are the generalized linear estimator
and b are the generalized linear estimator  where
where  and the posterior mean,
and the posterior mean,  The estimates
The estimates  and
and  jointly maximize the function [12]:
jointly maximize the function [12]:

The above function is the logarithm of the posterior density of  (up to a constant) for fixed
(up to a constant) for fixed  and for fixed
and for fixed  is the log-likelihood for
is the log-likelihood for  (up to a constant). Equation (9) has two terms, a sum of squares term and a quadratic term in b. By transforming the quadratic term in b to an equivalent sum of squares term, the optimization can be treated purely as a least squares problem. Then it is straightforward to translate it into the nonlinear setting.
(up to a constant). Equation (9) has two terms, a sum of squares term and a quadratic term in b. By transforming the quadratic term in b to an equivalent sum of squares term, the optimization can be treated purely as a least squares problem. Then it is straightforward to translate it into the nonlinear setting.
5. Linear Mixed-Effects Model Applied to Real-Time Wireless Spectrum Analysis
5.1. Regression Fit for Percentage Spectrum Occupancy
The model for the performed analysis on the spectrum occupancy percentage using a linear mixed model is as follows:

As seen from the above model, we have selected three indicator variables (i.e., either 1 or 0) for the types of the wireless service (TV, PCS, WCS), three indicator variables for the cities (Rochester, Buffalo, Pittsburgh), one indicator variable for afternoon/before noon, and one indicator variable for weekend/weekday. The intercept represents the spectrum occupancy in the paging band for Worcester, Massachusetts. As mentioned previously, the response variable in the regression analysis that we considered is the percentage spectrum occupancy which is calculated after applying Otsu's thresholding algorithm. Also, notice that the population density of the sites is chosen as the random-effects term which is specific to each of  groups (4 cities
groups (4 cities  5 sites). Since, we collected 25 wireless spectrum sweeps in each of the 5 sites from each city, the population density is chosen as the random effect that is different among the sites. Moreover, the population density is rounded off to the next highest multiple of 100. Thus, discrete values are considered, which helps in the interpretation of the obtained results. Fitting the linear mixed model gives the following results in Table 2. The parameters associated with the random effects are as follows: standard deviation of the intercept =
5 sites). Since, we collected 25 wireless spectrum sweeps in each of the 5 sites from each city, the population density is chosen as the random effect that is different among the sites. Moreover, the population density is rounded off to the next highest multiple of 100. Thus, discrete values are considered, which helps in the interpretation of the obtained results. Fitting the linear mixed model gives the following results in Table 2. The parameters associated with the random effects are as follows: standard deviation of the intercept =  , standard deviation of the population density =
, standard deviation of the population density =  and the correlation coefficient of the population density =
and the correlation coefficient of the population density =  .
.
From the above random effects, the covariance matrix of the random effects [13] can be calculated as follows:

5.1.1. Interpretation of the Obtained Regression Fit
From Table 2 mark (in Tables 2 and 3, DF is short for degrees of freedom), we see that the percentage spectrum occupancy for Worcester in the paging band is 13.28% with a  -value of
-value of  . With all other regressors remaining constant, the percentage spectrum occupancy for the city of Rochester in the paging band increases to 14.65%; that is, it is 1.37% higher than that of the city of Worcester with the associated
. With all other regressors remaining constant, the percentage spectrum occupancy for the city of Rochester in the paging band increases to 14.65%; that is, it is 1.37% higher than that of the city of Worcester with the associated  -value being
-value being  . Similarly, with the city under consideration, the type of the wireless service, and the time of the day remaining constant, the spectrum occupancy decreases by 1.12% on the weekends for a
. Similarly, with the city under consideration, the type of the wireless service, and the time of the day remaining constant, the spectrum occupancy decreases by 1.12% on the weekends for a  -value of
-value of  . Notice that we have obtained all of the above coefficients at very low
. Notice that we have obtained all of the above coefficients at very low  -values indicating the statistical significance of each of the regressors. Also, the structure of the
-values indicating the statistical significance of each of the regressors. Also, the structure of the  matrix which is almost diagonal suggests that the assumed normality assumption on the random effects is valid. The plot of the standardized residuals shown in Figure 2(a) also supports this assumption on the residuals since approximately 95% of the residuals lie in the range
matrix which is almost diagonal suggests that the assumed normality assumption on the random effects is valid. The plot of the standardized residuals shown in Figure 2(a) also supports this assumption on the residuals since approximately 95% of the residuals lie in the range  ; that is, they follow a standard normal distribution very closely.
; that is, they follow a standard normal distribution very closely.
5.2. Regression Fit for ON Time Duration of the Licensed Signal Transmissions
The model for the performed analysis on the ON time duration of the licensed signal transmissions in the four bands considered is similar to that of the spectrum occupancy percentage. Thus, it follows that

In this case, the response variable in the regression analysis performed is the ON time duration which is calculated after applying Otsu's thresholding algorithm. We calculated the amount of time during which the licensed signal transmission was consistently above the calculated threshold. The regressor variables are the same. Fitting the linear mixed model gives the following results presented in Table 3. The parameters associated with the random effects are as follows: standard deviation of the intercept =  , standard deviation of the population density =
, standard deviation of the population density =  and the correlation coefficient of the population density =
and the correlation coefficient of the population density =  .
.
From the above random effects, the covariance matrix of the random effects can be calculated as follows:

5.2.1. Interpretation of the Obtained Regression Fit
From Table 3, we see that the ON time duration for the city of Worcester in the PCS band is 3.35 s with a  -value of <.0001. It is 1.02 higher than that of the paging band. With all other regressors remaining constant, the ON time duration of the licensed signal transmissions for the city of Pittsburgh in the PCS band increases to 6.09 s; that is, it is 3.76 s higher than that of the city of Worcester with the associated
-value of <.0001. It is 1.02 higher than that of the paging band. With all other regressors remaining constant, the ON time duration of the licensed signal transmissions for the city of Pittsburgh in the PCS band increases to 6.09 s; that is, it is 3.76 s higher than that of the city of Worcester with the associated  -value being
-value being  . Similarly, with the city under consideration, the type of the wireless service, and the time of the day remaining constant, the ON time duration decreases by 1.87 s on the weekends for a
. Similarly, with the city under consideration, the type of the wireless service, and the time of the day remaining constant, the ON time duration decreases by 1.87 s on the weekends for a  -value of
-value of  . Again, we have obtained all of the above coefficients at very low
. Again, we have obtained all of the above coefficients at very low  -values indicating the statistical significance of each of the regressors. Again, the normality assumption on the random effects is validated by the structure of the
-values indicating the statistical significance of each of the regressors. Again, the normality assumption on the random effects is validated by the structure of the  matrix which is almost diagonal. We also show the quantile-quantile plot of the standardized residuals in Figure 2(b). Even though, towards the lower tail of the distribution, there is a slight deviation from the normal scores, we believe that it is not significant enough to seriously violate the normal distribution assumption.
matrix which is almost diagonal. We also show the quantile-quantile plot of the standardized residuals in Figure 2(b). Even though, towards the lower tail of the distribution, there is a slight deviation from the normal scores, we believe that it is not significant enough to seriously violate the normal distribution assumption.
6. Conclusion
In this paper, we analyzed the spectrum occupancy characteristics for four mid-size US cities in four frequency bands from a spectrum survey point of view. A linear mixed-effects model fit was obtained, and the selected regressor variables were shown to be statistically significant. The residual plots shown are a good indicator of this. Extending the considered models to include other regressor variables without making the interpretability of the models difficult is an important area in the field of regression analysis. In future work, we plan to study other techniques available in order to explain the spectrum occupancy characteristics for the other bands.
References
McHenry MA: NSF Spectrum Occupancy Measurements Project Summary. Shared Spectrum Company; 2005.
Mitola J III: Cognitive Radio: An Integrated Agent Architecture for Software Defined Radio, Ph.D. dissertation. KTH (Royal Institute of Technology), Stockholm, Sweden; 2000.
Federal Communications Commission : In the Matter of Unlicensed Operation in the TV Broadcast Bands, Additional Spectrum for Unlicensed Devices Below 900 MHz and in the 3 GHz Band.
Petrin AJ: Maximizing the Utility of Radio Spectrum: Broadband Spectrum Measurements and Occupancy Model for Use by Cognitive Radio, Ph.D. dissertation. Georgia Institute of Technology, Atlanta, Ga, USA; 2005.
Geirhofer S, Tong L, Sadler BM: A measurement-based model for dynamic spectrum access in WLAN channels. Proceedings of IEEE Military Communications Conference (MILCOM '06), 2006, Washington, DC, USA 1-7.
Marshall PF: Closed-form analysis of spectrum characteristics for cognitive radio performance analysis. Proceedings of the 3rd IEEE Symposium on New Frontiers in Dynamic Spectrum Access Networks (DySPAN '08), October 2008 1-12.
Pagadarai S, Wyglinski AM: A quantitative assessment of wireless spectrum measurements for dynamic spectrum access. Proceedings of the IEEE Cognitive Radio Oriented Wireless Networks and Communications (CROWNCOM '06), 2009, Hannover, Germany
Chiang RIC, Rowe GB, Sowerby KW: A quantitative analysis of spectral occupancy measurements for cognitive radio. Proceedings of the IEEE 65th Vehicular Technology Conference (VTC '07), April 2007 3016-3020.
Wellens M, de Baynast A, Mahonen P: Exploiting historical spectrum occupancy information for adaptive spectrum sensing. Proceedings of the IEEE Wireless Communications and Networking Conference, 2008, Las Vegas, Nev, USA 717-722.
Nekovee M: Quantifying the availability of TV white spaces for cognitive radio operation in the UK. Proceedings of the IEEE International Conference on Communications (ICC '09), 2009, Dresden, Germany
Otsu N: A threshold selection method from gray-level histograms. IEEE Transactions on Systems, Man, and Cybernetics 1979, 9(1):62-66.
Lindstrom MJ, Bates DM: Nonlinear mixed effects models for repeated measures data. Biometrics 1990, 46(3):673-687. 10.2307/2532087
Fox J: Applied Regression, Generalized Linear Models, and Related Methods. Sage Publications, Beverly Hills, Calif, USA; 2008.
Acknowledgment
This paper was supported by the National Science Foundation (NSF) via Grant CNS-0754315.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Pagadarai, S., Wyglinski, A. A Linear Mixed-Effects Model of Wireless Spectrum Occupancy. J Wireless Com Network 2010, 203178 (2010). https://doi.org/10.1155/2010/203178
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/203178

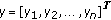 is the response vector;
is the response vector; is the model matrix;
is the model matrix; is the vector of regression coefficients;
is the vector of regression coefficients; is the vector of errors;
is the vector of errors;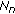 represents the n-variable multivariate normal distribution.
represents the n-variable multivariate normal distribution.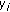 is the
is the  response variable for observations in the
response variable for observations in the  group;
group;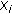 is the
is the  model vector for the fixed effects for observations in the
model vector for the fixed effects for observations in the 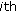 group;
group; is the
is the 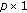 vector of fixed-effects coefficients for the
vector of fixed-effects coefficients for the 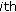 group;
group; is the
is the  model matrix for the random effects for observations in the
model matrix for the random effects for observations in the 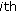 group;
group;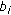 is the
is the 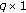 vector of random-effects coefficients for the
vector of random-effects coefficients for the 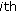 group;
group; is the
is the  variable of error for the
variable of error for the  group;
group; is the
is the  covariance matrix for the random-effects;
covariance matrix for the random-effects;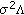 is the
is the  covariance matrix for the errors in the
covariance matrix for the errors in the  group.
group.