- Research Article
- Open access
- Published:
Advances in Relay Networks: Performance and Capacity Analysis of Space-Time Analog Network Coding
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 232754 (2010)
Abstract
We propose modified space-time-coding-based analog network coding (ANC) for multiple-relay network, termed space-time analog network coding (STANC). We present the performance and capacity analysis of the proposed network in terms of SER and ergodic capacity. We derive the closed-form expressions for the moment-generating function (MGF) of the equivalent signal-to-noise ratio (SNR) of the multiple-relay STANC network over independent and identically distributed (i.i.d.) Rayleigh, Nakagami, and Rician channels. Average SER of the system is evaluated using MGF-based approach. We further derive the approximate closed-form expressions of ergodic capacity. These expressions are simple and enable effective evaluation of the performance and capacity of STANC system.
1. Introduction
Relay nodes are considered as the main candidates for long-term-evolution-(LTE-) advanced standardization to provide incremental capacity growth and in-building coverage [1]. IEEE 802.16j standardization is developed for cooperative techniques to describe different modes of operation and frame structures [2]. In addition to the various advancements in the field of relay networks, it has also become vital to apply channel coding techniques to achieve high capacity and coding gain. Methods for implementing code diversity in fading scenario using higher-order coded modulation schemes are reported in [3, 4]. The idea of network coding (NC) was first introduced by Ahlswede et al. [5] to enhance the capacity of the wired networks. The essential idea of NC was further extended to wireless networks to explore the broadcast nature of wireless medium and to yield significant performance improvements in the wireless networks [5]. In [6–9], authors analyze the bit error rate (BER) and network capacity of physical-layer network coding (PNC) for frequency flat-fading channel and report that the capacity of bidirectional communication in a cooperative transmission (CT) increases by employing PNC. In PNC, the logical operation, that is XOR, is used by relay to map received signal into a digital bit stream, so that the interference becomes part of the arithmetic operation in network coding. In analog network coding (ANC), the relay simply amplifies and broadcasts the received signal without any processing.
The interference is always considered as a most harmful factor for wireless transmission. Wireless networks attempt to avoid scheduling multiple transmissions at the same time in order to prevent interference. Analog network coding (ANC), recognized as a variant of PNC, follows the opposite approach, which strategically allows the selected senders to interfere in order to exploits interference instead of avoiding it. The concept of ANC was first proposed by the author of [10], in which the terminals are allowed to simultaneously transmit their signals. The wireless channel naturally combines the signals, and the relay amplifies and forwards the resultant signal instead of forwarding combined packets as in digital network coding. The potential of analog network coding is recognized in information theory where it almost doubles the canonical relay network capacity in comparison with the conventional point-to-point transmission [10–12]. However, most of the research works reported in the literature so far focus only on the capacity bounds and do not provide the theoretical performance bound for symbol error rate (SER). In [7], an algorithm for PNC was proposed with certain assumptions of synchronization; symbol level, phase, and frequency. To make it more practical, the authors of [10] introduced an algorithm without those assumptions to exploit the lack of synchronization between interfering signals. In [13], the authors investigated the broadband bidirectional transmission with ANC scheme based on OFDM radio access in a frequency-selective fading channel. Most recently, a differential modulation scheme is proposed for analog network coding (ANC-DM) in which the channel state information (CSI) is not required at both sources and the relay [14], but the differential scheme is about 3 dB away as compared with the coherent detection scheme.
This paper presents the novel extension of analog network coding based on space-time coding technique (STANC) in a multihop scenario in view of further enhancing the network capacity and coverage area. In STANC, two terminals transmit their signals at the same instant to  number of relays, and each relay forwards the amplified version of the signal (the sum of signals from both terminals as received at the relay) to both the terminals in the second phase. Both terminals transmit signals simultaneously as discussed in [15]. Each signal takes two time slots to reach the destination terminal with the same throughput as in ANC but with improved performance. Although our work builds on earlier work, it exploits the space diversity by involving space time coding as a new aspect. We derive the theoretical closed-form expressions of moment-generating function (MGF) for STANC system over Nakagami-
number of relays, and each relay forwards the amplified version of the signal (the sum of signals from both terminals as received at the relay) to both the terminals in the second phase. Both terminals transmit signals simultaneously as discussed in [15]. Each signal takes two time slots to reach the destination terminal with the same throughput as in ANC but with improved performance. Although our work builds on earlier work, it exploits the space diversity by involving space time coding as a new aspect. We derive the theoretical closed-form expressions of moment-generating function (MGF) for STANC system over Nakagami- and Rician fading channels. Further, we analyze the performance of STANC in terms of SER using the MGF-based approach. The approximate closed-form expressions of ergodic capacity over both Nakagami-
and Rician fading channels. Further, we analyze the performance of STANC in terms of SER using the MGF-based approach. The approximate closed-form expressions of ergodic capacity over both Nakagami- and Rician fading channels are derived.
and Rician fading channels are derived.
This paper is organized as follows: Section 2 introduces the system model, channel model, transmission protocol, and equivalent SNR. Section 3 gives detailed derivations of closed-form MGF expressions. Section 4 presents the approximate closed-form expressions of ergodic capacity for both Nakagami and Rician distributions. Section 5 discusses the analytical and simulation results of the system performance. Finally, Section 6 concludes the paper.
Notations
 ,
,  ,
,  , and
, and  denote the expectation operator, the magnitude of complex value, the gamma function, and confluent hypergeometric function of the second kind, respectively.
denote the expectation operator, the magnitude of complex value, the gamma function, and confluent hypergeometric function of the second kind, respectively.  describes the link from node
describes the link from node  to
to  .
.  ,
,  , and
, and  represent the multipath gain coefficient, Rician-
represent the multipath gain coefficient, Rician- factor, and the Nakagami-
factor, and the Nakagami- factor, respectively from
factor, respectively from  th terminal to
th terminal to  th relay.
th relay.  ,
,  ,
,  , and
, and  represent the transmitted symbol energy of terminal
represent the transmitted symbol energy of terminal  over
over  link, equivalent signal-to-noise ratio (SNR) at
link, equivalent signal-to-noise ratio (SNR) at  th terminal, total unconditional moment-generating function of
th terminal, total unconditional moment-generating function of  , and AWGN at terminal
, and AWGN at terminal  in the
in the  th time slot, respectively.
th time slot, respectively.  and
and  denote the
denote the  th terminal and
th terminal and  th relay, respectively.
th relay, respectively.
2. System Model
The STANC cooperation model is shown in Figure 1. The terminals  and
and  communicate with each other through an
communicate with each other through an  number of relays
number of relays  , where
, where  . All the terminals are equipped with a single antenna and the relays operate in amplify-and-forward mode.
. All the terminals are equipped with a single antenna and the relays operate in amplify-and-forward mode.
2.1. Channel Model
It is assumed that the channel fading coefficients will remain the same for the two phases. It is also assumed that the transmitter (source terminal) has no channel information, but only the receiver (destination terminal) has perfect channel state information (CSI), which can be acquired by applying the training-based channel estimation schemes as reported in [16], where the entire channel link from source terminal to destination terminal is only estimated at the destination terminal. Here, we assume identical and independently distributed (i.i.d) Nakagami- fading channels and Rician fading channels for all the links between terminals and relay.
fading channels and Rician fading channels for all the links between terminals and relay.  is the fading magnitude of the link between
is the fading magnitude of the link between  th terminal and
th terminal and  th relay.
th relay.  (
( and
and  ) are gamma-distributed random variables. The probability density function of
) are gamma-distributed random variables. The probability density function of  for Nakagami-
for Nakagami- distribution is given in [17] as
distribution is given in [17] as

where  is a gamma function. Here, we consider
is a gamma function. Here, we consider  , where
, where  is the expectation operator. For
is the expectation operator. For  the Nakagami-
the Nakagami- distribution becomes the exponential distribution.
distribution becomes the exponential distribution.
Using [18, equation (2.15)], the probability density function of  for Rician distribution is given as:
for Rician distribution is given as:

where  is the zero-th order modified Bessel function of the first kind and
is the zero-th order modified Bessel function of the first kind and  is the Rician fading factor for the link from
is the Rician fading factor for the link from  th to
th to  th terminal. For
th terminal. For  , the Rician distribution becomes the Rayleigh distribution.
, the Rician distribution becomes the Rayleigh distribution.
2.2. STANC Transmission Protocol
The signaling in the proposed protocol is explained in Table 1.  represents the signal of
represents the signal of  th symbol from
th symbol from  th terminal. For the basic analog network coding scheme (ANC) [13] as given in Table 1, the
th terminal. For the basic analog network coding scheme (ANC) [13] as given in Table 1, the  denotes
denotes  th relay, (where
th relay, (where  ) and
) and  is the total number of relays.
is the total number of relays.  implies that the system uses the basic ANC scheme without STC. As the number of relays increases, the system starts using STANC based on STC codes and orthogonal STANC (OSTANC) based on OSTBC codes. Further, we compare the basic ANC scheme with STANC and OSTANC in terms of the three cases listed below.
implies that the system uses the basic ANC scheme without STC. As the number of relays increases, the system starts using STANC based on STC codes and orthogonal STANC (OSTANC) based on OSTBC codes. Further, we compare the basic ANC scheme with STANC and OSTANC in terms of the three cases listed below.
-
(i)
Case A: 2-relay STANC
-
(ii)
Case B: 3-relay OSTANC
-
(iii)
Case C:
 -relay STANC (general condition).
-relay STANC (general condition).
Case A.
The Alamouti code for  th terminal is given as
th terminal is given as

Terminals  and
and  send
send  and
and  , respectively, to
, respectively, to  in first time slot and
in first time slot and  and
and  , respectively, to
, respectively, to  in second time slot. The ANC scheme exploits the interference of the simultaneously transmitted signals in wireless channels. Therefore, in third time slot,
in second time slot. The ANC scheme exploits the interference of the simultaneously transmitted signals in wireless channels. Therefore, in third time slot,  and
and  amplify and forward the received signals to both
amplify and forward the received signals to both  and
and  on two orthogonal channels (FDMA-based rather than TDMA). In the fourth time slot,
on two orthogonal channels (FDMA-based rather than TDMA). In the fourth time slot,  and
and  send
send  and
and  , respectively, to
, respectively, to  , and
, and  and
and  , respectively, to
, respectively, to  in fifth time slot. In sixth time slot,
in fifth time slot. In sixth time slot,  and
and  amplify the information and the combined signals are forwarded to
amplify the information and the combined signals are forwarded to  and
and  through orthogonal subcarriers.
through orthogonal subcarriers.
Case B.
For simplicity, we assume  OSTBC for
OSTBC for  th terminal by considering three-relay ANC scenario.
th terminal by considering three-relay ANC scenario.

We focus only on the message sent by the source terminal  to the destination terminal
to the destination terminal  through
through  ,
,  , and
, and  . In first, second, and third time slots, terminal
. In first, second, and third time slots, terminal  transmits signal
transmits signal  ,
,  , and
, and  to
to  ,
,  , and
, and  , respectively. In fourth time slot, the relays retransmit the combined signals to both the terminals through orthogonal channels.
, respectively. In fourth time slot, the relays retransmit the combined signals to both the terminals through orthogonal channels.
In fifth and sixth time slots,  transmits
transmits  to
to  and
and  to
to  , respectively. In seventh time slot,
, respectively. In seventh time slot,  and
and  forward the scaled received signals to
forward the scaled received signals to  . Similarly, in eighth, ninth, and tenth time slots,
. Similarly, in eighth, ninth, and tenth time slots,  and
and  are transmitted to
are transmitted to  through
through  and
and  , respectively. In eleventh, twelfth, and thirteenth time slots, signals
, respectively. In eleventh, twelfth, and thirteenth time slots, signals  and
and  are transmitted through
are transmitted through  and
and  , respectively, to terminal
, respectively, to terminal  .
.
Case C.
In orthogonal transmission, the number of time slots increases with the increase in the number of transmitted symbols. The general form of OSTBC is given in [19] as:

where  is the total number of time slots used by
is the total number of time slots used by  number of relays.
number of relays.
2.3. Input-Output Equations
Case A.
The signals  and
and  are transmitted by
are transmitted by  (where
(where  ) to the relays
) to the relays  and
and  , respectively. The signals received at
, respectively. The signals received at  and
and  are given by:
are given by:

where  and
and  is the transmitted symbol energy at
is the transmitted symbol energy at  th terminal.
th terminal.
The  th relay normalizes the received signal by a factor of
th relay normalizes the received signal by a factor of  and transmits the analog network coded signal to
and transmits the analog network coded signal to  and
and  . The amplification factor (
. The amplification factor ( ) at the
) at the  th relay is given by
th relay is given by

where  is the average transmitted symbol energy at
is the average transmitted symbol energy at  . The two terminals
. The two terminals  (
( ) receive the signal from
) receive the signal from  th relay through two orthogonal channels and the general form of received signal is given as:
th relay through two orthogonal channels and the general form of received signal is given as:

where  at
at  th terminal
th terminal  .
.  knows
knows  and
and  . We assume that each terminal knows the value of
. We assume that each terminal knows the value of  . Knowing all these values, the terminals
. Knowing all these values, the terminals  and
and  can recover the data by removing their self information as given below:
can recover the data by removing their self information as given below:

Hence, the recovered signals from both the relays can be written as:

where  , having variance
, having variance  .
.
Similarly, the signals  and
and  are transmitted by
are transmitted by  (where
(where  ) to the relays
) to the relays  and
and  , respectively. The signals received at
, respectively. The signals received at  th terminal through
th terminal through  and
and  are given by:
are given by:

where  , having variance
, having variance  . The received signals at
. The received signals at  can be written in matrix form as:
can be written in matrix form as:

where

and  ,
,  , where
, where  is a normalizing factor at the receiver. By multiplying
is a normalizing factor at the receiver. By multiplying  on both side of (12), we arrive at:
on both side of (12), we arrive at:

Case B.
Using the TDMA-based protocol for the OSTANC system, the received signal from  at
at  in
in  th time slot is given as
th time slot is given as

where  . The relays
. The relays  normalize the received signal by a factor
normalize the received signal by a factor  and transmit the analog network coded signal to both the terminals
and transmit the analog network coded signal to both the terminals  . The two terminals
. The two terminals  (
( ) receive the signals from the relays through three orthogonal channels, and the general form of received signal is given as:
) receive the signals from the relays through three orthogonal channels, and the general form of received signal is given as:

where  at
at  th terminal
th terminal  .
.  knows
knows  and
and  . We assume that each terminal knows the value of
. We assume that each terminal knows the value of  . Knowing all these values, the terminal
. Knowing all these values, the terminal  amd
amd  can recover the data
can recover the data  and
and  , respectively, and the received signals can be written in matrix form as
, respectively, and the received signals can be written in matrix form as

where  ,
,  ,
,  , and
, and  are given as
are given as

 , and
, and  , where
, where  is a normalizing factor at the receiver. The equivalent SISO model is obtained by premultiplying with
is a normalizing factor at the receiver. The equivalent SISO model is obtained by premultiplying with  both sides of (18).
both sides of (18).

Case C.
Similarly, the equivalent SISO model obtained for  number of relays is given as:
number of relays is given as:

3. Performance Analysis
3.1. STANC Equivalent SNR
At terminal  , maximal ratio combining (MRC) is used to combine the signals received from
, maximal ratio combining (MRC) is used to combine the signals received from  relays. In general, the STANC equivalent SNR at
relays. In general, the STANC equivalent SNR at  th terminal can be expressed as:
th terminal can be expressed as:

where  and
and  . Here,
. Here,  and
and  give the equivalent SNR for Cases A and B, respectively.
give the equivalent SNR for Cases A and B, respectively.
3.2. Average SER
The SER equations ( ) for
) for  -PSK and
-PSK and  -QAM modulation are as given below.
-QAM modulation are as given below.
-
(1)
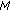 -PSK: the average SER for
-PSK: the average SER for  -PSK is given in [18] as:
-PSK is given in [18] as: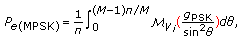 (22)
(22)where
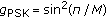 .
. -
(2)
 -QAM: the average SER for
-QAM: the average SER for  -QAM is given in [18] as:
-QAM is given in [18] as: (23)
(23)where
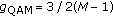 .
.
3.3. General STANC Moment Generating Function
In this section, we derive the expressions for unconditional MGFs to evaluate the above-average SER for ANC communication over Nakagami- , Rician, and Rayleigh fading channels. The MGF of
, Rician, and Rayleigh fading channels. The MGF of  is given as
is given as

We assume that  and
and  are independent random variables. The MGF for given
are independent random variables. The MGF for given  is represented as:
is represented as:

3.3.1. For Nakagami- Fading Channels
Fading Channels
As  (for
(for  ) are gamma-distributed random variables, (25) can be written as
) are gamma-distributed random variables, (25) can be written as

Equation (25) can also be written as

Equation (27) can be further simplified as:

where  , with
, with  as real constants. The unconditional MGF is obtained by averaging (28) over
as real constants. The unconditional MGF is obtained by averaging (28) over  and given as
and given as


where,  is given in (30), and
is given in (30), and  is the confluent hypergeometric function of the second kind.
is the confluent hypergeometric function of the second kind.
3.3.2. For Rician Fading Channels
The conditional MGF for given  of the SNR for STANC over Rician fading channels is given by:
of the SNR for STANC over Rician fading channels is given by:

where  and
and  are the Rician factor for link
are the Rician factor for link  and
and  , respectively. The unconditional MGF is obtained by averaging (31) over
, respectively. The unconditional MGF is obtained by averaging (31) over  and given as
and given as

where  is the confluent hypergeometric function of the second kind [20].
is the confluent hypergeometric function of the second kind [20].
3.3.3. For Rayleigh Fading Channels
The unconditional MGF of the SNR for  or
or  (special case: Rayleigh) is given as
(special case: Rayleigh) is given as

where  and
and  is an exponential integral function.
is an exponential integral function.
4. Ergodic Capacity Analysis
The ergodic capacity is the expectation of the information rate over the channel distribution between the source and destination and is defined in [21] as

which is upper bounded by Jensen's Inequality in [22] and is given as:

It is more important to determine the capacity of STANC two-way channels in a multipath fading environment. In this context, we propose that the STANC channel ergodic capacity can be accurately approximated by a Gaussian random variable, for the case where the channel state information (CSI) is not available at the transmitter but the receiver has the perfect channel state information. We present the ergodic capacity analysis of STANC two-way relay network based on the Gaussian approximation [13] under Nakagami and Rician fading channels. The implication of this Gaussian approximation is that only the capacity mean and variance are required to obtain an accurate approximation even for a lower number of relays, for various fading scenarios, and with a wide range of transmitting signal-to-noise ratio (TSNR). We resort to the numerical computation approach by using the Taylor expansion of  with the mean of
with the mean of  to obtain the second-order approximation expression for
to obtain the second-order approximation expression for  given in [23] as:
given in [23] as:

where  is given by (21) and
is given by (21) and  and
and  is the equivalent SNR at terminal
is the equivalent SNR at terminal  from
from  th relay in second phase of STANC bidirectional scheme. Now, the mean and second moment of
th relay in second phase of STANC bidirectional scheme. Now, the mean and second moment of  can be given as:
can be given as:

The probability density function of  in case of Nakagami-
in case of Nakagami- distribution is given in [17] as:
distribution is given in [17] as:

where  ,
,  is a gamma function. Here we consider
is a gamma function. Here we consider  , where
, where  is the expectation operator. For
is the expectation operator. For  , the Nakagami-
, the Nakagami- distribution becomes the exponential distribution.
distribution becomes the exponential distribution.
Using [18, equation (2.15)], the probability density function of  for Rician distribution is given as:
for Rician distribution is given as:

where  is the zero-th order modified Bessel function of the first kind and
is the zero-th order modified Bessel function of the first kind and  is the Rician fading factor for the link from
is the Rician fading factor for the link from  th to
th to  th terminal. For
th terminal. For  , the Ricean distribution becomes the Rayleigh distribution. Now, by substituting (38) in (37), the mean and second moment of
, the Ricean distribution becomes the Rayleigh distribution. Now, by substituting (38) in (37), the mean and second moment of  over Nakagami-
over Nakagami- fading channels are respectively given by
fading channels are respectively given by


where  denotes the confluent hypergeometric function of the second kind. Similarly, by substituting (39) in (37) we compute the mean and second moment of
denotes the confluent hypergeometric function of the second kind. Similarly, by substituting (39) in (37) we compute the mean and second moment of  over Rician-
over Rician- fading channels as given in (42) and (43), respectively.
fading channels as given in (42) and (43), respectively.


Consequently, the second-order approximated ergodic capacity for amplify and forward (AF) of STANC two-way relay network systems can be obtained by substituting (40), (41) and (42), (43) in (36) for Nakagami and Rician fading channels, respectively.
5. Results and Discussions
Numerical study results illustrate the performance and capacity analysis of our proposed STANC system. The exact SER and ergodic capacity performance are analytically derived in Section 3 and 4, respectively, and are drawn by using Mathematica software and shown together with the results obtained from Monte Carlo simulations. We obtained the analytical results for SER performance by substituting (29) and (32) in (22) and (23) for Nakagami and Rician fading channels, respectively. Similarly, we obtain analytical results for ergodic capacity as discussed in Section 4 for Nakagami and Rician fading channels. All the SER and capacity results are drawn w.r.t. the average SNR.
We initially present the SER performance of the two sources in the two-way relay network. Since, the SER performance at  and
and  are symmetrical, therefore, for simplicity, we compute the SER performance only at
are symmetrical, therefore, for simplicity, we compute the SER performance only at  . We assume that the channel coefficients remain constant during the time slots for transmission from terminals to relay and relay to terminals. Perfect channel estimation is assumed at the receiver, but transmitter does not know the channel conditions in terms of CSI. The uncorrelated propagation channel coefficients are Rayleigh, Nakagami, and Rician distributed. We consider the three types of ideal coherent modulation/demodulation schemes that is: BPSK, QPSK, and 16-QAM. The analysis is performed in terms of symbol error rate (SER). As a future work, this work can be extended to analyze the performance of the proposed STANC networks by taking path loss and shadowing effect into consideration.
. We assume that the channel coefficients remain constant during the time slots for transmission from terminals to relay and relay to terminals. Perfect channel estimation is assumed at the receiver, but transmitter does not know the channel conditions in terms of CSI. The uncorrelated propagation channel coefficients are Rayleigh, Nakagami, and Rician distributed. We consider the three types of ideal coherent modulation/demodulation schemes that is: BPSK, QPSK, and 16-QAM. The analysis is performed in terms of symbol error rate (SER). As a future work, this work can be extended to analyze the performance of the proposed STANC networks by taking path loss and shadowing effect into consideration.
5.1. SER Performance
Figures 2 and 3 show a good agreement between numerical analysis and simulation results for Nakagami  and Rician
and Rician  fading channels, respectively. A negligible difference can be seen in numerical and Monte-Carlo simulation results because at relatively high SNR values it was not possible to compute the numerical integration, since the crossing points no longer exist. At such points, numerical integration errors start to appear. These curves present the performance of the system with 2 relays operating in AF mode. In this case, at the destination end, each received signal carry data-modulated symbol which is exploited through STANC to obtain spatial-diversity gain resulting in improved performance. The figures also illustrate that the performance of STANC improves due to the channel coding gain in a block frequency flat-fading channel. It can be seen from Figures 2, 3, and 4 that the average SER exhibits decreasing coding gain as the constellation size increases for example, BPSK, QPSK, and 16-QAM, while full diversity is always achieved for sufficiently higher SNR. The coding gain can be certainly improved by invoking error control coding (ECC) at the expense of rate loss.
fading channels, respectively. A negligible difference can be seen in numerical and Monte-Carlo simulation results because at relatively high SNR values it was not possible to compute the numerical integration, since the crossing points no longer exist. At such points, numerical integration errors start to appear. These curves present the performance of the system with 2 relays operating in AF mode. In this case, at the destination end, each received signal carry data-modulated symbol which is exploited through STANC to obtain spatial-diversity gain resulting in improved performance. The figures also illustrate that the performance of STANC improves due to the channel coding gain in a block frequency flat-fading channel. It can be seen from Figures 2, 3, and 4 that the average SER exhibits decreasing coding gain as the constellation size increases for example, BPSK, QPSK, and 16-QAM, while full diversity is always achieved for sufficiently higher SNR. The coding gain can be certainly improved by invoking error control coding (ECC) at the expense of rate loss.
Figure 4 shows the performance improvement achieved in case of STANC-based transmission compared to ANC for  , the SNR (
, the SNR ( ) gain of approximately 10 dB is achieved in Rayleigh fading channels. It can be seen from the figure that the
) gain of approximately 10 dB is achieved in Rayleigh fading channels. It can be seen from the figure that the  gain of STANC is more for lower SER when compared to ANC scheme without STC and the dependence of the SER performance on the
gain of STANC is more for lower SER when compared to ANC scheme without STC and the dependence of the SER performance on the  with the number of channel links
with the number of channel links  (
( = no. of relays). The performance of STANC increases as
= no. of relays). The performance of STANC increases as  increases owing to more spatial diversity gain. The figure also shows the SER curves for STANC and OSTANC by implementing Alamouti codes
increases owing to more spatial diversity gain. The figure also shows the SER curves for STANC and OSTANC by implementing Alamouti codes  and OSTBC codes
and OSTBC codes  for
for  and
and  , respectively, for BPSK, QPSK, and 16QAM.
, respectively, for BPSK, QPSK, and 16QAM.
5.2. Ergodic Capacity
Analytically, the upper bound is derived from Jensen's inequality approach for Nakagami and Rician fading as in [22], which discussed only the Rayleigh fading channel. The ergodic capacity can be upper bounded by (35) because of concavity and with (40) and (42), this upper bound can be evaluated for Nakagami and Rician fading channels, respectively. The capacity given in (36) is evaluated using Monte Carlo numerical computational method to investigate the accuracy of the Gaussian approximations in a Nakagami and Rician fading environment. It can be seen from Figures 5 and 6 that the approximate ergodic capacity expressions of (36) are very stringent. The difference is negligible with the increase in the number of relays and in practical SNR regions. With a fewer number of relays, the simple upper bound is not so tight.
Figures 5 and 6 also illustrate the achievable ergodic capacity over Nakagami  and Rician
and Rician  , respectively, as a function of the
, respectively, as a function of the  with number of paths (Relays)
with number of paths (Relays)  for (i) analog network coding (ANC), (i.e., single source, destination terminal with single relay), (ii) analog network coding with space-time Alamouti codes
for (i) analog network coding (ANC), (i.e., single source, destination terminal with single relay), (ii) analog network coding with space-time Alamouti codes  (STANC), and (iii) analog network coding with orthogonal space time OSTBC codes
(STANC), and (iii) analog network coding with orthogonal space time OSTBC codes  (OSTANC). It can be observed that STANC is defined as 2 terminals communicating with each other through 2 relays by using Alamouti codes and 3, 4 relays by using OSTBC codes in the case of OSTANC. Both the source and destination terminals fully exploit the two-way transmission scheme of ANC and transmit their signals simultaneously to the relays in the first stage and receive the interfered signal from the relays in the second stage. Figures 5 and 6 show that the ergodic capacity of analog network coding (ANC), that is, single source, destination terminal with single relay is considerably increased in comparison with STANC and OSTANC scheme. This is because of the orthogonal partitioning of system resources. In ANC, the total available transmit power is divided only among the source terminals and the single relay whereas in STANC relaying, the total power is divided among the source terminals and also increasing number of relay terminals that is,
(OSTANC). It can be observed that STANC is defined as 2 terminals communicating with each other through 2 relays by using Alamouti codes and 3, 4 relays by using OSTBC codes in the case of OSTANC. Both the source and destination terminals fully exploit the two-way transmission scheme of ANC and transmit their signals simultaneously to the relays in the first stage and receive the interfered signal from the relays in the second stage. Figures 5 and 6 show that the ergodic capacity of analog network coding (ANC), that is, single source, destination terminal with single relay is considerably increased in comparison with STANC and OSTANC scheme. This is because of the orthogonal partitioning of system resources. In ANC, the total available transmit power is divided only among the source terminals and the single relay whereas in STANC relaying, the total power is divided among the source terminals and also increasing number of relay terminals that is,  . It can also be observed from the figures that the performance of the networks involving more number of relays that is, STANC and OSTANC is considerably better than ANC due to the gain obtained through diversity combining.
. It can also be observed from the figures that the performance of the networks involving more number of relays that is, STANC and OSTANC is considerably better than ANC due to the gain obtained through diversity combining.
6. Conclusion
In this paper, the novel extension of analog network coding based on space-time coding technique in multiple relay network under different fading scenarios is presented. The SER of  -ary QAM and PSK modulated signals are evaluated using the derived MGF expressions over Nakagami-
-ary QAM and PSK modulated signals are evaluated using the derived MGF expressions over Nakagami- and Rician fading channels. The approximate closed-form expressions of ergodic capacity are derived for STANC system. Numerical results indicate that all the approximate analytical expressions derived are very tight and can be effectively used for performance and capacity analysis of the proposed STANC system by arbitrarily changing different parameters of interest and in any SNR region. The analysis shows that the STANC system has significant performance improvement compared to ANC due to the diversity of combining. Reduction in ergodic capacity performance is also observed due to the orthogonal partitioning of system resources.
and Rician fading channels. The approximate closed-form expressions of ergodic capacity are derived for STANC system. Numerical results indicate that all the approximate analytical expressions derived are very tight and can be effectively used for performance and capacity analysis of the proposed STANC system by arbitrarily changing different parameters of interest and in any SNR region. The analysis shows that the STANC system has significant performance improvement compared to ANC due to the diversity of combining. Reduction in ergodic capacity performance is also observed due to the orthogonal partitioning of system resources.
References
Mogensen PE, Koivisto T, Pedersen KI, Kovács IZ, Raaf B, Pajukoski K, Rinne MJ: LTE-advanced: the path towards gigabit/s in wireless mobile communications. Proceedings of the 1st International Conference on Wireless Communication, Vehicular Technology, Information Theory and Aerospace and Electronic Systems Technology, Wireless (VITAE '09), May 2009, Aalborg, Denmark 147-151.
Genc V, Murphy S, Yu Y, Murphy J: IEEE 802.16j relay-based wireless access networks: an overview. IEEE Wireless Communications 2008, 15(5):56-63.
Tanoli SAK, Khan I, Rajatheva N: Cooperative Networks: bitinterleavedcoded modulation with iterative decoding. Journal of Communications 2010, 5(7):562-570.
Tanoli SAK, Khan I, Rajatheva N: Performance comparison of BICM-ID and BILDPCM-ID based cooperative network. Proceedings of the 72nd IEEE Vehicular Technology Conference (VTC '10), September 2010, Ottawa, Canada
Ahlswede R, Cai N, Li S-YR, Yeung RW: Network information flow. IEEE Transactions on Information Theory 2000, 46(4):1204-1216. 10.1109/18.850663
Popovski P, Yomo H: Bi-directional amplification of throughput in a wireless multi-hop network. Proceedings of the 63rd Vehicular Technology Conference (VTC '06), May 2006, Melbourne, Australia 2: 588-593.
Zhang S, Liew SC, Lam PP: Hot topic: physical-layer network coding. Proceedings of the 12th Annual International Conference on Mobile Computing and Networking (MOBICOM '06), September 2006, Los Angeles, Calif, USA 358-365.
Zhang S, Liew SC, Lu L: Physical layer network coding schemes over finite and infinite fields. Proceedings of IEEE Global Telecommunications Conference (GLOBECOM '08), November-December 2008, New Orleans, La, USA 3784-3789.
Wang T, Giannakis GB: Complex field network coding for multiuser cooperative communications. IEEE Journal on Selected Areas in Communications 2008, 26(3):561-571.
Katti S, Gollakota S, Katabi D: Embracing wireless interference: analog network coding. Proceeding of ACM Conference on Computer Communications (SIGCOMM '07), August 2007, Kyoto, Japan 397-408.
Katti S, Marić I, Goldsmith A, Katabi D, Medard M: Joint relaying and network coding in wireless networks. Proceedings of IEEE International Symposium on Information Theory (ISIT '07), June 2007, Nice, France 1101-1105.
Rankov B, Wittneben A: Spectral efficient protocols for half-duplex fading relay channels. IEEE Journal on Selected Areas in Communications 2007, 25(2):379-389.
Gacanin H, Adachi F: Broadband analog network coding. IEEE Transactions on Wireless Communications 2010, 9(5):1577-1583.
Song L, Li Y, Huang A, Jiao B, Vasilakos AV: Differential modulation for bidirectional relaying with analog network coding. IEEE Transactions on Signal Processing 2010, 58(7):3933-3938.
Cui T, Gao F, Ho T, Nallanathan A: Distributed space-time coding for two-way wireless relay networks. IEEE Transactions on Signal Processing 2009, 57(2):658-671.
Gao F, Cui T, Nallanathan A: On channel estimation and optimal training design for amplify and forward relay networks. IEEE Transactions on Wireless Communications 2008, 7(5):1907-1916.
Atapattu S, Rajatheva N, Tellambura C: Performance analysis of TDMA relay protocols over Nakagami-m fading. IEEE Transactions on Vehicular Technology 2010, 59(1):93-104.
Simon MK, Alouini M-S: Digital Communication over Fading Channels. John Wiley & Sons, New York, NY, USA; 2005.
Tarokh V, Seshadri N, Calderbank AR: Space-time codes for high data rate wireless communication: performance criterion and code construction. IEEE Transactions on Information Theory 1998, 44(2):744-765. 10.1109/18.661517
Gradshteyn IS, Ryzhik IM: Table of Integrals, Series and Products. 6th edition. Academic Press, New York, NY, USA; 2000.
Proakis JG: Digital Communications. 3rd edition. McGraw-Hill, New York, NY, USA; 1995.
Farhadi G, Beaulieu NC: Ergodic capacity of multi-hop wireless relaying systems in rayleigh fading. Proceedings of IEEE Global Telecommunications Conference (GLOBECOM '08), November-December 2008, usa 4477-4482.
Chen S, Wang W, Zhang X: Ergodic and outage capacity analysis of cooperative diversity systems under rayleigh fading channels. Proceedings of IEEE International Conference on Communications Workshops (ICC '09), June 2009
Author information
Authors and Affiliations
Corresponding authors
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Tanoli, S., Khan, I., Rajatheva, N. et al. Advances in Relay Networks: Performance and Capacity Analysis of Space-Time Analog Network Coding. J Wireless Com Network 2010, 232754 (2010). https://doi.org/10.1155/2010/232754
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/232754

 -relay STANC (general condition).
-relay STANC (general condition).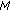 -PSK: the average SER for
-PSK: the average SER for  -PSK is given in [
-PSK is given in [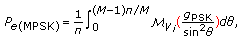
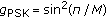 .
. -QAM: the average SER for
-QAM: the average SER for  -QAM is given in [
-QAM is given in [
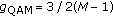 .
. Fading Channels
Fading Channels
 fading channels with different constellation size and orthogonal transmission from the relays (
fading channels with different constellation size and orthogonal transmission from the relays ( ).
).
 ).
).

 fading channels. The approximated analytical results given in (36) using (40) and (41).
fading channels. The approximated analytical results given in (36) using (40) and (41).