- Research Article
- Open access
- Published:
A Semianalytical PDF of Downlink SINR for Femtocell Networks
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 256370 (2010)
Abstract
This paper presents a derivation of the probability density function (PDF) of the signal-to-interference and noise ratio (SINR) for the downlink of a cell in multicellular networks. The mathematical model considers uncoordinated locations and transmission powers of base stations (BSs) which reflect accurately the deployment of randomly located femtocells in an indoor environment. The derivation is semianalytical, in that the PDF is obtained by analysis and can be easily calculated by employing standard numerical methods. Thus, it obviates the need for time-consuming simulation efforts. The derivation of the PDF takes into account practical propagation models including shadow fading. The effect of background noise is also considered. Numerical experiments are performed assuming various environments and deployment scenarios to examine the performance of femtocell networks. The results are compared with Monte Carlo simulations for verification purposes and show good agreement.
1. Introduction
Signal-to-interference and noise ratio (SINR) is one of the most important performance measures in cellular systems. Its probability distribution plays an important role for system performance evaluation, radio resource management, and radio network planning. With an accurate probability density function (PDF) of SINR, the capacity and coverage of a system can be easily predicted, which otherwise should rely on complicated and time-consuming simulations.
There have been various approaches to investigate the statistical characteristics of received signal and interference. The other-cell interference statistics for the uplink of code division multiple access (CDMA) system was investigated in [1], where the ratio of other-cell to own-cell interference was presented. The result was extended to both the uplink and the downlink of general cellular systems by [2]. In [3], the second-order statistics of SIR for a mobile station (MS) were investigated. In [4, 5], the prediction of coverage probability was addressed which is imperative in the radio network planning process. The probability that SINR goes below a certain threshold, which is termed outage probability, is another performance measure that has been extensively explored. The derivation of the outage probability can be found in [6–8] and references therein.
While most of the contributions have focused on a particular performance measure such as coverage probability or outage probability, an explicit derivation of the probability distribution for signal and interference has also been investigated [9, 10]. In [9], a PDF of adjacent channel interference (ACI) was derived in the uplink of cellular system. A PDF of SIR in an ad hoc system was studied in [10] assuming single transmitter and receiver pair.
In this paper, we derive the PDF of the SINR for the downlink of a cell area in a semianalytical fashion. A practical propagation loss model combined with shadow fading is considered in the derivation of the PDF. We also consider background noise in the derivation, which is often ignored in the references. Uncoordinated locations and transmission powers of interfering base stations (BSs) are considered in the model to take into account the deployment of femtocells (or home BSs) [11] in an indoor environment. It has been suggested that femto BSs can significantly improve system spectral efficiency by up to a factor of five [12]. It has also been found that in closed-access femtocell networks macrocell MSs in close vicinity to a femtocell greatly suffer from high interference and that such macrocell MSs cause destructive interference to femtocell BSs [13]. Thus, an accurate model for the probability distribution of the SINR assuming an uncoordinated placement of indoor BSs can be vital for further system improvements. In spite of the recent efforts for the performance evaluation of femtocells, most of the works relied on system simulation experiments [12–17]. To the best of our knowledge, the PDF of SINR for the outlined conditions and environment has not been derived before.
Since shadow fading is generally considered to follow a log-normal distribution, the PDF of the sum of log-normal RVs should be provided as a first step in the derivation of the SINR distribution. During the last few decades numerous approximations have been proposed to obtain the PDF of the sum of log-normal RVs since the exact closed-form expression is still unknown [18–23]. So far, no method offers significant advantages over another [18], and sometimes a tradeoff exists between the accuracy of the approximation and the computational complexity. We adopt two methods of approximation proposed by Fenton and Wilkinson [19] and Mehta et al. [20] which provide a good balance between accuracy and complexity. The performance of both methods is examined in various environments and a guideline is provided for choosing one of the methods.
The derivation of SINR distribution in this paper is semianalytical in the sense that the PDF can be easily calculated by applying standard numerical methods to equations obtained from analysis. Numerical experiments are performed to investigate the effects of standard deviation of shadow fading, the number of interfering BSs, wall penetration loss, and transmission powers of BSs. The results obtained are also validated by comparison with Monte Carlo simulations.
The paper is organised as follows. In Section 2, the PDF of the downlink SINR is derived. Numerical experiments are performed in various environments and the results are compared with Monte Carlo simulations in Section 3. Finally, the conclusions are provided in Section 4.
2. Derivation of the PDF of Downlink SINR
The derivation of the PDF of downlink SINR is divided into two parts. First, the SINR of an arbitrary MS is expressed depending on its location in Section 2.1. Methods of approximating the sum probability distribution of log-normal RVs are discussed and adopted in the SINR derivation. Second, the PDF of SINR unconditional on the location of the MS is derived in Section 2.2.
2.1. Location-Dependent SINR
Let us consider a femtocell which will be termed the cell of interest (CoI). The CoI is assumed to be circular with a cell radius  . We assume the MSs in the CoI to be uniformly distributed in the cell area. An arbitrary MS
. We assume the MSs in the CoI to be uniformly distributed in the cell area. An arbitrary MS  is considered whose location is
is considered whose location is  , where
, where  and
and  . The MS
. The MS  receives interference from
receives interference from  BSs that are a mixture of femto and macro-BSs. The network is modelled using polar coordinates where the BS of the CoI is located at the center and the location of the
BSs that are a mixture of femto and macro-BSs. The network is modelled using polar coordinates where the BS of the CoI is located at the center and the location of the  th interfering BS is denoted by
th interfering BS is denoted by  . In a practical deployment of femtocell systems, the placement of BSs in a random and uncoordinated fashion is unavoidable and may generate high interference scenarios and dead spots particularly in an indoor environment.
. In a practical deployment of femtocell systems, the placement of BSs in a random and uncoordinated fashion is unavoidable and may generate high interference scenarios and dead spots particularly in an indoor environment.
Let  be the transmission power of the BS in the CoI. It is attenuated by path loss and shadow fading. Let
be the transmission power of the BS in the CoI. It is attenuated by path loss and shadow fading. Let  be the RV which models the shadow fading. It is generally assumed that
be the RV which models the shadow fading. It is generally assumed that  follows a Gaussian distribution with zero mean and variance
follows a Gaussian distribution with zero mean and variance  in dB. Thus the received signal power at the MS
in dB. Thus the received signal power at the MS  from the serving BS,
from the serving BS,  , is denoted by
, is denoted by

where  and
and  are antenna gains of the BS and the MS, respectively,
are antenna gains of the BS and the MS, respectively,  is constant of path loss in the CoI,
is constant of path loss in the CoI,  is path loss exponent of CoI, and
is path loss exponent of CoI, and  . The
. The  denotes natural logarithm.
denotes natural logarithm.  can be rewritten as follows:
can be rewritten as follows:

Note that an RV  follows a log-normal distribution if
follows a log-normal distribution if  is a Gaussian distributed RV. Thus,
is a Gaussian distributed RV. Thus,  follows a log-normal distribution conditioned on the location of MS
follows a log-normal distribution conditioned on the location of MS  . The PDF of
. The PDF of  is given by
is given by

where  and
and  .
.
Let  be the received interference power from the
be the received interference power from the  th interfering BS. By denoting
th interfering BS. By denoting  as the transmission power from the
as the transmission power from the  th BS,
th BS,  results in
results in

where  and
and  are the path loss constant and exponent, respectively, on the link between the
are the path loss constant and exponent, respectively, on the link between the  th BS and MS
th BS and MS  , and
, and  is a Gaussian RV for shadow fading with zero mean and variance
is a Gaussian RV for shadow fading with zero mean and variance  on the link between the
on the link between the  th BS and MS
th BS and MS  . Note that the transmission power of each interfering BS can be different since an uncoordinated femtocell deployment is considered. Path loss parameters and standard deviation of shadow fading can also be different in each BS in practical systems. The distance between MS
. Note that the transmission power of each interfering BS can be different since an uncoordinated femtocell deployment is considered. Path loss parameters and standard deviation of shadow fading can also be different in each BS in practical systems. The distance between MS  and the
and the  th interfering BS is
th interfering BS is  , which is obtained from
, which is obtained from

In a similar fashion to  ,
,  follows a log-normal distribution with PDF given by
follows a log-normal distribution with PDF given by

where  and
and  .
.
Background noise can be regarded as a constant value by assuming the constant noise figure and the noise temperature. Let  be the background noise power at MS
be the background noise power at MS  , given by
, given by

where  is the Boltzmann constant,
is the Boltzmann constant,  is the ambient temperature in Kelvin,
is the ambient temperature in Kelvin,  is the channel bandwidth, and
is the channel bandwidth, and  is the noise figure of the MS. In order to make
is the noise figure of the MS. In order to make  mathematically tractable, we introduce an auxiliary Gaussian RV
mathematically tractable, we introduce an auxiliary Gaussian RV  with zero mean and zero variance so that
with zero mean and zero variance so that  can be treated as log-normal RV with parameters of
can be treated as log-normal RV with parameters of  and
and  . Note that
. Note that  has a constant value, and this is accounted for by the fact that the defined RV has zero variance. This particular definition is useful for the determination of the final PDF. By introducing
has a constant value, and this is accounted for by the fact that the defined RV has zero variance. This particular definition is useful for the determination of the final PDF. By introducing  ,
,  can be rewritten as follows:
can be rewritten as follows:

Let us consider a system with no interference arising from the serving cell such as an OFDMA or a TDMA system. The downlink SINR of MS  is denoted by
is denoted by  , which is given by
, which is given by

In (9),  denotes the sum of the interference powers and the background noise power. Since all of
denotes the sum of the interference powers and the background noise power. Since all of  and
and  are log-normally distributed,
are log-normally distributed,  is the sum of
is the sum of  log-normal RVs. Note that the exact closed-form expression is not known for the PDF of the sum of log-normal RVs. The most widely accepted approximation approach is to assume that the sum of log-normal RVs follows a log-normal distribution. Various methods have been proposed to find out parameters of the distribution [19–21].
log-normal RVs. Note that the exact closed-form expression is not known for the PDF of the sum of log-normal RVs. The most widely accepted approximation approach is to assume that the sum of log-normal RVs follows a log-normal distribution. Various methods have been proposed to find out parameters of the distribution [19–21].
Let  be
be  independent but not necessarily identical log-normal RVs, where
independent but not necessarily identical log-normal RVs, where  and
and  is a Gaussian distributed RV with mean
is a Gaussian distributed RV with mean  and variance
and variance  . The sum of
. The sum of  RVs is denoted by
RVs is denoted by  such that
such that  . Approximations assume that
. Approximations assume that  follows a log-normal distribution with parameters
follows a log-normal distribution with parameters  and
and  .
.
The Fenton and Wilkinson (FW) method [19] is one of the most frequently adopted approximations in literature. It obtains  and
and  by assuming that the first and second moments of
by assuming that the first and second moments of  match the sum of the moments of
match the sum of the moments of  . It should be noted that the FW method is the only approximate method that provides a closed-form expression of
. It should be noted that the FW method is the only approximate method that provides a closed-form expression of  and
and  [20]. Let us denote
[20]. Let us denote  as
as  and
and  as
as  . From [19], the PDF of
. From [19], the PDF of  conditioned on the location of MS
conditioned on the location of MS  is given as follows:
is given as follows:

where  and
and  are given by
are given by

In spite of its simplicity, the accuracy of the FW method suffers at high values of  . This means that the method may break down when an MS experiences a large standard deviation of shadow fading from interfering BSs. Thus, we adopt another method of approximating the sum of log-normal RVs which gives a more accurate result at a cost of increased computational complexity.
. This means that the method may break down when an MS experiences a large standard deviation of shadow fading from interfering BSs. Thus, we adopt another method of approximating the sum of log-normal RVs which gives a more accurate result at a cost of increased computational complexity.
The method proposed in [20], which is called MWMZ method in this paper after the initials of authors, exploits the property of the moment-generating function (MGF) that the product of MGFs of independent RVs equals to the MGF of the sum of RVs. The MGF of RV  is defined as
is defined as

By the property of MGF,

While the closed-form expression for the MGF of log-normal distribution is not available, a series expansion based on Gauss-Hermite integration was employed in [20] to approximate the MGF. For a real coefficient  , the MGF of the log-normal RV
, the MGF of the log-normal RV  is given by
is given by

where  and
and  are weights and abscissas of the Gauss-Hermite series which can be found in [24, Table
are weights and abscissas of the Gauss-Hermite series which can be found in [24, Table  ]. From (13), a system of two nonlinear equations can be set up with two real and positive coefficients
]. From (13), a system of two nonlinear equations can be set up with two real and positive coefficients  and
and  as follows:
as follows:

The variables to be solved by (15) are  and
and  . The right-hand side of (15) is a constant value which can be calculated with known parameters.
. The right-hand side of (15) is a constant value which can be calculated with known parameters.
By employing (15),  and
and  in (10) can be effectively obtained by standard numerical methods such as the function "fsolve" in Matlab. The coefficient
in (10) can be effectively obtained by standard numerical methods such as the function "fsolve" in Matlab. The coefficient  adjusts weight of penalty for inaccuracy of the PDF. Increasing
adjusts weight of penalty for inaccuracy of the PDF. Increasing  imposes more penalty for errors in the head portion of the PDF of
imposes more penalty for errors in the head portion of the PDF of  , whereas smaller
, whereas smaller  penalises errors in the tail portion. Thus, smaller
penalises errors in the tail portion. Thus, smaller  is recommended if one is interested in the PDF of poor SINR region, while larger
is recommended if one is interested in the PDF of poor SINR region, while larger  should be used to examine statistics of higher SINR.
should be used to examine statistics of higher SINR.
As shown in (3), the received signal power,  , follows a log-normal distribution. The sum of the received interference and the background noise power,
, follows a log-normal distribution. The sum of the received interference and the background noise power,  , was also approximated as a log-normal RV. Thus, the SINR of the MS
, was also approximated as a log-normal RV. Thus, the SINR of the MS  ,
,  , is the ratio of two log-normal RVs, which also follows a log-normal distribution. From (3) and (10), the PDF of
, is the ratio of two log-normal RVs, which also follows a log-normal distribution. From (3) and (10), the PDF of  is shown as
is shown as

where  and
and  .
.
2.2. The PDF of Downlink SINR in a Cell
Up to this point, the PDF of the downlink SINR has been derived conditionally on the location of the MS  . Let us denote the location of MS
. Let us denote the location of MS  by
by  . Since it is assumed that MSs are uniformly distributed within a circular area, the PDF of
. Since it is assumed that MSs are uniformly distributed within a circular area, the PDF of  ,
,  , is as follows:
, is as follows:

From (16) and (17), the joint distribution of the SINR and the MS location is

Let  be the RV of the downlink SINR of an MS in an arbitrary location within a circular cell area. The PDF of
be the RV of the downlink SINR of an MS in an arbitrary location within a circular cell area. The PDF of  can be obtained by integrating
can be obtained by integrating  over
over  and
and  . Thus, we get
. Thus, we get

Note that  in (19) is a function of
in (19) is a function of  . We employ numerical integration methods to obtain the final PDF.
. We employ numerical integration methods to obtain the final PDF.
3. Numerical Results
The PDF of downlink SINR derived in (19) is calculated numerically and compared with a Monte Carlo simulation result in order to validate the analysis. We consider the nonline of sight (NLOS) indoor environment at 5.25 GHz as specified in [25, page 19] to be the basic environment for the comparison. The path loss formula is given as follows:

where  is a reference distance in the far field. The interfering BSs are assumed to be femto BSs located on the same floor of a building throughout the experiments. However, interference scenarios such as femto BSs in different floors or outdoor macro-BSs can be easily examined by employing appropriate path loss models. The basic parameters used for the comparison are summarised in Table 1.
is a reference distance in the far field. The interfering BSs are assumed to be femto BSs located on the same floor of a building throughout the experiments. However, interference scenarios such as femto BSs in different floors or outdoor macro-BSs can be easily examined by employing appropriate path loss models. The basic parameters used for the comparison are summarised in Table 1.
We assume that all interfering BSs are located at the same distance from the serving BS as shown in Figure 1. Cells are assumed to overlap each other to consider a dense deployment of the femto BSs. Although it is unlikely that the interfering BSs are in regular shapes in practical deployments, it is useful to consider this topology for examining the effects of parameters such as standard deviation of shadow fading, the number of BSs, wall penetration loss, and transmission power of BSs. It should be emphasised that the PDF derived in Section 2 can effectively take into account irregular locations and transmission powers of BSs.
The result of the comparison is illustrated in Figure 2 where the PDFs derived by FW and MWMZ methods are compared with the Monte Carlo simulation result in Figure 2(a) and the cumulative distribution functions (CDFs) of the PDFs are depicted in Figure 2(b). The standard deviation of shadow fading,  and
and  , is considered to be 3.5 dB since it represents a typical value in an indoor office environment according to the measurement results in [25]. It is observed that the numerically obtained PDFs from both of the methods are in good agreement with the Monte Carlo simulation.
, is considered to be 3.5 dB since it represents a typical value in an indoor office environment according to the measurement results in [25]. It is observed that the numerically obtained PDFs from both of the methods are in good agreement with the Monte Carlo simulation.
The impact of the parameter  on the performance of MWMZ method is shown in Figure 3 where the tail portion of the CDF (low SINR region) is depicted in Figure 3(a) and the head portion of the CDF (high SINR regime) is illustrated in Figure 3(b). Smaller
on the performance of MWMZ method is shown in Figure 3 where the tail portion of the CDF (low SINR region) is depicted in Figure 3(a) and the head portion of the CDF (high SINR regime) is illustrated in Figure 3(b). Smaller  tends to give more accurate match in low SINR region while resulting in larger error in high SINR region.
tends to give more accurate match in low SINR region while resulting in larger error in high SINR region.  is chosen in the experiments since it brings about relatively small difference from simulations throughout the whole SINR region.
is chosen in the experiments since it brings about relatively small difference from simulations throughout the whole SINR region.
Figure 4 shows the CDFs when the standard deviation of shadow fading is 8.0 dB. While the SINR obtained by MWMZ method is still in good agreement with the simulation result, the difference between the analysis and the simulation is apparent in case of FW method. It means that FW method cannot be used in an environment where high shadow fading is experienced by MSs. In order to quantify the effect of shadow fading standard deviation, we introduce Kullback-Leibler Distance (KLD) which is a measure of divergence between two probability distributions [26]. For the two PDFs  and
and  the KLD is defined as
the KLD is defined as

The KLD is a nonnegative entity which measures the difference of the estimated distribution  from the real distribution
from the real distribution  in a statistical sense. It becomes zero if and only if
in a statistical sense. It becomes zero if and only if  =
=  . Table 2 presents the KLD for various standard deviations of shadow fading by assuming that the simulation results represent the true PDFs of SINR. It is shown in the table that the KLD of FW method soars when the standard deviation of shadow fading is higher than 6 dB. This implies that the range of standard deviation in which FW method can be adopted is between 3 dB and 6 dB, which is a typical range of shadow fading in an in-building environment [14, 25]. On the contrary, the MWMZ method maintains an acceptable level of the KLD even for the high shadow fading standard deviation. FW method is preferred if both of the methods are applicable due to its simplicity.
. Table 2 presents the KLD for various standard deviations of shadow fading by assuming that the simulation results represent the true PDFs of SINR. It is shown in the table that the KLD of FW method soars when the standard deviation of shadow fading is higher than 6 dB. This implies that the range of standard deviation in which FW method can be adopted is between 3 dB and 6 dB, which is a typical range of shadow fading in an in-building environment [14, 25]. On the contrary, the MWMZ method maintains an acceptable level of the KLD even for the high shadow fading standard deviation. FW method is preferred if both of the methods are applicable due to its simplicity.
 ).
).The effect of the number of interfering BSs is examined in Figure 5. It is known that the sum of log-normal RVs is not accurately approximated by a log-normal distribution as the number of summands increases [22]. This means that the derived SINR may not be accurate for a large number of interfering BSs. Figure 5 shows the KLD of FW and MWMZ methods compared to simulation results when  is between 2 and 60. An impairment in the accuracy is not observed as
is between 2 and 60. An impairment in the accuracy is not observed as  increases, which means that the derivation of SINR in this paper is useful for the practical range of interfering BSs in the downlink of cellular systems.
increases, which means that the derivation of SINR in this paper is useful for the practical range of interfering BSs in the downlink of cellular systems.
The numerical results so far have focused on the verification of the derived PDF. Now we investigate the performance of femtocell network in various environments. An important observation in Figure 2 is that the probability of the SINR below 2.2 dB (a typical threshold for binary phase shift keying (BPSK) to achieve reasonable BER performance [27]) is about 0.38 for the parameters in Table 1. In other words, the outage probability is around 38%. This means that a dense deployment of femtocells in a building results in unacceptable outage, unless intelligent interference avoidance and interference mitigation techniques are put in place.
Clearly isolation of a cell by wall penetration loss is an inherent property of indoor femtocell networks which can be utilised as a means of interference mitigation. Let  be the wall penetration loss between the CoI and the interfering BS
be the wall penetration loss between the CoI and the interfering BS  . The effect of
. The effect of  is examined in Figure 6 where
is examined in Figure 6 where  is assumed to be identical for all interfering BSs. It is shown that
is assumed to be identical for all interfering BSs. It is shown that  has significant impact on the SINR of the femtocell. The outage probability drops to 3.7% when
has significant impact on the SINR of the femtocell. The outage probability drops to 3.7% when  dB and to 0.5% when
dB and to 0.5% when  dB. This result implies that the implementation of the femtocell network is viable without complicated interference mitigation method if the wall isolation between BSs is provided.
dB. This result implies that the implementation of the femtocell network is viable without complicated interference mitigation method if the wall isolation between BSs is provided.
In Figure 7, different wall losses,  , are considered. We examine the following scenarios:
, are considered. We examine the following scenarios:
-
(i)
scenario 1:
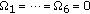 dB,
dB, -
(ii)
scenario 2:
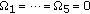 dB and
dB and 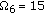 dB,
dB, -
(iii)
scenario 3:
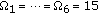 dB,
dB, -
(iv)
scenario 4:
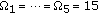 dB and
dB and 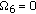 dB.
dB.
It is shown that scenarios 1 and 2 give similar performance. This means that the isolation from one or few BSs does not result in the performance improvement when the CoI is not protected from the majority of interfering BSs. On the contrary, a considerable difference is observed between scenarios 3 and 4. Significant degradation in the SINR is caused by one BS which is not isolated by the wall.
Similar behaviours are observed in Figure 8 where different BS transmission powers are considered. The effect of the uncoordinated power is examined by considering the following scenarios where  dBm:
dBm:
-
(i)
scenario 5:
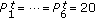 dBm,
dBm, -
(ii)
(ii)scenario 6:
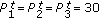 dBm and
dBm and 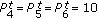 dBm,
dBm, -
(iii)
scenario 7:
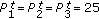 dBm and
dBm and 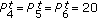 dBm,
dBm, -
(iv)
scenario 8:
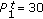 dBm and
dBm and  dBm.
dBm.
Figure 8 shows the CDFs of SINR by FW method with the assumption that  dB
dB  . It is observed that scenario 6 results in the worst SINR. This means that the higher transmission powers of a few BSs result in significantly decreased SINR. However, reduced transmission power in only a subset of neighbouring BSs does not necessarily improve the SINR because the predominant interference largely depends on the BSs which use high transmission powers. A similar trend is shown when comparing scenario 7 and scenario 8. The SINR performance is worse in scenario 8 than in scenario 7 for the same reason.
. It is observed that scenario 6 results in the worst SINR. This means that the higher transmission powers of a few BSs result in significantly decreased SINR. However, reduced transmission power in only a subset of neighbouring BSs does not necessarily improve the SINR because the predominant interference largely depends on the BSs which use high transmission powers. A similar trend is shown when comparing scenario 7 and scenario 8. The SINR performance is worse in scenario 8 than in scenario 7 for the same reason.
Finally, the effects of the BSs transmission power and the background noise are shown in Figure 9. If the transmit power drops below a certain level, a change in the PDF can be observed. For 10 dBm transmit power, for example, a noticeable impairment of the SINR can be seen. This is because the noise power remains the same regardless of the transmission power. In the case of increased transmission power, however, little change in the SINR distribution is observed. This means that the SINR is already interference limited with a transmission power of 20 dBm. Thus, the increase in the transmit power of BSs does not result in an improvement as expected.
4. Conclusion
In this paper, the PDF of the SINR for the downlink of a cell has been derived in a semianalytical fashion. It models an uncoordinated deployment of BSs which is particularly useful for the analysis of femtocells in an indoor environment. A practical propagation model including log-normal shadow fading is considered in the derivation of the PDF. The PDF presented in this paper has been obtained through analysis and calculated through standard numerical methods. The comparison with Monte Carlo simulation shows a good agreement, which indicates that the semianalytical PDF obviates the need for complicated and time-consuming simulations. The results also provide some insights into the performance of the indoor femtocells with universal frequency reuse. First, significant outage can be expected for a scenario where femto BSs are densely deployed in an in-building environment. This highlights that interference avoidance and mitigation techniques are needed. The isolation offered by wall penetration loss is an attractive solution to cope with the interference. Second, the SINR can be worsened by uncoordinated transmission powers of BSs. Thus, a coordination of BSs transmission power is needed to prevent a significant decrease in SINR.
References
Viterbi AJ, Viterbi AM, Zehavi E: Other-cell interference in cellular power-controlled CDMA. IEEE Transactions on Communications 1994, 42(4):1501-1504. 10.1109/TCOMM.1994.582830
Zorzi M: On the analytical computation of the interference statistics with applications to the performance evaluation of mobile radio systems. IEEE Transactions on Communications 1997, 45(1):103-109. 10.1109/26.554292
Graziosi F, Fuciarelli L, Santucci F: Second order statistics of the SIR for cellular mobile networks in the presence of correlated co-channel interferers. Proceedings of the 53th IEEE Vehicular Technology Conference (VTC '01), May 2001, Rhodes, Greece 2499-2503.
Koshi V: Coverage uncertainty and reliability estimation for microcellular radio network planning. Proceedings of the 51th IEEE Vehicular Technology Conference (VTC '00), May 2000, Tokyo, Japan 468-472.
Stachle D: An analytic method for coverage prediction in the UMTS radio network planning process. Proceedings of the 61th IEEE Vehicular Technology Conference (VTC '05), May-June 2005, Stockholm, Sweden 1945-1949.
Pratesi M, Santucci F, Graziosi F, Ruggieri M: Outage analysis in mobile radio systems with generically correlated log-normal interferers. IEEE Transactions on Communications 2000, 48(3):381-385. 10.1109/26.837041
Pratesi M, Santucci F, Graziosi F: Generalized moment matching for the linear combination of lognormal RVs: application to outage analysis in wireless systems. IEEE Transactions on Wireless Communications 2006, 5(5):1122-1132.
Berggren F, Slimane SB: A simple bound on the outage probability with lognormally distributed interferers. IEEE Communications Letters 2004, 8(5):271-273. 10.1109/LCOMM.2004.827448
Haas H, McLaughlin S: A derivation of the PDF of adjacent channel interference in a cellular system. IEEE Communications Letters 2004, 8(2):102-104. 10.1109/LCOMM.2004.823431
Mudesir A, Bode M, Sung KW, Haas H: Analytical SIR for self-organizing wireless networks. EURASIP Journal on Wireless Communications and Networking 2009, 2009:-8.
Chandrasekhar V, Andrews JG, Gatherer A: Femtocell networks: a survey. IEEE Communications Magazine 2008, 46(9):59-67.
Bharucha Z, Haas H: Application of the TDD underlay concept to home nodeB scenario. Proceedings of the 7th IEEE Vehicular Technology Conference (VTC '08), May 2008, Singapore 56-60.
Bharucha Z, Ćosović I, Haas H, Auer G: Throughput enhancement through femto-cell deployment. Proceedings of the IEEE 7th International Workshop on Multi-Carrier Systems & Solutions (MC-SS '09), May 2009, Herrsching, Germany 311-319.
Claussen H: Performance of macro—and co-channel femtocells in a hierarchical cell structure. Proceedings of the 18th IEEE International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC '07), November 2007, Athens, Greece
Espino J, Markendahl J: Analysis of macro—femtocell interference and implications for spectrum allocation. Proceedings of the 20th IEEE International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC '09), September 2009, Tokyo, Japan 13-16.
Valcarce A, Roche GDL, Jüttner A, Lopez-Perez D, Zhang J: Applying FDTD to the coverage prediction of wiMAX femtocells. Eurasip Journal on Wireless Communications and Networking 2009, 2009:-13.
Yavuz M, Meshkati F, Nanda S, et al.: Interference management and performance analysis of UMTS/HSPA+ femtocells. IEEE Communications Magazine 2009, 47(9):102-109.
Beaulieu NC, Xie Q: An optimal lognormal approximation to lognormal sum distributions. IEEE Transactions on Vehicular Technology 2004, 53(2):479-489. 10.1109/TVT.2004.823494
Fenton LF: The sum of log-normal probability distributions in scatter transmission systems. IRE Transactions on Communications Systems 1960, 8(1):57-67.
Mehta NB, Wu J, Molisch AF, Zhang J: Approximating a sum of random variables with a lognormal. IEEE Transactions on Wireless Communications 2007, 6(7):2690-2699.
Schwartz SC, Yeh YS: On the distribution function and moments of power sums with log-normal components. The Bell System Technical Journal 1982, 61(7):1441-1462.
Szyszkowicz SS, Yanikomeroglu H: On the tails of the distribution of the sum of lognormals. Proceedings of the IEEE International Conference on Communications (ICC '07), June 2007, Glasgow, UK 5324-5329.
Nie H, Chen S: Lognormal sum approximation with type IV pearson distribution. IEEE Communications Letters 2007, 11(10):790-792.
Abramowitz M, Stegun IA: Handbook of mathematical functions with fomulas. In Graphs, and Mathematical Tables. 9th edition. Dover, New York, NY, USA; 1972.
IST-4-027756 WINNER II : D1.1.2 v1.2 WINNER II Channel Models. February 2008, http://www.ist-winner.org/WINNER2-Deliverables/D7.1.5_Final-Report_v1.0.pdf
Cover TM, Thomas JA: Elements of Information Theory, D. L. Schilling, Ed., Wiley Series in Telecommunications. 1st edition. John Wiley & Sons, New York, NY, USA; 1991.
Persson A, Ottosson T, Auer G: Inter-sector scheduling in multi-user OFDM. Proceedings of the IEEE International Conference on Communications (ICC '06), June 2006, Istanbul, Turkey 10: 4415-4419.
Acknowledgment
This work was supported by the National Research Foundation of Korea, Grant funded by the Korean Government (NRF-2007-357-D00165).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Sung, K., Haas, H. & McLaughlin, S. A Semianalytical PDF of Downlink SINR for Femtocell Networks. J Wireless Com Network 2010, 256370 (2010). https://doi.org/10.1155/2010/256370
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/256370


 =
=  = 3. 5 dB).PDF of the downlink SINRCDF of the downlink SINR
= 3. 5 dB).PDF of the downlink SINRCDF of the downlink SINR
 on the performance of MWMZ method: tail and head portions of CDF (
on the performance of MWMZ method: tail and head portions of CDF ( =
=  = 3. 5 dB).Tail portion of the CDFHead portion of the CDF
= 3. 5 dB).Tail portion of the CDFHead portion of the CDF
 =
=  = 8. 0 dB).
= 8. 0 dB).
 =
=  = 3. 5 dB).
= 3. 5 dB).
 =
=  = 3. 5 dB).
= 3. 5 dB).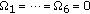 dB,
dB,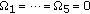 dB and
dB and 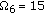 dB,
dB,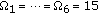 dB,
dB,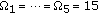 dB and
dB and 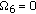 dB.
dB.
 =
=  = 3. 5 dB).
= 3. 5 dB).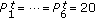 dBm,
dBm,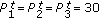 dBm and
dBm and 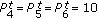 dBm,
dBm,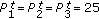 dBm and
dBm and 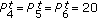 dBm,
dBm,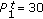 dBm and
dBm and  dBm.
dBm.
 =
=  = 3. 5 dB).
= 3. 5 dB).
 =
=  = 3. 5 dB).
= 3. 5 dB).