- Research Article
- Open access
- Published:
Spherical Statistics and Spatial Correlation for Multielement Antenna Systems
EURASIP Journal on Wireless Communications and Networking volume 2010, Article number: 307265 (2010)
Abstract
The well-known assumption of horizontal plane wave propagation is investigated and evidence suggests that elevation plays a crucial role in defining the spatial correlation between signals on adjacent antenna array elements. To augment previously published studies, an explicit relationship between the distribution of scatterers in three-dimensional (3D) space and the spatial correlation is formulated. A novel approach is taken for modeling of the distribution of scatterers in space. More specifically, the distribution of scatterers is modeled by the 3D von Mises-Fisher (vMF) distribution. In addition, a closed-form expression is derived for the harmonic coefficients of the vMF density. The main derivation expresses the spherical harmonic coefficients associated with an arbitrary mean direction on the sphere. Further, a closed-form expression for the spatial correlation function (SCF) is derived, based on the spherical harmonic expansion (SHE) of plane waves as well as the harmonic coefficients of the expanded vMF density. A novel approach is proposed for including the effect of directional antenna responses in the SCF. Finally, the SCF is evaluated under the existence of multiple scatterer clusters in the channel.
1. Introduction
Multielement antenna systems have been the centre of wireless communication research over the past decade due to the significant increase in capacity that they offer. Operators worldwide strive for capacity and coverage increase as the number of subscribers grows and demanding multimedia services are implemented. Complicated, expensive, and time-consuming optimization techniques that aim to improve the system performance, for example, drive test analysis; antenna and/or power optimization should ideally be avoided. Multielement antenna systems have been proven to increase capacity and decrease interference through spatial multiplexing and/or beamforming. Significant efforts are continuously made to analyse and simulate such systems with a high degree of accuracy although the nature of the assumptions often being made is sometimes doubtful. For instance, some studies in the literature assume that the signals received at adjacent antenna elements are uncorrelated. This may be considered an oversimplification of the challenges encountered in a wireless propagation channel. Further, occassionally elevation is ignored, and the effect of spatial correlation on the systems performance can be misleading, especially in urban clutter types. Our conjecture that elevation can have a significant effect on the correlation function has motivated this work. Various spatial correlation models have been proposed, where elevation is ignored and the distribution of scatterers or equivalently the angle of arrival (AoA) of paths at the mobile station (MS) (or even base station (BS)) is modeled as a two-dimensional (2D) uniform, Gaussian, von Mises, or Laplacian [1–5] distribution. A drawback associated with distributions that are defined on the line (e.g., Gaussian) is that the summary statistics are calculated in such a way that the directionality of the variables is not taken into consideration.
The need to investigate the spatial correlation between signals on adjacent antenna elements is well known in the research community. In [6], closed-form expressions for the spatial correlation function (SCF) of antenna arrays in a three-dimensional (3D) multipath environment are derived. However, in [6] the distribution of the angle of arrival of multipaths is assumed to be uniform over a given range of angles, and the azimuth is independently distributed from elevation. In [7], a thorough review of different 2D spatial correlation models is provided. By including the spatial information, the authors derive a closed-form expression for the ergodic capacity. In [8], the authors provide a capacity analysis of a dense multielement antenna system having obtained the spatial correlation values between the antenna elements. In addition, the idea of 3D propagation has also been considered in a number of other research works [9–11]. Toeltsch et al. provided a statistical analysis of 3D wideband measurement data after the application of a multipath parameter extraction algorithm, namely Unitary ESPRIT. The multipath components estimated were then clustered in the angular and delay domains, allowing a detailed statistical analysis of the propagation properties. In [10], the authors derived a cross-polarized multielement antenna channel model that takes into consideration the azimuth as well as the elevation domains. In [11], a spherical outdoor to indoor power spectrum model is developed for the MS, where the necessity of including the third dimension, that is, elevation becomes evident.
In this paper, the spatial correlation model derived in [12] is reviewed under a three-dimensional scattering distribution function, namely the von Mises-Fisher (vMF) distribution. It is shown that the correlation is not insensitive to elevation and that it is dependent on three key parameters, that is, angular spread (concentration of scatterers within a cluster), mean AoA in azimuth and elevation, and position of the elements. The results of this paper suggest that the correlation decreases significantly as elevation increases while this is dependent on the three parameters stated previously. To better understand this effect, the vMF distribution is expanded into spherical harmonics, and the harmonic coefficients are obtained in a closed-form expression. This closed-form expression is later used in the formulation of the spatial correlation function (SCF).
The arguments for proposing the vMF model are outlined in [13, 14], where it is shown that this distribution possesses excellent characteristics in describing the AoA of paths at the MS. In [14], a mixture of distributions is used in order to describe the scattering distribution function. This is in agreement with the natural phenomenon reported in [15, 16], that the channel clusters the incoming paths. For the same reasons, in this paper, the concept of mixture modeling is adopted for the characterization of the spatial correlation function. Consequently, the spatial correlation is scaled by the probability that each cluster contributes to the channel. The estimated priors of the vMF mixture model may define the magnitude of this relationship in terms of an assumed or otherwise estimated power value emanating from each scatterer cluster. The estimation of the parameters of the vMF mixture model is achieved using a soft-Expectation Maximization (soft-EM) algorithm [13]. The organization of this paper is as follows. In Section 2, the basics on spherical harmonics are provided, and a closed-form expression for the harmonic coefficients of the vMF density is further derived. In Section 3, a closed-form expression for the spatial correlation based on the unimodal vMF assumption is provided. In Section 3, the spatial correlation function is evaluated for various scenarios (of a constrained spherical array topology), where it is shown that elevation plays a major role in defining correlation. Later in Section 4, one element is elevated with respect to the other, and the correlation is re-examined. In this section, a detailed analysis on the effect of directional array responses on the SCF is provided. In Section 5, the SCF is extended so to capture the effect of multiple clusters of scatterers in the channel. Finally, the conclusions are presented in Section 6.
2. Spherical Phase Modes and the vMF Density
The vMF is a generic 3D model for directional data distributed unimodally on the sphere. It can therefore be considered as a suitable candidate for applications where the variables are angular in nature [17]. These variables are signified by  and
and  denoting the angles of the random vector
denoting the angles of the random vector  widely used in the forthcoming analysis. The distribution is closely related, and it is in fact analogous to the multivariate Gaussian distribution. If the distribution is defined on the normal sphere
widely used in the forthcoming analysis. The distribution is closely related, and it is in fact analogous to the multivariate Gaussian distribution. If the distribution is defined on the normal sphere  , its density function is significantly simplified. More specifically, the density function takes the following form:
, its density function is significantly simplified. More specifically, the density function takes the following form:

This equation is known as the general form of the vMF distribution [17] and is dependent on the modal direction  (known as the axis of symmetry) and the dispersion parameter
(known as the axis of symmetry) and the dispersion parameter  . Note that
. Note that  is defined in terms of
is defined in terms of  . The interested reader is referred to [14] for further mathematical details of the distribution and graphical illustrations for its interpretation within a scattering context. The spherical phase modes of the vMF are analyzed in the sequel.
. The interested reader is referred to [14] for further mathematical details of the distribution and graphical illustrations for its interpretation within a scattering context. The spherical phase modes of the vMF are analyzed in the sequel.
2.1. Spherical Phase Modes
The spherical phase modes or spherical harmonics are the angular portion of an orthonormal set of solutions (on the surface of the sphere) to Laplaces equation. The spherical harmonics are defined as follows [18, 19]:

where  and
and  are the elevation and azimuthal angles in the spherical co-ordinate system,
are the elevation and azimuthal angles in the spherical co-ordinate system,  is the degree of the spherical harmonic, and
is the degree of the spherical harmonic, and  is the order.
is the order.  are the associated Legendre functions. The orthonormality principle of spherical harmonics may be stated as [18]
are the associated Legendre functions. The orthonormality principle of spherical harmonics may be stated as [18]

where  ,
,  denote the Kronecker delta defined by
denote the Kronecker delta defined by  ,
, ,
,  ,
, . Knowing that the spherical harmonics form a complete orthonormal basis over
. Knowing that the spherical harmonics form a complete orthonormal basis over  allows the expansion of any square-integrable function (i.e., vMF) as a linear combination of these
allows the expansion of any square-integrable function (i.e., vMF) as a linear combination of these

The spherical harmonic coefficients  can be obtained (in a closed-form expression) using the spherical Fourier transform, otherwise the use of numerical integration techniques might be necessary. The spherical harmonic coefficients can be found by
can be obtained (in a closed-form expression) using the spherical Fourier transform, otherwise the use of numerical integration techniques might be necessary. The spherical harmonic coefficients can be found by

where  denotes complex conjugation and
denotes complex conjugation and  is the element of the solid angle. Note that since we introduce
is the element of the solid angle. Note that since we introduce  inside the double integral, there is no need to include the
inside the double integral, there is no need to include the  term of the vMF distribution in (1). It is important to distinguish between the pdf of (1) and the volumetric pdf [20]. In the next sections, the volumetric pdf is used, that is ignoring the last
term of the vMF distribution in (1). It is important to distinguish between the pdf of (1) and the volumetric pdf [20]. In the next sections, the volumetric pdf is used, that is ignoring the last  term in (1).
term in (1).
2.2. Closed-Form Expression for the Harmonic Coefficients of the vMF Density
It is known that a function,  , can be expanded as follows [21]:
, can be expanded as follows [21]:

By (6), it follows that (1) can be expressed as

where  is the displacement vector between the mean direction vector and a vector pointing in a scatterer's direction. Making use of (5) and the Addition Theorem for spherical harmonics in (A.2), the coefficients can be written in a closed-form expression as follows:
is the displacement vector between the mean direction vector and a vector pointing in a scatterer's direction. Making use of (5) and the Addition Theorem for spherical harmonics in (A.2), the coefficients can be written in a closed-form expression as follows:

The derivation of (8) for an arbitrary direction on the sphere is detailed in Appendix A.1. In Appendix A.2, it is shown that by conditioning the mean elevation angle,  (North Pole), a different spherical harmonic coefficient formulae is obtained. The latter being a special case of the main derivation.
(North Pole), a different spherical harmonic coefficient formulae is obtained. The latter being a special case of the main derivation.
3. Wavefield Decomposition and Spatial Correlation Using Constrained Spherical Antenna Arrays
Prior to proceeding into the relationship between the spherical harmonic expansion (SHE) of plane waves and the proposed vMF correlation function, it is vital to explain how the characteristics of the antenna array are integrated into this model. In the initial setup, each antenna comprising the array is assumed to be an isotropic radiator (three dimensions). In two dimensions, this corresponds to a circular aperture being equally sensitive in all azimuthal directions, thus revealing an omnidirectional pattern. Whilst recognizing that this assumption hinders the realistic performance of a multielement antenna system, it enables us to study the broader picture of the spatial correlation effect on the system's performance (e.g., capacity). Including realistic antenna patterns greatly complicates further analysis, making analytical solutions very difficult if not impossible. This simplification has helped us to decompose the rather complicated problem posed by the inclusion of mathematically untractable antenna patterns.
We proceed in the following directions. In Section 3.1, a definition of spatial correlation is provided. The vMF SCF is derived in Section 3.2. The rest of the parts comprising this section are organised as follows. We begin with analyzing the effect of an elevated cluster of scatterers in a constrained spherical antenna topology (e.g., two elements are placed in the median plane  ) in Section 3.3. Our primary interest is to later compare the spatial correlation estimation of a 3D incoming wavefield (i.e., vMF distributed) to a 2D and 3D element arrangements. Finally, it is shown in Section 3.4 that under the condition of isotropy the vMF SCF reduces to the sinc function.
) in Section 3.3. Our primary interest is to later compare the spatial correlation estimation of a 3D incoming wavefield (i.e., vMF distributed) to a 2D and 3D element arrangements. Finally, it is shown in Section 3.4 that under the condition of isotropy the vMF SCF reduces to the sinc function.
3.1. Spatial Correlation of Narrowband Sources
In [12], an expression is derived that characterizes the SCF for an arbitrary distribution of scatterers on the sphere. It was shown that if the harmonic coefficients of the scattering distribution function are obtained, a closed-form expression for the spatial correlation can be derived. Note that it is important to obtain those coefficients in an analytical form which is often a difficult task. In case the coefficients are not obtainable in a compact closed-form, then other numerical integration techniques need to be identified, that is, Monte Carlo integration. In [12], the authors conclude that the correlation is relatively insensitive to restriction in elevation having assumed a field uniform in azimuth. One of the arguments of this paper is concerned with the scattering distribution function to be used during this analysis. It is reasonable that the correlation will be relatively insensitive to elevation if the azimuth is uniformly distributed. In order to identify the effect of elevation on the correlation function, more realistic distribution functions need to be used. In the sequel, it will be shown that using the vMF distribution we can see exactly how the correlation scales as the elevation changes. We observed that correlation decreases as elevation increases and that the spatial correlation is dependent on elevation.
First consider the signals  and
and  impinging on an array with elements
impinging on an array with elements  and
and  . Each element pattern is assumed to be isotropic, and therefore each signal is assumed to be received by an isotropic sensor. Under these conditions the normalized spatial correlation between the complex envelopes of the two received signals is defined as in [12] and may be expressed as
. Each element pattern is assumed to be isotropic, and therefore each signal is assumed to be received by an isotropic sensor. Under these conditions the normalized spatial correlation between the complex envelopes of the two received signals is defined as in [12] and may be expressed as

where  is the wave number and
is the wave number and  is a unit vector in the direction of wave propagation. Note that
is a unit vector in the direction of wave propagation. Note that  is the distribution function of scatterers on the unit sphere. Since
is the distribution function of scatterers on the unit sphere. Since  is defined on
is defined on  , the scattering environment can be specified given the spherical harmonic coefficients in (4), so that
, the scattering environment can be specified given the spherical harmonic coefficients in (4), so that  . In the following section, we attempt to integrate the spatial correlation definition presented above with the wavefield decomposition using a spherical antenna array.
. In the following section, we attempt to integrate the spatial correlation definition presented above with the wavefield decomposition using a spherical antenna array.
3.2. Spherical Harmonic Expansion of Plane Waves and the Proposed vMF SCF
From the Jacobi-Anger expansion in (10) and the Addition Theorem of spherical harmonics in (A.2), the spherical harmonic expansion of plane waves can be written as in (11) [22]

where  denotes the spherical Bessel function of order
denotes the spherical Bessel function of order 

This equation expresses the expansion of plane waves into spherical co-ordinates and shows that the spherical harmonics only exhibit a spatial dependence related to the directions of the distribution of scatterers (i.e.,  ). This result is due to a spherical aperture that employs a unity weighting function, and therefore is equally sensitive in all directions (isotropic). Confining the elements in the 2D plane results in the expansion of a plane wave on a circular aperture of omnidirectional elements. Combining (9) and (11) results in [22]
). This result is due to a spherical aperture that employs a unity weighting function, and therefore is equally sensitive in all directions (isotropic). Confining the elements in the 2D plane results in the expansion of a plane wave on a circular aperture of omnidirectional elements. Combining (9) and (11) results in [22]

In (12),  is obtained from (8) to finally produce the closed-form expression for the vMF spatial fading correlation function
is obtained from (8) to finally produce the closed-form expression for the vMF spatial fading correlation function

The vMF correlation function proposed in (13) is expressed as a sum of terms, where each term either characterizes the scattering environment or the antenna locations. As a result, the effects of arbitrary antenna configurations and the complex scattering environment on the SCF can easily be investigated [7]. The correlation function in (13) has been evaluated for element position  and
and  . In this array architecture, the elements are positioned in the median plane. Consequently, the limiting case of a spherical array reveals a circular topology of elements. A circular aperture cannot discriminate 3D incoming signals with the same level of accuracy as a spherical aperture. This becomes apparent by realizing that the elevation of the incoming source is considered only within the argument of the
. In this array architecture, the elements are positioned in the median plane. Consequently, the limiting case of a spherical array reveals a circular topology of elements. A circular aperture cannot discriminate 3D incoming signals with the same level of accuracy as a spherical aperture. This becomes apparent by realizing that the elevation of the incoming source is considered only within the argument of the  th order Bessel function. The azimuthal dependence, however, is expressed in the exponential term. Thus, circular harmonics can be rotated in azimuth but not in elevation. Also if the directions of sources are not significantly attenuated in elevation, then a circular topology cannot unambiguously resolve the angles of arrival of the impinging signals. Herein, a comparison is performed between the spatial correlation estimates of the two array topologies under the assumption of a 3D incoming wavefield. The choice of angular position of elements was selected at random. Note that the angular position of elements in (13) produces a new two-dimensional (2D) vector given by
th order Bessel function. The azimuthal dependence, however, is expressed in the exponential term. Thus, circular harmonics can be rotated in azimuth but not in elevation. Also if the directions of sources are not significantly attenuated in elevation, then a circular topology cannot unambiguously resolve the angles of arrival of the impinging signals. Herein, a comparison is performed between the spatial correlation estimates of the two array topologies under the assumption of a 3D incoming wavefield. The choice of angular position of elements was selected at random. Note that the angular position of elements in (13) produces a new two-dimensional (2D) vector given by  . Note that the vector
. Note that the vector  depicted in Figure 4 will be abbreviated as
depicted in Figure 4 will be abbreviated as  for convenience. In spatial correlation terms, the quantity
for convenience. In spatial correlation terms, the quantity  should give the same value although this time its corresponding resultant vector
should give the same value although this time its corresponding resultant vector  . Subsequently, the correlation function is dependent on the angular position of elements. The assumptions above can be generalized to any antenna array topology, that is, linear or rectangular, which is a distinctive feature of the proposed spatial channel model. To carry out the multiple simulation scenarios presented in the following section, the number of terms (
. Subsequently, the correlation function is dependent on the angular position of elements. The assumptions above can be generalized to any antenna array topology, that is, linear or rectangular, which is a distinctive feature of the proposed spatial channel model. To carry out the multiple simulation scenarios presented in the following section, the number of terms ( ) in the sum of (13) was set equal to thirteen (
) in the sum of (13) was set equal to thirteen ( ). The decision on the appropriate number of terms to be used in the sum of (13) was based on the extensive analysis provided in [23]. The authors showed that the multipath field can be safely truncated by
). The decision on the appropriate number of terms to be used in the sum of (13) was based on the extensive analysis provided in [23]. The authors showed that the multipath field can be safely truncated by  terms, where
terms, where  ,
,  is the ceiling operator,
is the ceiling operator,  , and
, and  indicates the region of space to which the field is coupled or equivalently the radius of the circular or spherical region in consideration. This region of space is where multiple antenna elements may be located. In the analysis provided in this section, we consider that all elements lie in a circular ring with a maximum interelement spacing of
indicates the region of space to which the field is coupled or equivalently the radius of the circular or spherical region in consideration. This region of space is where multiple antenna elements may be located. In the analysis provided in this section, we consider that all elements lie in a circular ring with a maximum interelement spacing of  . Note that
. Note that  denotes the interelement spacing distance, where
denotes the interelement spacing distance, where  , and this should not be confused with the radius
, and this should not be confused with the radius  of the circular array. With the use of simple trigonometrical identities, it can be shown that if
of the circular array. With the use of simple trigonometrical identities, it can be shown that if  and the angle between the two elements is
and the angle between the two elements is  , the radius
, the radius  . As a result, the maximum number of terms required is
. As a result, the maximum number of terms required is  . However, due to the restriction in the multipath field, as defined by the concentration parameter
. However, due to the restriction in the multipath field, as defined by the concentration parameter  , the total number of terms required may be further reduced in accordance with
, the total number of terms required may be further reduced in accordance with  , where
, where  defines the spread of the distribution [23].
defines the spread of the distribution [23].
3.3. Evaluation of the Closed-Form SCF
The aim of this section is threefold: firstly, to identify the effect of elevation on the vMF SCF proposed in (13) (Section 3.3.1); secondly, to examine the effect of the azimuth of arrival of propagating waves on the SCF (Section 3.3.2); finally, to investigate the influence of the concentration parameter  on the vMF correlation function (Section 3.3.3).
on the vMF correlation function (Section 3.3.3).
3.3.1. SCF for Varying Mean Elevation of Arrival
To generate the coefficients  , the concentration parameter
, the concentration parameter  and the MAoA of the cluster must be specified a priori (or estimated [13, 14]). To proceed, the initial
and the MAoA of the cluster must be specified a priori (or estimated [13, 14]). To proceed, the initial  value was set to twenty (
value was set to twenty ( ) (Please note that in the proposed unimodal vMF model the distance between the scatterer cluster and the antenna array is not explicitly considered. If the MS is moving towards this cluster of scatterers, its associated
) (Please note that in the proposed unimodal vMF model the distance between the scatterer cluster and the antenna array is not explicitly considered. If the MS is moving towards this cluster of scatterers, its associated  value as seen at the MS will decrease. Consequently, a decreasing concentration parameter
value as seen at the MS will decrease. Consequently, a decreasing concentration parameter  can capture this effect. By setting
can capture this effect. By setting  to a large value, that is,
to a large value, that is,  , scenarios where the scatterers are located in the far field of the multielement antenna system can be modeled. A decreasing
, scenarios where the scatterers are located in the far field of the multielement antenna system can be modeled. A decreasing  value can therefore model the contribution of local scattering to the spatial correlation experienced between the receiving antennas. For this reason, a smaller value of
value can therefore model the contribution of local scattering to the spatial correlation experienced between the receiving antennas. For this reason, a smaller value of  is later introduced in this section, and its effect on the correlation function is investigated.) with a varying MAoA
is later introduced in this section, and its effect on the correlation function is investigated.) with a varying MAoA  (varying
(varying  , constant
, constant  ). The choice of the mean azimuth angle
). The choice of the mean azimuth angle  can be explained by geometry since
can be explained by geometry since  lies in the fourth quadrant opposite to
lies in the fourth quadrant opposite to  . Figure 1(a) illustrates the evaluated vMF correlation function in (13) for various elevation values
. Figure 1(a) illustrates the evaluated vMF correlation function in (13) for various elevation values  , within
, within  degrees and
degrees and  .
.
Spatial correlation between 2 elements located at 45° and 90°, respectively. Elevation is varied from  . This assessment also includes multiple mean azimuthal angles for a given value of the concentration parameter
. This assessment also includes multiple mean azimuthal angles for a given value of the concentration parameter  .Spatial correlation for a constant mean azimuth
.Spatial correlation for a constant mean azimuth  Spatial correlation for a constant mean azimuth
Spatial correlation for a constant mean azimuth  Spatial correlation for a constant mean azimuth
Spatial correlation for a constant mean azimuth  Spatial correlation for a constant mean azimuth
Spatial correlation for a constant mean azimuth 
Because of symmetry, there is no need to evaluate (13) for  greater than 90°. It is evident that the correlation decreases as elevation increases (as measured from
greater than 90°. It is evident that the correlation decreases as elevation increases (as measured from  ) and vice versa. Further, consider that a cluster is located at mean azimuth
) and vice versa. Further, consider that a cluster is located at mean azimuth  with concentration parameter
with concentration parameter  . The evaluation of (13) for this mean azimuth angle results in Figure 1(b). Note again that as elevation increases (from
. The evaluation of (13) for this mean azimuth angle results in Figure 1(b). Note again that as elevation increases (from  ) correlation decreases, although the difference between the lowest and maximum elevation points (
) correlation decreases, although the difference between the lowest and maximum elevation points ( and
and  , resp.) is now smaller. The correlation experienced between elements
, resp.) is now smaller. The correlation experienced between elements  and
and  at a mean azimuth cluster angle
at a mean azimuth cluster angle  is identical to the one presented in Figure 1(a) (due to symmetry). The underlying reason is illustrated by geometry in Figure 4. In Figure 1(c), the scaling of correlation with elevation at
is identical to the one presented in Figure 1(a) (due to symmetry). The underlying reason is illustrated by geometry in Figure 4. In Figure 1(c), the scaling of correlation with elevation at  is further provided. The spatial correlation difference between minimum and maximum
is further provided. The spatial correlation difference between minimum and maximum  's has now been increased, since the vector
's has now been increased, since the vector  is closer to the resultant
is closer to the resultant  than the vector
than the vector  is to
is to  . Intuitively, this can be explained by the fact that the angular difference between the first pair of vectors is only 37.5° compared to the second pair whose angular difference equals 52.5°. The wider angular range implies lower correlation values since as the distance between any given pair of vectors increases as their associated correlation decreases. Additionally, an interpretation of the observable decrease in the SCF during the ascent of the scatterer cluster to the north region of the sphere is that as the spatial cluster is elevated, a larger deviation is projected in the azimuthal plane. Consequently, maximum deviation is realized when the mean direction vector aligns with the vector directed along the
. Intuitively, this can be explained by the fact that the angular difference between the first pair of vectors is only 37.5° compared to the second pair whose angular difference equals 52.5°. The wider angular range implies lower correlation values since as the distance between any given pair of vectors increases as their associated correlation decreases. Additionally, an interpretation of the observable decrease in the SCF during the ascent of the scatterer cluster to the north region of the sphere is that as the spatial cluster is elevated, a larger deviation is projected in the azimuthal plane. Consequently, maximum deviation is realized when the mean direction vector aligns with the vector directed along the  -axis. In view of this, we speculate that the decrease in spatial correlation due to the spatial cluster's disposition from the azimuthal plane is justified. The assumption of elements being positioned strictly on the azimuthal plane needs to be retained.
-axis. In view of this, we speculate that the decrease in spatial correlation due to the spatial cluster's disposition from the azimuthal plane is justified. The assumption of elements being positioned strictly on the azimuthal plane needs to be retained.
3.3.2. SCF for Varying Mean Azimuth of Arrival
The problem is now reversed in order to examine how the spatial correlation scales while the mean azimuthal angle  is varied, and the mean elevation angle
is varied, and the mean elevation angle  is kept constant at 90∘. Figure 2 illustrates this for
is kept constant at 90∘. Figure 2 illustrates this for  . Because of symmetry, we do not need to evaluate for
. Because of symmetry, we do not need to evaluate for  . It is apparent that maximum correlation is obtained at
. It is apparent that maximum correlation is obtained at  (Figure 2) for this range of angles. Note, however, that maximum correlation for a varying
(Figure 2) for this range of angles. Note, however, that maximum correlation for a varying  is theoretically obtained at
is theoretically obtained at  and/or
and/or  . This is because the two vectors coincide with the corresponding
. This is because the two vectors coincide with the corresponding  vectors, producing a 0 angle, the cosine of which is 1 (hence maximum spatial correlation). The spatial correlation slightly exceeds
vectors, producing a 0 angle, the cosine of which is 1 (hence maximum spatial correlation). The spatial correlation slightly exceeds  at
at  and
and  .
.
3.3.3. SCF for Different Angular Spread
To extend the results presented above, the concentration parameter  is now varied in order to investigate its effect on the SCF. As expected, decreasing the value of
is now varied in order to investigate its effect on the SCF. As expected, decreasing the value of  decreases the spatial correlation experienced between adjacent antenna elements. In Figure 3, the estimated spatial correlation values for
decreases the spatial correlation experienced between adjacent antenna elements. In Figure 3, the estimated spatial correlation values for  ,
,  , and
, and  , respectively, are shown. The results can be compared with the correlation values depicted in Figure 1(a), where the concentration parameter
, respectively, are shown. The results can be compared with the correlation values depicted in Figure 1(a), where the concentration parameter  . A decrease in the spatial correlation is evident.
. A decrease in the spatial correlation is evident.
The correlation function is clearly not insensitive to elevation. This was also confirmed in [24], where the authors made use of the more complex Fisher-Bingham 5-parameter model. The Fisher-Bingham 5-parameter (FB5) model does not have a well-known series expansion, andas a result, its spherical harmonic coefficients cannot be obtained in a closed-form expression. Although the FB5 model is more generic, its complexity is a limiting factor. In [25], Shafi et al. also showed that ignoring elevation can significantly underestimate capacity. This can be thought of as a direct consequence of the fact that at higher elevation angles correlation decreases, and therefore capacity increases. Interestingly, the only angles at which the elevation effect vanishes are at  and
and  , respectively (see Figure 1(d)). The reason behind this observation is that at
, respectively (see Figure 1(d)). The reason behind this observation is that at  and
and  , the cosine of the angle between the
, the cosine of the angle between the  and both of the vectors is 0. The vectors are at right angles to each other. Figure 4 provides a geometrical explanation for this effect. The spatial correlation is minimum at both locations even for different elevation angles. Therefore, according to this study, the correlation becomes insensitive to elevation when
and both of the vectors is 0. The vectors are at right angles to each other. Figure 4 provides a geometrical explanation for this effect. The spatial correlation is minimum at both locations even for different elevation angles. Therefore, according to this study, the correlation becomes insensitive to elevation when
-
(i)
the concentration parameter
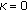 , in which case the distribution of scatterers over the sphere becomes completely isotropic;
, in which case the distribution of scatterers over the sphere becomes completely isotropic; -
(ii)
the mean azimuthal angle of a cluster is on the plane orthogonal to
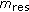 .
.
The above results are directly comparable to the results obtained in [12]. Here, we will not present the results of the uniform (although limited) azimuth/elevation scattering distribution function presented in [12]. It was shown that if the scatterer distribution is uniform in azimuth, the correlation becomes insensitive to restriction in elevation. As an addition to the significant work of [12], in this work, we show exactly how elevation affects correlation if a more realistic distribution of scatterers (i.e., vMF) is to be used. In [13, 14], it was shown that the vMF provides a very accurate fit for the AoA of multipaths at the MS and hence the distribution of scatterers in space. This result has therefore motivated the investigation of spatial correlation in antenna arrays under the 3D vMF model. In Section 3.4, it is shown that the proposed vMF model can also reduce to the well-known sinc function when one of its parameters, namely  , is set to zero. This implies that the scatterers are isotropically distributed on the surface of the sphere.
, is set to zero. This implies that the scatterers are isotropically distributed on the surface of the sphere.
3.4. Isotropic Distribution of Scatterers
If the distribution of scatterers is isotropic on the sphere, then the plane waves will be incident on the elements from all directions. Isotropic distribution implies that  , and therefore only the order
, and therefore only the order  is required for the calculation of the spherical harmonic coefficients. Consequently, the vMF density reduces to
is required for the calculation of the spherical harmonic coefficients. Consequently, the vMF density reduces to  (Appendix A.2) and (5) becomes
(Appendix A.2) and (5) becomes  . Upon substitution of
. Upon substitution of  and
and  in (12), the vMF SCF function reduces to the classic result obtained in [26]. Note that the spherical harmonic of degree
in (12), the vMF SCF function reduces to the classic result obtained in [26]. Note that the spherical harmonic of degree  is given by
is given by  . The same result was obtained in [12] under a uniform (limited) azimuth-elevation distribution on the sphere.
. The same result was obtained in [12] under a uniform (limited) azimuth-elevation distribution on the sphere.
4. Wavefield Decomposition and Spatial Correlation Using Directional Antenna Responses
In the previous section, the so-called constrained spherical array topology was examined under the condition of omnidirectional antenna responses. In this section, focus is mainly shifted towards antenna responses that are directional in nature, and the effect of an elevated element on SCF is only briefly discussed. To achieve this, we introduce a weighting function  in order to include the effect of a realistic antenna pattern while computing the spatial correlation. This function describes the degree of sensitivity of the antenna pattern towards some specific direction of interest. Unfortunately, its introduction hinders the emergence of an analytical solution as it will soon become evident. Therefore, here, a numerical solution is sought due to the complexity of the problem. This complexity escalates by adding other impacting factors of antenna pattern properties, that is, mutual coupling and antenna mounting platform effects. The effect of the antenna mounting platform on the spatial correlation function will be investigated in future work.
in order to include the effect of a realistic antenna pattern while computing the spatial correlation. This function describes the degree of sensitivity of the antenna pattern towards some specific direction of interest. Unfortunately, its introduction hinders the emergence of an analytical solution as it will soon become evident. Therefore, here, a numerical solution is sought due to the complexity of the problem. This complexity escalates by adding other impacting factors of antenna pattern properties, that is, mutual coupling and antenna mounting platform effects. The effect of the antenna mounting platform on the spatial correlation function will be investigated in future work.
4.1. Spatial Correlation with an Elevated Element
A change in both element's positions with respect to elevation was initially performed. Note that the rest of the parameters related to the vMF distribution were left unchanged. Therefore, an element was positioned at  and a second element positioned at
and a second element positioned at  , where the first angle in each element denotes its elevation
, where the first angle in each element denotes its elevation  and the second its azimuthal
and the second its azimuthal  position. Therein, the azimuthal position of both elements examined earlier is unaffected, while they are both shifted by
position. Therein, the azimuthal position of both elements examined earlier is unaffected, while they are both shifted by  towards the North Pole. In this case, the mean resultant vector's (
towards the North Pole. In this case, the mean resultant vector's ( ) angles are
) angles are  , and consequently the SCF behaves identically. Note that this applies for all cases in which the two elements are shifted equally in the elevation plane. However, if one element's position is elevated with respect to its adjacent element position, then the resultant vector's orientation angles significantly change causing a change in the spatial correlation as well. For instance, consider that the position of
, and consequently the SCF behaves identically. Note that this applies for all cases in which the two elements are shifted equally in the elevation plane. However, if one element's position is elevated with respect to its adjacent element position, then the resultant vector's orientation angles significantly change causing a change in the spatial correlation as well. For instance, consider that the position of  , while
, while  . The resultant vector is now at
. The resultant vector is now at  . The evaluation of the vMF SCF for this
. The evaluation of the vMF SCF for this  reveals the dependency of the SCF on the resultant vector. Maximum correlation is attained when a spatial cluster is located around
reveals the dependency of the SCF on the resultant vector. Maximum correlation is attained when a spatial cluster is located around  . Interestingly, the mean direction vector that produces minimum correlation is at the mean elevation angles
. Interestingly, the mean direction vector that produces minimum correlation is at the mean elevation angles  . A similar interpretation may be given as the one provided earlier for the constrained spherical topology. the key point in here is that as the cluster mean direction vector approaches the resultant vector, correlation increases.
. A similar interpretation may be given as the one provided earlier for the constrained spherical topology. the key point in here is that as the cluster mean direction vector approaches the resultant vector, correlation increases.
4.2. Spatial Correlation with Directional Antenna Patterns
Directional antenna patterns are commonly used in practice, and therefore the extension of this work to capture their influence on spatial correlation is noteworthy. Base stations usually employ directional patterns as opposed to mobile terminals that should not in most cases favor any direction. The influence of antenna directivity on the performance of multipath channels is multidimensional. From a propagation viewpoint, the antenna directivity not only affects the power received at a terminal, but it also has a significant impact on the angle spread of the channel. It is an important realization that a directive antenna has the potential to change our perception on the physical distribution of scatterers. Of course, this is dependent on the antenna effective aperture, which is in turn related to the gain of the antenna. Also, nonisotropic antenna patterns yield weighted AoA components, and as a result, they alter the power angular spectrum received at the MS/BS. At this moment, the weighting function  is introduced, which essentially describes the sensitivity of an infinitesimal point located on the array at
is introduced, which essentially describes the sensitivity of an infinitesimal point located on the array at  . Note that the weighting function is also associated with the look-direction
. Note that the weighting function is also associated with the look-direction  of the antenna pattern. This means that the pattern may be rotated at any azimuth-elevation pair of angles. Following the approach presented in [27], the weighting function may be expressed as
of the antenna pattern. This means that the pattern may be rotated at any azimuth-elevation pair of angles. Following the approach presented in [27], the weighting function may be expressed as

where  was defined earlier in (7). Applying the Addition Theorem for spherical harmonics (A.2) to (14) transforms the above equation to
was defined earlier in (7). Applying the Addition Theorem for spherical harmonics (A.2) to (14) transforms the above equation to

The application of this weighting factor to the inverse spherical harmonics transform of a plane wave (5) results in an expression for the harmonic coefficients (decomposed wavefield) due to a directional antenna being present. This expression can be written as

After substitution of the weighting function in (15) and the equation corresponding to the plane wave expansion in (11) to (16), it can be seen that the spherical harmonic coefficients cannot be obtained in an analytical form since the integral contains the product of three spherical harmonics. Consequently, the equation that defines the expansion of plane waves in spherical co-ordinates under a directional antenna cannot be derived in a closed-form solution. In this respect, (17) can only be evaluated numerically, and may be rewritten as follows:

where  . This rearrangement has a meaningful interpretation since the product
. This rearrangement has a meaningful interpretation since the product  defines the overall scattering response through the multiplication of the azimuth-elevation scattering response
defines the overall scattering response through the multiplication of the azimuth-elevation scattering response  with the complex antenna pattern
with the complex antenna pattern  . To exemplify this, let us consider the case where the elements exhibit dipole-like characteristics. Under this assumption, the weighting function in (15) may be rewritten as
. To exemplify this, let us consider the case where the elements exhibit dipole-like characteristics. Under this assumption, the weighting function in (15) may be rewritten as

whose associated expansion coefficients are given by

However, this is of little significance at the moment since the SCF will be evaluated numerically. Note that this is a first-order dipole response whose elevation beamwidth is  . Increasing the order of the array reduces the corresponding beamwidth. Second- and third-order dipole responses have elevation beamwidths of 65° and 54°, respectively, which can be met in practical scenarios. The elevation beamwidth of dipoles varies depending on the application. Typically, antenna designs with high-directivity index have reduced elevation beamwidths. Of course, elevation beamwidths of azimuthally omnidirectional dipole patterns can be as small as 7°, but this should not compromise the generality of the approach followed in here. Other practical designs include the second- and third-order dipole, cardioid, and hypercardioid directional responses. In general, a
. Increasing the order of the array reduces the corresponding beamwidth. Second- and third-order dipole responses have elevation beamwidths of 65° and 54°, respectively, which can be met in practical scenarios. The elevation beamwidth of dipoles varies depending on the application. Typically, antenna designs with high-directivity index have reduced elevation beamwidths. Of course, elevation beamwidths of azimuthally omnidirectional dipole patterns can be as small as 7°, but this should not compromise the generality of the approach followed in here. Other practical designs include the second- and third-order dipole, cardioid, and hypercardioid directional responses. In general, a  th order array response may be expressed as [28]
th order array response may be expressed as [28]

This is the canonic form of the antenna response, and it actually factors (21) into its first-order terms. The normalised directional array response may be rewritten in the following form as a function of  :
:

Solving (20) results in expressions for the  s in terms of the
s in terms of the  s. For a third-order array, for example, (20) and (21) become
s. For a third-order array, for example, (20) and (21) become


respectively. In Table 2, some of these patterns are listed and subsequently plotted in Figure 5.
In Figure 6, the correlation estimates of (17) are displayed for various interelement spacings and concentration parameters. The look direction for all antenna responses is set at  ,
,  , and therefore the cluster mean direction vector coincides with the look direction of each antenna. This configuration produces the highest correlation estimates. It becomes clear that the isotropic element pattern assumption serves as a lower bound to the spatial correlation function. Also, as the concentration parameter increases, the weighted (including antenna effect) SCF approaches the unweighted SCF. For low concentration parameter values, that is,
, and therefore the cluster mean direction vector coincides with the look direction of each antenna. This configuration produces the highest correlation estimates. It becomes clear that the isotropic element pattern assumption serves as a lower bound to the spatial correlation function. Also, as the concentration parameter increases, the weighted (including antenna effect) SCF approaches the unweighted SCF. For low concentration parameter values, that is,  , the dipole response produces the highest spatial correlation estimates due to possessing the highest directivity index in comparison to the other responses. The choice of antenna response clearly depends on different factors, for example, front-to-back ratio, beamwidth, and directivity, and therefore an antenna response is application specific. The approach followed is generic enough to allow any antenna response to be included in the model. In the next section, we mathematically describe the scenario of multiple scatterer clusters and its inclusion on the spatial correlation function.
, the dipole response produces the highest spatial correlation estimates due to possessing the highest directivity index in comparison to the other responses. The choice of antenna response clearly depends on different factors, for example, front-to-back ratio, beamwidth, and directivity, and therefore an antenna response is application specific. The approach followed is generic enough to allow any antenna response to be included in the model. In the next section, we mathematically describe the scenario of multiple scatterer clusters and its inclusion on the spatial correlation function.
5. Mixtures of vMF Distributions in a Spatial Correlation Context
During the last decade, directional channel measurements have been extensively used in various measurement campaigns worldwide. This is due to the fact that directional channel measurements can reveal the clustered nature of the propagation channel. Important findings related to these measurements have been reported in [9, 15, 29–32], all of which establish that channels with multiple scatterer clusters often occur in nature. In [29], the authors identify the existence of far scatterer clusters using measurements from a campaign in Frankfurt, Germany. In [30], Kuchar et al. not only mention the existence of far scatterer clusters that result in increased delay dispersion but also report that  of the incoming signal energy is incident with an elevation larger than 10°. The latter experiment was carried out in Paris, France. The work in [31, 32] also confirmed the existence of multiple scatterer clusters. Standardized models, such as the one developed by the third-generation partnership project (3GPP), namely the spatial channel model (SCM), also accounts for multiple scatterer clusters. It is therefore important to include the multiple scatterer cluster effect in future channel models and to also recognize that far scatterer clusters are an important propagation scenario in urban environments.
of the incoming signal energy is incident with an elevation larger than 10°. The latter experiment was carried out in Paris, France. The work in [31, 32] also confirmed the existence of multiple scatterer clusters. Standardized models, such as the one developed by the third-generation partnership project (3GPP), namely the spatial channel model (SCM), also accounts for multiple scatterer clusters. It is therefore important to include the multiple scatterer cluster effect in future channel models and to also recognize that far scatterer clusters are an important propagation scenario in urban environments.
The definition of a cluster is subject to different analysis constraints. Usually the clusterization of multipath components takes place in spatial, power, and temporal domains. This paper aims at understanding of fading effects by exploiting the spatial domain. In [13, 14], clustering is performed in the spatial domain. It was shown that the vMF mixture model provides a good fit to the angular estimates of the multidimensional parameter extraction algorithm, namely RiMAX [33]. The model-based approach followed uses the soft-EM for mixtures of vMF distributions. Mathematically, each distribution in the mixture of  VMFs can be described as
VMFs can be described as  with parameter
with parameter  . The overall density of the mixture model comprising of
. The overall density of the mixture model comprising of  vMF distributions can be described as
vMF distributions can be described as

where the parameter vector  , and
, and  defines the prior probability that vector
defines the prior probability that vector  was generated by the
was generated by the  th component. After taking into consideration (24), the SCF in (13) can be modified accordingly, where the priors
th component. After taking into consideration (24), the SCF in (13) can be modified accordingly, where the priors  . The resultant equation is the multimodal vMF SCF function, the mathematical details of which are omitted in here. A similar approach was followed in [34], where the authors considered a mixture of 2D von Mises distributions. To understand the implications of the multimodal density on the SCF, let us assume that in a radio propagation channel exist 3 clusters with different MAoAs, and concentration parameters
. The resultant equation is the multimodal vMF SCF function, the mathematical details of which are omitted in here. A similar approach was followed in [34], where the authors considered a mixture of 2D von Mises distributions. To understand the implications of the multimodal density on the SCF, let us assume that in a radio propagation channel exist 3 clusters with different MAoAs, and concentration parameters  . In Table 1, the parameters are shown. We have assumed equal contribution from each cluster. However, the results can be generalized to any set of parameters, any number of clusters, and any contribution from each cluster. To sample a point from the mixture density in (24), the
. In Table 1, the parameters are shown. We have assumed equal contribution from each cluster. However, the results can be generalized to any set of parameters, any number of clusters, and any contribution from each cluster. To sample a point from the mixture density in (24), the  th vMF was randomly chosen with probability
th vMF was randomly chosen with probability  and subsequently sample a point from
and subsequently sample a point from  [35]. The evaluation of the multimodal SCF for this set of parameters produces Figure 7. It is evident that maximum correlation is obtained at
[35]. The evaluation of the multimodal SCF for this set of parameters produces Figure 7. It is evident that maximum correlation is obtained at  . To further explore the concept of mixture modeling, we consider that the 2nd cluster has a higher assigned prior (
. To further explore the concept of mixture modeling, we consider that the 2nd cluster has a higher assigned prior ( ) and that the rest of the parameters remain the same (as in Table 1). In this case, the contribution of the rest of the spatial clusters in the mixture is
) and that the rest of the parameters remain the same (as in Table 1). In this case, the contribution of the rest of the spatial clusters in the mixture is  and
and  , respectively. Evidently, the priors of each cluster in the mixture can have a dramatic effect on the correlation function as shown in Figure 8. The mixture correlation function does not only depend on the prior contribution of each component, but on the mean elevation AoA, mean azimuth AoA, and concentration parameter of each cluster. Note that the priors can be a function of the total power in a cluster. It is of common interest to direct focus on the power-dominating clusters. Therefore, the priors
, respectively. Evidently, the priors of each cluster in the mixture can have a dramatic effect on the correlation function as shown in Figure 8. The mixture correlation function does not only depend on the prior contribution of each component, but on the mean elevation AoA, mean azimuth AoA, and concentration parameter of each cluster. Note that the priors can be a function of the total power in a cluster. It is of common interest to direct focus on the power-dominating clusters. Therefore, the priors  in the mixture density proposed can be changed to normalized power-weighted values (after the soft-EM estimation). This can be achieved by estimating the total power in each cluster, and changing the
in the mixture density proposed can be changed to normalized power-weighted values (after the soft-EM estimation). This can be achieved by estimating the total power in each cluster, and changing the  term to
term to  , where
, where  is the total power in each cluster.
is the total power in each cluster.
It is important to observe that in the proposed vMF mixture model, the distance from the scatterer cluster to the antenna array system is considered, although indirectly, as opposed to the unimodal case presented earlier. This is due to the fact that the contribution of each cluster in the vMF mixture is scaled in accordance with the power emanated from it. It is therefore valid to expect that scatterer clusters in the vicinity of the MS will have a higher associated power, contributing more to the spatial correlation between the receiving antennas. Equivalently, scatterer clusters in the far field of the multielement antenna system are expected to have a higher value of concentration and a lower value of power. Evidently, the proposed model can fit to a wider range of propagation scenarios.
6. Conclusions
In this paper, the assumption of traditional horizontal wave propagation and its effect on the SCF have been reviewed. A novel approach is proposed (vMF) for modeling the distribution of scatterers in space. The spherical harmonic coefficients of the vMF distribution were derived and various simulations on the modified SCF function indicate that the correlation decreases as elevation increases when the elements are positioned on the median plane. The proposed method directly links the spatial correlation with the elevation of the incoming cluster of multipaths. It was also observed that if an element is elevated while the other is kept on the horizontal plane, signal correlations change significantly. Since most of the practical array designs include two-dimensional element configurations, the first case applies. The proposed model was further enhanced by the inclusion of an arbitrary weighting function to describe the effect of the antenna pattern on the spatial correlation. Finally, the effect of multiple clusters of scatterers that is frequently reported in the literature was also included in the SCF. The proposed model can be used to study the capacity in multielement antenna systems.
Appendix
A. Closed-Form Expressions for the Harmonic Coefficients of the vMF Density
A.1. Proof for the Harmonic Coefficients of the vMF Density for an Arbitrary Mean Direction on the Sphere
To begin with we rewrite (5) as follows:

According to the Addition Theorem of spherical harmonics,

We substitute (A.2) into (A.1) and make use of the orthonormality principle in (3) in order to obtain the closed-form expression for the harmonic coefficients

Substituting (A.3) into the synthesis equation (4), we obtain the expanded vMF density as follows:

A.2. Special Case: Proof for the Harmonic Coefficients of the vMF Density When 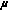 Is Directed along the
Is Directed along the  -Axis
-Axis
A special case of the main derivation arises by conditioning the mean direction vector of the distribution. More specifically, if the mean direction  , the vMF density simplifies to
, the vMF density simplifies to

In (A.5), the marginal pdf of  is given by
is given by

The marginal (uniform) pdf of  is given by
is given by  . Clearly, coelevation is independently distributed from the azimuth and its pdf as
. Clearly, coelevation is independently distributed from the azimuth and its pdf as  goes to zero tends to
goes to zero tends to  (since
(since  ). Combining
). Combining  and
and  , the isotropic pdf on the sphere is obtained,
, the isotropic pdf on the sphere is obtained,  . From the above analysis, it is straightforward to derive the spherical harmonic coefficients when
. From the above analysis, it is straightforward to derive the spherical harmonic coefficients when  . When
. When  and from (6), it follows that the series representation of the marginal pdf of
and from (6), it follows that the series representation of the marginal pdf of  is
is

Note that since the function  is independent of the azimuthal angle
is independent of the azimuthal angle  , the spherical harmonic in (2) is independent of
, the spherical harmonic in (2) is independent of  too. In this case,
too. In this case,  and (2) reduces to
and (2) reduces to  . By substitution of (A.7) into (5) and noting that when
. By substitution of (A.7) into (5) and noting that when  , the spherical harmonic becomes independent of the azimuthal angle
, the spherical harmonic becomes independent of the azimuthal angle  , we obtain
, we obtain

Upon substitution of (A.8) into (4) and making use of the  relationship stated earlier, the vMF pdf when
relationship stated earlier, the vMF pdf when  is obtained in (A.5). In the above derivation, we have used the orthogonality principle of Legendre polynomials which states that
is obtained in (A.5). In the above derivation, we have used the orthogonality principle of Legendre polynomials which states that

It is important to note that the spherical harmonic coefficients derived are independent of the antenna positions.
References
Durrani S, Bialkowski ME: Effect of angular energy distribution of an incident signal on the spatial fading correlation of a uniform linear array. Proceedings of the 15th International Conference on Microwaves, Radar and Wireless Communications (MIKON '04), May 2004 2: 493-496.
Salz J, Winters JH: Effect of fading correlation on adaptive arrays in digital mobile radio. IEEE Transactions on Vehicular Technology 1994, 43(4):1049-1057. 10.1109/25.330168
Tepedelenlioglu C, Giannakis B: Effects of nonisotropic scattering on the correlation properties of mobile fading channels. Proceedings of Conference on Information Sciences and Systems (CISS '00), March 2000 WP4.13-WP4.17.
Wang J, Huang C, Zhou J, Kikuchi H: The impact of AOA energy distribution on the spatial fading correlation and SER performance of antenna array communication systems. Proceedings of International Conference on Communications, Circuits and Systems (ICCCAS '06), June 2006 2: 803-806.
Zhou Z, Ishizawa K, Kikuchi H, Sengoku M, Onozato Y: Generalized spatial correlation equations for antenna arrays in wireless diversity reception exact and approximate analyses. Proceedings of the International Conference on Neural Networks and Signal Processing, December 2003 1: 180-184.
Yong SK, Thompson JS: Three-dimensional spatial fading correlation models for compact MIMO receivers. IEEE Transactions on Wireless Communications 2005, 4(6):2856-2868.
Pollock TS, Abhayapala TD, Kennedy RA: Introducing space into MIMO capacity calculations. Telecommunication Systems 2003, 24(2–4):415-436.
Gesbert D, Ekman T, Christophersen N: Capacity limits of dense palm-sized MIMO arrays. Proceedings of IEEE Global Telecommunications Conference (GLOBECOM '02), November 2002 2: 1187-1191.
Toeltsch M, Laurila J, Kalliola K, Molisch AF, Vainikainen P, Bonek E: Statistical characterization of urban spatial radio channels. IEEE Journal on Selected Areas in Communications 2002, 20(3):539-549. 10.1109/49.995513
Shafi M, Zhang M, Moustakas AL, Smith PJ, Molisch AF, Tufvesson F, Simon SH: Polarized MIMO channels in 3-D: models, measurements and mutual information. IEEE Journal on Selected Areas in Communications 2006, 24(3):514-526.
Knudsen MB, Pedersen GF: Spherical outdoor to indoor power spectrum model at the mobile terminal. IEEE Journal on Selected Areas in Communications 2002, 20(6):1156-1169. 10.1109/JSAC.2002.801216
Teal PD, Abhayapala TD, Kennedy RA: Spatial correlation for general distributions of scatterers. IEEE Signal Processing Letters 2002, 9(10):305-308. 10.1109/LSP.2002.804138
Mammasis K, Pfann E, Stewart RW, Freeland G: Three-dimensional channel modelling using spherical statistics for smart antennas. Electronics Letters 2008, 44(2):136-138. 10.1049/el:20082462
Mammasis K, Stewart RW, Pfann E, Freeland G: 3-dimensional channel modelling using spherical statistics for multiple-input multiple-output systems. IET Communications 2009, 3(1):48-56. 10.1049/iet-com:20070518
Molisch AF: Effect of far scatterer clusters in MIMO outdoor channel models. Proceedings of the 57th IEEE Semiannual Vehicular Technology Conference (VTC '03), April 2003 1: 534-538.
3GPP-SCM : Spatial channel model for multiple input multiple output (MIMO) simulations. tr.25.966 v.6.10. September 2003, http://www.3gpp.org/
Mardia KV, Jupp PE: Directional Statistics. John Wiley & Sons, New York, NY, USA; 2000.
Hassani S: Mathematical Physics a Modern Introduction to Its Foundation. Springer, New York, NY, USA; 1999.
MacRobert T: An Elementary Treatise on Harmonic Functions, with Applications. Pergamon Press, Elmsford, NY, USA; 1967.
Tarantola A: Mapping of Probabilities, Theory of the Interpretation of Uncertain Physical Measurements. Cambridge University Press, Cambridge, UK; 2007.
Abramowitz M, Stegun IA: Handbook of Mathematical Functions. Dover, New York, NY, USA; 1964.
Kolton D, Kress R: Inverse Accoustic and Electromagnetic Scattering Theory. 2nd edition. Springer, New York, NY, USA; 1998.
Kennedy RA, Sadeghi P, Abhayapala TD, Jones HM: Intrinsic limits of dimensionality and richness in random multipath fields. IEEE Transactions on Signal Processing 2007, 55(6):2542-2556.
Mammasis K, Stewart RW: The Fisher-Bingham spatial correlation model for multielement antenna systems. IEEE Transactions on Vehicular Technology 2009, 58(5):2130-2136.
Shafi M, Zhang M, Smith PJ, Moustakas AL, Molisch AF: The impact of elevation angle on MIMO capacity. Proceedings of IEEE International Conference on Communications (ICC '06), July 2006 9: 4155-4160.
Cook RK, Waterhouse RV, Berendt RD, Edelman S, Thompson JR: Measurement of correlation coefficients in reverberant sound fields. Journal of the Acoustical Society of America 1995, 27(6):1072-1077.
Teutsch H: Modal Array Signal Processing: Principles and Applications of Accoustic Wavefield Decomposition. Springer, New York, NY, USA; 2007.
Huang YA, Benesty J: Audio Signal Processing for Next-Generation Multimedia Communication Systems. Kluwer Academic Publishers, Boston, Mass, USA; 2004.
Martin U: Spatio-temporal radio channel characteristics in urban macrocells. IEE Proceedings: Radar, Sonar and Navigation 1998, 145(1):42-49. 10.1049/ip-rsn:19981780
Kuchar A, Rossi JP, Bonek E: Directional macro-cell channel characterization from urban measurements. IEEE Transactions on Antennas and Propagation 2000, 48(2):137-146. 10.1109/8.833062
Pedersen KI, Mogensen PE, Fleury BH: Spatial channel characteristics in outdoor environments and their impact on BS antenna system performance. Proceedings of the 48th IEEE Vehicular Technology Conference (VTC '98), May 1998 2: 719-723.
Kalliola K, Laitinen H, Vainikainen P, Toeltsch M, Laurila J, Bonek E: 3-D double-directional radio channel characterization for urban macrocellular applications. IEEE Transactions on Antennas and Propagation 2003, 51(11):3122-3133. 10.1109/TAP.2003.816393
Richter A, Landmann M, Thoma R: A flexible algorithm for channel parameter estimation from channel sounding measurements. Proceedings of International Symposium on Antennas and Propagation, January 2004 COST 273 Temporary Document, no. TD(04) 045
Lamahewa TA, Abhayapala TD, Kennedy RA, Ho JTY: Space-time cross correlation and space-frequency cross spectrum in non-isotropic scattering environments. Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '06), May 2006, Toulouse, France 4: 609-612.
Banerjee A, Dhillon IS, Ghosh J, Sra S: Clustering on the unit hypersphere using von Mises-Fisher distributions. Journal of Machine Learning Research 2005, 6: 1345-1382.
Acknowledgment
The authors would like to acknowledge the valuable suggestions made by Dr. Paul Teal, Senior Lecturer in Signal Processing and Communications at the Victoria University of Wellinton, New Zealand.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Mammasis, K., Stewart, R. Spherical Statistics and Spatial Correlation for Multielement Antenna Systems. J Wireless Com Network 2010, 307265 (2010). https://doi.org/10.1155/2010/307265
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/307265


 for a constant mean elevation
for a constant mean elevation  and
and  .
.
 on the spatial correlation experienced between 2 elements located at 45° and
on the spatial correlation experienced between 2 elements located at 45° and  , respectively. Elevation is varied from
, respectively. Elevation is varied from  to 90° for a constant mean azimuth
to 90° for a constant mean azimuth  and
and  .
.
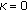 , in which case the distribution of scatterers over the sphere becomes completely isotropic;
, in which case the distribution of scatterers over the sphere becomes completely isotropic;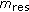 .
.

 .
.

 , and the remaining two spatial clusters have
, and the remaining two spatial clusters have  and
and  , respectively.
, respectively.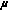 Is Directed along the
Is Directed along the  -Axis
-Axis